Small-Amplitude Nonlinear Modes under the Combined Effect of the Parabolic Potential, Nonlocality and PT Symmetry
Abstract
:1. Introduction
2. The Models
3. Bifurcations of Nonlinear Modes
4. Linear Stability of Nonlinear Modes
4.1. Statement of the Problem
4.2. Linear Stability of Small-Amplitude Modes
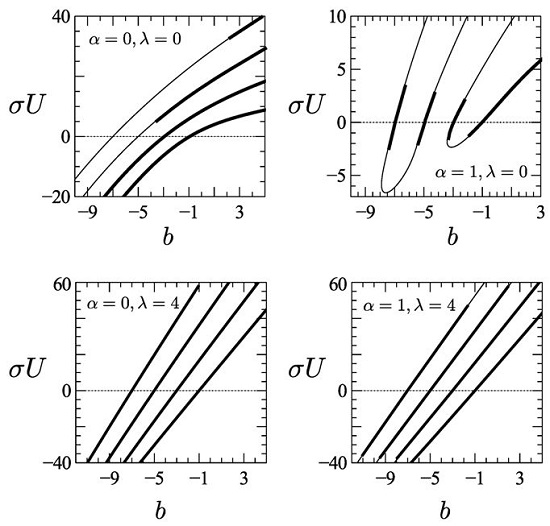
5. Results for the Real Parabolic Potential
6. Results for the -Symmetric Parabolic Potential
7. Nonlinear Modes of Finite Amplitude
8. Conclusions
- A set of continuous families of nonlinear modes exists in the nonlocal -symmetric nonlinear Schrödinger equation. The spectrum of the corresponding linear eigenvalue problem is available in the analytical form, and thus the stability problem for the small-amplitude nonlinear modes can be reduced to the searching real roots of certain analytical expressions.
- In the conservative case, small-amplitude nonlinear modes of arbitrary order become stable for sufficiently strong nonlocality, provided that the kernel is a sufficiently smooth function in the vicinity of the origin. If the kernel feature a singularity at , no stabilization of higher-order nonlinear modes is observed.
- Both the degree of nonlocality and the strength of the symmetry can be used to manage stability of the small-amplitude modes.
- The above stability conclusions remain valid for nonlinear modes of finite amplitude.
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| Parity-Time | |
| BEC | Bose-Einstein condensate |
Appendix A. Examples of Expressions for
Appendix B. Definition and Some Properties of the Fourier Transform
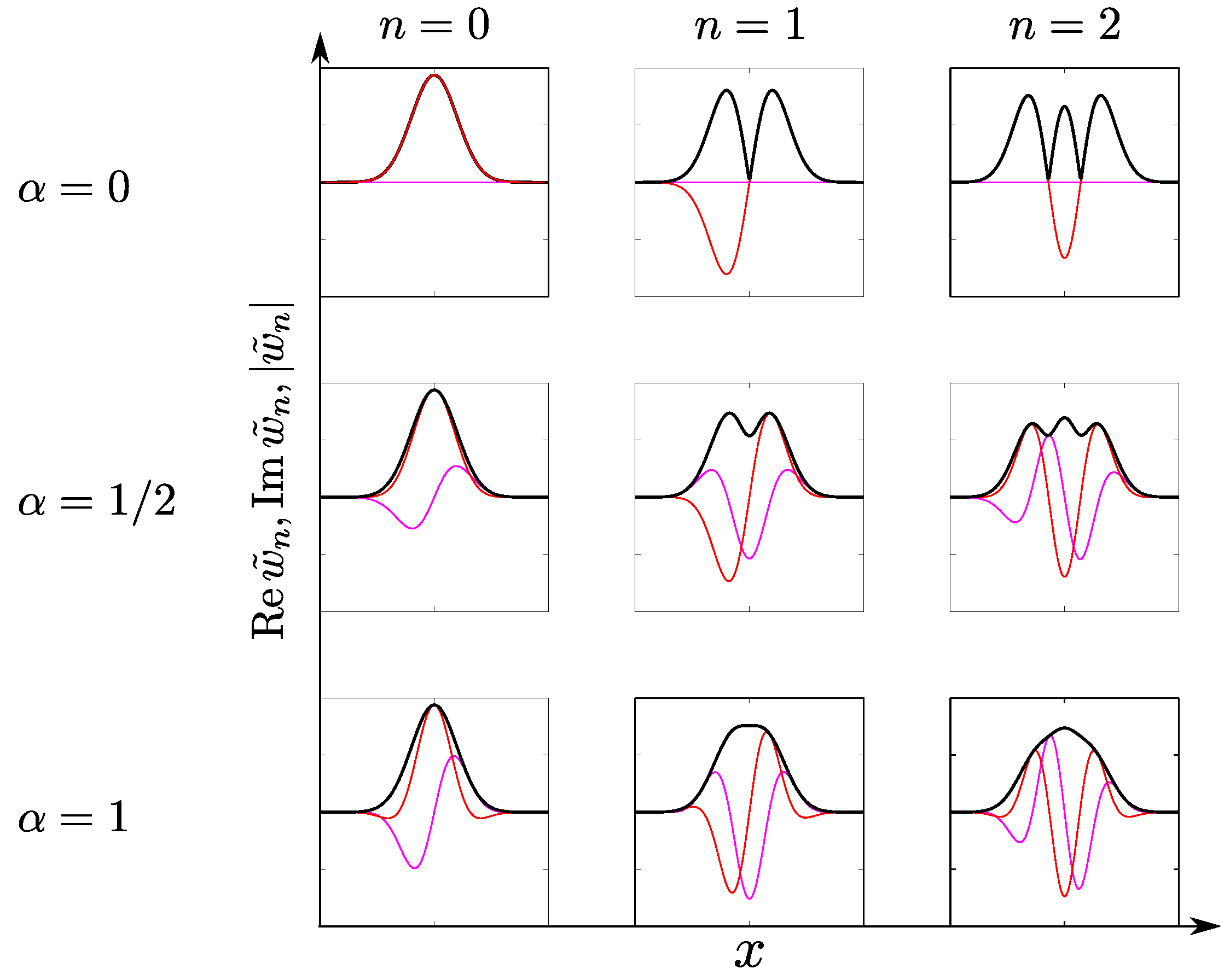
Appendix C. Some Properties of the Hermite—Gauss Eigenfunctions
Appendix D. Asymptotics in the Strongly Nonlocal Limit
References
- Litvak, A.G. Self-Focusing of Powerful Light Beams by Thermal Effects. JETF Lett. 1966, 4, 230–233. [Google Scholar]
- Tam, A.C.; Happer, W. Long-Range Interactions between cw Self-Focused Laser Beams in an Atomic Vapor. Phys. Rev. Lett. 1977, 38, 278. [Google Scholar] [CrossRef]
- Suter, D.; Blasberg, T. Stabilization of Transverse Solitary Waves by a Nonlocal Response of the Nonlinear Medium. Phys. Rev. A 1993, 48, 4583. [Google Scholar] [CrossRef] [PubMed]
- Turitsyn, S.K. Spatial Dispersion of Nonlinearity and Stability of Multidimensional Solitons. Theor. Math. Phys. (Engl. Transl.) 1985, 64, 797. [Google Scholar] [CrossRef]
- Krolikowski, W.; Bang, O. Solitons in Nonlocal Nonlinear Media: Exact Solutions. Phys. Rev. E 2000, 63, 016610. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, Z.; Kartashov, Y.V.; Torner, L. Upper Threshold for Stability of Multipole-Mode Solitons in Nonlocal Nonlinear media. Opt. Lett. 2005, 30, 3171. [Google Scholar] [CrossRef] [PubMed]
- Skupin, S.; Bang, O.; Edmundson, D.; Krolikowski, W. Stability of Two-Dimensional Spatial Solitons in Nonlocal Nonlinear media. Phys. Rev. E 2006, 73, 066603. [Google Scholar] [CrossRef] [PubMed]
- Bang, O.; Krolikowski, W.; Wyller, J.; Rasmussen, J.J. Collapse Arrest and Soliton Stabilization in Nonlocal Nonlinear Media. Phys. Rev. E 2002, 66, 046619. [Google Scholar] [CrossRef] [PubMed]
- Dreischuh, A.; Neshev, D.N.; Petersen, D.E.; Bang, O.; Krolikowski, W. Observation of Attraction between Dark Solitons. Phys. Rev. Lett. 2006, 96, 043901. [Google Scholar] [CrossRef] [PubMed]
- Pitaevskii, L.P.; Stringari, S. Bose-Einstein Condensation; Clarendon Press: Oxford, UK; New York, NY, USA, 2003. [Google Scholar]
- Pérez-García, V.M.; Konotop, V.V.; García-Ripoll, J.J. Dynamics of Quasicollapse in Nonlinear Schrödinger Systems with Nonlocal Interactions. Phys. Rev. E 2000, 62, 4300. [Google Scholar] [CrossRef]
- Henkel, N.; Nath, R.; Pohl, T. Three-Dimensional Roton Excitations and Supersolid Formation in Rydberg-Excited Bose-Einstein Condensates. Phys. Rev. Lett. 2010, 104, 195302. [Google Scholar] [CrossRef] [PubMed]
- Góral, K.; Rza̧żewski, K.; Pfau, T. Bose-Einstein Condensation with Magnetic Dipole-Dipole Forces. Phys. Rev. A 2000, 61, 051601(R). [Google Scholar] [CrossRef]
- Yi, S.; You, L. Trapped Atomic Condensates with Anisotropic Interactions. Phys. Rev. A 2000, 61, 041604(R). [Google Scholar] [CrossRef]
- Santos, L.; Shlyapnikov, G.V.; Zoller, P.; Lewenstein, M. Bose-Einstein Condensation in Trapped Dipolar Gases. Phys. Rev. Lett. 2000, 85, 1791. [Google Scholar] [CrossRef] [PubMed]
- Pedri, P.; Santos, L. Two-Dimensional Bright Solitons in Dipolar Bose-Einstein Condensates. Phys. Rev. Lett. 2005, 95, 200404. [Google Scholar] [CrossRef] [PubMed]
- Sinha, S.; Santos, L. Cold Dipolar Gases in Quasi-One-Dimensional Geometries. Phys. Rev. Lett. 2007, 99, 140406. [Google Scholar] [CrossRef] [PubMed]
- Maucher, F.; Pohl, T.; Skupin, S.; Krolikowski, W. Self-Organization of Light in Optical Media with Competing Nonlinearities. Phys. Rev. Lett. 2016, 116, 163902. [Google Scholar] [CrossRef] [PubMed]
- Litvak, A.G.; Sergeev, A.M. One-Dimensional Collapse of Plasma Waves. JETP Lett. 1978, 27, 517–520. [Google Scholar]
- Conti, C.; Peccianti, M.; Assanto, G. Route to Nonlocality and Observation of Accessible Solitons. Phys. Rev. Lett. 2003, 91, 073901. [Google Scholar] [CrossRef] [PubMed]
- Conti, C.; Peccianti, M.; Assanto, G. Observation of Optical Spatial Solitons in a Highly Nonlocal Medium. Phys. Rev. Lett. 2004, 92, 113902. [Google Scholar] [CrossRef] [PubMed]
- Sevinçli, S.; Henkel, N.; Pohl, T. Nonlocal Nonlinear Optics in Cold Rydberg Gases. Phys. Rev. Lett. 2011, 107, 153001. [Google Scholar] [CrossRef] [PubMed]
- Kunze, M.; Küpper, T.; Mezentsev, V.K.; Shapiro, E.G.; Turitsyn, S. Nonlinear Solitary Waves with Gaussian Tails. Physica D 1999, 128, 273–295. [Google Scholar] [CrossRef]
- Kivshar, Y.S.; Alexander, T.; Turitsyn, S.K. Nonlinear Modes of a Macroscopic Quantum Oscillator. Phys. Lett. A 2001, 278, 225–230. [Google Scholar] [CrossRef]
- Yukalov, V.I.; Yukalova, E.P.; Bagnato, V.S. Nonlinear Coherent Modes of Trapped Bose-Einstein Condensates. Phys. Rev. A 2002, 66, 043602. [Google Scholar] [CrossRef]
- D’Agosta, R.; Malomed, B.A.; Presilla, C. Stationary States of Bose-Einstein Condensates in Single- and Multi-Well Trapping Potentials. Laser Phys. 2002, 12, 37–42. [Google Scholar]
- Konotop, V.V.; Kevrekidis, P.G. Bohr-Sommerfeld Quantization Condition for the Gross-Pitaevskii Equation. Phys. Rev. Lett. 2003, 91, 230402. [Google Scholar] [CrossRef] [PubMed]
- Kevrekidis, P.G.; Konotop, V.V.; Rodrigues, A.; Frantzeskakis, D.J. Dynamic Generation of Matter Solitons from Linear States via Time-Dependent Scattering Lengths. J. Phys. B At. Mol. Opt. Phys. 2005, 38, 1173–1188. [Google Scholar] [CrossRef]
- Edwards, M.; Burnett, K. Numerical Solution of the Nonlinear Schrödinger Equation for Small Samples of Trapped Neutral Atoms. Phys. Rev. A 1995, 51, 1382–1386. [Google Scholar] [CrossRef] [PubMed]
- Ruprecht, P.A.; Holland, M.J.; Burnett, K.; Edwards, M. Time-Dependent Solution of the Nonlinear Schrödinger Equation for Bose-Condensed Trapped Neutral Atoms. Phys. Rev. A 1995, 51, 4704–4711. [Google Scholar] [CrossRef] [PubMed]
- Dalfovo, F.; Stringari, S. Bosons in Anisotropic Traps: Ground State and Vortices. Phys. Rev. A 1996, 53, 2477–2485. [Google Scholar] [CrossRef] [PubMed]
- Yukalov, V.I.; Yukalova, E.P.; Bagnato, V.S. Non-Ground-State Bose-Einstein Condensates of Trapped Atoms. Phys. Rev. A 1997, 56, 4845. [Google Scholar] [CrossRef]
- Wang, C.; Kevrekidis, P.G.; Frantzeskakis, D.J.; Malomed, B.A. Effects of Long-Range Nonlinear Interactions in Double-Well Potentials. Physica D 2011, 240, 805–813. [Google Scholar] [CrossRef]
- Tsilifis, P.A.; Kevrekidis, P.G.; Rothos, V.M. Cubic-Quintic Long-Range Interactions with Double Well Potentials. J. Phys. A: Math. Theor. 2014, 47, 035201. [Google Scholar] [CrossRef]
- Kartashov, Y.V.; Vysloukh, V.A.; Torner, L. Tunable Soliton Self-Bending in Optical Lattices with Nonlocal Nonlinearity. Phys. Rev. Lett. 2004, 93, 153903. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Kartashov, Y.V.; Torner, L. Soliton Mobility in Nonlocal Optical Lattices. Phys. Rev. Lett. 2005, 95, 113901. [Google Scholar] [CrossRef] [PubMed]
- Efremidis, N.K. Nonlocal Lattice Solitons in Thermal Media. Phys. Rev. A 2008, 77, 063824. [Google Scholar] [CrossRef]
- Cuevas, J.; Malomed, B.A.; Kevrekidis, P.G.; Frantzeskakis, D.J. Solitons in Quasi-One-Dimensional Bose-Einstein Condensates with Competing Dipolar and Local Interactions. Phys. Rev. A 2009, 79, 053608. [Google Scholar] [CrossRef]
- Konotop, V.V.; Yang, J.; Zezyulin, D.A. Nonlinear Waves in -Symmetric Systems. Rev. Mod. Phys. 2016, 88, 035002. [Google Scholar] [CrossRef]
- Zezyulin, D.A.; Alfimov, G.L.; Konotop, V.V.; Pérez-García, V.M. Stability of Excited States of a Bose-Einstein Condensate in an Anharmonic Trap. Phys. Rev. A 2008, 78, 013606. [Google Scholar] [CrossRef]
- Bender, C.M.; Boettcher, S. Real Spectra in Non-Hermitian Hamiltonians Having Symmetry. Phys. Rev. Lett. 1998, 80, 5243. [Google Scholar] [CrossRef]
- Rüter, C.E.; Makris, K.G.; El-Ganainy, R.; Christodoulides, D.N.; Segev, M.; Kip, D. Observation of Parity-Time Symmetry in Optics. Nat. Phys. 2010, 6, 192–195. [Google Scholar] [CrossRef]
- Hang, C.; Huang, G.; Konotop, V.V. Symmetry with a System of Three-Level Atoms. Phys. Rev. Lett. 2013, 110, 083604. [Google Scholar] [CrossRef] [PubMed]
- Hang, C.; Zezyulin, D.A.; Huang, G.; Konotop, V.V.; Malomed, B.A. Tunable Nonlinear Double-Core -Symmetric Waveguides. Opt. Lett. 2014, 39, 5387–5390. [Google Scholar] [CrossRef] [PubMed]
- Hang, C.; Zezyulin, D.A.; Konotop, V.V.; Huang, G. Tunable Nonlinear Parity-Time-Symmetric Defect Modes with an Atomic Cell. Opt. Lett. 2013, 38, 4033–4036. [Google Scholar] [CrossRef] [PubMed]
- Klaiman, S.; Günther, U.; Moiseyev, N. Visualization of Branch Points in -Symmetric Waveguides. Phys. Rev. Lett. 2008, 101, 080402. [Google Scholar] [CrossRef] [PubMed]
- Musslimani, Z.H.; Makris, K.G.; El-Ganainy, R.; Christodoulides, D.N. Optical Solitons in Periodic Potentials. Phys. Rev. Lett. 2008, 100, 030402. [Google Scholar] [CrossRef] [PubMed]
- Hu, S.; Ma, X.; Lu, D.; Yang, Z.; Zheng, Y.; Hu, W. Solitons Supported by Complex -Symmetric Gaussian Potentials. Phys. Rev. A 2011, 84, 043818. [Google Scholar] [CrossRef]
- Shi, Z.; Jiang, X.; Zhu, X.; Li, H. Bright Spatial Solitons in Defocusing Kerr Media with -Symmetric Potentials. Phys. Rev. A 2011, 84, 053855. [Google Scholar] [CrossRef]
- Nixon, S.; Ge, L.; Yang, J. Stability Analysis for Solitons in -Symmetric Optical Lattices. Phys. Rev. A 2012, 85, 023822. [Google Scholar] [CrossRef]
- Achilleos, V.; Kevrekidis, P.G.; Frantzeskakis, D.J.; Carretero-González, R. Dark Solitons and Vortices in -Symmetric Nonlinear Media: From Spontaneous Symmetry Breaking to Nonlinear Phase Transitions. Phys. Rev. A 2012, 86, 013808. [Google Scholar] [CrossRef]
- Zhu, X.; Wang, H.; Zheng, L.X.; Li, H.; He, Y.J. Gap Solitons in Parity-Time Complex Periodic Optical Lattices with the Real Part of Superlattices. Opt. Lett. 2011, 36, 2680–2682. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Wang, J. Defect Solitons in Parity-Time Periodic Potentials. Opt. Express 2011, 19, 4030–4035. [Google Scholar] [CrossRef] [PubMed]
- Lu, Z.; Zhang, Z.-M. Defect Solitons in Parity-Time Symmetric Superlattices. Opt. Express. 2011, 19, 11457–11462. [Google Scholar] [CrossRef] [PubMed]
- Zezyulin, D.A.; Konotop, V.V. Nonlinear Modes in the Harmonic -Symmetric Potential. Phys. Rev. A 2012, 85, 043840. [Google Scholar] [CrossRef]
- Shi, Z.H.; Li, H.; Zhu, X.; Jiang, X. Nonlocal Bright Spatial Solitons in Defocusing Kerr Media Supported by Symmetric Potentials. EPL 2012, 98, 64006. [Google Scholar] [CrossRef]
- Hu, S.; Lu, D.; Ma, X.; Guo, Q.; Hu, W. Defect Solitons Supported by Nonlocal PT Symmetric Superlattices. EPL 2012, 98, 14006. [Google Scholar] [CrossRef]
- Zhu, X.; Li, H.; Wang, H.; He, Y. Nonlocal Multihump Solitons in Parity-Time Symmetric Periodic Potentials. J. Opt. Soc. Am. B 2013, 30, 1987. [Google Scholar] [CrossRef]
- Hu, S.; Ma, X.; Lu, D.; Zheng, Y.; Hu, W. Defect Solitons in Parity-Time-Symmetric Optical Lattices with Nonlocal Nonlinearity. Phys. Rev. A 2012, 85, 043826. [Google Scholar] [CrossRef]
- Li, H.; Jiang, X.; Zhu, X.; Shi, Z. Nonlocal Solitons in Dual-Periodic -Symmetric Optical Lattices. Phys. Rev. A 2012, 86, 023840. [Google Scholar] [CrossRef]
- Jisha, C.P.; Alberucci, A.; Brazhnyi, V.A.; Assanto, G. Nonlocal Gap Solitons in -Symmetric Periodic Potentials with Defocusing Nonlinearity. Phys. Rev. A. 2014, 89, 013812. [Google Scholar] [CrossRef]
- Fang, L.; Gao, J.; Shi, Z.; Zhu, X.; Li, H. Nonlocal Defect Solitons in Parity-Time-Symmetric Superlattices with Defocusing Nonlinearity. Eur. Phys. J. D 2014, 68. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Musslimani, Z.H. Integrable Nonlocal Nonlinear Schrödinger Equation. Phys. Rev. Lett. 2013, 110, 064105. [Google Scholar] [CrossRef] [PubMed]
- García-Ripoll, J.J.; Konotop, V.V.; Malomed, B.; Pérez-García, V.M. A Quasi-Local Gross-Pitaevskii Equation for Attractive Bose-Einstein condensates. Math. Comput. Simul. 2003, 62, 21–30. [Google Scholar] [CrossRef]
- Konotop, V.V.; Pérez-García, V.M. On the Applicability of the Classical Dipole-Dipole Interaction for Polar Bose-Einstein Condensates. Phys. Lett. A 2002, 300, 348–352. [Google Scholar] [CrossRef]
- Mayteevarunyoo, T.; Malomed, B.A.; Reoksabutr, A. Solvable Model for Solitons Pinned to a Parity-Time-Symmetric Dipole. Phys. Rev. E 2013, 88, 022919. [Google Scholar] [CrossRef] [PubMed]
- Kato, T. Perturbation Theory for Linear Operators; Springer-Verlag: Berlin, Germany, 1966. [Google Scholar]
- Znojil, M. -Symmetric Harmonic Oscillators. Phys. Lett. A 1999, 259, 220–223. [Google Scholar] [CrossRef]
- Abramovitz, M.; Stegun, I.A. Handbook of Mathematical Functions; National Bureau of Standards: Washington, DC, USA, 1972.
- Dohnal, T.; Siegl, P. Bifurcation of Nonlinear Eigenvalues in Problems with Antilinear Symmetry. 2015; preprint: arXiv:1504.00054 [math-ph]. [Google Scholar]
- Huang, C.; Ye, F.; Kartashov, Y.V.; Malomed, B.A.; Chen, X. Symmetry in Optics Beyond the Paraxial Approximation. Opt. Lett. 2014, 39, 5443–5446. [Google Scholar] [CrossRef] [PubMed]
- Coles, M.P.; Pelinovsky, D.E.; Kevrekidis, P.G. Excited States in the Large Density Limit: A Variational Approach. Nonlinearity 2010, 23. [Google Scholar] [CrossRef]
- Gallo, C.; Pelinovsky, D.E. On the Thomas-Fermi Approximation of the Ground State in a PT-Symmetric Confining Potential. Stud. Appl. Math. 2014, 133, 398–421. [Google Scholar] [CrossRef]

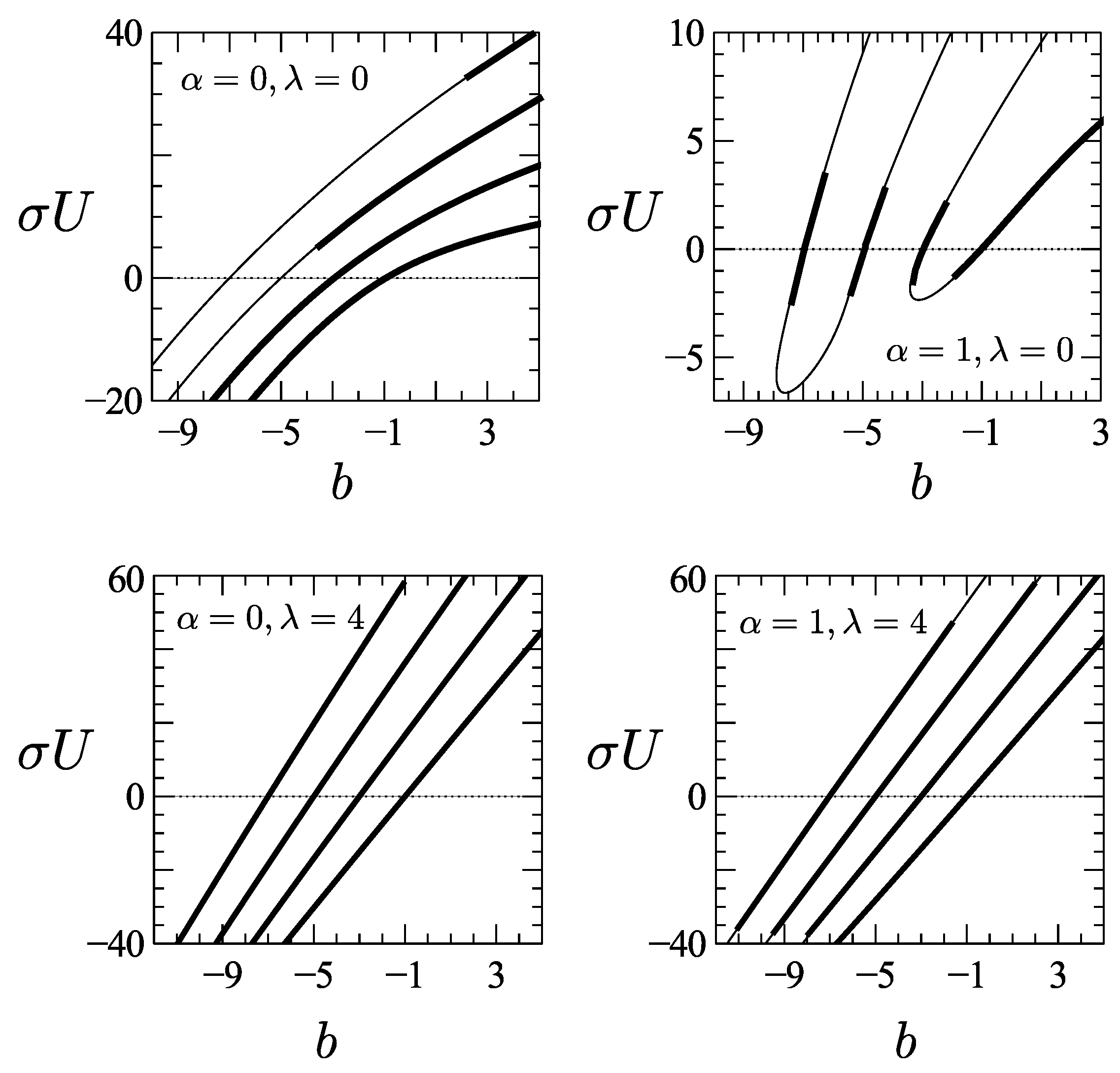
| n | k | Zeros of | Interval of Stability in λ | |
|---|---|---|---|---|
| 1 | 0 | + | no zeros | |
| 2 | 0 | − | 1.82 | |
| 1 | + | no zeros | ||
| 3 | 0 | − | 2.36 | |
| 1 | − | 2.04 | ||
| 2 | + | no zeros | ||
| 4 | 0 | + | 2.61 2.85 | |
| 1 | − | 2.64 | ||
| 2 | − | 2.26 | ||
| 3 | + | no zeros | ||
| 5 | 0 | + | 3.23 3.25 | |
| 1 | − | 3.12 | ||
| 2 | − | 2.90 | ||
| 3 | − | 2.45 | ||
| 4 | + | no zeros | ||
| 6 | 0 | + | 3.566 3.568 | |
| 1 | + | 3.45 3.51 | ||
| 2 | − | 3.37 | ||
| 3 | − | 3.13 | ||
| 4 | − | 2.64 | ||
| 5 | + | no zeros |
| n | k | Zeros of | Interval of Stability in λ | |
|---|---|---|---|---|
| 1 | 0 | + | no zeros | |
| 2 | 0 | − | 1.31 | |
| 1 | + | no zeros | ||
| 3 | 0 | − | no zeros | always unstable |
| 1 | − | 1.54 | ||
| 2 | + | no zeros | ||
| 4 | 0 | + | 7.25 | always unstable |
| 1 | − | no zeros | ||
| 2 | − | 1.70 | ||
| 3 | + | no zeros | ||
| 5 | 0 | + | no zeros | always unstable |
| 1 | − | no zeros | ||
| 2 | − | no zeros | ||
| 3 | − | 1.84 | ||
| 4 | + | no zeros | ||
| 6 | 0 | + | no zeros | always unstable |
| 1 | + | no zeros | ||
| 2 | − | no zeros | ||
| 3 | − | no zeros | ||
| 4 | − | 1.97 | ||
| 5 | + | no zeros |
| n | k | Zeros of | Interval of Stability in λ | |
|---|---|---|---|---|
| 1 | 0 | + | no zeros | |
| 2 | 0 | − | 1.52 | |
| 1 | + | no zeros | ||
| 3 | 0 | − | 2.70 | |
| 1 | − | 1.66 | ||
| 2 | + | no zeros | ||
| 4 | 0 | + | 2.77 3.45 | |
| 1 | − | 2.96 | ||
| 2 | − | 1.77 | ||
| 3 | + | no zeros | ||
| 5 | 0 | + | 3.88 3.99 | |
| 1 | − | 3.74 | ||
| 2 | − | 3.21 | ||
| 3 | − | 1.87 | ||
| 4 | + | no zeros | ||
| 6 | 0 | + | 4.39 4.42 | |
| 1 | + | 3.98 4.28 | ||
| 2 | − | 4.00 | ||
| 3 | − | 3.44 | ||
| 4 | − | 1.97 | ||
| 5 | + | no zeros |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zezyulin, D.A.; Konotop, V.V. Small-Amplitude Nonlinear Modes under the Combined Effect of the Parabolic Potential, Nonlocality and PT Symmetry. Symmetry 2016, 8, 72. https://doi.org/10.3390/sym8080072
Zezyulin DA, Konotop VV. Small-Amplitude Nonlinear Modes under the Combined Effect of the Parabolic Potential, Nonlocality and PT Symmetry. Symmetry. 2016; 8(8):72. https://doi.org/10.3390/sym8080072
Chicago/Turabian StyleZezyulin, Dmitry A., and Vladimir V. Konotop. 2016. "Small-Amplitude Nonlinear Modes under the Combined Effect of the Parabolic Potential, Nonlocality and PT Symmetry" Symmetry 8, no. 8: 72. https://doi.org/10.3390/sym8080072
APA StyleZezyulin, D. A., & Konotop, V. V. (2016). Small-Amplitude Nonlinear Modes under the Combined Effect of the Parabolic Potential, Nonlocality and PT Symmetry. Symmetry, 8(8), 72. https://doi.org/10.3390/sym8080072