Next Article in Journal
Cosmological Reflection of Particle Symmetry
Previous Article in Journal
Modeling Bottom-Up Visual Attention Using Dihedral Group D4
Previous Article in Special Issue
Fluctuating Charge Order: A Universal Phenomenon in Unconventional Superconductivity?
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Symmetry
Volume 8
Issue 8
10.3390/sym8080080
symmetry-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Superconducting Gap Symmetry of LaFeP(O,F) Observed by Impurity Doping Effect

by
Shigeki Miyasaka
*,
Sinnosuke Suzuki
and
Setsuko Tajima
Department of Physics, Graduate School of Science, Osaka University, Toyonaka, Osaka 560-0043, Japan
*
Author to whom correspondence should be addressed.
Symmetry 2016, 8(8), 80; https://doi.org/10.3390/sym8080080
Submission received: 30 May 2016 / Revised: 9 August 2016 / Accepted: 11 August 2016 / Published: 17 August 2016
(This article belongs to the Special Issue Symmetry of the Order Parameter in Iron-Based Superconductors)
Browse Figures
Versions Notes

Abstract

:
We have investigated Mn, Co and Ni substitution effects on polycrystalline samples of LaFePO0.95F0.05 by resistivity and magnetoresistance measurements. In LaFe1-xMxPO0.95F0.05 (M = Mn, Co and Ni), the superconducting transition temperature (Tc) monotonously decreases with increasing the impurity doping level of x. There is a clear difference of Tc suppression rates among Mn, Co and Ni doping cases, and the decreasing rate of Tc by Mn doping as a magnetic impurity is larger than those by the nonmagnetic doping impurities (Co/Ni). This result indicates that in LaFePO0.95F0.05, Tc is rapidly suppressed by the pair-breaking effect of magnetic impurities, and the pairing symmetry is a full-gapped s-wave. In the nonmagnetic impurity-doped systems, the residual resistivity in the normal state has nearly the same value when Tc becomes zero. The residual resistivity value is almost consistent with the universal value of sheet resistance for two-dimensional superconductors, suggesting that Tc is suppressed by electron localization in Co/Ni-doped LaFePO0.95F0.05.

Graphical Abstract

1. Introduction

More than a quarter of a century ago, high-Tc superconducting (SC) cuprates were discovered. Since then, the research field of cuprate superconductors has become one of the most investigated topics in condensed matter physics, and a lot of experimental and theoretical studies have been performed in order to explore new superconductivity in other layered transition metal compounds. Recently, Kamihara and co-workers found new high-Tc superconductors, LaFeP(O,F) and LaFeAs(O,F) [1,2]. The discovery of the iron arsenide superconductor has stimulated many researchers and many families of iron-based SC systems have been found by experimental investigations [3].
Since the discovery of the iron-pnictide superconductor, many researchers have made great efforts to clarify its SC mechanism. Several theoretical research groups have argued that spin or orbital fluctuations play an important role in the pairing mechanism, but this issue is under debate. In spin fluctuation–mediated superconductivity [4,5], the nesting between hole and electron Fermi surfaces induces a sign-changing s±-wave SC state, while the sign-preserving s++-wave SC state is predicted in the orbital fluctuation–mediated superconductivity [6,7].
In order to understand the pairing mechanism in iron-based SC systems, it is crucial to clarify the SC gap symmetry. After eight years of intensive research on these systems, however, no consensus on a universal gap structure has been reached. The pioneering works by angle resolved photoemission spectroscopy (ARPES) reported a full-gapped symmetry on several Fermi surfaces in (Ba,K)Fe2As2 and NdFeAs(O,F) [8,9]. On the other hand, the results of NMR, penetration depth and thermal conductivity measurements have proposed the existence of line nodes of the SC order parameter in BaFe2(As,P)2 [10,11].
The theoretical report by Kuroki et al. has explained that the difference of local structural parameters around Fe ions, such as the pnictogen height from the Fe plane, etc., causes the different electronic structures and SC gap symmetries [4]. Hashimoto et al. performed a systematic comparison of quasi-particle excitations estimated by the penetration depth measurements in various iron-based SC systems. Their results suggested that the nodeless SC gap is changed to a nodal one when the pnictogen height from the Fe plane is shortened below a threshold value [12]. Kinouchi et al. also found the relationship between the pnictogen height and the nodal/nodeless SC gap states in the isovalent-substituted systems [13]. On the other hand, Thomale et al. have theoretically demonstrated that the d-wave SC symmetry appears in the heavily hole-doped systems such as (Ba,K)Fe2As2 [14]. Pressure also causes the various changes of SC gap symmetry in iron-based SC systems. The results of muon spin rotation under high pressure have indicated that pressure induces the nodal SC gap in (Ba,Rb)Fe2As2, while the nodeless SC gap seems to be robust against pressure in LaFeAs(O,F) [15,16]. These previous studies have indicated that small differences in structural and electronic properties can lead to a strong diversity of the SC gap structure in iron-based SC systems.
Several research groups have experimentally suggested that the first iron-based SC material LaFePO has a nodal SC gap [17,18,19]. In this study, we revisited the LaFePO system and tried to get information about the gap symmetry using a different approach, i.e., the impurity doping effect. We have synthesized the impurity-doped polycrystalline samples of LaFe1-xMxP(O,F) (M = Mn, Co and Ni) and measured electrical resistivity and magnetoresistance. In the present work, we studied the impurity doping effects on the 5% F-doped system, LaFePO0.95F0.05. The F doping enhanced Tc in the LaFeP(O,F) system [20] and enabled us to easily observe the Tc suppression using impurity doping.

2. Materials and Methods

Polycrystalline LaFe1-xMxPO0.95F0.05 were prepared by solid-state reaction. The precursor of LaP powder was synthesized by heating a mixture of La and P powders in evacuated silica tube. The mixtures of LaP, Fe, Fe2O3, FeF2, Mn3O4, Co, and NiO in stoichiometric ratio of LaFe1-xMxPO0.95F0.05 were pressed into pellets in a pure Ar filled glove box and annealed at 1100 °C for 40 h in evacuated silica tubes.
The samples were checked by powder X-ray diffraction using Cu Kα1 radiation at room temperature. Almost all the diffraction peaks can be assigned to the calculated Bragg peaks for the tetragonal P4/nmm symmetry, indicating that the samples are a single phase. Any broadening of diffraction peaks by impurity doping was not observed, suggesting that the doped impurities were homogenously distributed in the samples. The in-plane (a) and out-of-plane lattice constants (c) are obtained by using least squares fitting of the peak positions of the powder X-ray diffraction profile. In the doping region of 0 ≤ x ≤ 0.10 for Mn-doped system, the lattice constants increase with x and the variation rates are +2.1%/x for a-axis and +3.6%/x for c-axis, respectively. On the other hand, the lattice constants hardly change in the same doping region of Co and Ni. We have synthesized the several samples of Co- and Ni-doped systems with the wider doping level of x = 0–1.0 and estimated the lattice constants. With the doping level of Co and Ni, the lattice constant of c-axis systematically decreases. This result indicates that the Mn, Co and Ni substitutions on Fe site succeed in this system.
Magnetic susceptibility was measured using a SQUID magnetometer (Quantum Design MPMS-7) under a magnetic field of 10 Oe and the SC diamagnetism has been observed in the samples which show resistive transition to SC state. Electrical resistivity was measured by a standard four-probe method from room temperature down to 1.8 K. Temperature of the midpoint of the resistive transition nearly agrees with the onset of the SC diamagnetic transition temperature. Magnetoresistance were measured up to 7 T at various temperatures in a SC magnet.

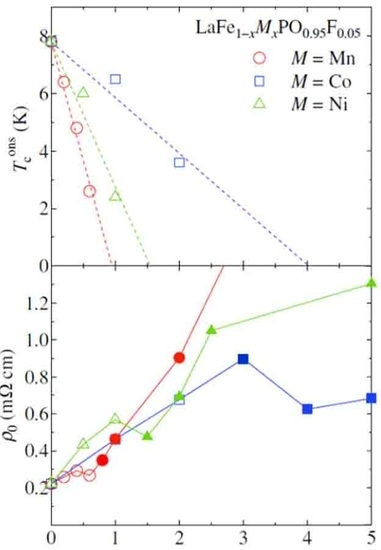
3. Results

Figure 1 shows temperature dependence of electrical resistivity for LaFe1−xMxPO0.95F0.05. The resistivity for all the samples with x = 0–0.10 shows a metallic behavior and the value almost systematically increases with x. The increasing rate of the resistivity value is dependent on the impurity, and the resistivity for the samples with M = Mn is much more strongly enhanced than in those with M = Co and Ni. The different ratio of the resistivity enhancement with x may be related to the ground states for each end member. LaMnPO is a semiconductor, and resultantly the Mn substitution to this system causes a large change of resistivity [21]. On the other hand, LaCoPO and LaNiPO are metal, as is LaFePO0.95F0.05, and the resistivity for the Co- and Ni-doped samples shows a smaller change with the increasing x [22,23].
Figure 2 presents the low-temperature part of the resistivity for LaFe1−xMxPO0.95F0.05 with low xs. The impurity doping enhances the residual resistivity almost monotonically, indicating that the impurities are successfully introduced into the Fe site of LaFePO0.95F0.05. On the other hand, Tc is systematically suppressed with x, and the SC transition almost disappears around x = 0.8% for M = Mn, x = 3.0% for M = Co, and x = 1.5% for M = Ni, respectively.
Figure 3a shows the x dependence of the onset temperature of the resistive transition to the SC state (Tcons) for LaFe1−xMxPO0.95F0.05. Tcons is defined as the temperature at which the resistivity becomes 95% of the extrapolated normal-state value of the resistivity. Tcons decreases almost linearly with x. However, the suppression rate dTcons/dx is strikingly dependent on the impurity element, that is −8.2 K/% for M = Mn, −1.9 K/% for M = Co, and −5.0 K/% for M = Ni. Figure 3b shows the x dependence of the residual resistivity ρ0 in the normal state. As shown in Figure 2 and Figure 3b, it is interesting that Tcons becomes almost zero, when ρ0 reaches approximately 0.6 mΩ·cm for M = Co and Ni.
In order to clarify the magnetic feature of the doped impurities, we have measured the temperature dependence of longitudinal magnetoresistance at a magnetic field of H = 7 T for the x = 0.05 samples, which show no superconductivity down to 1.8 K. As shown in Figure 4, the magnetoresistance for Mn-doped LaFePO0.95F0.05 shows a different behavior from the cases of Co and Ni doping at low temperatures. The magnetoresistance remains positive down to the lowest temperature for Co- and Ni-doped compounds, while its sign turns negative for M = Mn. In general, the negative magnetoresistance appears when the charge carriers are scattered by the magnetic ions in the compounds. Therefore, the results of the magnetoresistance indicate that Co and Ni play as nonmagnetic impurities in the present system, while Mn as a magnetic one. This is consistent with the previous studies for Co- and Mn-doped BaFe2As2 which have pointed out that the doped Co does not create any localized magnetic moments, but Mn plays as a magnetic impurity in the Fe layer [24,25,26].

4. Discussion

The suppression of Tc by impurity doping is dependent on the impurity elements, and the Mn doping most strongly destabilizes the superconductivity. The results of magnetoresistance have indicated that the doped Mn acts as a magnetic impurity in this system. This fact reveals that Tc is suppressed by the pair-breaking effect of the magnetic moments of Mn. On the other hand, the doped Co and Ni have no magnetic moment, and the suppression ratios of Tc in these impurity doping cases are smaller than that in the Mn-doped system. In general, the magnetic impurity induces the magnetic pair-breaking effect and, resultantly, larger Tc suppression than that by the nonmagnetic impurity in full-gapped s-wave superconductors. On the other hand, the magnetic and nonmagnetic impurities similarly destabilize the nodal s-wave or d-wave SC sates. These different behaviors by Mn, Co and Ni doping suggest that the SC gap of LaFeP(O,F) has a finite value at all k points, i.e., the SC gap symmetry is a full-gapped s-wave. In contrast, the previous reports have indicated that LaFePO has a nodal SC gap via the measurements of penetration depth and thermal transport [17,18,19]. The techniques of penetration depth and thermal transport are conventional ones for the determination of SC gap symmetry, but they observe the SC gap indirectly. The impurity doping effect is also an indirect way of probing the pairing symmetry. To resolve this inconsistency between the present and previous results, we need further experimental studies using different methods for the direct observation of the SC gap such as ARPES.
As shown Figure 3, the Tc suppression rate by Ni doping is smaller than that of the Mn doping case, but larger than that of Co doping. As compared with Co, Ni has a more different ionic radius compared to Fe. The doped Ni case has a larger mismatch of crystal structure and plays a role of a stronger scattering center. The carrier localization occurs and the SC state is destabilized in the lower doping region in the Ni-doped samples. As a result, different Tc suppression behaviors may be observed in the cases of nonmagnetic Co and Ni doping.
We have pointed out that ρ0 in the normal state has nearly the same values (~0.6 mΩ·cm), when Tcons goes to zero in LaFe1-xMxPO0.95F0.05. For two-dimensional superconductors such as cuprates, it has been well known that the SC transition disappears when the electrical resistivity at low temperatures exceeds the universal value h/4e2 = 6.45 kΩ of sheet resistance [27]. For LaFeP(O,F), ρ0 ~ 0.6 mΩ·cm corresponds to the sheet resistance of ~7.1 kΩ, which is approximately consistent with the universal value. Therefore, it is suggested that Tc is suppressed by electronic localization in the nonmagnetic Co- and Ni-doped systems. Here, we note that there is uncertainty in the present results, because we have measured the resistivity for polycrystalline samples which include not only in-plane but also out-of-plane resistivity information. However, the anisotropy of the out-of-plane to in-plane electrical resistivity for LaFePO is large, ~13 to 17 [28]. Therefore, the in-plane resistivity mainly dominates the present resistivity behaviors using polycrystalline samples, and we can discuss the present results from the viewpoint of two-dimensional superconductors.
Since the discovery of iron-based superconductors, many groups have investigated the impurity doping effects in RFeAs(O,F) (R = rare earth elements) with the same crystal structure of LaFePO but with higher Tc. The behaviors of Tc suppression by impurity doping in both RFeAs(O,F) and LaFeP(O,F) are very similar, i.e., the magnetic impurity of Mn strongly reduces Tc, while the nonmagnetic impurities do not largely destabilize the SC state [29,30,31,32]. The previous and present experimental results may have indicated that these effects of destabilization of superconductivity by magnetic and nonmagnetic impurities are a common feature in iron-based SC materials.
Both RFeAs(O,F) and LaFeP(O,F) are multi-band systems with several Fermi surfaces, but their different Tc values indicate that these systems have different electronic states. The theoretical studies have predicted that the 1111-type FeAs and FeP systems have different Fermi surface conditions depending on the local crystal structure around the Fe site [4]. Actually, our recent studies for RFeP1−xAsx(O,F) systems (R = La, Pr and Nd) have revealed that the transport properties in the normal state and the relationship between Tc and the resistivity show anomalies around x = 0.6~0.8, indicating the two different Fermi surface states and the different SC mechanisms in RFeP(O,F) and RFeAs(O,F) [33,34]. These results also have suggested that the RFeP(O,F) and RFeAs(O,F) systems have different SC gap symmetries.

5. Conclusions

We have investigated the impurity doping effect on the electrical resistivity and magnetoresistance for polycrystalline LaFe1−xMxPO0.95F0.05. The results of the magnetoresistance indicate that the doped Mn has local magnetic moments, while Co and Ni are nonmagnetic. Tc is suppressed by impurity doping. In the Mn-doped case, the Tc decreasing rate is larger than in the case of nonmagnetic Co and Ni doping. The different behaviors of Mn and Co/Ni doping indicate that in this system, Tc is rapidly suppressed by the pair-breaking effect of magnetic impurity, and the pairing symmetry is a full-gapped s-wave. In Co- and Ni-doped LaFePO0.95F0.05, the residual resistivity in the normal state is approximately 0.6 mΩ·cm when Tc becomes zero. This value corresponds to the sheet resistance of ~7.1 kΩ, which is approximately consistent with the universal value for two-dimensional superconductors. The present result suggests that Tc is suppressed by electronic localization in the nonmagnetic Co- and Ni-doped systems.

Acknowledgments

We thank Kiyohisa Tanaka for fruitful discussion. This work was supported by JST, TRIP, IRONSEA, and Grants-in-Aid for Scientific Research from MEXT and JSPS, Japan.

Author Contributions

Shigeki Miyasaka and Setsuko Tajima conceived and designed the experiments; Shigeki Miyasaka and Sinnosuke Suzuki performed the experiments and analyzed the data; Shigeki Miyasaka and Setsuko Tajima wrote the paper.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Kamihara, Y.; Hiramatsu, H.; Hirano, M.; Kawamura, R.; Yanagi, H.; Kamiya, T.; Hosono, H. Iron-Based Layered Superconductor: LaOFeP. J. Am. Chem. Soc. 2006, 128, 10012–10013. [Google Scholar] [CrossRef] [PubMed]
  2. Kamihara, Y.; Watanabe, T.; Hirano, M.; Hosono, H. Iron-Based Layered Superconductor La[O1−xFx]FeAs (x = 0.05–0.12) with Tc = 26 K. J. Am. Chem. Soc. 2008, 130, 3296–3297. [Google Scholar] [CrossRef] [PubMed]
  3. Hosono, H.; Kuroki, K. Iron-based superconductors: Current status of materials and pairing mechanism. Phys. C 2015, 514, 399–422. [Google Scholar] [CrossRef]
  4. Kuroki, K.; Usui, H.; Onari, S.; Arita, R.; Aoki, H. Pnictogen height as a possible switch between high-Tc nodeless and low-Tc nodal pairings in the iron-based superconductors. Phys. Rev. B 2009, 79. [Google Scholar] [CrossRef]
  5. Mazin, I.I.; Singh, D.J.; Johannes, M.D.; Du, M.H. Unconventional Superconductivity with a Sign Reversal in the Order Parameter of LaFeAsO1−xFx. Phys. Rev. Lett. 2008, 101. [Google Scholar] [CrossRef] [PubMed]
  6. Kontani, H.; Onari, S. Orbital-Fluctuation-Mediated Superconductivity in Iron Pnictides: Analysis of the Five-Orbital Hubbard-Holstein. Model. Phys. Rev. Lett. 2010, 104. [Google Scholar] [CrossRef] [PubMed]
  7. Onari, S.; Kontani, H. Self-consistent Vertex Correction Analysis for Iron-based Superconductors: Mechanism of Coulomb Interaction-Driven Orbital Fluctuations. Phys. Rev. Lett. 2012, 109. [Google Scholar] [CrossRef] [PubMed]
  8. Ding, H.; Richard, P.; Nakayama, K.; Sugawara, K.; Arakane, T.; Sekiba, Y.; Takayama, A.; Souma, S.; Sato, T.; Takahashi, T.; et al. Observation of Fermi-surface–dependent nodeless superconducting gaps in Ba0.6K0.4Fe2As2. Europhys. Lett. 2008, 83. [Google Scholar] [CrossRef]
  9. Kondo, T.; Santander-Syro, A.F.; Copie, O.; Liu, C.; Tillman, M.E.; Mun, E.D.; Schmalian, J.; Bud’ko, S.L.; Tanatar, M.A.; Canfield, P.C.; et al. Momentum Dependence of the Superconducting Gap in NdFeAsO0.9F0.1 Single Crystals Measured by Angle Resolved Photoemission Spectroscopy. Phys. Rev. Lett. 2008, 101. [Google Scholar] [CrossRef] [PubMed]
  10. Nakai, Y.; Iye, T.; Kitagawa, S.; Ishida, K.; Kasahara, S.; Shibauchi, T.; Matsuda, Y.; Terashima, T. 31P and 75As NMR evidence for a residual density of states at zero energy in superconducting BaFe2(As0.67P0.33)2. Phys. Rev. B 2010, 81. [Google Scholar] [CrossRef]
  11. Hashimoto, K.; Yamashita, M.; Kasahara, S.; Senshu, Y.; Nakata, N.; Tonegawa, S.; Ikada, K.; Serafin, A.; Carrington, A.; Terashima, T.; et al. Line nodes in the energy gap of superconducting BaFe2(As1−xPx)2 single crystals as seen via penetration depth and thermal conductivity. Phys. Rev. B 2010, 81. [Google Scholar] [CrossRef]
  12. Hashimoto, K.; Kasahara, S.; Katsumata, R.; Mizukami, Y.; Yamashita, M.; Ikeda, H.; Terashima, T.; Carrington, A.; Matsuda, Y.; Shibauchi, T. Nodal versus Nodeless Behaviors of the Order Parameters of LiFeP and LiFeAs Superconductors from Magnetic Penetration-Depth Measurements. Phys. Rev. Lett. 2012, 108. [Google Scholar] [CrossRef] [PubMed]
  13. Kinouchi, H.; Mukuda, H.; Kitaoka, Y.; Shirage, P.M.; Fujihisa, H.; Gotoh, Y.; Eisaki, H.; Iyo, A. Emergent phases of nodeless and nodal superconductivity separated by antiferromagnetic order in iron-based superconductor (Ca4Al2O6)Fe2(As1−xPx)2: 75As- and 31P-NMR studies. Phys. Rev. B 2013, 87. [Google Scholar] [CrossRef]
  14. Thomale, R.; Platt, C.; Hanke, W.; Hu, J.; Bernevig, B.A. Exotic d-Wave Superconducting State of Strongly Hole-Doped KxBa1-xFe2As2. Phys. Rev. Lett. 2011, 107. [Google Scholar] [CrossRef] [PubMed]
  15. Guguchia, Z.; Amato, A.; Kang, J.; Luetkens, H.; Biswas, P.K.; Prando, G.; von Rohr, F.; Bukowski, Z.; Shengelaya, A.; Keller, H.; et al. Direct evidence for a pressure-induced nodal superconducting gap in the Ba0.65Rb0.35Fe2As2 superconductor. Nat. Commun. 2015, 6. [Google Scholar] [CrossRef] [PubMed]
  16. Prando, G.; Hartmann, T.; Schottenhamel, W.; Guguchia, Z.; Sanna, S.; Ahn, F.; Nekrasov, I.; Blum, C.G.F.; Wolter, A.U.B.; Wurmehl, S.; et al. Mutual Independence of Critical Temperature and Superfluid Density under Pressure in Optimally Electron-Doped Superconducting LaFeAsO1−xFx. Phys. Rev. Lett. 2015, 114. [Google Scholar] [CrossRef] [PubMed]
  17. Fletcher, J.D.; Serafin, A.; Malone, L.; Analytis, J.G.; Chu, J.-H.; Erickson, A.S.; Fisher, I.R.; Carrington, A. Evidence for a Nodal-Line Superconducting State in LaFePO. Phys. Rev. Lett. 2009, 102. [Google Scholar] [CrossRef] [PubMed]
  18. Yamashita, M.; Nakata, N.; Senshu, Y.; Tonegawa, S.; Ikada, K.; Hashimoto, K.; Sugawara, H.; Shibauchi, T.; Matsuda, Y. Thermal conductivity measurements of the energy-gap anisotropy of superconducting LaFePO at low temperatures. Phys. Rev. B 2009, 80. [Google Scholar] [CrossRef]
  19. Sutherland, M.; Dunn, J.; Toews, W.H.; O’Farrell, E.; Analytis, J.; Fisher, I.; Hill, R.W. Low-energy quasiparticles probed by heat transport in the iron-based superconductor LaFePO. Phys. Rev. B 2012, 85. [Google Scholar] [CrossRef]
  20. Suzuki, S.; Miyasaka, S.; Tajima, S.; Kida, T.; Hagiwara, M. Systematic Study on Fluorine-Doping Dependence of Superconducting and Normal State Properties in LaFePO1−xFx. J. Phys. Soc. Jpn. 2009, 78, 114712. [Google Scholar] [CrossRef]
  21. Yanagi, H.; Watanabe, T.; Kodama, K.; Iikubo, S.; Shamoto, S.; Kamiya, T.; Hirano, M.; Hosono, H. Antiferromagnetic bipolar semiconductor LaMnPO with ZrCuSiAs-type structure. J. Appl. Phys. 2009, 105. [Google Scholar] [CrossRef]
  22. Yanagi, H.; Kawamura, R.; Kamiya, T.; Kamihara, Y.; Hirano, M.; Nakamura, T.; Osawa, H.; Hosono, H. Itinerant ferromagnetism in the layered crystals LaCoOX (X = P,As). Phys. Rev. B 2008, 77. [Google Scholar] [CrossRef]
  23. Watanabe, T.; Yanagi, H.; Kamiya, T.; Kamihara, Y.; Hiramatsu, H.; Hirano, M.; Hosono, H. Nickel-Based Oxyphosphide Superconductor with a Layered Crystal Structure, LaNiOP. Inorg. Chem. 2007, 46, 7719–7721. [Google Scholar] [CrossRef] [PubMed]
  24. Ning, F.; Ahilan, K.; Imai, T.; Sefat, A.S.; Jin, R.; McGuire, M.A.; Sales, B.C.; Mandrus, D. 59Co and 75As NMR Investigation of Electron-Doped High Tc Superconductor BaFe1.8Co0.2As2 (Tc = 22 K). J. Phys. Soc. Jpn. 2008, 77. [Google Scholar] [CrossRef]
  25. Tucker, G.S.; Pratt, D.K.; Kim, M.G.; Ran, S.; Thaler, A.; Granroth, G.E.; Marty, K.; Tian, W.; Zarestky, J.L.; Lumsden, M.D.; et al. Competition between stripe and checkerboard magnetic instabilities in Mn-doped BaFe2As2. Phys. Rev. B 2012, 86. [Google Scholar] [CrossRef]
  26. Thaler, A.; Hodovanets, H.; Torikachvili, M.S.; Ran, S.; Kracher, A.; Straszheim, W.; Yan, J.Q.; Mun, E.; Canfield, P.C. Physical and magnetic properties of Ba(Fe1−xMnx)2As2 single crystals. Phys. Rev. B 2011, 84. [Google Scholar] [CrossRef]
  27. Mizuhashi, K.; Takenaka, K.; Fukuzumi, Y.; Uchida, S. Effect of Zn doping on charge transport in YBa2Cu3O7-δ. Phys. Rev. B 1995, 52, R3884–R3887. [Google Scholar] [CrossRef]
  28. Analytis, J.G.; Chu, J.-H.; Erickson, S.; Kucharczyk, C.; Serafin, A.; Carrington, A.; Cox, C.; Kauzlarich, S.M.; Hope, H.; Fisher, I.R. Bulk superconductivity and disorder in single crystals of LaFePO. arXiv:0810.5368v3.
  29. Sato, M.; Kobayashi, Y.; Lee, S.C.; Takahashi, H.; Satomi, E.; Miura, Y. Studies of Effects of Impurity Doping and NMR Measurements of La 1111 and/or Nd 1111 Fe-Pnictide Superconductors. J. Phys. Soc. Jpn. 2010, 79. [Google Scholar] [CrossRef]
  30. Satomi, E.; Lee, S.C.; Kobayashi, Y.; Sato, M. Superconducting Transition Temperatures and Transport Properties of LaFe1-yRuyAsO0.89F0.11 and LaFeAsO0.89-xF0.11+x. J. Phys. Soc. Jpn. 2010, 79. [Google Scholar] [CrossRef]
  31. Kawamata, T.; Satomi, E.; Kobayashi, Y.; Itoh, M.; Sato, M. Study of Ni-Doping Effect of Specific Heat and Transport Properties for LaFe1-yNiyAsO0.89F0.11. J. Phys. Soc. Jpn. 2011, 80. [Google Scholar] [CrossRef]
  32. Guo, Y.F.; Shi, Y.G.; Yu, S.; Belik, A.A.; Matsushita, Y.; Tanaka, M.; Katsuya, Y.; Kobayashi, K.; Nowik, I.; Felner, I.; et al. Large decrease in the critical temperature of superconducting LaFeAsO0.85 compounds doped with 3% atomic weight of nonmagnetic Zn impurities. Phys. Rev. B 2010, 82. [Google Scholar] [CrossRef]
  33. Miyasaka, S.; Takemori, A.; Kobayashi, T.; Suzuki, S.; Saijo, S.; Tajima, S. Two Fermi Surface States and Two Tc-Rising Mechanisms Revealed by Transport Properties in RFeP1-xAsxO0.9F0.1 (R = La, Pr, and Nd). J. Phys. Soc. Jpn. 2013, 82. [Google Scholar] [CrossRef]
  34. Lai, T.; Takemori, A.; Miyasaka, S.; Engetsu, F.; Mukuda, H.; Tajima, S. Evolution of the phase diagram of LaFeP1−xAsxO1−yFy (y = 0–0.1). Phys. Rev. B 2014, 90. [Google Scholar] [CrossRef]
Symmetry 08 00080 g001 1024
Figure 1. Temperature (T) dependence of electrical resistivity (ρ) for LaFe1−xMxPO0.95F0.05 with various doping levels (x = 0–0.10) of (a) M = Mn, (b) Co and (c) Ni in the wide T-region of T < 300 K. The scale of the vertical axis of panel (a) is different from the others.
Figure 1. Temperature (T) dependence of electrical resistivity (ρ) for LaFe1−xMxPO0.95F0.05 with various doping levels (x = 0–0.10) of (a) M = Mn, (b) Co and (c) Ni in the wide T-region of T < 300 K. The scale of the vertical axis of panel (a) is different from the others.
Symmetry 08 00080 g001
Symmetry 08 00080 g002 1024
Figure 2. Temperature (T) dependence of electrical resistivity (ρ) for LaFe1−xMxPO0.95F0.05 with various xs of (a) M = Mn; (b) Co and (c) Ni below 10 K, respectively.
Figure 2. Temperature (T) dependence of electrical resistivity (ρ) for LaFe1−xMxPO0.95F0.05 with various xs of (a) M = Mn; (b) Co and (c) Ni below 10 K, respectively.
Symmetry 08 00080 g002
Symmetry 08 00080 g003 1024
Figure 3. (a) x dependence of Tcons for LaFe1-xMxPO0.95F0.05 with M = Mn (red circles), Co (blue squares) and Ni (green triangles), respectively. The broken lines indicate linear fitting results; (b) x dependence of residual resistivity (ρ0) in the normal state for SC (open symbols) and non-SC (closed ones) samples. The resistivity for the 3% Co-doped sample shows a small drop due to resistive transition at low temperatures, as seen in Figure 2b. The low-temperature drop of resistivity for this sample is too small to determine Tcons by using the definition of Tcons in the present work. In this figure, we regard the 3% Co-doped sample as the non-SC one, but this sample may show an SC transition below 1.8 K.
Figure 3. (a) x dependence of Tcons for LaFe1-xMxPO0.95F0.05 with M = Mn (red circles), Co (blue squares) and Ni (green triangles), respectively. The broken lines indicate linear fitting results; (b) x dependence of residual resistivity (ρ0) in the normal state for SC (open symbols) and non-SC (closed ones) samples. The resistivity for the 3% Co-doped sample shows a small drop due to resistive transition at low temperatures, as seen in Figure 2b. The low-temperature drop of resistivity for this sample is too small to determine Tcons by using the definition of Tcons in the present work. In this figure, we regard the 3% Co-doped sample as the non-SC one, but this sample may show an SC transition below 1.8 K.
Symmetry 08 00080 g003
Symmetry 08 00080 g004 1024
Figure 4. Temperature dependence of longitudinal magnetoresistance at a magnetic field of H = 7 T for LaFe0.95M0.05PO0.95F0.05 with M = Mn (red circles), Co (blue squares) and Ni (green triangles), respectively. Magnetoresistance Δρxx(7 T)/ρxx(0) = (ρxx(H = 7 T)-ρxx(H = 0 T))/ρxx(H = 0 T), here ρxx(H) is resistivity in H parallel to current. The solid lines are the guide for eyes.
Figure 4. Temperature dependence of longitudinal magnetoresistance at a magnetic field of H = 7 T for LaFe0.95M0.05PO0.95F0.05 with M = Mn (red circles), Co (blue squares) and Ni (green triangles), respectively. Magnetoresistance Δρxx(7 T)/ρxx(0) = (ρxx(H = 7 T)-ρxx(H = 0 T))/ρxx(H = 0 T), here ρxx(H) is resistivity in H parallel to current. The solid lines are the guide for eyes.
Symmetry 08 00080 g004

Share and Cite

MDPI and ACS Style

Miyasaka, S.; Suzuki, S.; Tajima, S. Superconducting Gap Symmetry of LaFeP(O,F) Observed by Impurity Doping Effect. Symmetry 2016, 8, 80. https://doi.org/10.3390/sym8080080

AMA Style

Miyasaka S, Suzuki S, Tajima S. Superconducting Gap Symmetry of LaFeP(O,F) Observed by Impurity Doping Effect. Symmetry. 2016; 8(8):80. https://doi.org/10.3390/sym8080080

Chicago/Turabian Style

Miyasaka, Shigeki, Sinnosuke Suzuki, and Setsuko Tajima. 2016. "Superconducting Gap Symmetry of LaFeP(O,F) Observed by Impurity Doping Effect" Symmetry 8, no. 8: 80. https://doi.org/10.3390/sym8080080

APA Style

Miyasaka, S., Suzuki, S., & Tajima, S. (2016). Superconducting Gap Symmetry of LaFeP(O,F) Observed by Impurity Doping Effect. Symmetry, 8(8), 80. https://doi.org/10.3390/sym8080080

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop