An Orthogonal Multi-Swarm Cooperative PSO Algorithm with a Particle Trajectory Knowledge Base
Abstract
:1. Introduction
2. PSO and Other PSO Variants
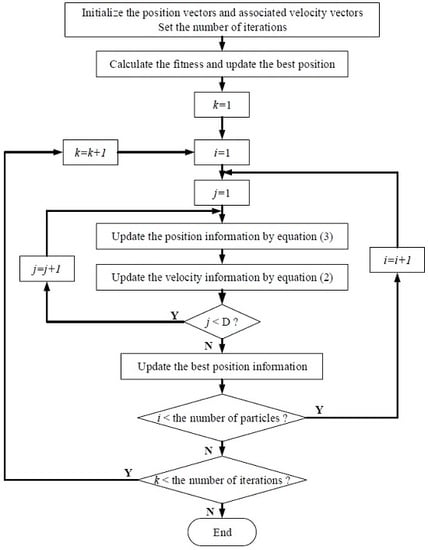
3. Multi-Swarm Orthogonal Cooperative PSO Algorithm with a Particle Trajectory Knowledge Base
3.1. Adaptive Cooperative Mechanism of Multi-Swarm Particles
3.2. Orthogonal Initialization Mechanism
3.3. Particle Trajectory Knowledge Base
3.4. Further Discussion about the MCPSO-K Model
4. Experiments and Analysis
4.1. Test Functions
4.2. Test on The Number of Computation on Similar Positions
4.3. Reliability and Accuracy of Algorithms
5. Conclusions
- (1)
- A new information interaction mechanism is conceived, which is similar to gravitational action mechanism in astrophysics field. In this way, the algorithm can update the velocity of each particle dynamically. In other words, there is an adaptive mechanism to control the searching speed based on the fitness value and the distance of swarms.
- (2)
- Our MCPSO-K adopts an orthogonal initialization method to guarantee the uniform distribution of particles in search space, which avoids local minimum value and the premature convergence.
- (3)
- To greatly decrease the computational cost, a matrix recording the information of particle trajectory is proposed and used during the iteration. By defining a reasonable error range, a group of particles whose variable combination are similar to the particles in the database can be assigned by the value in the matrix directly. Thus, the computational cost by repetitive searches and useless searches is decreased. The test results show that the introduction of the particle trajectory database can decrease the computation cost significantly without influencing the final convergence value.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the International Symposium on MICRO Machine and Human Science, Nagoya, Japan, 4–6 October 1995.
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995.
- Cheng, Q.; Zhan, C.; Liu, Z.; Zhao, Y.; Gu, P. Sensitivity-based Multidisciplinary Optimal Design of a Hydrostatic Rotary Table with Particle Swarm Optimization. Strojniski Vestnik 2015, 61, 432–447. [Google Scholar] [CrossRef]
- Zouache, D.; Nouioua, F.; Moussaoui, A. Quantum-inspired firefly algorithm with particle swarm optimization for discrete optimization problems. Soft Comput. 2016, 20, 2781–2799. [Google Scholar] [CrossRef]
- Lian, K.L.; Jhang, J.H.; Tian, I.S. A Maximum Power Point Tracking Method Based on Perturb-and-Observe Combined With Particle Swarm Optimization. IEEE J. Photovolt. 2014, 4, 626–633. [Google Scholar] [CrossRef]
- Bonyadi, M.R.; Michalewicz, Z. Locating Potentially Disjoint Feasible Regions of a Search Space with a Particle Swarm Optimizer; Springer: New Delhi, India, 2015; pp. 205–230. [Google Scholar]
- Abd-Elazim, S.M.; Ali, E.S. A hybrid particle swarm optimization and bacterial foraging for power system stability enhancement. Complexity 2015, 21, 245–255. [Google Scholar] [CrossRef]
- Tran, Q.A.; Quan, D.D.; Jiang, F. Binary Hybrid Particle Swarm Optimization with Wavelet Mutation. In Knowledge and Systems Engineering; Springer International Publishing: Cham, Switzerland, 2015; pp. 261–272. [Google Scholar]
- Yazdani, D.; Nasiri, B.; Sepas-Moghaddam, A.; Meybodi, M.R. A novel multi-swarm algorithm for optimization in dynamic environments based on particle swarm optimization. Appl. Soft Comput. 2013, 13, 2144–2158. [Google Scholar] [CrossRef]
- Gülcü, Ş.; Kodaz, H. A novel parallel multi-swarm algorithm based on comprehensive learning particle swarm optimization. Eng. Appl. Artif. Intell. 2015, 45, 33–45. [Google Scholar] [CrossRef]
- Dey, S.; Bhattacharyya, S.; Maulik, U. Quantum Behaved Multi-objective PSO and ACO Optimization for Multi-level Thresholding. In Proceedings of the International Conference on Computational Intelligence and Communication Networks, Bhopal, India, 14–16 November 2014.
- An, Z.Z.; Zhou, H.; Yang, Y.; Shi, X.L. A Study on Particle Trajectory of Particle Swarm Optimization. Appl. Mech. Mater. 2013, 433–435, 662–666. [Google Scholar] [CrossRef]
- Bonyadi, M.; Michalewicz, Z. Stability analysis of the particle swarm optimization without stagnation assumption. IEEE Trans. Evolut. Comput. 2016, 20, 814–819. [Google Scholar] [CrossRef]
- Chen, D.B.; Zhao, C.X. Particle swarm optimization with adaptive population size and its application. Appl. Soft Comput. 2009, 9, 39–48. [Google Scholar] [CrossRef]
- Jin’no, K.; Sano, R.; Saito, T. Particle swarm optimization with switched topology. Nonlinear Theory Its Appl. Ieice 2015, 6, 181–193. [Google Scholar] [CrossRef]
- Ayatollahi, F.; Shokouhi, S.B.; Ayatollahi, A. A new hybrid particle swarm optimization for multimodal brain image registration. J. Biomed. Sci. Eng. 2012, 5, 18508. [Google Scholar] [CrossRef]
- Van den Bergh, F.; Engelbrecht, A.P. A Cooperative approach to particle swarm optimization. IEEE Trans. Evolut. Comput. 2004, 8, 225–239. [Google Scholar] [CrossRef]
- Liang, J.J.; Suganthan, P.N. Dynamic multi-swarm particle swarm optimizer. In Proceedings of the Swarm Intelligence Symposium, Pasadena, CA, USA, 8–10 June 2005.
- Cheng, S.; Shi, Y. Diversity control in particle swarm optimization. In Proceedings of the Second International Conference on Swarm Intelligence, Chongqing, China, 12–15 June 2011.
- Trelea, I.C. The particle swarm optimization algorithm: convergence analysis and parameter selection. Inf. Process. Lett. 2003, 85, 317–325. [Google Scholar] [CrossRef]
- Ahila, R.; Sadasivam, V.; Manimala, K. An integrated PSO for parameter determination and feature selection of ELM and its application in classification of power system disturbances. Appl. Soft Comput. 2015, 32, 23–37. [Google Scholar] [CrossRef]
- Cazzaniga, P.; Nobile, M.S.; Besozzi, D. The impact of particles initialization in PSO: Parameter estimation as a case in point. In Proceedings of the IEEE Conference on Computational Intelligence in Bioinformatics and Computational Biology, Niagara Falls, ON, Canada, 12–15 August 2015.
- Liang, J.J.; Qin, A.K.; Baskar, S. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions. IEEE Trans. Evolut. Comput. 2006, 10, 281–295. [Google Scholar] [CrossRef]
- Branke, J.; Kaußler, T.; Smidt, C.; Schmeck, H. A Multi-population Approach to Dynamic Optimization Problems. In Evolutionary Design and Manufacture; Springer: London, UK, 2000; pp. 299–307. [Google Scholar]
- Li, C.; Yang, S. Fast Multi-Swarm Optimization for Dynamic Optimization Problems. In Proceedings of the 2008 Fourth International Conference on Natural Computation, ICNC ’08, Jinan, China, 18–20 October 2008.
- Mohais, A.S. Random Dynamic Neighborhood Structures in Particle Swarm Optimization. Ph.D. Thesis, University of the West Indies, Mona, Jamaica, 2008. [Google Scholar]
- Huang, T.; Mohan, A.S. Significance of neighborhood topologies for the reconstruction of microwave images using particle swarm optimization. In Proceedings of the 2005 Asia-Pacific Microwave Conference, Suzhou International Conference Center, Suzhou, China, 4–7 December 2005; p. 4.
- Kennedy, J. Small worlds and mega-minds: Effects of neighborhood topology on particle swarm performance. In Proceedings of the 1999 Congress on Evolutionary Computation, CEC ’99, Washington, DC, USA, 6–9 July 1999.
- Kennedy, J.; Mendes, R. Population structure and particle swarm performance. In Proceedings of the 2002 Congress on Evolutionary Computation, CEC ’02, Honolulu, HI, USA, 12–17 May 2002.
- Hu, X.; Eberhart, R. Multiobjective optimization using dynamic neighborhood particle swarm optimization. In Proceedings of the 2002 Congress on Evolutionary Computation, CEC ’02, Honolulu, HI, USA, 12–17 May 2002.
- Wang, Q.-H.; Tong, Q.; Han, J.-J.; Bao, B.-Y.-M.Q.-E.; Wu, J.-S.; Han, N.-R.-C.-K.-T.; Dai, N.-Y.-T.; Wu, R.-J. Orthogonal test design for optimization of the isolation and purification of total favonoids from Artemisia frigida Willd using macroporous resin chromatography. Afr. J. Pharm. Pharmacol. 2016, 10, 192–199. [Google Scholar] [CrossRef]



















| The Implementation Process of MCPSO |
| n: the number of swarms p: each swarm’s population size h: information exchange frequency in swarm level and specific iterative node for orthogonal initialization Max_gen: max number of generations for stopping criteria : evaluation index for similarity between particles : adaptive index for similarity evaluation index = []: the number of partition in each dimension Implementation sensitivity analysis on a m dimensional optimization problem Determine the value of = [] Determine an orthogonal combination of parameters value interval based on the sensitivity analysis Create n swarms and each swarm has p particles Initialize particles and create a trajectory database base on the fitness value of particles For j = 1 to h For i = 1 to For i = 1 to n Update the position of each particle in swarm i and calculate the fitness value Calculate the similarity index for each particle If the similarity index calculated above Update the fitness value of particle by the trajectory database End Update the trajectory database End Update the position of each particle by the cooperative mechanism defined by Equations (4)–(13) Execute the orthogonal initialization operation Update the best fitness of n swarms End End Output the best fitness value |
| Function | n | Stopping Criteria | |
|---|---|---|---|
| Iteration | Threshold | ||
| 20 | 500 | 100 | |
| 20 | 500 | 0.01 | |
| 20 | 500 | 5.00 | |
| 20 | 500 | 100 | |
| 20 | 500 | 0.1 | |
| Function | Similar Computation | Identical Computation | |||
|---|---|---|---|---|---|
| Criteria | ≤10 | ≤5 | ≤1 | ≤0.5 | ≤0.1 |
| 342.1/5010 | 232.7/5010 | 55.8/5010 | 33/5010 | 0/5010 | |
| 1055.5/10,020 | 683.6/10,020 | 19.7/10,020 | 0.8/10,020 | 0/10,020 | |
| 362.6/20,020 | 560.2/20,020 | 17.8/20,020 | 440.2/20,020 | 0.4/20,020 | |
| 1424/6000 | 1719.8/6000 | 490.3/6000 | 756.3/6000 | 0.7/6000 | |
| 1775.9/10,020 | 1198.8/10,020 | 402.4/10,020 | 352/10,020 | 0/10,020 | |
| Function | ITERATION | ||
|---|---|---|---|
| 50 | 150 | 250 | |
| Function | The Final Convergence Value |
|---|---|
| 6005 | |
| 5.138 | |
| 20.28 | |
| 551.7 | |
| 0.0103 |
| Function | ITERATION | ||
|---|---|---|---|
| 50 | 150 | 250 | |
| Function | The Final Convergence Value |
|---|---|
| 1346 | |
| 2.138 | |
| 0.7105 | |
| 551.7 | |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Zhu, H.; Wang, Y. An Orthogonal Multi-Swarm Cooperative PSO Algorithm with a Particle Trajectory Knowledge Base. Symmetry 2017, 9, 15. https://doi.org/10.3390/sym9010015
Yang J, Zhu H, Wang Y. An Orthogonal Multi-Swarm Cooperative PSO Algorithm with a Particle Trajectory Knowledge Base. Symmetry. 2017; 9(1):15. https://doi.org/10.3390/sym9010015
Chicago/Turabian StyleYang, Jun, Haihua Zhu, and Yingcong Wang. 2017. "An Orthogonal Multi-Swarm Cooperative PSO Algorithm with a Particle Trajectory Knowledge Base" Symmetry 9, no. 1: 15. https://doi.org/10.3390/sym9010015
APA StyleYang, J., Zhu, H., & Wang, Y. (2017). An Orthogonal Multi-Swarm Cooperative PSO Algorithm with a Particle Trajectory Knowledge Base. Symmetry, 9(1), 15. https://doi.org/10.3390/sym9010015