Algebraic Aspects of the Supersymmetric Minimal Surface Equation
Abstract
:1. Introduction
2. Supersymmetric Version of the Minimal Surface Equation
3. Lie Symmetries of the Supersymmetric Minimal Surface Equation

4. Classification of Subalgebras for the Lie Superalgebra
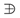 using the method of splitting and non-splitting subalgebras [29]. The splitting subalgebras of are formed by combining the dilation or the trivial element with each of the subalgebras of in a semidirect sum of the form F
using the method of splitting and non-splitting subalgebras [29]. The splitting subalgebras of are formed by combining the dilation or the trivial element with each of the subalgebras of in a semidirect sum of the form F 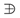 N, where or and N is a subalgebra of the classification of . The splitting one-dimensional subalgebras of are the combined subalgebras to listed in Equations (26), (27), (29) and (31) together with the subalgebra . For non-splitting subalgebras, we consider spaces of the form:
N, where or and N is a subalgebra of the classification of . The splitting one-dimensional subalgebras of are the combined subalgebras to listed in Equations (26), (27), (29) and (31) together with the subalgebra . For non-splitting subalgebras, we consider spaces of the form:5. Symmetry Group Reductions and Solutions of the SUSY Minimal Surface Equation
5.1. Translation-Invariant Solutions
5.2. Scaling-Invariant Solution
6. Group Analysis of the Classical Minimal Surface Equation
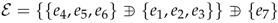
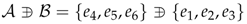
 are conjugate to an element of the list , where m is any real number. Finally, if we consider the full Lie algebra , we also obtain the subalgebra . Thus, the full classification of the one-dimensional subalgebras of :
are conjugate to an element of the list , where m is any real number. Finally, if we consider the full Lie algebra , we also obtain the subalgebra . Thus, the full classification of the one-dimensional subalgebras of :7. Final Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Aitchison, I. Supersymmetry in Particle Physics; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Labelle, P.; Mathieu, P. A new N = 2 supersymmetric Korteweg-de Vries equation. J. Math. Phys. 1991, 32, 923–927. [Google Scholar] [CrossRef]
- Barcelos-Neto, J.; Constandache, A.; Das, A. Dispersionless fermionic KdV. Phys. Lett. A 2000, 268, 342–351. [Google Scholar] [CrossRef]
- Tan, K.; Liu, Q.P. A supersymmetric Sawada-Kotera equation. Phys. Lett. A 2009, 373, 1807–1810. [Google Scholar]
- Das, A.; Popowicz, Z. Supersymmetric polytropic gas dynamics. Phys. Lett. A 2002, 296, 15–26. [Google Scholar] [CrossRef]
- Grundland, A.M.; Hariton, A.J. Supersymmetric formulation of polytropic gas dynamics and its invariant solutions. J. Math. Phys. 2011, 52, 043501. [Google Scholar] [CrossRef]
- Grundland, A.M.; Hariton, A.J. Supersymmetric version of a Gaussian irrotational compressible fluid flow. J. Phys. A Math. Theor. 2007, 40, 15113–15129. [Google Scholar] [CrossRef]
- Henkel, M.; Unterberger, J. Supersymmetric extensions of Schrödinger-invariance. Nucl. Phys. B 2006, 746, 155–201. [Google Scholar] [CrossRef]
- Grammaticos, B.; Ramani, A.; Carstea, A.S. Bilinearization and soliton solutions for the N = 1 supersymmetric sine-Gordon equation. J. Phys. A Math. Gen. 2001, 34, 4881–4886. [Google Scholar] [CrossRef]
- Gomes, J.F.; Ymai, L.H.; Zimerman, A.H. Permutability of Backlund transformation for N = 1 supersymmetric sinh-Gordon equation. Phys. Lett. A 2009, 373, 1401–1404. [Google Scholar] [CrossRef]
- Grundland, A.M.; Hariton, A.J.; Snobl, L. Invariant solutions of the supersymmetric sine-Gordon equation. J. Phys. A Math. Theor. 2009, 42, 335203. [Google Scholar] [CrossRef]
- Jackiw, R. A Particle Theorist’s Lectures on Supersymmetric Non-Abelian Fluid Mechanics and d-Branes; Springer: New York, NY, USA, 2002. [Google Scholar]
- Bianchi, L. Lezioni di Geometria Differentiale, 2nd ed.; Spoerri: Pisa, Italy, 1902. [Google Scholar]
- Spivak, M. A Comprehensive Introduction to Differential Geometry; Publish or Perish Inc.: Houston, TX, USA, 1979. [Google Scholar]
- Lamb, H. Hydrodynamics; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Chandrasekhar, S. Hydrodynamic and Hydromagnetic Stability; Dover: New York, NY, USA, 1981. [Google Scholar]
- Nelson, D.; Piran, T.; Weinberg, S. Statistical Mechanics of Membranes and Surfaces; World Scientific: Singapore, 1992. [Google Scholar]
- David, F.; Ginsparg, P.; Zinn-Justin, Y. Fluctuating Geometries in Statistical Mechanics and Field Theory; Elsevier: Amsterdam, The Netherlands, 1996. [Google Scholar]
- Chen, F. Introduction to Plasma Physics and Controlled Fusion, Volume 1: Plasma Physics; Plenum Press: New York, NY, USA, 1983. [Google Scholar]
- Luneburg, R.K. Mathematical Theory of Optics; University California Press: Berkeley, CA, USA, 1964. [Google Scholar]
- Davidov, A. Solitons in Molecular Systems; Kluwer: New York, NY, USA, 1991. [Google Scholar]
- Ou-Yang, Z.; Liu, J.; Xie, Y. Geometric Methods in the Elastic Theory of Membranes in Liquid Crystal Phases; World Scientific: Singapore, 1999. [Google Scholar]
- Whitham, G.B. Linear and Nonlinear Waves; John Wiley Publishing: New York, NY, USA, 1974. [Google Scholar]
- Manno, G.; Oliveri, F.; Vitolo, R. On differential equations characterized by their Lie point symmetries. J. Math. Anal. Appl. 2007, 332, 767–786. [Google Scholar] [CrossRef]
- Freed, D.S. Five Lectures on Supersymmetry; AMS: New York, NY, USA, 1999. [Google Scholar]
- Varadarajan, V.S. Reflections on Quanta, Symmetries and Supersymmetries; Springer: New York, NY, USA, 2011. [Google Scholar]
- Olver, P.J. Applications of Lie Groups to Differential Equations; Springer: New York, NY, USA, 1986. [Google Scholar]
- Bertrand, S.; Grundland, A.M.; Hariton, A.J. Supersymmetric versions of the equations of conformally parametrized surfaces. J. Phys. A Math. Theor. 2015, 48, 175208. [Google Scholar] [CrossRef]
- Winternitz, P. Lie Groups and Solutions of Nonlinear Partial Differential Equations. In Integrable Systems, Quantum Groups and Quantum Field Theories; Ibort, L.A., Rodriguez, M.A., Eds.; Kluwer: Dordrech, The Netherlands, 1993; p. 429. [Google Scholar]
- Goursat, E. Sur les substitutions orthogonales et les divisions régulières de l’espace. Ann. Sci. Ecole Norm. Supér. 1880, 6, 9–102. [Google Scholar] [CrossRef]
- Byrd, P.F.; Friedman, M.D. Handbook of Elliptic Integrals for Engineers and Scientists; Springer: Berlin, Germany, 1971. [Google Scholar]
- Bila, N. Lie groups applications to minimal surfaces PDE. Differ. Geom. Dyn. Syst. 1999, 1, 1–9. [Google Scholar]
- Patera, J.; Winternitz, P. Subalgebras of real three- and four-dimensional Lie algebras. J. Math. Phys. 1977, 18, 1–9. [Google Scholar] [CrossRef]
| D | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0 | ||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 0 | 0 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | ||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 0 | 0 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | ||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grundland, A.M.; Hariton, A. Algebraic Aspects of the Supersymmetric Minimal Surface Equation. Symmetry 2017, 9, 318. https://doi.org/10.3390/sym9120318
Grundland AM, Hariton A. Algebraic Aspects of the Supersymmetric Minimal Surface Equation. Symmetry. 2017; 9(12):318. https://doi.org/10.3390/sym9120318
Chicago/Turabian StyleGrundland, Alfred Michel, and Alexander Hariton. 2017. "Algebraic Aspects of the Supersymmetric Minimal Surface Equation" Symmetry 9, no. 12: 318. https://doi.org/10.3390/sym9120318
APA StyleGrundland, A. M., & Hariton, A. (2017). Algebraic Aspects of the Supersymmetric Minimal Surface Equation. Symmetry, 9(12), 318. https://doi.org/10.3390/sym9120318




