Minimal-Entanglement Entanglement-Assisted Quantum Error Correction Codes from Modified Circulant Matrices

Abstract

In this paper, new construction methods of entanglement-assisted quantum error correction code (EAQECC) from circulant matrices are proposed. We first construct the matrices from two vectors of constraint size, and determine the isotropic subgroup. Then, we also propose a method for calculation of the entanglement subgroup based on standard forms of binary matrices to satisfy the constraint conditions of EAQECC. With isotropic and entanglement subgroups, we determine all the parameters and the minimum distance of the EAQECC. The proposed EAQECC with small lengths are presented to explain the practicality of this construction of EAQECC. Comparison with some earlier constructions of EAQECC shows that the proposed EAQECC is better.

1. Introduction

The theory of quantum information is a result of the effort to generalize classical information theory. However, an aspect that is commonly tacitly referred to the background, is the reversible character of the quantum mechanical processes, underlying the computations [1]. An important milestone in quantum computations occurred in 1994 when Shor published computationally efficient quantum algorithms for factoring integers and for evaluating discrete logarithms [2]. With these algorithms, the owner of a quantum computer could crack popular, highly utilized public key cryptosystems. In addition, Grover [3] discovered a quantum algorithm for the important problem of searching an unstructured database, which yields a substantial speed-up over classical search algorithms. Hence, performance of these quantum algorithms promised a great deal. However, the effects of noise and imperfectly applied quantum gates would quash their performance advantages [4]. To deal with the problems, the theory of quantum error correction codes was developed to protect quantum states against noise. Discoveries of 9-qubit codes by Shor [5] and 7-qubit codes by Steane [6] showed how data could be protected by containing more redundancy after encoding by quantum systems; these were the first examples of quantum error correction code (QECC). The purpose of QECC is to encode a k-qubit state into an n-qubit state, such that all 2^k complex coefficients are perfectly stored and used to correct errors.

Stabilizer codes, first introduced by Gottesman [7], have become an important class of QECC, since these codes are useful for building quantum fault-tolerant circuits [8]. Stabilizer codes append ancilla qubits to qubits to be protected, and the most important advantage of stabilizer codes is that errors can be detected and removed from stabilizer operators, rather than from the quantum state itself. In addition, the stabilizer formalism allows us to construct quantum stabilizer codes from binary matrices over binary in the constraint referred to as the symplectic inner product (SIP) [7]. With Calderbank-Shor-Steane (CSS)-based construction [9], the problem turned out to be utilizing self-orthogonal classical codes. However, self-orthogonal codes with high error-correcting capacity are restricted, and therefore, further investigation was required to generate good stabilizer codes. Introduction of entanglement-assisted quantum error correction code (EAQECC) by Brun et al. [10] is one answer to this problem. More precisely, it enables us to construct the quantum error-correction codes not only from self-orthogonal classical codes, but also from arbitrary classical codes with the help of copies of maximally entangled quantum states shared between encoder and decoder. To design efficient EAQECC, however, it is desirable to use the fewest entangled states possible, because the cost to prepare those states is relatively high. Hence, the construction of EAQECC with small amounts of entangled states is a much more attractive issue [10,11]. Therefore, several constructions of EAQECC have been proposed, such as construction from arbitrary matrices where the number of ebits is determined by parameters of classical codes [12], from low-density parity-check (LDPC) codes [11], from generalized quadrangles [13], from circulant permutation matrices [14], and from shortened Hamming codes [15]. Almost all existing constructions consider classical codes to calculate the number of ebits. To do so, the problem of transforming the classical form to basic form of EAQECC was proposed in the Gram–Schmidt procedure. This aims to classify the classical form into isotropic and entanglement subgroups, but the complexity of the Gram–Schmidt procedure also increases in proportion to the length of the codes [16]. Furthermore, the encoding transforms the non-commuting set of generators into its canonical form [17]. Then, quantum circuits composed of CNOT, H, and S gates can be derived directly with complexity O(n²). The canonical form gives the relationship between EAQECC and quantum stabilizer codes, even though we can use the property of the stabilizer code that is useful for fault-tolerant computation [18].

The key result of this paper is to propose novel approaches to construction of EAQECC. First, we propose a new method for the construction of the isotropic subgroup based on circulant matrices. Then, the entanglement subgroup can be determined from a method of transforming the isotropic group into standard form; hence, the parameters of codes are found, and for effective preparation of the entangled state, the number of ebits should be as few as possible. To explain the practical construction of the quantum codes, design of the proposed EAQECC with lengths up to 12 are shown. In addition, the minimum distance is calculated and explained to show that the proposed construction has good correctable capability, in comparison with recent EAQECC. The organization of this paper is as follows. In Section 2, we review the theory of quantum mechanics, the role of quantum stabilizer codes in quantum error correction, and the constraints on the construction of EAQECC. In Section 3, we propose the construction of two new types of circulant matrices. Following that, we construct the isotropic subgroup, and the calculation for entanglement subgroups is proposed. From the subgroup of isotropic and entanglement, parameters and minimum distances of EAQECC have been determined. Finally, conclusions are presented in Section 4.

2. Background

In this section, we give some preliminary explanations about quantum mechanics, quantum error correction codes, and the entanglement-assisted quantum stabilizer codes used throughout the paper.

2.1. Introduction to Quantum Mechanics

The bit is the fundamental concept of classical computation and classical information. Quantum computation and quantum information are built upon an analogous concept, the quantum bit, or qubit for short [4]. Then, just as the classical bit has a state (either 0 or 1), the state in a quantum system is instead a vector over the complex number C; the state denoted as $|\psi \rangle$ = α$|0\rangle$ + β$|1\rangle$ can be considered to have both values of $|0\rangle$ and $|1\rangle$ at the same time, where the probability of value $|0\rangle$ and $|1\rangle$ are |α|² and |β|² respectively. This concept, known as superposition, is the main property of quantum computation, since it allows gate operations to deal with several values in one step. Hence, the amount of information that can be represented is infinite. A qubit can be represented in vector form:

$$|\psi \rangle =\alpha |0\rangle +\beta |1\rangle =\alpha \left[\begin{array}{c}1\\ 0\end{array}\right]+\beta \left[\begin{array}{c}0\\ 1\end{array}\right]=\left[\begin{array}{c}\alpha \\ \beta \end{array}\right].$$

According to the probability, the condition |α|² + |β|² = 1 must be satisfied. A quantum memory register is a physical system composed of n qubits, that is, multiples of the tensor product of some qubits. Generally, the n-qubit state is denoted as:

$$|\psi \rangle ={\displaystyle {\sum }_{i_k=\{0,1\}}{\alpha }_{i_1{i}_2...i_n}|i_1\rangle \otimes |i_2\rangle \otimes ...\otimes |i_n\rangle }={\displaystyle {\sum }_i{\alpha }_i|i\rangle },$$

where $i={\displaystyle {\sum }_{k=1}^n{2}^{n-k}{i}_k}$. Hence, a state vector of an n-qubit quantum system is considered a superposition of the states that make up a base in a 2ⁿ dimensional complex Hilbert space, H^⊗n.

A particularly fruitful way to understand a quantum system is to look at the behavior of various operators acting on the states of the system. Quantum information processing requires unitary transformations operating on states. For example, Pauli operators are one of the unitary transformations. The single Pauli operators (matrices) I, X, Y, and Z are represented as

$$I=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right],X=\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right],Y=\left[\begin{array}{cc}0& -j\\ j& 0\end{array}\right],Z=\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]$$

where $j=\sqrt{-1}$. The Pauli operation acts on the qubit as follows:

$$\begin{array}{l}I|\psi \rangle =\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]\times \left[\begin{array}{c}\alpha \\ \beta \end{array}\right]=\left[\begin{array}{c}\alpha \\ \beta \end{array}\right]=\alpha |0\rangle +\beta |1\rangle ,X|\psi \rangle =\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right]\times \left[\begin{array}{c}\alpha \\ \beta \end{array}\right]=\left[\begin{array}{c}\beta \\ \alpha \end{array}\right]=\beta |0\rangle +\alpha |1\rangle ,\hfill \\ Z|\psi \rangle =\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]\times \left[\begin{array}{c}\alpha \\ \beta \end{array}\right]=\left[\begin{array}{c}\alpha \\ -\beta \end{array}\right]=\alpha |0\rangle -\beta |1\rangle ,Y|\psi \rangle =\left[\begin{array}{cc}0& -j\\ j& 0\end{array}\right]\times \left[\begin{array}{c}\alpha \\ \beta \end{array}\right]=\left[\begin{array}{c}-j\beta \\ j\alpha \end{array}\right]=j(-\beta |0\rangle +\alpha |1\rangle ).\hfill \end{array}$$

Thus, the Pauli operators X, Z, and Y are regarded as a bit flip, a phase flip, and a combination of bit and phase flips, respectively. Multiplication of two Pauli operators satisfies the following equations.

$$\begin{array}{c}{X}^2=Y^2=Z^2=I;\hfill \\ X\times Y=jZ;Y\times X=-jZ\to X\times Y=-Y\times X;\hfill \\ Y\times Z=jX;Z\times Y=-jX\to Y\times Z=-Z\times Y;\hfill \\ Z\times X=jY;X\times Z=-jY\to Z\times X=-X\times Z.\hfill \end{array}$$

The single Pauli group P₁ is a group formed by the Pauli operators, which is closed under multiplication. Therefore, the Pauli group consists of all the Pauli matrices, together with the multiplicative factors ±1, ±j. We have: P₁ = ±{I, jI, X, jX, Y, jY, Z, jZ}. The n-fold tensor product of single Pauli operators forms an n-qubit Pauli group P_n. The main property of P_n is that any two elements, $A,B\in P_n$, either commute or anti-commute. For n-qubit Pauli operators $A,B\in P_n$, the operator ◦ for commutativity is defined as

$$A\circ B={\displaystyle {\prod }_{i=1}^n{A}_i•B_i},\mathrm{where}{A}_i•B_i=\{\begin{array}{c}+1,\mathrm{if}{A}_i\times B_i=B_i\times A_i\hfill \\ -1,\mathrm{if}{A}_i\times B_i=-B_i\times A_i\hfill \end{array}$$

The two operators A and B are commutative if and only if A◦B = +1; otherwise, they are anti-commutative. Commutativity is an important feature of the Pauli group, since this can be used to detect errors within the stabilizer formalism described in the next section.

2.2. Standard QECC: Stabilizers Code

Let $H^{\otimes n}=\left\{|\psi \rangle \right\}$ be the quantum state space of n qubits. A stabilizer group, S, closed under multiplication, is an Abelian subgroup of P_n, such that a non-trivial subspace, C_S of $H^{\otimes n}$, is fixed (or stabilized) by S. The stabilized C_S defines a quantum code space such that

$$C_{\mathit{S}}=\{|\psi \rangle \in H^{\otimes n}|g|\psi \rangle =|\psi \rangle ,\forall g\in \mathit{S}\}.$$

If S is generated by g = {g₁, g₂, …, g_m}, where g is m = n − k independent stabilizer operators, the code space C_S encodes k logical qubits into n physical qubits and can correct t = $⎿$(d_min − 1)/2$⏌$ errors. This code C_S is called [[n, k, d_min]] quantum stabilizer code. Note that quantum stabilizer code C_S has the following features:

• $-I\notin \mathit{S}.$
• For any two stabilizers $E,F\in S,E\circ F=+1.$

Then, it is enough to check the commutative property of the generators of C_S: g = {g₁, g₂, …, g_m}; every two elements must be commutative to each other. Considering a set of error operators, $\left\{{\rm E}\right\}\subset P_n$, the collection of Pauli operators takes a state $|\psi \rangle$ to the corrupted state $E|\psi \rangle$. A given operator E either commutes or anti-commutes with each stabilizer S_i. Then, the corrupted state $E|\psi \rangle$ is diagnosed by elements S_i of the set S. The outcome of the diagnostic procedure is a vector, {+1, −1}, indicating whether E can be detected or not. The indication for the error detection is expressed as follows:

$${\mathit{S}}_i\times E|\psi \rangle =\{\begin{array}{cc}\hfill E\times {\mathit{S}}_i|\psi \rangle =E|\psi \rangle ,& \mathrm{Error}\mathrm{undetected}.\hfill \\ \hfill -E\times {\mathit{S}}_i|\psi \rangle =-E|\psi \rangle ,& \mathrm{Error}\mathrm{detected}.\hfill \end{array}$$

The condition for quantum error correction is that E is a set of correctable error operators for C_S if

$$E_i{}^{†}{E}_j\notin N(\mathit{S})\backslash \mathit{S},\forall E_i,E_j\in E,$$

where ${E_i}^{†}$ is the conjugate transpose of E_i, and N(S) is the normalizer of S in P_n, such as

$$N(\mathit{S})=\{A\in P_n|A^{†}EA\in \mathit{S},\forall E\in \mathit{S}\}.$$

Note that N(S) is the collection of all operators in P_n that commute with S, and $\mathit{S}\subset P_n$. Then, minimum distance d_min of stabilizer code is determined by

$$d_{\min }=\min \{\mathrm{W}(E)\} \mathrm{s}.\mathrm{t}. E\in N(\mathit{S})\backslash \mathit{S},$$

where the weight of an operator, W(*), is the number of positions not equal to Pauli operator I.

Quantum stabilizer codes can be expressed in the binary field, since any given Pauli operator on n qubits can be composed into an X–containing operator and a Z–containing operator, as well as a phase factor, $\{\pm 1,\pm j\}$. This is achieved by mapping I, X, Y, Z as follows: $I\to (0,0);X\to (1,0)$ and $Y\to (1,1);Z\to (0,1)$. Then, the (n − k) generators of an [[n, k]] stabilizer code can be expressed as a concatenation of a pair of $(n-k)\times n$ binary matrices, H_X, H_Z. Then, the parity-check matrix H of the quantum stabilizer code is defined as

$$H=[H_X|H_Z].$$

(1)

The commutative property of the stabilizers can be transformed into the orthogonality of rows in the matrix forms with respect to the symplectic product. If the m-th row, r_m, is expressed as r_m = [x_m | z_m], where z_m and x_m are binary strings for Z and X, respectively, then the symplectic product of the m₁ row and m₂ row in the parity-check matrix H in (1) is expressed as

$$r_{m_1}\odot r_{m_2}=[x_{m_1}|z_{m_1}]\odot [x_{m_2}|z_{m_2}]=x_{m_1}\ast z_{m_2}+x_{m_2}\ast z_{m_1}\mathrm{modulo}2,$$

where $x_k\ast z_l={\displaystyle {\sum }_{i=1}^n{x}_{ki}}\times z_{li}$. The symplectic product between two rows is zero if the total number of positions with different values in X and Z is even. This condition is also needed to satisfy the commutativity property. In other words, for a binary matrix, size $(n-k)\times 2n$, H = [H_X | H_Z], the symplectic product is satisfied for all rows if and only if

$$H_X\times H_Z{}^T+H_Z\times H_X{}^T=0_{n-k}\mathrm{modulo}2$$

(2)

where $0_a$ is the $a\times a$ zero matrix. (2) is the SIP condition, which can be used to determine generators of stabilizer codes.

2.3. Entanglement-Assisted Quantum Error Correction Code

An EAQECC is an extension of quantum stabilizer codes with parameter [[n, k, d_min; c]]. Like classical coding theory, it also encodes k logical qubits into n physical qubits but with the help of c copies of maximally entangled Bell states. It has been shown that EAQECCs have considerable advantages over standard quantum stabilizer codes from pre-existing entanglement between transmitter and receiver to improve the reliability of transmission. In addition, while quantum stabilizer codes based on CSS can use dual-containing classical linear binary or quaternary code, non-self-orthogonal codes can be transformed into an EAQECCs.

Let a size of a group be the number of elements in the group. If S is the non-Abelian in Pauli group P_n of size m, then there exists a set of generators for S of the form {Z₁, Z₂, …, Z_s+c, X_s+1, X_s+2, …, X_s+c} (where s + c = m) with the following commutation properties:

$$\{\begin{array}{c}[Z_i,Z_j]=0\mathrm{and}[X_i,X_j]=0\mathrm{for}\mathrm{all}i,j;\hfill \\ [X_i,Z_j]=0\mathrm{for}\mathrm{all}i\ne j;\hfill \\ \{X_i,Z_i\}=0\mathrm{for}\mathrm{all}i,\hfill \end{array}$$

(3)

where [A, B] and {A, B} are a commutator and a anti-commutator of generator A and B, respectively. The [A, B] and {A, B} of generator A and B can be expressed as A × B − B × A and A × B + B × A, respectively. Then, the non-Abelian group can be partitioned into:

• a commuting subgroup, the isotropic group S_I = {Z_c+1, Z_c+2, …, Z_c+s}.
• entanglement subgroup pairs S_E = {Z₁, Z₂, …, Z_c, X₁, X₂, …, X_c} with anti-commuting pairs; the anti-commuting pairs (Z_i, X_i) being shared between source and receiver.

The Gram–Schmidt procedure to drop the non-Abelian group into the partitions of operators with the above properties (called the isotropic and entanglement subgroup) was introduced and discussed [10]. From the isotropic and entanglement subgroup, EAQECC code C_EA are defined as [[n, k; c]] that encodes k = n − s − c qubits into n physical qubits with the help of s = n − k − c ancillas qubits and c ebits shared between the sender and receiver, that can correct any error from the following set of errors, N:

$$N=\left\{E_m|\forall E_1,E_2\Rightarrow E_2{}^{†}{E}_1\in {\mathit{S}}_I\cup ({\mathrm{P}}_n-N(\mathit{S}))\right\}.$$

Code space C_EA is a simultaneous eigenspace of the Abelian extension of S [16]. The Abelian extension is Galois extension by using ancilla operators. From N, we can determine d_min, and it tells us the detectable and correctable EAQECCs.

From the isotropic and entanglement subgroup, the operation of EAQECC can be considered. For example, the following state shared between A (Alice) and B (Bob) is an entanglement state:

$$|\mathrm{\Phi }\rangle =\frac{1}{\sqrt{2}}\left(|0\rangle \otimes |0\rangle +|1\rangle \otimes |1\rangle \right)$$

The first half of the entanglement pair belongs to Alice and the second half to Bob. Then, the operating principle is illustrated in Figure 1 [16]. The Sender A encodes the quantum information state $|\psi \rangle$ with the help of local ancillary qubits $|0\rangle$ and her half of shared ebits, $|\mathrm{\Phi }\rangle$, and then shares the encoded qubits over a noisy quantum channel. The Receiver B performs multi-qubit measurement on all qubits to diagnose the channel error and perform recovery unitary operation R to reserve the action of the channel.

The most important relationship between EAQECCs and classical codes is given in the following theorem [10,12]:

Theorem 1.

Let C be a binary classical code [n, k, d] with parity check matrix H. We can obtain a corresponding [[n, 2k − n + c, d; c]] EAQECC, where $c=rank\left\{H{H}^T\right\}$ is the number of ebits needed.

As a consequence, there are lots of papers using this theorem for EAQECC construction. From binary code C with parameter [n, k, d] and the generator matrix G = [I_k | A_kx(n-k)], the EAQECC with [[2n − k, k, d’; c]] can be made [12], where c = 2n − 2k and d’ $\ge$ d. Tomas [13] used the generalized quadrangle GQ(s,1) for the construction of classical binary code and proved the number of ebits is 2. The circulant matrix $P_m=\left[\begin{array}{ccccc}0& 1& 0& \cdots & 0\\ 0& 0& 1& \cdots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 0& 0& \dots & 1\\ 1& 0& 0& \dots & 0\end{array}\right]$, and A_m⁽ⁱ⁾ (i = 0, 1, 2, …, m − 1) is an $m\times m$ binary matrix where the (i + 1) row is 1 and other rows are 0, and defines classical binary codes [14]. Then, the number of ebits is proven to be 1 for some conditions. Qian and Zhang [15] used shortened Hamming codes with parameter $\left[\frac{m(m-1)}{2},\frac{(m-1)(m-2)}{2},3\right]$, and proved EAQECCs with parameter $\left[\left[\frac{m(m-1)}{2},\frac{(m-1)(m-4)}{2}+1,3;1\right]\right]$ exist if m is even.

3. Construction Method of the Proposed EAQECC

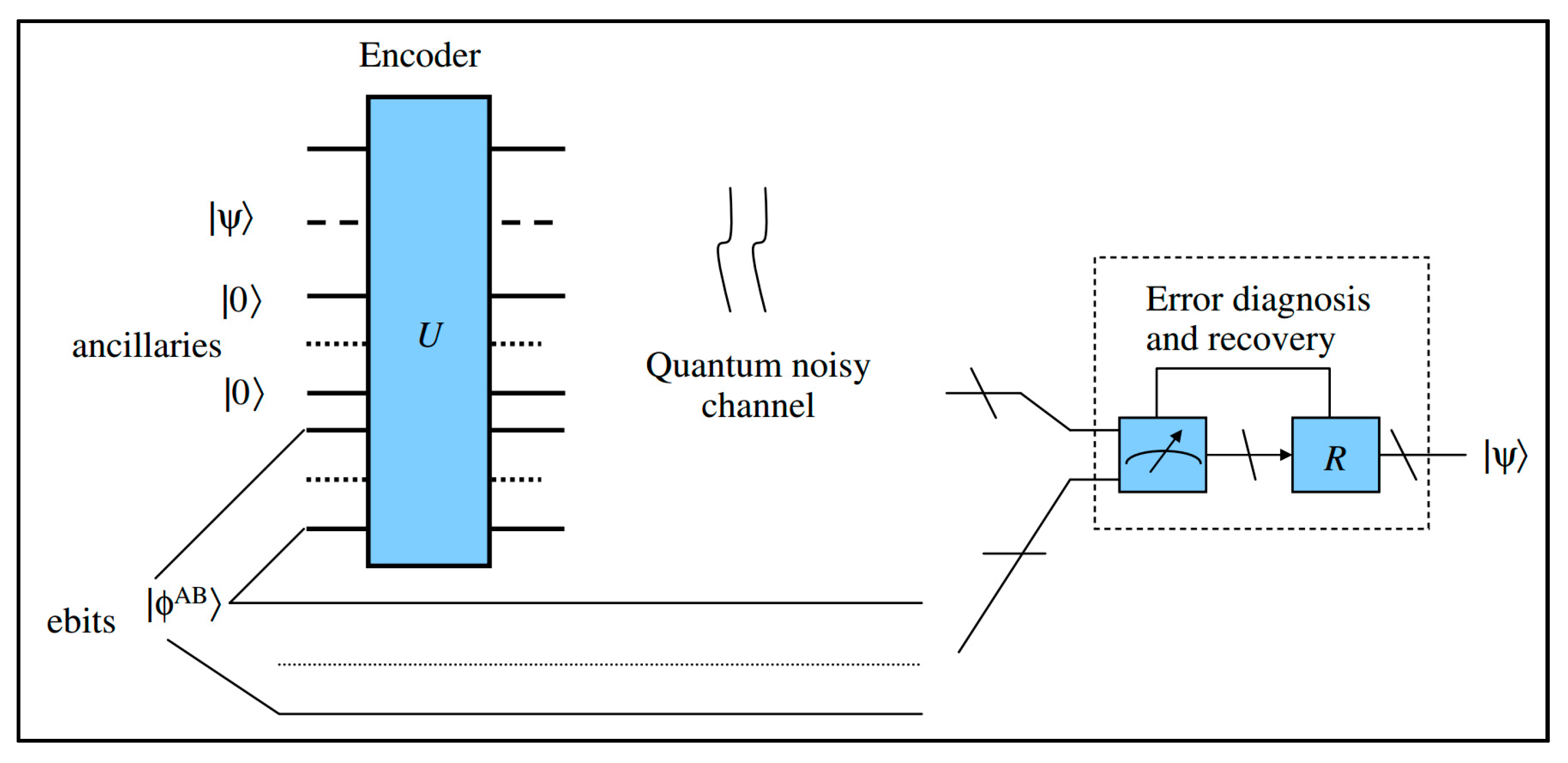
In this section, general properties of cyclic matrices and circulant matrices are introduced first. Then, we discuss the construction of the isotropic subgroup from the proposed modified circulant matrix, and then the calculation for an entanglement group is given. As a consequence, the parameters for EAQECC are obtained.

3.1. Cyclic Matrices

Definition 1.

(Cyclic Matrix) Let I_n be the $n\times n$ identity matrix. A cyclic matrix I_n(x) is a shifted identity matrix with the rows of I_n circularly shifted to the right by x positions, where $x\in \{0,1,...,n-1\}$ is the offset.

In general, it is known that I_n(0) = I_n and $I_n(x\pm kn)=I_n(x)$ for any integer k. The multiplication of I_n(1) and I_n(1) is I_n(2). Therefore, if I_n(1)^c is denoted as c times the multiplication of I_n(1), then I_n(1)^c = I_n(c).

Example 1.

For n = 4, the cyclic matrix and relations are given as follows:

$$I_4=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right],I_4(1)=\left[\begin{array}{cccc}0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\\ 1& 0& 0& 0\end{array}\right],\mathrm{and}{I}_4{(1)}^2=\left[\begin{array}{cccc}0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\\ 1& 0& 0& 0\end{array}\right]\times \left[\begin{array}{cccc}0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\\ 1& 0& 0& 0\end{array}\right]=\left[\begin{array}{cccc}0& 0& 1& 0\\ 0& 0& 0& 1\\ 1& 0& 0& 0\\ 0& 1& 0& 0\end{array}\right]=I_4(2).$$

Definition 2.

(Left-cyclic Matrix) Let J_n be the $n\times n$ binary matrix made from the $\pi$-rotation of identity matrix I_n. A cyclic matrix $J_n(x)$ is a shifted J_n with the rows of J_n circularly shifted to the right by $x$ positions, where $x\in \{0,1,...,n-1\}$ is the offset.

In general, it is known that the transpose matrix of any Left-cyclic matrix is equal to itself. Therefore, any Left-cyclic matrix is a symmetric matrix.

Example 2.

For n = 4, the following Left-cyclic matrix and relations are given:

$$J_4=\left[\begin{array}{cccc}0& 0& 0& 1\\ 0& 0& 1& 0\\ 0& 1& 0& 0\\ 1& 0& 0& 0\end{array}\right],J_4(1)=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 0& 1\\ 0& 0& 1& 0\\ 0& 1& 0& 0\end{array}\right]\mathrm{and}{J}_4{(1)}^T=J_4(1)=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 0& 1\\ 0& 0& 1& 0\\ 0& 1& 0& 0\end{array}\right].$$

3.2. Circulant Matrices

Definition 3.

(Circulant Matrix-CM) An $n\times n$ binary matrix Q₁ is called a CM if it is expressed as

$$Q_1=\left[\begin{array}{ccccc}{i}_0& i_1& i_2& \cdots & i_{n-1}\\ i_{n-1}& i_0& i_1& \cdots & i_{n-2}\\ i_{n-2}& i_{n-1}& i_0& \cdots & i_{n-3}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ i_1& i_2& i_3& \cdots & i_0\end{array}\right],$$

where the entries $\{i_0,i_1,...,i_{n-1}\}$ of matrix Q₁ are the binary values.

Circulant matrix Q₁ can be expressed by using a cyclic matrix as follows:

$$Q_1=i_0\times I_n(0)+i_1\times I_n(1)+i_2\times I_n(2)+...+i_{n-1}\times I_n(n-1)=\left[\begin{array}{c}u\times I_n(0)\\ u\times I_n(1)\\ ⋮\\ u\times I_n(n-1)\end{array}\right],$$

where u = [i₀ i₁ … i_n−1]. Therefore, we can denote Q₁ as the function of vector u and variable n. Hereafter, we denote Q₁ as P₁(u, n).

Definition 4.

(Left-circulant Matrix—Left-CM) An $n\times n$ binary matrix Q₂ is called a Left-CM if it is expressed as

$$Q_2=\left[\begin{array}{ccccc}{j}_0& j_1& j_2& \cdots & j_{n-1}\\ j_1& j_2& j_3& \cdots & j_0\\ j_2& j_3& j_4& \cdots & j_1\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ j_{n-1}& j_0& j_1& \cdots & j_{n-2}\end{array}\right],$$

where the entries {j₀, j₁, …, j_n−1} of matrix Q₂ are the binary values.

Circulant matrix Q₂ can be expressed by using a left-cyclic matrix, such as

$$Q_2=j_0\times J_n(1)+j_1\times J_n(2)+j_2\times J_n(3)+...+j_{n-2}\times J_n(n-1)+j_{n-1}\times J_n(0)=\left[\begin{array}{c}v\times I_n(0)\\ v\times I_n(n-1)\\ ⋮\\ v\times I_n(1)\end{array}\right],$$

where v = [j₀ j₁ … j_n-1]. Therefore, we can denote Q₂ as the function of vector v and variable n. Hereafter, we denote Q₂ as P₂(v, n).

3.3. Construction of Parity Check Matrices of EAQECC Based on Modified Circulant Matrices

From the combination of circulant matrices and the left-circulant matrices, the parity check matrix that corresponds to isotropic subgroup have been formed in Theorem 2, then the anti-commuting subgroup are determined as logical operators of the parity check matrix as Theorem 3. Finally, the EAQECCs [[n, k, d_min; 1]] are found as the Corollary 1.

Theorem 2.

For any two binary vectors u, v of size n, two circulant matrices are P₁(u, n) and P₂(v, n). Then, the parity-check matrix H = [H_X | H_Z], where H_X and H_Z correspond to P₁(u, n) and P₂(v, n), respectively, satisfies the SIP condition in (2).

Proof. 

From Definitions 3 and 4, P₁(u, n) and P₂(v, n) can be written as

$$P_1(u,n)=I_n(i_{u_1})+I_n(i_{u_2})+...+I_n(i_{u_k})\iff H_X=I_n(i_{u_1})+I_n(i_{u_2})+...+I_n(i_{u_k}),$$

$$P_2(v,n)=J_n(i_{v_1})+J_n(i_{v_2})+...+J_n(i_{v_h})\iff H_Z=J_n(i_{v_1})+J_n(i_{v_2})+...+J_n(i_{v_h}),$$

where {u₁, u₂, …, u_k} and {v₁, v₂, …, v_k} are the positions of 1 at vectors u and v, respectively.

From the properties of circulant matrices, we get following equation for any 0 < m, l ≪ n:

$$\{\begin{array}{c}{J}_n(m)=J_n(0)\times I_n(m),\\ I_n(l)\times J_n(0)=J_n(0)\times I_n(n-l),\\ I_n{(l)}^T=I_n(n-l).\end{array}$$

In addition, any left-cyclic matrix is a symmetric matrix. So, the following equation is always true:

$$I_n(l)\times J_n(m)=J_n(m)\times I_n{(l)}^T\iff I_n(l)\times J_n{(m)}^T=J_n(m)\times I_n{(l)}^T.$$

(4)

From (4), we get:

$$(I_n(i_{u_1})+I_n(i_{u_2})+...+I_n(i_{u_k})){(J_n(i_{v_1})+J_n(i_{v_2})+...+J_n(i_{v_h}))}^T=(J_n(i_{v_1})+J_n(i_{v_2})+...+J_n(i_{v_h})){(I_n(i_{u_1})+I_n(i_{u_2})+...+I_n(i_{u_k}))}^T.$$

$$\iff H_X\times H_Z{}^T=H_Z\times H_X{}^T\iff H_X\times H_Z{}^T+H_Z\times H_X{}^T=0_n\mathrm{modulo}2.$$

Therefore, the matrix H = [H_X | H_Z] satisfies the SIP condition in (2), and Theorem 2 is proven. ☐

Since the parity-check matrices constructed from Theorem 2 satisfy the SIP condition in (2), we can choose the independent vectors from H to create corresponding isotropic subgroup S_I. To have the entanglement subgroup, the following theorem can be considered to satisfy the conditions.

Theorem 3.

Given that parity-check matrix H of size (n − k) × 2n and its vectors are an independent relationship, we can transform H into the standard form H_st in the following form:

$$H_{\mathrm{st}}=\left[\begin{array}{cccccc}\stackrel{r}{\overbrace{I}}& \stackrel{n-k-r}{\overbrace{A_1}}& \stackrel{k}{\overbrace{A_2}}& \stackrel{r}{\overbrace{B}}& \stackrel{n-k-r}{\overbrace{C_1}}& \stackrel{k}{\overbrace{C_2}}\\ 0& 0& 0& D& I& E\end{array}\right]\begin{array}{c}\hfill \}r\\ \hfill \}n-k-r\end{array}$$

(5)

Then, the pairs of anti-commuting can be determined as

$$\{\begin{array}{c}{X}_{\mathrm{E}}=\\ Z_{\mathrm{E}}=\end{array}\begin{array}{cccccccc}[& 0& E^T& I& (E^T{C}_1+C_2{}^T)& 0& 0& ]\\ [& 0& 0& 0& A_2{}^T& 0& I& ]\end{array}$$

(6)

where the rank of matrix X_E and Z_E are k.

Proof. 

(1)

To transform the parity-check matrix to standard form, we use the Gauss-Jordan elimination, swap the qubits, and add one row to another. The codewords and stabilizer are invariant to these changes. So, step by step, the standard form can be obtained with (5).

(2)

From the standard form, H_st, we calculate the encoded Pauli operators $\overline{X}$ and $\overline{Z}$ that satisfy the following conditions:

$$\{\begin{array}{c}[\overline{X_i},\overline{X_j}]=0,\\ [\overline{Z_i},\overline{Z_j}]=0,\\ [\overline{X_i},\overline{Z_j}]=0\mathrm{for}i\ne j,\\ \{\overline{X_i},\overline{Z_j}\}=0\mathrm{for}i=j.\end{array}$$

Consequently, encoded Pauli operators $\overline{X}$ and $\overline{Z}$ can be used as X_E and Z_E. Theorem 3 is proven. ☐

EAQECCs use pre-existing entanglement between transmitter and receiver to improve the reliability of transmission. Hence, before transmission we must manufacture the entanglement state between transmitter and receiver. It will be difficult to set up if the number of ebits becomes larger. So, an EAQECC design to minimize the numbers of ebits is an important constraint. In following Corollary, we will consider the result of the Theorem 2 when the number of ebits is 1.

Corollary 1.

From the Theorem 3, firstly we choose one pair of anti-commuting from S_E, it denotes as {X₁, Z₁}. Then, we choose n − k − 1 generators {Z₂, Z₃, …, Z_n-k} from parity check matrix that satisfy the commutation property of isotropic sub-group S_I. The minimum distance d_min is calculated from the generators of S_E and S_I. The EAQECCs with parameter [[n, k, d_min;1]] is constructed.

Proof. 

 

As the definition of EAQECC in Section 2.3, the non-Abelian group can be partitioned into:

• a commuting subgroup, the isotropic group S_I = {Z_c+1, Z_c+2, …, Z_c+s}.
• entanglement subgroup pairs S_E = {Z₁, Z₂, …, Z_c, X₁, X₂, …, X_c} with anti-commuting pairs; the anti-commuting pairs (Z_i, X_i) being shared between source and receiver.

Then, from the isotropic and entanglement subgroup, EAQECC code C_EA are defined as [[n, k; c]] that encodes k = n − s − c qubits into n physical qubits with the help of s = n − k − c ancillas qubits and c ebits shared between the sender and receiver. As the expectation to get the minimum distance, one entanglement pair is chosen, hence c = 1, the operators are chosen above, the minimum distance is determined by the minimum weights of operators in the error set N:

$$N=\left\{E_m|\forall E_1,E_2\Rightarrow E_2{}^{†}{E}_1\in {\mathit{S}}_I\cup ({\mathrm{P}}_n-N(\mathit{S}))\right\}.$$

Finally, the parameter of EAQECC [[n, k, d_min;1]] are determined and the Corollary is proven. ☐

Following examples show the outputs of Corollary 1 where the minimum distance d_min ≥ 3, we search vectors which make codes with various minimum distance. Then, among many candidates of the vectors, to achieve largest minimum distance that has the error correctable ability the number of error t = ⎿(d_min − 1)/2⏌ ≥ 1 when the length of code up to 12.

Example 3.

For n = 7, let us consider the EAQECC when u = [1 1 0 0 1 0 1] and v = [1 0 0 1 0 1 1]. We have a code with the minimum number of ebits and good minimum distance, as in the following explanations.

Per Theorem 2, we have the corresponding parity-check matrix:

$$H=\left[\begin{array}{cccccccccccccc}1& 1& 0& 0& 1& 0& 1& 1& 0& 0& 1& 0& 1& 1\\ 1& 1& 1& 0& 0& 1& 0& 0& 0& 1& 0& 1& 1& 1\\ 0& 1& 1& 1& 0& 0& 1& 0& 1& 0& 1& 1& 1& 0\\ 1& 0& 1& 1& 1& 0& 0& 1& 0& 1& 1& 1& 0& 0\\ 0& 1& 0& 1& 1& 1& 0& 0& 1& 1& 1& 0& 0& 1\\ 0& 0& 1& 0& 1& 1& 1& 1& 1& 1& 0& 0& 1& 0\\ 1& 0& 0& 1& 0& 1& 1& 1& 1& 0& 0& 1& 0& 1\end{array}\right]$$

(7)

The six generators are chosen from the first six rows of matrix H, which satisfy the independent condition to generate all elements of an inotropic subgroup. By using Gaussian elimination and interchanges of columns, matrix H in (7) takes the standard form:

$$H_{\mathrm{st}}=\left[\begin{array}{cccccccccccccc}1& 0& 0& 1& 0& 1& 1& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 1& 1& 1& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 1& 1& 1& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 1& 1& 1& 0& 0& 1\\ 0& 0& 0& 0& 0& 0& 0& 1& 1& 0& 0& 1& 0& 1\\ 0& 0& 0& 0& 0& 0& 0& 1& 1& 1& 0& 0& 1& 0\end{array}\right]$$

(8)

And the corresponding entanglement subgroup pair is calculated as:

$$\begin{array}{l}{X}_1=\left[\begin{array}{cccccccccccccc}0& 0& 0& 1& 1& 0& 1& 0& 0& 0& 0& 0& 0& 0\end{array}\right],\\ Z_1=\left[\begin{array}{cccccccccccccc}0& 0& 0& 0& 0& 0& 0& 1& 0& 1& 0& 0& 0& 1\end{array}\right].\end{array}$$

(9)

Then, from vectors in (8) and (9) we have the generators for EAQECC as follows: S_E = {X₁, Z₁} and S_I = {Z₂, Z₃, Z₄, Z₅, Z₆} where

$$\begin{array}{l}{Z}_2=\left[11001011001011\right],\\ Z_3=\left[11100100010111\right],\\ Z_4=\left[01110010101110\right],\\ Z_5=\left[10111001011100\right],\\ Z_6=\left[00101111110010\right].\end{array}$$

The generators S = <S_I, S_E > correspond to EAQECC [[7,1,3;1]] that encodes one information qubit into seven physical qubits with the help of s = 6 ancilla qubits and only one pair entanglement -assisted ebit, and they can correct one error.

Example 4.

For n = 9, let us consider the EAQECC where u = [0 1 1 0 0 1 0 0 1] and v = [1 1 0 0 1 0 0 1 0]. We have a code with the minimum number of ebits and good minimum distance, as in the following explanations.

From Theorem 2, we have the corresponding parity-check matrix:

$$H=\left[\begin{array}{l}011001001110010010\\ 101100100100100101\\ 010110010001001011\\ 001011001010010110\\ 100101100100101100\\ 010010110001011001\\ 001001011010110010\\ 100100101101100100\\ 110010010011001001\end{array}\right]$$

(10)

The eight generators are chosen from the first eight rows of matrix H, which satisfies the independent condition to generate all elements of an inotropic subgroup. By using Gaussian elimination and interchange of columns, matrix H in (10) takes the standard form:

$$H_{\mathrm{st}}=\left[\begin{array}{l}100000001101110110\\ 010000001110011011\\ 001000001001000001\\ 000100001111110100\\ 000010001010011111\\ 000001001001001000\\ 000000101111100110\\ 000000011010111011\end{array}\right]$$

(11)

And the corresponding entanglement subgroup pair is calculated as:

$$\begin{array}{l}{X}_1=\left[000000001011010010\right],\\ Z_1=\left[000000000111111111\right].\end{array}$$

(12)

Then, from vectors in (11) and (12), we have the generators for EAQECC as follows: S_E = {X₁, Z₁} and S_I = {Z₂, Z₃, Z₄, Z₅, Z₆, Z₇, Z₈}, where

$$\begin{array}{l}{Z}_2=\left[011001001110010010\right],\\ Z_3=\left[101100100100100101\right],\\ Z_4=\left[010110010001001011\right],\\ Z_5=\left[001011001010010110\right],\\ Z_6=\left[010010110001011001\right],\\ Z_7=\left[001001011010110010\right],\\ Z_8=\left[100100101101100100\right].\end{array}$$

The generators S = < S_I, S_E > correspond to EAQECC [[9,1,3;1]] that encodes one information qubit into nine physical qubits with the help of s = 7 ancilla qubits and one pair entanglement -assisted ebit, and they can also correct one error.

Example 5.

For n = 10, let us consider the EAQECC when u = [0 1 1 1 0 1 1 0 1 0] and v = [1 1 1 0 1 1 0 1 0 0]. We have a code with the minimum number of ebits and good minimum distance as in the following explanations.

Per Theorem 2, we have the corresponding parity-check matrix:

$$H=\left[\begin{array}{l}01110110101110110100\\ 00111011011101101001\\ 10011101101011010011\\ 01001110110110100111\\ 10100111011101001110\\ 11010011101010011101\\ 01101001110100111011\\ 10110100111001110110\\ 11011010010011101101\end{array}\right]$$

(13)

The nine rows of matrix H satisfy the independent condition to generate all elements of an inotropic subgroup. By using Gaussian elimination and interchange of columns, matrix H in (13) takes the standard form:

$$H_{\mathrm{st}}=\left[\begin{array}{l}10000000011111010010\\ 01000000010001110111\\ 00100000011100111100\\ 00010000010110101011\\ 00001000010010000100\\ 00000100011011011010\\ 00000010011001100111\\ 00000001011100011101\\ 00000000110111101001\end{array}\right]$$

(14)

And the corresponding entanglement subgroup pair is calculated as:

$$\begin{array}{l}{X}_1=\left[00000000010101001110\right],\\ Z_1=\left[00000000001111111111\right].\end{array}$$

(15)

a/ Then, from vectors in (14) and (15) we have the generators for EAQECC as follows: S_E = {X₁, Z₁} and S_I = {Z₂, Z₃, Z₄, Z₅, Z₆, Z₇, Z₈, Z₉} where

$$\begin{array}{l}{Z}_2=\left[01110110101110110100\right],\\ Z_3=\left[00111011011101101001\right],\\ Z_4=\left[10011101101011010011\right],\\ Z_5=\left[01001110110110100111\right],\\ Z_6=\left[10100111011101001110\right],\\ Z_7=\left[11010011101010011101\right],\\ Z_8=\left[01101001110100111011\right],\\ Z_9=\left[10110100111001110110\right].\end{array}$$

The generators S = < S_I, S_E > correspond to EAQECC [[10,1,3;1]] that encodes one information qubit into 10 physical qubits with the help of s = 8 ancilla qubits and only one pair entanglement-assisted ebit, and they can correct one error.

b/ When we calculate with S_E = {X₁, Z₁} where

$$\begin{array}{l}{X}_1=\left[00000000010101001110\right],\\ Z_1=\left[00000000001111111111\right].\end{array}$$

and S_I = {Z₂, Z₃, Z₄, Z₅, Z₆, Z₇, Z₈} where

$$\begin{array}{l}{Z}_2=\left[01110110101110110100\right],\\ Z_3=\left[00111011011101101001\right],\\ Z_4=\left[01001110110110100111\right],\\ Z_5=\left[10100111011101001110\right],\\ Z_6=\left[01101001110100111011\right],\\ Z_7=\left[10110100111001110110\right],\\ Z_8=\left[11011010010011101101\right].\end{array}$$

The generator S = < S_I, S_E > correspond to EAQECC [[10,2,3;1]] that encodes two information qubits into 10 physical qubits with the help of s = 7 ancilla qubits and only one pair entanglement-assisted ebit, and they can correct one error.

Example 6.

For n = 11, let us consider the EAQECC when u = [1 1 1 0 0 1 1 0 0 0 1], v = [1 1 0 0 1 1 0 0 0 1 1]. We have a code with the minimum number of ebits and good minimum distance as in the following explanations.

Per Theorem 2, we have the corresponding parity-check matrix:

$$H=\left[\begin{array}{l}1110011000111001100011\\ 1111001100010011000111\\ 0111100110000110001111\\ 0011110011001100011110\\ 0001111001111000111100\\ 1000111100110001111001\\ 1100011110000011110011\\ 0110001111000111100110\\ 0011000111101111001100\\ 1001100011111110011000\end{array}\right]$$

(16)

The ten rows of matrix H satisfy the independent condition to generate all elements of an inotropic subgroup. By using Gaussian elimination and interchange of columns, matrix H in (16) takes the standard form:

$$H_{\mathrm{st}}=\left[\begin{array}{l}1000000000101100100111\\ 0100000000110101101001\\ 0010000000100111110100\\ 0001000000100011001111\\ 0000100000101010111001\\ 0000010000111001010101\\ 0000001000111110001100\\ 0000000100110000111110\\ 0000000010101101011010\\ 0000000001110110010011\end{array}\right]$$

(17)

And the corresponding entanglement subgroup pair is calculated as:

$$\begin{array}{l}{X}_1=\left[0000000000111011100010\right],\\ Z_1=\left[0000000000011111111111\right].\end{array}$$

(18)

a/ Then, from vectors in (14) and (15), we have the generators for EAQECC as follows: S_E = {X₁, Z₁} and S_I = {Z₂, Z₃, Z₄, Z₅, Z₆, Z₇, Z₈, Z₉, Z₁₀} where

$$\begin{array}{l}{Z}_2=\left[1110011000111001100011\right],\\ Z_3=\left[1111001100010011000111\right],\\ Z_4=\left[0011110011001100011110\right],\\ Z_5=\left[0001111001111000111100\right],\\ Z_6=\left[1000111100110001111001\right],\\ Z_7=\left[1100011110000011110011\right],\\ Z_8=\left[0110001111000111100110\right],\\ Z_9=\left[0011000111101111001100\right],\\ Z_{10}=\left[1001100011111110011000\right].\end{array}$$

The generators S = < S_I, S_E > correspond to EAQECC [[11,1,4;1]] that encodes one information qubit into 11 physical qubits with the help of s = 9 ancilla qubits and only one entanglement-assisted ebit, and the minimum distance is four.

b/ When we calculate with S_E = {X₁, Z₁} where

$$\begin{array}{l}{X}_1=\left[0000000000111011100010\right],\\ Z_1=\left[0000000000011111111111\right].\end{array}$$

and S_I = {Z₂, Z₃, Z₄, Z₅, Z₆, Z₇, Z₈, Z₉} where

$$\begin{array}{l}{Z}_2=\left[1110011000111001100011\right],\\ Z_3=\left[0011110011001100011110\right],\\ Z_4=\left[0001111001111000111100\right],\\ Z_5=\left[1000111100110001111001\right],\end{array}$$

$$\begin{array}{l}{Z}_6=\left[1100011110000011110011\right],\\ Z_7=\left[0110001111000111100110\right],\\ Z_8=\left[0011000111101111001100\right],\\ Z_9=\left[1001100011111110011000\right].\end{array}$$

The generator S = < S_I, S_E > correspond to EAQECC [[11,2,3;1]] that encodes two information qubits into 11 physical qubits with the help of s = 8 ancilla qubits and only one pair entanglement-assisted ebit, and they can correct one error.

c/ When we calculate with S_E = {X₁, Z₁} where

$$\begin{array}{l}{X}_1=\left[0000000000111011100010\right],\\ Z_1=\left[0000000000011111111111\right].\end{array}$$

and S_I = {Z₂, Z₃, Z₄, Z₅, Z₆, Z₇, Z₈} where

$$\begin{array}{l}{Z}_2=\left[1110011000111001100011\right],\\ Z_3=\left[0001111001111000111100\right],\\ Z_4=\left[1000111100110001111001\right],\\ Z_5=\left[1100011110000011110011\right],\\ Z_6=\left[0110001111000111100110\right],\\ Z_7=\left[0011000111101111001100\right],\\ Z_8=\left[1001100011111110011000\right].\end{array}$$

The generator S = <S_I, S_E > correspond to EAQECC [[11,3,3;1]] that encodes three information qubits into 11 physical qubits with the help of s = 7 ancilla qubits and only one pair entanglement-assisted ebit, and they can correct one error.

d/ When we calculate with S_E = {X₁, Z₁} where

$$\begin{array}{l}{X}_1=\left[0000000000111011100010\right],\\ Z_1=\left[0000000000011111111111\right].\end{array}$$

and S_I = { Z₂, Z₃, Z₄, Z₅, Z₆, Z₇} where

$$\begin{array}{l}{Z}_2=\left[1110011000111001100011\right],\\ Z_3=\left[0001111001111000111100\right],\\ Z_4=\left[1000111100110001111001\right],\\ Z_5=\left[1100011110000011110011\right],\\ Z_6=\left[0110001111000111100110\right],\\ Z_7=\left[0011000111101111001100\right].\end{array}$$

The generator S = <S_I, S_E > correspond to EAQECC [[11,4,3;1]] that encodes four information qubits into 11 physical qubits with the help of s = 6 ancilla qubits and only one pair entanglement-assisted ebit, and they can correct one error.

Example 7.

For n = 12, let us consider the EAQECC where u = [1 1 1 0 0 1 0 1 0 1 0 1], v = [1 1 0 0 1 0 1 0 1 0 1 1]. We have a code with the minimum number of ebits and good minimum distance, as in the following explanations.

Per Theorem 2, we have the corresponding parity-check matrix:

$$H=\left[\begin{array}{l}111001010101110010101011\\ 111100101010100101010111\\ 011110010101001010101111\\ 101111001010010101011110\\ 010111100101101010111100\\ 101011110010010101111001\\ 010101111001101011110010\\ 101010111100010111100101\\ 010101011110101111001010\\ 001010101111011110010101\\ 100101010111111100101010\end{array}\right]$$

(19)

The eleven rows of matrix H satisfy the independent condition to generate all elements of an inotropic subgroup. By using Gaussian elimination and interchange of columns, matrix H in (19) takes the standard form:

$$H_{\mathrm{st}}=\left[\begin{array}{l}100000000000000010011101\\ 010000000000000100111010\\ 001000000001101000111010\\ 000100000001110010100110\\ 000010000000100111010000\\ 000001000001101111101111\\ 000000100001111100001100\\ 000000010001011011001010\\ 000000001001010101000111\\ 000000000100101000010011\\ 000000000010010000100111\end{array}\right]$$

(20)

And the corresponding entanglement subgroup pair is calculated as:

$$\begin{array}{l}{X}_1=\left[000000000001100001001110\right],\\ Z_1=\left[000000000000001101111001\right].\end{array}$$

(21)

a/ Then, from vectors in (14) and (15) we have the generators for EAQECC as follows: S_E = {X₁, Z₁} and S_I = {Z₂, Z₃, Z₄, Z₅, Z₆, Z₇, Z₈, Z₉, Z₁₀, Z₁₁} where

$$\begin{array}{l}{Z}_2=\left[111001010101110010101011\right],\\ Z_3=\left[111100101010100101010111\right],\\ Z_4=\left[011110010101001010101111\right],\\ Z_5=\left[101111001010010101011110\right],\\ Z_6=\left[010111100101101010111100\right],\\ Z_7=\left[101011110010010101111001\right],\\ Z_8=\left[010101111001101011110010\right],\\ Z_9=\left[101010111100010111100101\right],\\ Z_{10}=\left[010101011110101111001010\right],\\ Z_{11}=\left[001010101111011110010101\right].\end{array}$$

The generators S = <S_I, S_E > correspond to EAQECC [[12,1,4;1]] that encodes one information qubit into 12 physical qubits with the help of s = 10 ancilla qubits and only one pair entanglement -assisted ebit and the minimum distance is four.

b/ When we calculate with S_E = {X₁, Z₁} where

$$\begin{array}{l}{X}_1=\left[000000000001100001001110\right],\\ Z_1=\left[000000000000001101111001\right].\end{array}$$

and S_I = {Z₂, Z₃, Z₄, Z₅, Z₆, Z₇, Z₈, Z₉, Z₁₀} where

$$\begin{array}{l}{Z}_2=\left[111100101010100101010111\right],\\ Z_3=\left[011110010101001010101111\right],\\ Z_4=\left[101111001010010101011110\right],\\ Z_5=\left[010111100101101010111100\right],\\ Z_6=\left[101011110010010101111001\right],\\ Z_7=\left[010101111001101011110010\right],\\ Z_8=\left[101010111100010111100101\right],\\ Z_9=\left[010101011110101111001010\right],\\ Z_{10}=\left[001010101111011110010101\right].\end{array}$$

The generator S = <S_I, S_E > correspond to EAQECC [[12,2,4;1]] that encodes two information qubits into 12 physical qubits with the help of s = 9 ancilla qubits and only one pair entanglement-assisted ebit, and they can correct one error.

The results of the proposed EAQECC with lengths up to 12 are listed in

Table 1. Entanglement-assisted quantum error correction code (EAQECC) [[n, k, d; c]] from proposed method with c = 1 and d ≥ 3.

n	k	d
7	1	3
8	1	3
9	1	3
10	1	3
10	2	3
11	1	4
11	2	3
11	3	3
11	4	3
12	1	4
12	2	4
12	3	3
12	4	3
12	5	3

. The detailed values of the operators are calculated in Examples 3–7.

In comparison with the results of referenced studies [12,13,14,15], the proposed EAQECC shows outperform as a smaller number of ebits and larger minimum distance. As the construction of EAQECC by generalized quadrangles in [13] and circulant matrix in [14], the two main things are clearly to conclude the advances of proposed methods that are code lengths and the classification of generators. Firstly, in [13,14], the code lengths are limited as the conditions to construct the parity check matrix, in contrast the proposed method can find the corresponding EAQECCs for any length. In addition, proposed codes are expressed as the standard form transformation to classify subgroups S_I and S_E; hence, the operators of subgroups are clearly determined, instead of knowing the numbers and operators not being determined, as seen in elsewhere, hence the minimum distance of outputs are not calculated in [13,14], furthermore the determined generators also open the effective way to implement the quantum system in future works. For more details, the comparisons are listed in

Table 2. Comparison of this proposed paper to other research.

EAQECC Based on	Number of Ebits	To Classify Subgroups	Minimum Distance
Arbitrary binary linear code [12]	2n – 2k	Gram-Schmidt procedure	$\ge$3
Generalized quadrangles [13]	2	Gram-Schmidt procedure	Not mentioned
Circulant permutation [14]	1	Gram-Schmidt procedure	Not mentioned
Shortened Hamming code [15]	1	Gram-Schmidt procedure	3
The proposed method	1	Standard form transformation of matrix	3,$\ge$4

.

4. Conclusions

In this paper, the construction of EAQECC-based on circulant matrices has been studied. Not using the Gram-Schmidt procedure to classify the subgroups of EAQECC, we first propose the construction and calculation for each subgroup. This work aims to reduce the complexity in the classification and determination of ebits. Some EAQECCs with a minimum number of ebits, and the capability to correct errors were showed clearly, with generators of each subgroup. This promises effective codes in comparison with other results.