Density of NaAlSi2O6 Melt at High Pressure and Temperature Measured by In-Situ X-ray Microtomography
Abstract
:1. Introduction
2. Materials and Methods
2.1. Starting Materials
2.2. High-Pressure Experiments
2.3. X-Ray Microtomography Measurements
2.4. Tomographic Reconstruction and 3D Volume Rendering
3. Results and Discussions
3.1. Density of Jadeite Melt at High Pressures
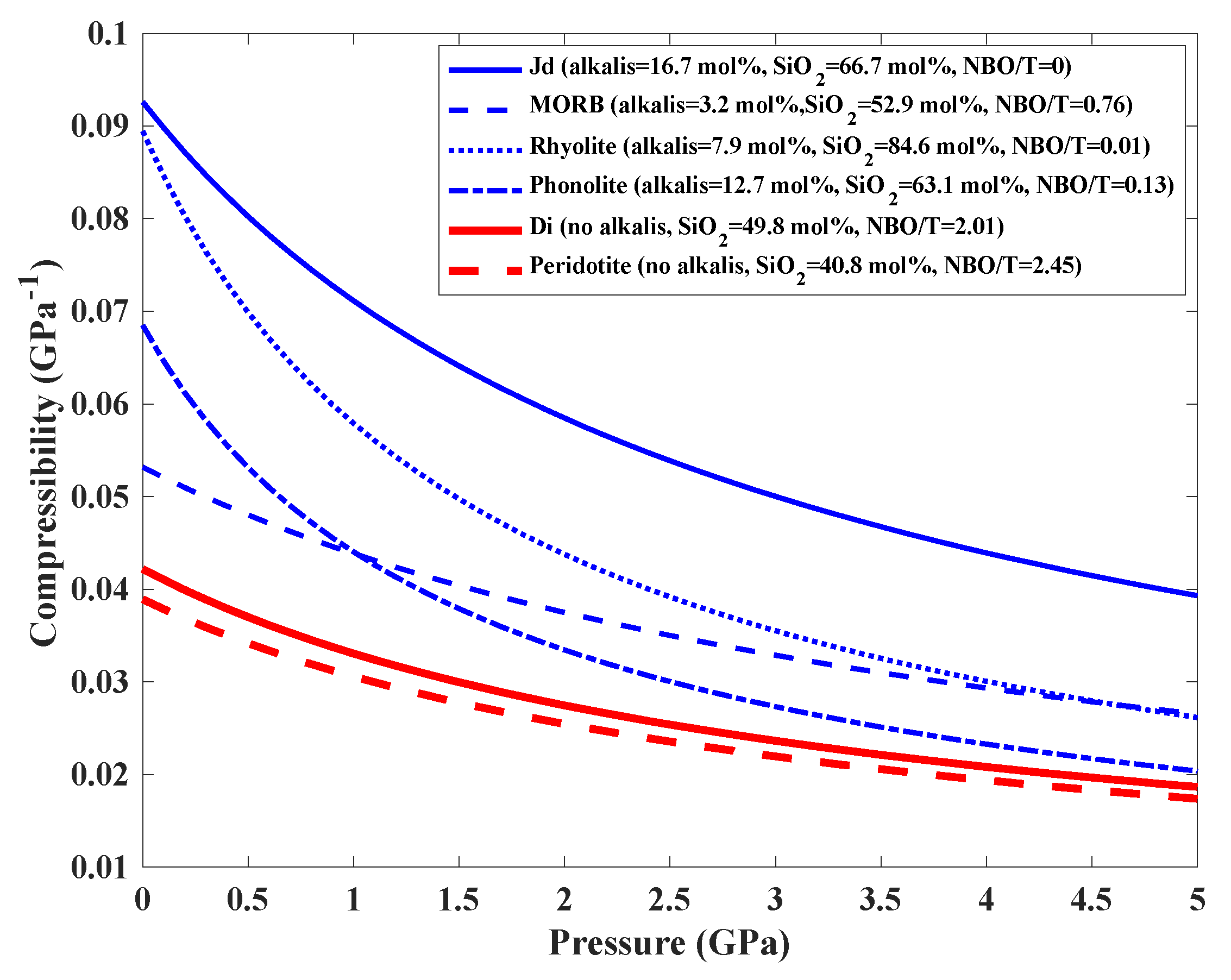
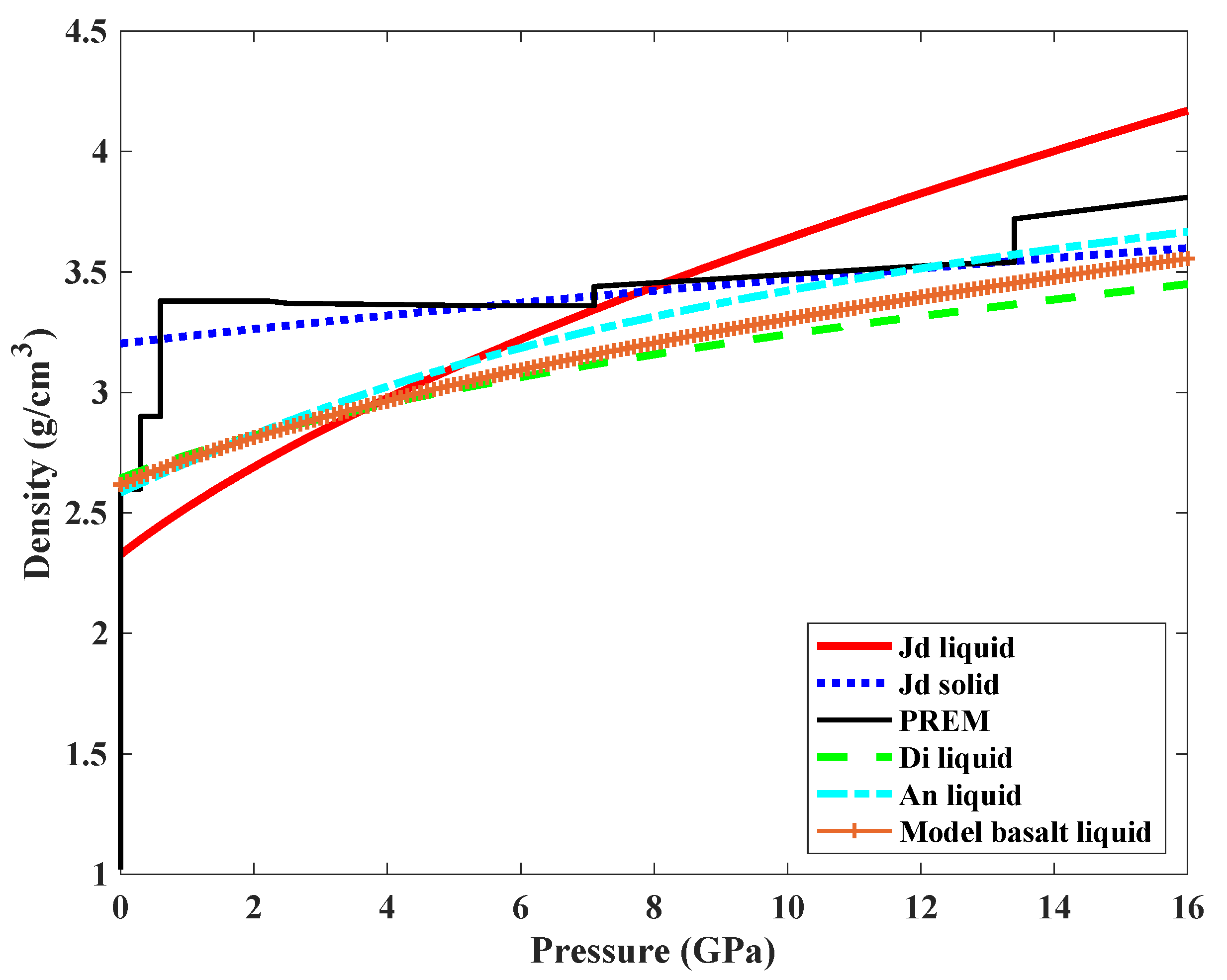
3.2. Comparison of the Compressibility with Other Silicate Melts and Geological Implications
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Agee, C.B. Crystal-liquid density inversions in terrestrial and lunar magmas. Phys. Earth Planet. Inter. 1998, 107, 63–74. [Google Scholar] [CrossRef]
- Sanloup, C. Density of magmas at depth. Chem. Geol. 2016, 429, 51–59. [Google Scholar] [CrossRef] [Green Version]
- Stolper, E.; Walker, D.; Hager, B.H.; Hays, J.F. Melt segregation from partially molten source regions: The importance of melt density and source region size. J. Geophys. Res. 1981, 86, 6261–6271. [Google Scholar] [CrossRef] [Green Version]
- Faul, U.H. Melt retention and segregation beneath mid-ocean ridges. Nature 2001, 410, 920–923. [Google Scholar] [CrossRef] [PubMed]
- Schmerr, N. The gutenberg discontinuity: Melt at the lithosphere-asthenosphere boundary. Science 2012, 335, 1480–1483. [Google Scholar] [CrossRef] [Green Version]
- Naif, S.; Key, K.; Constable, S.; Evans, R.L. Melt-rich channel observed at the lithosphere-asthenosphere boundary. Nature 2013, 495, 356–359. [Google Scholar] [CrossRef]
- Tauzin, B.; Debayle, E.; Wittlinger, G. Seismic evidence for a global low-velocity layer within the Earth’s upper mantle. Nat. Geosci. 2010, 3, 718–721. [Google Scholar] [CrossRef]
- Schmandt, B.; Jacobsen, S.D.; Becker, T.W.; Liu, Z.; Dueker, K.G. Dehydration melting at the top of the lower mantle. Science 2014, 344, 1265–1268. [Google Scholar] [CrossRef]
- Williams, Q.; Garnero, E.J. Seismic evidence for partial melt at the base of earth’s mantle. Science 1996, 273, 1528–1530. [Google Scholar] [CrossRef] [Green Version]
- Nakajima, M.; Stevenson, D.J. Melting and mixing states of the Earth’s mantle after the Moon-forming impact. Earth Planet. Sci. Lett. 2015, 427, 286–295. [Google Scholar] [CrossRef] [Green Version]
- Hosono, N.; Karato, S.; Makino, J.; Saitoh, T.R. Terrestrial magma ocean origin of the Moon. Nat. Geosci. 2019, 12, 418–423. [Google Scholar] [CrossRef]
- Hirschmann, M.M. Mantle solidus: Experimental constraints and the effects of peridotite composition. Geochem. Geophys. Geosyst. 2000, 1, 2000GC000070. [Google Scholar] [CrossRef]
- Baker, M.B.; Hirschmann, M.M.; Ghiorso, M.S.; Stolper, E.M. Compositions of near-solidus peridotite melts from experiments and thermodynamic calculations. Nature 1995, 375, 308–311. [Google Scholar] [CrossRef]
- Schiano, P.; Clocchiatti, R. Worldwide occurrence of silica-rich melts in sub-continental and sub-oceanic mantle minerals. Nature 1994, 368, 621–624. [Google Scholar] [CrossRef]
- Falloon, T.J.; Green, D.H.; O’Neill, H.S.C.; Hibberson, W.O. Experimental tests of low degree peridotite partial melt compositions: Implications for the nature of anhydrous near-solidus peridotite melts at 1 GPa. Earth Planet. Sci. Lett. 1997, 152, 149–162. [Google Scholar] [CrossRef]
- Falloon, T.J.; Green, D.H.; Danyushevsky, L.V.; Mcneill, A.W. The composition of near-solidus partial melts of fertile peridotite at 1 and 1.5 GPa: Implications for the petrogenesis of Morb. J. Petrol. 2008, 49, 591–613. [Google Scholar] [CrossRef]
- Pommier, A.; Garnero, E.J. Petrology-based modeling of mantle melt electrical conductivity and joint interpretation of electromagnetic and seismic results. J. Geophys. Res. Solid Earth 2014, 119, 4001–4016. [Google Scholar] [CrossRef]
- Kushiro, I. Changes in viscosity and structure of melt of NaAlSi2O6 composition at high pressures. J. Geophys. Res. 1976, 81, 6347–6350. [Google Scholar] [CrossRef]
- Shimizu, N.; Kushiro, I. Diffusivity of oxygen in jadeite and diopside melts at high pressures. Geochim. Cosmochim. Acta 1984, 48, 1295–1303. [Google Scholar] [CrossRef]
- Litvin, Y.A.; Gasparik, T. Melting of jadeite to 16.5 GPa and melting relations on the enstatite-jadeite join. Geochim. Cosmochim. Acta 1993, 57, 2033–2040. [Google Scholar] [CrossRef]
- Suzuki, A.; Ohtani, E.; Terasaki, H.; Nishida, K.; Hayashi, H.; Sakamaki, T.; Shibazaki, Y.; Kikegawa, T. Pressure and temperature dependence of the viscosity of a NaAlSi2O6 melt. Phys. Chem. Miner. 2011, 38, 59–64. [Google Scholar] [CrossRef]
- Zhao, Y.; Von Dreele, R.B.; Shankland, T.J.; Weidner, D.J.; Zhang, J.; Wang, Y.; Gasparik, T. Thermoelastic equation of state of jadeite NaAlSi2O6: An energy-dispersive Reitveld refinement study of low symmetry and multiple phases diffraction. Geophys. Res. Lett. 1997, 24, 5–8. [Google Scholar] [CrossRef]
- Liu, L. High-pressure phase transformations of albite, jadeite and nepheline. Earth Planet. Sci. Lett. 1978, 37, 438–444. [Google Scholar] [CrossRef]
- Nestola, F.; Boffa-Ballaran, T.; Liebske, C.; Bruno, M.; Tribaudino, M. High-pressure behaviour along the jadeite NaAlSi2O6—Aegirine NaFeSi2O6 solid solution up to 10 GPa. Phys. Chem. Miner. 2006, 33, 417–425. [Google Scholar] [CrossRef]
- Wu, X.; Fan, X.; Qin, F.; Meng, D.; Zhang, X.; Chen, L.; Liu, W.; Zheng, J. Compressibility and structural properties of Jadeite, NaAlSi2O6 at high pressure. J. Earth Sci. 2013, 24, 57–64. [Google Scholar] [CrossRef]
- Agee, C.B.; Walker, D. Olivine flotation in mantle melt. Earth Planet. Sci. Lett. 1993, 114, 315–324. [Google Scholar] [CrossRef]
- Ghosh, S.; Ohtani, E.; Litasov, K.; Suzuki, A.; Sakamaki, T. Stability of carbonated magmas at the base of the Earth’s upper mantle. Geophys. Res. Lett. 2007, 34, L22312. [Google Scholar] [CrossRef]
- Jing, Z.; Karato, S. Effect of H2O on the density of silicate melts at high pressures: Static experiments and the application of a modified hard-sphere model of equation of state. Geochim. Cosmochim. Acta 2012, 85, 357–372. [Google Scholar] [CrossRef]
- Matsukage, K.N.; Jing, Z.; Karato, S. Density of hydrous silicate melt at the conditions of Earth’s deep upper mantle. Nature 2005, 438, 488–491. [Google Scholar] [CrossRef]
- Asimow, P.D.; Ahrens, T.J. Shock compression of liquid silicates to 125 GPa: The anorthite-diopside join. J. Geophys. Res. Solid Earth 2010, 115, B10209. [Google Scholar] [CrossRef] [Green Version]
- Rigden, S.M.; Ahrens, T.J.; Stolper, E.M. High pressure equation of state of molten Anorthite and Diopside. J. Geophys. Res. 1989, 94, 9508–9522. [Google Scholar] [CrossRef]
- Thomas, C.W.; Asimow, P.D. Preheated shock experiments in the molten CaAl2Si2O8–CaFeSi2O6–CaMgSi2O6 ternary: A test for linear mixing of liquid volumes at high pressure and temperature. J. Geophys. Res. Solid Earth 2013, 118, 3354–3365. [Google Scholar] [CrossRef] [Green Version]
- Sakamaki, T. Density of jadeite melts under high pressure and high temperature conditions. J. Mineral. Petrol. Sci. 2017, 112, 300–307. [Google Scholar] [CrossRef] [Green Version]
- Sato, T.; Funamori, N. Sixfold-coordinated amorphous Polymorph of SiO2 under high pressure. Phys. Rev. Lett. 2008, 101, 255502. [Google Scholar] [CrossRef] [PubMed]
- Seifert, R.; Malfait, W.J.; Petitgirard, S.; Sanchez-Valle, C. Density of phonolitic magmas and time scales of crystal fractionation in magma chambers. Earth Planet. Sci. Lett. 2013, 381, 12–20. [Google Scholar] [CrossRef]
- Malfait, W.J.; Seifert, R.; Petitgirard, S.; Perrillat, J.P.; Mezouar, M.; Ota, T.; Nakamura, E.; Lerch, P.; Sanchez-Valle, C. Supervolcano eruptions driven by melt buoyancy in large silicic magma chambers. Nat. Geosci. 2014, 7, 122–125. [Google Scholar] [CrossRef]
- Petitgirard, S.; Malfait, W.J.; Sinmyo, R.; Kupenko, I.; Hennet, L.; Harries, D.; Dane, T.; Burghammer, M.; Rubie, D.C. Fate of MgSiO3 melts at core—Mantle boundary conditions. Proc. Natl. Acad. Sci. USA 2015, 112, 14186–14190. [Google Scholar] [CrossRef] [Green Version]
- Bajgain, S.K.; Peng, Y.; Mookherjee, M.; Jing, Z.; Solomon, M. Properties of hydrous aluminosilicate melts at high pressures. ACS Earth Space Chem. 2019, 3, 390–402. [Google Scholar] [CrossRef]
- Lesher, C.E.; Wang, Y.; Gaudio, S.; Clark, A.; Nishiyama, N.; Rivers, M. Volumetric properties of magnesium silicate glasses and supercooled liquid at high pressure by X-ray microtomography. Phys. Earth Planet. Inter. 2009, 174, 292–301. [Google Scholar] [CrossRef]
- Clark, A.N.; Lesher, C.E.; Jacobsen, S.D.; Wang, Y. Anomalous density and elastic properties of basalt at high pressure: Reevaluating of the effect of melt fraction on seismic velocity in the Earth’s crust and upper mantle. J. Geophys. Res. Solid Earth 2016, 121, 4232–4248. [Google Scholar] [CrossRef] [Green Version]
- Li, R.; Li, L.; Yu, T.; Wang, L.; Chen, J.; Wang, Y.; Cai, Z.; Chen, J.; Rivers, M.L.; Liu, H. Study of liquid gallium as a function of pressure and temperature using synchrotron x-ray microtomography and x-ray diffraction. Appl. Phys. Lett. 2014, 105, 041906. [Google Scholar] [CrossRef]
- Li, R.; Wang, L.; Li, L.; Yu, T.; Zhao, H.; Chapman, K.W.; Wang, Y.; Rivers, M.L.; Chupas, P.J.; Mao, H.; et al. Local structure of liquid gallium under pressure. Sci. Rep. 2017, 7, 5666. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kono, Y.; Yamada, A.; Wang, Y.; Yu, T.; Inoue, T. Combined ultrasonic elastic wave velocity and microtomography measurements at high pressures. Rev. Sci. Instrum. 2011, 82, 023906. [Google Scholar] [CrossRef] [PubMed]
- Rivers, M.L. Synchrotron “pink beam” tomography for the study of dynamic processes. SPIE Newsroom 2016. [Google Scholar] [CrossRef]
- Jing, Z.; Karato, S. A new approach to the equation of state of silicate melts: An application of the theory of hard sphere mixtures. Geochim. Cosmochim. Acta 2011, 75, 6780–6802. [Google Scholar] [CrossRef]
- Wang, Y.; Uchida, T.; Westferro, F.; Rivers, M.L.; Nishiyama, N.; Gebhardt, J.; Lesher, C.E.; Sutton, S.R. High-pressure X-ray tomography microscope: Synchrotron computed microtomography at high pressure and temperature. Rev. Sci. Instrum. 2005, 76, 073709. [Google Scholar] [CrossRef] [Green Version]
- Yu, T.; Wang, Y.; Rivers, M.L. Imaging in 3D under pressure: A decade of high-pressure X-ray microtomography development at GSECARS. Prog. Earth Planet. Sci. 2016, 3, 17. [Google Scholar] [CrossRef] [Green Version]
- Xu, M.; Jing, Z.; Chantel, J.; Jiang, P.; Yu, T.; Wang, Y. Ultrasonic velocity of diopside liquid at high pressure and temperature: Constraints on velocity reduction in the upper mantle due to partial melts. J. Geophys. Res. Solid Earth 2018, 123, 8676–8690. [Google Scholar] [CrossRef]
- Tange, Y.; Nishihara, Y.; Tsuchiya, T. Unified analyses for P-V-T equation of state of MgO: A solution for pressure-scale problems in high P-T experiments. J. Geophys. Res. 2009, 114, B03208. [Google Scholar] [CrossRef]
- Rivers, M.L. tomoRecon: High-speed tomography reconstruction on workstations using multi-threading. Proc. SPIE 2012, 8506, 85060U. [Google Scholar] [CrossRef]
- Rivers, M.L.; Wang, Y. Recent developments in microtomography at GeoSoilEnviroCARS. Proc. SPIE 2006, 6318, 63180J. [Google Scholar] [CrossRef]
- Ketcham, R.A. Computational methods for quantitative analysis of three-dimensional features in geological specimens. Geosphere 2005, 1, 32–41. [Google Scholar] [CrossRef]
- Ketcham, R.A.; Carlson, W.D. Acquisition, optimization and interpretation of X-ray computed tomographic imagery: Applications to the geosciences. Comput. Geosci. 2001, 27, 381–400. [Google Scholar] [CrossRef]
- Lange, R.A. A revised model for the density and thermal expansivity of K2O–Na2O–CaO–MgO–Al2O3–SiO2 liquids from 700 to 1900 K: Extension to crustal magmatic temperatures. Contrib. Mineral. Petrol. 1997, 130, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Birch, F. Elasticity and constitution of the Earth’s interior. J. Geophys. Res. 1952, 57, 227–286. [Google Scholar] [CrossRef]
- Murnaghan, F.D. Finite Deformation of an Elastic Solid; Dover: New York, NY, USA, 1967. [Google Scholar]
- Kress, V.C.; Williams, Q.; Carmichael, I.S.E. Ultrasonic investigation of melts in the system Na2O–Al2O3–SiO2. Geochim. Cosmochim. Acta 1988, 52, 283–293. [Google Scholar] [CrossRef]
- Ni, H.; De Koker, N. Thermodynamics, diffusion and structure of NaAlSi2O6 liquid at mantle conditions: A first-principles molecular dynamics investigation. J. Geophys. Res. 2011, 116, B09202. [Google Scholar] [CrossRef]
- Sakamaki, T.; Ohtani, E.; Urakawa, S.; Suzuki, A.; Katayama, Y. Density of dry peridotite magma at high pressure using an X-ray absorption method. Am. Mineral. 2010, 95, 144–147. [Google Scholar] [CrossRef]
- Ai, Y.; Lange, R.A. New acoustic velocity measurements on CaO–MgO–Al2O3–SiO2 liquids: Reevaluation of the volume and compressibility of CaMgSi2O6-CaAl2Si2O8 liquids to 25 GPa. J. Geophys. Res. 2008, 113, B04203. [Google Scholar] [CrossRef] [Green Version]
- Mysen, B.O.; Virgo, D.; Seifert, F.A. Relationships between properties and structure of aluminosilicate melts. Am. Mineral. 1985, 70, 88–105. [Google Scholar]
- Hirose, K.; Kushiro, I. Partial melting of dry peridotites at high pressures: Determination of compositions of melts segregated from peridotite using aggregates of diamond. Earth Planet. Sci. Lett. 1993, 114, 477–489. [Google Scholar] [CrossRef]
- Robinson, J.A.C.; Wood, B.J.; Blundy, J.D. The beginning of melting of fertile and depleted peridotite at 1.5 GPa. Earth Planet. Sci. Lett. 1998, 155, 97–111. [Google Scholar] [CrossRef]
- Ghiorso, M.S.; Hirschmann, M.M.; Reiners, P.W.; Kress, V.C. The pMELTS: A revision of MELTS for improved calculation of phase relations and major element partitioning related to partial melting of the mantle to 3 GPa. Geochem. Geophys. Geosyst. 2002, 3, 1–35. [Google Scholar] [CrossRef]
- Dziewonski, A.M.; Anderson, D.L. Preliminary reference Earth model. Phys. Earth Planet. Inter. 1981, 25, 297–356. [Google Scholar] [CrossRef]
- Ritsema, J.; Van Heijst, H. New seismic model of the upper mantle beneath Africa. Geology 2000, 28, 63–66. [Google Scholar] [CrossRef]
- Mibe, K.; Fujii, T.; Yasuda, A.; Ono, S. Mg–Fe partitioning between olivine and ultramafic melts at high pressures. Geochim. Cosmochim. Acta 2006, 70, 757–766. [Google Scholar] [CrossRef]
- Jing, Z.; Karato, S. The density of volatile bearing melts in the Earth’s deep mantle: The role of chemical composition. Chem. Geol. 2009, 262, 100–107. [Google Scholar] [CrossRef]
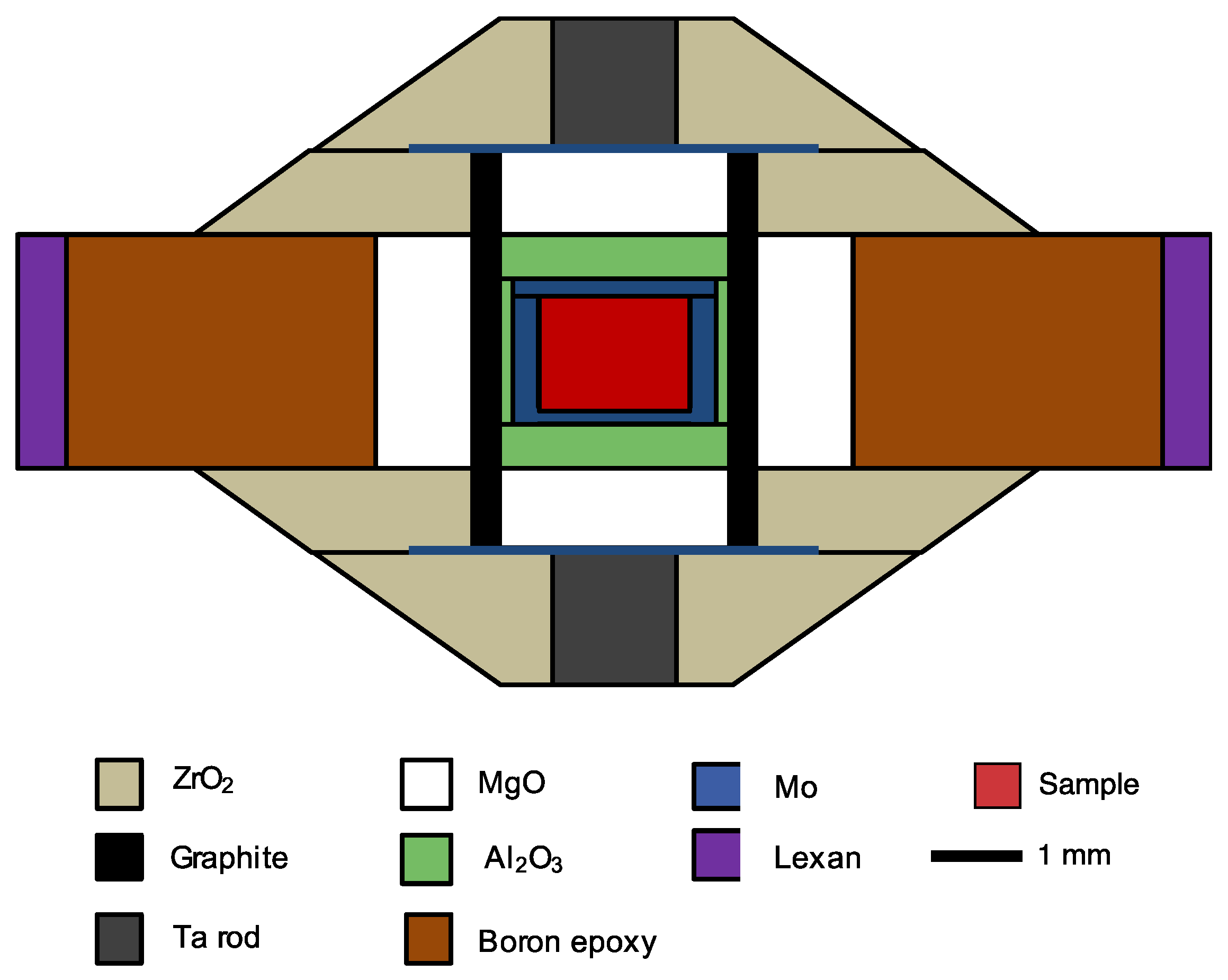


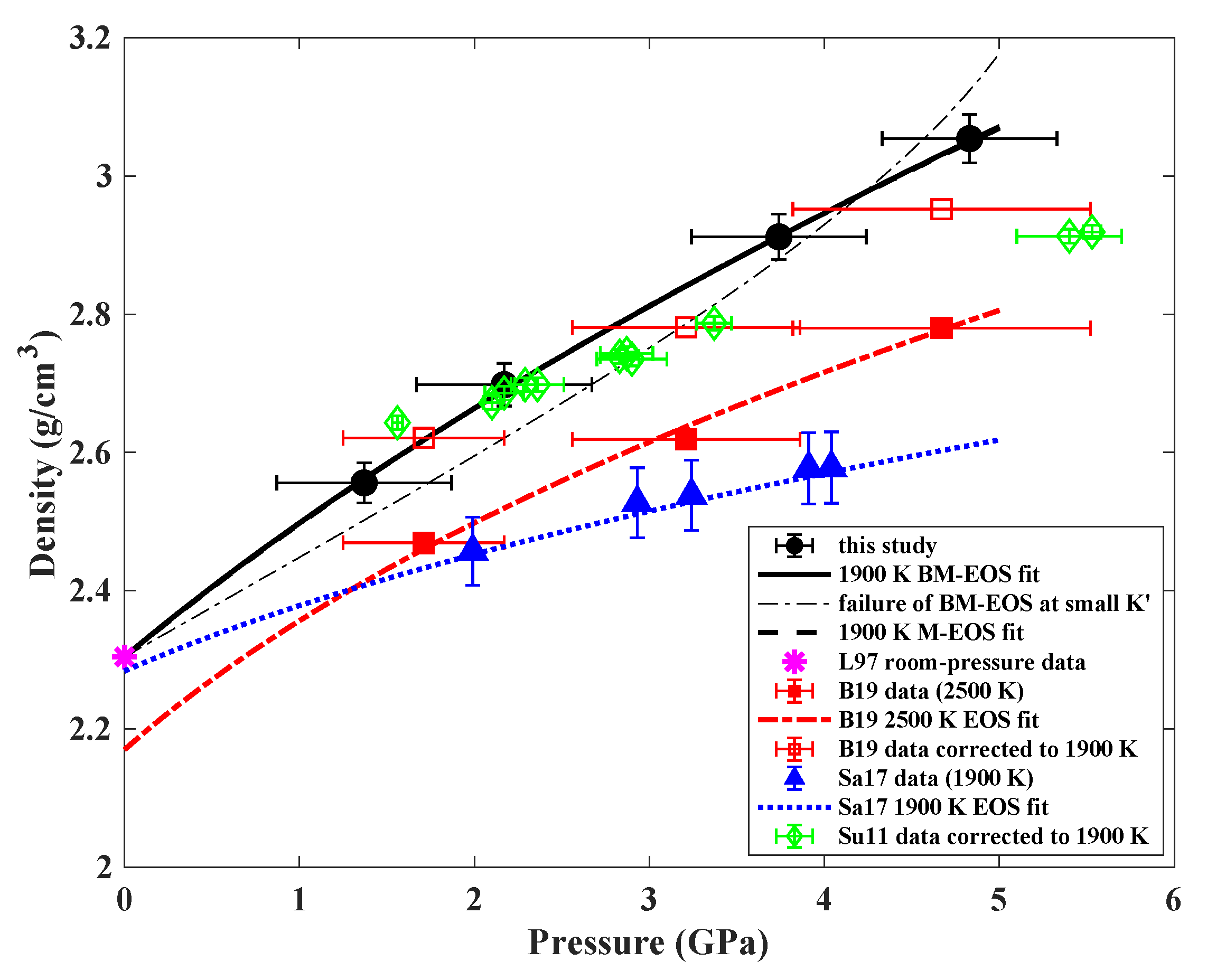
| Load (tons) | P (GPa) | T (K) | V (mm3) | V1900 K (mm3) | ρ (g/cm3) |
|---|---|---|---|---|---|
| 10 | 1.4 | 1741 | 1.704 | 1.716 | 2.556 |
| 10 | 2.2 | 1955 | 1.629 | 1.625 | 2.698 |
| 20 | 3.7 | 1934 | 1.508 | 1.506 | 2.912 |
| 30 | 4.8 | 1921 | 1.437 | 1.436 | 3.054 |
| References | T (K) | Method | ||
|---|---|---|---|---|
| This study (BM-EOS) | 1900 | HPXTM | ||
| 4 (fixed) | 1900 | |||
| This study (M-EOS) | 1900 | |||
| Bajgain et al. [38] | 9.70 ± 3.88 | 5.42 ± 1.35 | 2500 | FPMD |
| Ni and de Koker [58]* | 15.0 | 3.56 | 3000 | FPMD |
| Sakamaki [33] | 21.5 ± 0.8 | 8.9 ± 1.2 | 1473 | X-ray absorption |
| Kress et al. [57]# | 19.1 | 1773 | Room-pressure ultrasonics |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, M.; Jing, Z.; Van Orman, J.A.; Yu, T.; Wang, Y. Density of NaAlSi2O6 Melt at High Pressure and Temperature Measured by In-Situ X-ray Microtomography. Minerals 2020, 10, 161. https://doi.org/10.3390/min10020161
Xu M, Jing Z, Van Orman JA, Yu T, Wang Y. Density of NaAlSi2O6 Melt at High Pressure and Temperature Measured by In-Situ X-ray Microtomography. Minerals. 2020; 10(2):161. https://doi.org/10.3390/min10020161
Chicago/Turabian StyleXu, Man, Zhicheng Jing, James A. Van Orman, Tony Yu, and Yanbin Wang. 2020. "Density of NaAlSi2O6 Melt at High Pressure and Temperature Measured by In-Situ X-ray Microtomography" Minerals 10, no. 2: 161. https://doi.org/10.3390/min10020161
APA StyleXu, M., Jing, Z., Van Orman, J. A., Yu, T., & Wang, Y. (2020). Density of NaAlSi2O6 Melt at High Pressure and Temperature Measured by In-Situ X-ray Microtomography. Minerals, 10(2), 161. https://doi.org/10.3390/min10020161





