Abstract
Although near-surface seawater is supersaturated with CaCO3, only a minor part of it is abiogenic (e.g., carbonate cements). The possible reason for such a phenomenon has attracted much attention in the past decades. Substrate effects on the heterogeneous nucleation and growth of CaCO3 at various Mg2+/Ca2+ ratios may contribute to the understanding of the origin of abiogenic CaCO3 cements. Here, we used in situ atomic force microscopy (AFM), scanning electron microscopy (SEM), X-ray diffraction (XRD) and Raman spectroscopy to study the heterogeneous nucleation and growth of CaCO3 on both calcite (104) and aragonite (110) surfaces. The results show that (1) calcite spiral growth occurs on calcite (104) surfaces by monomer-by-monomer addition; (2) the aggregative growth of aragonite appears on aragonite (110) surfaces through a substrate-controlled oriented attachment (OA) along the [001] direction, followed by the formation of elongated columnar aragonite; and (3) Mg2+ inhibits the crystallization of both calcite and aragonite without impacting on crystallization pathways. These findings disclose that calcite and aragonite substrates determine the crystallization pathways, while the Mg2+/Ca2+ ratios control the growth rate of CaCO3, indicating that both types of CaCO3 substrate in shallow sediments and aqueous Mg2+/Ca2+ ratios constrain the deposition of abiogenic CaCO3 cements in the ocean.
1. Introduction
The supersaturation of near-surface seawater is about six and four times higher than that with respect to calcite and aragonite, respectively, whereas a much smaller fraction of the total sedimentary CaCO3 minerals is abiogenic [1], which contradicts traditional thermodynamics [2,3]. These abiogenic CaCO3 minerals, composed of aragonite and high-magnesium calcite in shoal-shallow marine environments [4,5,6], typically form either as heterogeneously precipitated primary marine cements or through post-depositional and diagenetic reactions [1]. In order to further understand the lack of abiogenic CaCO3 in the modern ocean, many efforts have been conducted to ascertain factors which affect the precipitation of abiogenic CaCO3 [7,8,9,10,11].
The precipitation of abiogenic CaCO3 correlates with aqueous chemistry [12]. The pH, temperature, and affect the saturation index (SI, which is defined as SI = logΩ = log(IAP/ Ksp), where Ω denotes saturation state, and IAP and Ksp represent activity product and solubility product, respectively) of solutions [13] and play key roles in determining the precipitate rate (r) of CaCO3 polymorphs. The r is constrained by Ω, following the equation r = k (Ω − 1)n [2]. In addition, the formation of CaCO3 minerals is partly kinetically driven, i.e., calcite growth favors a low reaction rate, while aragonite and vaterite prefer to form in relatively fast reactions [14]. In addition, the precipitation of CaCO3 (e.g., calcite) depends on the of solutions. Due to the differences in the dehydration properties between Ca2+ and CO32− and the geometry of calcite step kink sites, the step velocities of the obtuse and acute angled edges can reverse with the variation of at a fixed SI [15,16,17]. On the other hand, impurity ions and molecules in solutions can also influence CaCO3 precipitation. Inorganic anions (e.g., PO43−and SO42−) exert the impacts by competing with CO32− for Ca2+ sites or incorporating in a crystal lattice [13]. Divalent metal cations, such as Mg2+, Ba2+ and Sr2+, inhibit calcite growth by step pining, incorporation or kink blocking [18,19,20,21]. Similarly, soluble organic molecules (such as humate, fulvate, citrate and polyfunctional aromatic acids) inhibit the precipitation of aragonite by the modification of functional groups in these additives [11,22,23].
The surface properties of the growth substrate are another factor affecting the precipitation of abiogenic CaCO3 [24,25,26,27]. The surface charge of an inorganic substrate relates to the growth of CaCO3 polymorphs. Metastable CaCO3 phases (e.g., aragonite or vaterite) are favored by negatively charged substrates, whereas positively charged substrates contribute to the formation of the stable CaCO3 phase (i.e., calcite) [28]. In addition, the lattice mismatch between substrates and surface precipitates is also vital in the growth of abiogenic CaCO3 [29]. Based on classical nucleation theory, the energy barrier (ΔGC) to form a critical nucleus is positively correlated with γ3 (ΔGc ∝ γ3/(−RTlnσ)2, where γ denotes the interfacial free energy, σ the supersaturation, and R and T represent gas constant and Kelvin temperature, respectively [30]. The precipitation rate is subsequently controlled by the lattice mismatch, because a larger lattice mismatch leads to a higher ΔGC [31].
Abiogenic CaCO3 cements tend to overgrow on shoal-shallow calcium carbonate-rich sediments [32]. Different types of CaCO3 inorganic substrate should be taken into consideration, to study the precipitation of abiogenic CaCO3 cements. The substrate effects of CaCO3 have been found to control the mineralogical properties of carbonate cements [7,13], and plenty of works have also been conducted on the heterogeneous nucleation and growth of CaCO3 on calcite and aragonite seeds [33,34,35]. However, little attention has been paid to the internal mechanism and crystallization pathways of CaCO3 precipitates in these systems. Although the precipitation of CaCO3 on calcite (104) surfaces has been well documented [3,23,36,37], it may not represent the formation of abiogenic aragonite cements, due to the distinct surface properties of the two polymorphs [38]. Additionally, there are some controversies regarding aragonite nucleation and growth in Mg2+-bearing solutions. Mg2+-induced inhibition was reported in both nucleation and growth [39], whereas either inhibition [33] or non-inhibition [40] was merely found in the growth processes. Therefore, the evolution and mechanism of heterogeneous nucleation and growth of both calcite and aragonite at the nanoscale on CaCO3 substrates in Mg2+-bearing solutions with different concentrations should be investigated, to deeply understand the formation of abiogenic carbonate cements in the ocean.
In this study, we used AFM, SEM, XRD and Raman spectroscopy to investigate how calcite (104) and aragonite (110) substrates affect the heterogeneous nucleation and growth of CaCO3 under different solution supersaturations at pH = 8.0 ± 0.1. Since Mg2+ is a chief modifier for CaCO3 precipitation in sedimentary environments, we altered the Mg2+/Ca2+ ratios from 0 to 3 in the growth experiment. We observed that both the mineral phases and crystallization pathways of CaCO3 precipitated on different types of CaCO3 substrates are disparate. In addition, the precipitation rates of CaCO3 generated on calcite and aragonite substrates are negatively correlated to Mg2+/Ca2+ ratios. These findings reveal the different crystallization processes of CaCO3 grown on calcite (104) and aragonite (110) surfaces, providing a new perspective on the origin of abiogenic CaCO3 cements in the ocean.
2. Materials and Methods
2.1. Sample Preparation
An Iceland spar (from Guizhou, China) was cleaned using ethanol and deionized water (resistivity = 18.2 MΩ cm−1). Then, fresh calcite (104) surfaces (2 × 2 × 1 mm3) were prepared by scalpel cutting along the cleavage plane. Additionally, a diamond wire cutter (STX-202A, Kejing Auto-instrument Co., Ltd., Shenyang, China) was used to slice aragonite (110) surfaces (2 × 2 × 1 mm3) from single crystals (from Morocco). To obtain polished aragonite (110) surfaces, a Leica SP1600 (Leica, Wetzlar, Germany) saw microtome was employed. Since polished aragonite (110) surfaces would enhance the growth rate of CaCO3 by the increase in surface defects (which will reduce the energy barrier (ΔGC) to form a critical nucleus, and the number of nanoparticles will increase after increasing surface defects, thus causing the increase in growth rate), we used them in the next experiments to elevate experimental efficiency. Next, 15 mL acetone was used to wash these polished (110) surfaces through ultrasonic bathing for 1 h, and then these (110) surfaces were taken out from acetone and dried with pure N2. Afterwards, these prepared calcite (104) and aragonite (110) samples were glued onto steel pucks with wax for AFM experiments.
2.2. Solution Preparation
High-purity CaCl2, MgCl2, NaHCO3, NaCl (purchased from Aldrich and Macklin) and deionized water were used to prepare solutions with different Mg2+/Ca2+ ratios (0 and 3) and saturation indexes, with respect to calcite and aragonite (i.e., SIcalcite and SIaragonite), based on Visual MINTEQ [41] calculations (Table 1). Since the SIcalcite is 0.13 greater than SIaragonite (SIcalcite = SIaragonite + 0.13) in the same solution, we only used the former to label saturation states of solutions. Solution chemistry in the system is constrained by the amounts of [Mg2+], [Ca2+], ∑CO2, pH, and ionic strength (IS). The pH was maintained at 8.0 ± 0.1, and the IS was controlled up to 0.10 M (to avoid the coverage of substrates by too much NaCl, we did not used the salinity of seawater). All solutions were freshly prepared before the growth experiment, to prevent the precipitation of supersaturated solutions. Before introducing growth solutions, the solution with SIcalcite = 0.07 was injected into the fluid cell for at least one hour to make the surface of samples flatter. Based on solution chemistry, equilibriums in chemical reactions were taken into consideration as the following.
Mg(OH)2 + 2H+ → Mg2+ + 2H2O Ksp-1
MgCO3·3H2O → Mg2+ + CO32− + 3H2O Ksp-2
H2CO3 → H+ + HCO3− Ka1
HCO3- → H+ + CO32− Ka2

Table 1.
Compositions and solution chemistry calculated by Visual MINTEQ.
From the definition of Ksp, we derived
where (Mg2+) represents the activity of Mg2+, and ∑CO2 is the total concentration of carbonate species. Equations (5) and (6) define the stability fields of brucite and nesquehonite in the two-dimensional stability diagram of log (Mg2+) – pH, respectively (Figure 1). The concentrations of ∑CO2 (10 × [Ca2+]) and [Ca2+] (1/3 × [Mg2+]) in these equations were determined based on additive amounts.
log(Mg2+) = −2pH + logKsp-1
log(Mg2+) = log(Ksp-2[1+10−pH/Ka2 + 10−2pH/ Ka1Ka2 ]/ΣCO2)
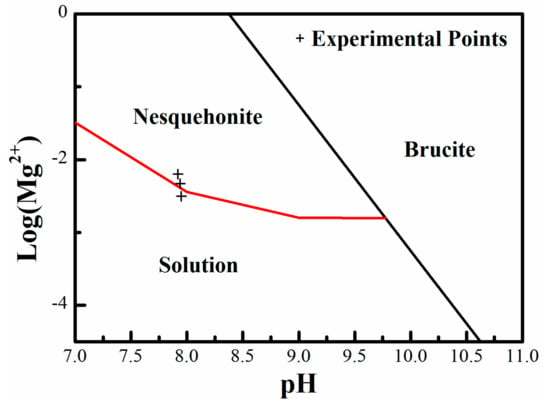
Figure 1.
Stability diagram of brucite and nesquehonite with respect to Mg2+ activity and solution pH. The cross symbols mark the compositions of experimental solutions in this study.
2.3. Growth Experiments Measured by In Situ AFM
A Bruker Nanoscope IV Scanning Probe Microscope equipped with a flow-through fluid cell and Si3N4 cantilevers was used to collect AFM images. The operational process was similar to that in our previous study [42]. After flatjaw pinchcocks were turned on, a flowing system formed between the O-ring installed on the fluid cell and sample. The flow rate of solutions was performed at 550 uL/min throughout the in situ growth experiment.
2.4. SEM, XRD and Raman Spectroscopy Analysis
SU8010 cold field emission SEM (FESEM, Hitachi, Japan), equipped with energy dispersive X-ray spectroscopy (EDS) (AMETEK-EDAX, Mahwah, NJ, USA), was utilized to observe surface morphologies and chemical compositions after growth under different conditions. In addition, mineral phases precipitated on the surfaces of substrates were analyzed by a Rigaku DMAX Rapid II X-ray diffraction system (Rigaku, Tokyo, Japan) (MoKα radiation), at 50 mV and 30 mA. A Micro-confocal Raman spectrometer (in Via, Renishaw-RM 2000 (Renishaw, Gloucestershire, UK)) at 532 nm laser extinction was also used to identify precipitates formed on these substrates.
3. Results
3.1. The Heterogeneous Nucleation and Growth of CaCO3 on Calcite (104) Surfaces
Under Mg2+/Ca2+ = 0 conditions, spiral growth of calcite, with the monomolecular of growth hillock around 3.1 Å, is observed as the solution system reaches a steady-state (Figure S1a–c and Figure 2a). The morphology of growth hillock is a rhombus which consists of two acute and obtuse angles (Figure S1d). The terrace width (λ) of steps is negatively correlated to the increase in solution SIcalcite (Figure S1a–c) [3]. When the SIcalcite of the solutions is equal to 0.50, 0.83 and 1.05, the λ values of obtuse steps are 175.43, 171.25 and 123.60 nm, respectively, while those of acute steps are 77.33, 74.25 and 62.80 nm, respectively. In addition, the calcite (104) surface after growing in the solution at SIcalcite = 1.05 and Mg2+/Ca2+ = 0 was characterized by SEM and EDS. We observed that these growth hillocks are covered by a layer of CaCO3 crust, which is smooth and evenly distributed (Figure S1e–g).
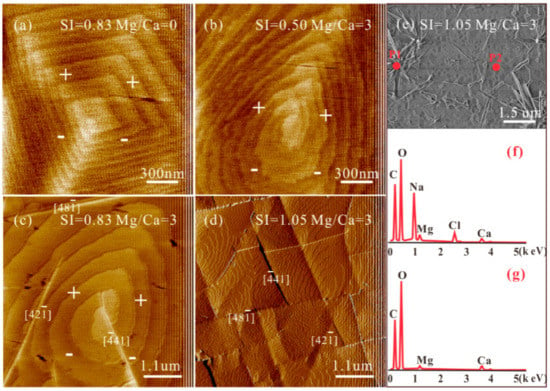
Figure 2.
AFM results of the calcite (104) cleavage surfaces in solutions at pH = 8.0 ± 0.1 of height images with (a) SIcalcite = 0.83, Mg2+/Ca2+ = 0; (b) SIcalcite = 0.50, Mg2+/Ca2+ = 3; (c) SIcalcite = 0.83, Mg2+/Ca2+ = 3; and deflection image with (d) SIcalcite = 1.05, Mg2+/Ca2+ = 3; and (e) SEM image with SIcalcite = 1.05 and Mg2+/Ca2+ = 3, and (f) and (g) represent EDS analysis of P1 and P2 labeled in (e), respectively.
The effects of SIcalcite and Mg2+/Ca2+ ratios on calcite growth were investigated. Under the condition of Mg2+/Ca2+ = 3 and SIcalcite = 0.50, a tear-drop shaped morphology of growth hillock emerges on the calcite (104) surface (Figure 2b). With a modest increase in SIcalcite to 0.83, a sudden buckling of terraces cutting through multiple steps forms. These buckled terraces possess ridges in the direction of [42], [41] and [48], segmenting the calcite surface into multiple area blocks (Figure 2c). Continuously elevating the SIcalcite to 1.05, the number of segments increases on the calcite (104) surface (Figure 2d). SEM images and EDS spectra of the calcite (104) surface after growing at SIcalcite = 1.05 and Mg2+/Ca2+ = 3 were acquired (Figure 2e). Except for the needlelike NaCl crystals produced on the substrate, the other precipitates are Ca(1-x)MgxCO3 with segmented surfaces. We also used EDS to semi-quantify the Mg2+ contents in these overgrowths precipitated on calcite (104) substrates in the solution at Mg2+/Ca2+ =3 and SIcalcite = 1.05, discovering that it ranges from 24.68 at% (P2) to 43.20 at% (P1).
3.2. The Heterogeneous Nucleation and Growth of CaCO3 on Aragonite (110) Surfaces
Under conditions of Mg2+/Ca2+ = 0, the heterogeneous nucleation and growth of CaCO3 on aragonite (110) substrates were investigated at low, intermediate, and high SIcalcite. At SIcalcite = 0.50, nanoparticles gradually precipitated on the aragonite (110) growth surface. These nanoparticles increase in size and number with time (Figure 3). After 190 min, we observed that these individual nanoparticles elongate along the [10] direction, while the aggregates of these nanoparticles form crystals extending along the [001] direction (Figure 3f), indicating a substrate-controlled OA growth pathway. Nevertheless, we can only observe columnar crystals extending along the [001] direction on polished aragonite (110) surfaces, without discovering the solid-solid interfaces among these nanoparticles in the solution at SIcalcite = 0.50 (Figure 4). Increasing SIcalcite to 0.83, the aggregation rate of nanoparticles is enhanced (Figure 5). Crusts composed of nanoparticles cover the substrate after 5 min (Figure 5c), and these crusts rapidly evolve to elongated columnar crystals (Figure 5c–h). Further increasing SIcalcite to 1.05, the phenomena are generally similar to what is observed in the solution at SIcalcite = 0.83, except that crusts only sporadically cover the substrate (Figure S2).

Figure 3.
AFM height images of the aragonite (110) growth surface in solutions (Mg2+/Ca2+ = 0, SIcalcite = 0.50) under flowing conditions at pH = 8.0 ± 0.1 for (a) 0, (b) 5, (c) 30, (d) 160 and (e) 190 min, and (f) denotes the same zone marked with red box in (e). The region marked with the red box in (a) represents the same zones in (b–e).

Figure 4.
AFM height images of the polished aragonite (110) surface in solution (Mg2+/Ca2+ = 0, SIcalcite = 0.50) under static conditions at pH = 8.0 ± 0.1 for (a) 3, (b) 6, (c) 9, (d) 12, (e) 24 and (f) 52 min.

Figure 5.
AFM height images of the polished aragonite (110) surface in solution (Mg2+/Ca2+ = 0, SIcalcite = 0.83) under flowing conditions at pH = 8.0 ± 0.1 for (a) 0, (b) 2, (c) 5, (d) 10, (e) 20 and (f) 50 min.
SEM was used to observe aragonite (110) surfaces after the heterogeneous nucleation and growth of CaCO3 in solutions with different SIcalcite. The size and morphology of these crystals are identical, while the orientation of crystals in the lower and upper layers is disparate. Crystals in the lower layer have their c axes parallel to aragonite (110) substrates, whereas those in the upper layer have their c axes perpendicular to the substrates (Figure 6). The surfaces of these crystals are generally smooth, only with local cracks and holes (as indexed by the red arrows in Figure 6f,h). In addition, nanoparticles are observed from the broken parts and a few crystal surfaces (as indexed by the red arrows in Figure 6e,f).

Figure 6.
SEM images of (a) the polished aragonite (110) surface, and polished aragonite (110) surfaces after growing in solutions with Mg2+/Ca2+ = 0 and (b,c) SIcalcite = 0.50; (d–f) SIcalcite = 0.83; (g–i) SIcalcite = 1.05.
The heterogeneous nucleation and growth of CaCO3 on polished aragonite (110) substrates were investigated in solutions under Mg2+/Ca2+ = 3. The aggregation process of nanoparticles, which is similar to that without Mg2+ addition, can be captured by in situ AFM (Figure 7). Meanwhile, the interfaces among these nanoparticles are extremely obvious, even after 180 min (as indexed by the red arrows in Figure 7h). Increasing SIcalcite to 0.83 and eventually to 1.05, the aggregation rate of nanoparticles soars, while their solid-solid interfaces are still preserved (Figure 8 and Figure S3).

Figure 7.
AFM height images of the polished aragonite (110) surface in the solution (Mg2+/Ca2+ = 3, SIcalcite = 0.50) under flowing conditions at pH = 8.0 ± 0.1 for (a) 0, (b) 5, (c) 11, (d) 20, (e) 30, (f) 50, (g) 80 and (h) 180 min.

Figure 8.
AFM height images of the polished aragonite (110) surface in the solution (Mg2+/Ca2+ = 3, SIcalcite = 0.83) under flowing conditions at pH = 8.0 ± 0.1 for (a) 0, (b) 5, (c) 20, (d) 30 and (e) 70 min, and (f) represents the same zone marked with red box in (e), which grows for 80 min.
The surfaces after growing in supersaturated solutions with Mg2+/Ca2+ = 3 were analyzed by SEM. Although some rhombohedral particles form on these substrates, tower-like and elongated columnar crystals are major precipitates (Figure 9a,c,e). Additionally, some crystals with smooth surfaces generate around these tower-like crystals (Figure 9c,f). The surface roughness of these tower-like crystals, positively correlated with the increase in SIcalcite, is greater than that of crystals precipitated in Mg2+-free solutions (Figure 9b,d,f).

Figure 9.
SEM images of the polished aragonite (110) surfaces after growing in solutions with Mg2+/Ca2+ = 0 and (a,b) SIcalcite = 0.50; (c,d) SIcalcite = 0.83; (e,f) SIcalcite = 1.05.
3.3. Mineral Phases of CaCO3 Dependent on Calcite (104) and Aragonite (110) Substrates
Mineral phases of CaCO3 precipitates have been identified by XRD and Raman analyses. The XRD results show that calcite and aragonite tend to precipitate on calcite (104) and aragonite (110) substrates, respectively (Figure 10a). Under our experimental conditions, the addition of Mg2+ does not induce the formation of protodolomite, dolomite, hydromagnesite (e.g., nesquehonite) or magnesite (Figure 10b). In addition, the relative intensity of XRD reflections is distinct after CaCO3 grows on calcite (104) and aragonite (110) substrates in different solutions. The Raman results demonstrate that the mineral phase of aragonite formed on aragonite (110) substrates will not be affected by solution SIcalcite (Figure 11a). In addition, we cannot observe the obvious change in mineral phase under Mg2+/Ca2+ = 3 compared with that under Mg2+/Ca2+ = 0 (Figure 11b).
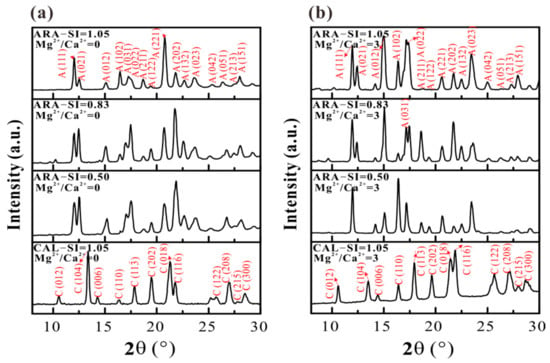
Figure 10.
XRD patterns of the calcite (104) and aragonite (110) substrates after growing in solutions at SIcalcite = 0.50 – 1.05 with (a) Mg2+/Ca2+ = 0, and (b) Mg2+/Ca2+ = 3.
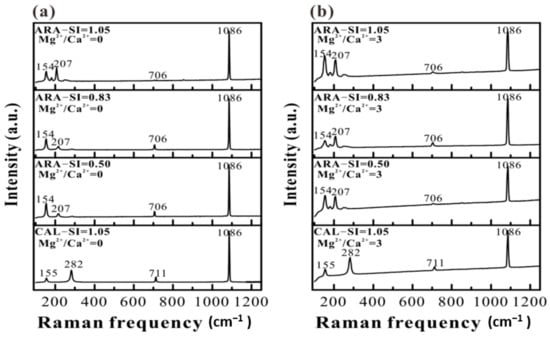
Figure 11.
Raman spectra of the calcite (104) and aragonite (110) substrates after growing in solutions at SIcalcite = 0.50–1.05 with (a) Mg2+/Ca2+ = 0, and (b) Mg2+/Ca2+ = 3.
4. Discussion
4.1. Different Crystallization Pathways of Heterogeneous Nucleation and Growth of CaCO3 on Calcite (104) and Aragonite (110) Surfaces
Classical and nonclassical nucleation and growth theories play critical roles in understanding the formation of minerals. The former stresses the whole processes, including the diffusion of monomers from solution to solid surfaces, the transformation of monomers from surfaces to active sites, and eventually the growth of crystals [43]. The latter emphasizes the formation and aggregation of precursors in the solution [44]. Based on our results, CaCO3 crystals formed on calcite (104) surfaces crystallize by spiral growth, and these CaCO3 crystals are not typical rhombohedral calcite particles. In contrast, nanoparticles are initially generated on aragonite (110) surfaces, and then followed by OA and finally form elongated columnar crystals. These crystals precipitated on aragonite (110) surfaces are divided into two layers. The crystals in the first layer are arranged with their c axes parallel to the substrate, while those in the second layer are perpendicular to the substrate. These two different orientations of crystals can be ascribed to the limitation of growth space [45]. The growth of crystals in the second layer is constrained by gaps between crystals formed in the first layer, leading to vertical extension. The SEM results show that the crystals are composed of nanoparticles, which is evidence of particle aggregation. Therefore, we proposed that the heterogeneous nucleation and growth of CaCO3 on calcite (104) surfaces are in accordance with classical nucleation and growth theory (i.e., monomer-by-monomer addition), while those on aragonite (110) surfaces conform to nonclassical nucleation and growth theory (i.e., precursor attachment).
The results of XRD and Raman analyses demonstrate that the CaCO3 precipitated on calcite (104) surfaces is calcite, whereas that formed on aragonite (110) surfaces is aragonite, which is attributed to the complete lattice match between minerals with identical phases [31,46]. The relative intensity of XRD reflections, as well as Raman frequencies, of the same type of substrate grown in different solutions is distinct, which is ascribed to different orientations of CaCO3 precipitates on local surfaces. Additionally, the surface roughness of aragonite (110) is greater than that of the calcite (104) surfaces in this study, causing the drop in local supersaturation on aragonite (110) surfaces and the eventual formation of sporadic rhombohedral CaCO3 (probably calcite) (Figure 9).
The crystallization pathways of calcite and aragonite on calcite (104) and aragonite (110) surfaces in this study are similar to those precipitated in homogeneous systems [47,48,49]. Hence, the differences in crystallization pathways between calcite and aragonite may be decided by their own crystalline behaviors. A previous study proposed that the binding force of rhombic crystals in 3D directions is identical, while that of prismatic crystals along the c axes is greater than that in both the a and b directions [50], which perfectly explains our AFM observations that aggregates of nanoparticles formed on aragonite (110) surfaces extend along the c axes.
4.2. Effects of Mg2+ and Saturation States on the Heterogeneous Nucleation and Growth of CaCO3 on Calcite (104) and Aragonite (110) Surfaces
Both Mg2+/Ca2+ ratios and solution supersaturations impact CaCO3 growth. On the one hand, when Mg2+/Ca2+ ratios increase from 0 to 3, the spiral growth of calcite is inhibited. Sethmann et al. (2010) observed the segmentation of Mg-calcite thin films on calcite (104) surfaces, and they discovered that the premise of ridge formation is to break through the critical thickness (about 12 nm), which signifies the release of compress stress when the thickness exceeds the critical value [51]. Due to the ionic radius of Mg2+ (0.86 Å) being about 30% smaller than that of Ca2+ (1.14 Å) [52], the Mg2+ substitution of Ca2+ will increase the compress stress. This stress will be released through layer buckling and breaking along the [41], [48] and [42] directions [37].
On the other hand, Mg2+ also decreases the crystallization rate of aragonite. The magnitude of the kinetic coefficient (β) is controlled by the density of kink sites along the step (nk) and the net probability of attachment to a site ((exp(Ek/kT), where k and T represent the Boltzmann constant and Kelvin temperature, respectively, and Ek denotes an effective barriers to attachment at a kink). Namely, β ~ nk exp(-Ek/kT) [53]. As many nanoparticles form on aragonite (110) surfaces, the nk reaches the maximum value. Therefore, the exp(Ek/kT), instead of the nk, is the major factor affecting β. Since the exp(Ek/kT) is related to the desolvation of cations, which is the rate-limiting step during CaCO3 growth, the dynamics of particle aggregation would be restricted when solvation layers are strongly bounded [44]. The desolvation of Mg2+ is more difficult than that of Ca2+, resulting in a slower crystallization rate of aragonite in Mg2+-bearing solutions. As a result, the OA of nanoparticles aggregates along the [001] direction is much easier to be observed.
As supersaturations of solutions are positively correlated with growth rates of CaCO3 [2], the aggregation rate of nanoparticles is obviously accelerated in solutions with higher supersaturation. However, the solid-solid interfaces among nanoparticles are still obvious under these conditions (Figure 8 and Figure S3), indicating that it is difficult to eliminate the inhibition of Mg2+ on the crystalline rate of CaCO3, even in highly supersaturated solutions (from 0.50 to 1.05).
4.3. Comparison with Previous Studies
The IS and Mg2+/Ca2+ ratios in our study are different with those in seawater and some previous studies; nevertheless, our results can be reasonably inferred to CaCO3 precipitation in the ocean. Although the IS in our study (0.1 M) is much lower than that in seawater (IS = 0.7 M), Zhong and Mucci (1989) discovered that salinity variations alone will not significantly affect both the precipitation rates and overgrowth compositions of calcite and aragonite [35]. In addition, the critical Mg2+/Ca2+ ratios favoring calcite or aragonite ranges from 1.5 to 2 [30,54], and when the Mg2+/Ca2+ ratios in solutions are less than 7.5, the distribution coefficients of Mg2+, both in mineral overgrowths and on their adsorbed layers, are positively correlated with Mg2+/Ca2+ ratios of solutions [34]. Therefore, the experimental consequences obtained at Mg2+/Ca2+ = 3 in this study can represent those in real seawater at Mg2+/Ca2+ = 5.
4.3.1. Calcite Precipitation
The growth features of calcite in Mg2+-free solutions (Figure S1a–c) are used for comparison with previous studies. We discovered that the differences in terrace width between obtuse and acute steps (Δλ) are 98.10, 97.00 and 60.80 nm at SIcalcite = 0.50, 0.83 and 1.05, respectively. Since the λ of steps is negatively related to the step velocity [3], the difference in step velocity between obtuse and acute steps is positively correlated with solution SIcalcite at = 10, which is consistent with previous experimental and fitting data [16,17]. Additionally, when we convert SIcalcite = 0.50 to supersaturation σ (SIcalcite = log(exp(σ))), the σ value is equal to 1.15, and we found that the λ values of obtuse and acute steps under our experiment (175.43 and 77.33 nm) are slightly higher than those (152.67 and 75.00 nm) reported by Wasylenki et al. (2005), which may be caused by the minor differences of [55].
The inhibiting effect of Mg2+ on the spreading rate of the calcite growth hillock in this study is similar to that in previous studies. Two basic impurity models for the inhibiting effect of Mg2+ on the growth of calcite (104) surfaces are widely accepted. One is step pinning [56,57], while the other is incorporation [57,58]. In the former model, the adsorption of Mg2+ on step sites is a reversible process, while Mg2+ incorporated into the calcite lattice cannot be reversed in the latter. Based on the inhibiting effect of a newly formed monolayer on the growth of subsequent monolayers, Astilleros et al. (2010) proposed a new solid solution-aqueous solution model, providing an explanation for the formation of “dead zones” in the step pinning model [59]. According to our AFM results (Figure 2b–d), these three models probably coexist. The Mg2+ ions can pin at non-specific sites, while only incorporated at specific sites. Additionally, the surface properties of the first monolayer formed on the calcite (104) surface would be altered upon Mg2+ incorporation, causing the growth inhibition of subsequent monolayers. Some researchers have declared that the incorporation of Mg2+ into calcite leads to the increase in mineral solubility, which contributes to aragonite precipitation [33]. However, based on the thermodynamic simulation, the increase of surface energy by incorporating Mg2+ into calcite is the main reason for the rise of the energy barrier (ΔGC) to form a critical nucleus of calcite [30]. Similarly, the spreading rates of calcite steps are negatively correlated with the free energy (Δg±) (Δg± = –(L/b)Δμ + 2c<γ>±, where L, b, Δμ, c and <γ>± denote step length, 6.4 Å intermolecular distance along the steps, chemical potential, 3.1 Å distance between rows and step edge free energies along the + and − steps, respectively.) [36]. When the Δg± increases with the incorporation of Mg2+ into the steps, the compress stress increases and the spreading rates are inhibited.
The overgrowth compositions of calcite in Mg2+-bearing solutions are also compared. Since the concentration of Mg2+ in calcite overgrowth is independent of precipitation rates [34], the SIcalcite of solutions will not change Mg2+ contents in overgrowth. The contents of Mg2+ semi-quantified in our study (24.68–43.20 at%) are in accordance with Hong et al. (2016)’s calculation that the maximal Mg2+ content which a calcite lattice can sustain before plastic deformation is around 40 at% [37]. However, our value is greater than that obtained in a previous study using the constant disequilibrium technique (crystal-seed systems) (7–10 at%), which is attributed to the effects of the surface or adsorbed layer. As the Mg2+/Ca2+ ratios in the surface or adsorbed layer are higher than those in the overgrowth layer, Mg2+ contents detected in precipitates are greater when the thickness of the overgrowth layer is extremely thin [34].
4.3.2. Aragonite Precipitation
The influence of Mg2+ on aragonite precipitation is a controversial topic [33,39,40], which might be partly ascribed to the limitation of research techniques in the late 20th century. These studies determined the precipitation rate by measuring weight change per unit of time, neglecting the reaction pathways. Fortunately, the in situ AFM has been successfully employed to monitor chemical reaction pathways in the past decades [3,9,16,17,20,36,37,53,55]. Our in situ AFM study discovered that the interfaces among nanoparticles formed on aragonite (110) substrates in solutions with Mg2+/Ca2+ = 3 are more obvious than those in Mg2+-free solutions, demonstrating that the precipitation rate of aragonite is actually inhibited by Mg2+ through retarding the dehydration rate of precursors. However, since these previous experiments were carried out in extremely high supersaturated solutions for several hours, the inhibition of Mg2+ on the precipitation rate of aragonite is not easily detected on the macro-scale. According to our investigation, the aragonite precipitated on aragonite (110) substrates undergoes the oriented attachment of nanoparticles, and thus impacts of Mg2+ on these nanoparticles should not be ignored.
The stability of Mg2+ in aragonite structure directly determines overgrowth compositions. Since the coordination number of Ca2+ in aragonite structure is nine, Mg2+, commonly occurring in six and eight coordination, cannot be preserved in aragonite for a long time. Nevertheless, a small amount of Mg2+ can be conserved in aragonite precursors (e.g., ACC and monoclinic aragonite, i.e., mAra), and the contents of Mg2+ incorporated in structures are gradually released with the transformation of mineral phases [53,60]. This prolonged precipitation provides suitable conditions for releasing Mg2+ from the particle precursors back into the solution, leading to low Mg2+ contents in the ultimate aragonite crystals (<10 at%, which is the maximum value for mAra).
4.4. Implications for the Formation of Abiogenic Carbonate Cements
Our experimental results are consistent with previous inhibition models of Mg2+ on the growth of calcite (104) surfaces. We discovered that the modification mechanisms of Mg2+ on the growth of calcite (104) and aragonite (110) substrates act on the step sites and nanoparticles, respectively, providing a new perspective on the precipitation of abiogenic CaCO3 in the ocean.
It was discovered that the ACC preferentially deposits at the edges of nacreous tablets in the early stage of precipitation, and then transforms into tower-like aragonite with time [61]. This precipitation behavior of CaCO3 is similar to the template effect of soluble macromolecules (SM) on CaCO3 aggregation [62], which is ascribed to the change in interfacial free energy by organic templates. The regulation of organic templates on nucleation widely exists in the formation of CaCO3 in vivo or on organic membranes [63,64].
In shallow marine sedimentary environments, the precipitation of CaCO3 can be divided into three stages. In the first stage, phytoplankton and zooplankton produce biogenic CaCO3 shells through photosynthesis and metabolism [63], respectively, belonging to direct biological regulation. When these plankton die, the precipitation of CaCO3 proceeds into the second stage, in which organic membranes on these shells chiefly control the formation of CaCO3 cements. After these CaCO3 cements cover the majority of organic membranes, the precipitation of CaCO3 enters the third stage, in which abiogenic CaCO3 cements directly overgrow on the CaCO3 substrate.
The findings presented in this study mainly contribute to the CaCO3 precipitation in the third stage, without direct or indirect biological regulation. We observed that elongated columnar aragonite in two layers with different orientations forms on aragonite (110) surfaces, while smooth layered calcite precipitates form on calcite (104) surfaces. That is to say, the heterogeneous nucleation and growth of CaCO3 on aragonite are an important origin of acicular and fibrous aragonite cements, whereas those on calcite are conducive to the formation of the secondary enlargement of calcite cements. Additionally, Mg2+ will inhibit the step growth of calcite and the dehydration rate of aragonite precursors, without changing the crystallization pathways of CaCO3 on these two substrates, suggesting that the precipitation rate of CaCO3 cements is subject to Mg2+/Ca2+ ratios in the ocean. These discussions indicate that the distribution of different types of CaCO3 in shallow-water sediments and Mg2+/Ca2+ ratios in seawater chiefly control the formation and subsequent input flux of abiogenic CaCO3 cements.
5. Conclusions
AFM, SEM, XRD and Raman analyses were utilized to investigate the heterogeneous nucleation and growth of CaCO3 on calcite (104) and aragonite (110) surfaces in abiotic environments, leading to the following conclusions: (1) smooth layered calcite forms on calcite (104) surfaces; (2) elongated columnar aragonite generated by OA of nanoparticles, aggregating along the [001] directions, precipitates on aragonite (110) surfaces; (3) Mg2+ inhibits the growth of aragonite and calcite formed on aragonite (110) and calcite (104) surfaces, by retarding the dehydration of precursors and blocking step growth, respectively, without affecting the crystallization pathways of CaCO3 on these two substrates. The aforementioned conclusions suggest that different types of CaCO3 in shallow-water sediments determine the mineralogy and morphology of abiotic CaCO3 cements, and the lack of abiogenic CaCO3 cements can be partly ascribed to the retardation of Mg2+ on the crystallization rates of both calcite and aragonite.
Supplementary Materials
The following are available online at https://www.mdpi.com/2075-163X/10/4/294/s1, Figure S1. AFM height images of the calcite (104) cleavage surfaces in solutions at Mg2+/Ca2+ = 0 and pH = 8.0 ± 0.1 with (a) SIcalcite = 0.50; (b) SIcalcite = 0.83; (c) SIcalcite = 1.05. (d) Sketch of the atomic arrangements in calcite (104) surface. The cross-section illustrates the angular relationship of the acute and obtuse step edges with terraces. And SEM image with (e) SIcalcite = 1.05; and (f) represents the image of the red box marked zone in (e); and (g) denotes the EDS analysis of P labeled in (f). Figure S2: AFM height images of the polished aragonite (110) surface in solution (Mg2+/Ca2+ = 0, SIcalcite = 1.05) under flowing conditions at pH = 8.0 ± 0.1 for (a) 0, (b) 5, (c) 10, (d) 25, (e) 45 and (f) 80 min. Figure S3: AFM height images of the polished aragonite (110) surface in solution (Mg2+/Ca2+ = 3, SIcalcite = 1.05) under flowing conditions at pH = 8.0 ± 0.1 for (a) 0, (b) 2, (c) 5, (d) 10, (e) 20 and (f) 40 min.
Author Contributions
Conceptualization, H.T., H.X., J.Z., J.W. and H.H.; Methodology, H.T., H.X. and X.W.; Experiments, H.T., J.W. and H.L.; Data curation, H.T., H.X., J.Z. and X.W. Writing—review and editing, H.T., X.W., H.X., J.Z., J.W., H.L., and H.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key R&D Program of China (Grant No. 2017YFC0602305), the National Natural Science Foundation of China (Grant No. 41825003), the Science and Technology Planning Project of Guangdong Province, China (Grant No. 2017B030314175) and the China Postdoctoral Science Foundation (Grant Nos. 2018M643220 and 2019T120755). The APC was funded by the China Postdoctoral Science Foundation (Grant No. 2019T120755).
Acknowledgments
The authors would like to thank Qin Zhou for technical assistants for SEM-EDS analysis. We are grateful to Tingting Chen, Jianlin Liao and Xin Yang for XRD analysis. We thank editors of MDPI and two anonymous reviewers who help us improve this manuscript. This is contribution No.IS-2839 from GIGCAS.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Morse, J.W.; Arvidson, R.S.; Lüttge, A. Calcium Carbonate Formation and Dissolution. Chem. Rev. 2007, 107, 342–381. [Google Scholar] [CrossRef]
- Lasaga, A.C. Kinetic Theory in the Earth Sciences; Princeton University Press: Princeton, NJ, USA, 1998; Available online: https://www.jstor.org/stable/j.ctt7zvgxm (accessed on 23 March 2019).
- Teng, H.H.; Dove, P.M.; De Yoreo, J.J. Kinetics of calcite growth: Surface processes and relationships to macroscopic rate laws. Geochim. Cosmochim. Acta 2000, 64, 2255–2266. [Google Scholar] [CrossRef]
- Davies, G.R. Former magnesian calcite and aragonite submarine cements in upper Paleozoic reefs of the Canadian Arctic: A summary. Geology 1977, 5, 11–15. [Google Scholar] [CrossRef]
- Kendall, A.C. Fascicular-optic calcite; a replacement of bundled acicular carbonate cements. J. Sediment. Res. 1977, 47, 1056–1062. [Google Scholar] [CrossRef]
- Reid, R.P.; Macintyre, I.G. Carbonate recrystallization in shallow marine environments: A widespread diagenetic process forming micritized grains. J. Sediment. Res. 1998, 68, 928–946. [Google Scholar] [CrossRef]
- Walter, L.M. Relative efficiency of carbonate dissolution and precipitation during diagenesis: A progress report on the role of solution chemistry. Soc. Econ. Paleontol. Mineral. Spec. Publ. 1986, 38, 1–12. [Google Scholar]
- Burton, E.A.; Walter, L.M. The role of pH in phosphate inhibition of calcite and aragonite precipitation rates in seawater. Geochim. Cosmochim. Acta 1990, 54, 797–808. [Google Scholar] [CrossRef]
- Renard, F.; Montes-Hernandez, G.; Ruiz-Agudo, E.; Putnis, C.V. Selenium incorporation into calcite and its effect on crystal growth: An atomic force microscopy study. Chem. Geol. 2013, 340, 151–161. [Google Scholar] [CrossRef]
- Xu, M.; Riechers, S.L.; Ilton, E.S.; Du, Y.; Kovarik, L.; Varga, T.; Arey, B.W.; Qafoku, O.; Kerisit, S. Manganese-calcium intermixing facilitates heteroepitaxial growth at the (101¯4) calcite-water interface. Chem. Geol. 2017, 470, 152–163. [Google Scholar] [CrossRef]
- Dobberschutz, S.; Nielsen, M.R.; Sand, K.K.; Civioc, R.; Bovet, N.; Stipp, S.L.S.; Andersson, M.P. The mechanisms of crystal growth inhibition by organic and inorganic inhibitors. Nat. Commun. 2018, 9, 1–6. [Google Scholar] [CrossRef]
- Schott, J.; Pokrovsky, O.S.; Oelkers, E.H. The Link between Mineral Dissolution/Precipitation Kinetics and Solution Chemistry. Rev. Mineral. Geochem. 2009, 70, 207–258. [Google Scholar] [CrossRef]
- Burton, E.A. Controls on marine carbonate cement mineralogy: Review and reassessment. Chem. Geol. 1993, 105, 163–179. [Google Scholar] [CrossRef]
- Sunagawa, I. Crystals: Growth, Morphology and Perfection; Cambridge University Press: Cambridge, UK, 2005; pp. 1–308. [Google Scholar]
- Stack, A.G.; Grantham, M.C. Growth rate of calcite steps as a function of aqueous calcium-to-carbonate ratio: Independent attachment and detachment of calcium and carbonate ions. Cryst. Growth Des. 2010, 10, 1409–1413. [Google Scholar] [CrossRef]
- Larsen, K.; Bechgaard, K.; Stipp, S.L.S. The effect of the Ca2+ to CO32− activity ratio on spiral growth at the calcite (101¯4) surface. Geochim. Cosmochim. Acta 2010, 74, 2099–2109. [Google Scholar] [CrossRef]
- Sand, K.K.; Tobler, D.J.; Larsen, K.K.; Makovicky, E.; Andersson, M.P.; Stipp, S.L.S. Calcite growth kinetics: Dependence on saturation index, Ca2+:CO32−activity ratio, and surface atomic structure. Cryst. Growth Des. 2016, 16, 3602–3612. [Google Scholar] [CrossRef]
- Gutjahr, A.; Dabringhaus, H.; Lacmann, R. Studies of the growth and dissolution kinetics of the CaCO3 polymorphs calcite and aragonite II. The influence of divalent cation additives on the growth and dissolution rates. J. Cryst. Growth 1996, 158, 310–315. [Google Scholar] [CrossRef]
- Dove, P.M.; De Yoreo, J.J.; Weiner, S. Biomineralization: Reviews in Mineralogy and Geochemistry; Mineralogical Society of America; Geochemical Society: Chantilly, VA, USA; Washington, DC, USA, 2003; pp. 1–377. [Google Scholar]
- Xu, J.; Wang, J.; Hong, M.; Teng, H.H. Solution-chemistry control of Mg2+-calcite interaction mechanisms: Implication for biomineralization. Am. Mineral. 2016, 101, 1104–1112. [Google Scholar] [CrossRef]
- Mavromatis, V.; Goetschl, K.E.; Grengg, C.; Konrad, F.; Purgstaller, B.; Dietzel, M. Barium partitioning in calcite and aragonite as a function of growth rate. Geochim. Cosmochim. Acta 2018, 237, 65–78. [Google Scholar] [CrossRef]
- Berner, R.; Westrich, J.; Graber, R.; Smith, J.; Martens, C. Inhibition of Aragonite precipitation from Supersaturated Seawater: A Laboratory and Field Study. Am. J. Sci. 1978, 278, 816–837. [Google Scholar] [CrossRef]
- Morse, J.W.; Mucci, A. Composition of carbonate overgrowths produced on Iceland spar calcite crystals buried in Bahamian carbonate-rich sediments. Sediment. Geol. 1984, 40, 287–291. [Google Scholar] [CrossRef]
- Lioliou, M.G.; Paraskeva, C.A.; Koutsoukos, P.G.; Payatakes, A.C. Heterogeneous nucleation and growth of calcium carbonate on calcite and quartz. J. Colloid Interface Sci. 2007, 308, 421–428. [Google Scholar] [CrossRef] [PubMed]
- Ren, D.; Feng, Q.; Bourrat, X. Effects of additives and templates on calcium carbonate mineralization in vitro. Micron 2011, 42, 228–245. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Fernandez-Martinez, A.; Lee, B.; Waychunas, G.A.; Jun, Y.S. Interfacial energies for heterogeneous nucleation of calcium carbonate on mica and quartz. Environ. Sci. Technol. 2014, 48, 5745–5753. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Jun, Y.S. The apparent activation energy and pre-exponential kinetic factor for heterogeneous calcium carbonate nucleation on quartz. Commun. Chem. 2018, 1, 1–9. [Google Scholar] [CrossRef]
- Lin, Y.; Hu, Q.; Chen, J.; Ji, J.; Teng, H.H. Formation of metastable CaCO3 polymorphs in the presence of oxides and silicates. Cryst. Growth Des. 2009, 9, 4634–4641. [Google Scholar] [CrossRef]
- Xu, H.; Zhou, M.; Fang, Y.; Teng, H.H. Effect of mica and hematite (001) surfaces on the precipitation of calcite. Minerals 2018, 8, 17. [Google Scholar] [CrossRef]
- Sun, W.; Jayaraman, S.; Chen, W.; Persson, K.A.; Ceder, G. Nucleation of metastable aragonite CaCO3 in seawater. Proc. Natl. Acad. Sci. USA 2015, 112, 3199–3204. [Google Scholar] [CrossRef]
- Li, L.; Fijneman, A.J.; Kaandorp, J.A.; Aizenberg, J.; Noorduin, W.L. Directed nucleation and growth by balancing local supersaturation and substrate/nucleus lattice mismatch. Proc. Natl. Acad. Sci. USA 2018, 115, 3575–3580. [Google Scholar] [CrossRef]
- Bathurst, R.G. Diagenetically enhanced bedding in argillaceous platform limestones: Stratified cementation and selective compaction. Sedimentology 1987, 34, 749–778. [Google Scholar] [CrossRef]
- Berner, R.A. The role of magnesium in the crystal growth of calcite and aragonite from sea water. Geochim. Cosmochim. Acta 1975, 39, 489–504. [Google Scholar] [CrossRef]
- Mucci, A.; Morse, J.W. The incorporation of Mg2+ and Sr2+ into calcite overgrowths: Influences of growth rate and solution composition. Geochim. Cosmochim. Acta 1983, 47, 217–233. [Google Scholar] [CrossRef]
- Zhong, S.; Mucci, A. Calcite and aragonite precipitation from seawater solutions of various salinities: Precipitation rates and overgrowth compositions. Chem. Geol. 1989, 78, 283–299. [Google Scholar] [CrossRef]
- Teng, H.H.; Dove, P.M.; Orme, C.A.; Yoreo, J.J.D. Thermodynamics of Calcite Growth: Baseline for Understanding Biomineral Formation. Science 1998, 282, 724–727. [Google Scholar] [CrossRef] [PubMed]
- Hong, M.; Xu, J.; Teng, H.H. Evolution of calcite growth morphology in the presence of magnesium: Implications for the dolomite problem. Geochim. Cosmochim. Acta 2016, 172, 55–64. [Google Scholar] [CrossRef]
- Sinha, S.; Rez, P. Distortions of the calcite and aragonite atomic structures from interstitial water. Mater. Chem. Phys. 2015, 157, 56–62. [Google Scholar] [CrossRef]
- Pytkowicz, R.M. Rates of inorganic calcium carbonate nucleation. J. Geol. 1965, 73, 196–199. [Google Scholar] [CrossRef]
- Lippmann, F. Sedimentary Carbonate Minerals; Springer: Berlin/Heidelberg, Germany, 1973; pp. 1–233. [Google Scholar]
- Gustafsson, J.P. Visual MINTEQ 3.0 User Guide; KTH, Department of Land and Water Recources: Stockholm, Sweden, 2011; Available online: http://www2.lwr.kth.se/English/OurSoftware/vminteq/contact.html (accessed on 20 March 2012).
- Tang, H.; Xian, H.; He, H.; Wei, J.; Liu, H.; Zhu, J.; Zhu, R. Kinetics and mechanisms of the interaction between the calcite (10.4) surface and Cu2+-bearing solutions. Sci. Total Environ. 2019, 668, 602–616. [Google Scholar] [CrossRef]
- Van Driessche, A.E.; Kellermeier, M.; Benning, L.G.; Gebauer, D. New Perspectives on Mineral Nucleation and Growth: From Solution Precursors to Solid Materials; Springer: Cham, Switzerland, 2016; pp. 1–380. [Google Scholar]
- De Yoreo, J.J.; Gilbert, P.U.P.A.; Sommerdijk, N.A.J.M.; Penn, R.L.; Whitelam, S.; Joester, D.; Zhang, H.; Rimer, J.D.; Navrotsky, A.; Banfield, J.F.; et al. Crystallization by particle attachment in synthetic, biogenic, and geologic environments. Science 2015, 349, 498–507. [Google Scholar] [CrossRef]
- Gránásy, L.; Pusztai, T.; Tegze, G.; Warren, J.A.; Douglas, J.F. Growth and form of spherulites. Phys. Rev. E 2005, 72, 11605. [Google Scholar] [CrossRef]
- Cubillas, P.; Köhler, S.; Prieto, M.; Causserand, C.; Oelkers, E.H. How do mineral coatings affect dissolution rates? An experimental study of coupled CaCO3 dissolution—CdCO3 precipitation. Geochim. Cosmochim. Acta 2005, 69, 5459–5476. [Google Scholar] [CrossRef]
- Zhou, G.T.; Yao, Q.Z.; Ni, J.; Jin, G. Formation of aragonite mesocrystals and implication for biomineralization. Am. Mineral. 2009, 94, 293–302. [Google Scholar] [CrossRef]
- Nielsen, M.H.; Aloni, S.; De Yoreo, J.J. In situ TEM imaging of CaCO3 nucleation reveals coexistence of direct and indirect pathways. Science 2014, 345, 1158–1162. [Google Scholar] [CrossRef] [PubMed]
- Walker, J.M.; Marzec, B.; Nudelman, F. Solid-State Transformation of Amorphous Calcium Carbonate to Aragonite Captured by CryoTEM. Angew. Chem. Int. Edit. 2017, 56, 11740–11743. [Google Scholar] [CrossRef] [PubMed]
- Alberstein, R.G.; Tezcan, F.A. Observations of the birth of crystals. Nature 2018, 556, 41–42. [Google Scholar] [CrossRef] [PubMed]
- Sethmann, I.; Wang, J.; Becker, U.; Putnis, A. Strain-induced segmentation of magnesian calcite thin films growing on a calcite substrate. Cryst. Growth Des. 2010, 10, 4319–4326. [Google Scholar] [CrossRef]
- Shannon, R.D. Revised effective ionic-radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr. Sect. A. 1976, 32, 751–767. [Google Scholar] [CrossRef]
- Elhadj, S.; De Yoreo, J.J.; Hoyer, J.R.; Dove, P.M. Role of molecular charge and hydrophilicity in regulating the kinetics of crystal growth. Proc. Natl. Acad. Sci. USA 2006, 103, 19237–19242. [Google Scholar] [CrossRef]
- Nemeth, P.; Mugnaioli, E.; Gemmi, M.; Czuppon, G.; Demeny, A.; Spoetl, C. A nanocrystalline monoclinic CaCO3 precursor of metastable aragonite. Sci. Adv. 2018, 4, eaau6178. [Google Scholar] [CrossRef]
- Wasylenki, L.E.; Dove, P.M.; Wilson, D.S.; De Yoreo, J.J. Nanoscale effects of strontium on calcite growth: An in situ AFM study in the absence of vital effects. Geochim. Cosmochim. Acta 2005, 69, 3017–3027. [Google Scholar] [CrossRef]
- Teng, H.H.; Dove, P.M.; DeYoreo, J.J. Reversed calcite morphologies induced by microscopic growth kinetics: Insight into biomineralization. Geochim. Cosmochim. Acta 1999, 63, 2507–2512. [Google Scholar] [CrossRef]
- De Yoreo, J.J.; Vekilov, P.G. Principles of crystal nucleation and growth. In Biomineralization: Reviews in Mineralogy and Geochemistry; Mineralogical Society of America; Geochemical Society: Chantilly, VA, USA; Washington, DC, USA, 2003; Volume 54, pp. 57–93. [Google Scholar]
- Davis, K.J.; Dove, P.M.; De Yoreo, J.J. The role of Mg2+ as an impurity in calcite growth. Science 2000, 290, 1134–1137. [Google Scholar] [CrossRef] [PubMed]
- Astilleros, J.; Fernández-Díaz, L.; Putnis, A. The role of magnesium in the growth of calcite: An AFM study. Chem. Geol. 2010, 271, 52–58. [Google Scholar] [CrossRef]
- Mass, T.; Giuffre, A.J.; Sun, C.Y.; Stifler, C.A.; Frazier, M.J.; Neder, M.; Tamura, N.; Stan, C.V.; Marcus, M.A.; Gilbert, P.U. Amorphous calcium carbonate particles form coral skeletons. Proc. Natl. Acad. Sci. USA 2017, 114, 7670–7678. [Google Scholar] [CrossRef]
- Luo, C.; Xie, L.; Wang, X.X. In vitro growth of aragonite crystal on nacre surface. Key Eng. Mat. 2007, 330, 1335–1338. [Google Scholar] [CrossRef]
- Gal, A.; Wirth, R.; Kopka, J.; Fratzl, P.; Faivre, D.; Scheffel, A. Macromolecular recognition directs calcium ions to coccolith mineralization sites. Science 2016, 353, 590–593. [Google Scholar] [CrossRef] [PubMed]
- Branson, O.; Bonnin, E.A.; Perea, D.E.; Spero, H.J.; Zhu, Z.; Winters, M.; Hönisch, B.; Russell, A.D.; Fehrenbacher, J.S.; Gagnon, A.C. Nanometer-scale chemistry of a calcite biomineralization template: Implications for skeletal composition and nucleation. Proc. Natl. Acad. Sci. USA 2016, 113, 12934–12939. [Google Scholar] [CrossRef]
- Gal, A.; Wirth, R.; Barkay, Z.; Eliaz, N.; Scheffel, A.; Faivre, D. Templated and self-limiting calcite formation directed by coccolith organic macromolecules. Chem. Commun. 2017, 53, 7740–7743. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).