Characterisation and Modelling of Gravity Pre-Concentration Amenability Using LST Fluidisation in a REFLUXTM Classifier
Abstract
:1. Introduction
2. Experimental
2.1. REFLUXTM Classifier Fractionation
2.2. Extraction of Partition Data
3. Results and Discussion
3.1. Partition Surface of the REFLUXTM Classifier
3.1.1. Sink/Float versus LST Flow Fractionation
3.1.2. Partition Surface for Gold-Bearing Ore based on LST Flow Fractionation
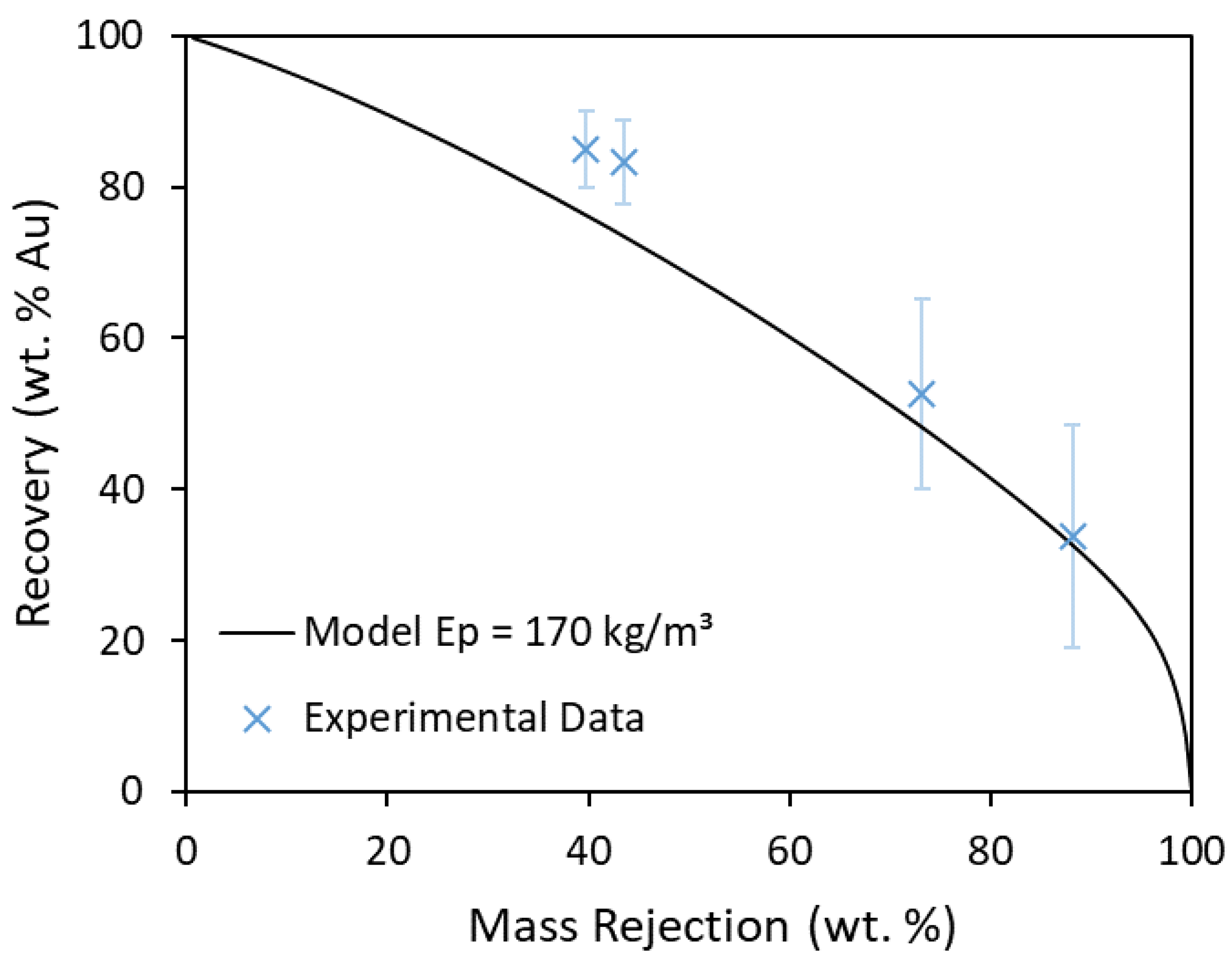
3.2. Process Modelling
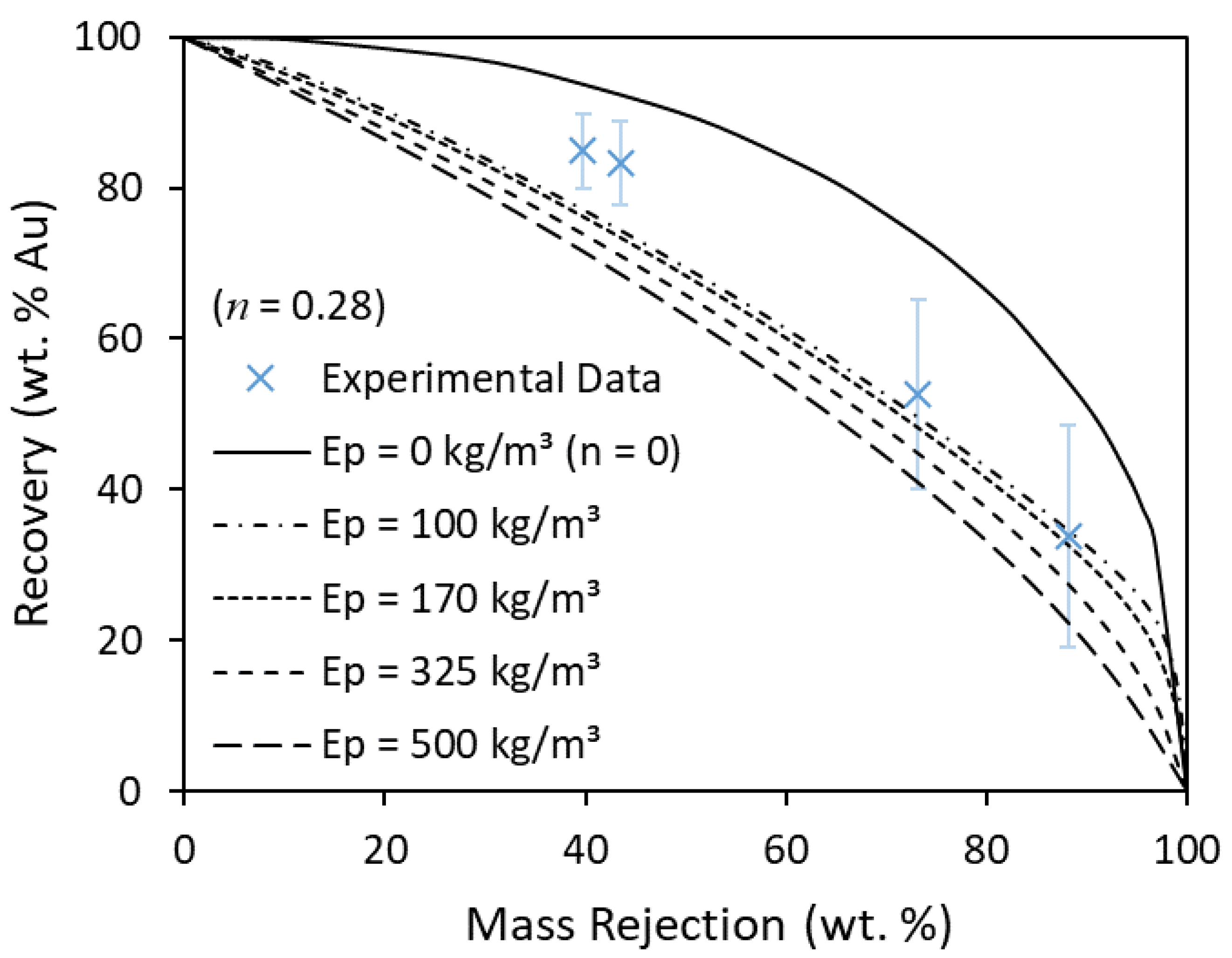
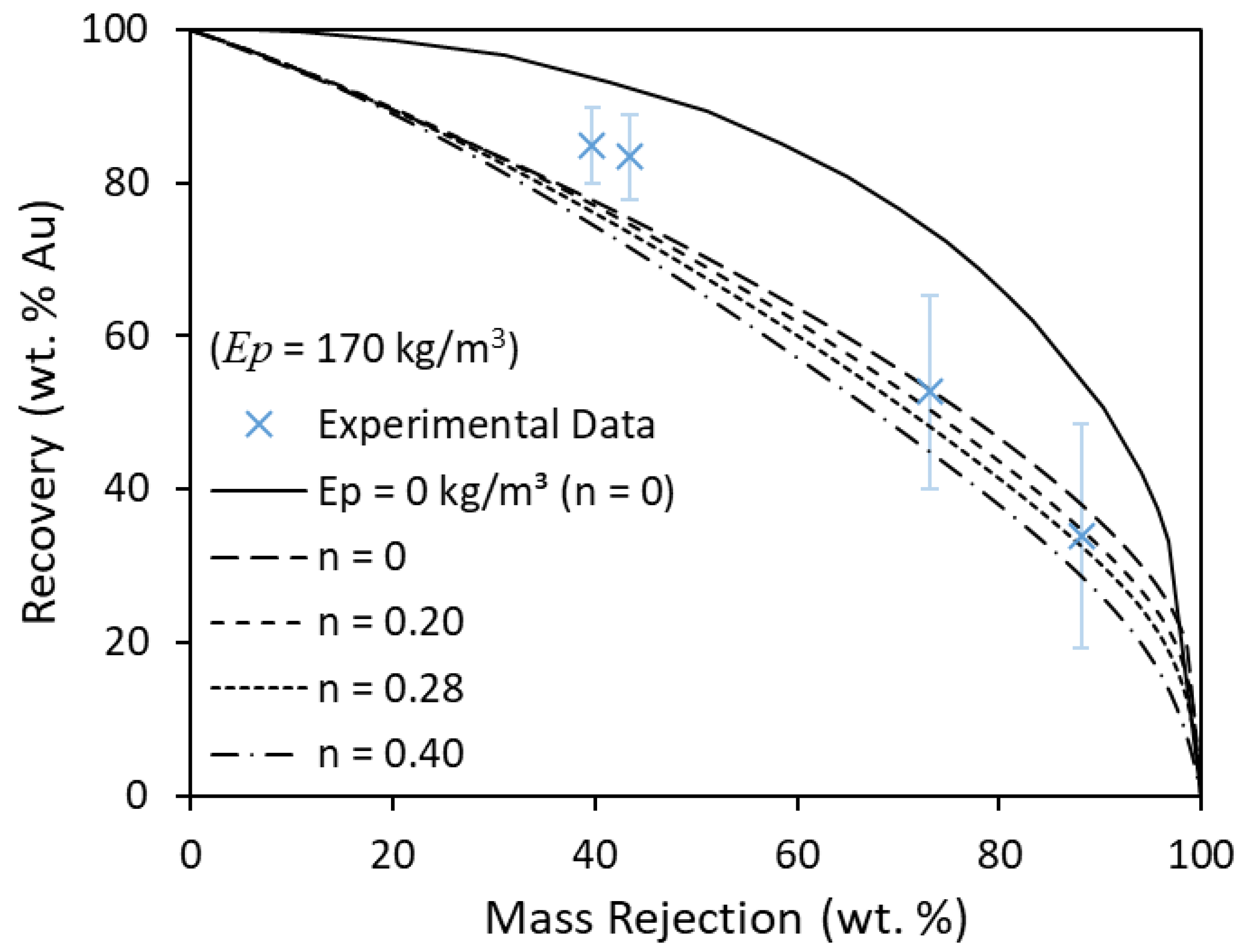
3.3. Sensitivity Analysis on Ep and n
3.4. Final Discussion
4. Conclusions
5. Patents
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Feed | Underflow | Overflow | |||||
|---|---|---|---|---|---|---|---|
| Flow Fraction | Size Interval | Mass | Average Density | Mass | Average Density | Mass | Average Density |
| (-) | (µm) | (g) | (kg/m3) | (g) | (kg/m3) | (g) | (kg/m3) |
| 1 | −300 + 212 | 11.0 | 2753.0 | 10.0 | 2837.8 | 5.7 | 2706.8 |
| −212 + 150 | 19.8 | 2751.3 | 6.4 | 2951.0 | 10.5 | 2700.2 | |
| −150 + 106 | 28.4 | 2750.6 | 4.0 | 3124.3 | 13.7 | 2692.6 | |
| −106 + 75 | 30.7 | 2762.9 | 4.1 | 3277.0 | 23.7 | 2698.6 | |
| −75 + 53 | 35.1 | 2794.7 | 3.8 | 3403.2 | 18.6 | 2702.3 | |
| −53 + 38 | 29.0 | 2851.5 | 3.0 | 3840.5 | 14.3 | 2712.6 | |
| 2 | −300 + 212 | 11.7 | 2945.1 | 24.4 | 3233.8 | 10.7 | 2748.9 |
| −212 + 150 | 20.6 | 2993.6 | 28.3 | 3295.9 | 26.4 | 2756.3 | |
| −150 + 106 | 27.3 | 3067.2 | 18.0 | 3332.1 | 33.0 | 2756.7 | |
| −106 + 75 | 50.0 | 3220.7 | 5.0 | 3393.4 | 42.3 | 2787.8 | |
| −75 + 53 | 42.0 | 3285.9 | 6.3 | 4302.7 | 29.5 | 2688.2 | |
| −53 + 38 | 31.1 | 3316.2 | 15.9 | 4472.5 | 25.1 | 2979.6 | |
| 3 | −300 + 212 | 16.1 | 3231.8 | 41.0 | 3368.6 | 18.9 | 2968.5 |
| −212 + 150 | 28.8 | 3274.8 | 38.0 | 3387.5 | 46.3 | 3017.2 | |
| −150 + 106 | 33.2 | 3301.7 | 17.8 | 3442.8 | 57.9 | 3075.0 | |
| −106 + 75 | 44.4 | 3349.8 | 10.3 | 4199.9 | 51.0 | 3159.2 | |
| −75 + 53 | 27.6 | 3430.9 | 46.0 | 4504.9 | 43.1 | 3237.4 | |
| −53 + 38 | 18.4 | 3692.5 | 18.5 | 4517.8 | 29.4 | 3303.6 | |
| 4 | −300 + 212 | 25.0 | 3358.6 | 7.3 | 3643.4 | 20.7 | 3295.6 |
| −212 + 150 | 43.6 | 3366.8 | 8.8 | 3912.6 | 53.6 | 3314.5 | |
| −150 + 106 | 46.3 | 3376.3 | 17.9 | 4337.2 | 69.4 | 3327.3 | |
| −106 + 75 | 36.5 | 3486.2 | 62.2 | 4497.0 | 67.3 | 3343.8 | |
| −75 + 53 | 30.4 | 3985.5 | 58.2 | 4520.5 | 45.5 | 3365.9 | |
| −53 + 38 | 25.0 | 4245.9 | 12.6 | 4516.5 | 17.3 | 3427.0 | |
| 5 | −300 + 212 | 22.2 | 3621.5 | 32.0 | 4457.2 | 24.0 | 3383.9 |
| −212 + 150 | 27.7 | 3753.5 | 72.9 | 4494.0 | 75.4 | 3389.4 | |
| −150 + 106 | 33.1 | 4028.7 | 125.7 | 4507.5 | 72.7 | 3409.9 | |
| −106 + 75 | 68.4 | 4373.0 | 86.4 | 4519.2 | 78.8 | 3547.8 | |
| −75 + 53 | 45.9 | 4449.1 | 26.0 | 4529.3 | 52.9 | 3793.1 | |
| −53 + 38 | 20.2 | 4434.4 | 5.4 | 4491.7 | 33.6 | 4088.5 | |
| 6 | −300 + 212 | 18.3 | 4437.8 | 58.3 | 4514.8 | 4.1 | 3467.4 |
| −212 + 150 | 52.8 | 4495.1 | 93.0 | 4514.1 | 10.7 | 3654.7 | |
| −150 + 106 | 76.1 | 4508.8 | 76.1 | 4518.0 | 19.7 | 3909.8 | |
| −106 + 75 | 46.8 | 4515.2 | 24.2 | 4520.1 | 33.9 | 4277.9 | |
| −75 + 53 | 21.1 | 4509.0 | 6.0 | 4494.8 | 30.0 | 4426.2 | |
| −53 + 38 | 6.6 | 4461.4 | 1.0 | 4487.4 | 16.2 | 4475.2 | |
| 7 | −300 + 212 | 38.8 | 4518.9 | 18.1 | 4515.6 | 1.0 | 2804.1 |
| −212 + 150 | 42.9 | 4515.7 | 26.1 | 4524.9 | 3.1 | 4108.7 | |
| −150 + 106 | 34.7 | 4514.4 | 23.8 | 4534.8 | 8.4 | 4344.1 | |
| −106 + 75 | 13.3 | 4518.9 | 7.8 | 4572.8 | 12.2 | 4407.2 | |
| −75 + 53 | 6.0 | 4462.5 | 2.8 | 4394.0 | 13.1 | 4453.5 | |
| −53 + 38 | 1.9 | 4315.0 | 0.8 | 10.4 | 4446.7 | ||
| Feed | Underflow | Overflow | |||||
|---|---|---|---|---|---|---|---|
| Flow Fraction | Size Interval | Mass | Average Density | Mass | Average Density | Mass | Average Density |
| (-) | (µm) | (g) | (kg/m3) | (g) | (kg/m3) | (g) | (kg/m3) |
| 1 | −1000 + 710 | 0.1 | 5.6 | 2611.1 | 0.2 | ||
| −710 + 500 | 0.6 | 2583.2 | 23.1 | 2625.1 | 0.8 | 2514.9 | |
| −500 + 355 | 1.1 | 2546.7 | 25.2 | 2639.9 | 1.8 | 2668.3 | |
| −355 + 250 | 3.0 | 2562.5 | 24.4 | 2656.8 | 4.2 | 2586.3 | |
| −250 + 180 | 7.5 | 2582.9 | 10.1 | 2677.2 | 9.5 | 2603.8 | |
| −180 + 125 | 22.1 | 2603.5 | 2.6 | 2693.7 | 27.3 | 2614.7 | |
| −125 + 90 | 35.5 | 2606.3 | 0.6 | 2724.7 | 55.5 | 2623.2 | |
| 2 | −1000 + 710 | 0.1 | 8.0 | 2624.6 | 0.3 | ||
| −710 + 500 | 0.8 | 2610.1 | 35.4 | 2643.5 | 3.8 | 2612.6 | |
| −500 + 355 | 3.6 | 2631.6 | 30.7 | 2659.3 | 12.0 | 2633.1 | |
| −355 + 250 | 13.4 | 2629.2 | 15.6 | 2685.3 | 23.2 | 2639.9 | |
| −250 + 180 | 22.6 | 2631.4 | 3.3 | 2723.4 | 36.0 | 2641.6 | |
| −180 + 125 | 37.2 | 2639.8 | 0.6 | 2820.4 | 65.7 | 2647.6 | |
| −125 + 90 | 41.6 | 2650.5 | 0.1 | 80.2 | 2662.1 | ||
| 3 | −1000 + 710 | 0.3 | 20.7 | 2643.6 | 0.1 | ||
| −710 + 500 | 3.0 | 2625.8 | 79.0 | 2659.9 | 1.7 | 2623.9 | |
| −500 + 355 | 11.6 | 2628.7 | 47.4 | 2674.5 | 5.9 | 2631.5 | |
| −355 + 250 | 25.7 | 2637.9 | 17.4 | 2708.6 | 16.2 | 2633.3 | |
| −250 + 180 | 30.6 | 2646.8 | 3.4 | 2807.5 | 26.8 | 2639.5 | |
| −180 + 125 | 35.2 | 2652.4 | 1.0 | 3072.2 | 40.3 | 2651.0 | |
| −125 + 90 | 25.6 | 2668.5 | 0.5 | 2991.7 | 35.0 | 2670.2 | |
| 4 | −1000 + 710 | 1.3 | 2640.7 | 40.4 | 2592.2 | 0.1 | |
| −710 + 500 | 17.1 | 2634.1 | 100.1 | 2672.6 | 1.0 | 2616.6 | |
| −500 + 355 | 47.8 | 2644.2 | 39.2 | 2694.6 | 4.0 | 2619.2 | |
| −355 + 250 | 64.6 | 2650.9 | 9.5 | 2748.4 | 12.0 | 2622.2 | |
| −250 + 180 | 50.0 | 2657.2 | 1.5 | 2867.9 | 15.4 | 2625.4 | |
| −180 + 125 | 48.1 | 2665.2 | 0.6 | 3118.6 | 16.6 | 2644.4 | |
| −125 + 90 | 30.7 | 2686.5 | 0.2 | 3482.7 | 12.3 | 2666.3 | |
| 5 | −1000 + 710 | 1.1 | 2617.3 | 89.6 | 2671.8 | 0.2 | |
| −710 + 500 | 13.4 | 2641.1 | 154.0 | 2685.5 | 3.8 | 2631.5 | |
| −500 + 355 | 31.5 | 2654.3 | 45.0 | 2721.4 | 14.6 | 2626.0 | |
| −355 + 250 | 33.3 | 2664.2 | 10.0 | 2797.7 | 30.5 | 2640. | |
| −250 + 180 | 24.9 | 2669.2 | 2.1 | 3060.6 | 32.9 | 2647.4 | |
| −180 + 125 | 25.5 | 2681.1 | 1.1 | 3032.9 | 31.7 | 2657.3 | |
| −125 + 90 | 13.4 | 2710.8 | 0.5 | 2804.9 | 18.0 | 2677.3 | |
| 6 | −1000 + 710 | 3.5 | 2638.3 | 115.4 | 2677.7 | 3.4 | 2639.1 |
| −710 + 500 | 33.1 | 2649.4 | 146.9 | 2700.0 | 37.5 | 2648.8 | |
| −500 + 355 | 52.1 | 2659.8 | 33.9 | 2745.3 | 70.5 | 2654.4 | |
| −355 + 250 | 42.0 | 2670.3 | 7.5 | 2822.6 | 73.1 | 2662.1 | |
| −250 + 180 | 31.4 | 2677.8 | 2.2 | 2895.7 | 49.9 | 2655.9 | |
| −180 + 125 | 29.9 | 2692.1 | 1.2 | 3199.3 | 35.3 | 2671.9 | |
| −125 + 90 | 13.3 | 2730.6 | 0.8 | 3136.3 | 14.5 | 2699.7 | |
| 7 | −1000 + 710 | 16.6 | 2640.6 | 164.6 | 2706.5 | 2.6 | 2655.3 |
| −710 + 500 | 72.2 | 2657.6 | 148.4 | 2748.0 | 32.2 | 2654.6 | |
| −500 + 355 | 59.6 | 2673.3 | 32.8 | 2809.5 | 61.0 | 2662.0 | |
| −355 + 250 | 44.8 | 2687.6 | 8.4 | 2916.7 | 64.4 | 2667.1 | |
| −250 + 180 | 31.9 | 2696.1 | 3.4 | 3055.9 | 42.3 | 2671.4 | |
| −180 + 125 | 23.5 | 2718.1 | 1.7 | 3213.4 | 31.0 | 2681.6 | |
| −125 + 90 | 11.6 | 2764.7 | 0.7 | 3209.6 | 12.8 | 2714.5 | |
| 8 | −1000 + 710 | 21.7 | 2657.9 | 75.3 | 2731.4 | 2.7 | 2650.6 |
| −710 + 500 | 83.9 | 2674.9 | 80.4 | 2798.3 | 31.7 | 2662.0 | |
| −500 + 355 | 65.2 | 2693.4 | 20.5 | 2892.1 | 56.6 | 2669.2 | |
| −355 + 250 | 56.0 | 2715.4 | 6.8 | 3018.0 | 51.6 | 2675.9 | |
| −250 + 180 | 43.5 | 2733.1 | 3.1 | 3178.6 | 34.1 | 2680.1 | |
| −180 + 125 | 27.3 | 2766.0 | 1.5 | 3464.4 | 27.8 | 2689.3 | |
| −125 + 90 | 7.6 | 2849.3 | 0.9 | 3901.3 | 11.8 | 2729.3 | |
| 9 | −1000 + 710 | 25.4 | 2673.1 | 46.0 | 2756.7 | 16.5 | 2663.8 |
| −710 + 500 | 91.1 | 2702.0 | 37.0 | 2838.4 | 102.8 | 2675.1 | |
| −500 + 355 | 62.4 | 2733.1 | 9.1 | 2965.0 | 92.3 | 2686.6 | |
| −355 + 250 | 39.6 | 2772.0 | 3.9 | 3131.8 | 62.6 | 2700.3 | |
| −250 + 180 | 22.2 | 2813.9 | 1.8 | 3305.2 | 39.7 | 2704.8 | |
| −180 + 125 | 13.6 | 2862.0 | 1.1 | 3548.6 | 26.9 | 2715.6 | |
| −125 + 90 | 4.6 | 2949.6 | 0.8 | 4077.6 | 11.0 | 2757.1 | |
| 10 | −1000 + 710 | 24.4 | 2690.9 | 32.8 | 2790.6 | 17.4 | 2681.8 |
| −710 + 500 | 74.9 | 2732.6 | 24.0 | 2925.1 | 100.6 | 2700.9 | |
| -500 + 355 | 34.6 | 2791.9 | 9.4 | 3055.3 | 96.3 | 2685.6 | |
| −355 + 250 | 15.2 | 2867.2 | 5.8 | 3193.1 | 87.4 | 2732.9 | |
| −250 + 180 | 7.2 | 2927.6 | 2.9 | 3413.7 | 67.9 | 2742.7 | |
| −180 + 125 | 4.8 | 3012.4 | 2.9 | 3870.2 | 50.2 | 2758.8 | |
| −125 + 90 | 2.7 | 3157.2 | 3.1 | 4333.0 | 16.1 | 2820.1 | |
| 11 | −1000 + 710 | 45.2 | 2703.3 | 24.3 | 2851.0 | 10.0 | 2701.3 |
| −710 + 500 | 41.6 | 2787.3 | 14.3 | 3049.9 | 51.5 | 2743.8 | |
| −500 + 355 | 13.0 | 2900.5 | 7.2 | 3214.7 | 47.7 | 2783.3 | |
| −355 + 250 | 6.4 | 2996.8 | 5.0 | 3372.7 | 36.4 | 2814.0 | |
| −250 + 180 | 3.2 | 3141.6 | 2.8 | 3761.9 | 27.6 | 2836.7 | |
| −180 + 125 | 2.7 | 3376.3 | 3.9 | 4231.7 | 25.4 | 2858.2 | |
| −125 + 90 | 2.2 | 3651.7 | 3.4 | 4635.9 | 11.7 | 2923.5 | |
| 12 | −1000 + 710 | 32.1 | 2743.7 | 11.0 | 2946.1 | 5.0 | 2736.6 |
| −710 + 500 | 11.3 | 2869.8 | 8.3 | 3177.2 | 18.8 | 2785.5 | |
| −500 + 355 | 2.5 | 3018.1 | 4.4 | 3400.7 | 14.4 | 2843.3 | |
| −355 + 250 | 2.0 | 3104.7 | 4.5 | 3759.6 | 10.1 | 2911.5 | |
| −250 + 180 | 1.0 | 3181.9 | 5.7 | 4255.3 | 6.6 | 2979.3 | |
| −180 + 125 | 1.5 | 3399.1 | 9.1 | 4594.3 | 5.4 | 3042.3 | |
| −125 + 90 | 1.5 | 3512.4 | 5.1 | 4717.4 | 3.4 | 3165.2 | |
| 13 | −1000 + 710 | 16.2 | 2905.4 | 7.5 | 3282.4 | 5.2 | 2770.5 |
| −710 + 500 | 9.6 | 3233.5 | 9.3 | 3786.9 | 10.8 | 2819.0 | |
| −500 + 355 | 4.5 | 3708.1 | 8.1 | 4234.0 | 8.0 | 2891.2 | |
| −355 + 250 | 5.1 | 4033.6 | 12.3 | 4453.3 | 5.7 | 2978.1 | |
| −250 + 180 | 4.0 | 4279.1 | 11.6 | 4670.2 | 3.5 | 3087.4 | |
| −180 + 125 | 3.8 | 4447.7 | 10.6 | 4758.6 | 3.4 | 3193.9 | |
| −125 + 90 | 2.1 | 4333.0 | 3.9 | 4793.4 | 2.8 | 3374.5 | |
References
- Franks, G.V.; Forbes, E.; Oshitani, J.; Batterham, R.J. Economic, water and energy evaluation of early rejection of gangue from copper ores using a dry sand fluidised bed separator. Int. J. Miner. Process. 2015, 137, 43–51. [Google Scholar] [CrossRef]
- McGrath, T.D.; Eksteen, J.J.; Bode, P. Assessing the amenability of a free milling gold ore to coarse particle gangue rejection. Miner. Eng. 2018, 120, 110–117. [Google Scholar] [CrossRef]
- Bergerman, M.G.; Jose Neto, D.; Mano, E.S.; Chaves, A.P. Impacts on Energy Consumption and Wear in Grinding Circuits With a Pre-Concentration Stage. In Proceedings of the XXIX International Mineral Processing Congress, Moscow, Russia, 15–21 September 2018; pp. 92–102. [Google Scholar]
- de Kretser, R.G.; Powell, M.; Scales, P.J.; Lim, J. The Water Efficient Plant of the Future—Towards a Holistic Process Chain Approach. In Proceedings of the Water in Mining, Perth, Australia, 15–17 September 2009; pp. 65–70. [Google Scholar]
- Napier-Munn, T.J. Modelling and simulating dense medium separation processes—A progress report. Miner. Eng. 1991, 4, 329–346. [Google Scholar] [CrossRef]
- Rong, R.X.; Lyman, J. Computational Techniques for Coal Washery Optimization—Parallel Gravity and Flotation Separation. Coal Prep. 1985, 2, 51–67. [Google Scholar] [CrossRef]
- Rosenblum, S. A mineral separation procedure using hot Clerici solution. J. Res. US Geol. Surv. 1974, 2, 479–481. [Google Scholar]
- Jahns, R.H. Clerici solution for the specific gravity determination of small mineral grains. Am. Mineral. 1939, 24, 116–122. [Google Scholar]
- Central Chemical Consulting. Available online: https://www.chem.com.au/comparison.html (accessed on 9 April 2020).
- Galvin, K.P.; Walton, K.; Zhou, J. How to elutriate particles according to their density. Chem. Eng. Sci. 2009, 64, 2003–2010. [Google Scholar] [CrossRef]
- Galvin, K.P.; Liu, H. Role of inertial lift in elutriating particles according to their density. Chem. Eng. Sci. 2011, 66, 3687–3691. [Google Scholar] [CrossRef]
- King, M.R.; Leighton, D.T. Measurement of the inertial lift on a moving sphere in contact with a plane wall in a shear flow. Phys. Fluids 1997, 9, 1248–1255. [Google Scholar] [CrossRef]
- Walton, K.; Zhou, J.; Galvin, K.P. Processing of fine particles using closely spaced inclined channels. Adv. Powder Technol. 2010, 21, 386–391. [Google Scholar] [CrossRef]
- Hunter, D.M.; Iveson, S.M.; Galvin, K.P. The role of viscosity in the density fractionation of particles in a laboratory-scale Reflux Classifier. Fuel 2014, 129, 188–196. [Google Scholar] [CrossRef]
- Campbell, Q.P.; le Roux, M.; Smith, I.G. Water-only laboratory coal fractionation using the reflux classifier. Miner. Eng. 2015, 83, 59–63. [Google Scholar] [CrossRef]
- Iveson, S.M.; Hunter, D.M.; Galvin, K.P. A water-based method for measuring density-based partition curves of separators used in coal and mineral processing. Miner. Eng. 2015, 79, 196–211. [Google Scholar] [CrossRef]
- Galvin, K.P.; Iveson, S.M.; Zhou, J.; Lowes, C.P. Influence of Inclined Channel Spacing on Dense Mineral Partition in a REFLUX™ Classifier. Part 1: Continuous Steady State. Miner. Eng. 2020, 146, 106112. [Google Scholar] [CrossRef]
- Galvin, K.P.; Iveson, S.M.; Hunter, D.M. Deconvolution of fractionation data to deduce consistent washability and partition curves for a mineral separator. Miner. Eng. 2018, 125, 94–110. [Google Scholar] [CrossRef]
- Galvin, K.P.; Iveson, S.M.; Zhou, J.; Lowes, C.P. Influence of Inclined Channel Spacing on Dense Mineral Partition in a REFLUX™ Classifier. Part 2: Water Based Fractionation. Miner. Eng. 2020, 155, 106442. [Google Scholar] [CrossRef]
- Lowes, C.P.; Zhou, J.; Galvin, K.P. Improved Density Fractionation of Minerals in the REFLUX™ Classifier Using LST as a Novel Fluidising Medium. Miner. Eng. 2020, 146, 106145. [Google Scholar] [CrossRef]
- Lowes, C.P.; Zhou, J.; McGrath, T.D.; Eksteen, J.J.; Galvin, K.P. Characterising the amenability of gold ore for gravity pre-concentration using LST fluidization in the REFLUX™ Classifier. In Proceedings of the MineXchange 2020 SME Annual Conference & Expo, Phoenix, AZ, USA, 23–26 February 2020. [Google Scholar]
- Lowes, C.P.; Zhou, J.; Galvin, K.P. Gravity Separation of Gold Ore Using the REFLUX™ Classifier to Achieve Coarse Particle Gangue Rejection. In Proceedings of the Chemeca, Queenstown, New Zealand, 30 September–3 October 2018. [Google Scholar]
- Scott, I.A.; Napier-Munn, T.J. A dense medium cyclone model based on the pivot phenomenon. Trans. Inst. Min. Metall. 1992, 101, C61–C76. [Google Scholar]
- Mitchell, K.; Hoffman, D.; Hartmann, T. Full scale plant operation of reflux classifier circuits. In Proceedings of the 15th Australian Coal Preparation Conference and Exhibition, Broadbeach, Australia, 14–18 September 2014. [Google Scholar]
- Galvin, K.P.; Zhou, J.; Walton, K. Application of closely spaced inclined channels in gravity separation of fine particles. Miner. Eng. 2010, 23, 326–338. [Google Scholar] [CrossRef]
- Rao, V.B.; Kapur, P.C.; Konnur, R. Modeling the size-density partition surface of dense medium separators. Int. J. Miner. Process. 2003, 72, 443–453. [Google Scholar] [CrossRef]
- Jowett, A. An appraisal of partition curves for coal-cleaning processes. Int. J. Miner. Process. 1986, 16, 75–95. [Google Scholar] [CrossRef]
- Couto, H.J.; Braga, P.F.; França, S.C. Use of gas pycnometry for estimating the iron content in mineral samples. Miner. Eng. 2012, 39, 45–47. [Google Scholar] [CrossRef]


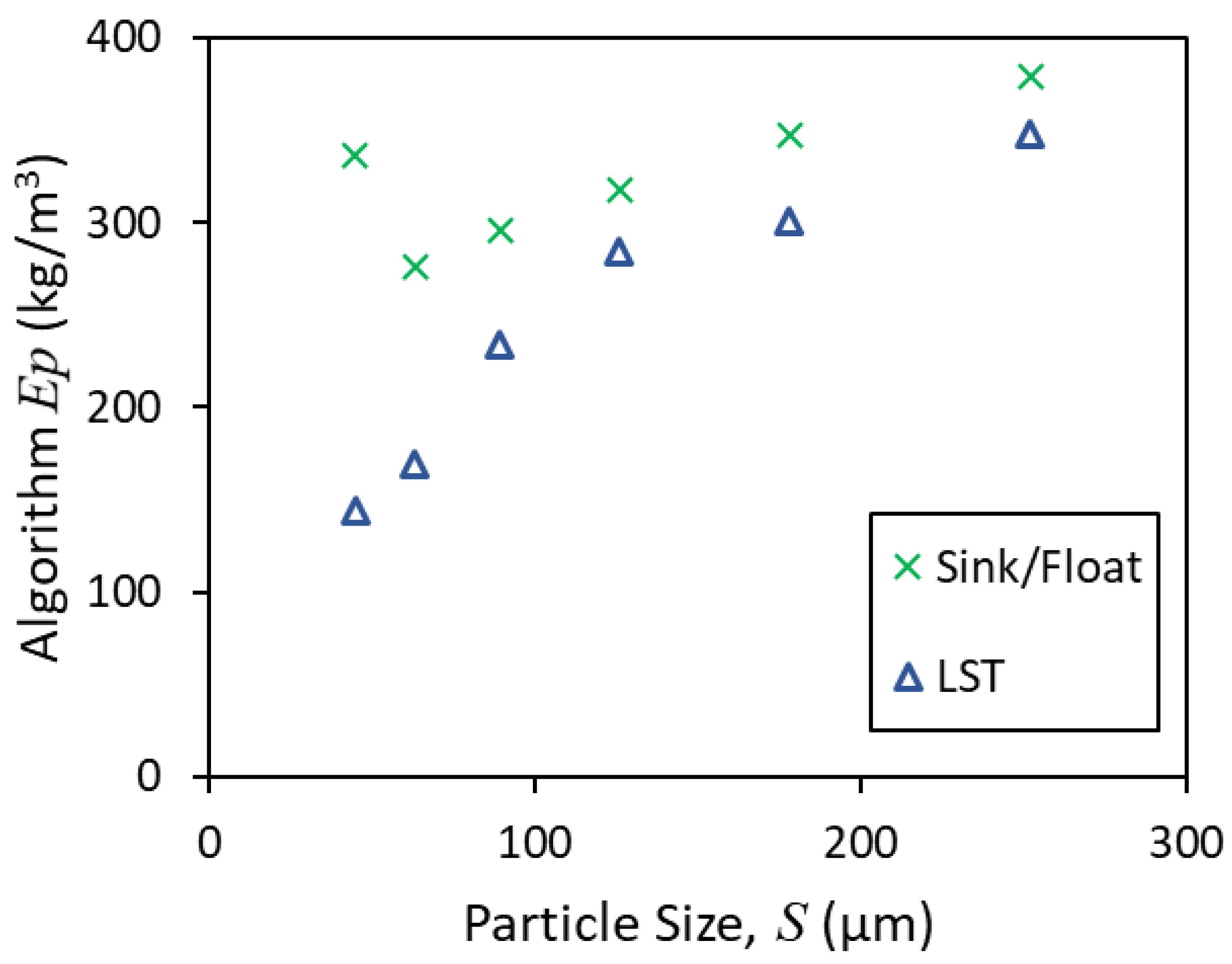

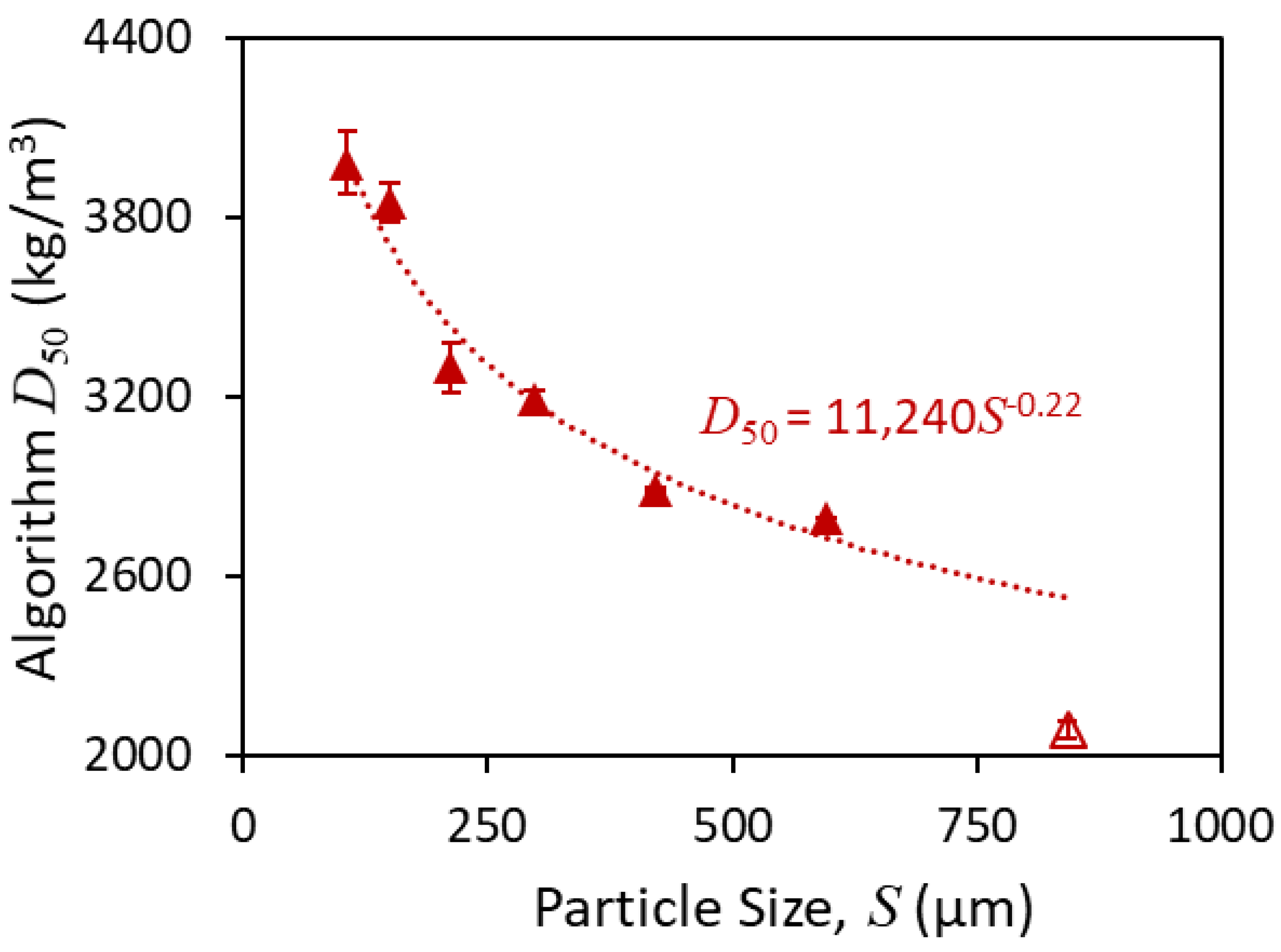

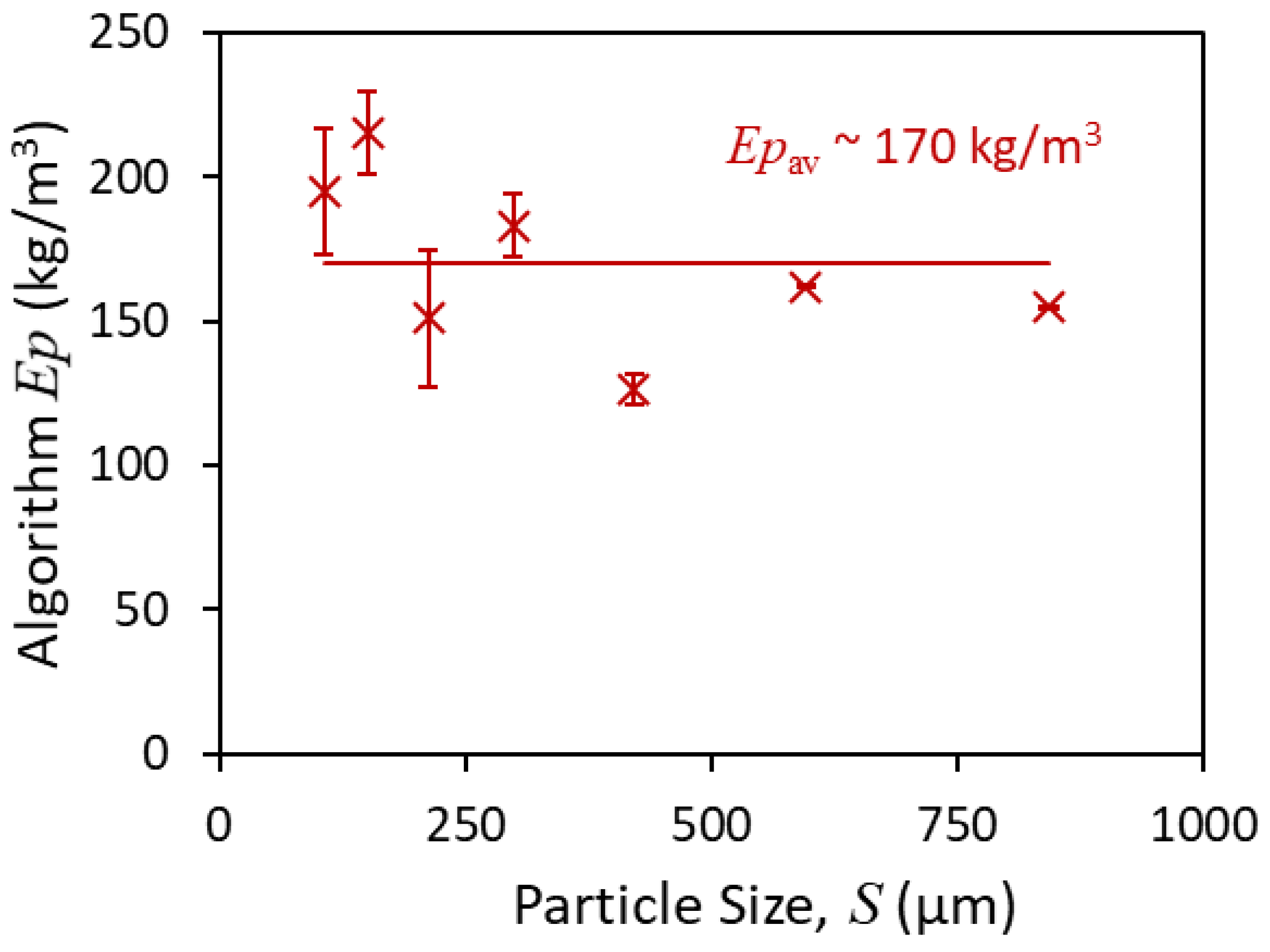
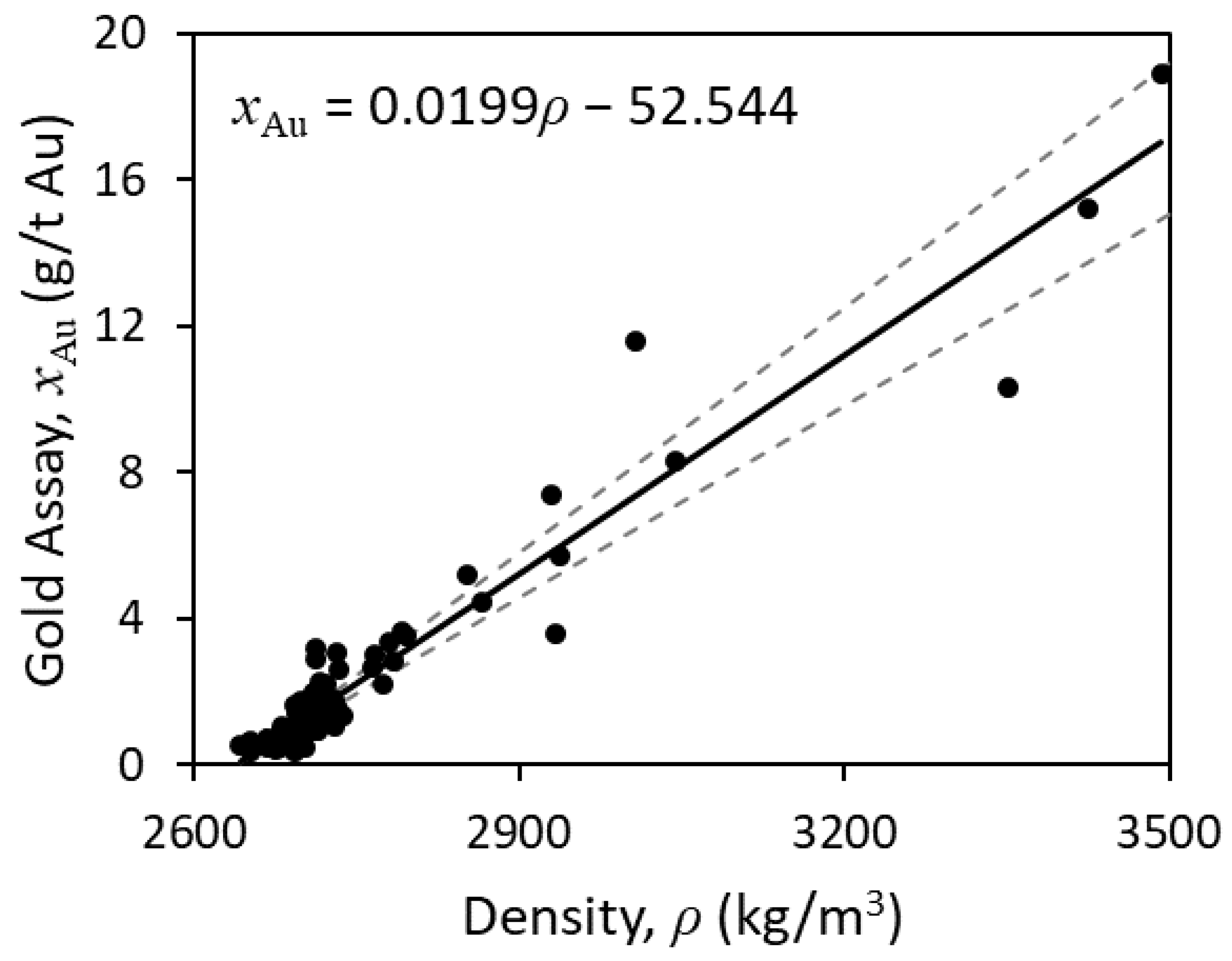
| Sink/Float | LST Flow Fractionation | |||
|---|---|---|---|---|
| Size Range | D50 | Ep | D50 | Ep |
| (µm) | (kg/m3) | (kg/m3) | (kg/m3) | (kg/m3) |
| −300 + 212 | 3090 | 379 | 3151 | 348 |
| −212 + 150 | 3477 | 347 | 3518 | 301 |
| −150 + 106 | 3828 | 318 | 3821 | 284 |
| −106 + 75 | 4096 | 296 | 4128 | 234 |
| −75 + 53 | 4389 | 276 | 4352 | 169 |
| −53 + 38 | 4573 | 336 | 4539 | 145 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lowes, C.; Zhou, J.; McGrath, T.; Eksteen, J.; Galvin, K. Characterisation and Modelling of Gravity Pre-Concentration Amenability Using LST Fluidisation in a REFLUXTM Classifier. Minerals 2020, 10, 545. https://doi.org/10.3390/min10060545
Lowes C, Zhou J, McGrath T, Eksteen J, Galvin K. Characterisation and Modelling of Gravity Pre-Concentration Amenability Using LST Fluidisation in a REFLUXTM Classifier. Minerals. 2020; 10(6):545. https://doi.org/10.3390/min10060545
Chicago/Turabian StyleLowes, Callan, James Zhou, Teresa McGrath, Jacques Eksteen, and Kevin Galvin. 2020. "Characterisation and Modelling of Gravity Pre-Concentration Amenability Using LST Fluidisation in a REFLUXTM Classifier" Minerals 10, no. 6: 545. https://doi.org/10.3390/min10060545
APA StyleLowes, C., Zhou, J., McGrath, T., Eksteen, J., & Galvin, K. (2020). Characterisation and Modelling of Gravity Pre-Concentration Amenability Using LST Fluidisation in a REFLUXTM Classifier. Minerals, 10(6), 545. https://doi.org/10.3390/min10060545





