The Influence of Selected Properties of Particles in the Jigging Process of Aggregates on an Example of Chalcedonite
Abstract
:1. Introduction
2. Materials and Methods
2.1. Investigations of the Projection Diameter and Shape Coefficients of Particles
2.2. Chalcedonite Particles’ Chemistry Examination
3. Results and Discussion
3.1. Analysis of the Geometric and Physical Properties
3.2. Analysis of the Chalcedonite Particles’ Surface Chemistry
4. Conclusions
5. Patents
Author Contributions
Funding

Acknowledgments
Conflicts of Interest
References
- Osoba, M. Osadzarki wodne pulsacyjne typu KOMAG, maszyny sprawdzone w przeróbce surowców mineralnych. Masz. Gór. 2005, 4, 104. (In Polish) [Google Scholar]
- Lutyński, A.; Osoba, M. Wpływ charakterystyki pulsacji wody w wodnych osadzarkach pulsacyjnych na proces pozyskiwania wybranych produktów mineralnych. In Prace Naukowe—Monografie; CMG KOMA: Gliwice, Poland, 2007. (In Polish) [Google Scholar]
- Lutyński, A.; Osoba, M. Dobór technologiczny osadzarek wodnych pulsacyjnych w procesie projektowania. Gór. Geoinż. 2009, 33, 259–268. (In Polish) [Google Scholar]
- Osoba, M. Osadzarki Wodne Pulsacyjne Typu KOMAG do Przeróbki Żwiru i Piasku, Prace Naukowe Instytutu Górnictwa Politechniki Wrocławskiej nr 119, Seria: Konferencje nr 48. In Kruszywa Mineralne; Szklarska Poręba, oficyna Wydawnicza Politechniki Wrocławskiej: Wrocław, Poland, 2007. (In Polish) [Google Scholar]
- Osoba, M. Polskie osadzarki wodne pulsacyjne do wzbogacania surowców mineralnych. Inż. Miner. 2014, 34, 287–294. (In Polish) [Google Scholar]
- Cazacliu, B.; Sampaio, C.H.; Miltzarek, G.; Petter, C.; Le Guen, L.; Paranhos, R.; Huchet, F.; Kirchheim, A.P. The potential to using air jigging to sort recycled aggregates. J. Clean. Prod. 2014, 66, 46–53. [Google Scholar] [CrossRef] [Green Version]
- Sampaio, C.H.; Ambrós, W.M.; Miranda, L.R.; Gerson, L.; Miltzarek, G.M.; Kronbauer, M.A. Improve the quality of recycled aggregate concrete by sorting in air jig. In Proceedings of the IIIrd Progress of Recycling in the Built Environment, São Paulo, Brazil, 3–5 August 2015. [Google Scholar]
- Sampaio, C.H.; Cazacliu, B.G.; Miltzarek, G.L.; Huchet, F.; le Guen, L.; Petter, C.O.; Paranhos, R.; Ambros, W.M.; Oliveira, M.L.S. Stratification in air jigs of concrete/brick/gypsum particles. Constr. Build. Mater. 2016, 109, 63–72. [Google Scholar] [CrossRef]
- Naziemiec, Z.; Pichniarczyk, P.; Saramak, D. Current issues of processing and industrial utilization of chalcedonite. Inż. Miner. 2017, 1, 89–96. [Google Scholar]
- Naziemiec, Z.; Pichniarczyk, P.; Saramak, D. Methods of improvement chalcedonite processing effectiveness with the use of density separation. Miner. Resourc. Manag. 2017, 33, 163–178. [Google Scholar] [CrossRef] [Green Version]
- Gawenda, T.; Saramak, D.; Nad, A.; Surowiak, A.; Krawczykowska, A.; Foszcz, D. Badania procesu uszlachetniania kruszyw w innowacyjnym układzie technologicznym. In Kruszywa Mineralne; Glapa, W., Ed.; Wrocław Wydział Geoinżynierii, Górnictwa i Geologii Politechniki Wrocławskiej: Wrocław, Poland, 2019. (In Polish) [Google Scholar]
- Kowol, D.; Matusiak, P. Optymalizacja parametrów procesowych oczyszczania nadaw żwirowych w klasyfikatorze pulsacyjnym w zależności od typu zanieczyszczeń i udziału ziaren piaskowych. ITG KOMAG 2012. Unpublished Materials (In Polish) [Google Scholar]
- Matusiak, P.; Kowol, D. Możliwości poprawy jakości kruszywa poprzez zastosowanie klasyfikatora pulsacyjnego typu KOMAG. Stud. Mater. 2013, 43, 109–118. (In Polish) [Google Scholar]
- Kowol, D.; Matusiak, P. Badania skuteczności osadzarkowego oczyszczania kruszywa z ziaren węglanowych. Min. Sci. Miner. Aggreg. 2015, 22, 83–92. [Google Scholar]
- Gawenda, T.; Krawczykowski, D.; Krawczykowska, A.; Saramak, A.; Nad, A. Application of dynamic analysis methods into assessment of geometric properties of chalcedonite aggregates obtained by means of gravitational upgrading operations. Minerals 2020, 10, 180. [Google Scholar] [CrossRef] [Green Version]
- Phengsaart, T.; Ito, M.; Azuma, A.; Tabelin, C.B.; Hiroyoshi, N. Jig separation of crushed plastics: The effects of particle geometry on separation efficiency. J. Mater. Cycles Waste Manag. 2020, 22, 787–800. [Google Scholar] [CrossRef]
- Gradziński, R. Zarys Sedymentologii; WG Wrocław: Wrocław, Poland, 1986. (In Polish) [Google Scholar]
- Brożek, M.; Surowiak, A. Argument of separation at upgrading in the JIG. Arch. Min. Sci. 2010, 55, 1–40. [Google Scholar]
- Finkey, J. Die Wissenschaftlichen Grundlagen der Nassen Erzaufbereitung; Springer: Berlin, Germany, 1924. (In German) [Google Scholar]
- Laszczenko, P.V. Gravitacionnyje Metody Obogaszczenija; Gostoptechizdat: Moscow, Russia, 1940. (In Russian) [Google Scholar]
- Olevskij, V.A. O Svobodnom Padenii Czastic v Żidkoj Srede; Trudy Instituta Mechanobr: Leningrad, Vypusk, 1953; pp. 88–96. (In Russian) [Google Scholar]
- Heiss, J.F.; Coull, J. On the settling velocity of non-isometric particles in a viscous medium. Chem. Eng. Prog. 1952, 48, 133–140. [Google Scholar]
- Akkerman, J.E. Skorost svobodnogo padenija mineralnych zeren v żidkostiach. Obogaszczenie Rud 1966, 6, 22–25. (In Russian) [Google Scholar]
- Chrisiansen, E.B.; Barker, D.E. The effect of shape and density on the free settling of particles at high Reynolds numbers. AIChE J. 1965, 11, 145–151. [Google Scholar] [CrossRef]
- Bedran, N.G.; Denisenko, A.I.; Pilov, P.I. Rasczet skorosti svobodnogo dvi-żenija mineralnych zeren v srede. Izv. VUZ Gornyj Ż. 1976, 9, 141–144. (In Russian) [Google Scholar]
- Concha, F.; Almendra, E.R. Settling velocities of particulate systems, 1. Settling velocities of individual spherical particles. Int. J. Miner. Process. 1979, 5, 349–367. [Google Scholar] [CrossRef]
- Haide, A.; Levenspiel, O. Drag coefficient and terminal velocity of spherical and non-spherical particles. Powder Technol. 1989, 58, 63–70. [Google Scholar] [CrossRef]
- Briens, C.L. Correlation for the direct calculation of the terminal velocity of spherical particles in newtonian and pseudoplastic (power-law) fluids. Powder Technol. 1991, 67, 87–91. [Google Scholar] [CrossRef]
- Abraham, F. Functional dependence of drag coefficient of a sphere on Reynolds number. Phys. Fluids 1970, 13, 2194–2195. [Google Scholar] [CrossRef]
- Thompson, T.L.; Clark, N.N. A holistic approach to particle drag prediction. Powder Technol. 1991, 67, 57–66. [Google Scholar] [CrossRef]
- Ganser, G.H. A rational approach to drag prediction of spherical and non-spherical particles. Powder Technol. 1993, 77, 143–152. [Google Scholar] [CrossRef]
- Gawenda, T.; Saramak, D.; Naziemiec, Z. Układ Urządzeń do Produkcji Kruszyw Oraz Sposób Produkcji Kruszyw. Poland Patent No. PL 233318B1, 7 June 2019. (In Polish). [Google Scholar]
- Gawenda, T. Innovative technological circuits for regular aggregates production. IOP Conf. Ser. Mater. Sci. Eng. 2019, 641, 012013. [Google Scholar] [CrossRef]
- Stempkowska, A.; Gawenda, T. Analiza właściwości cieplnych kruszywa chalcedonitowego na podstawie badań wykorzystujących metody termowizyjne. In Kruszywa Mineralne Vol. 4; Glapa, W., Ed.; Wrocław Wydział Geoinżynierii, Górnictwa i Geologii Politechniki Wrocławskiej: Wrocław, Poland, 2020. (In Polish) [Google Scholar]
- Kosk, L. Complex management of chalcedonite waste fractions from Inowłódz mine clarifiers in environment prevention and in building material industry. Gospod. Surow. Miner. Miner. Resourc. Manag. 2010, 26, 5–22. (In Polish) [Google Scholar]
- Michel, M. Charakterystyka chalcedonitu ze złoża Teofilów pod kątem możliwości wykorzystania w technologii uzdatniania wody i oczyszczania ścieków. Gospod. Surow. Miner. Miner. Resourc. Manag. 2011, 27, 49–67. (In Polish) [Google Scholar]
- Bolewski, A.; Manecki, A. Mineralogia Szczegółowa; PAE: Warsaw, Poland, 1993. (In Polish) [Google Scholar]
- Gawenda, T. Układ Urządzeń Do Produkcji Kruszyw Foremnych. Poland Patent nr PL233689, 8 July 2019. (In Polish). [Google Scholar]
- PN-EN 933-3. Badania Geometrycznych Właściwości Kruszyw. Część 3: Oznaczanie Kształtu Ziarn za Pomocą Wskaźnika Płaskości; Polski Komitet Normalizacyjny: Warsaw, Poland, 2012. (In Polish) [Google Scholar]
- Szurgot, M.; Tszydel, I. Zastosowanie spektroskopii Ramana do identyfikacji minerałów meteorytu NWA 4967. Acta Soc. Metheorol. Pol. 2011, 2, 158–170. [Google Scholar]
- Hodenberg, M. Gravimetric and optical particle analysis of mixed particle samples. Aufbereit. Tech. 1998, 39, 461–466. [Google Scholar]
- Stark, U.; Muller, A. Effective methods for measurement of particle size and shape. Aufbereit. Tech. 2005, 45, 6–16. [Google Scholar]
- Surowiak, A. Influence of particle density distributions of their settling velocity for narrow size fractions. Miner. Resourc. Manag. 2014, 30, 105–122. (In Polish) [Google Scholar]
- Brozek, M.; Surowiak, A. Effect of particle shape on jig separation efficiency. Physicochem. Probl. Miner. Proc. 2007, 41, 397–413. [Google Scholar]
- Surowiak, A.; Brożek, M. Methodology of calculation the terminal settling velocity distribution of irregular particles for values of the Reynold’s number. Arch. Min. Sci. 2014, 59, 553–562. [Google Scholar]
- Hanesh, M. Raman spectroscopy of iron oxides and (oxy)hydroxides at low laser power and possible applications in environmental magnetic studies. Geophys. J. Int. 2009, 177, 941–948. [Google Scholar] [CrossRef]
- Henderson, P. Inorganic Geochemistry; Pergamon: Oxford, UK, 1982. [Google Scholar]
- Jeż-Walkowiak, J.; Komorowska-Kaufmann, M.; Dymaczewski, Z.; Sozański, M.; Zakrzewski, P. Properties of catalyst for iron and manganese oxidation in filter materials. E3S Web Conf. 2018, 59, 00014. [Google Scholar] [CrossRef] [Green Version]

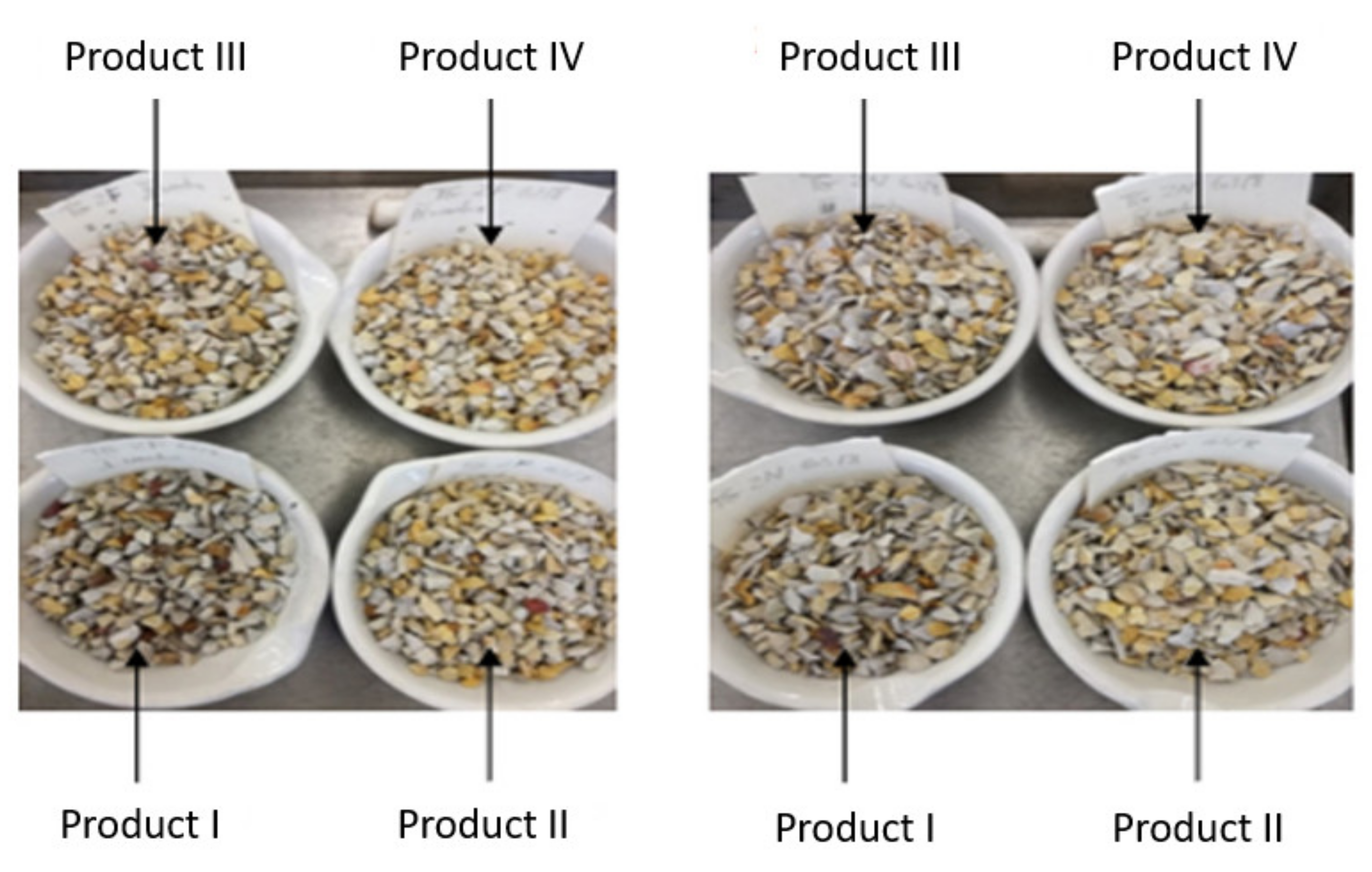


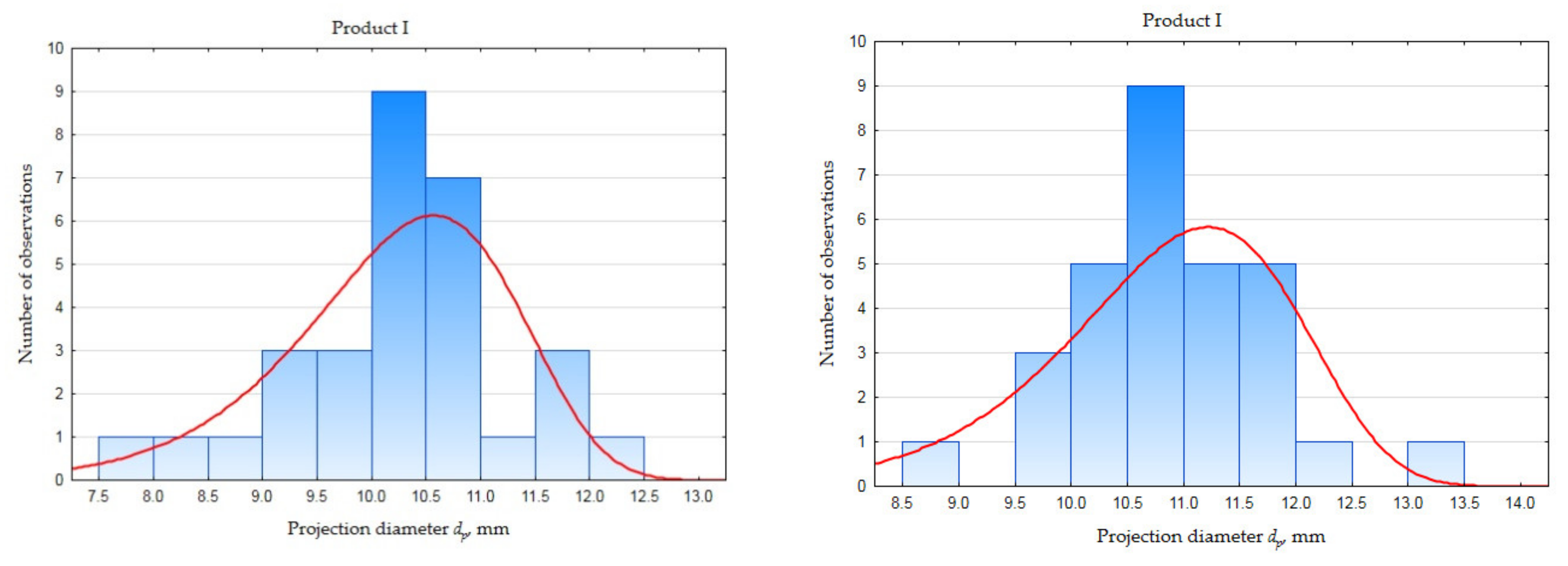
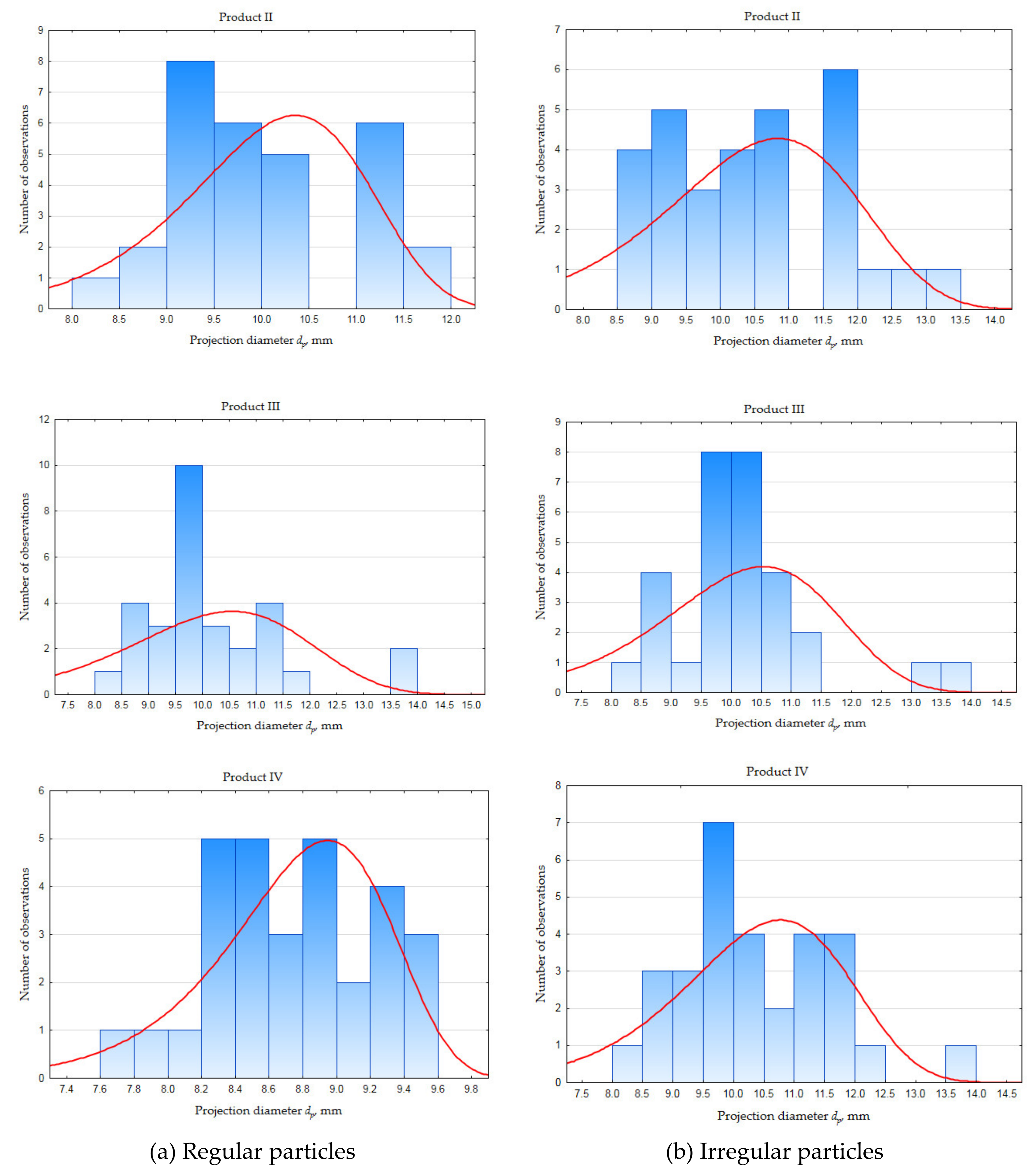
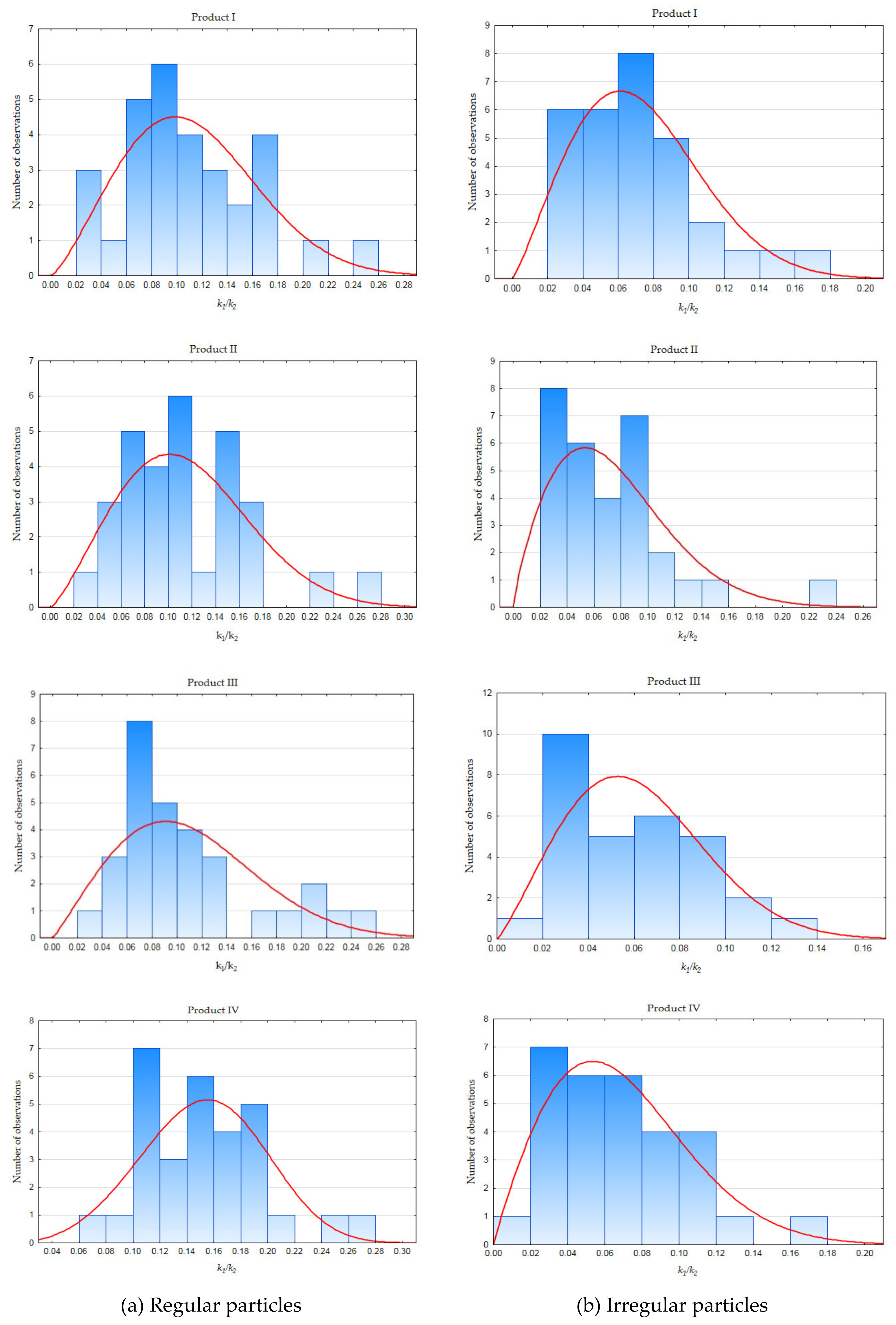
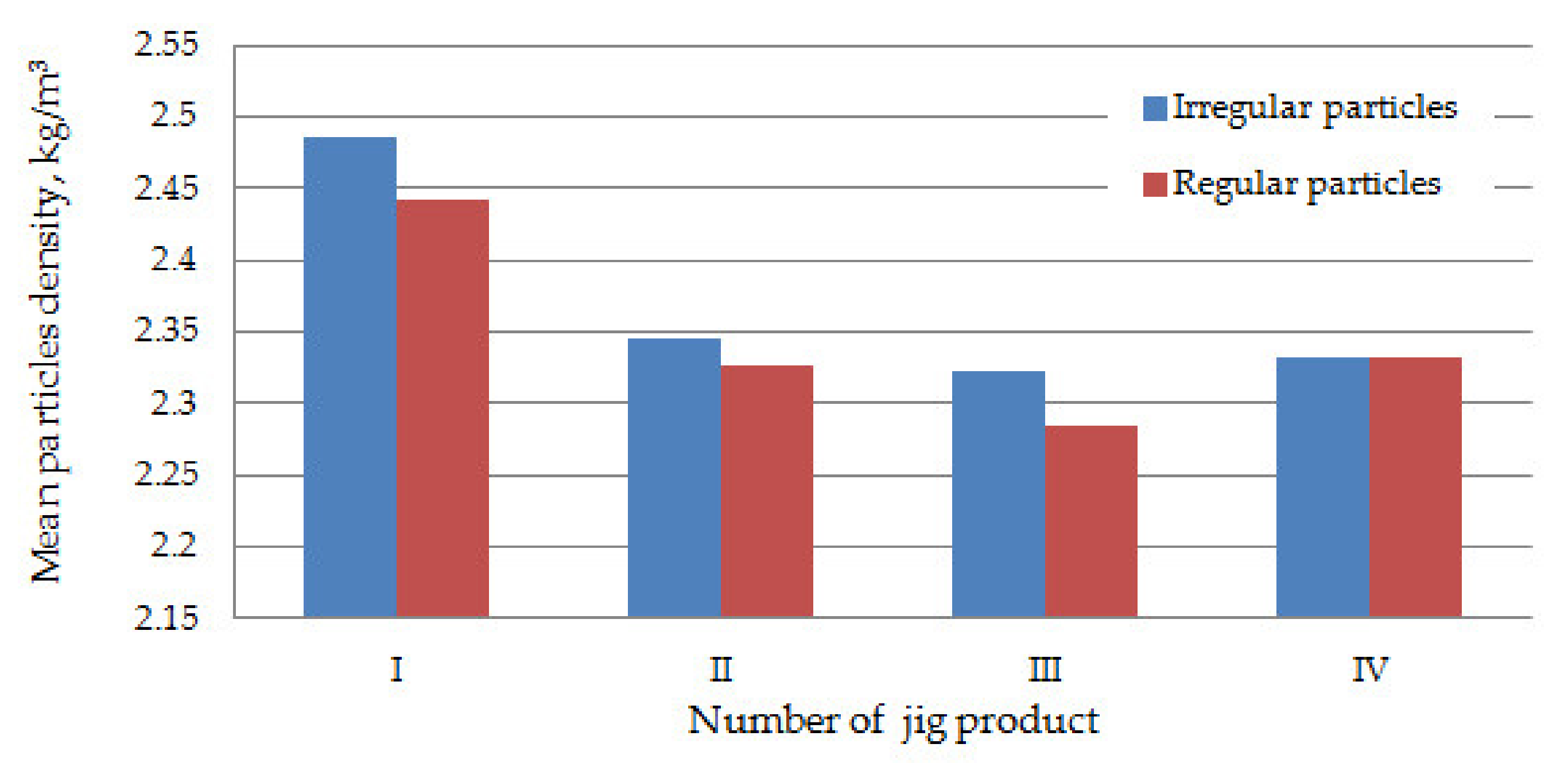
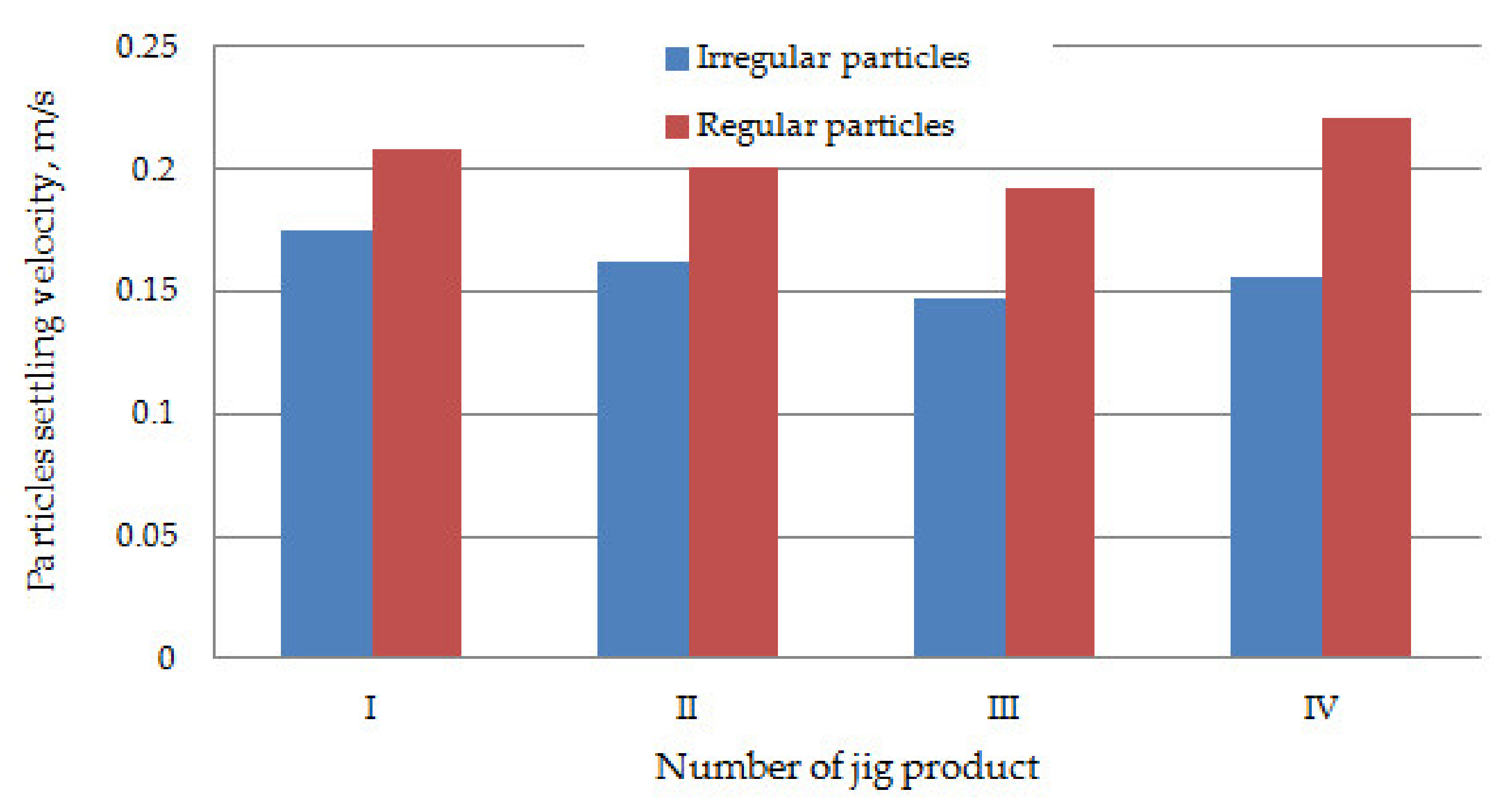
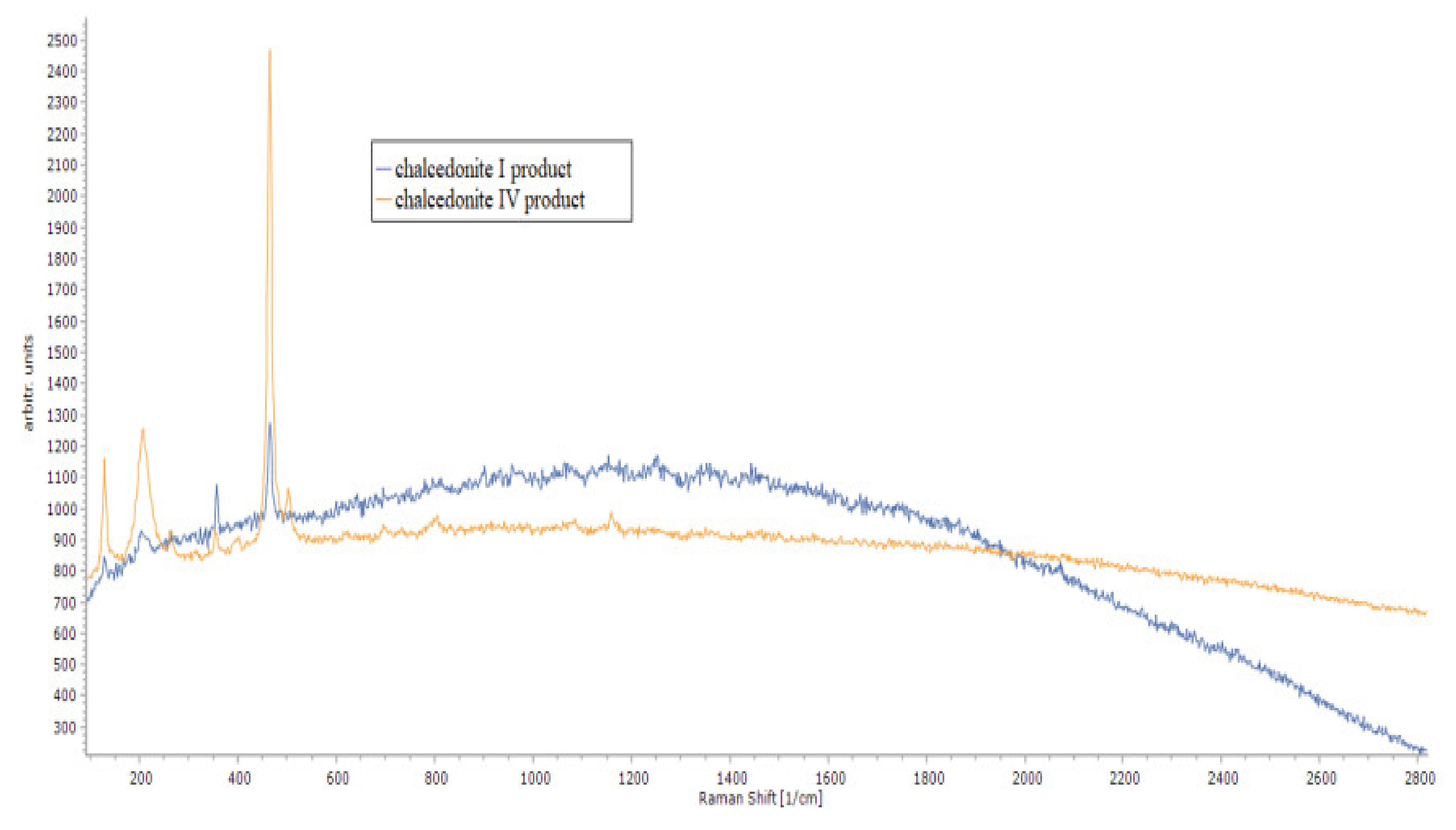
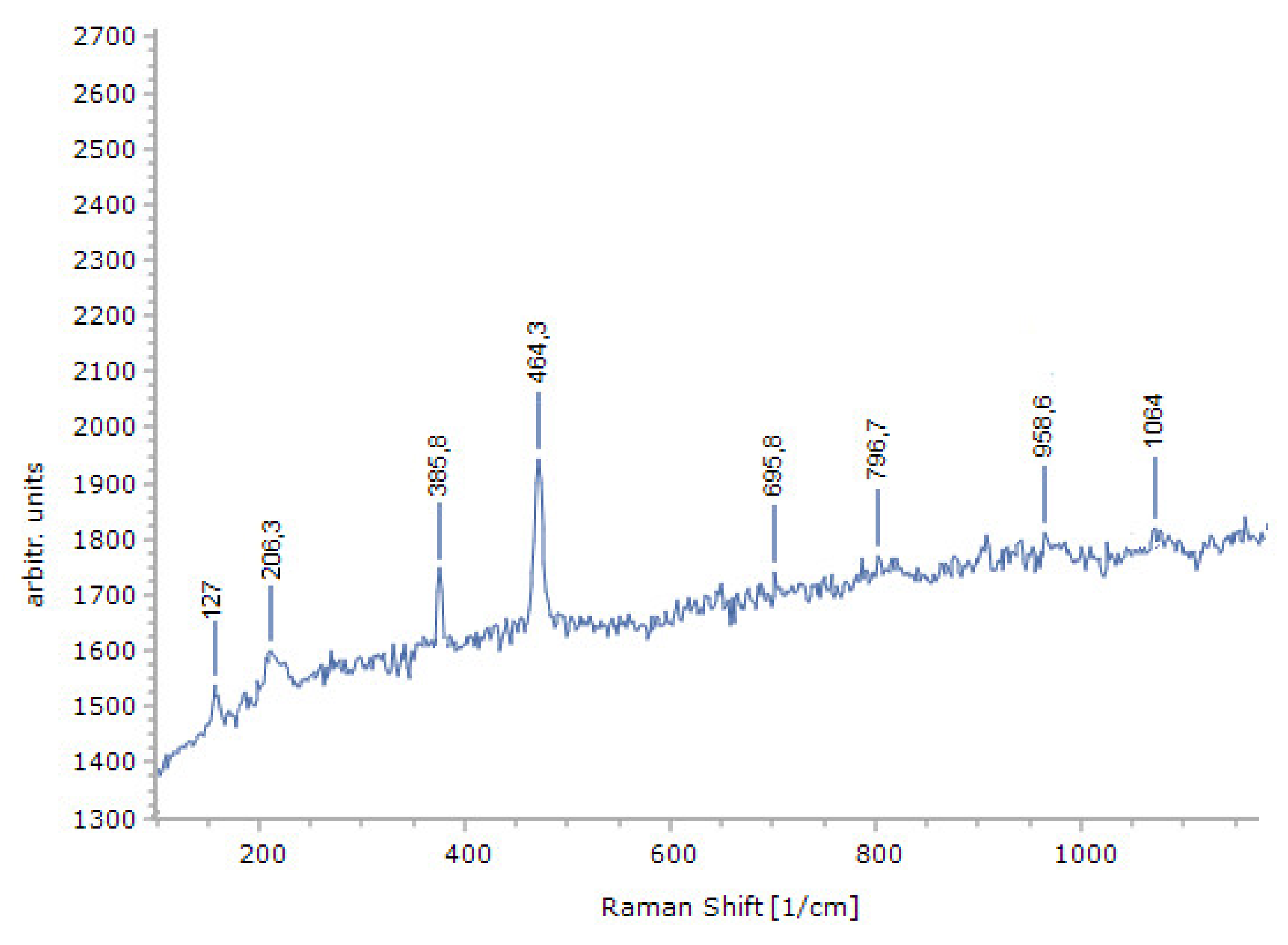
| Regular Particles | Irregular Particles | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| No. of product | dp | k1 | k2 | k1/k2 | ρ | dp | k1 | k2 | k1/k2 | ρ |
| I | 0.988 | 0.131 | 1.812 | 0.052 | 0.110 | 0.874 | 0.097 | 0.972 | 0.035 | 0.116 |
| II | 0.906 | 0.115 | 1.236 | 0.054 | 0.152 | 1.284 | 0.117 | 0.642 | 0.044 | 0.119 |
| III | 1.289 | 0.123 | 0.790 | 0.056 | 0.090 | 1.118 | 0.079 | 0.829 | 0.030 | 0.167 |
| IV | 0.482 | 0.096 | 0.584 | 0.042 | 0.173 | 1.181 | 0.081 | 0.948 | 0.038 | 0.158 |
| Regular Particles | Irregular Particles | |||||
|---|---|---|---|---|---|---|
| Product | k1 | k2 | k1/k2 | k1 | k2 | k1/k2 |
| I | 0.364 | 3.728 | 0.098 | 0.210 | 3.095 | 0.068 |
| II | 0.369 | 3.613 | 0.102 | 0.225 | 3.220 | 0.070 |
| III | 0.350 | 3.512 | 0.100 | 0.191 | 3.336 | 0.057 |
| IV | 0.454 | 3.093 | 0.147 | 0.208 | 3.349 | 0.062 |
| Total mean | 0.384 | 3.486 | 0.110 | 0.208 | 3.250 | 0.064 |
| Mineral | Values of Raman Shifts (cm−1) | |||||
|---|---|---|---|---|---|---|
| quartz | 127 | 206 | 464 | - | - | - |
| cristobalite | 114 | 230 | 420 | - | - | - |
| tridymite | 210 | 304 | 349 | 431 | 799 | 1073 |
| hematite Fe2O3 | 225 | 245 | 290–300 | 412 | - | - |
| magnetite FeO. Fe2O3 | 310 | 540 | 670 | |||
| goethite αFeOOH | 244 | 299 | 385 | 480 | 548 | 681 |
| lepidocrocite γFeOOH | 250 | 348 | 379 | 528 | 650 | - |
| siderite FeCO3 | 184 | 287 | 731 | 1090 | - | - |
| Values of Raman Shifts (cm−1) | |
|---|---|
| Fourth product | First product |
| 127.6 | 127.0 |
| 207.2 | 206.3 |
| 353.9 | 385.8 |
| 464.1 | 464.3 |
| 675.7 | 675.8 |
| 804.8 | 796.7 |
| 913.6 | 958.6 |
| 1085.8 | 1083.0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Surowiak, A.; Gawenda, T.; Stempkowska, A.; Niedoba, T.; Nad, A. The Influence of Selected Properties of Particles in the Jigging Process of Aggregates on an Example of Chalcedonite. Minerals 2020, 10, 600. https://doi.org/10.3390/min10070600
Surowiak A, Gawenda T, Stempkowska A, Niedoba T, Nad A. The Influence of Selected Properties of Particles in the Jigging Process of Aggregates on an Example of Chalcedonite. Minerals. 2020; 10(7):600. https://doi.org/10.3390/min10070600
Chicago/Turabian StyleSurowiak, Agnieszka, Tomasz Gawenda, Agata Stempkowska, Tomasz Niedoba, and Alona Nad. 2020. "The Influence of Selected Properties of Particles in the Jigging Process of Aggregates on an Example of Chalcedonite" Minerals 10, no. 7: 600. https://doi.org/10.3390/min10070600
APA StyleSurowiak, A., Gawenda, T., Stempkowska, A., Niedoba, T., & Nad, A. (2020). The Influence of Selected Properties of Particles in the Jigging Process of Aggregates on an Example of Chalcedonite. Minerals, 10(7), 600. https://doi.org/10.3390/min10070600








