Correlation between the Pore Structure and Water Retention of Cemented Paste Backfill Using Centrifugal and Nuclear Magnetic Resonance Methods
Abstract
1. Introduction
2. Materials and Methods
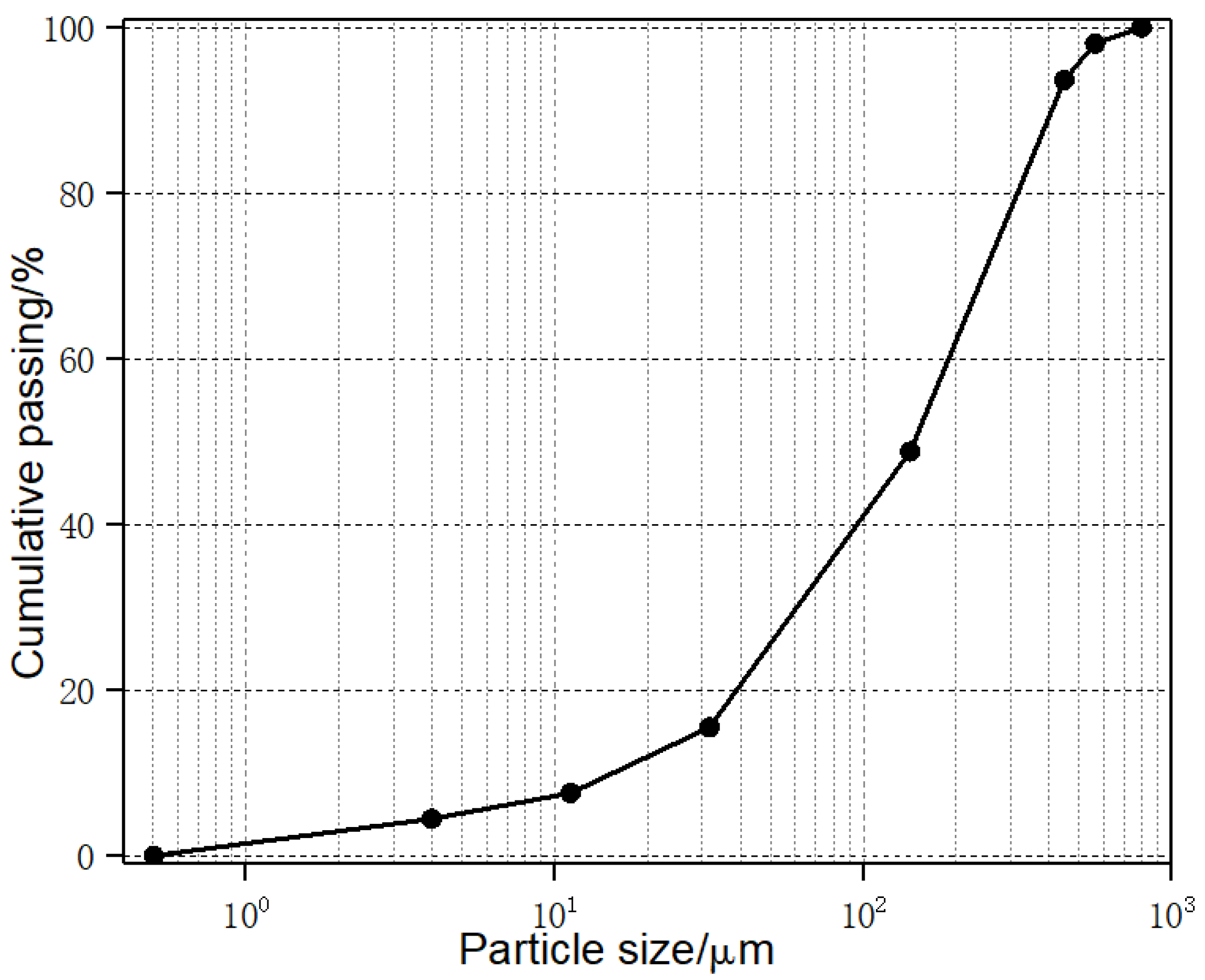
2.1. Testing Materials
2.2. Sample Preparation
2.3. NMR Theories
2.3.1. NMR Technology
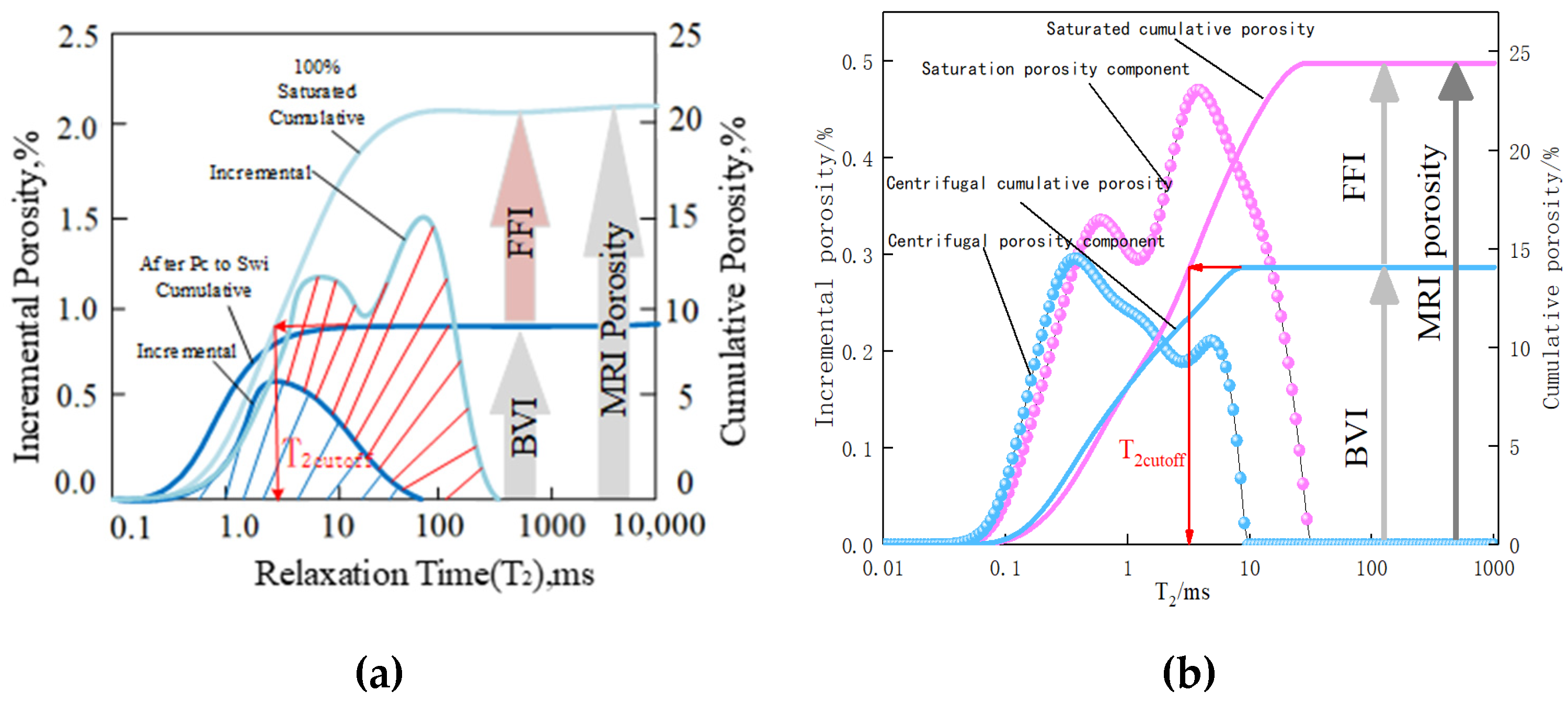
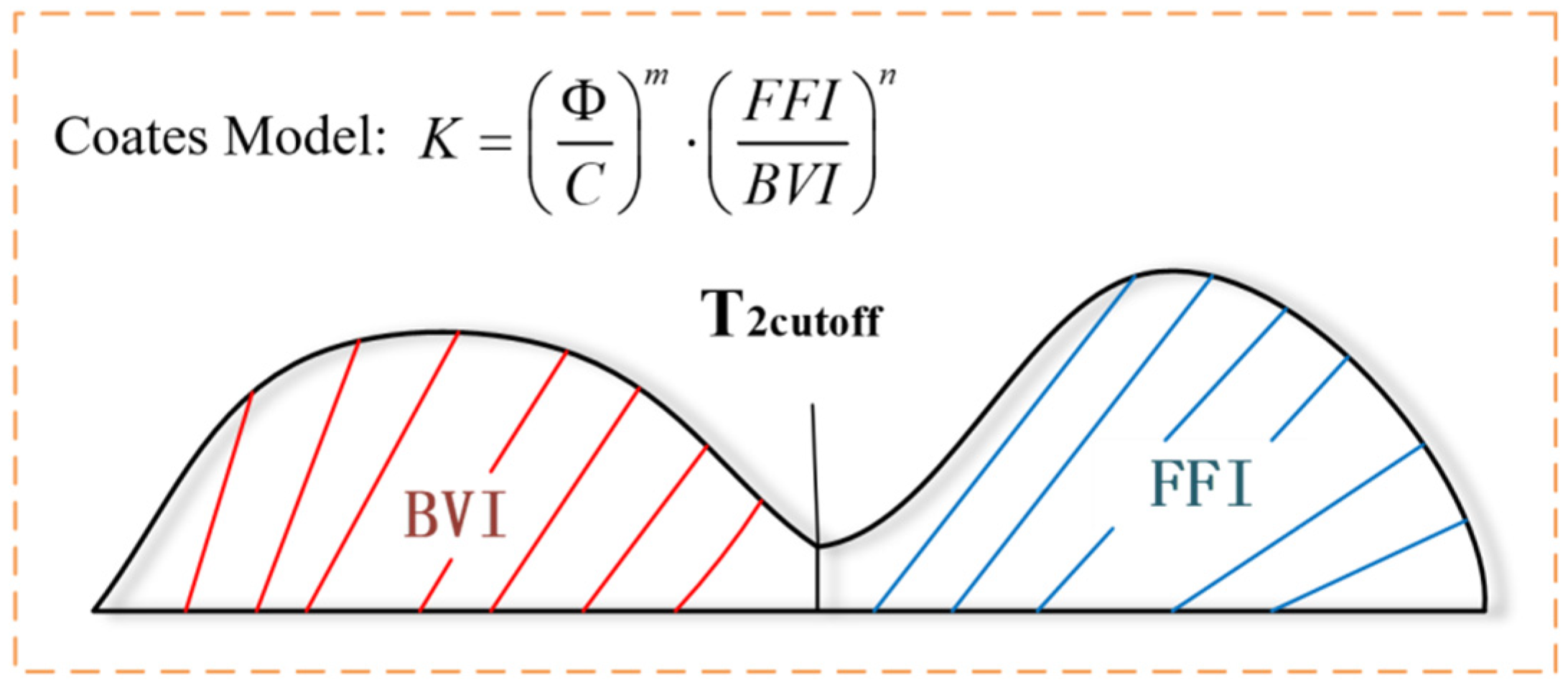
2.3.2. Bound Volume Index (BVI) Cutoff Value
2.3.3. Centrifugal Methods
- (1)
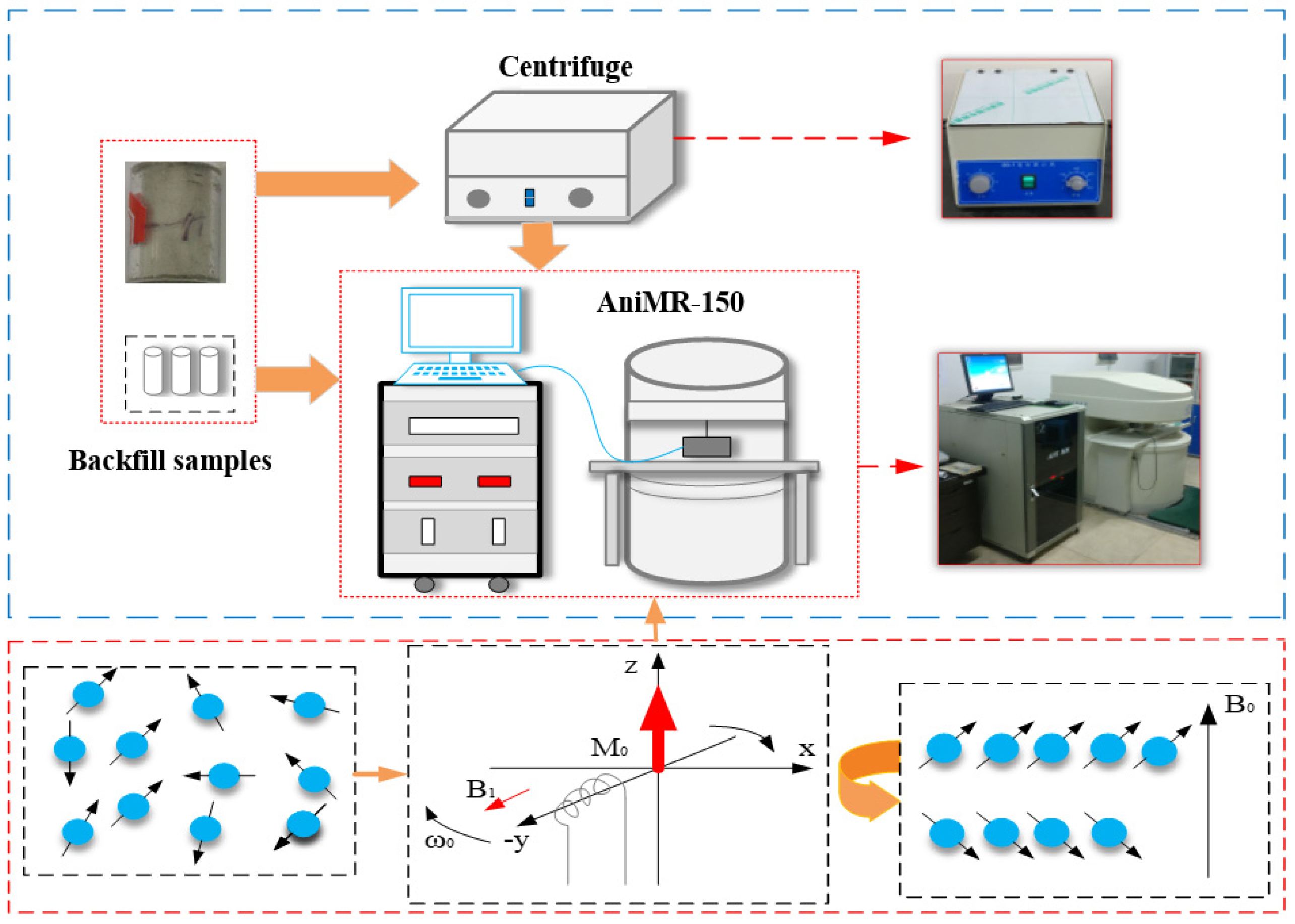
- NMR test: After placing the backfill sample in the magnetic field, the hydrogen ion resonates by emitting a radio frequency (RF) pulse at a certain frequency and absorbs its energy. When the RF pulse is stopped, the hydrogen ion will release the absorbed energy, the process of which can be detected through the nuclear magnetic resonance signal. The energy release rates of samples with different properties are distinct, and the differences between the signals can intuitively reflect the variation of pore water retention.
- (2)
- Centrifugal separation: Centrifugal separation is used to encourage the moisture in the sample pores to pass out through the pore throat and channel and become a filtrate under the strong centrifugal force generated by high-speed rotating equipment, thereby achieving solid–liquid or liquid–liquid separation in a short time [33]. Usually, the relative centrifugal force () is used to express the magnitude of the centrifugal force, which is calculated as follows:where n and r denote the same meanings but in different units of r·s−1 and cm. The unit of is gravitational acceleration, 9.81 m/s2.
2.4. Testing Procedures
- (1)
- Before conducting subsequent tests, all backfill samples need to be saturated [34]. This study used the method of staged immersion saturation. The 28-day-old backfill sample was placed into the water tank. Water was next injected to 1/4 of the sample height, and then the same amount of water was injected every 2 h. All samples were completely submerged within 6 h.
- (2)
- After every four hours, the weights of the sample during the drying and wetting procedures were measured using an electronic balance (with an accuracy of 0.01 g). If the weight difference was less than 1%, the sample was considered to be saturated.
- (3)
- After the sample was completely saturated with water, an NMR analysis was performed to obtain the initial relaxation time spectrum. The NMR relaxation measurements were conducted on the AniMR-150 NMR system. The magnetic field strength of the NMR instrument was 0.3 T, the echo time was 0.301 ms, the waiting time was 1500 s, the sampling frequency was 200 KHz, and the magnet control temperature was 25–35 °C. After sampling and inversion operations were conducted in the NMR testing system itself, the spectrum was obtained as the T2 relaxation time versus signal intensity. The porosity calculated by the built-in program of the NMR system was output along with the spectrum.
- (4)
- The sample was taken out of the nuclear magnetic equipment and then centrifuged at an initial rotation speed of 1500 rpm. The instrument that was used for the centrifugation was an 80-1 Desktop Electric Centrifuge made by Changzhou Ronghua Instrument Manufacturing Co., Ltd., Changzhou, China. Following this, the sample was subjected to NMR analysis to obtain the relaxation time spectrum after centrifugation. If the difference ratio of water retention before and after the centrifugation was larger than 3%, the centrifugation operation was conducted again with the rotation speed increased by 500 rpm. The maximum limitation of rotation speed was set as 4000 rpm. The cycle of centrifugation and NMR analysis was repeated until the difference ratio of water retention was within 3%.
- (5)
- A specimen of approximately 1 mm3 was taken from the core of samples and dehydrated with absolute ethanol to stop the hydration. The specimen was dried at 45 °C to a constant weight and was used to conduct SEM scanning on the a Czech TESCAN MIRA3 field-emission SEM (Taisken Co., Ltd., Shanghai, China). In order to observe the pore structure, the scale of the SEM images was restricted to 2 μm.
- (6)
- The above experimental procedures were repeated for all cemented paste backfill samples. The testing instruments and process are shown in Figure 5.
3. Results and Discussion
3.1. Porosity Analysis of the Backfills in a Water-Saturated State
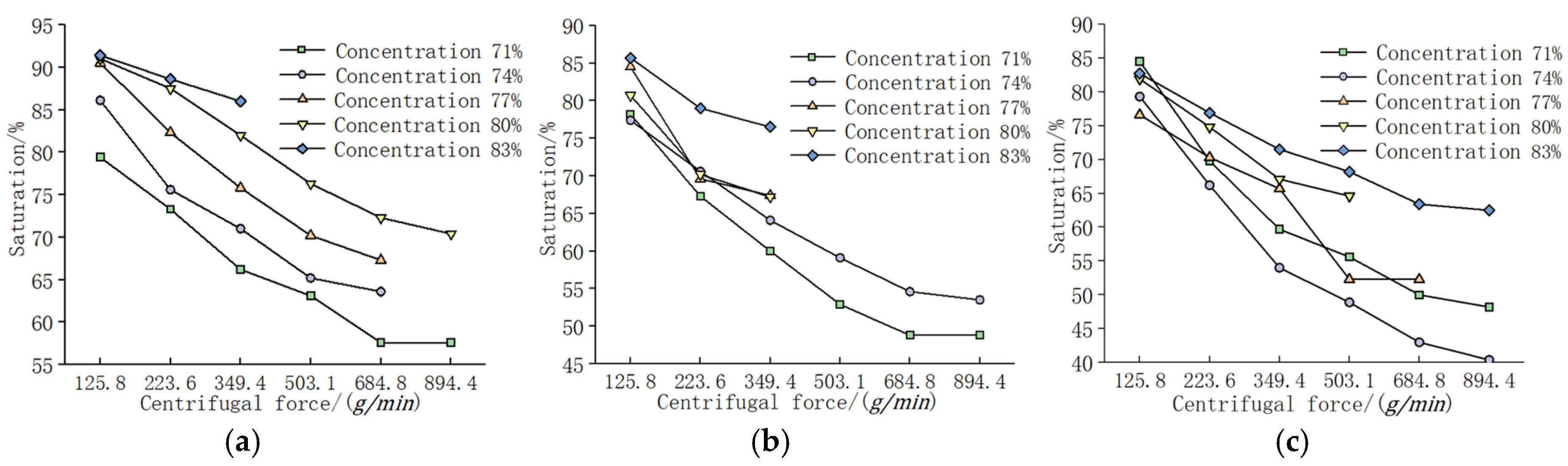
3.2. Analysis of Backfill Porosity before and after Centrifugation
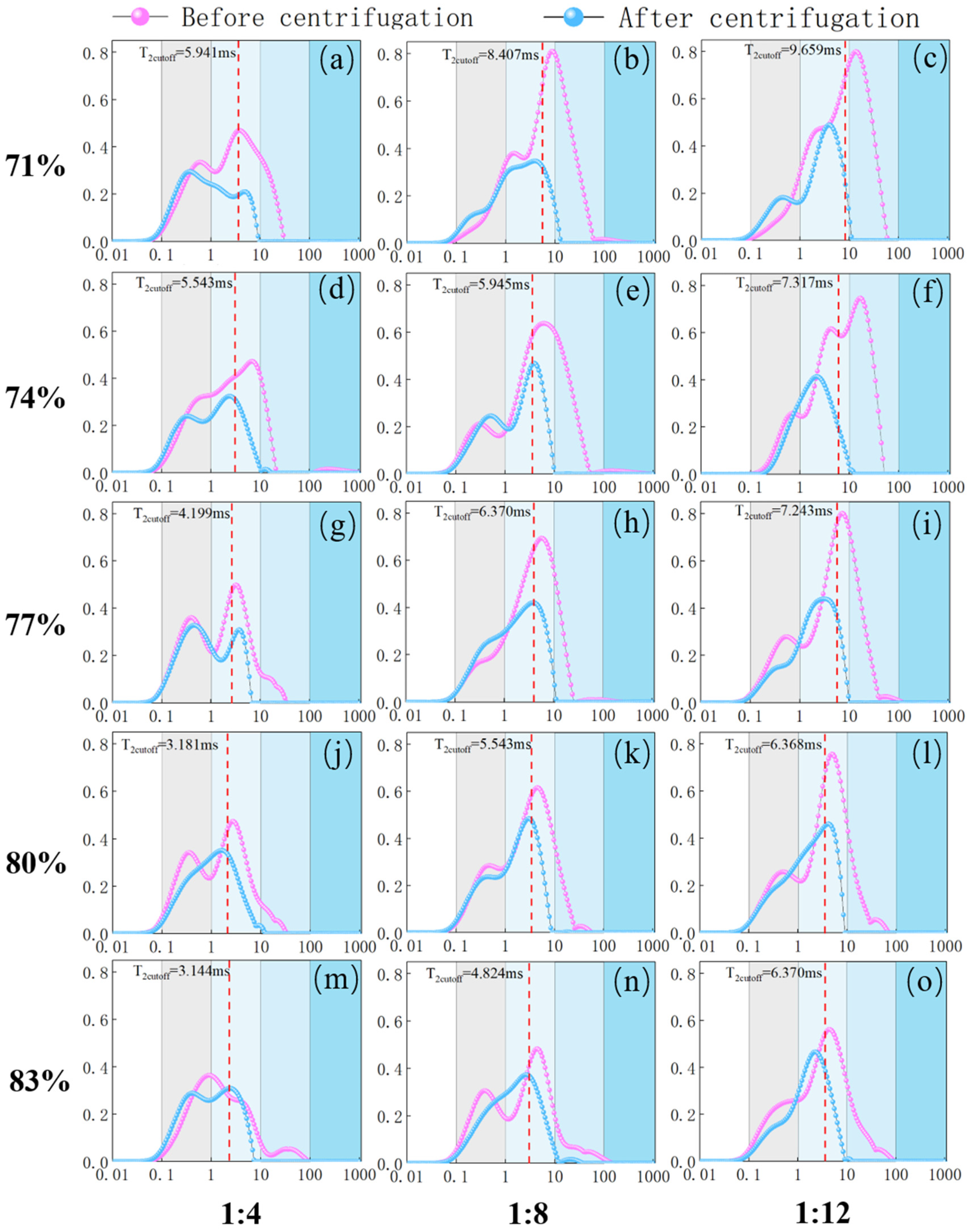
3.3. Analysis of the Optimal Centrifugal Force and T2 Cutoff Value
3.3.1. Calibration of the Optimal Centrifugal Force and T2 Cutoff
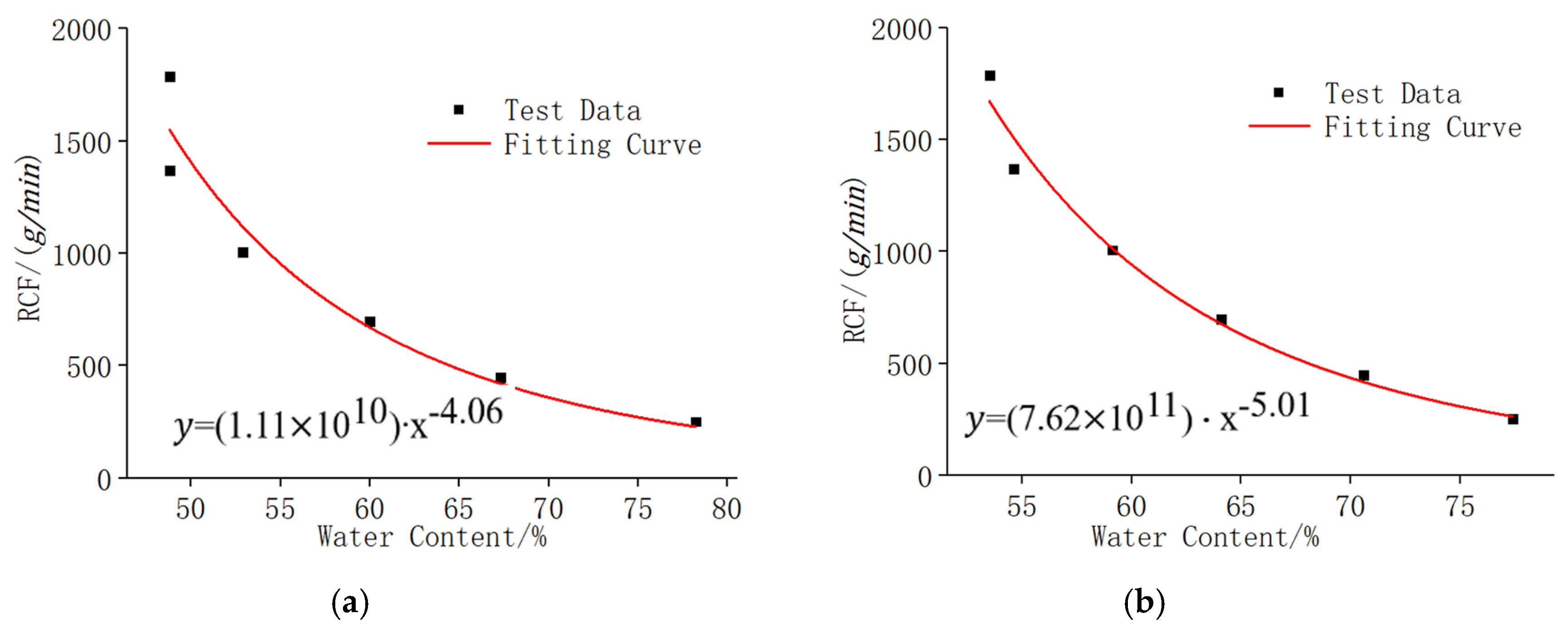
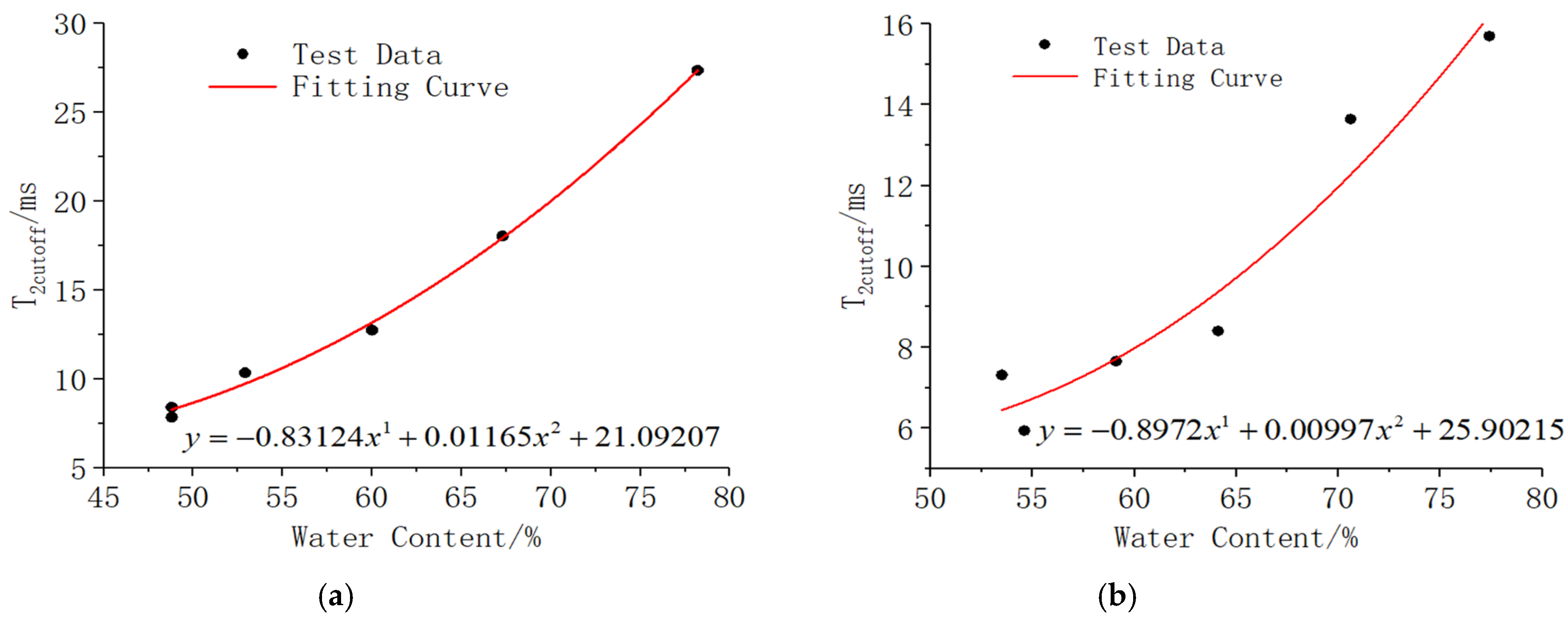
3.3.2. Regression Analysis of Centrifugal Force, T2 Cutoff, and Water Retention Curve
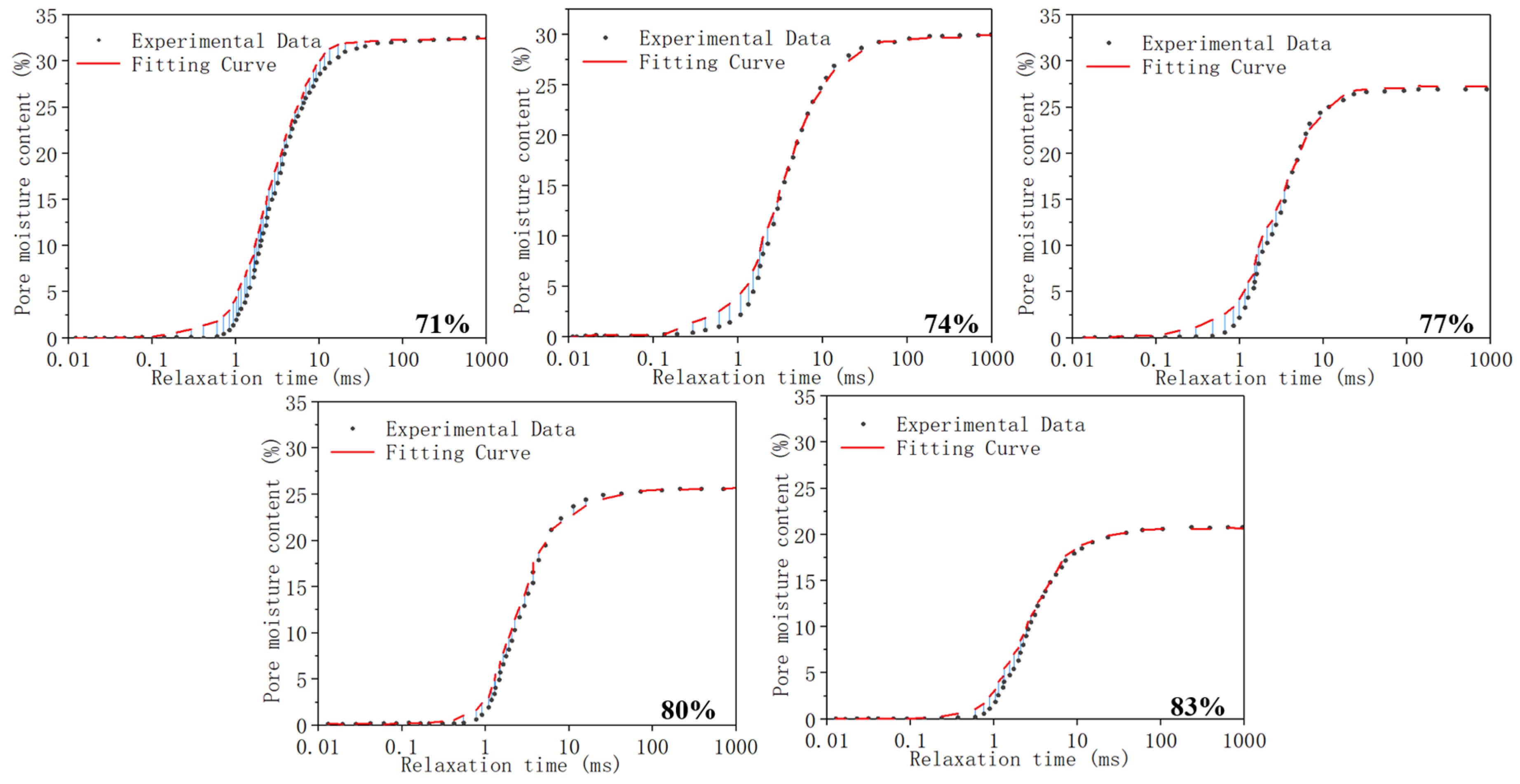
3.4. NMR Pore Water Retention Model Based on SWCC
3.4.1. Establishment of a Pore Water Retention Model
3.4.2. Regression Analysis of the Pore Water Retention Model
4. Conclusions
- (1)
- The optimal centrifugal force of the backfills with different solid concentrations and cement–tailings ratios were analyzed by an NMR-centrifugation test. This test also achieved a comparison of the porosities of the backfill samples between the saturated water stage and the free water separation stage. The values were between 125.8 and 894.4 when the concentration ranged from 71% to 83% at cement–tailings ratios of 1:4 and 1:8, respectively.
- (2)
- The range of the T2 cutoff of the backfill samples ranged from 3 to 10 ms. The centrifugal force and the water retention conformed to the overall power function distribution, and the T2 cutoff and the water retention conformed to the quadratic polynomial distribution. When the concentration and ratio accelerated, the T2 cutoff decreased; hence, the corresponding permeability increased, demonstrating that the higher the concentration and cement–tailings ratios are, the better the pore connectivity and guttation effect. The lower the concentration and cement–tailings ratio are, the more concentrated the occurrence of large pores, thereby forming long-term water retention.
- (3)
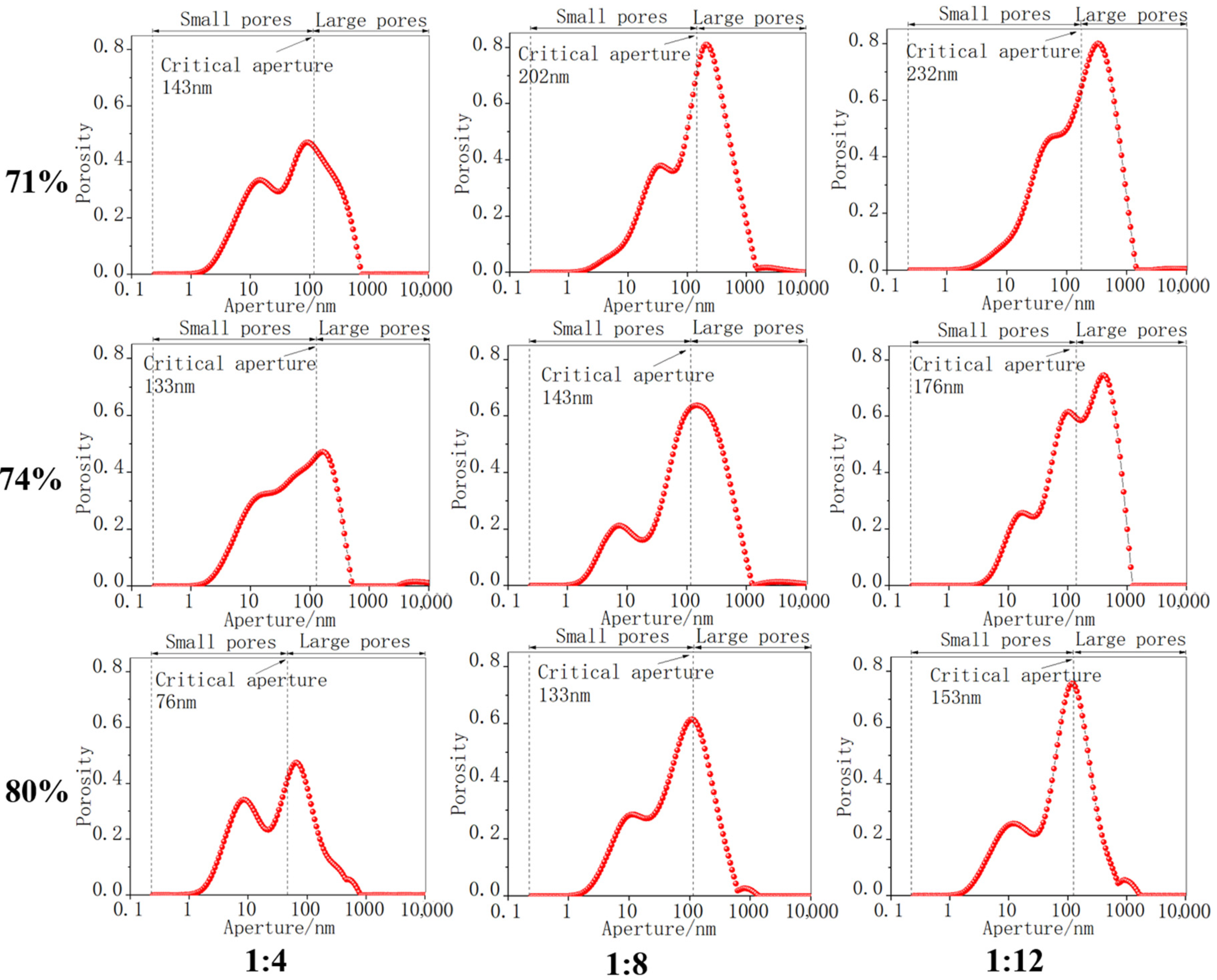
- By establishing an SWCC-based NMR pore water distribution model, the proportion distribution of large and small pores was obtained. Further, the pore size distribution curve presents bimodal characteristics. The higher the solid concentration and cement–tailings ratio, the smaller the critical pore size needed to reduce concentrated water retention in the area. This research lays a theoretical foundation for revealing the migration law of water molecules in backfill and to further study the probability density of pore size.
Author Contributions
Funding
Conflicts of Interest
References
- Du, X.; Feng, G.; Zhang, Y.; Wang, Z.; Guo, Y.; Qi, T. Bearing mechanism and stability monitoring of cemented gangue-fly ash backfill column with stirrups in partial backfill engineering. Eng. Struct. 2019, 188, 876–881. [Google Scholar] [CrossRef]
- Wang, D.L.; Zhang, Q.L.; Chen, Q.S.; Qi, C.C.; Feng, Y.; Xiao, C.C. Temperature variation characteristics in flocculation settlement of tailings and its mechanism. Int. J. Min. Met. Mater. 2020. [Google Scholar] [CrossRef]
- Hou, D.; Li, D.; Hua, P.; Jiang, J.; Zhang, G. Statistical modelling of compressive strength controlled by porosity and pore size distribution for cementitious materials. Cem. Concr. Compos. 2019, 96, 11–20. [Google Scholar] [CrossRef]
- Chidiac, S.E.; Moutassem, F.; Mahmoodzadeh, F. Compressive strength model for concrete. Mag. Concr. Res. 2013, 65, 557–572. [Google Scholar] [CrossRef]
- Rong, H.; Zhou, M.; Hou, H. Pore structure evolution and its effect on strength development of sulfate-containing cemented paste backfill. Minerals 2017, 7, 8. [Google Scholar] [CrossRef]
- Li, J.-S.; Wang, D.; Kang, T.-H. Algorithmic study on rock pore structure based on micro-CT experiment. Chin. J. Geotech. Eng. 2010, 32, 1703–1708. [Google Scholar]
- Liu, L.; Fang, Z.; Qi, C.; Zhang, B.; Guo, L.; Song, K.I.I.L. Experimental investigation on the relationship between pore characteristics and unconfined compressive strength of cemented paste backfill. Constr. Build. Mater. 2018, 179, 254–264. [Google Scholar] [CrossRef]
- Yao, Y.; Liu, D.; Che, Y.; Tang, D.; Tang, S.; Huang, W. Petrophysical characterization of coals by low-field nuclear magnetic resonance (NMR). Fuel 2010, 89, 1371–1380. [Google Scholar] [CrossRef]
- Hu, J.H.; Ren, Q.F.; Jiang, Q.; Jiang, Y.J.; Shang, J.L.; Luo, Z.Q. Macroscopic and microscopic trans-scale characteristics of pore structure of mine grouting materials. Trans. Nonferr. Met. Soc. China 2019, 29, 1067–1081. [Google Scholar] [CrossRef]
- al Hinai, A.; Rezaee, R.; Esteban, L.; Labani, M. Comparisons of pore size distribution: A case from the Western Australian gas shale formations. J. Unconv. Oil Gas Resour. 2014, 8, 1–13. [Google Scholar] [CrossRef]
- Liu, L.; Xin, J.; Huan, C.; Qi, C.; Zhou, W.; Song, K.I.I.L. Pore and strength characteristics of cemented paste backfill using sulphide tailings: Effect of sulphur content. Constr. Build. Mater. 2020, 237, 117452. [Google Scholar] [CrossRef]
- Hu, J.; Ren, Q.; Ding, X.; Jiang, Q. Trans-scale relationship analysis between the pore structure and macro parameters of backfill and slurry. R. Soc. Open Sci. 2019, 6. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Shao, M. Advances and perspectives on soil water research in China’s Loess Plateau. Earth Sci. Rev. 2019, 199, 102962. [Google Scholar] [CrossRef]
- van Genuchten, M.T. Closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Xing, A.Q. Equations for the soil–water characteristic curve. Can. Geotech. J. 1994, 31, 521–532. [Google Scholar] [CrossRef]
- Gitirana, G.D.N.; Fredlund, D.G. Soil–water characteristic curve equation with independent properties. J. Geotech. Geoenvironmental. Eng. 2004, 130, 209–212. [Google Scholar] [CrossRef]
- Rahardjo, H.; Satyanaga, A.; D’Amore, G.A.R.; Leong, E.C. Soil–water characteristic curves of gap-graded soils. Eng. Geol. 2012, 125, 102–107. [Google Scholar] [CrossRef]
- Chen, R.P.; Liu, P.; Liu, X.M.; Wang, P.F.; Kang, X. Pore-scale model for estimating the bimodal soil–water characteristic curve and hydraulic conductivity of compacted soils with different initial densities. Eng. Geol. 2019, 260, 105199. [Google Scholar] [CrossRef]
- Zhai, Q.; Rahardjo, H.; Satyanaga, A.; Priono. Effect of bimodal soil–water characteristic curve on the estimation of permeability function. Eng. Geol. 2017, 230, 142–151. [Google Scholar] [CrossRef]
- Li, X.; Li, J.H.; Zhang, L.M. Predicting bimodal soil–water characteristic curves and permeability functions using physically based parameters. Comput. Geotech. 2014, 57, 85–96. [Google Scholar] [CrossRef]
- Ren, X.; Kang, J.; Ren, J.; Chen, X.; Zhang, M. A method for estimating soil water characteristic curve with limited experimental data. Geoderma 2020, 360, 114013. [Google Scholar] [CrossRef]
- Li, Z.; Liu, D.; Cai, Y.; Wang, Y.; Si, G. Evaluation of coal petrophysics incorporating fractal characteristics by mercury intrusion porosimetry and low-field NMR. Fuel 2020, 263, 116802. [Google Scholar] [CrossRef]
- Belem, T.; Benzaazoua, M. Predictive models for prefeasibility cemented paste backfill mix design. In Proceedings of the 3rd International Conference on Post-Mining, Nancy, France, 6–8 February 2008; Volume 8, pp. 6–8. [Google Scholar]
- Gao, R.; Zhou, K.; Zhang, J.; Guo, H.; Ren, Q. Research on the Dynamic Characteristics in the Flocculation Process of Mineral Processing Tailings. IEEE Access 2019, 7, 129244–129259. [Google Scholar] [CrossRef]
- Sadrossadat, E.; Basarir, H.; Luo, G.; Karrech, A.; Durham, R.; Fourie, A.; Elchalakani, M. Multi-objective mixture design of cemented paste backfill using particle swarm optimisation algorithm. Miner. Eng. 2020, 153, 106385. [Google Scholar] [CrossRef]
- Zhai, C.; Wu, S.; Liu, S.; Qin, L.; Xu, J. Experimental study on coal pore structure deterioration under freeze–thaw cycles. Environ. Earth Sci. 2017, 76, 507. [Google Scholar] [CrossRef]
- Li, J.L.; Zhou, K.P.; Zhang, Y.M.; Xu, Y.J. Study on freeze-thaw damage of rock pore structure based on nuclear magnetic resonance. Chin. J. Rock Mech. Eng. 2012, 31, 1208–1214. [Google Scholar]
- Li, J.; Liu, H.; Ai, K.; Zhu, L. An NMR-based experimental study on the pore structure of the hydration process of mine filling slurry. Adv. Civ. Eng. 2018, 2018. [Google Scholar] [CrossRef]
- Li, J.; Zhu, L.; Zhou, K.; Cao, S.; Liu, H. Experimental Investigation on the Effects of Ambient Freeze–Thaw Cycling on Creep Mechanical Properties of Sandstone Under Step Loading. IEEE Access 2019, 7, 108513–108520. [Google Scholar] [CrossRef]
- Liu, K.; Cheng, X.; Zhang, X.; Li, Z.; Zhuang, J.; Guo, X. Relationship between the microstructure/pore structure of oil-well cement and hydrostatic pressure. Transp. Porous Media 2018, 124, 463–478. [Google Scholar] [CrossRef]
- Testamanti, M.N.; Rezaee, R. Determination of NMR T2 cut-off for clay bound water in shales: A case study of Carynginia Formation, Perth Basin, Western Australia. J. Pet. Sci. Eng. 2017, 149, 497–503. [Google Scholar] [CrossRef]
- Ge, X.; Fan, Y.; Zhu, X.; Chen, Y.; Li, R. Determination of pore structure of rock based on nuclear magnetic resonance technique. J. Cent. South Univ. (Sci. Technol.) 2012, 43, 4796–4800. [Google Scholar]
- Wahhab, H.I.A.A.; Dalhat, M.A. Oil-Sludge Extended Asphalt Mastic Filled with Heavy Oil Fly Ash and Cement Waste for Waterproofing. J. Eng. Res. 2014, 11, 27–38. [Google Scholar] [CrossRef]
- Fall, M.; Célestin, J.C.; Pokharel, M.; Touré, M. A contribution to understanding the effects of curing temperature on the mechanical properties of mine cemented tailings backfill. Eng. Geol. 2010, 114, 397–413. [Google Scholar] [CrossRef]
- Lyu, C.; Ning, Z.; Wang, Q.; Chen, M. Application of NMR T2 to pore size distribution and movable fluid distribution in tight sandstones. Energy Fuels 2018, 32, 1395–1405. [Google Scholar] [CrossRef]
- Wu, T.; Li, X.; Zhao, J.; Zhang, D. Multiscale pore structure and its effect on gas transport in organic-rich shale. Water Resour. Res. 2017, 53, 5438–5450. [Google Scholar] [CrossRef]
- Liu, J.Z.; Zhu, J.F.; Cheng, J.; Zhou, J.H.; Cen, K.F. Pore structure and fractal analysis of Ximeng lignite under microwave irradiation. Fuel 2015, 146, 41–50. [Google Scholar] [CrossRef]
- Durner, W. Hydraulic conductivity estimation for soils with heterogeneous pore structure. Water Resour. Res. 1994, 30, 211–223. [Google Scholar] [CrossRef]



| Element | O | Na | Mg | Al | Si | S | Cl | K | Ca | Ti |
| Content | 42.5 | 0.019 | 5.695 | 0.781 | 2.29 | 0.676 | 0.018 | 0.239 | 33.02 | 0.037 |
| Element | Cr | Mn | Fe | Cu | Zn | As | Rb | Sr | Zr | Pb |
| Content | 0.006 | 0.468 | 1.316 | 0.0141 | 0.104 | 0.13 | 0.002 | 0.0252 | 0.0013 | 0.179 |
| Sample No. | 1:4 | 1:8 | 1:12 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 71% | 74% | 77% | 80% | 83% | 71% | 74% | 77% | 80% | 83% | 71% | 74% | 77% | 80% | 83% | |
| Mean value | 24.65 | 23.58 | 21.62 | 20.87 | 17.27 | 32.62 | 30.37 | 27.42 | 26.13 | 20.90 | 34.35 | 33.54 | 34.27 | 27.55 | 24.72 |
| Standard deviation | 0.17 | 0.22 | 0.30 | 0.23 | 0.19 | 0.15 | 0.10 | 0.12 | 0.19 | 0.24 | 0.17 | 0.22 | 0.13 | 0.30 | 0.30 |
| Cement–Tailings Ratio | Concentration/% | Φ/% | Variation of Sample Porosity after Different Centrifugal Forces/% | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Centrifuge Time/min | 125.8 | 223.6 | 349.4 | 503.1 | 684.8 | 894.4 g/min | |||
| 1:4 | 71 | 24.646 | 6 | 19.557 | 18.063 | 16.234 | 15.547 | 14.206 | 14.203 |
| 74 | 23.581 | 5 | 20.310 | 17.837 | 16.743 | 15.371 | 14.990 | (-) | |
| 77 | 21.618 | 5 | 19.559 | 17.834 | 16.385 | 15.168 | 14.549 | (-) | |
| 80 | 20.866 | 6 | 18.999 | 18.260 | 17.132 | 15.915 | 15.079 | 14.697 | |
| 83 | 17.266 | 3 | 15.778 | 15.292 | 14.850 | (-) | (-) | (-) | |
| 1:8 | 71 | 32.624 | 6 | 25.517 | 21.958 | 19.571 | 17.259 | 15.938 | 15.909 |
| 74 | 30.365 | 6 | 23.491 | 21.429 | 19.451 | 17.942 | 16.558 | 16.242 | |
| 77 | 27.421 | 3 | 23.161 | 19.085 | 18.487 | (-) | (-) | (-) | |
| 80 | 26.128 | 3 | 21.087 | 18.345 | 17.550 | (-) | (-) | (-) | |
| 83 | 20.896 | 3 | 17.911 | 16.512 | 15.988 | (-) | (-) | (-) | |
| 1:12 | 71 | 34.347 | 6 | 29.029 | 23.974 | 20.501 | 19.083 | 17.185 | 16.155 |
| 74 | 33.537 | 6 | 26.620 | 22.204 | 18.115 | 16.401 | 14.434 | 13.568 | |
| 77 | 31.265 | 5 | 23.952 | 21.995 | 20.546 | 16.358 | 16.376 | (-) | |
| 80 | 27.546 | 4 | 22.558 | 20.598 | 18.469 | 17.773 | (-) | (-) | |
| 83 | 24.723 | 6 | 20.429 | 18.995 | 17.683 | 16.862 | 15.693 | 15.437 | |
| Concentration | 1:4 | 1:8 | 1:12 | |||
|---|---|---|---|---|---|---|
| T2cutoff/ms | T2cutoff/ms | T2cutoff/ms | ||||
| 71% | 894.4 | 5.941 | 894.4 | 8.407 | 894.4 | 9.659 |
| 74% | 684.8 | 5.941 | 894.4 | 7.317 | 894.4 | 5.543 |
| 77% | 684.8 | 4.199 | 349.4 | 7.843 | 684.8 | 6.368 |
| 80% | 894.4 | 3.181 | 349.4 | 5.543 | 503.1 | 6.368 |
| 83% | 349.4 | 3.144 | 349.4 | 6.368 | 894.4 | 4.824 |
| Fitting Parameters of Water Retention Model of Backfill | ||||||||
|---|---|---|---|---|---|---|---|---|
| Concentration | ||||||||
| 71% | 0.312 | 0.062 | 0.935 | 0.938 | 1.621 | 1.524 | 2.260 | 0.98 |
| 74% | 0.324 | 0.071 | 1.035 | 1.138 | 1.581 | 1.289 | 2.240 | 0.99 |
| 77% | 0.353 | 0.120 | 0.635 | 0.238 | 1.632 | 1.568 | 2.140 | 0.99 |
| 80% | 0.386 | 0.732 | 0.935 | 0.656 | 1.721 | 1.524 | 2.040 | 0.99 |
| 83% | 0.402 | 0.965 | 0.865 | 0.234 | 1.821 | 1.424 | 1.820 | 0.98 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, R.; Zhou, K.; Liu, W.; Ren, Q. Correlation between the Pore Structure and Water Retention of Cemented Paste Backfill Using Centrifugal and Nuclear Magnetic Resonance Methods. Minerals 2020, 10, 610. https://doi.org/10.3390/min10070610
Gao R, Zhou K, Liu W, Ren Q. Correlation between the Pore Structure and Water Retention of Cemented Paste Backfill Using Centrifugal and Nuclear Magnetic Resonance Methods. Minerals. 2020; 10(7):610. https://doi.org/10.3390/min10070610
Chicago/Turabian StyleGao, Rugao, Keping Zhou, Wei Liu, and Qifan Ren. 2020. "Correlation between the Pore Structure and Water Retention of Cemented Paste Backfill Using Centrifugal and Nuclear Magnetic Resonance Methods" Minerals 10, no. 7: 610. https://doi.org/10.3390/min10070610
APA StyleGao, R., Zhou, K., Liu, W., & Ren, Q. (2020). Correlation between the Pore Structure and Water Retention of Cemented Paste Backfill Using Centrifugal and Nuclear Magnetic Resonance Methods. Minerals, 10(7), 610. https://doi.org/10.3390/min10070610





