Evolution of Fracture Aperture in Quartz Sandstone under Hydrothermal Conditions: Mechanical and Chemical Effects
Abstract
:1. Introduction
2. Sample Material and Experimental Methods
2.1. Sample Preparation and Experimental Apparatus
2.2. Experimental Procedures
2.3. Sampling and Chemical Fluid Analysis
2.4. Determination of Fracture Aperture
2.5. X-ray Computed Micro Tomography (µCT)
3. Results
3.1. Effects of Pressure and Temperature on Fracture Aperture
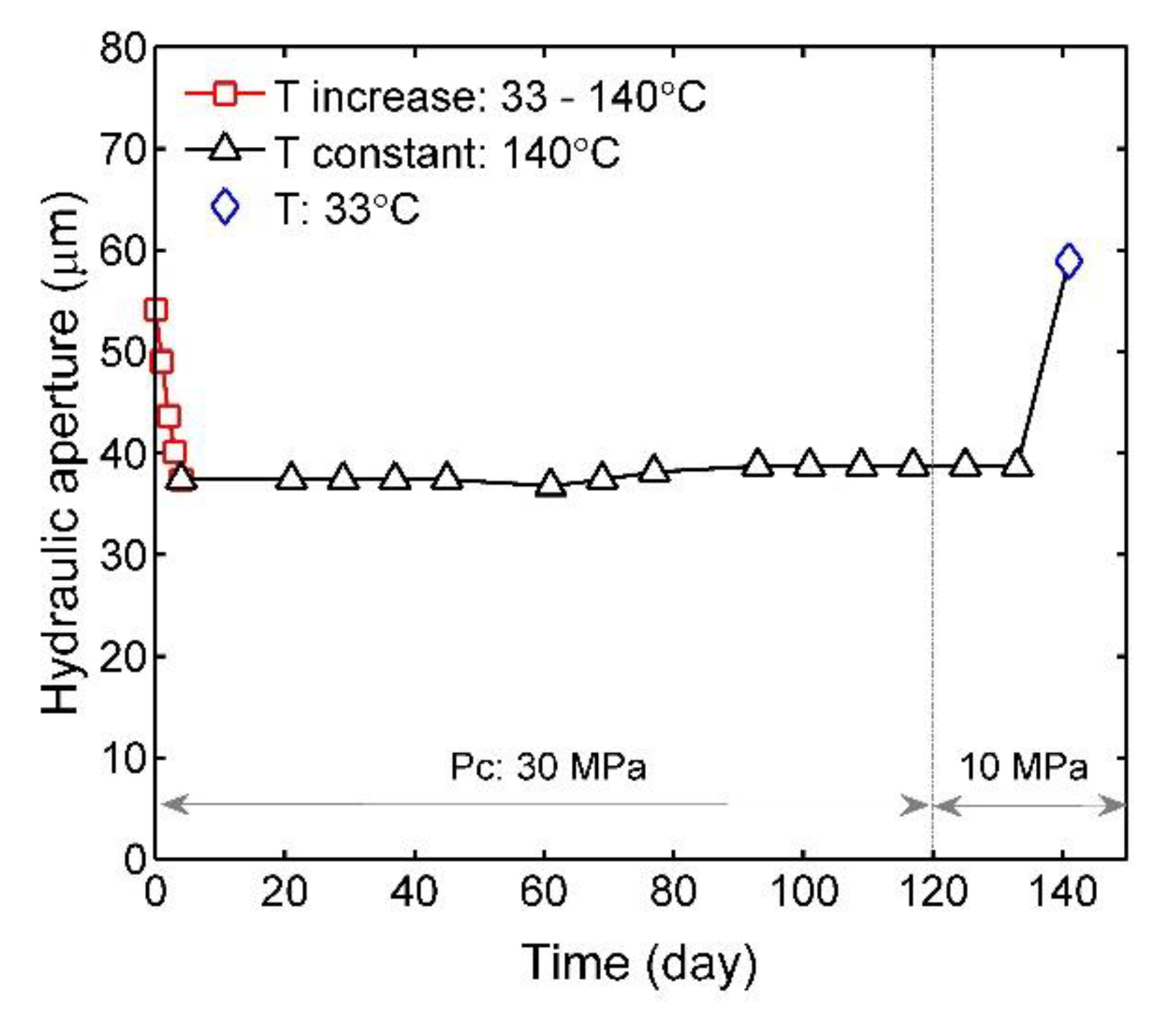
3.2. Time-Dependent Evolution of Fracture Aperture
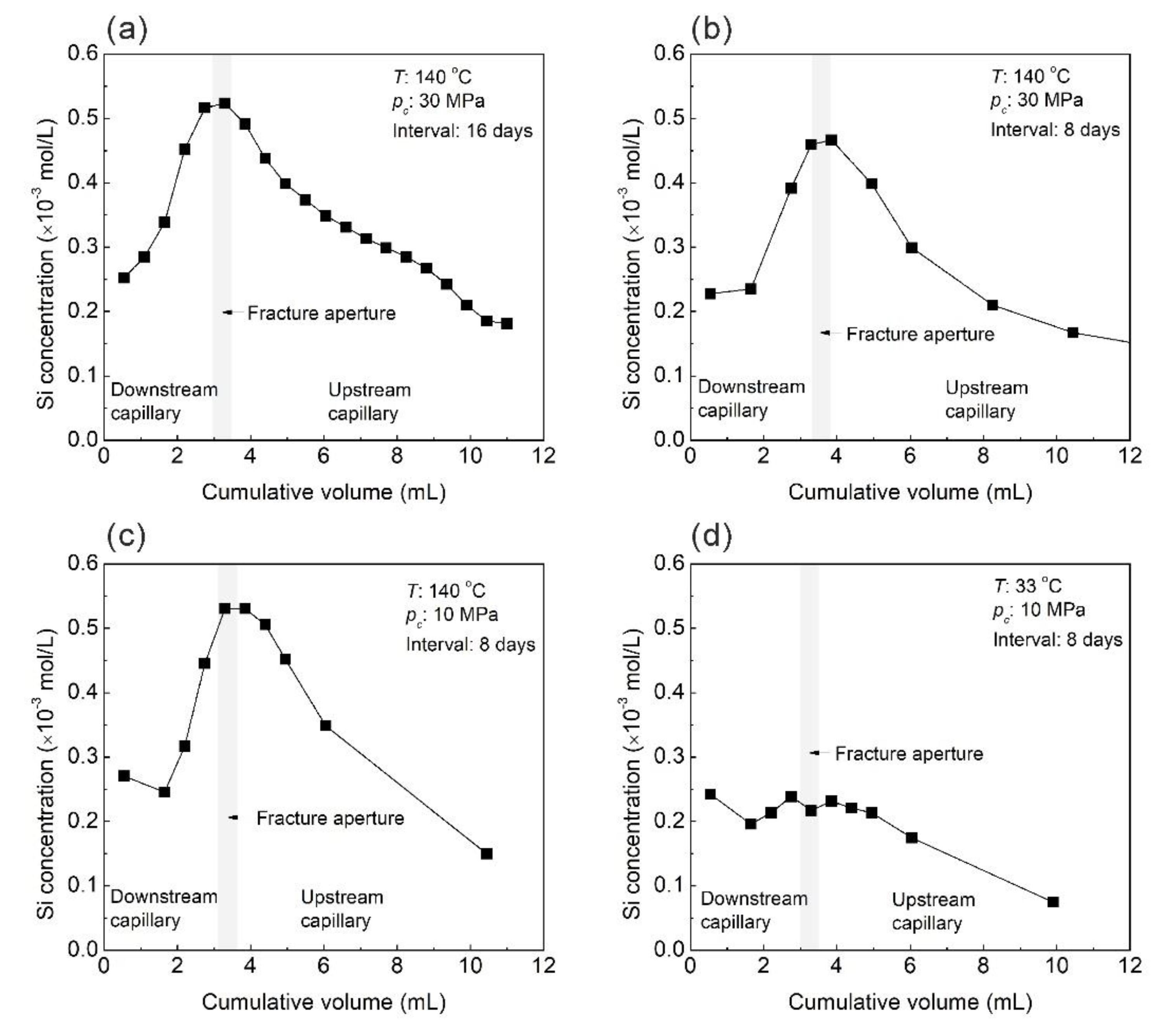
3.3. Evolution of Effluent Si Concentration
3.4. Microstructure Variations
4. Discussion
4.1. Mechanical and Thermal Effects on Fracture Aperture
4.2. Chemical Effects on Fracture Aperture in the Long Term
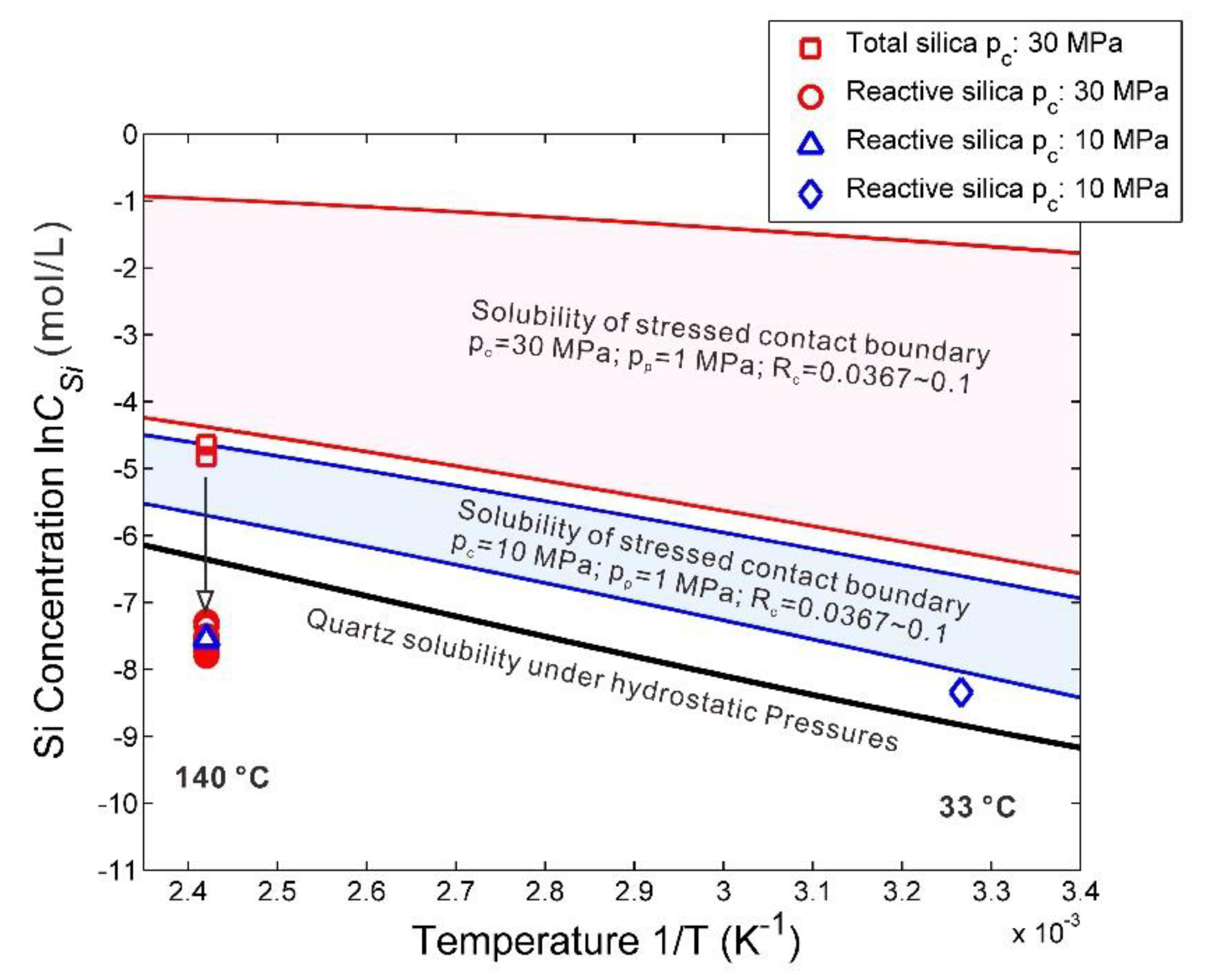
4.2.1. Quartz Solubility
4.2.2. Pressure Solution-Induced Deformation
4.3. Effects of Stress Corrosion-Induced Subcritical Cracking
4.4. Implications
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Schutjens, P.M. Experimental compaction of quartz sand at low effective stress and temperature conditions. J. Geol. Soc. Lond. 1991, 148, 3. [Google Scholar] [CrossRef]
- Polak, A.; Elsworth, D.; Yasuhara, H.; Grader, A.S.; Halleck, P.M. Permeability reduction of a natural fracture under net dissolution by hydrothermal fluids. Geophys. Res. Lett. 2003, 30, 20. [Google Scholar] [CrossRef]
- Yasuhara, H.; Polak, A.; Mitani, Y.; Grader, A.; Halleck, P.; Elsworth, D. Evolution of fracture permeability through fluid–rock reaction under hydrothermal conditions. Earth Planet. Sci. Lett. 2006, 244, 1–2. [Google Scholar] [CrossRef]
- Weyl, P.K. Pressure solution and the force of crystallization: A phenomenological theory. J. Geophys. Res. 1959, 64, 11. [Google Scholar] [CrossRef]
- De Boer, R. On the thermodynamics of pressure solution—Interaction between chemical and mechanical forces. Geochim. Cosmochim. Acta 1977, 41, 2. [Google Scholar] [CrossRef]
- De Boer, R. Pressure solution: Theory and experiments. Tectonophysics 1977, 39, 1–3. [Google Scholar] [CrossRef]
- Robin, P.-Y.F. Pressure solution at grain-to-grain contacts. Geochim. Cosmochim. Acta 1978, 42. [Google Scholar] [CrossRef]
- Van Noort, R.; Spiers, C.J.; Pennock, G.M. Compaction of granular quartz under hydrothermal conditions: Controlling mechanisms and grain boundary processes. J. Geophys. Res. 2008, 113, B12. [Google Scholar] [CrossRef] [Green Version]
- Niemeijer, A.; Spiers, C.; Bos, B. Compaction creep of quartz sand at 400–600 °C: Experimental evidence for dissolution-controlled pressure solution. Earth Planet. Sci. Lett. 2002, 195, 3–4. [Google Scholar] [CrossRef]
- Polak, A.; Elsworth, D.; Liu, J.; Grader, A.S. Spontaneous switching of permeability changes in a limestone fracture with net dissolution. Water Resour. Res. 2004, 40, 3. [Google Scholar] [CrossRef]
- Yasuhara, H.; Elsworth, D.; Polak, A. Evolution of permeability in a natural fracture: Significant role of pressure solution. J. Geophys. Res. 2004, 109, B3. [Google Scholar] [CrossRef]
- Yasuhara, H.; Kinoshita, N.; Ohfuji, H.; Takahashi, M.; Ito, K.; Kishida, K. Long-term observation of permeability in sedimentary rocks under high-temperature and stress conditions and its interpretation mediated by microstructural investigations. Water Resour. Res. 2015, 51, 7. [Google Scholar] [CrossRef] [Green Version]
- Tada, R.; Maliva, R.; Siever, R. A new mechanism for pressure solution in porous quartzose sandstone. Geochim. Cosmochim. Acta 1987, 51, 9. [Google Scholar] [CrossRef]
- Yasuhara, H.; Elsworth, D. Compaction of a Rock Fracture Moderated by Competing Roles of Stress Corrosion and Pressure Solution. Pure Appl. Geophys. 2008, 165, 7. [Google Scholar] [CrossRef] [Green Version]
- Lu, R.; Nagel, T.; Shao, H.; Kolditz, O.; Shao, H. Modeling of dissolution-induced permeability evolution of a granite fracture under crustal conditions. J. Geophys. Res. Solid Earth 2018, 123, 7. [Google Scholar] [CrossRef]
- Elias, B.P.; Hajash, J.A. Changes in quartz solubility and porosity due to effective stress: An experimental investigation of pressure solution. Geology 1992, 20, 5. [Google Scholar] [CrossRef]
- Milsch, H.; Spangenberg, E.; Kulenkampff, J.; Meyhöfer, S. A new apparatus for long-term petrophysical investigations on geothermal reservoir rocks at simulated in-situ conditions. Transp. Porous Med. 2008, 74, 1. [Google Scholar] [CrossRef] [Green Version]
- Engelder, T. A natural example of the simultaneous operation of free-face dissolution and pressure solution. Geochim. Cosmochim. Acta 1982, 46, 69–74. [Google Scholar] [CrossRef]
- Aureli, F.; Ciprotti, M.; D’Amato, M.; do Nascimento da Silva, E.; Nisi, S.; Passeri, D.; Sorbo, A.; Raggi, A.; Rossi, M.; Cubadda, F. Determination of total silicon and SiO2 particles using an ICP-MS based analytical platform for toxicokinetic studies of synthetic amorphous silica. Nanomaterials 2020, 10, 5. [Google Scholar] [CrossRef]
- Witherspoon, P.A.; Wang, J.S.; Iwai, K.; Gale, J.E. Validity of cubic law for fluid flow in a deformable rock fracture. Water Resour. Res. 1980, 16, 6. [Google Scholar] [CrossRef] [Green Version]
- Zimmerman, R.W.; Bodvarsson, G.S. Hydraulic conductivity of rock fractures. Transp. Porous Med. 1996, 23, 1. [Google Scholar] [CrossRef] [Green Version]
- Carroll, M.M.; Katsube, N. The role of Terzaghi effective stress in linearly elastic deformation. J. Energ. Resour. Tech. 1983, 105, 4. [Google Scholar] [CrossRef]
- Arns, C.H.; Knackstedt, M.A.; Pinczewski, W.V.; Garboczi, E.J. Computation of linear elastic properties from microtomographic images: Methodology and agreement between theory and experiment. Geophysics 2002, 67, 5. [Google Scholar] [CrossRef]
- David, E.C.; Fortin, J.; Schubnel, A.; Guéguen, Y.; Zimmerman, R.W. Laboratory measurements of low- and high-frequency elastic moduli in Fontainebleau sandstone. Geophysics 2013, 78, 5. [Google Scholar] [CrossRef]
- Sulem, J.; Ouffroukh, H. Hydromechanical behaviour of Fontainebleau sandstone. Rock Mech. Rock Eng. 2006, 39, 3. [Google Scholar] [CrossRef]
- Durham, W.B.; Bonner, B.P. Self-propping and fluid flow in slightly offset joints at high effective pressures. J. Geophys. Res. 1994, 99, B5. [Google Scholar] [CrossRef]
- Vogler, D.; Amann, F.; Bayer, P.; Elsworth, D. Permeability evolution in natural fractures subject to cyclic loading and gouge formation. Rock Mech. Rock Eng. 2016, 49, 9. [Google Scholar] [CrossRef]
- Crawford, B.R.; Tsenn, M.C.; Homburg, J.M.; Stehle, R.C.; Freysteinson, J.A.; Reese, W.C. Incorporating scale-dependent fracture stiffness for improved reservoir performance prediction. Rock Mech. Rock Eng. 2017, 50, 12. [Google Scholar] [CrossRef]
- Rutqvist, J. Fractured rock stress-permeability relationships from in situ data and effects of temperature and chemical-mechanical couplings. Geofluids 2015, 15, 1–2. [Google Scholar] [CrossRef] [Green Version]
- Fournier, R.O.; Potter II, R.W. An equation correlating the solubility of quartz in water from 25 to 900 C at pressures up to 10,000 bars. Geochim. Cosmochim. Acta 1982, 46, 10. [Google Scholar] [CrossRef]
- Paterson, M. Nonhydrostatic thermodynamics and its geologic applications. Rev. Geophys. 1973, 11, 2. [Google Scholar] [CrossRef]
- Renard, F.; Park, A.; Ortoleva, P.; Gratier, J.-P. An integrated model for transitional pressure solution in sandstones. Tectonophysics 1999, 312, 2–4. [Google Scholar] [CrossRef]
- Yasuhara, H. A mechanistic model for compaction of granular aggregates moderated by pressure solution. J. Geophys. Res. 2003, 108, B11. [Google Scholar] [CrossRef]
- Ogata, S.; Yasuhara, H.; Kinoshita, N.; Cheon, D.-S.; Kishida, K. Modeling of coupled thermal-hydraulic-mechanical-chemical processes for predicting the evolution in permeability and reactive transport behavior within single rock fractures. Int. J. Rock Mech. Min. Sci. 2018, 107. [Google Scholar] [CrossRef]
- Rimstidt, J.D.; Barnes, H. The kinetics of silica-water reactions. Geochim. Cosmochim. Acta 1980, 44, 11. [Google Scholar] [CrossRef]
- De Boer, R.; Nagtegaal, P.; Duyvis, E. Pressure solution experiments on quartz sand. Geochim. Cosmochim. Acta 1977, 41, 2. [Google Scholar] [CrossRef]
- Gratier, J.-P.; Dysthe, D.K.; Renard, F. The Role of Pressure Solution Creep in the Ductility of the Earth’s Upper Crust. In Advances in Geophysics; Dmowska, R., Ed.; Elsevier: Amsterdam, The Netherlands, 2013; pp. 47–179. [Google Scholar]
- Kling, T.; Vogler, D.; Pastewka, L.; Amann, F.; Blum, P. Numerical simulations and validation of contact mechanics in a granodiorite fracture. Rock Mech. Rock Eng. 2018, 51, 9. [Google Scholar] [CrossRef]
- Waza, T.; Kurita, K.; Mizutani, H. The effect of water on the subcritical crack growth in silicate rocks. Tectonophysics 1980, 67, 1–2. [Google Scholar] [CrossRef]
- Atkinson, B.K. Stress corrosion and the rate-dependent tensile failure of a fine-grained quartz rock. Tectonophysics 1980, 65, 3–4. [Google Scholar] [CrossRef]
- Nara, Y.; Hiroyoshi, N.; Yoneda, T.; Kaneko, K. Effects of relative humidity and temperature on subcritical crack growth in igneous rock. Int. J. Rock Mech. Min. Sci. 2010, 47, 4. [Google Scholar] [CrossRef] [Green Version]
- Yasuhara, H.; Kinoshita, N.; Ohfuji, H.; Lee, D.S.; Nakashima, S.; Kishida, K. Temporal alteration of fracture permeability in granite under hydrothermal conditions and its interpretation by coupled chemo-mechanical model. Appl. Geochem. 2011, 26, 12. [Google Scholar] [CrossRef]






| No. | Operation | Duration (Days) | pc (MPa) | pp (MPa) | Temperature T (°C) |
|---|---|---|---|---|---|
| 1 | Mechanical | Short-term | 5↔10↔15↔20↔25↔30 a | 1 | 26 |
| 2 | Thermal | Short-term | 10 | 1 | 26↔60↔95↔140 b |
| 3 | 0–4 | 30 | 1 | 33→59→86→112→140 c | |
| 4 | Chemical | 4–117 | 30 | 1 | 140 |
| 5 | 117–133 | 10 | 1 | 140 | |
| 6 | 133–141 | 10 | 1 | 33 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, C.; Milsch, H. Evolution of Fracture Aperture in Quartz Sandstone under Hydrothermal Conditions: Mechanical and Chemical Effects. Minerals 2020, 10, 657. https://doi.org/10.3390/min10080657
Cheng C, Milsch H. Evolution of Fracture Aperture in Quartz Sandstone under Hydrothermal Conditions: Mechanical and Chemical Effects. Minerals. 2020; 10(8):657. https://doi.org/10.3390/min10080657
Chicago/Turabian StyleCheng, Chaojie, and Harald Milsch. 2020. "Evolution of Fracture Aperture in Quartz Sandstone under Hydrothermal Conditions: Mechanical and Chemical Effects" Minerals 10, no. 8: 657. https://doi.org/10.3390/min10080657
APA StyleCheng, C., & Milsch, H. (2020). Evolution of Fracture Aperture in Quartz Sandstone under Hydrothermal Conditions: Mechanical and Chemical Effects. Minerals, 10(8), 657. https://doi.org/10.3390/min10080657





