On the Adsorption Mechanism of Humic Substances on Kaolinite and Their Microscopic Structure
Abstract
:1. Introduction
2. Materials and Methods
2.1. Initial Configuration
2.2. Simulation Settings
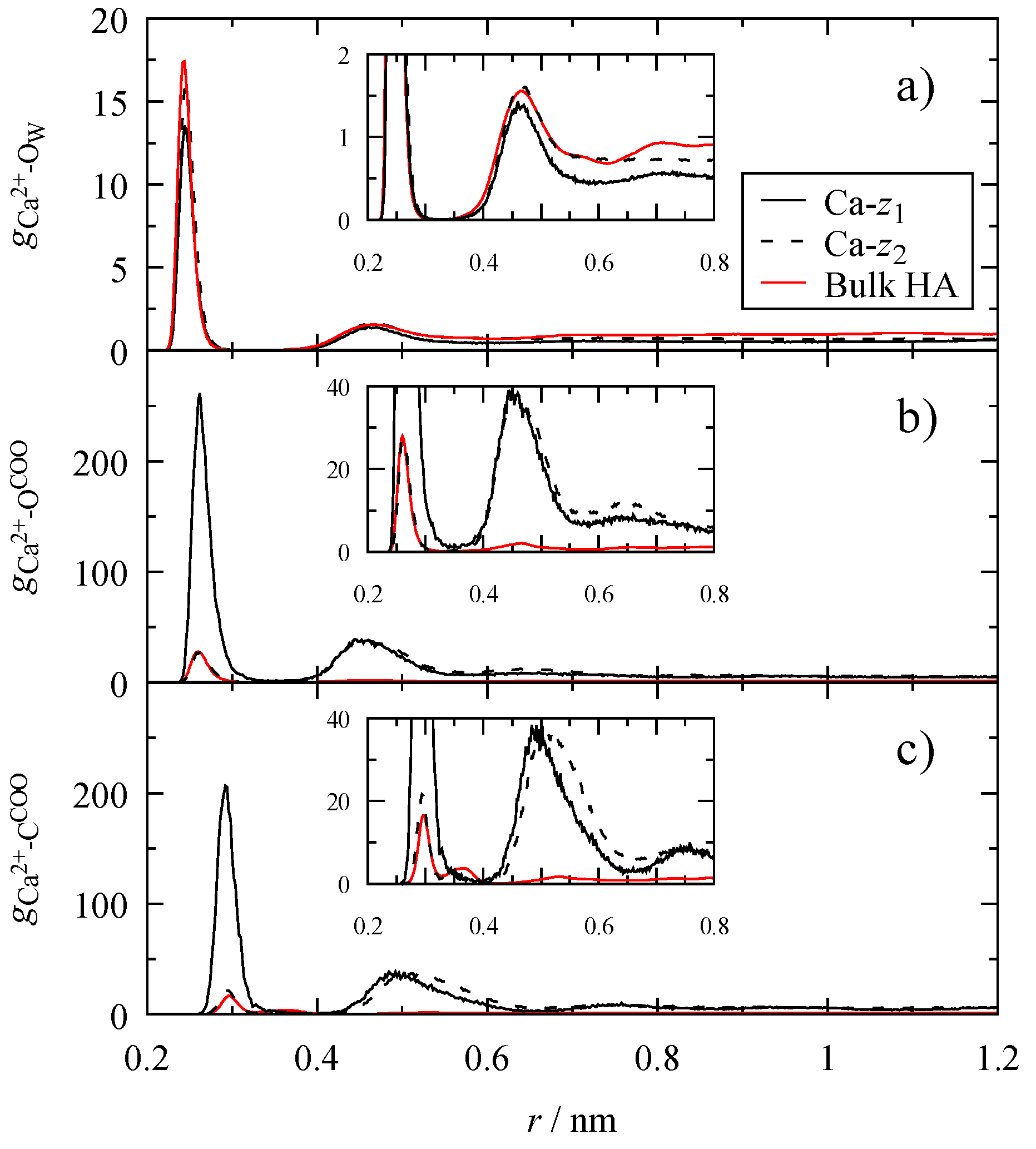
2.3. Radial Distribution Functions
3. Results
3.1. HA Adsorption
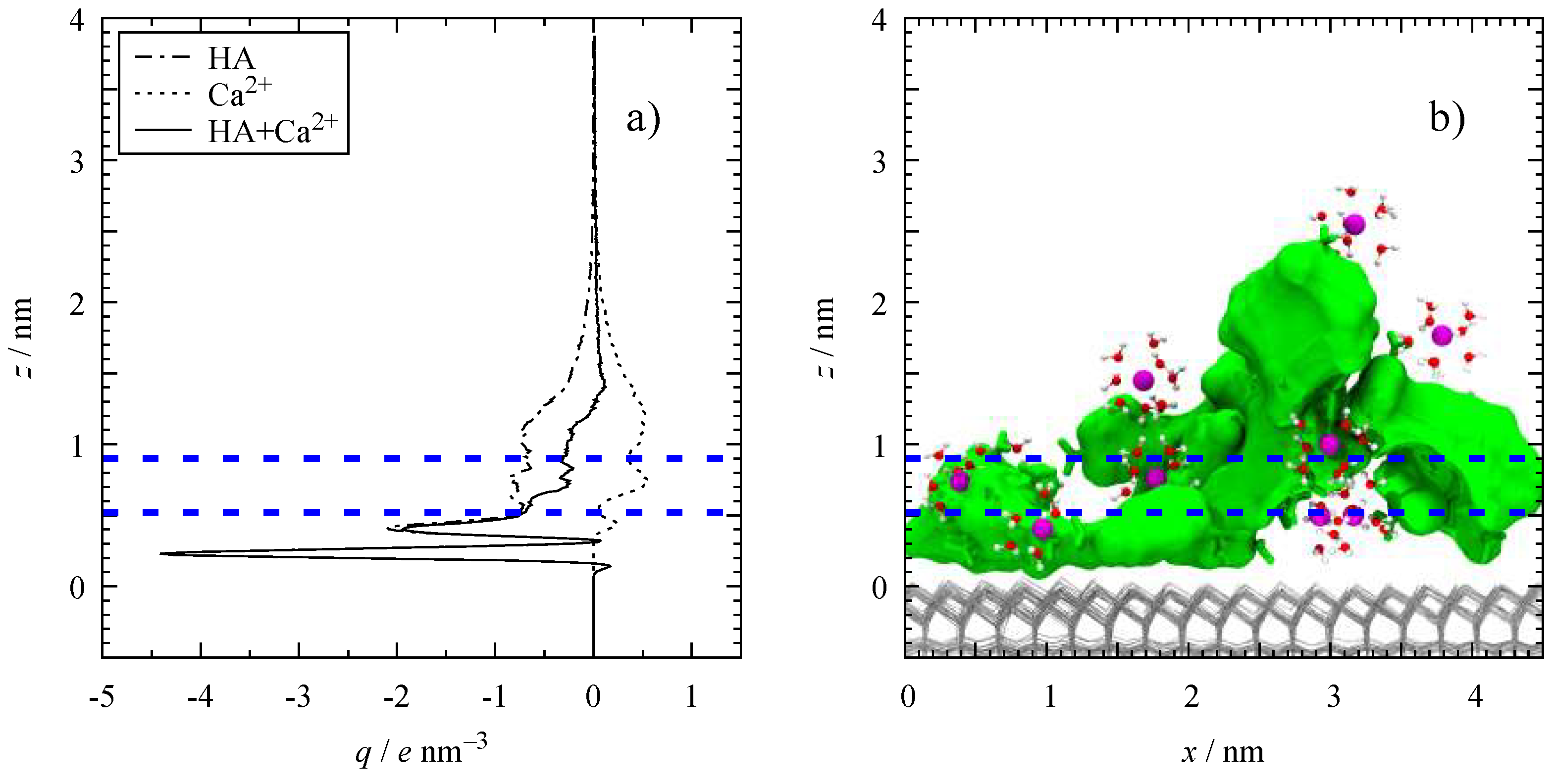
3.2. Molar Distribution Profiles
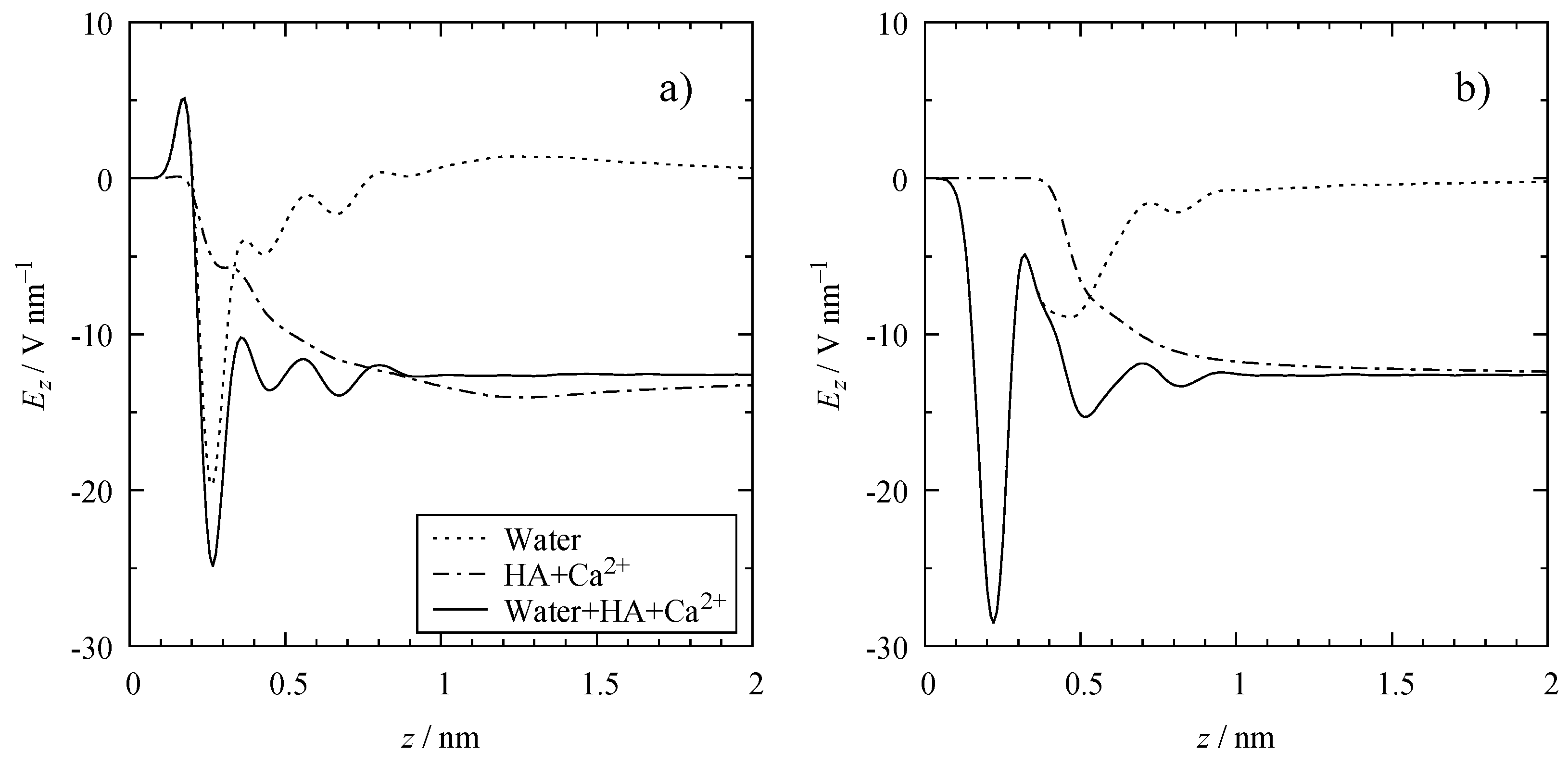
3.3. Electrostatic Interactions
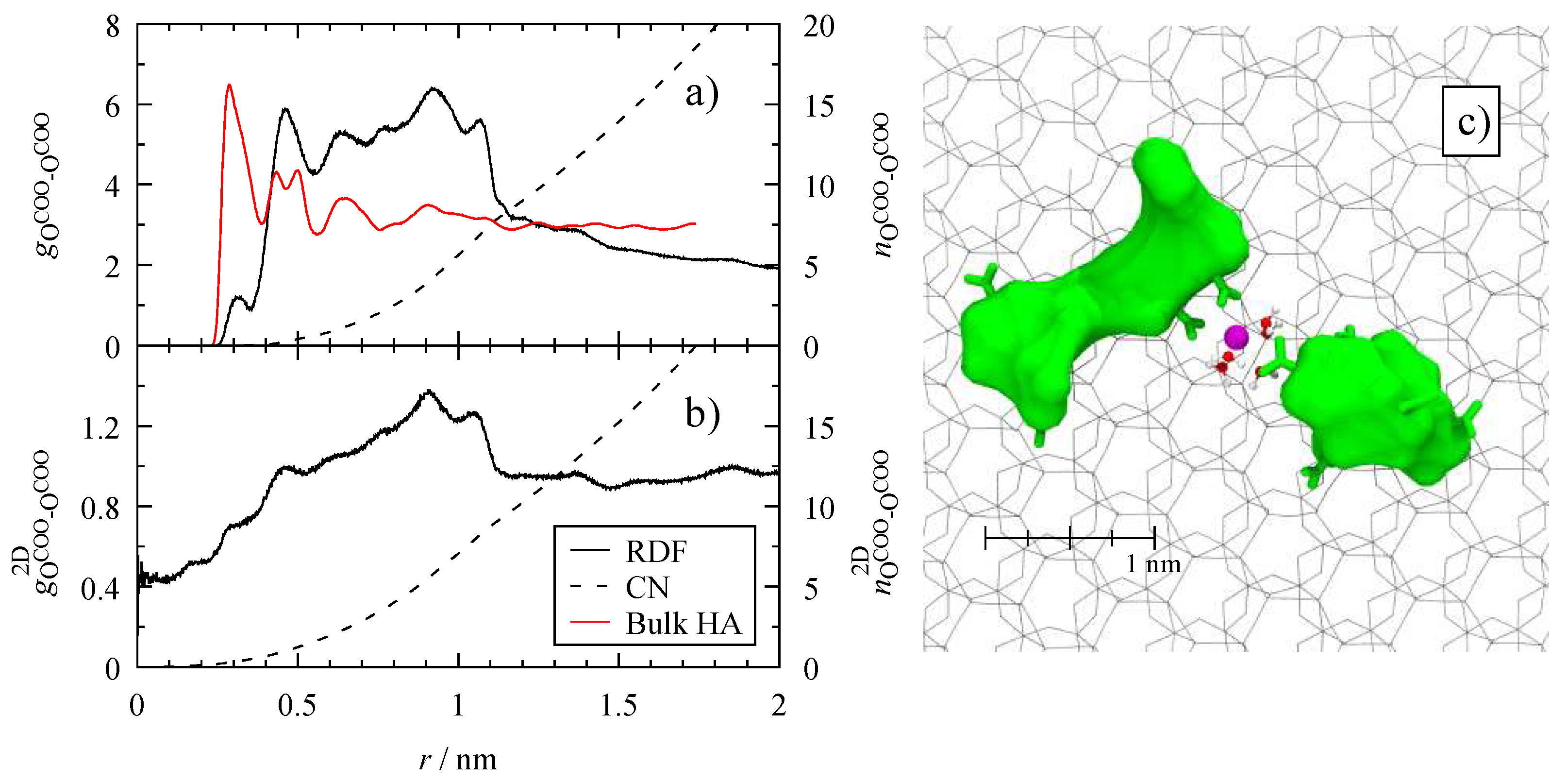
3.4. Microscopic Structure
4. Discussion
4.1. Influence of Kaolinite on HA Aggregates
- Disaggregation and separation of the supramolecular structure (HA and Ca2+ desorption);
- HA (Ca2+) fixation on the aluminol (siloxane) surface;
- HA (Ca2+) dispersion on the aluminol (siloxane) surface.
4.2. Polarization of the Cavity
4.3. Electrical Double Layer (EDL)
4.4. Dispersion of Humic Substances
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Baldock, J.A.; Broos, K. Soil organic matter. In Handbook of Soil Science: Properties and Processes; Huang, P.M., Li, Y., Summer, M.E., Eds.; CRC Press: Boca Raton, FL, USA, 2012; p. 1442. ISBN 978-1-4398-0306-6. [Google Scholar]
- Lehmann, J.; Kleber, M. The contentious nature of soil organic matter. Nature 2015, 528, 60–68. [Google Scholar] [CrossRef]
- Kleber, M. What is recalcitrant soil organic matter? Environ. Chem. 2010, 7, 320–332. [Google Scholar] [CrossRef]
- Totsche, K.U.; Amelung, W.; Gerzabek, M.H.; Guggenberger, G.; Klumpp, E.; Knief, C.; Lehndorff, E.; Mikutta, R.; Peth, S.; Prechtel, A.; et al. Microaggregates in soils. J. Plant Nutr. Soil Sci. 2018, 181, 104–136. [Google Scholar] [CrossRef] [Green Version]
- Baldock, J.A.; Skjemstad, J.O. Role of the soil matrix and minerals in protecting natural organic materials against biological attack. Org. Geochem. 2000, 31, 697–710. [Google Scholar] [CrossRef]
- Vrdoljak, G.; Sposito, G. Soil aggregate hierarchy in a Brazilian oxisol. In Developments in Soil Science; Elsevier: Amsterdam, The Netherlands, 2002; pp. 197–217. [Google Scholar]
- Tisdall, J.M.; Oades, J.M. Organic matter and water–stable aggregates in soils. J. Soil Sci. 1982, 33, 141–163. [Google Scholar] [CrossRef]
- Six, J.; Conant, R.T.; Paul, E.A.; Paustian, K. Stabilization mechanisms of soil organic matter: Implications for C–saturation of soils. Plant Soil 2002, 241, 155–176. [Google Scholar] [CrossRef]
- Schmidt, M.W.I.; Torn, M.S.; Abiven, S.; Dittmar, T.; Guggenberger, G.; Janssens, I.A.; Kleber, M.; Kögel–Knabner, I.; Lehmann, J.; Manning, D.A.C.; et al. Persistence of soil organic matter as an ecosystem property. Nature 2011, 478, 49–56. [Google Scholar] [CrossRef] [Green Version]
- Kleber, M.; Sollins, P.; Sutton, R. A conceptual model of organo–mineral interactions in soils: Self–assembly of organic molecular fragments into zonal structures on mineral surfaces. Biogeochemistry 2007, 85, 9–24. [Google Scholar] [CrossRef]
- Kleber, M.; Eusterhues, K.; Keiluweit, M.; Mikutta, C.; Mikutta, R.; Nico, P.S. Mineral–organic associations: Formation, properties, and relevance in soil environments. Adv. Agron. 2015, 130, 1–140. [Google Scholar]
- Newcomb, C.J.; Qafoku, N.P.; Grate, J.W.; Bailey, V.L.; De Yoreo, J.J. Developing a molecular picture of soil organic matter–mineral interactions by quantifying organo–mineral binding. Nat. Commun. 2017, 8, 396. [Google Scholar] [CrossRef]
- Aquino, A.J.A.; Tunega, D.; Schaumann, G.E.; Haberhauer, G.; Gerzabek, M.H.; Lischka, H. The functionality of cation bridges for binding polar groups in soil aggregates. Int. J. Quantum Chem. 2011, 111, 1531–1542. [Google Scholar] [CrossRef]
- Aquino, A.J.A.; Tunega, D.; Schaumann, G.E.; Haberhauer, G.; Gerzabek, M.H.; Lischka, H. Stabilizing capacity of water bridges in nanopore segments of humic substances: A theoretical investigation. J. Phys. Chem. C 2009, 113, 16468–16475. [Google Scholar] [CrossRef]
- Mouvenchery, Y.K.; Kučerík, J.; Diehl, D.; Schaumann, G.E. Cation–mediated cross–linking in natural organic matter: A review. Rev. Environ. Sci. Biotechnol. 2012, 11, 41–54. [Google Scholar] [CrossRef]
- Mouvenchery, Y.K.; Jaeger, A.; Aquino, A.J.A.; Tunega, D.; Diehl, D.; Bertmer, M.; Schaumann, G.E. Restructuring of a peat in interaction with multivalent cations: Effect of cation type and aging time. PLoS ONE 2013, 8, e65359. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Piccolo, A. The supramolecular structure of humic substances. Soil Sci. 2001, 166, 810–832. [Google Scholar] [CrossRef] [Green Version]
- Schaumann, G.E.; Bertmer, M. Do water molecules bridge soil organic matter molecule segments? Eur. J. Soil Sci. 2008, 59, 423–429. [Google Scholar] [CrossRef]
- Tunega, D.; Aquino, A.J.A.; Haberhauer, G.; Lischka, H.; Schaumann, G.E.; Gerzabek, M.H. Molecular models of cation and water molecule bridges in humic substances. In Soil Carbon; Hartemink, A., McSweeney, K., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 107–115. [Google Scholar]
- Galicia–Andrés, E.; Escalona, Y.; Oostenbrink, C.; Tunega, D.; Gerzabek, M.H. Soil organic matter stabilization at molecular scale: The role of metal cations and hydrogen bonds. Geoderma 2021, 401, 115237. [Google Scholar] [CrossRef]
- US Geological Survey. Characterization of the International Humic Substances Society Standard and Reference Fulvic and Humic Acids by Solution State Carbon–13 (13C) and Hydrogen–1 (1H) Nuclear Magnetic Resonance Spectrometry; U.S. Dept. of the Interior, U.S. Geological Survey: Books and Open–File Reports Section: Denver, CO, USA, 1989.
- Schaumann, G.E. Soil organic matter beyond molecular structure Part I: Macromolecular and supramolecular characteristics. J. Plant Nutr. Soil Sci. 2006, 169, 145–156. [Google Scholar] [CrossRef]
- Ai, Y.; Zhao, C.; Sun, L.; Wang, X.; Liang, L. Coagulation mechanisms of humic acid in metal ions solution under different pH conditions: A molecular dynamics simulation. Sci. Total Environ. 2020, 702, 135072. [Google Scholar] [CrossRef]
- Iskrenova–Tchoukova, E.; Kalinichev, A.G.; Kirkpatrick, R.J. Metal cation complexation with natural organic matter in aqueous solutions: Molecular dynamics simulations and potentials of mean force. Langmuir 2010, 26, 15909–15919. [Google Scholar] [CrossRef] [Green Version]
- Kalinichev, A.G.; Iskrenova–Tchoukova, E.; Ahn, W.Y.; Clark, M.M.; Kirkpatrick, R.J. Effects of Ca2+ on supramolecular aggregation of natural organic matter in aqueous solutions: A comparison of molecular modeling approaches. Geoderma 2011, 169, 27–32. [Google Scholar] [CrossRef] [Green Version]
- Kalinichev, A.G.; Kirkpatrick, R.J. Molecular dynamics simulation of cationic complexation with natural organic matter. Eur. J. Soil Sci. 2007, 58, 909–917. [Google Scholar] [CrossRef]
- Tan, L.; Yu, Z.; Tan, X.; Fang, M.; Wang, X.; Wang, J.; Xing, J.; Ai, Y.; Wang, X. Systematic studies on the binding of metal ions in aggregates of humic acid: Aggregation kinetics, spectroscopic analyses and MD simulations. Environ. Pollut. 2019, 246, 999–1007. [Google Scholar] [CrossRef]
- Escalona, Y.; Petrov, D.; Oostenbrink, C. Vienna soil organic matter modeler 2 (VSOMM2). J. Mol. Graph. Model. 2021, 103, 107817. [Google Scholar] [CrossRef]
- Sündermann, A.; Solc, R.; Tunega, D.; Haberhauer, G.; Gerzabek, M.H.; Oostenbrink, C. Vienna Soil-Organic-Matter Modeler—Generating condensed–phase models of humic substances. J. Mol. Graph. Model. 2015, 62, 253–261. [Google Scholar] [CrossRef] [Green Version]
- Ritschel, T.; Totsche, K.U. Modeling the formation of soil microaggregates. Comput. Geosci. 2019, 127, 36–43. [Google Scholar] [CrossRef]
- Loganathan, N.; Ferguson, B.O.; Arey, B.; Argersinger, H.E.; Bowers, G.M. A Mechanistic Exploration of Natural Organic Matter Aggregation and Surface Complexation in Smectite Mesopores. J. Phys. Chem. A 2020, 124, 9832–9843. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, X.; Zhang, C.; Lu, X. A combined first principles and classical molecular dynamics study of clay–soil organic matters (SOMs) interactions. Geochim. Cosmochim. Acta 2020, 291, 110–125. [Google Scholar] [CrossRef]
- Schmickler, W.; Santos, E. Interfacial Electrochemistry; Springer: Berlin/Heidelberg, Germany, 2010; ISBN 978-3-642-04936-1. [Google Scholar]
- Zhang, C. Note: On the dielectric constant of nanoconfined water. J. Chem. Phys. 2018, 148, 156101. [Google Scholar] [CrossRef] [Green Version]
- Sayer, T.; Zhang, C.; Sprik, M. Charge compensation at the interface between the polar NaCl(111) surface and a NaCl aqueous solution. J. Chem. Phys. 2017, 147, 104702. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Sprik, M. Computing the dielectric constant of liquid water at constant dielectric displacement. Phys. Rev. B 2016, 93, 144201. [Google Scholar] [CrossRef] [Green Version]
- Petrov, D.; Tunega, D.; Gerzabek, M.H.; Oostenbrink, C. Molecular dynamics simulations of the standard Leonardite humic acid: Microscopic analysis of the structure and dynamics. Environ. Sci. Technol. 2017, 51, 5414–5424. [Google Scholar] [CrossRef] [PubMed]
- Petrov, D.; Tunega, D.; Gerzabek, M.H.; Oostenbrink, C. Molecular modelling of sorption processes of a range of diverse small organic molecules in Leonardite humic acid. Eur. J. Soil Sci. 2020, 71, 831–844. [Google Scholar] [CrossRef] [Green Version]
- Escalona, Y.; Petrov, D.; Oostenbrink, C. Modeling Soil Organic Matter: Changes in Macroscopic Properties due to Microscopic Changes. Geochim. Cosmochim. Acta 2021, 307, 228–241. [Google Scholar] [CrossRef]
- Gerzabek, M.H.; Tunega, D.; Galicia–Andrés, E.; Oostenbrink, C. Soil organic matter and molecular simulations (Accepted). In Encyclopedia of Soils in the Environment; Staunton, S., Xing, B., Eds.; Elsevier: Amsterdam, The Netherlands, 2021. [Google Scholar]
- Galicia–Andrés, E.; Grančič, P.; Gerzabek, M.H.; Oostenbrink, C.; Tunega, D. Modeling of interactions in natural and synthetic organoclays. In Computational Modeling in Clay Mineralogy; Sainz Diaz, I.C., Ed.; Digilabs: Bari, Italy, 2021; pp. 211–254. ISBN 978-88-7522-048-8. [Google Scholar]
- Bish, D.L. Rietveld refinement of the kaolinite structure at 1.5 K. Clays Clay Miner. 1993, 41, 738–744. [Google Scholar] [CrossRef]
- Galicia–Andrés, E.; Petrov, D.; Gerzabek, M.H.; Oostenbrink, C.; Tunega, D. Polarization effects in simulations of kaolinite–water interfaces. Langmuir 2019, 35, 15086–15099. [Google Scholar] [CrossRef] [PubMed]
- Galicia–Andrés, E.; Tunega, D.; Gerzabek, M.H.; Oostenbrink, C. On glyphosate–kaolinite surface interactions. A molecular dynamic study. Eur. J. Soil Sci. 2021, 72, 1231–1242. [Google Scholar] [CrossRef] [PubMed]
- Schmid, N.; Eichenberger, A.P.; Choutko, A.; Riniker, S.; Winger, M.; Mark, A.E.; Van Gunsteren, W.F. Definition and testing of the GROMOS force–field versions 54A7 and 54B7. Eur. Biophys. J. 2011, 40, 843–856. [Google Scholar] [CrossRef]
- Vasconcelos, I.F.; Bunker, B.A.; Cygan, R.T. Molecular Dynamics Modeling of Ion Adsorption to the Basal Surfaces of Kaolinite. J. Phys. Chem. C 2007, 111, 6753–6762. [Google Scholar] [CrossRef]
- Cygan, R.T.; Liang, J.-J.; Kalinichev, A.G. Molecular models of hydroxide, oxyhydroxide, and clay phases and the development of a general force field. J. Phys. Chem. B 2004, 108, 1255–1266. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; Hermans, J. Interaction models for water in relation to protein hydration. In Intermolecular Forces, Proceedings of the Fourteenth Jerusalem Symposium on Quantum Chemistry and Biochemistry Held in Jerusalem, Israel, 13–16 April 1981; Pullman, B., Ed.; Springer: Dordrecht, The Netherlands, 1981; pp. 331–342. ISBN 978-94-015-7658-1. [Google Scholar]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi–level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef] [Green Version]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; DiNola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef] [Green Version]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef] [Green Version]
- Linse, B.; Linse, P. Tuning the smooth particle mesh Ewald sum: Application on ionic solutions and dipolar fluids. J. Chem. Phys. 2014, 141, 184114. [Google Scholar] [CrossRef]
- Ewald, P.P. Die Berechnung optischer und elektrostatischer Gitterpotentiale. Ann. Phys. 1921, 369, 253–287. [Google Scholar] [CrossRef] [Green Version]
- Miyamoto, S.; Kollman, P.A. Settle: An analytical version of the SHAKE and RATTLE algorithm for rigid water models. J. Comput. Chem. 1992, 13, 952–962. [Google Scholar] [CrossRef]
- Hess, B.; Bekker, H.; Berendsen, H.J.C.; Fraaije, J.G.E.M. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 1997, 18, 1463–1472. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Rapaport, D.C. The Art of Molecular Dynamics Simulation; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Lehmann, J.; Hansel, C.M.; Kaiser, C.; Kleber, M.; Maher, K.; Manzoni, S.; Nunan, N.; Reichstein, M.; Schimel, J.P.; Torn, M.S.; et al. Persistence of soil organic carbon caused by functional complexity. Nat. Geosci. 2020, 13, 529–534. [Google Scholar] [CrossRef]
- Ivanić, M.; Vdović, N.; Sandra Brito Baretto, D.; Bermanec, V.; Sondi, I. Mineralogy, surface properties and electrokinetic behaviour of kaolin clays from the naturally occurring pegmatite deposits. Geol. Croat. 2015, 68, 139–145. [Google Scholar] [CrossRef] [Green Version]
- Siretanu, I.; van den Ende, D.; Mugele, F. Atomic structure and surface defects at mineral–water interfaces probed by in situ atomic force microscopy. Nanoscale 2016, 8, 8220–8227. [Google Scholar] [CrossRef]
- Wang, G.; Ran, L.; Xu, J.; Wang, Y.; Ma, L.; Zhu, R.; Wei, J.; He, H.; Xi, Y.; Zhu, J. Technical development of characterization methods provides insights into clay mineral–water interactions: A comprehensive review. Appl. Clay Sci. 2021, 206, 106088. [Google Scholar] [CrossRef]
- Morais, L.; Cordão–Neto, M.; Tarantino, A. Aggregation process of kaolinite clay. E3S Web Conf. 2019, 92, 03002. [Google Scholar] [CrossRef]
- Gupta, V.; Miller, J.D. Surface force measurements at the basal planes of ordered kaolinite particles. J. Colloid Interface Sci. 2010, 344, 362–371. [Google Scholar] [CrossRef] [PubMed]
- Gupta, V.; Hampton, M.A.; Stokes, J.R.; Nguyen, A.V.; Miller, J.D. Particle interactions in kaolinite suspensions and corresponding aggregate structures. J. Colloid Interface Sci. 2011, 359, 95–103. [Google Scholar] [CrossRef]
- Raj, P.P. Soil Mechanics and Foundation Engineering, 2nd ed.; Pearson: New Delhi, India, 2013; ISBN 9788131790816. [Google Scholar]
- Yeh, I.-C.; Berkowitz, M.L. Dielectric constant of water at high electric fields: Molecular dynamics study. J. Chem. Phys. 1999, 110, 7935–7942. [Google Scholar] [CrossRef]
- Yeh, I.-C.; Berkowitz, M.L. Ewald summation for systems with slab geometry. J. Chem. Phys. 1999, 111, 3155–3162. [Google Scholar] [CrossRef]


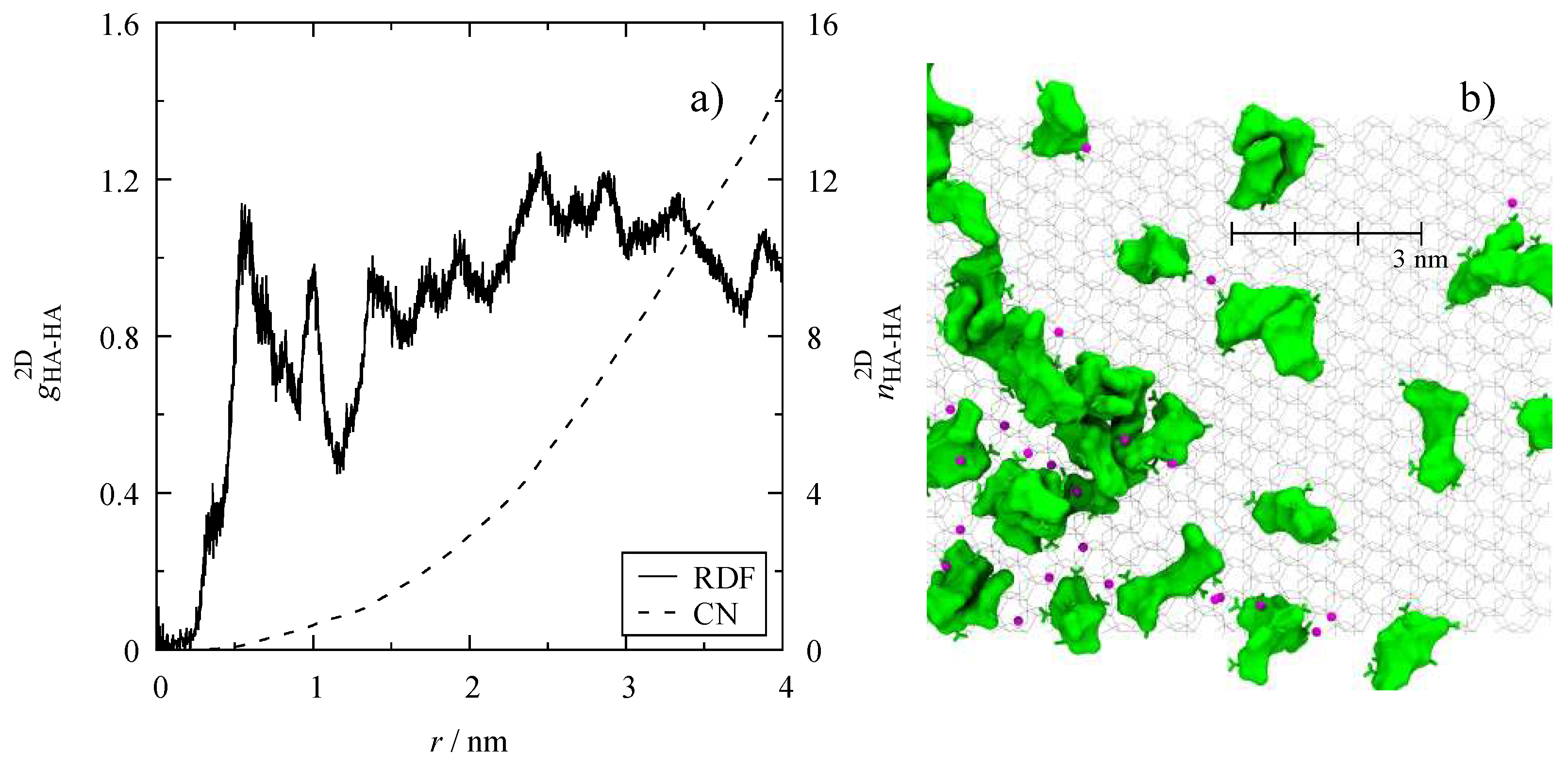
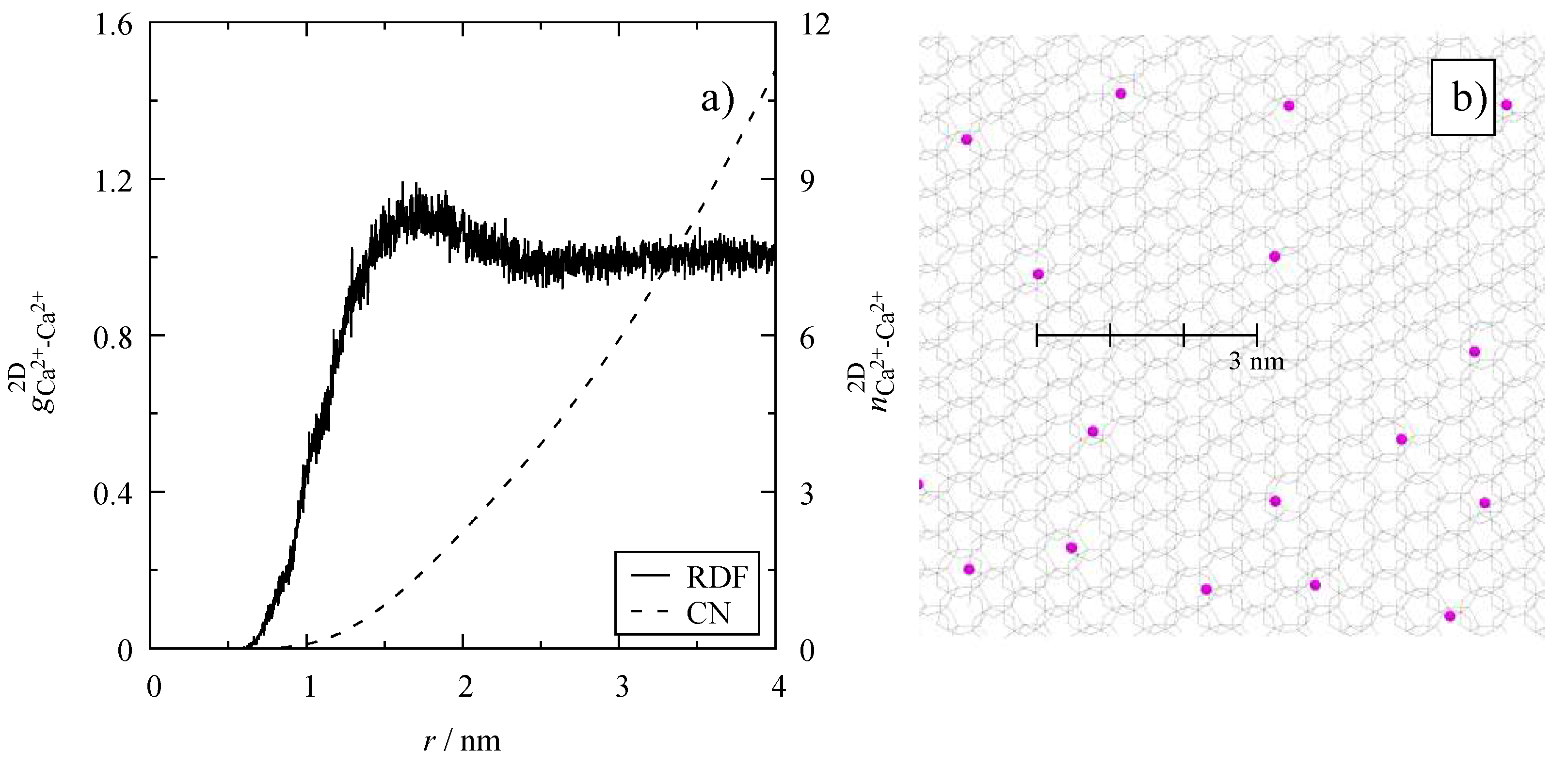
| Position | ISC(b)/nm | RL/nm | OSC/nm | RU/nm | Keq |
|---|---|---|---|---|---|
| Ca–z1 | 0.29 | 0.40 | 0.48 | 0.62 | 2.14 |
| Ca–z2 | 0.29 | 0.40 | 0.51 | 0.66 | 23.83 |
| HA matrix 1 | 0.30 | 0.43 | 0.53 | 0.64 | 0.99 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Galicia-Andrés, E.; Oostenbrink, C.; Gerzabek, M.H.; Tunega, D. On the Adsorption Mechanism of Humic Substances on Kaolinite and Their Microscopic Structure. Minerals 2021, 11, 1138. https://doi.org/10.3390/min11101138
Galicia-Andrés E, Oostenbrink C, Gerzabek MH, Tunega D. On the Adsorption Mechanism of Humic Substances on Kaolinite and Their Microscopic Structure. Minerals. 2021; 11(10):1138. https://doi.org/10.3390/min11101138
Chicago/Turabian StyleGalicia-Andrés, Edgar, Chris Oostenbrink, Martin H. Gerzabek, and Daniel Tunega. 2021. "On the Adsorption Mechanism of Humic Substances on Kaolinite and Their Microscopic Structure" Minerals 11, no. 10: 1138. https://doi.org/10.3390/min11101138
APA StyleGalicia-Andrés, E., Oostenbrink, C., Gerzabek, M. H., & Tunega, D. (2021). On the Adsorption Mechanism of Humic Substances on Kaolinite and Their Microscopic Structure. Minerals, 11(10), 1138. https://doi.org/10.3390/min11101138






