Next Article in Journal
Specific Mixing Energy of Cemented Paste Backfill, Part II: Influence on the Rheological and Mechanical Properties and Practical Applications
Previous Article in Journal
Borehole-Based Monitoring of Mining-Induced Movement in Ultrathick-and-Hard Sandstone Strata of the Luohe Formation
Previous Article in Special Issue
Retaining Geochemical Signatures during Aragonite-Calcite Transformation at Hydrothermal Conditions
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Minerals
Volume 11
Issue 11
10.3390/min11111158
minerals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Mg/Ca Ratios in Synthetic Low-Magnesium Calcite: An Experimental Investigation

by
Jeremy M. Weremeichik
1,*,
Rinat I. Gabitov
2,
Aleksey Sadekov
3,
Aleksandra Novak
2,
Angel Jimenez
2,
Rooban Venkatesh K. G. Thirumalai
4,
Jac J. Varco
5 and
Andrew Dygert
5
1
Independent Researcher, Mount Arlington, NJ 07856, USA
2
Department of Geosciences, Mississippi State University, Mississippi State, MS 39762, USA
3
ARC Centre of Excellence for Coral Reef Studies, The University of Western Australia, Crawley, WA 6009, Australia
4
Institute for Imaging & Analytical Technologies, Mississippi State University, Mississippi State, MS 39762, USA
5
Department of Plant and Soil Sciences, Mississippi State University, Mississippi State, MS 39762, USA
*
Author to whom correspondence should be addressed.
Minerals 2021, 11(11), 1158; https://doi.org/10.3390/min11111158
Submission received: 15 August 2021 / Revised: 5 October 2021 / Accepted: 13 October 2021 / Published: 21 October 2021
(This article belongs to the Special Issue Trace Element Uptake by Carbonate Minerals)
Browse Figures
Versions Notes

Abstract

:
The work presented sought to determine the effects of Mg/Ca ratios in solution have on Mg partitioning (KMg) between precipitated abiotic low-Mg calcite and solution. Experiments were set up so that Mg/Ca in precipitated abiotic calcite would match the Mg/Ca in planktonic foraminifera. This research intended to investigate the effect of Mg/Ca(Fluid) on KMg when the molar value of Mg/Ca(Fluid) was below 0.5, which is below the previously reported Mg/Ca range. The values of pH, salinity, and aqueous Mg/Ca were monitored during calcite precipitation, and Mg/Ca of calcite was determined at the end of experiments. Partition coefficients of Mg were evaluated as a ratio of Mg/Ca in calcite to the averaged ratio of aqueous Mg/Ca for each experiment.

1. Introduction

Understanding the means and extent to which external environmental factors control Mg incorporation into calcite is of significant interest to the geoscientific community. The ability of calcite to accommodate trace and minor elements in its crystalline structure has been a topic of interest for inorganic and organic precipitation studies. Calcite precipitated in laboratory settings has been leveraged to better understand the influence of environmental factors that collectively and individually govern Mg incorporation. Biological representative Mg/Ca ratios of foraminifera shells are used to study temperature variations in the oceans over the past 541.0 ± 1.0 Ma (i.e., Phanerozoic). Previous studies have demonstrated that the Mg partition coefficient (KMg) is temperature-dependent; e.g., [1,2,3,4,5,6,7]. Numerous studies have also proposed other parameters that could influence KMg, such as salinity [8,9], pH [6,10,11], calcite growth rate [12,13,14,15,16], Mg/Ca ratio of the solution [15,17,18,19], or possibly a combination of calcite growth rate and the Mg/Ca ratio of the solution [16].
For example, Mavromatis et al. [15] assessed the calcite growth rate by conducting a series of experiments in which the pH was maintained constant by bubbling pure CO2 gas into the precipitation medium. This study found that pH did not have a direct effect on KMg. However, it is known that the pH of fluids influences calcite growth rate (i.e., fluids with a low pH cause carbonate dissolution), which influences KMg. The findings of Mavromatis et al. [15] and Gabitov et al. [16] demonstrated that the growth rate was responsible for controlling Mg partitioning. Though the two studies found opposite relationships between KMg and the growth rate, Gabitov et al. [16] explained that this could be due to differences in Mg/Ca ratios of the fluid, which would cause a change in the Mg incorporation mechanism.
It is known that the oceanic Mg/Ca ratio is not constant with respect to geologic time, and has varied from ~1 to 5.2 mol/mol between the present day and the Cretaceous [20,21,22,23,24,25,26,27,28,29,30,31,32]. The cause or causes for fluctuation of seawater Mg/Ca are not fully understood, but it is thought to be controlled by various parameters, including runoff [33], temperature [34], the rate of oceanic crust production [22,35], a change in the mode of calcium carbonate deposition [36], and the rate of dolomite formation [37]. Although there have been attempts to study variations in oceanic Mg/Ca over the geologic past using coccolithophores [38,39,40], Mg/Ca in foraminiferal calcite is far more studied. It has been demonstrated that temperature was the primary control on Mg/Ca in the tests of foraminifera [41,42,43,44]. Several studies suggested that salinity also influenced Mg/Ca in foraminifera [42,45,46,47], but in a lesser capacity than the temperature for marine surface waters.
The Mg/Ca ratio of oceanic waters can be inferred by studying Mg/Ca preserved in fossilized marine organisms (e.g., foraminifera, coccoliths, echinoids, corals, and algae) [28,48,49]. It is known that the Mg/Ca ratio in planktonic foraminifera is much lower than what is expected based on the Mg concentration in typical seawaters [50]. It has been postulated that the cause for depressed Mg in foraminiferal calcite is due to biological/physiological factors, which selectively occlude Mg at the site of calcification [50,51,52,53,54]. Moreover, it has been demonstrated by Branson et al. [54] that Mg is uniformly substituted for Ca in the calcite mineral lattice of foraminiferal tests.
In this study, experiments were conducted at 15 °C, a constant titration rate, and variable Mg/Ca of aqueous solutions for precipitating calcite, the Mg/Ca values for which cover the range observed in planktonic foraminifera.

2. Materials and Methods

2.1. Calcite Precipitation

Calcite was precipitated by continuous addition of CaCl2, MgCl2, and NaHCO3 titrates into a NaCl solution. These methods were modified from techniques described in several previous works; e.g., [15,55]. In all experiments, titrate fluids were delivered to a reaction vessel at a constant rate using a programmable multichannel peristaltic pump and 1.75 mm inner-diameter (i-d) tubing (Figure 1).

2.2. Experimental Design

Three series (i.e., series 9, 10, and 11) accounting for a total of 13 experiments were conducted for this study. Series 9 consisted of six experiments, series 10 was one experiment, and series 11 comprised six experiments. All experiments were conducted using a continuous-pumping method by which solutions were contemporaneously pumped into and out of a reaction vessel at a rate of 0.14 mL min–1 using a multichannel peristaltic pump. The diameter of the outlet tube was greater than twice the diameter of either inlet tube. To prevent a decrease in solution volume for the reaction vessel, the outlet tube was always kept at a fixed height. Therefore, the volume of the growth media was kept near-constant for the duration of each experiment. Solutions in the reaction vessel were maintained at 15 °C in a refrigerated water bath and continuously stirred at 150 rpm using a submersed stir plate and suspended magnetic stir bars (Figure 1). The selected experimental temperature represented the average global sea surface temperature.
For each experiment, three solutions were prepared using Fisher Chemical Certified ACS (American Chemical Society) salts. The first step in preparing all solutions was to mix NaCl with reverse osmosis (RO) H2O to achieve a concentration of 0.6 M. The solution in the reaction vessel comprised a mixture of NaCl (99.9%) and NaHCO3 (99.7%) chemical salts (values in parentheses denote chemical purity). For each experiment, two titrate vessels were prepared using the NaCl solution described above. In titrate vessel 1, MgCl2·6H2O and CaCl2·2H2O salts were added to the NaCl solution. The mass of MgCl2·6H2O and CaCl2·2H2O salts added for each experiment varied depended on the desired Mg/Ca ratio of the fluid. Titrate vessel 2 was prepared by the addition of NaHCO3 to the NaCl solution. For each experiment, the molar concentration of NaHCO3 in titrate 1 was equal to the molar concentration of MgCl2·6H2O + CaCl2·2H2O in titrate 2. The experimental design for the series 11 experiments varied slightly from the previous description, in that the addition of NaOH was used in specific experiments to elevate the pH of the fluid. The concentration of the chemical salts in the titrate solutions for each experiment is reported in Table 1. The fluid Mg/Ca ratio was calculated to have varied from 0.51 to 20.18 (mmol mol−1) between experiments in series 9. For the series 10 experiment, the fluid Mg/Ca ratio was calculated to be 5.0 (mmol mol−1). For the series 11 experiments, the fluid Mg/Ca ratio was calculated to be either 0.25 or 4.41 (mmol mol−1), depending on the respective experiment.
Subsamples were collected from the reaction vessel every 12–24 h throughout the duration of each experiment to measure pH, salinity, and Mg and Ca concentrations. The collection of subsamples and all other fluids (i.e., return flow fluid and final fluid) was done using a 60 mL syringe. and then the subsamples were filtered using a 0.45 µm nylon Whatman syringe filter. All pH measurements were conducted using a Denver Instrument UB-10 UltraBASIC benchtop meter equipped with a Sartorius PY-P11 pH Combination Electrode, Mississippi State, USA. Salinity measurements were carried out using an HI 5521 benchtop meter equipped with a HI 76312 4-ring platinum EC/TDS probe, Mississippi State, USA. Immediately following measurements, the subsamples were acidified for further chemical analysis. An aliquot of fluid from the return flow vessel was recovered approximately every two to three days and at the end of each experimental run to determine alkalinity of the fluids.

2.3. Analysis of Fluids

2.3.1. Atomic Absorption

Fluid samples from all experiments in series 9 and 10 were analyzed using a Shimadzu, AA-7000 Line-Source AAS, Mississippi State, USA. The LS-AAS was calibrated using 1000 ppm magnesium and calcium analytical standards (Fisher Scientific, Pittsburgh, PA, USA) as stock solutions. Six calibration standards were created for each element. The standards for calcium ranged from 0.5 ppm to 16 ppm, with the concentration of each successive standard being double the previous. The standards for magnesium ranged from 0.05 ppm to 1.6 ppm, with the concentration of each successive standard being double. Calibration curves showed that the actual concentrations measured using LS-AAS were close to the prepared concentration, as the minimum r2 value for the calibration curves was 0.993.

2.3.2. Alkalinity Titrations

Titrations were performed to determine the total alkalinity of each experiment in series 9 and 10 following protocols described by Rounds [56]. Titrations were conducted using a 25 mL burette, 100 mL glass beakers, a pH meter and electrode, magnetic stir plate and stir bars, disposable 10 mL volumetric pipets, phenolphthalein indicator, volumetric flasks, trace-metal-grade H2SO4, RO H2O, and ACS-grade Na2CO3.
Fluid collected from the return flow vessel at the beginning of each experiment and final fluid collected at the end of each experiment in series 9 and 10 underwent titration with known concentrations of H2SO4 to determine the alkalinity of the fluid. Titration was performed in triplicate for each sample, and the average of the three alkalinity values was taken to be the true value. The alkalinity values were converted from mg of CaCO3 L−1 to μmol kg−1 of H2O so that the values would be compatible with the CO2SYS (Version 2.1, U.S. Department of Energy, Oak Ridge, TN, USA), initially developed by Lewis et al. [57] and updated by Pierrot et al. [58].

2.4. Analysis of Solids

2.4.1. ICP-OES

Elemental (Mg and Ca) analyses of calcites were conducted at the University of Cambridge (UK) using an Algilent 5100 ICP-OES) and following protocols described in de Villiers et al. [59] and Greaves et al. [60]. Samples were cleaned prior to analysies by rapid (5–10 s) rinsing of the solids three times with RO H2O, followed by three rinses with trace-metal-grade methanol, once using 10% ultra-high-purity H2O2, then rinsed three more times using Nanopure H2O. The storage polypropylene vials were cleaned prior to the addition of the solid samples by soaking them in 10% ACS-grade HNO3 then 2% trace-metal-grade HNO3, and were lastly rinsed with Nanopure H2O and dried at 40 °C.

2.4.2. X-ray Diffraction (XRD) Analysis

Powdered X-ray diffraction (XRD) analyses were conducted for all solid samples collected from experiments in series 9, 10, and 11 to determine mineral composition. Analyses were carried out using a Rigaku Ultima III X-ray diffractometer. All data interpretations were conducted using the MDI Jade 2010 software package at the Mississippi State University Institute for Imaging and Analytical Technology (I2AT), USA. The XRD pattern for each sample was generated at 40 KV and 44 mA. Scan speed was set at 0.5° per minute with a scan step of 0.02° and an effective scan range of 20–40°.

2.4.3. Scanning Electron Microscopy (SEM) Imaging

Powdered samples were examined with SEM to determine the morphology of precipitated calcites. Imaging was conducted using a Carl Zeiss EVO50VP scanning electron microscope at the Institute of Imaging & Analytical Technologies (I2AT) at Mississippi State University, Mississippi State, USA. SEM imaging of secondary electrons (SE) was performed on platinum-coated crystalline powders while applying 5 KV and 300 pA.

3. Results

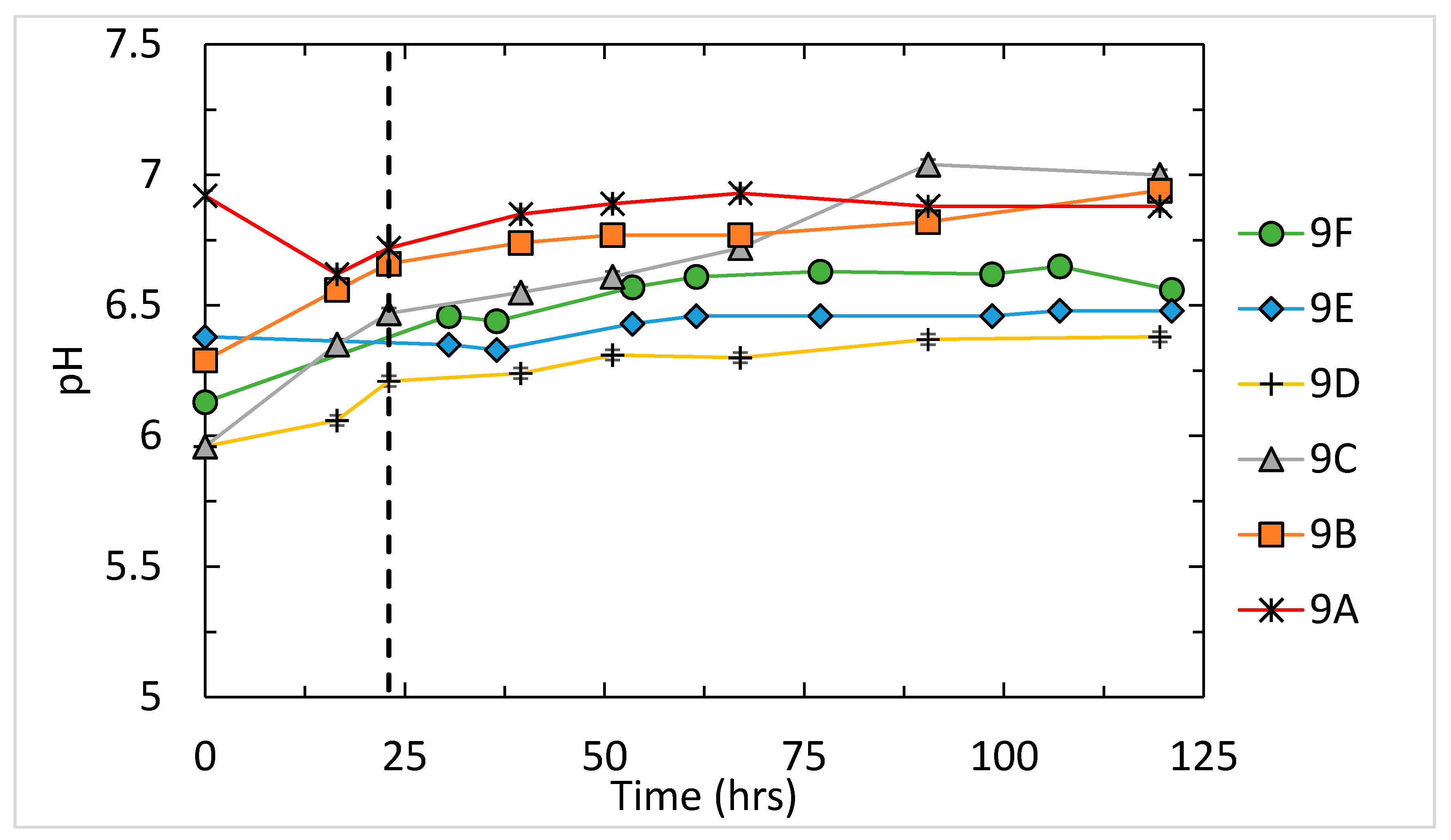
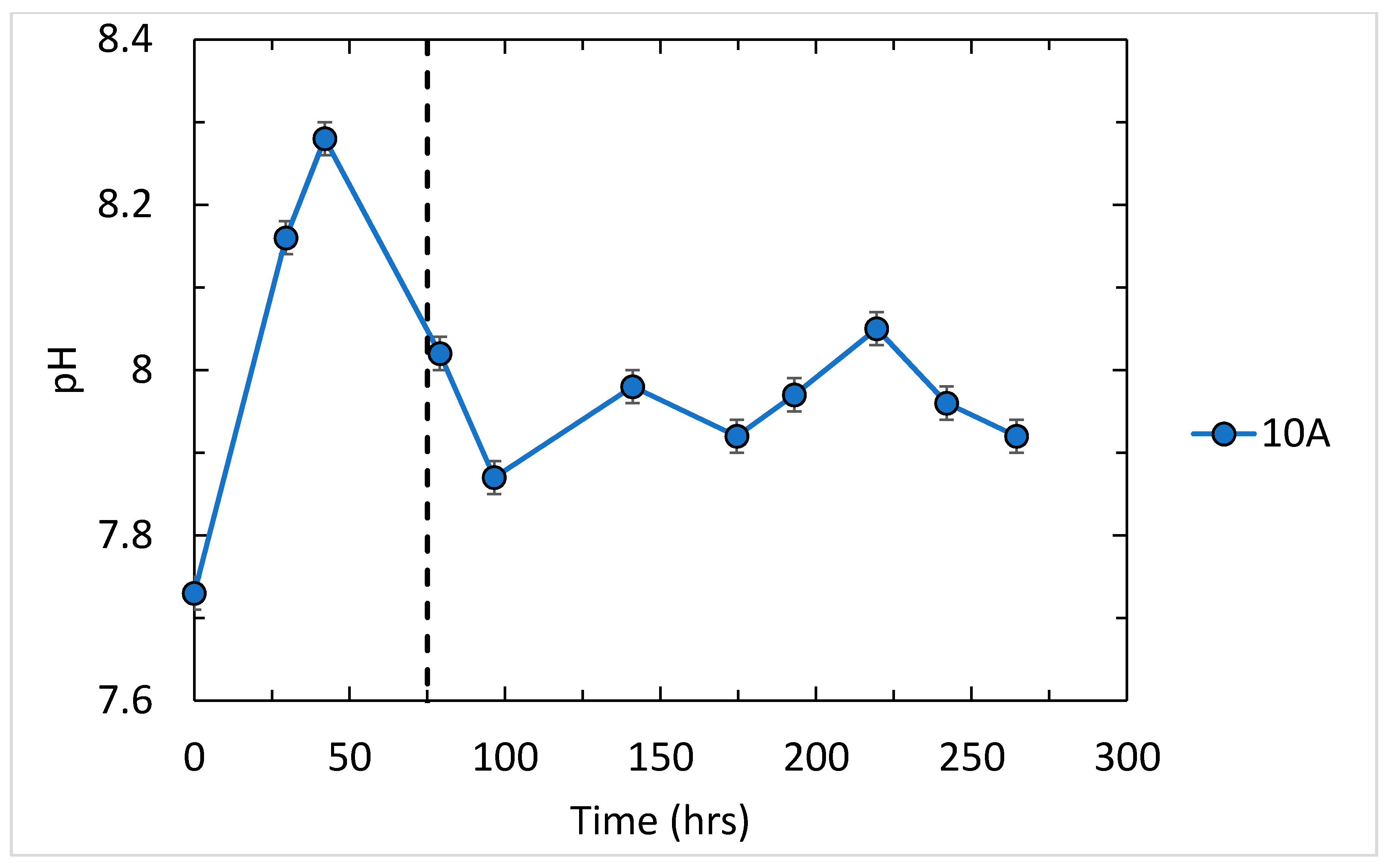
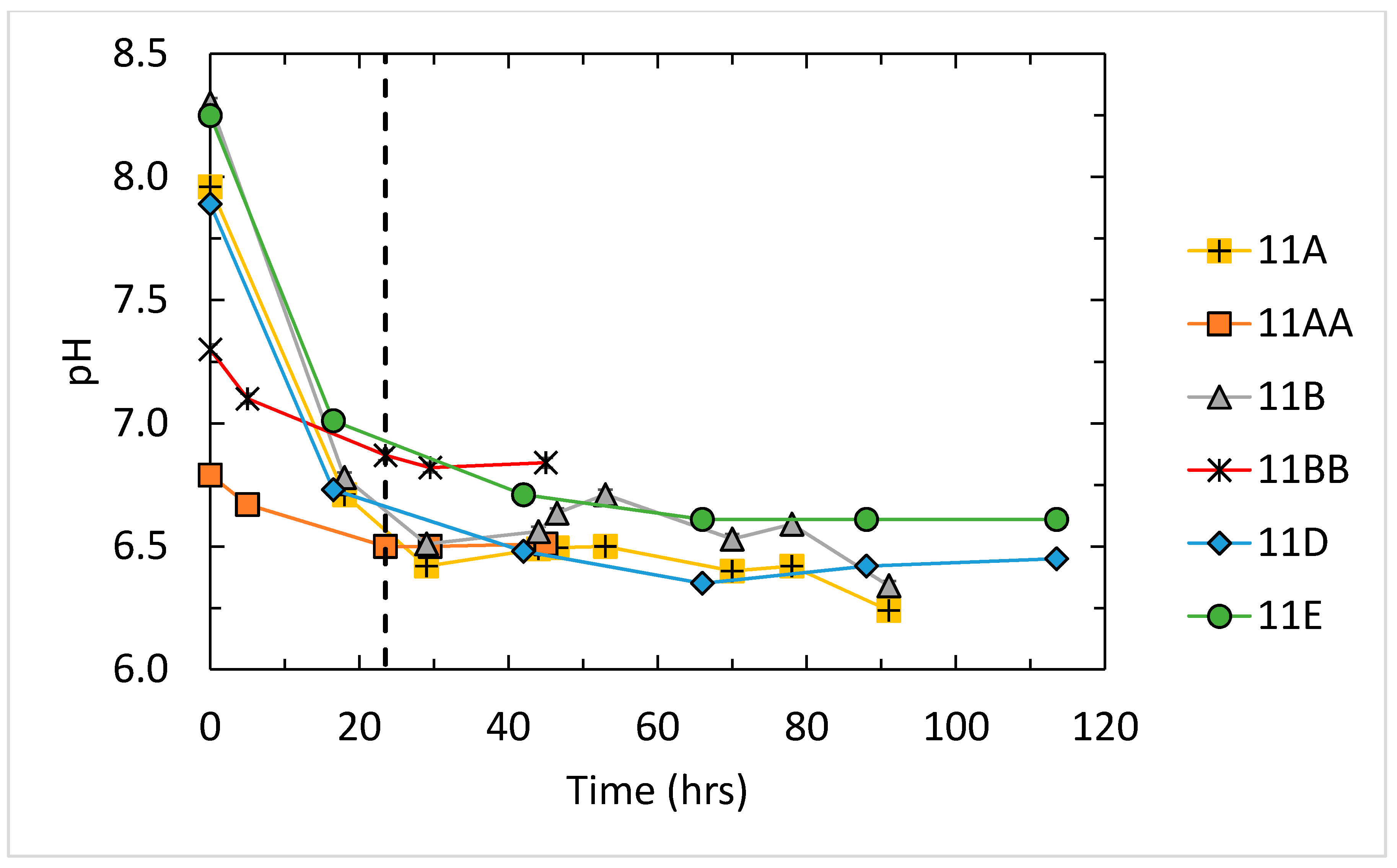
3.1. Results for Fluid pH, Salinity, and Saturation State

Graphical representations of pH and salinity data collected as part of series 9, 10, and 11 can be seen in Figure 2 and Figure 3 and Figure 4 for pH, and Figures S1 and S2 for salinity, in which the data was plotted as X–Y scatter plots. Although salinity data was not collected for series 11, the value of ~40 was expected due to the similarity in concentrations of major ions in titration solutions between series 9 and series 11. Additional information regarding salinity and pH can be found in Table S1. The average values of pH and salinity are reported in Table 2. Figure 2 shows that the pH at the beginning of experiments 9A through 9F was between ~6 and ~7. The onset of crystallization was observed approximately 24 h into the experiments for series 9, and it was at this time that the pH began to stabilize for all experiments, demonstrating steady-state conditions. Figure 3 shows the pH at the beginning of experiment 10A was approximately 7.75. Precipitation of crystals was not observed until 75 h into the experiment. After 100 h, the pH of the fluids in experiment 10A began to stabilize, demonstrating steady-state conditions. Figure 4 shows that the pH at the beginning of the experiments in series 11 was between 6.75 and 8.50. Precipitation of calcite was not observed until after 24 h had passed since the start of each experiment.
The CO2SYS program developed by Pierrot et al. [58] was utilized using the carbonate dissociation constants developed by Millero et al. [61] and dissociation constant for HSO4 defined by Dickson [62] to determine CO32−.
The terms “precip” and “final” refer to the time at which data was collected and the time at which precipitation began or the end of the experiment, respectively.
The subscript “ss” is an abbreviation of “steady-state”, and was the average of values collected when the standard deviation of the averaged values was less than 13%.
Other values reported in Table 2 include: average salinity, precip and final CO32− and Ca2+ aqueous concentrations, precip and final saturation state (Ω), and the mass of recovered calcite. The precip and final ΩC values reported in Table 2 were endmembers for conditions present in each experimental run. To determine the saturation state of the fluid, with respect to calcite or aragonite, the alkalinity, pH, Ca concentration, temperature, and salinity of the fluid must first be known. The calcium carbonate saturation state (Ω) is expressed as:
  Ω = [ Ca 2 + ] [ CO 3 2 − ] K * sp
where K*sp is the stoichiometric solubility product for a specific mineral phase of CaCO3 (e.g., calcite (calc), aragonite (arag), or low-magnesium calcite (lmc)); and [Ca2+] and [CO32−] are the total molar concentration of the reacting (free + complexed) ions. The saturation state was calculated for experiments in series 9 and 10 in this manner. [Ca2+] was determined from the data collected from the fluid samples using LA-AAS. [CO32−] was determined by utilizing the program CO2SYS, initially developed by Lewis et al. [57] and updated by Pierrot et al. [58], using the carbonate dissociation constants developed by Millero et al. [61] for carbonate systems and dissociation constant for HSO4 defined by Dickson [62] (to be included in alkalinity). The program uses two of four measurable input parameters of the aqueous carbonate system: TA, total dissolved inorganic carbon (TCO2), pH, and the partial pressure of CO2 (pCO2), to calculate the other two parameters at a set of input conditions (e.g., temperature and pressure) and a set of output conditions that included CO32− concentration [58]. K*sp was calculated using the expression developed by Mucci [8] and modified by Zeebe and Wolf-Gladrow [63].

3.2. X-ray Diffraction Results

The mass percentages of each calcium carbonate polymorph precipitated from the various experiments were determined by the MDI Jade 2010 software package, which analyzed XRD patterns of the scans. The XRD scans for series 9, 10, and 11 are shown in Figures S3–S5, respectively. Scans for all experiments indicated only one polymorph of calcium carbonate—calcite.

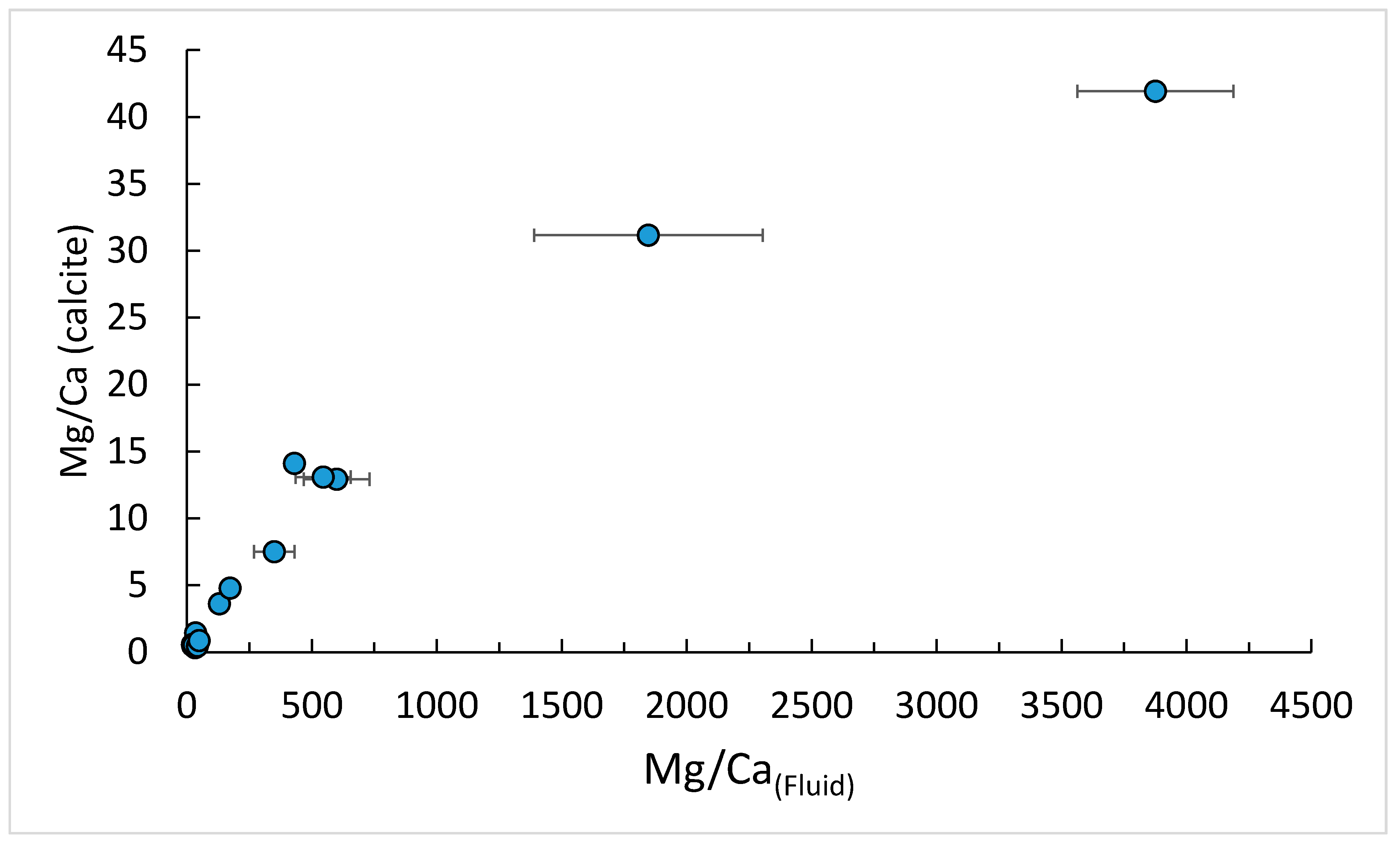
3.3. LS-AAS and ICP-OES Results

3.3.1. LS-AAS Results

The data collected from LS-AAS analysis were compiled and are presented in Table S1.

3.3.2. ICP-OES Results

The data collected from ICP-OES and LA-AAS were compiled into a plot of the aqueous Mg/Ca against the calcite Mg/Ca for all experiments (Figure 5). As shown, the calcite Mg/Ca ratio increased in a near-linear manner with an increase in the aqueous Mg/Ca ratio when 23 < Mg/Ca(Fluid) < 600 mmol/mol; however dependency became weaker at greater high aqueous Mg/Ca ratios; i.e., when 600 < Mg/Ca(Fluid) < 4000. The nonlinear nature of the observed relationship suggested a decrease in Mg partitioning between calcite and fluid with increasing aqueous Mg/Ca ratios, especially at high Mg/Ca(Fluid) values.

3.4. SEM Results

Figure 6 shows morphologies of calcite crystals imaged with SEM. Calcite crystals (runs 9A, 9B, and 11E) with relatively high Mg content (Mg/Ca = 41.9–13.1 mmol/mol) showed somewhat sharper edges compared to other crystals (runs 10A, 9D, and 11AA) with lower Mg content (Mg/Ca = 4.78–0.479 mmol/mol). In addition, the morphology of high-Mg crystals was pyramidal, whereas low-Mg calcite pyramids were truncated.

4. Discussion

Mg/Ca Ratios in Synthetic Low-Magnesium Calcite

For our experiments, KMg was calculated as a ratio of Mg/Ca in calcite to the averaged Mg/Ca in fluid:
( K Mg = Mg / Ca ( Solid ) Mg / Ca ( Fluid ) )
It has been shown that KMg is not dependent upon the calcium or magnesium concentration in solution, but is dependent on fluid Mg/Ca at Mg/Ca(Fluid) values above 0.35 mol/mol. For comparison, various ranges of Mg and Ca aqueous concentrations have been reported in the literature. Mavromatis et al. [15], reported Ca concentrations from 6.85 to 15.96 × 10 −3 M, and Mg concentrations ranged from 1.52 to 14.15 × 10−3 M while Gabitov et al. [16] demonstrated that Ca concentrations ranged from 2.38 to 8.17 × 10−3 M, and Mg concentrations ranged from 0.36 to 0.80 × 10−3 M. In the present study, Ca and Mg concentration ranges were 2.95 to 297 × 10−3 M and 0.32 to 45 × 10−3 M, respectively.
Using the values for Mg/Ca(Solid) and averaged Mg/Ca(Fluid), KMg was calculated (see Table 3). The values were plotted on a log–linear plot to determine the relationship between Mg/Ca(Fluid) and KMg. According to the data shown in Figure 7, KMg decreases by a factor of 3 (from 0.03 to 0.01) when Mg/Ca(Fluid) increases by a factor of 10 (from 0.43 to 3.9 mol/mol) for the crystals on which sharp edges were frequently observed (Figure 6: 9A, 9B, and 11E). No dependence of KMg on aqueous Mg/Ca ratio was observed at Mg/Ca(Fluid) < 0.4. The high scatter of KMg data at low aqueous Mg/Ca values (0.02 < Mg/Ca < 0.05 mol/mol) can be partially explained by the variability of pH values in the growth media (Figure 8). KMg decreased almost by a factor of four (from 0.041 to 0.014) when pH was increased by 0.7 units (from 6.23 to 6.95). This relationship could be explained by a reverse correlation between KMg and the growth rate observed by Gabitov et al. [16]; i.e., an increase of pH increased the growth and drove KMg down, when aqueous Mg/Ca did not vary much (0.02 < Mg/Ca < 0.05 mol/mol). Our findings agree with results reported by Mucci and Morse [18] and Mavromatis et al. [15] by replicating the inverse relationship of KMg on fluid Mg/Ca when Mg/Ca(Fluid) is greater than 0.4 and less than 20 mol/mol.

5. Conclusions

This study demonstrated that Mg/Ca(Solid) increased with increasing Mg/Ca(Fluid) when Mg/Ca(Fluid) increased from ~0.023 to ~0.6 mol/mol, implying that Mg uptake in low-Mg calcite was proportional to the Mg concentration in solution. The study results demonstrated that aqueous concentrations of Mg or Ca individually did not influence KMg.
This study reinforces the previously observed inverse relationship of KMg on fluid Mg/Ca ratios when 0.5 > Mg/Ca(Fluid) < 20 mol/mol, and extended it down to Mg/Ca = 0.4 mol/mol, demonstrating that KMg increased with decreasing Mg/Ca(Fluid). However, for Mg/Ca(Fluid) concentrations less than 0.4 and greater than 0.023 mol/mol, our results demonstrated a lack of a KMg–Mg/Ca(Fluid) trend, likely due to the combined effects of Mg/Ca and pH. Although additional research is needed to constrain accurate KMg–Mg/Ca(Fluid) relationships in low-Mg calcite, our results suggested that the KMg of low-Mg calcite was less sensitive to Mg/Ca(Fluid) compared to calcite with a higher Mg content.

Supplementary Materials

The following are available online at https://www.mdpi.com/article/10.3390/min11111158/s1, Figure S1: Graphical representation of salinity plotted against time for experiments 9A through 9F. Figure S2: Graphical representation of salinity plotted against time for experiments 10A. Figure S3: Series 9. Powdered X-ray diffraction scans with Cu-Kα radiation of different calcium carbonate polymorphs. Figure S4: Series 10. Powdered X-ray diffraction scans with Cu-Kα radiation of different calcium carbonate polymorphs. Figure S5. Series 11. Powdered X-ray diffraction scans with Cu-Kα radiation of different calcium carbonate polymorphs. Table S1: Compiled data documenting time of sample collection in hrs, measured pH value, salinity, and LS-AAS data for Mg and Ca (ppm) and Mg/Ca ratios.

Author Contributions

Conceptualization, J.M.W. and R.I.G.; methodology, J.M.W.; software, J.M.W., R.I.G. and A.S.; validation, A.N. and A.J.; formal analysis, J.M.W., R.I.G., A.S., A.N., A.J., R.V.K.G.T., J.J.V. and A.D.; investigation, J.M.W., R.I.G., A.S., A.N., A.J., R.V.K.G.T., J.J.V. and A.D.; resources, R.I.G., A.S., R.V.K.G.T., J.J.V. and A.D.; data curation, J.M.W., R.I.G., A.S., A.N. and A.J.; writing—original draft preparation, J.M.W.; writing—review and editing, J.M.W., R.I.G., A.S. and A.J.; visualization, J.M.W. and R.I.G.; supervision, R.I.G.; project administration, J.M.W. and R.I.G.; funding acquisition, R.I.G. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Not applicable.

Acknowledgments

The authors would like to acknowledge the Department of Geosciences, the College of Arts & Sciences, and the Institute for Imaging & Analytical Technologies at Mississippi State University.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Katz, A. The interaction of magnesium with calcite during crystal growth at 25–90 °C and one atmosphere. Geochim. Cosmochim. Acta 1973, 37, 1563–1586. [Google Scholar] [CrossRef]
  2. Füchtbauer, H.; Hardie, L.A. Experimentally determined homogeneous distribution coefficients for precipitated magnesian calcites: Application to marine carbonate cements. In Proceedings of the Geological Society of America Annual Meeting, Denver, CO, USA, 8–10 November 1976; Volume 8, p. 877. [Google Scholar]
  3. Burton, E.A.; Walter, L.M. Relative precipitation rates of aragonite and Mg calcite from seawater: Temperature or carbonate ion control? Geology 1987, 15, 111–114. [Google Scholar] [CrossRef]
  4. Howson, M.R.; Pethybridge, A.D.; House, W.A. Synthesis and distribution coefficient of low-magnesium calcites. Chem. Geol. 1987, 64, 79–87. [Google Scholar] [CrossRef]
  5. Mucci, A. Influence of temperature on the composition of magnesian calcite overgrowths precipitated from seawater. Geochim. Cosmochim. Acta 1987, 51, 1977–1984. [Google Scholar] [CrossRef]
  6. Oomori, T.; Kaneshima, H.; Maezato, Y.; Kitano, Y. Distribution coefficient of Mg2+ ions between calcite and solution at 10–50 °C. Mar. Chem. 1987, 20, 327–336. [Google Scholar] [CrossRef]
  7. Huang, Y.; Fairchild, I.J. Partitioning of Sr2+ and Mg2+ into calcite under karst-analogue experimental conditions. Geochim. Cosmochim. Acta 2001, 65, 47–62. [Google Scholar] [CrossRef]
  8. Mucci, A. The solubility of calcite and aragonite in seawater at various salinities, temperatures, and one atmosphere total pressure. Am. J. Sci. 1983, 283, 780–799. [Google Scholar] [CrossRef]
  9. Zhong, S.; Mucci, A. Calcite and aragonite precipitation from seawater solutions of various salinities: Precipitation rates and overgrowth compositions. Chem. Geol. 1989, 78, 283–299. [Google Scholar] [CrossRef]
  10. Burton, E.A.; Walter, L.M. The effects of P CO 2 and temperature on magnesium incorporation in calcite in seawater and MgCl2-CaCl2 solutions. Geochim. Cosmochim. Acta 1991, 55, 777–785. [Google Scholar] [CrossRef]
  11. Hartley, G.; Mucci, A. The influence of P CO 2 on the partitioning of magnesium in calcite overgrowths precipitated from artificial seawater at 25° and 1 atm total pressure. Geochim. Cosmochim. Acta 1996, 60, 315–324. [Google Scholar] [CrossRef]
  12. Given, R.K.; Wilkinson, B.H. Kinetic control of morphology, composition, and mineralogy of abiotic sedimentary carbonates. J. Sediment. Res. 1985, 55, 109–119. [Google Scholar]
  13. Given, R.K.; Wilkinson, B.H. Kinetic control of morphology, composition, and mineralogy of abiotic sedimentary carbonates–REPLY. J. Sediment. Res. 1985, 55, 921–926. [Google Scholar]
  14. Saulnier, S.; Rollion-Bard, C.; Vigier, N.; Chaussidon, M. Mg isotope fractionation during calcite precipitation: An experimental study. Geochim. Cosmochim. Acta 2012, 91, 75–91. [Google Scholar] [CrossRef]
  15. Mavromatis, V.; Gautier, Q.; Bosc, O.; Schott, J. Kinetics of Mg partition and Mg stable isotope fractionation during its incorporation in calcite. Geochim. Cosmochim. Acta 2013, 114, 188–203. [Google Scholar] [CrossRef]
  16. Gabitov, R.I.; Sadekov, A.; Leinweber, A. Crystal growth rate effect on Mg/Ca and Sr/Ca partitioning between calcite and fluid: An in situ approach. Chem. Geol. 2014, 367, 70–82. [Google Scholar] [CrossRef]
  17. Devery, D.M.; Ehlmann, A.J. Morphological changes in a series of synthetic Mg-calcites. Am. Mineral. 1981, 66, 592–595. [Google Scholar]
  18. Mucci, A.; Morse, J.W. The incorporation of Mg2+ and Sr2+ into calcite overgrowths: Influences of growth rate and solution composition. Geochim. Cosmochim. Acta 1983, 47, 217–233. [Google Scholar] [CrossRef]
  19. Busenberg, E.; Plummer, L.N. Thermodynamics of magnesian calcite solid-solutions at 25 °C and 1 atm total pressure. Geochim. Cosmochim. Acta 1989, 53, 1189–1208. [Google Scholar] [CrossRef]
  20. Sandberg, P.A. An oscillating trend in Phanerozoic non-skeletal carbonate mineralogy. Nature 1983, 305, 19–22. [Google Scholar] [CrossRef]
  21. Wilkinson, B.H.; Algeo, T.J. Sedimentary carbonate record of calcium-magnesium cycling. Am. J. Sci. 1989, 289, 1158–1194. [Google Scholar] [CrossRef]
  22. Hardie, L.A. Secular variation in seawater chemistry: An explanation for the coupled secular variation in the mineralogies of marine limestones and potash evaporites over the past 600 m.y. Geology 1996, 24, 279–283. [Google Scholar] [CrossRef]
  23. Horita, J.; Weinberg, A.; Das, N.; Holland, H.D. Brine inclusions in halite and the origin of the Middle Devonian Prairie evaporites of Western Canada. J. Sediment. Res. 1996, 66, 956–964. [Google Scholar]
  24. Stanley, S.M.; Hardie, L.A. Hypercalcification: Paleontology links plate tectonics and geochemistry to sedimentology. GSA Today 1999, 9, 1–7. [Google Scholar]
  25. Zimmermann, H.; Holland, H.D.; Horita, J.A.B. The evolution of seawater during the Phanerozoic; Record from marine evaporites and fluid inclusions in halite. In Proceedings of the Geological Society of America Annual Meeting, Reno, NV, USA, 5–8 November 2000; Volume 32, p. 67. [Google Scholar]
  26. Lowenstein, T.K.; Timofeeff, M.N.; Brennan, S.T.; Hardie, L.A.; Demicco, R.V. Oscillations in Phanerozoic seawater chemistry: Evidence from fluid inclusions. Science 2001, 294, 1086–1088. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  27. Horita, J.; Zimmermann, H.; Holland, H.D. Chemical evolution of seawater during the Phanerozoic: Implications from the record of marine evaporites. Geochim. Cosmochim. Acta 2002, 66, 3733–3756. [Google Scholar] [CrossRef]
  28. Dickson, J.A.D. Fossil echinoderms as monitor of the Mg/Ca ratio of Phanerozoic oceans. Science 2002, 298, 1222–1224. [Google Scholar] [CrossRef] [PubMed]
  29. Lowenstein, T.K.; Hardie, L.A.; Timofeeff, M.N.; Demicco, R.V. Secular variation in seawater chemistry and the origin and significance of calcium chloride basinal brines; Geological Society of America, 2003 Annual Meeting. In Proceedings of the Geological Society of America Annual Meeting, Seattle, WA, USA, 2–5 November 2003; Volume 35, p. 201. [Google Scholar] [CrossRef]
  30. Coggon, R.M.; Teagle, D.A.H.; Smith-Duque, C.E.; Alt, J.C.; Cooper, M.J. Reconstructing past seawater Mg/Ca and Sr/Ca from mid-ocean ridge flank calcium carbonate veins. Science 2010, 327, 1114–1117. [Google Scholar] [CrossRef] [Green Version]
  31. Hasiuk, F.J.; Lohmann, K.C. Application of calcite Mg partitioning functions to the reconstruction of paleocean Mg/Ca. Geochim. Cosmochim. Acta 2010, 74, 6751–6763. [Google Scholar] [CrossRef]
  32. Broecker, W.; Yu, J. What do we know about the evolution of Mg to Ca ratios in seawater? Paleoceanography 2011, 26, 1–8. [Google Scholar] [CrossRef] [Green Version]
  33. Demicco, R.V.; Lowenstein, T.K.; Hardie, L.A.; Spencer, R.J. Model of seawater composition for the Phanerozoic. Geology 2005, 33, 877–880. [Google Scholar] [CrossRef]
  34. Morse, J.W.; Wang, Q.; Tsio, M.Y. Influences of temperature and Mg:Ca ratio on CaCO3 precipitates from seawater. Geology 1997, 25, 85–87. [Google Scholar] [CrossRef]
  35. Spencer, R.J.; Hardie, L.A. Control of seawater composition by mixing of river waters and mid-ocean ridge hydrothermal brines. In Fluid-Mineral Interaction: A Tribute to HP Eugster Special Publication No. 2; Geochemical Society: Washington, DC, USA, 1990; Volume 19, pp. 409–419. [Google Scholar]
  36. Volk, T. Sensitivity of climate and atmospheric CO2 to deep-ocean and shallow-ocean carbonate burial. Nature 1989, 337, 637–640. [Google Scholar] [CrossRef]
  37. Holland, H.D.; Zimmermann, H. The Dolomite Problem Revisited. Int. Geol. Rev. 2000, 42, 481–490. [Google Scholar] [CrossRef]
  38. Schmidt, D.N.; Lazarus, D.; Young, J.R.; Kucera, M. Biogeography and evolution of body size in marine plankton. Earth Sci. Rev. 2006, 78, 239–266. [Google Scholar] [CrossRef]
  39. Stoll, H.M.; Ziveri, P.; Shimizu, N.; Conte, M.; Theroux, S. Relationship between coccolith Sr/Ca ratios and coccolithophore production and export in the Arabian Sea and Sargasso Sea. Deep. Res. Part II Top. Stud. Oceanogr. 2007, 54, 581–600. [Google Scholar] [CrossRef]
  40. Prentice, K.; Jones, T.D.; Lees, J.A.; Young, J.; Bown, P.; Langer, G.; Fearn, S.; EIMF. Trace metal (Mg/Ca and Sr/Ca) analyses of single coccoliths by Secondary Ion Mass Spectrometry. Geochim. Cosmochim. Acta 2014, 146, 90–106. [Google Scholar] [CrossRef]
  41. Nürnberg, D.; Bijma, J.; Hemleben, C. Assessing the reliability of magnesium in foraminiferal calcite as a proxy for water mass temperatures. Geochim. Cosmochim. Acta 1996, 60, 803–814. [Google Scholar] [CrossRef] [Green Version]
  42. Lea, D.W.; Mashiotta, T.A.; Spero, H.J. Controls on magnesium and strontium uptake in planktonic foraminifera determined by live culturing. Geochim. Cosmochim. Acta 1999, 63, 2369–2379. [Google Scholar] [CrossRef]
  43. Mashiotta, T.; Lea, D.W.; Spero, H.J. Glacial–interglacial changes in Subantarctic sea surface temperature and δ18O-water using foraminiferal Mg. Earth Planet. Sci. Lett. 1999, 170, 417–432. [Google Scholar] [CrossRef]
  44. Rosenthal, Y.; Boyle, E.A.; Slowey, N. Temperature control on the incorporation of magnesium, strontium, fluorine, and cadmium into benthic foraminiferal shells from Little Bahama Bank: Prospects for thermocline paleoceanography. Geochim. Cosmochim. Acta 1997, 61, 3633–3643. [Google Scholar] [CrossRef]
  45. Ferguson, J.E.; Henderson, G.M.; Kucera, M.; Rickaby, R.E.M. Systematic change of foraminiferal Mg/Ca ratios across a strong salinity gradient. Earth Planet. Sci. Lett. 2008, 265, 153–166. [Google Scholar] [CrossRef] [Green Version]
  46. Mathien-Blard, E.; Bassinot, F. Salinity bias on the foraminifera Mg/Ca thermometry: Correction procedure and implications for past ocean hydrographic reconstructions. Geochem. Geophys. Geosyst. 2009, 10. [Google Scholar] [CrossRef]
  47. Hönisch, B.; Allen, K.A.; Lea, D.W.; Spero, H.J.; Eggins, S.M.; Arbuszewski, J.; DeMenocal, P.; Rosenthal, Y.; Russell, A.D.; Elderfield, H. The influence of salinity on Mg/Ca in planktic foraminifers—Evidence from cultures, core-top sediments and complementary δ18O. Geochim. Cosmochim. Acta 2013, 121, 196–213. [Google Scholar] [CrossRef] [Green Version]
  48. Ries, J.B. Effect of ambient Mg/Ca ratio on Mg fractionation in calcareous marine invertebrates: A record of the oceanic Mg/Ca ratio over the Phanerozoic. Geology 2004, 32, 981–984. [Google Scholar] [CrossRef]
  49. Stanley, S.M.; Ries, J.B.; Hardie, L.A. Seawater chemistry, coccolithophore population growth, and the origin of Cretaceous chalk. Geology 2005, 33, 593–596. [Google Scholar] [CrossRef] [Green Version]
  50. Bentov, S.; Erez, J. Impact of biomineralization processes on the Mg content of foraminiferal shells: A biological perspective. Geochem. Geophys. Geosyst. 2006, 7. [Google Scholar] [CrossRef]
  51. Blackmon, P.D.; Todd, R. Mineralogy of some foraminifera as related to their classification and ecology. J. Paleontol. 1959, 33, 1–15. [Google Scholar]
  52. Erez, J. The Source of Ions for Biomineralization in Foraminifera and Their Implications for Paleoceanographic Proxies. Rev. Mineral. Geochem. 2003, 54, 115–149. [Google Scholar] [CrossRef] [Green Version]
  53. Sadekov, A.Y.; Eggins, S.M.; De Deckker, P. Characterization of Mg/Ca distributions in planktonic foraminifera species by electron microprobe mapping. Geochem. Geophys. Geosyst. 2005, 6. [Google Scholar] [CrossRef]
  54. Branson, O.; Redfern, S.A.T.; Tyliszczak, T.; Sadekov, A.; Langer, G.; Kimoto, K.; Elderfield, H. The coordination of Mg in foraminiferal calcite. Earth Planet. Sci. Lett. 2013, 383, 134–141. [Google Scholar] [CrossRef] [Green Version]
  55. Tesoriero, A.J.; Pankow, J.F. Solid solution partitioning of Sr2+, Ba2+, and Cd2+ to calcite. Geochim. Cosmochim. Acta 1996, 60, 1053–1063. [Google Scholar] [CrossRef]
  56. Rounds, S.A. Alkalinity and acid neutralizing capacity (ver. 4.0, September 2012). In U.S. Geological Survey Techniques of Water-Resources Investigations; U.S. Geological Survey: Reston, VA, USA, 2012; Book 9, Chapter 6.6. [Google Scholar]
  57. Lewis, E.; Wallace, D.; Allison, L.J. Program Developed for CO2 System Calculations; ORNL/CDIAC-105; Carbon Dioxide Information Analysis Center, Oak Ridge National Laboratory, US Department of Energy: Oak Ridge, TN, USA, 1998.
  58. Pierrot, D.; Lewis, E.; Wallace, D. MS Excel Program Developed for CO2 System Calculations; ORNL/CDIAC-105a; Carbon Dioxide Information Analysis Center, Oak Ridge National Laboratory, US Department of Energy: Oak Ridge, TN, USA, 2006.
  59. De Villiers, S.; Greaves, M.; Elderfield, H. An Intensity Ratio Calibration Method for the Accurate Determination of Mg/Ca and Sr/Ca of Marine Carbonates by ICP-AES. Geochem. Geophys. Geosyst. 2002, 3. [Google Scholar] [CrossRef]
  60. Greaves, M.; Barker, S.; Daunt, C.; Elderfield, H. Accuracy, Standardization, and Interlaboratory Calibration Standards for Foraminiferal Mg/Ca Thermometry. Geochem. Geophys. Geosyst. 2005, 6, 1–9. [Google Scholar] [CrossRef]
  61. Millero, F.J.; Graham, T.B.; Huang, F.; Bustos-Serrano, H.; Pierrot, D. Dissociation constants of carbonic acid in seawater as a function of salinity and temperature. Mar. Chem. 2006, 100, 80–94. [Google Scholar] [CrossRef]
  62. Dickson, A.G. Thermodynamics of the Dissociation of Boric Acid in Synthetic Seawater from 273.15 to 318.15 K. Deep Sea Res. Part A Oceanogr. Res. Pap. 1990, 37, 755–766. [Google Scholar] [CrossRef]
  63. Zeebe, R.E.; Wolf-Gladrow, D.A. CO2 in Seawater: Equilibrium, Kinetics, Isotopes; Elsevier: London, UK, 2001; p. 347. ISBN 9780444509468. [Google Scholar]
Minerals 11 01158 g001 550
Figure 1. Illustration depicting the experimental set-up for experiments conducted in series 9, 10, and 11. Colored lines and arrows are meant to depict fluid flow directions within tubing.
Figure 1. Illustration depicting the experimental set-up for experiments conducted in series 9, 10, and 11. Colored lines and arrows are meant to depict fluid flow directions within tubing.
Minerals 11 01158 g001
Minerals 11 01158 g002 550
Figure 2. Graphical representation of pH plotted against time for experiments 9A through 9F. The analytical uncertainty was ±0.02, and is included in the symbol size. The vertical dashed line indicates the observed onset of crystallization at approximately 24 h.
Figure 2. Graphical representation of pH plotted against time for experiments 9A through 9F. The analytical uncertainty was ±0.02, and is included in the symbol size. The vertical dashed line indicates the observed onset of crystallization at approximately 24 h.
Minerals 11 01158 g002
Minerals 11 01158 g003 550
Figure 3. Graphical representation of pH plotted against time for experiment 10A. The analytical uncertainty was ±0.02. The vertical dashed line indicates the observed onset of crystallization at approximately 75 h.
Figure 3. Graphical representation of pH plotted against time for experiment 10A. The analytical uncertainty was ±0.02. The vertical dashed line indicates the observed onset of crystallization at approximately 75 h.
Minerals 11 01158 g003
Minerals 11 01158 g004 550
Figure 4. Graphical representation of pH plotted against time for experiments 11A through 11E. The analytical uncertainty was ±0.02, and is included in symbol size. The vertical dashed line indicates the observed onset of crystallization at approximately 24 h.
Figure 4. Graphical representation of pH plotted against time for experiments 11A through 11E. The analytical uncertainty was ±0.02, and is included in symbol size. The vertical dashed line indicates the observed onset of crystallization at approximately 24 h.
Minerals 11 01158 g004
Minerals 11 01158 g005 550
Figure 5. Mg/Ca concentration as a ratio in precipitated calcite plotted as a function of averaged aqueous Mg/Ca concentration as a ratio (in mmol/mol). The Mg/Ca(Fluid) analytical uncertainty was determined in terms of the standard error.
Figure 5. Mg/Ca concentration as a ratio in precipitated calcite plotted as a function of averaged aqueous Mg/Ca concentration as a ratio (in mmol/mol). The Mg/Ca(Fluid) analytical uncertainty was determined in terms of the standard error.
Minerals 11 01158 g005
Minerals 11 01158 g006 550
Figure 6. SEM imaging of the crystals (scale bar is 10 µ). The order of the images corresponds to the decrease in Mg content of calcite. (A1–A3) correspond to calcite crystals collected from experiments 9A, 9B, and 11E respectively and are crystals with higher Mg content and sharper crystal edges. Comparatively, (B1–B3) which correspond to calcite crystals collected from experiments 10A, 9D, and 11AA respectively poses lower Mg content and truncated crystal edges.
Figure 6. SEM imaging of the crystals (scale bar is 10 µ). The order of the images corresponds to the decrease in Mg content of calcite. (A1–A3) correspond to calcite crystals collected from experiments 9A, 9B, and 11E respectively and are crystals with higher Mg content and sharper crystal edges. Comparatively, (B1–B3) which correspond to calcite crystals collected from experiments 10A, 9D, and 11AA respectively poses lower Mg content and truncated crystal edges.
Minerals 11 01158 g006
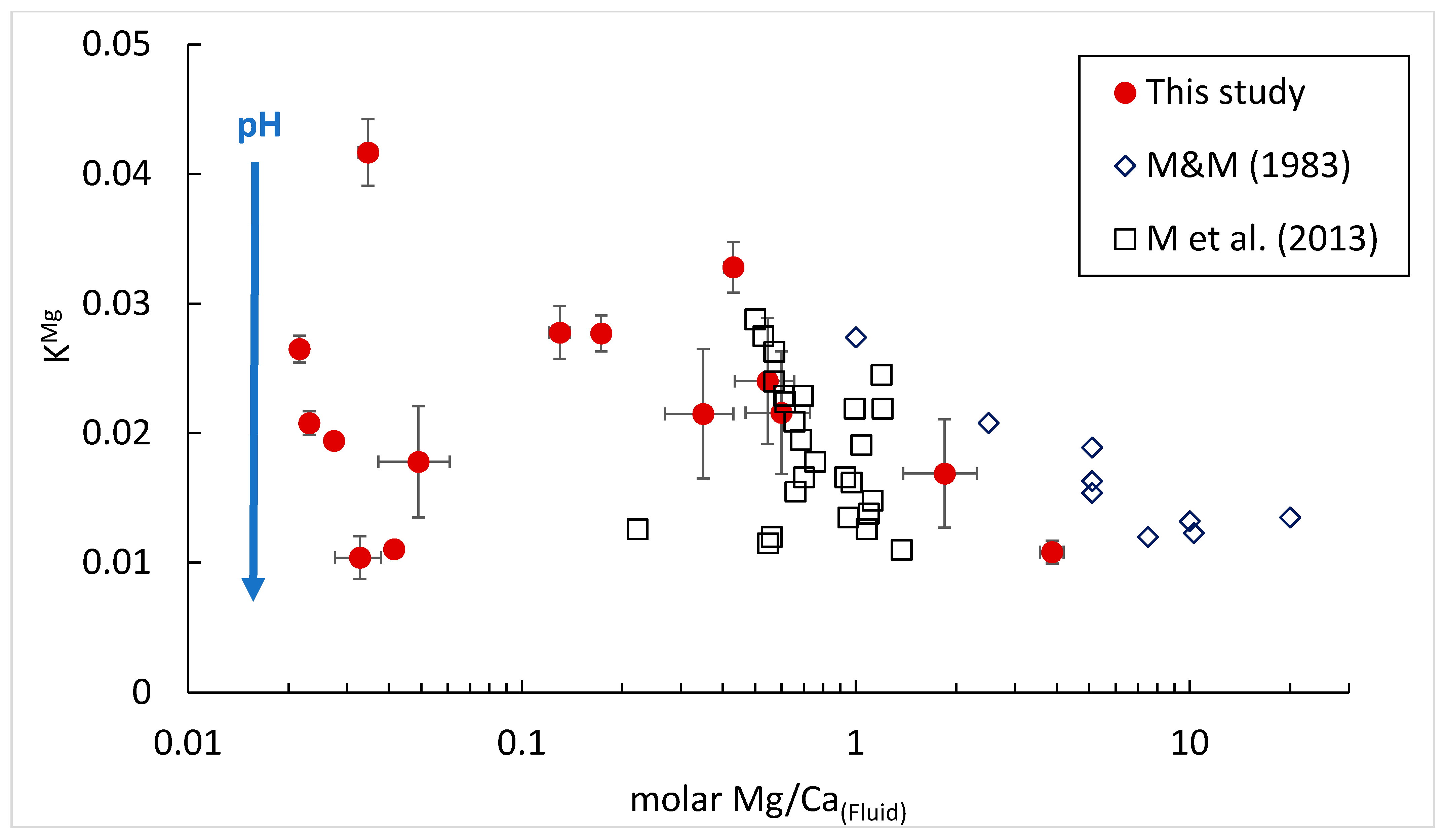
Minerals 11 01158 g007 550
Figure 7. A log–linear plot demonstrating the relationship between aqueous Mg/Ca and KMg. Red circles represent data from the present study, blue diamonds are data from Mucci and Morse [18], and grey squares are data from Mavromatis et al. [15]. The analytical uncertainty for Mg/Ca(Fluid) in the present study was determined in terms of the standard error. KMg analytical uncertainty in the present study was determined using the formula: √((Mg/Ca(Solid) Error)2/(Mg/Ca(Fluid))2 + (Mg/Ca(Fluid) Std.dev)2/(Mg/Ca(Fluid))4·(Mg/Ca(Solid))2). The method for determining analytical uncertainty was not reported by Mavromatis et al. [15]. The blue arrow indicates a negative effect of pH on KMg.
Figure 7. A log–linear plot demonstrating the relationship between aqueous Mg/Ca and KMg. Red circles represent data from the present study, blue diamonds are data from Mucci and Morse [18], and grey squares are data from Mavromatis et al. [15]. The analytical uncertainty for Mg/Ca(Fluid) in the present study was determined in terms of the standard error. KMg analytical uncertainty in the present study was determined using the formula: √((Mg/Ca(Solid) Error)2/(Mg/Ca(Fluid))2 + (Mg/Ca(Fluid) Std.dev)2/(Mg/Ca(Fluid))4·(Mg/Ca(Solid))2). The method for determining analytical uncertainty was not reported by Mavromatis et al. [15]. The blue arrow indicates a negative effect of pH on KMg.
Minerals 11 01158 g007
Minerals 11 01158 g008 550
Figure 8. (A) A plot of KMg versus pH for the experiments run at low aqueous Mg/Ca (0.02 < Mg/Ca < 0.05 mol/mol). (B) The averaging of the three data points with overlapped pH values due to the high error bars (red circle seen in A) yielded a better fit with r2 = 0.82.
Figure 8. (A) A plot of KMg versus pH for the experiments run at low aqueous Mg/Ca (0.02 < Mg/Ca < 0.05 mol/mol). (B) The averaging of the three data points with overlapped pH values due to the high error bars (red circle seen in A) yielded a better fit with r2 = 0.82.
Minerals 11 01158 g008
Table
Table 1. Concentrations of salts in the titration solutions.
Table 1. Concentrations of salts in the titration solutions.
RunConcentrations of Salts in Titrate Solutions (mmol L−1)Calculated Aqueous Mg/Ca (mmol/mol)
NaClNaHCO3NaOHMgCl2·6H2OCaCl2·2H2O
9A600300 134166807
9B600300 113187604
9C600300 50250200
9D600300 629420
9E600300 2327783
9F600300 66234282
10A60012 210200
11A-1,2,3600300 329710
11AA60030030329710
11B60030010329710
11BB-1,2,360030010329710
11D600300 45255176
11E6003001045255176
Table
Table 2. Steady-state pH; average salinity; CO32−, Ca2+, and Mg2+ aqueous concentrations, precipitation, and final saturation state (Ωc); and mass of precipitated calcium carbonate.
Table 2. Steady-state pH; average salinity; CO32−, Ca2+, and Mg2+ aqueous concentrations, precipitation, and final saturation state (Ωc); and mass of precipitated calcium carbonate.
RunCO32−Ca2+ TAΩCS (‰)CaCO3 (g)
9APrecip0.1514.2834.253.4545.3417.74
Final0.078.0922.181.01
9BPrecip0.0822.2825.823.0645.0818.68
Final0.118.322.421.57
9CPrecip0.0429.4711.091.847.3819.79
Final0.5116.7142.0113.21
9DPrecip0.0261.927.221.6745.8920.59
Final0.0543.599.793.18
9EPrecip0.0258.5112.071.85 44.8122.68
Final0.0436.1117.462.27
9FPrecip0.0445.0113.343.2145.2522.04
Final0.0633.225.963.23
10APrecip0.222.9515.832.5322.441.53
Final0.181.628.021.16
Ion concentration and total alkalinity (TA) are in mmol per kg of H2O. S (‰): average salinity. Ωc: saturation state.
Table
Table 3. Solid and aqueous Mg/Ca, KMg.
Table 3. Solid and aqueous Mg/Ca, KMg.
RunpHSEMg/Ca(Solid) (mol/mol)Mg/Ca(Fluid) (mmol/mol)SEMg/Ca(Fluid) (mol/mol)SEKMgSE
9A6.840.0641.923875311.93.87520.31190.01080.00087
9B6.770.0631.171846457.11.84650.45710.01690.00418
9C6.740.1312.92599.1131.50.59910.13150.02160.00474
9D6.230.011.44134.592.1310.03460.00210.04170.00257
9E6.440.023.608129.99.5310.12990.00950.02780.00204
9F6.510.0814.10429.825.820.42980.02580.03280.00197
10A7.990.054.785172.88.6300.17280.00860.02770.00138
11A-16.320.090.571021.560.8500.02160.00090.02650.00104
11A-2,36.910.420.340032.735.1600.03270.00520.01040.00164
11AA6.550.040.479023.061.0090.02310.00100.02080.00091
11B-16.430.090.531027.360.47500.02740.00050.01940.00034
11B-2,37.050.490.45741.40.47500.04140.00050.01100.00013
11BB6.910.060.8749.011.820.04900.01180.01780.00429
11D6.230.067.508349.481.280.34940.08130.0214860.00500
11E6.710.0813.09544.9110.00.54490.11000.02400.00485
SE: standard error. The SE of Mg/Ca(Solid) was calculated from the reproducibility of standard measurements using ICP-OES; pH and Mg/Ca(Fluid) are the average values of the subsamples. The error was determined using the formula: √((Mg/Ca(Solid) Error)2/(Mg/Ca(Fluid))2 + (Mg/Ca(Fluid) Std.dev)2/(Mg/Ca(Fluid))4×(Mg/Ca(Solid))2).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Weremeichik, J.M.; Gabitov, R.I.; Sadekov, A.; Novak, A.; Jimenez, A.; Thirumalai, R.V.K.G.; Varco, J.J.; Dygert, A. Mg/Ca Ratios in Synthetic Low-Magnesium Calcite: An Experimental Investigation. Minerals 2021, 11, 1158. https://doi.org/10.3390/min11111158

AMA Style

Weremeichik JM, Gabitov RI, Sadekov A, Novak A, Jimenez A, Thirumalai RVKG, Varco JJ, Dygert A. Mg/Ca Ratios in Synthetic Low-Magnesium Calcite: An Experimental Investigation. Minerals. 2021; 11(11):1158. https://doi.org/10.3390/min11111158

Chicago/Turabian Style

Weremeichik, Jeremy M., Rinat I. Gabitov, Aleksey Sadekov, Aleksandra Novak, Angel Jimenez, Rooban Venkatesh K. G. Thirumalai, Jac J. Varco, and Andrew Dygert. 2021. "Mg/Ca Ratios in Synthetic Low-Magnesium Calcite: An Experimental Investigation" Minerals 11, no. 11: 1158. https://doi.org/10.3390/min11111158

APA Style

Weremeichik, J. M., Gabitov, R. I., Sadekov, A., Novak, A., Jimenez, A., Thirumalai, R. V. K. G., Varco, J. J., & Dygert, A. (2021). Mg/Ca Ratios in Synthetic Low-Magnesium Calcite: An Experimental Investigation. Minerals, 11(11), 1158. https://doi.org/10.3390/min11111158

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop