Kinetic Energy Calculation in Granite Particles Comminution Considering Movement Characteristics and Spatial Distribution
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Materials
2.2. Experimental System
3. Results and Discussion
3.1. Force-Displacement Relationship of Uniaxial Compression
3.2. Characteristics of Uniaxial Compression Failure Fragments
3.3. Fragments Velocity Characteristics
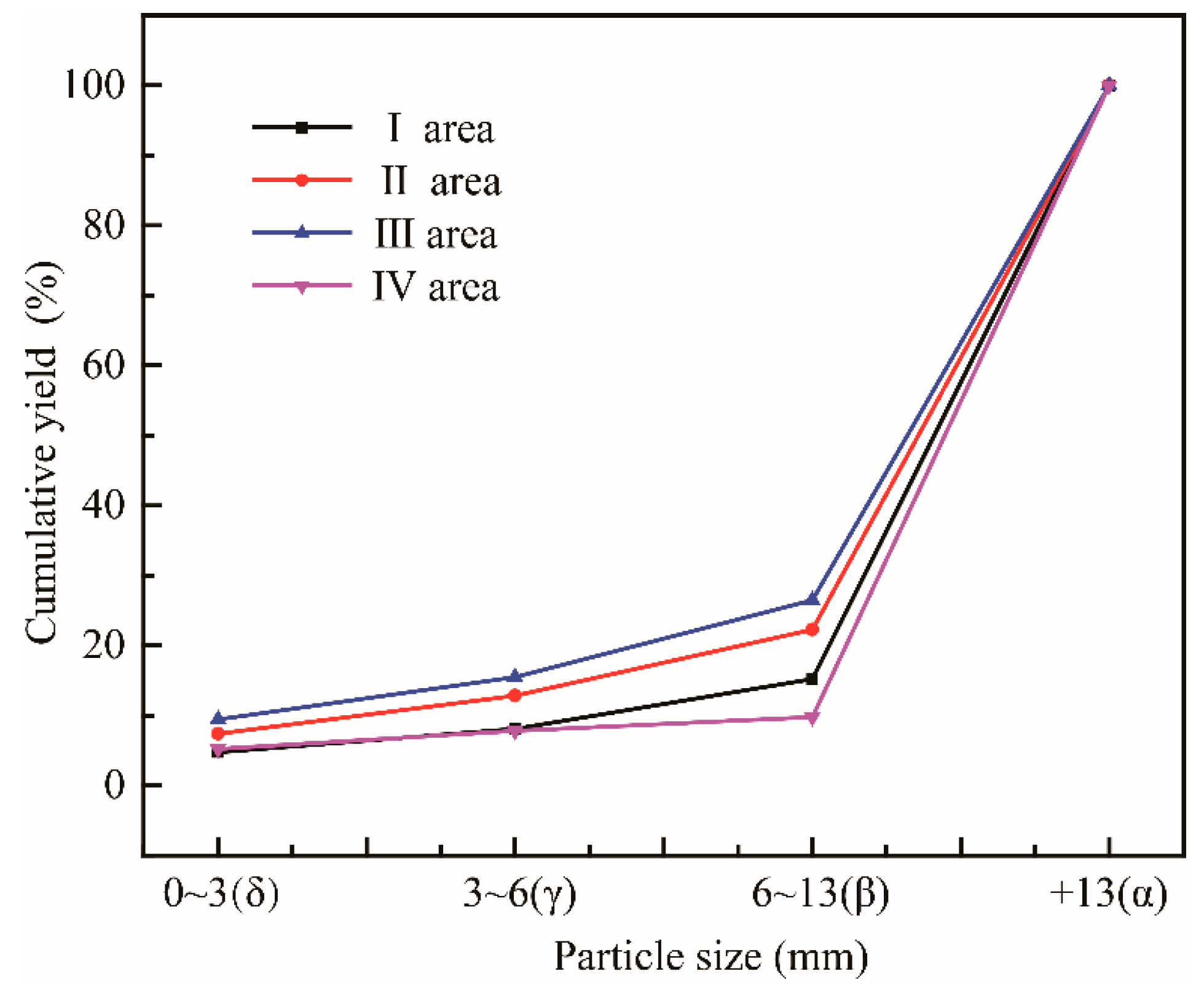
3.4. Mass Distribution of Fragments
3.5. Kinetic Energy of Single-Axis Destruction Fragments
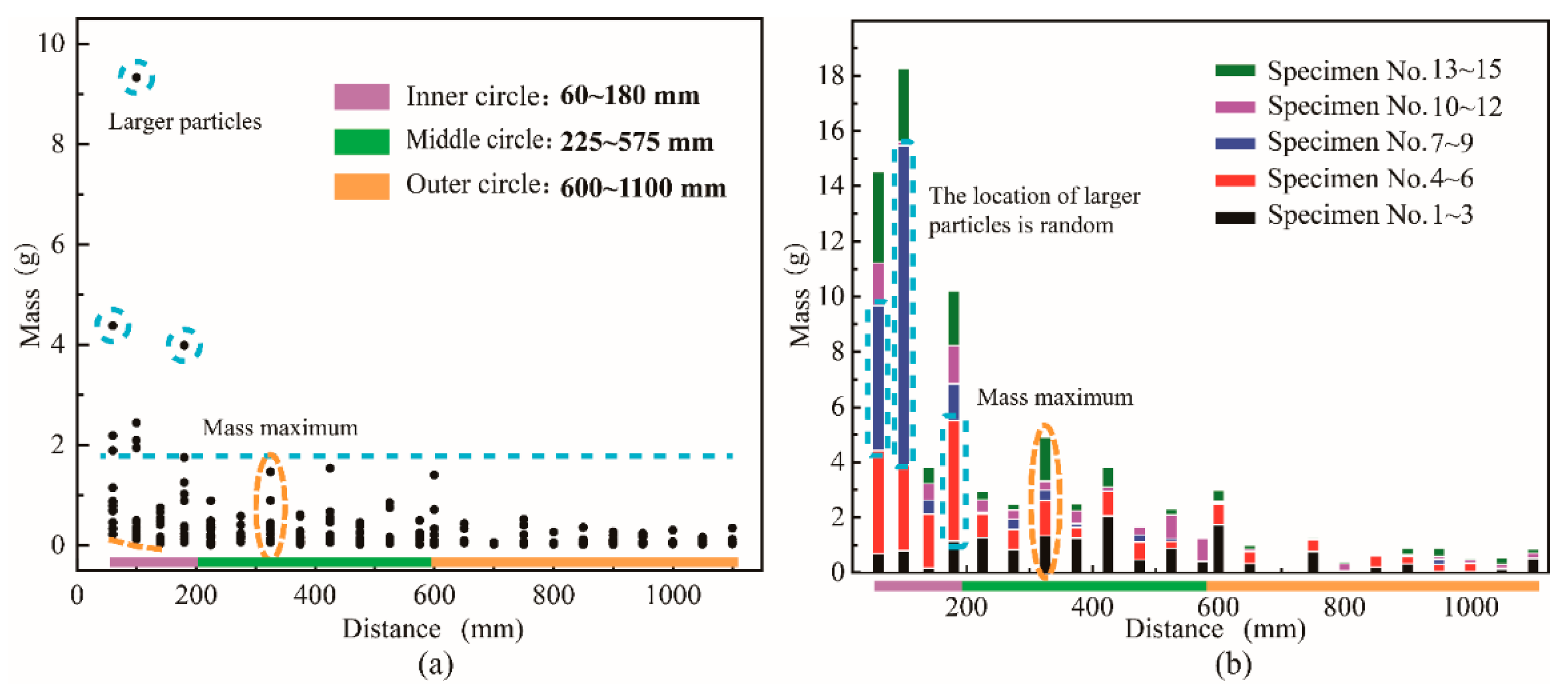
3.6. Spatial Distribution of Fragments
3.7. Location of Fragments
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Griffith, A.A. The Phenomena of Rupture and Flow in Solids. Philos. Trans. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1921, 221, 98–163. [Google Scholar] [CrossRef]
- Rice, J.R. Thermodynamics of the quasi-static growth of Griffith cracks. J. Mech. Phys. Solids 1978, 26, 61–78. [Google Scholar] [CrossRef]
- Irwin, G.R. Fracture Dynamics: Fracturing of Metals; American Society for Metals: Cleveland, OH, USA, 1948; pp. 147–166. [Google Scholar]
- Taddeucci, J.; Alatorre-Ibargueengoitia, M.A.; Cruz-Vazquez, O.; Del Bello, E.; Scarlato, P.; Ricci, T. In-flight dynamics of volcanic ballistic projectiles. Rev. Geophys. 2017, 55, 675–718. [Google Scholar] [CrossRef]
- Zhao, T.; Crosta, G.B.; Dattola, G.; Utili, S. Dynamic Fragmentation of Jointed Rock Blocks during Rockslide-Avalanches: Insights from Discrete Element Analyses. J. Geophys. Res. Solid Earth 2018, 123, 3250–3269. [Google Scholar] [CrossRef]
- Kim, E.; Garcia, A.; Changani, H. Fragmentation and energy absorption characteristics of Red, Berea and Buff sandstones based on different loading rates and water contents. Geomech. Eng. 2018, 14, 151–159. [Google Scholar] [CrossRef]
- Brannon, R.M.; Lee, M.Y.; Bronowski, D.R. Uniaxial and Triaxial Compression Tests of Silicon Carbide Ceramics under Quasi-Static Loading Condition; Sandia National Laboratories: Albuquerque, NM, USA, 2005; pp. 9–26. [Google Scholar]
- Mott, N.F. Fragmentation of shell cases. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1947, 189, 300–308. [Google Scholar] [CrossRef]
- Fondriest, M.; Doan, M.-L.; Aben, F.; Fusseis, F.; Mitchell, T.M.; Voorn, M.; Secco, M.; Di Toro, G. Static versus dynamic fracturing in shallow carbonate fault zones. Earth Planet. Sci. Lett. 2017, 461, 8–19. [Google Scholar] [CrossRef]
- Li, X.F.; Li, H.B.; Zhang, Q.B.; Jiang, J.L.; Zhao, J. Dynamic fragmentation of rock material: Characteristic size, fragment distribution and pulverization law. Eng. Fract. Mech. 2018, 199, 739–759. [Google Scholar] [CrossRef]
- Songlin, X.; Wen, W.; Hua, Z. Experimental study on dynamic unloading of the confining pressures for a marble under triaxial compression and simulation analyses of rock burst. J. Liaoning Tech. Univ. 2002, 21, 612–615. [Google Scholar] [CrossRef]
- Manchao, H.; Jinli, M.; Dejiang, L.; Chunguang, W. Experimental study on rockburst processes of granite specimen at great depth. Chin. J. Roc. Mech. Eng. 2007, 26, 865–876. [Google Scholar] [CrossRef]
- Guoshao, S.; Jianqing, J.; Xiating, F.; Chun, M.; Quan, J. Experimental study of ejection process in rockburst. Chin. J. Roc. Mech. Eng. 2016, 35, 1990–1999. [Google Scholar] [CrossRef]
- Hogan, J.D.; Spray, J.G.; Rogers, R.J.; Vincent, G.; Schneider, M. Dynamic fragmentation of natural ceramic tiles: Ejecta measurements and kinetic consequences. Int. J. Impact Eng. 2013, 58, 1–16. [Google Scholar] [CrossRef]
- Hogan, J.D.; Rogers, R.J.; Spray, J.G.; Vincent, G.; Schneider, M. Debris Field Kinetics during the Dynamic Fragmentation of Polyphase Natural Ceramic Blocks. Exp. Mech. 2014, 54, 211–228. [Google Scholar] [CrossRef]
- Gong, D.; Nadolski, S.; Sun, C.; Klein, B.; Kou, J. The effect of strain rate on particle breakage characteristics. Powder Technol. 2018, 339, 595–605. [Google Scholar] [CrossRef]
- Jiang, J.; Su, G.; Zhang, X.; Feng, X.-T. Effect of initial damage on remotely triggered rockburst in granite: An experimental study. Bull. Eng. Geol. Environ. 2020, 79, 3175–3194. [Google Scholar] [CrossRef]
- Hermalyn, B.; Schultz, P.H. Early-stage ejecta velocity distribution for vertical hypervelocity impacts into sand. Icarus 2010, 209, 866–870. [Google Scholar] [CrossRef]
- Fujiwara, A.; Tsukamoto, A. Experimental study on the velocity of fragments in collisional breakup. Icarus 1980, 44, 142–153. [Google Scholar] [CrossRef]
- Hogan, J.D.; Spray, J.G.; Rogers, R.J.; Boonsue, S.; Vincent, G.; Schneider, M. Micro-scale energy dissipation mechanisms during dynamic fracture in natural polyphase ceramic blocks. Int. J. Impact Eng. 2011, 38, 931–939. [Google Scholar] [CrossRef]
- Kimberley, J.; Ramesh, K.T.; Barnouin, O.S. Visualization of the failure of quartz under quasi-static and dynamic compression. J. Geophys. Res. Solid Earth 2010, 115. [Google Scholar] [CrossRef]
- Heping, X.; Yang, J.; Liyun, L.; Ruidong, P. Energy Mechanism of Deformation and Failure of Rock Masses. Chin. J. Rock Mech. Eng. 2008, 27, 1729–1739. [Google Scholar] [CrossRef]
- Zhou, Z.; Cai, X.; Li, X.; Cao, W.; Du, X. Dynamic Response and Energy Evolution of Sandstone Under Coupled Static-Dynamic Compression: Insights from Experimental Study into Deep Rock Engineering Applications. Rock Mech. Rock Eng. 2020, 53, 1305–1331. [Google Scholar] [CrossRef]
- Minh Phono, L. Infrared thermovision of damage processes in concrete and rock. Eng. Fract. Mech. 1990, 35, 291–301. [Google Scholar] [CrossRef]
- Heping, X.; Yang, J.; Liyun, L. Criteria for Strength and Structural Failure of Rocks Based on Energy Dissipation and Energy Release Principles. Chin. J. Rock Mech. Eng. 2005, 24, 3003–3010. [Google Scholar]
- Li, L.y.; Ju, Y.; Zhao, Z.w.; Wang, L.; Lu, J.; Ma, X. Energy analysis of rock structure under static and dyanmic loading conditions. J. China Coal Soc. 2009, 34, 737–740. [Google Scholar] [CrossRef]
- Rait, K.L.; Bowman, E.T.; Lambert, C. Dynamic fragmentation of rock clasts under normal compression in sturzstrom. Geotech. Lett. 2012, 2, 167–172. [Google Scholar] [CrossRef]
- Wang, P.; Arson, C. Energy distribution during the quasi-static confined comminution of granular materials. Acta Geotech. 2018, 13, 1075–1083. [Google Scholar] [CrossRef]
- Xiao, Y.; Yuan, Z.x.; Chu, J.; Liu, H.l.; Huang, J.y.; Luo, S.N.; Wang, S.; Lin, J. Particle breakage and energy dissipation of carbonate sands under quasi-static and dynamic compression. Acta Geotech. 2019, 14, 1741–1755. [Google Scholar] [CrossRef]
- Zhang, Q.; Zheng, Y.; Zhou, F.; Yu, T. Fragmentations of Alumina (Al2O3) and Silicon Carbide (SiC) under quasi-static compression. Int. J. Mech. Sci. 2020, 167, 105119. [Google Scholar] [CrossRef]
- Martin, C.D.; Chandler, N.A. The progressive fracture of Lac du Bonnet granite. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1994, 31, 643–659. [Google Scholar] [CrossRef]
- Huang, D.; Huang, R.Q.; Zhang, Y.X. Experimental investigations on static loading rate effects on mechanical properties and energy mechanism of coarse crystal grain marble under uniaxial compression. Chin. J. Rock Mech. Eng. 2012, 31, 245–255. [Google Scholar] [CrossRef]
- He, M.; Yang, G.; Miao, J.; Jia, X.; Jiang, T. Classification and research methods of rockburst experimental fragments. Chin. J. Rock Mech. Eng. 2009, 28, 1521–1529. [Google Scholar]
- Bowman, E.T.; Take, W.A.; Rait, K.L.; Hann, C. Physical models of rock avalanche spreading behaviour with dynamic fragmentation. Can. Geotech. J. 2012, 49, 460–476. [Google Scholar] [CrossRef]
- Wu, S.Z.; Chau, K.T.; Yu, T.X. Crushing and fragmentation of brittle spheres under double impact test. Powder Technol. 2004, 143–144, 41–55. [Google Scholar] [CrossRef]
- Sanchidrian, J.A.; Segarra, P.; Lopez, L.M. Energy components in rock blasting. Int. J. Rock Mech. Min. 2007, 44, 130–147. [Google Scholar] [CrossRef]
- Akdag, S.; Karakus, M.; Taheri, A.; Nguyen, G.; Manchao, H. Effects of Thermal Damage on Strain Burst Mechanism for Brittle Rocks Under True-Triaxial Loading Conditions. Rock Mech. Rock Eng. 2018, 51, 1657–1682. [Google Scholar] [CrossRef]
- Sun, Y.; Qi, C.; Zhu, H.; Guo, Y.; Wang, Y. Energy Analysis on Rock Dynamic Fracture Process. Chin. J. Undergr. Sp. Eng. 2020, 16, 43–49. [Google Scholar]












| SiO2% | Al2O3% | Na2O% | K2O% | CaO% | Fe2O3% | MgO% | TiO2% |
|---|---|---|---|---|---|---|---|
| 67.75 | 15.66 | 4.81 | 3.84 | 2.73 | 2.49 | 1.41 | 0.318 |
| Particle Type | Size/mm | Generation Time | Spatial Location | Movement Characteristics |
|---|---|---|---|---|
| +13 | Early stage of macro destruction | Front middle of the detrital cluster | Surface peeling, ejection, Roll along the length | |
| 6–13 | Early and mid-term macro destruction | Middle of detrital cluster | Surface peeling, rotating | |
| 3–6 | Early stage of macro destruction | Forward of the detrital cluster [34] | Ejection, extremely fast | |
| −3 | Mid- to late period of macro destruction | The tail of the detrital cluster | Friction occurs, slower |
| Serial Number | The Velocity of Particles m/s | |||
|---|---|---|---|---|
| α Particle | β Particle | γ Particle | δ Particle | |
| 1 | 14.75 | 8.11 | 13.28 | 2.23 |
| 2 | 4.86 | 8.25 | 15.08 | 1.94 |
| 3 | 8.58 | 6.55 | 14.97 | 2.39 |
| 4 | 4.33 | 8.44 | 12.15 | 2.42 |
| 5 | 3.78 | 8.59 | 13.09 | 1.64 |
| 6 | 6.77 | 6.58 | 7.63 | 1.74 |
| 7 | 6.13 | 7.59 | 7.71 | 1.83 |
| 8 | 6.11 | 7.91 | 6.63 | 1.92 |
| 9 | 7.27 | 6.83 | 6.40 | 2.56 |
| 10 | 6.42 | 7.09 | 7.90 | 1.70 |
| 6.900 | 7.594 | 10.483 | 2.036 | |
| STD. | 2.943 | 0.740 | 3.358 | 0.317 |
| Specimen Number | The Average Velocity of Particles m/s | |||
|---|---|---|---|---|
| α Particle | β Particle | γ Particle | δ Particle | |
| 1 | 3.052 | 5.827 | 9.913 | 1.403 |
| 2 | 4.945 | 5.151 | 8.009 | 2.826 |
| 3 | 2.480 | 2.825 | 4.972 | 1.278 |
| 4 | 2.111 | 2.104 | 8.797 | 1.476 |
| 5 | 4.194 | 4.052 | 7.821 | 3.583 |
| 6 | 2.950 | 4.864 | 7.263 | 2.074 |
| 7 | 4.238 | 4.856 | 8.206 | 2.634 |
| 8 | 2.015 | 3.604 | 5.530 | 1.313 |
| 9 | 3.154 | 3.160 | 6.511 | 1.718 |
| 10 | 6.017 | 6.357 | 18.094 | 2.830 |
| 11 | 6.900 | 7.594 | 10.483 | 2.036 |
| 12 | 5.163 | 6.834 | 9.829 | 2.162 |
| 13 | 6.519 | 5.434 | 10.068 | 2.489 |
| 14 | 2.404 | 4.109 | 7.228 | 1.050 |
| 15 | 2.254 | 4.909 | 8.749 | 1.822 |
| 3.893 | 4.779 | 8.765 | 2.046 | |
| STD. | 1.615 | 1.467 | 2.949 | 0.691 |
| Particle Type | I Area | II Area | III Area | IV Area | ||||
|---|---|---|---|---|---|---|---|---|
| /mJ | PCT.% | PCT.% | PCT.% | PCT.% | ||||
| 927.51 | 73.99 | 993.57 | 64.76 | 818.92 | 62.35 | 945.77 | 87.28 | |
| 167.85 | 13.39 | 249.76 | 16.28 | 235.87 | 17.96 | 38.06 | 3.51 | |
| 150.28 | 11.99 | 276.82 | 18.04 | 244.18 | 18.59 | 92.59 | 8.54 | |
| 7.94 | 0.63 | 14.13 | 0.92 | 14.49 | 1.10 | 7.15 | 0.66 | |
| Total | 1253.58 | 100 | 1534.29 | 100 | 1313.45 | 100 | 1083.57 | 100 |
| Specimen Number | |||||
|---|---|---|---|---|---|
| 1 | 56.21 | 30.87 | 1435.36 | 5.21 | 2.55 |
| 2 | 40.53 | 23.09 | 2414.18 | 13.36 | 5.96 |
| 3 | 25.39 | 12.53 | 626.53 | 5.85 | 2.47 |
| 4 | 33.78 | 15.88 | 1073.90 | 6.21 | 3.18 |
| 5 | 27.65 | 12.36 | 2281.99 | 18.50 | 8.25 |
| 6 | 44.28 | 25.69 | 1441.39 | 6.11 | 3.25 |
| 7 | 23.72 | 8.38 | 3481.25 | 30.44 | 14.68 |
| 8 | 25.98 | 14.05 | 823.46 | 5.98 | 3.17 |
| 9 | 26.09 | 10.62 | 1793.53 | 16.06 | 6.88 |
| 10 | 41.20 | 20.98 | 4369.55 | 25.84 | 10.61 |
| 11 | 47.16 | 24.43 | 5184.90 | 21.22 | 10.99 |
| 12 | 21.01 | 8.56 | 2542.20 | 30.55 | 12.10 |
| 13 | 27.90 | 11.87 | 7289.66 | 54.95 | 26.13 |
| 14 | 30.01 | 13.75 | 1557.10 | 9.01 | 5.19 |
| 15 | 41.37 | 20.81 | 1383.43 | 7.87 | 3.34 |
| Average | 34.15 | 16.25 | 2604.32 | 16.03% | 7.92% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Q.; Pan, Y.; Zhou, Q.; Zhang, C.; Bi, Y. Kinetic Energy Calculation in Granite Particles Comminution Considering Movement Characteristics and Spatial Distribution. Minerals 2021, 11, 217. https://doi.org/10.3390/min11020217
Guo Q, Pan Y, Zhou Q, Zhang C, Bi Y. Kinetic Energy Calculation in Granite Particles Comminution Considering Movement Characteristics and Spatial Distribution. Minerals. 2021; 11(2):217. https://doi.org/10.3390/min11020217
Chicago/Turabian StyleGuo, Qing, Yongtai Pan, Qiang Zhou, Chuan Zhang, and Yankun Bi. 2021. "Kinetic Energy Calculation in Granite Particles Comminution Considering Movement Characteristics and Spatial Distribution" Minerals 11, no. 2: 217. https://doi.org/10.3390/min11020217
APA StyleGuo, Q., Pan, Y., Zhou, Q., Zhang, C., & Bi, Y. (2021). Kinetic Energy Calculation in Granite Particles Comminution Considering Movement Characteristics and Spatial Distribution. Minerals, 11(2), 217. https://doi.org/10.3390/min11020217






