Three-Dimensional Anisotropic Inversions for Time-Domain Airborne Electromagnetic Data
Abstract
:1. Introduction
2. Basic Theory
2.1. Governing Equations
2.2. Regularized Inversion
2.3. Calculation of Sensitivity Matrix for 3-Axial Anisotropic Media
3. Numerical Experiments
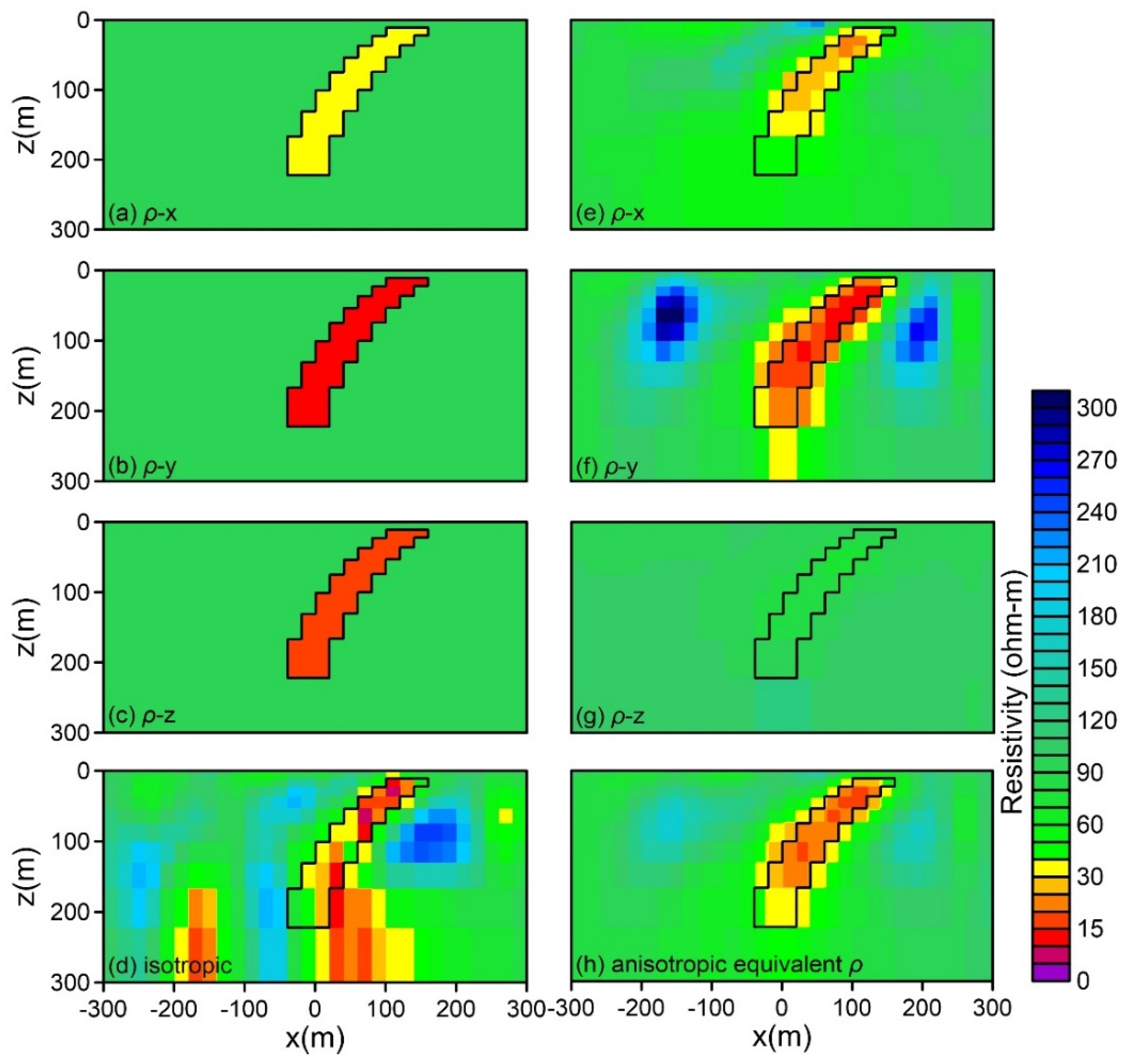
3.1. Synthetic Data Inversion for an Anisotropic Ore-Body
3.2. Synthetic Data Inversion for Anisotropic Host Rock
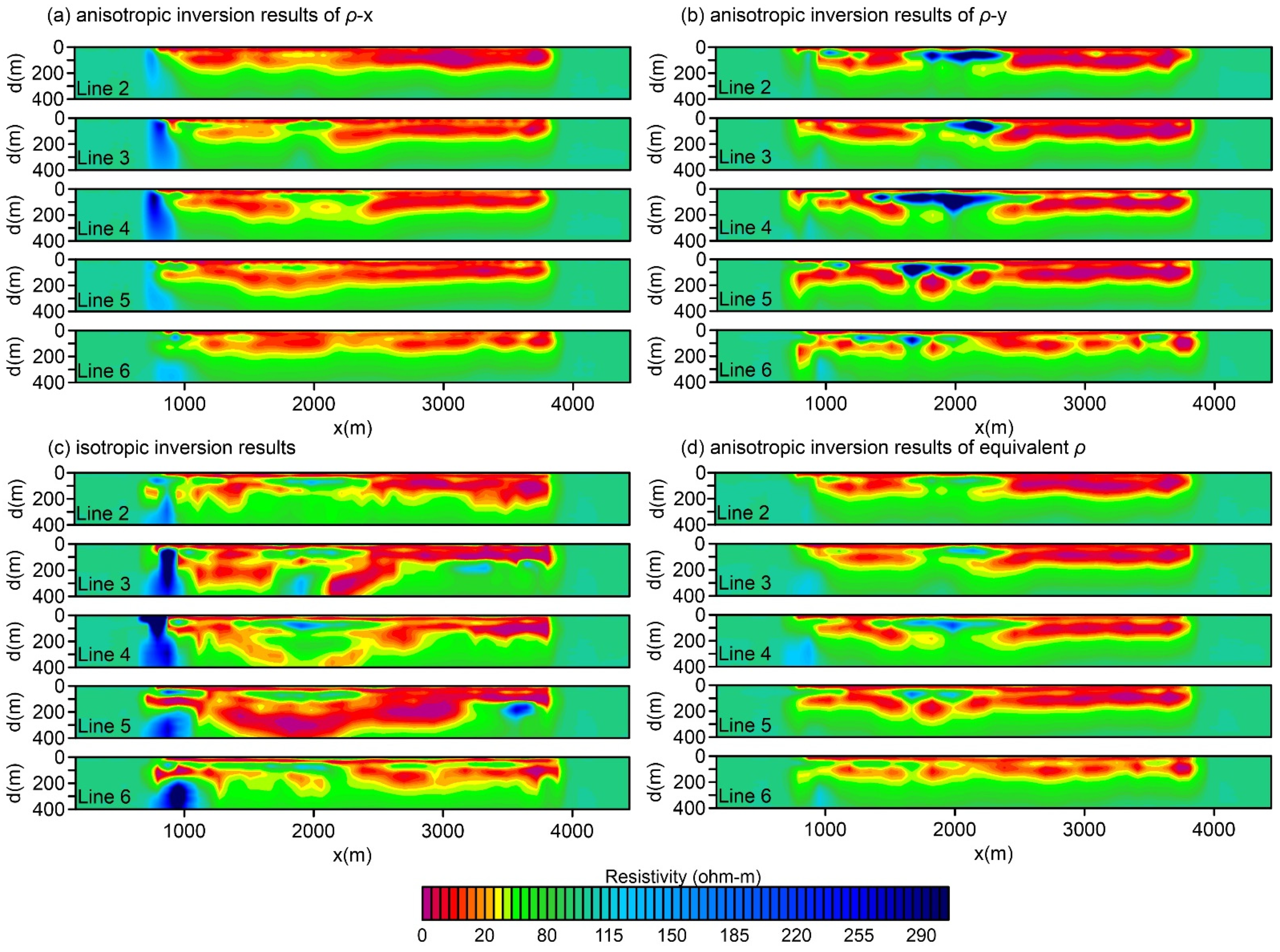
4. Field Data Example
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Sub-Model Based on the Moving Footprint

Appendix A.2. Grid Design for Our Synthetic Models

References
- Siemon, B.; Christiansen, A.V.; Auken, E. A review of helicopter-borne electromagnetic methods for groundwater exploration. Near Surf. Geophys. 2009, 7, 629–646. [Google Scholar] [CrossRef] [Green Version]
- Kaminski, V.; Legault, J.M.; Kumar, H. The Drybones Kimberlite: A case study of VTEM and ZTEM airborne EM results. Aseg Ext. Abstr. 2010, 2010, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Raiche, A. Inverting AEM data using a damped eigenparameter method. Explor. Geophys. 1998, 29, 128–132. [Google Scholar] [CrossRef]
- Huang, H.; Fraser, D.C. Dielectric permittivity and resistivity mapping using high frequency, helicopter-borne EM data. Geophysics 2002, 67, 727–738. [Google Scholar] [CrossRef] [Green Version]
- Auken, E.; Chistiansen, A.V.; Jacobsen, B.H.; Foged, N.; Sørensen, K.I. Piece-wise 1D laterally constrained inversion of resistivity data. Geophys. Prospect. 2005, 53, 497–506. [Google Scholar] [CrossRef]
- Sattel, D. Inverting airborne electromagnetic (AEM) data using Zohdy’s method. Geophysics 2005, 70, G77–G85. [Google Scholar] [CrossRef]
- Brodie, R.; Sambridge, M. A holistic approach to inversion of frequency-domain airborne EM data. Geophysics 2006, 71, G301–G312. [Google Scholar] [CrossRef]
- Viezzoli, A.; Auken, E.; Munday, T. Spatially constrained inversion for quasi 3D modeling of airborne electromagnetic data—An application for environmental assessment in the Lower Murray Region of South Australia. Explor. Geophys. 2009, 40, 173–183. [Google Scholar] [CrossRef] [Green Version]
- Christensen, N.B.; Fitzpatrick, A.; Munday, T. Fast approximate inversion of frequency-domain electromagnetic data. Near Surf. Geophys. 2010, 8, 1–15. [Google Scholar] [CrossRef]
- Sasaki, Y. Full 3-D inversion of electromagnetic data on PC. J. Appl. Geophys. 2001, 46, 45–54. [Google Scholar] [CrossRef]
- Cox, L.H.; Zhdanov, M.S. Advanced computational methods for rapid and rigorous 3D inversion of airborne electromagnetic data. Commun. Comput. Phys. 2008, 3, 160–179. [Google Scholar]
- Cox, L.H.; Wilson, G.A.; Zhdanov, M.S. 3D inversion of airborne electromagnetic data using a moving footprint. Explor. Geophys. 2010, 41, 250–259. [Google Scholar] [CrossRef]
- Liu, Y.; Yin, C. 3D inversion for multipulse airborne transient electromagnetic data. Geophysics 2016, 81, E401–E408. [Google Scholar] [CrossRef]
- Oldenburg, D.W.; Haber, E.; Shekhtman, R. Three dimensional inversion of multi-source time domain electromagnetic data. Geophysics 2013, 78, E47–E57. [Google Scholar] [CrossRef] [Green Version]
- Yang, D.; Oldenburg, D.W.; Haber, E. 3-D inversion of airborne electromagnetic data parallelized and accelerated by local mesh and adaptive soundings. Geophys. J. Int. 2014, 196, 1492–1507. [Google Scholar] [CrossRef] [Green Version]
- Régis, C.; da Cruz Luz, E.; Costa, M.D. Inversion of anisotropic MT data using approximate equality constrains. In Proceedings of the 2010 SEG Annual Meeting, Denver, CO, USA, 17–22 October 2010. [Google Scholar]
- Häuserer, M.; Junge, A. Electrical mantle anisotropy and crustal conductor: A 3-D conductivity model of the Rwenzori Region in western Uganda. Geophys. J. Int. 2011, 185, 1235–1242. [Google Scholar] [CrossRef] [Green Version]
- Miensopusτ, M.P.; Jones, A.G. Artefacts of isotropic inversion applied to magnetotelluric data from an anisotropic Earth. Geophys. J. Int. 2011, 187, 677–689. [Google Scholar] [CrossRef]
- Jones, A.G. Distortion decomposition of the magnetotelluric impedance tensors from a one-dimensional anisotropic Earth. Geophys. J. Int. 2012, 189, 268–284. [Google Scholar] [CrossRef]
- Guo, Z.Q.; Wei, W.B.; Ye, G.F.; Jin, S.; Jing, J.E. Canonical decomposition of magnetotelluric responses: Experiment on 1D anisotropic structures. J. Appl. Geophys. 2015, 119, 79–88. [Google Scholar] [CrossRef]
- Newman, G.A.; Commer, M.; Carazzone, J.J. Imaging CSEM data in the presence of electrical anisotropy. Geophysics 2010, 75, F51–F61. [Google Scholar] [CrossRef]
- Tseng, H.-W.; Stalnaker, J.; MacGregor, L.M.; Ackermann, R.V. Multi-dimensional analyses of the SEAM controlled source electromagnetic data—The story of a blind test of interpretation workflows. Geophys. Prospect. 2015, 63, 1383–1402. [Google Scholar] [CrossRef]
- Wiik, T.; Nordskag, J.I.; Dischler, E.Ø.; Nguyen, A.K. Inversion of inline and broadside marine controlled-source electromagnetic data with constraints derived from seismic data. Geophys. Prospect. 2015, 63, 1371–1382. [Google Scholar] [CrossRef]
- Hoversten, G.M.; Myer, D.; Key, K.; Alumbaugh, D.; Hermann, O.; Hobbet, R. Field test of sub-basalt hydrocarbon exploration with marine controlled source electromagnetic and magnetotelluric data. Geophys. Prospect. 2015, 63, 1284–1310. [Google Scholar] [CrossRef]
- Shen, J.S. Modeling of 3-D electromagnetic responses to the anisotropic medium by the edge finite element method. Well Logging Technol. 2004, 28, 11–15. [Google Scholar]
- Wang, H.; Tao, H.; Yao, J.; Chen, G. Fast multiparameter reconstruction of multicomponent induction well-logging datum in a deviated well in a horizontally stratified anisotropic formation. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1525–1534. [Google Scholar] [CrossRef]
- Yang, S.W.; Wang, H.N.; Chen, G.B.; Yao, D.H. The 3-D finite difference time domain (FDTD) algorithm of response of multicomponent electromagnetic well logging tool in a deviated and layered anisotropic formation. Chin. J. Geophys. 2009, 52, 833–841. (In Chinese) [Google Scholar] [CrossRef]
- Beer, R.; Zhang, P.; Alumbaugh, D.; Nalonnil, A. Anisotropy modeling and inversions of DeepLook-EM data from Brazil. In Proceedings of the 2010 SEG Annual Meeting, Denver, CO, USA, 17–22 October 2010. [Google Scholar]
- Zhang, G.Y.; Xiao, J.Q.; Hong, D.C.; Yang, S.D. A fast inversion method of 3D induction logging responses in layered anisotropic formation. Well Logging Technol. 2013, 37, 487–491. [Google Scholar]
- Liu, Y.; Yogeshwar, P.; Hu, X.; Peng, R.; Tezkan, B.; Morbe, W.; Li, J. Effects of electrical anisotropy on long-offset transient electromagnetic data. Geophys. J. Int. 2020, 222, 1074–1089. [Google Scholar] [CrossRef]
- Yin, C.; Fraser, D.C. The effect of the electrical anisotropy on the response of helicopter-borne frequency-domain electromagnetic systems. Geophys. Prospect. 2004, 52, 399–416. [Google Scholar] [CrossRef]
- Avdeev, D.B.; Newman, G.A.; Kuvshinov, A.V.; Pankratov, O.V. 3D frequency-domain modeling of airborne electromagnetic responses. Explor. Geophys. 1998, 29, 11–119. [Google Scholar]
- Liu, Y.; Yin, C. 3D anisotropic modeling for airborne EM systems using finite-difference method. J. Appl. Geophys. 2014, 109, 186–194. [Google Scholar] [CrossRef]
- Newman, G.A.; Alumbaugh, D.L. 3D induction logging problems. Part I. An integral equation solution and model comparisons. Geophysics 2002, 67, 484–491. [Google Scholar] [CrossRef]
- Yin, C.; Huang, W.; Ben, F. The full-time electromagnetic modeling for time-domain airborne electromagnetic systems. Chin. J. Geophys. 2013, 56, 3153–3162. (In Chinese) [Google Scholar]
- Haber, E. Computational Methods in Geophysical Electromagnetics; SIAM: Philadelphia, PA, USA, 2014. [Google Scholar]
- Yin, C. Geoelectrical inversion for a one-dimensional anisotropic model and inherent non-uniqueness. Geophys. J. Int. 2000, 1, 11–23. [Google Scholar] [CrossRef] [Green Version]
- Ley-Cooper, A.Y.; Viezzoli, A.; Guillemoteau, J.; Vignoli, G.; Macnae, J.; Cox, L.; Munday, T. Airborne electromagnetic modelling options and their consequences in target definition. Explor. Geophys. 2014, 46, 74–84. [Google Scholar] [CrossRef]













Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, Y.; Yin, C.; Liu, Y.; Ren, X.; Zhang, B.; Xiong, B. Three-Dimensional Anisotropic Inversions for Time-Domain Airborne Electromagnetic Data. Minerals 2021, 11, 218. https://doi.org/10.3390/min11020218
Su Y, Yin C, Liu Y, Ren X, Zhang B, Xiong B. Three-Dimensional Anisotropic Inversions for Time-Domain Airborne Electromagnetic Data. Minerals. 2021; 11(2):218. https://doi.org/10.3390/min11020218
Chicago/Turabian StyleSu, Yang, Changchun Yin, Yunhe Liu, Xiuyan Ren, Bo Zhang, and Bin Xiong. 2021. "Three-Dimensional Anisotropic Inversions for Time-Domain Airborne Electromagnetic Data" Minerals 11, no. 2: 218. https://doi.org/10.3390/min11020218
APA StyleSu, Y., Yin, C., Liu, Y., Ren, X., Zhang, B., & Xiong, B. (2021). Three-Dimensional Anisotropic Inversions for Time-Domain Airborne Electromagnetic Data. Minerals, 11(2), 218. https://doi.org/10.3390/min11020218






