Monitoring of Flotation Systems by Use of Multivariate Froth Image Analysis
Abstract
1. Introduction
2. Analytical Methodology
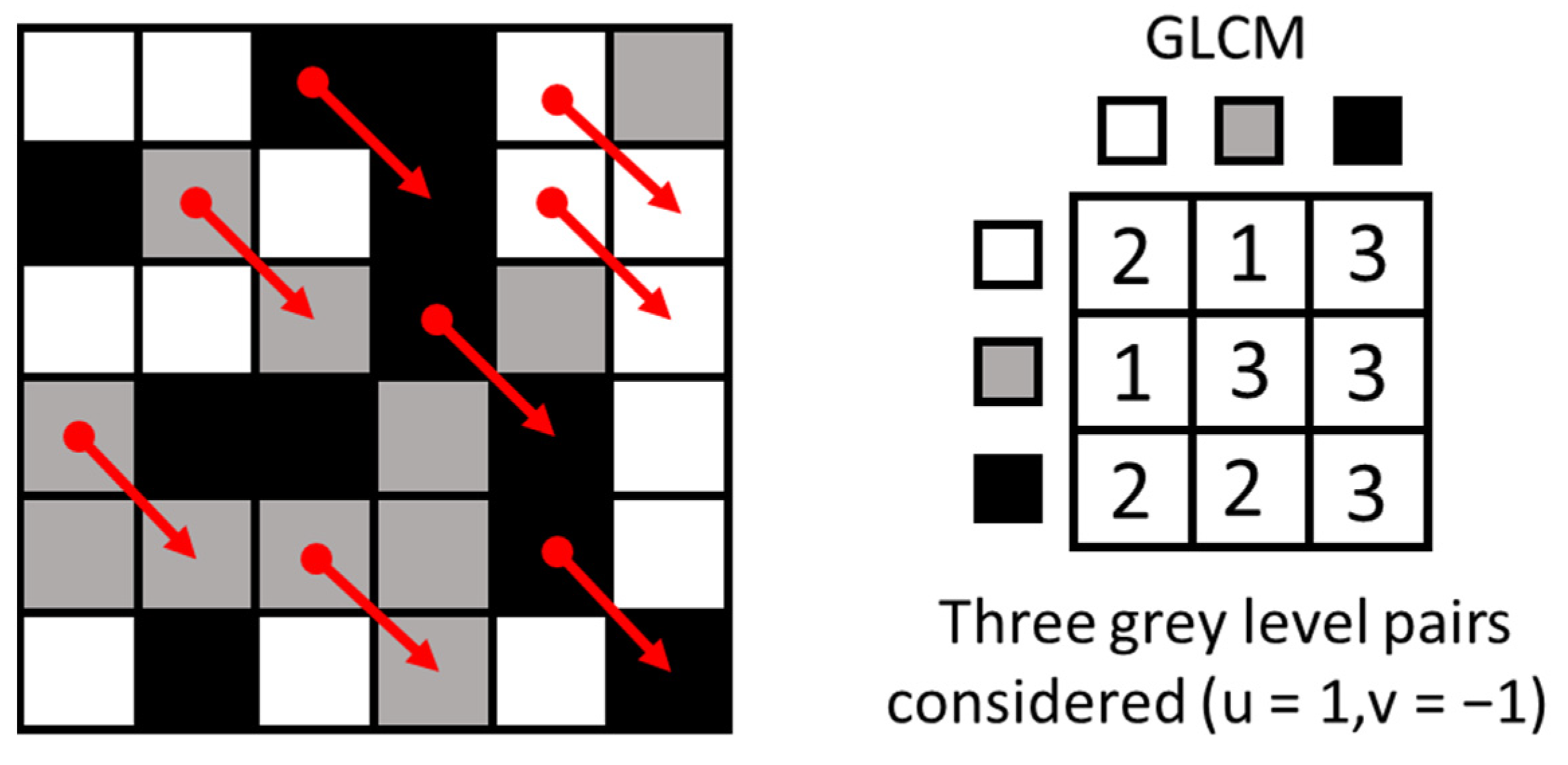
2.1. Feature Extraction with Grey Level Co-Occurrence Matrices
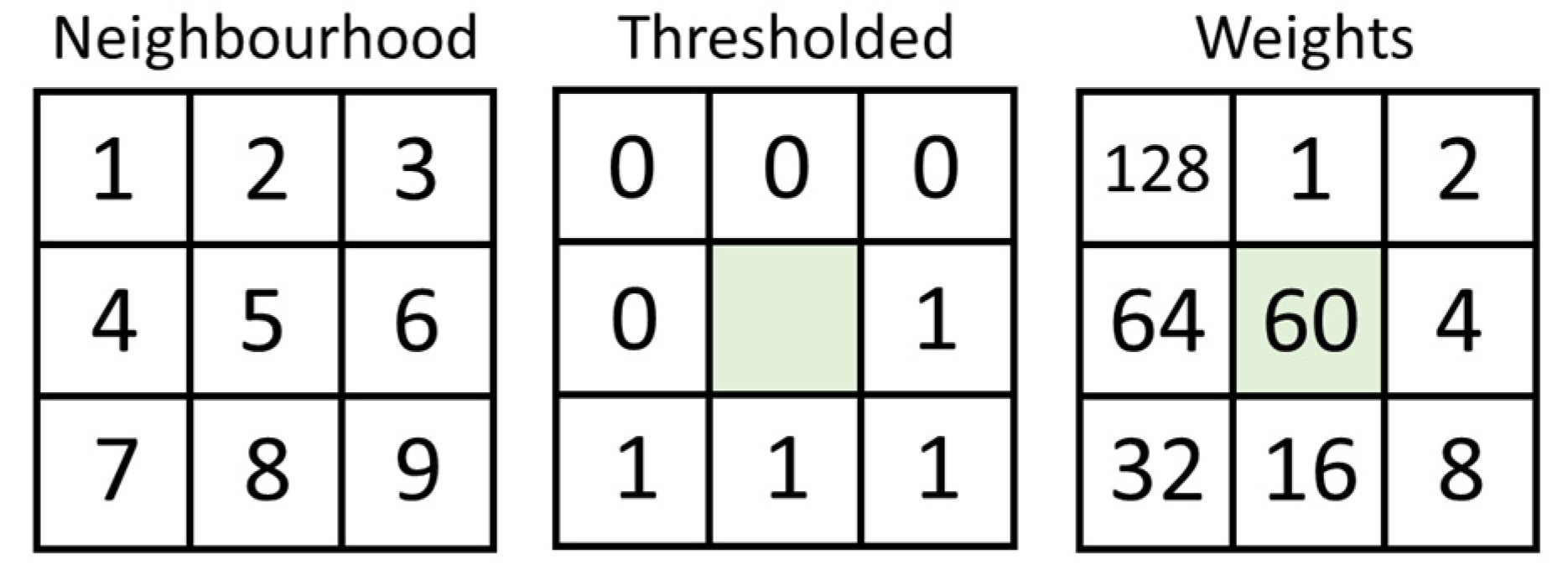
2.2. Feature Extraction with Local Binary Patterns
2.3. Construction of Principal Component Models
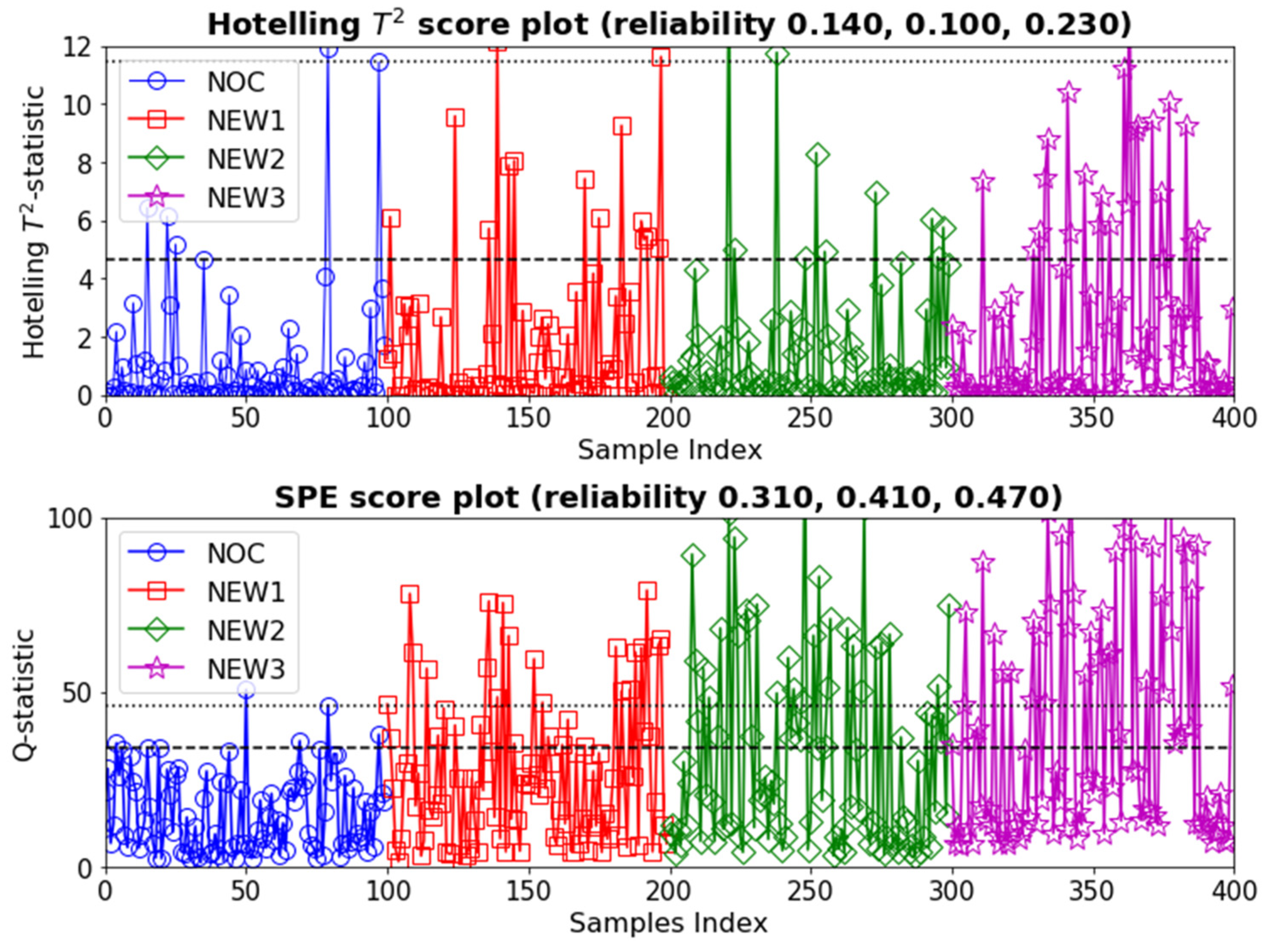
3. Case Study 1: Monitoring of PGM Froths
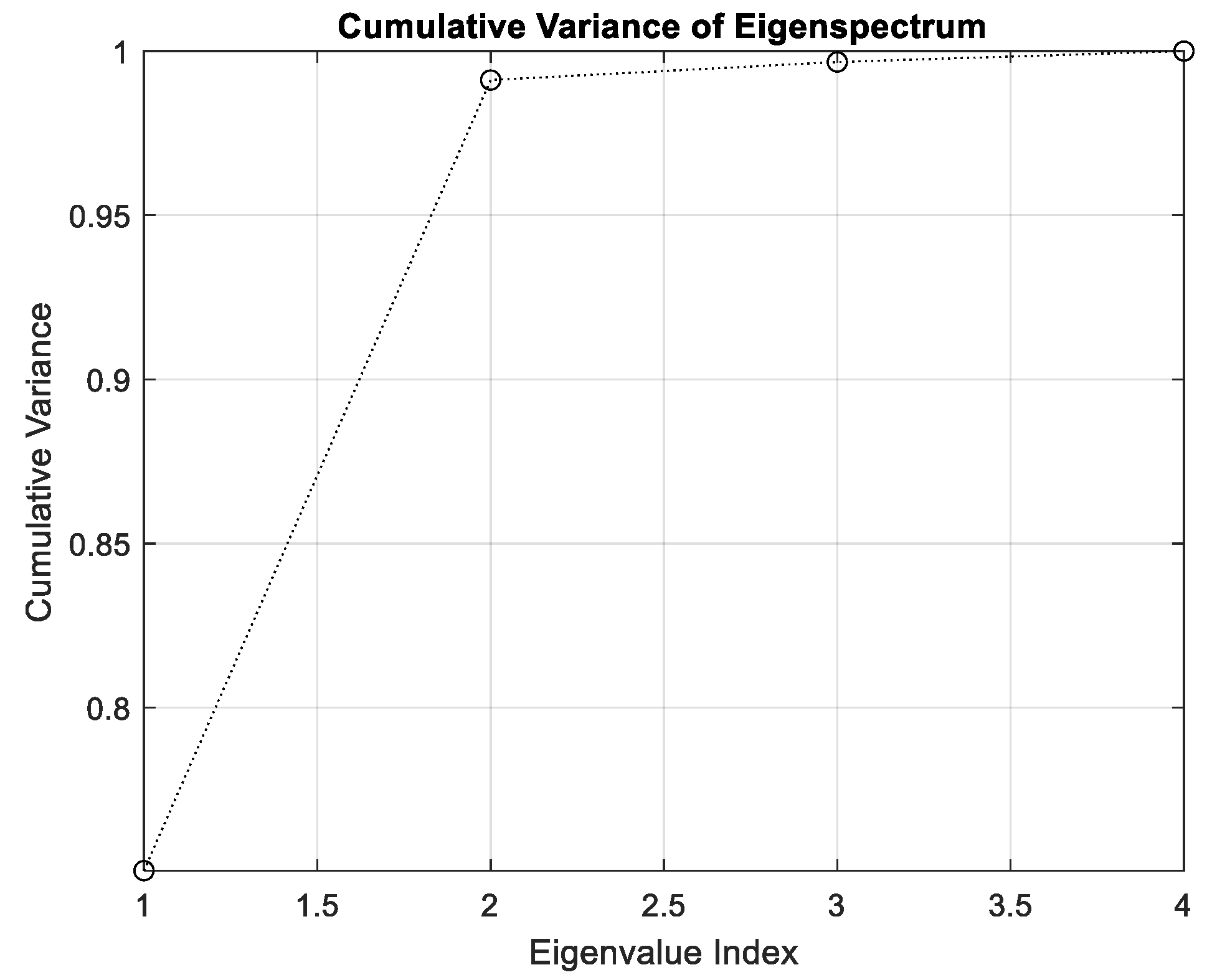
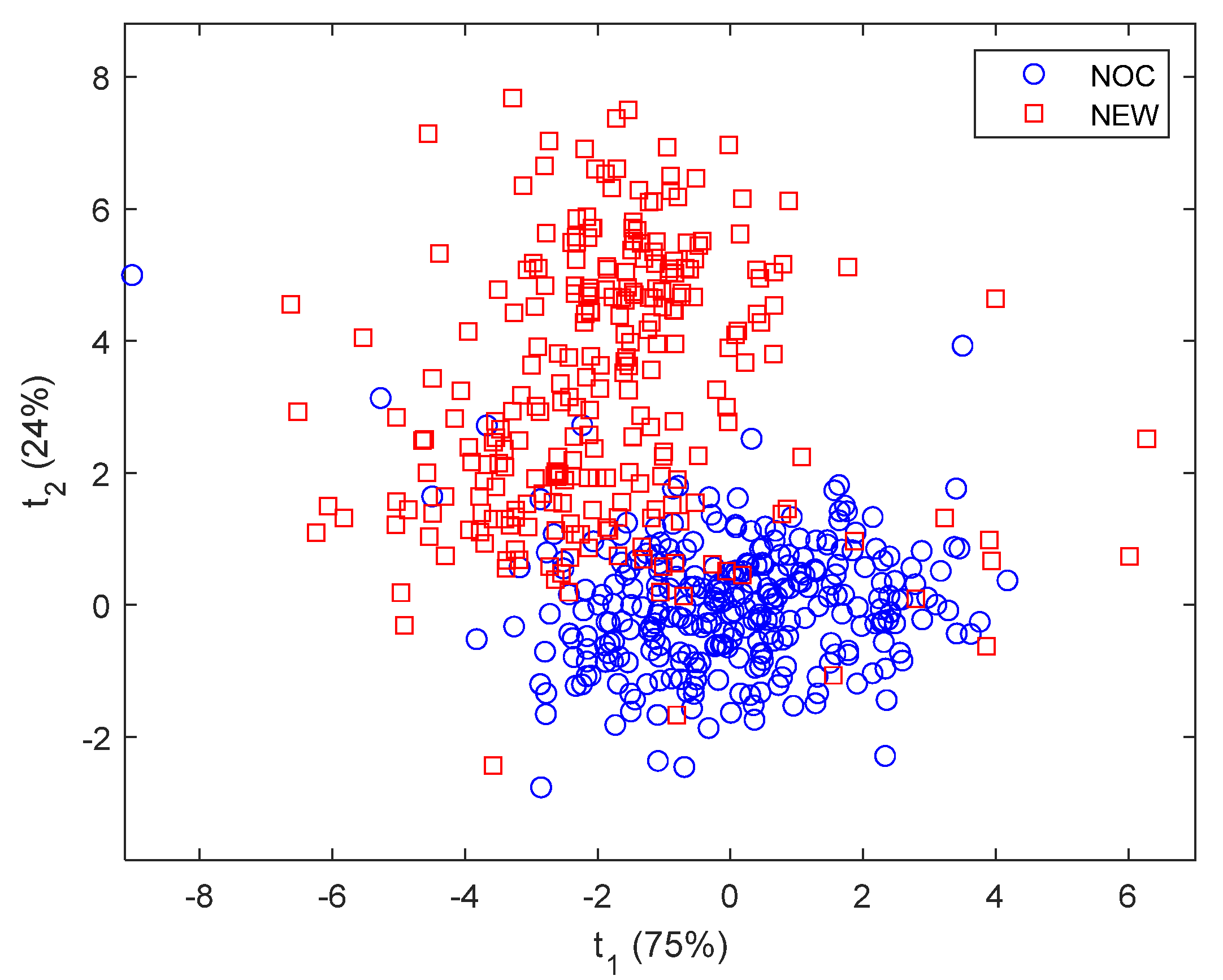
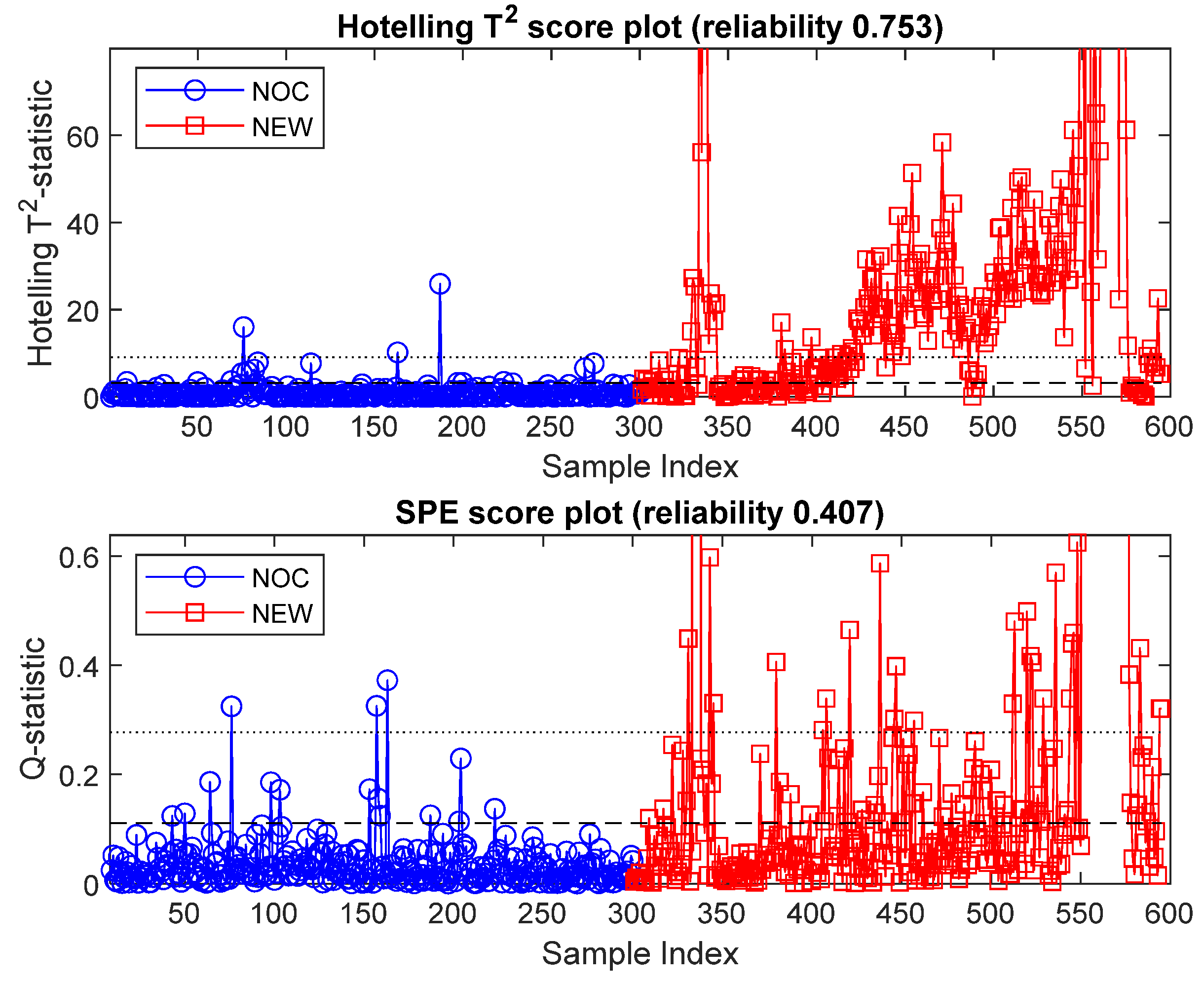
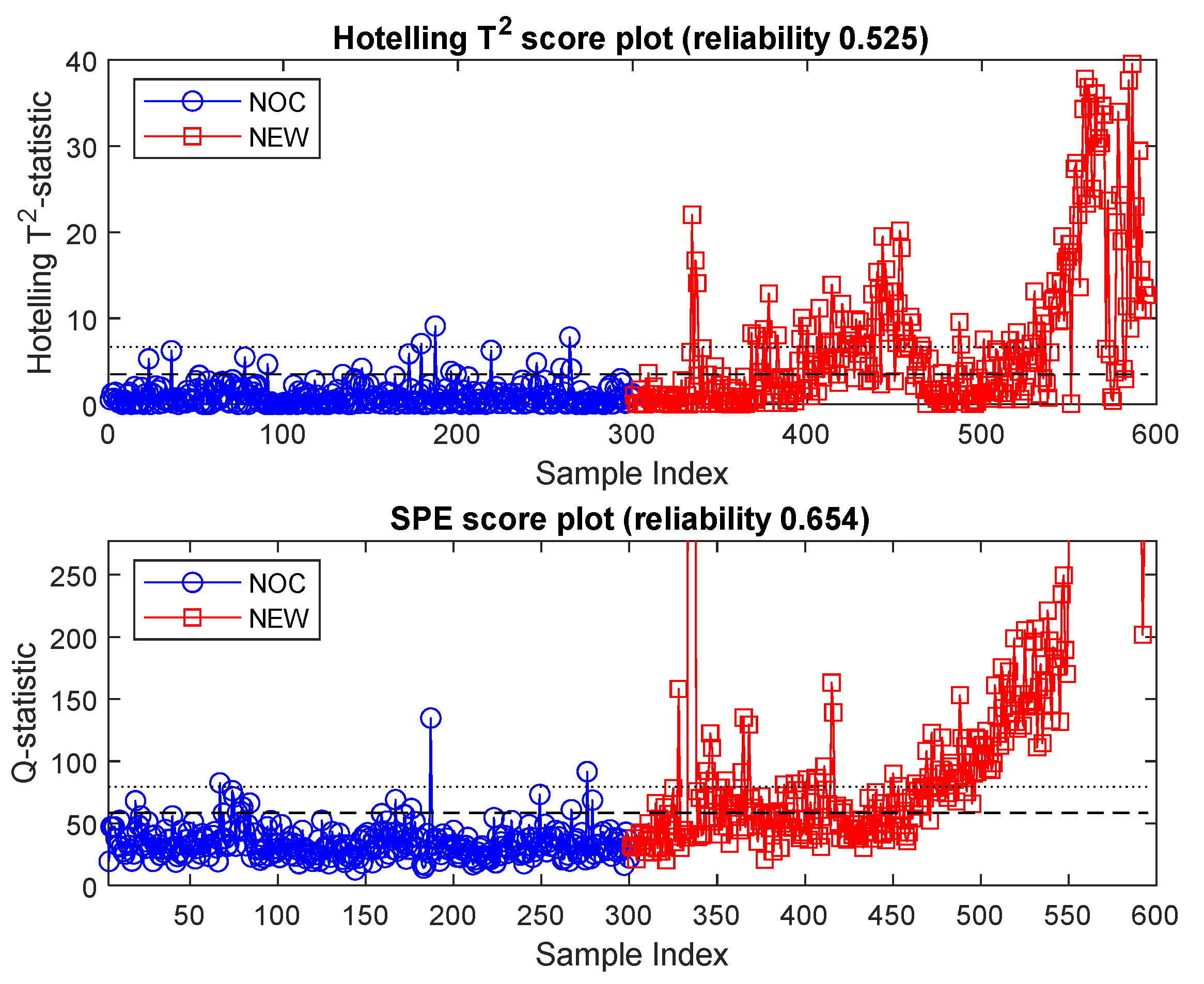
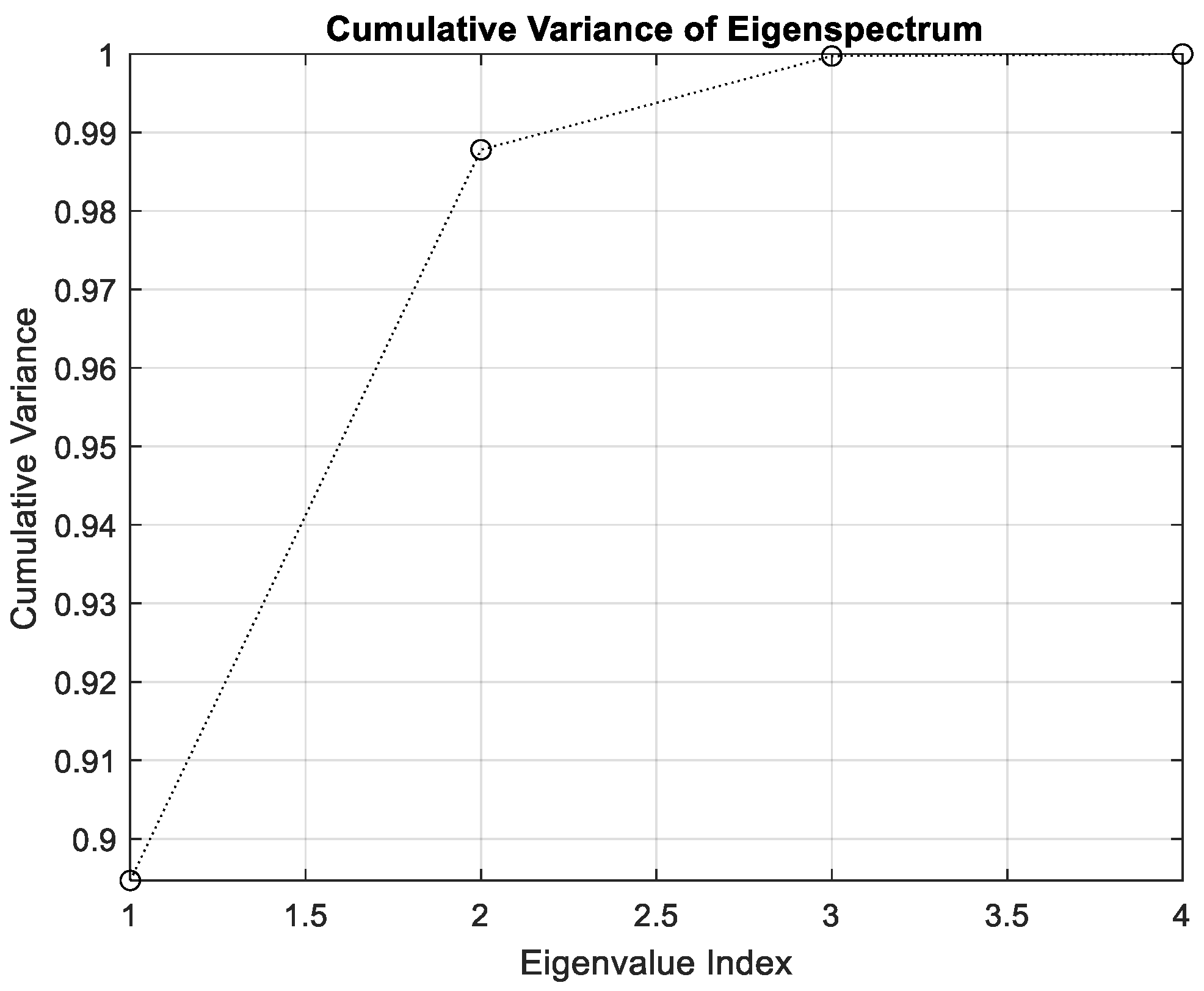
3.1. Monitoring Based on GLCM Features
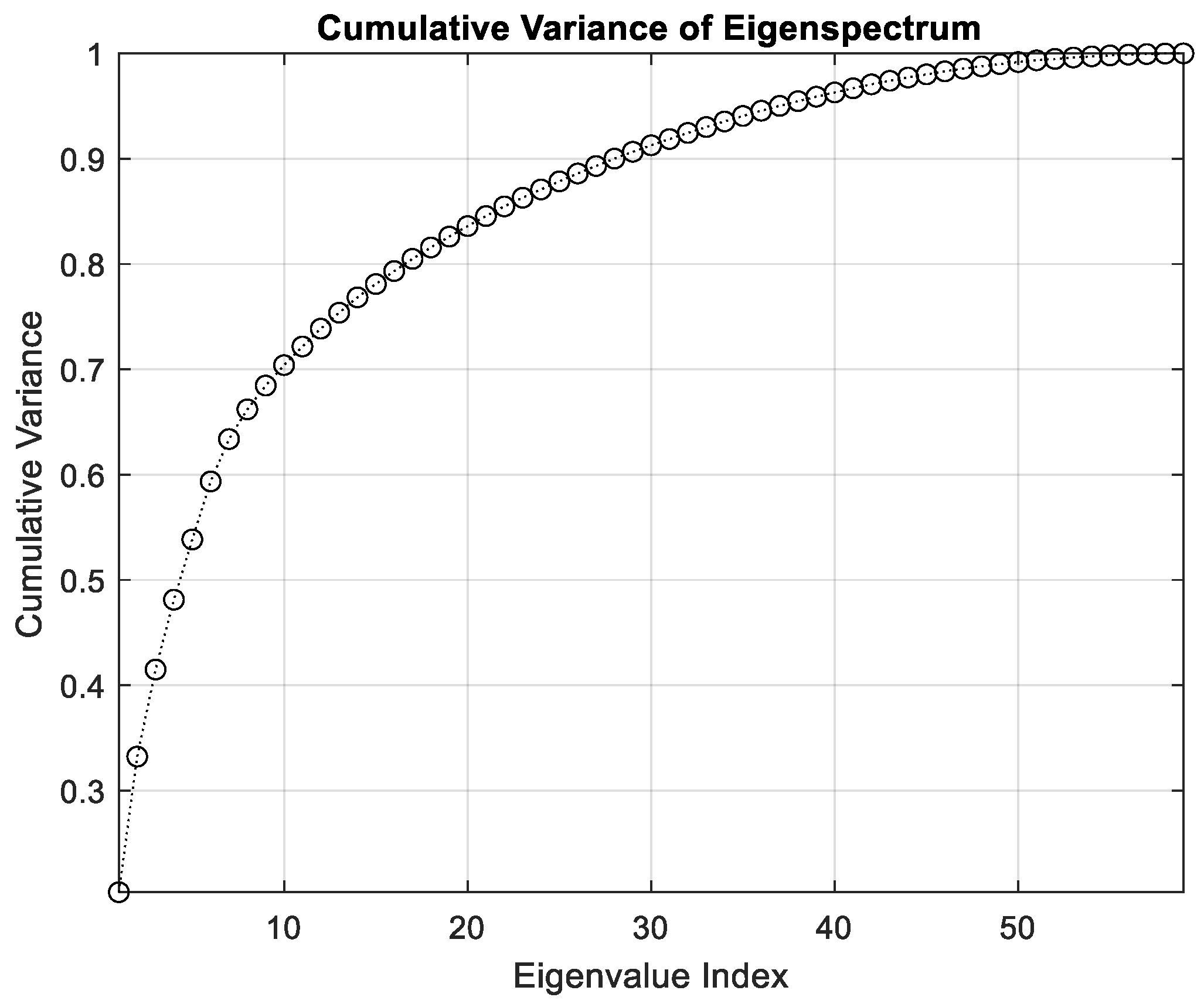
3.2. Monitoring Based on LBP Features
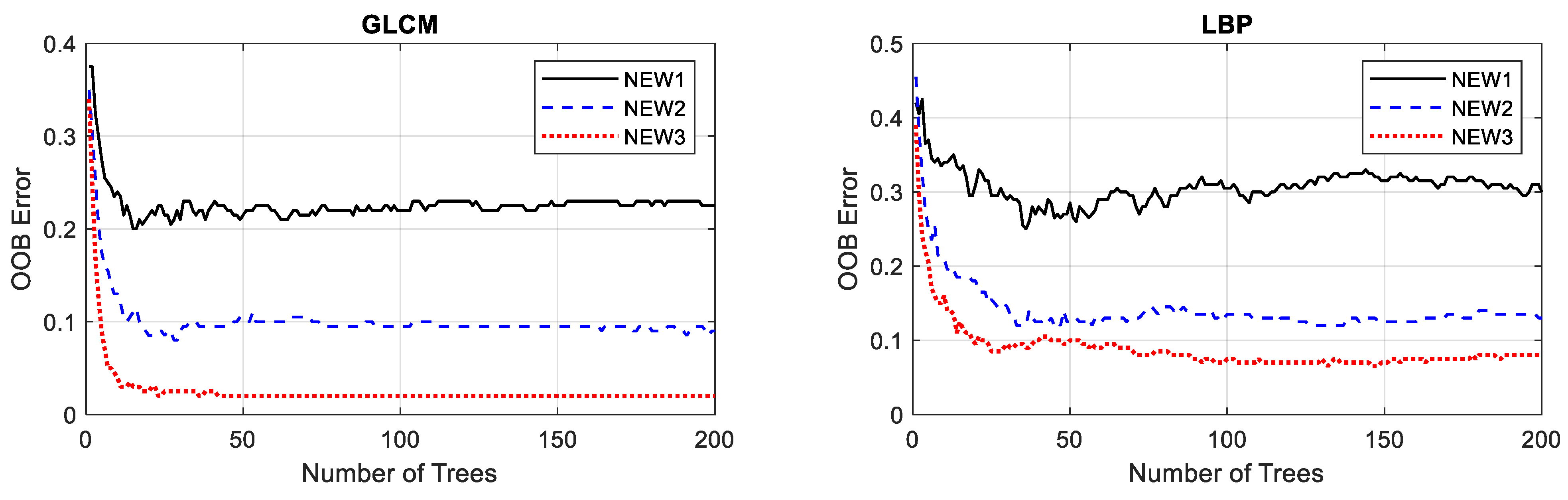
4. Case Study 2: Monitoring of Platinum Froths Associated with Different Grades
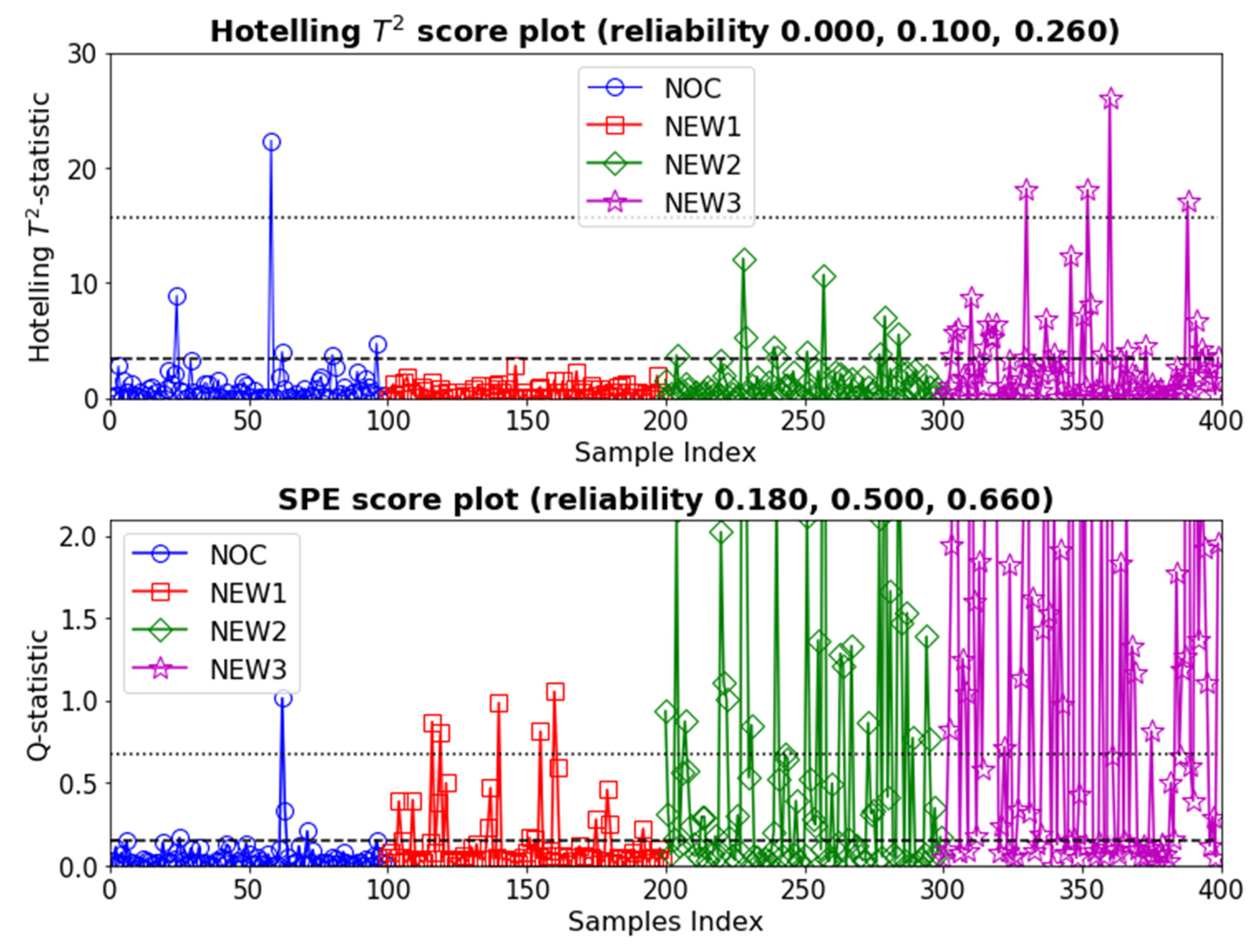
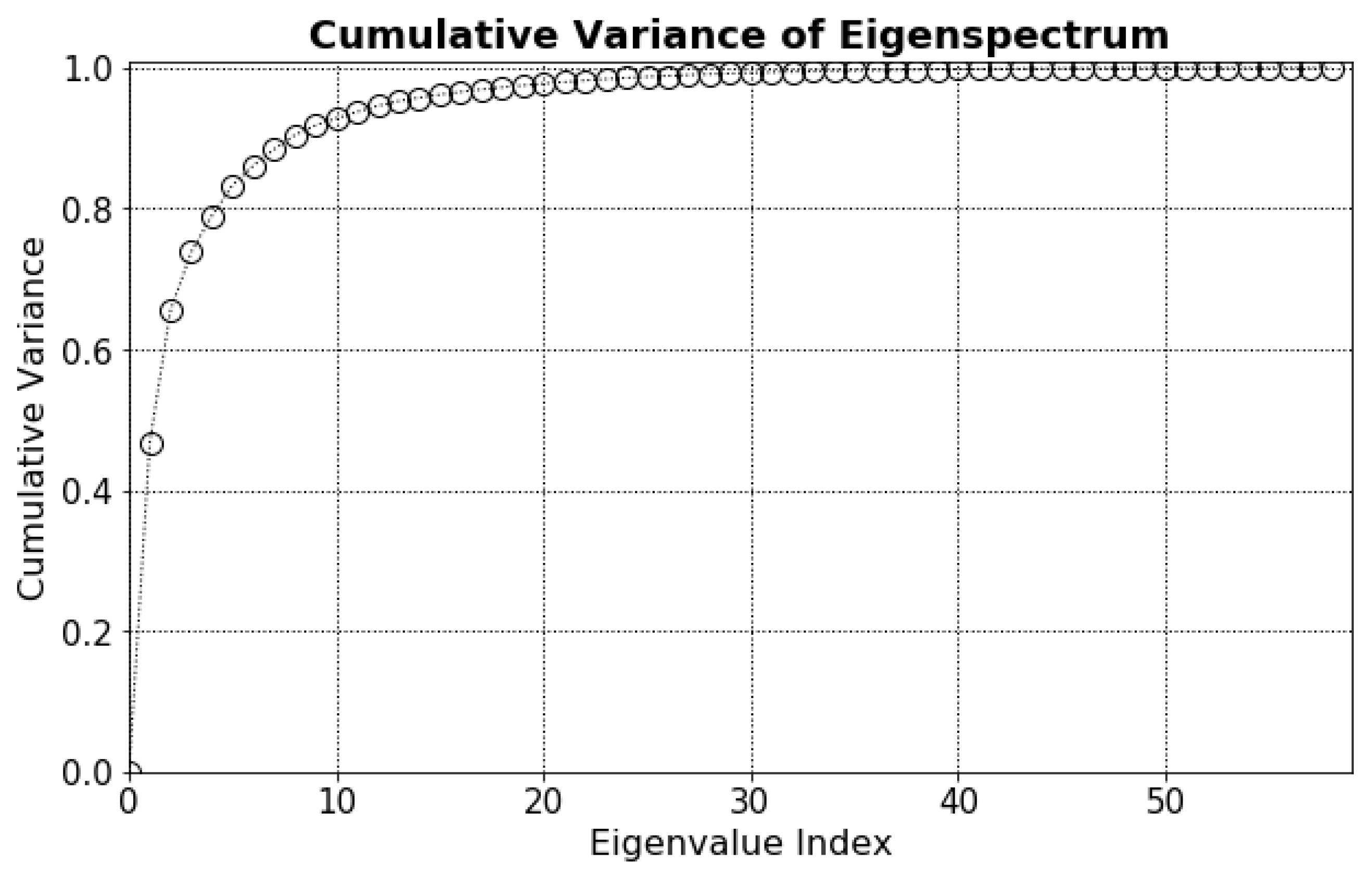
4.1. Monitoring Based on GLCM Features
4.2. Monitoring Based on LBP Vectors
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Random Forest Models with the Froth Image Features
| Number of Trees | GLCM Features | LBP Features | Variables at Split | Terminal Nodes |
|---|---|---|---|---|
| 200 | 4 | 59 | LBP (7), GLCM (2) | 5 samples |
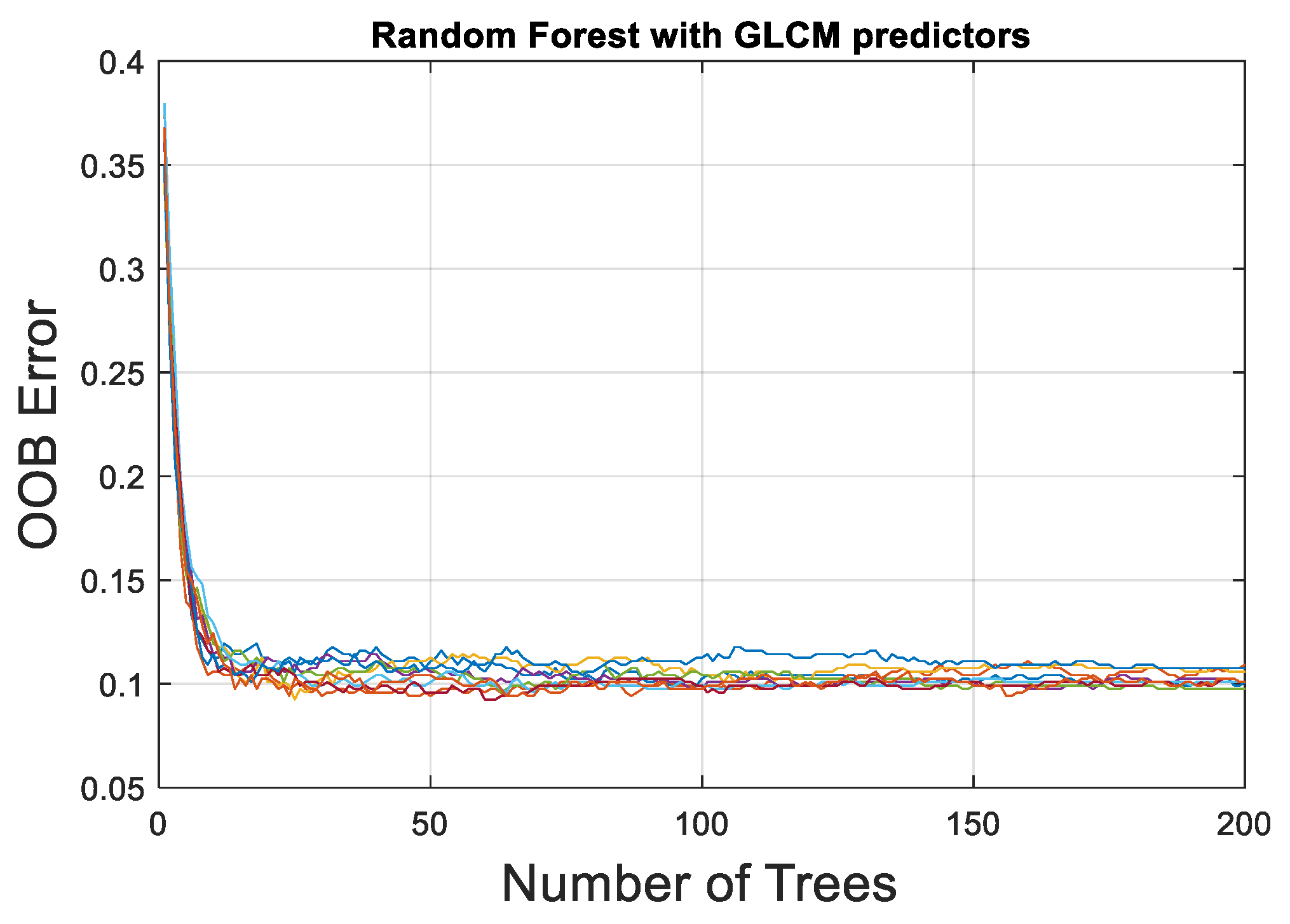
| Number of Trees | GLCM Features | LBP Features | Variables at Split | Terminal Nodes |
|---|---|---|---|---|
| 200 | 4 | 59 | LBP (7), GLCM (2) | 5 samples |
References
- Neethling, S.J.; Brito-Parada, P.R. Predicting flotation behaviour—The interaction between froth stability and performance. Miner. Eng. 2018, 120, 60–65. [Google Scholar] [CrossRef]
- Farrokhpay, S. The significance of froth stability in mineral flotation—A review. Adv. Colloid Interface Sci. 2011, 166, 1–7. [Google Scholar] [CrossRef]
- Cutting, G.W.; Barber, S.P.; Newton, S. Effects of froth structure and mobility on the performance and simulation of continuously operated flotation cells. Int. J. Miner. Process. 1986, 16, 43–61. [Google Scholar] [CrossRef]
- Ni, C.; Bu, X.; Xia, W.; Liu, B.; Peng, Y.; Xie, G. Improving lignite flotation performance by enhancing the froth properties using polyoxyethylene sorbitan monostearate. Int. J. Miner. Process. 2016, 155, 99–105. [Google Scholar] [CrossRef]
- Sheni, N.; Corin, K.; Wiese, J. Considering the effect of pulp chemistry during flotation on froth stability. Miner. Eng. 2018, 116, 15–23. [Google Scholar] [CrossRef]
- Ng, C.Y.; Park, H.; Wang, L. Improvement of coal flotation by exposure of the froth to acoustic sound. Miner. Eng. 2021, 168, 106920. [Google Scholar] [CrossRef]
- Mesa, D.; Morrison, A.J.; Brito-Parada, P.R. The effect of impeller-stator design on bubble size: Implications for froth stability and flotation performance. Miner. Eng. 2020, 157, 106533. [Google Scholar] [CrossRef]
- Nuorivaara, T.; Serna-Guerrero, R. Unlocking the potential of sustainable chemicals in mineral processing: Improving sphalerite flotation using amphiphilic cellulose and frother mixtures. J. Clean. Prod. 2020, 261, 121143. [Google Scholar] [CrossRef]
- Tsatouhas, G.; Grano, S.R.; Vera, M. Case studies on the performance and characterisation of the froth phase in industrial flotation circuits. Miner. Eng. 2006, 19, 774–783. [Google Scholar] [CrossRef]
- Quintanilla, P.; Neethling, S.J.; Brito-Parada, P.R. Modelling for froth flotation control: A review. Miner. Eng. 2021, 162, 106718. [Google Scholar] [CrossRef]
- Ai, M.; Xie, Y.; Xie, S.; Gui, W. Shape-weighted bubble size distribution based reagent predictive control for the antimony flotation process. Chemom. Intell. Lab. Syst. 2019, 192, 103821. [Google Scholar] [CrossRef]
- Zhang, L.; Xu, D. Flotation bubble size distribution detection based on semantic segmentation. IFAC Pap. 2020, 53, 11842–11847. [Google Scholar] [CrossRef]
- Zhang, H.; Tang, Z.; Xie, Y.; Gao, X.; Chen, Q. A watershed segmentation algorithm based on an optimal marker for bubble size measurement. Measurement 2019, 138, 182–193. [Google Scholar] [CrossRef]
- Zhao, L.; Peng, T.; Xie, Y.; Yang, C.; Gui, W. Recognition of flooding and sinking conditions in flotation process using soft measurement of froth surface level and QTA. Chemom. Intell. Lab. Syst. 2017, 169, 45–52. [Google Scholar] [CrossRef]
- He, Z.; Tang, Z.; Yan, Z.; Liu, J. DTCWT-based zinc fast roughing working condition identification. Chin. J. Chem. Eng. 2018, 26, 1721–1726. [Google Scholar] [CrossRef]
- Ming, L.; Wei-hua, G.; Tao, P.; Wei, C. Fault condition detection for a copper flotation process based on a wavelet multi-scale binary froth image. Rem Rev. Esc. Minas 2015, 68, 177–185. [Google Scholar] [CrossRef][Green Version]
- Moolman, D.W.; Aldrich, C.; Van Deventer, J.S.J.; Stange, W.W. Digital image processing as a tool for on-line monitoring of froth in flotation plants. Miner. Eng. 1994, 7, 1149–1164. [Google Scholar] [CrossRef]
- Moolman, D.W.; Aldrich, C.; Van Deventer, J.S.J.; Bradshaw, D.J. The interpretation of flotation froth surfaces by using digital image analysis and neural networks. Chem. Eng. Sci. 1995, 50, 3501–3513. [Google Scholar] [CrossRef]
- Moolman, D.W.; Aldrich, C.; van Deventer, J.S.J. The monitoring of froth surfaces on industrial flotation plants using connectionist image processing techniques. Miner. Eng. 1995, 8, 23–30. [Google Scholar] [CrossRef]
- Zhao, L.; Peng, T.; Han, H.; Cao, W.; Lou, Y.; Xie, X. Fault condition recognition based on multi-scale co-occurrence matrix for copper flotation process. IFAC Proc. Vol. 2014, 47, 7091–7097. [Google Scholar] [CrossRef]
- Zhang, J.; Tang, Z.; Liu, J.; Tan, Z.; Xu, P. Recognition of flotation working conditions through froth image statistical modeling for performance monitoring. Miner. Eng. 2016, 86, 116–129. [Google Scholar] [CrossRef]
- Fu, Y.; Aldrich, C. Flotation froth image analysis by use of a dynamic feature extraction algorithm. IFAC Pap. 2016, 49, 84–89. [Google Scholar] [CrossRef]
- Aldrich, C.; Smith, L.K.; Verrelli, D.I.; Bruckard, W.J.; Kistner, M. Multivariate image analysis of realgar–orpiment flotation froths. Miner. Process. Extr. Metall. 2017, 127, 146–156. [Google Scholar] [CrossRef]
- Luo, J.; Tang, Z.; Zhang, H.; Fan, Y.; Xie, Y. LTGH: A dynamic texture feature for working condition recognition in the froth flotation. IEEE Trans. Instrum. Meas. 2021, 70, 1–10. [Google Scholar]
- Tan, J.; Liang, L.; Peng, Y.; Xie, G. The concentrate ash content analysis of coal flotation based on froth images. Miner. Eng. 2016, 92, 9–20. [Google Scholar] [CrossRef]
- Xu, D.; Chen, X.; Xie, Y.; Yang, C.; Gui, W. Complex networks-based texture extraction and classification method for mineral flotation froth images. Miner. Eng. 2015, 83, 105–116. [Google Scholar] [CrossRef]
- Aldrich, C.; Marais, C.; Shean, B.J.; Cilliers, J.J. Online monitoring and control of froth flotation systems with machine vision: A review. Int. J. Miner. Process. 2010, 96, 1–13. [Google Scholar] [CrossRef]
- Ai, M.; Xie, Y.; Xu, D. Reagent predictive control using joint froth image feature for antimony flotation process. IFAC Pap. 2018, 51, 284–289. [Google Scholar] [CrossRef]
- Lyu, Y.; Chen, J.; Song, Z. Image-based process monitoring using deep learning framework. Chemom. Intell. Lab. Syst. 2019, 189, 8–17. [Google Scholar] [CrossRef]
- Liu, J.J.; MacGregor, J.F.; Duchesne, C.; Bartolacci, G. Flotation froth monitoring using multiresolutional multivariate image analysis. Miner. Eng. 2005, 18, 65–76. [Google Scholar] [CrossRef]
- MacGregor, J.F.; Kourti, T.; Liu, J.; Bradley, J.; Dunn, K.; Yu, H. Multivariate methods for the analysis of data-bases, Process monitoring, and control in the material processing industries. IFAC Proc. Vol. 2007, 40, 193–198. [Google Scholar] [CrossRef]
- Zhang, H.; Tang, Z.; Xie, Y.; Gao, X.; Chen, Q.; Gui, W. Long short-term memory-based grade monitoring in froth flotation using a froth video sequence. Miner. Eng. 2021, 160, 106677. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I.H. Textural features for image classification. IEEE Trans. Syst. Man Cybern. 1973, SMC-3, 610–621. [Google Scholar] [CrossRef]
- Ojala, T.; Pietikäinen, M.; Harwood, D. A comparative study of texture measures with classification based on featured distributions. Pattern Recognit. 1996, 29, 51–59. [Google Scholar] [CrossRef]
- Kistner, M.; Jemwa, G.T.; Aldrich, C. Monitoring of mineral processing systems by using textural image analysis. Miner. Eng. 2013, 52, 169–177. [Google Scholar] [CrossRef]
- Hubbard, R.; Allen, S.J. An empirical comparison of alternative methods for principal component extraction. J. Bus. Res. 1987, 15, 173–190. [Google Scholar] [CrossRef]
- Jackson, J.E. A User’s Guide to Principal Components; Jackson, J.E., Ed.; Wiley John and Sons: New York, NY, USA, 1991. [Google Scholar]
- Marais, C.; Aldrich, C. Estimation of platinum flotation grades from froth image data. Miner. Eng. 2011, 24, 433–441. [Google Scholar] [CrossRef]
- Horn, Z.C.; Auret, L.; McCoy, J.T.; Aldrich, C.; Herbst, B.M. Performance of convolutional neural networks for feature extraction in froth flotation sensing. IFAC Pap. 2017, 50, 13–18. [Google Scholar] [CrossRef]
- Fu, Y.; Aldrich, C. Froth image analysis by use of transfer learning and convolutional neural networks. Miner. Eng. 2018, 115, 68–78. [Google Scholar] [CrossRef]
- Fu, Y.; Aldrich, C. Flotation froth image recognition with convolutional neural networks. Miner. Eng. 2019, 132, 183–190. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aldrich, C.; Liu, X. Monitoring of Flotation Systems by Use of Multivariate Froth Image Analysis. Minerals 2021, 11, 683. https://doi.org/10.3390/min11070683
Aldrich C, Liu X. Monitoring of Flotation Systems by Use of Multivariate Froth Image Analysis. Minerals. 2021; 11(7):683. https://doi.org/10.3390/min11070683
Chicago/Turabian StyleAldrich, Chris, and Xiu Liu. 2021. "Monitoring of Flotation Systems by Use of Multivariate Froth Image Analysis" Minerals 11, no. 7: 683. https://doi.org/10.3390/min11070683
APA StyleAldrich, C., & Liu, X. (2021). Monitoring of Flotation Systems by Use of Multivariate Froth Image Analysis. Minerals, 11(7), 683. https://doi.org/10.3390/min11070683






