Freeze–Thaw Damage Model of Polypropylene Fiber Reinforced Cement Stabilized Waste Construction Slurry under Uniaxial Action
Abstract
:1. Introduction
2. Unconfined Compression Test of F–T Cycles
2.1. Materials
2.2. Test Scheme
2.2.1. UCS Test
2.2.2. SEM Test
2.2.3. Meso Random Damage Model
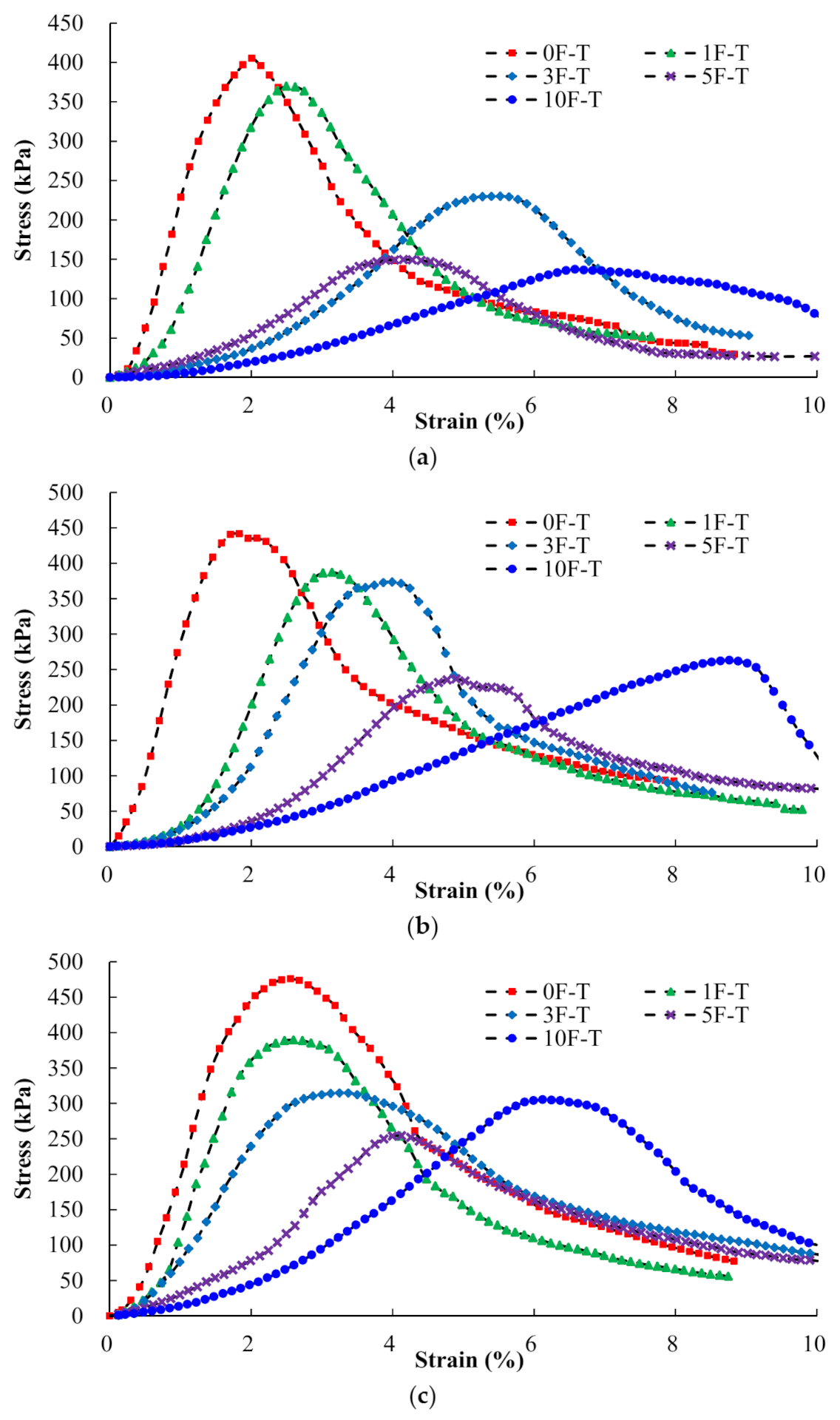
2.3. Analysis of UCS Test Results
2.4. SEM Test Results
3. F–T Damage Model of FCMS
3.1. Two-Stage F–T Damage Model of the FCMS
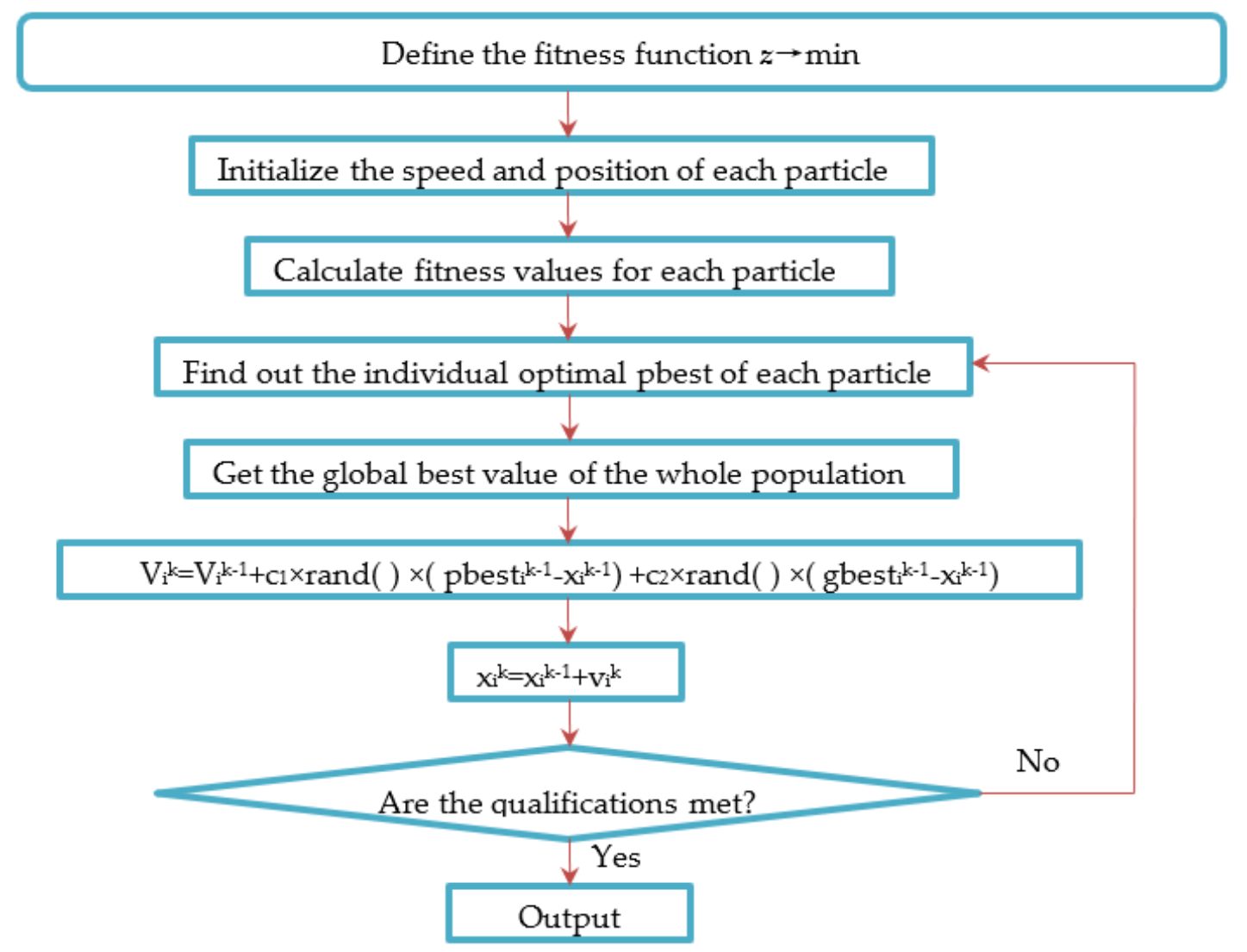
3.2. Particle Swarm Optimization
4. Mechanism Analysis of F–T Damage
5. Conclusions and Discussion
- (1)
- The mechanical properties of the FCMS at room temperature and in the F–T environment were significantly improved by the presence of fiber content. Undergoing the same number of F–T cycles, the strength of the FCMS increased when fiber content was increased. When the fiber content was 1%, the strength increased to 17.9% higher than that of modified construction slurry with 0.75% fiber content. The UCS of the FCMS decreased continually when the number of F–T cycles increased from 0 to 5. When the number of F–T cycles increased from 5 to 10, the UCS of the modified construction slurry was improved by adding fiber. When the fiber content was between 0.5% and 0.75%, the loss of UCS of the FCMS decreased with the increase of F–T cycles, which indicates that the addition of fiber can significantly improve the frost resistance of modified construction slurry.
- (2)
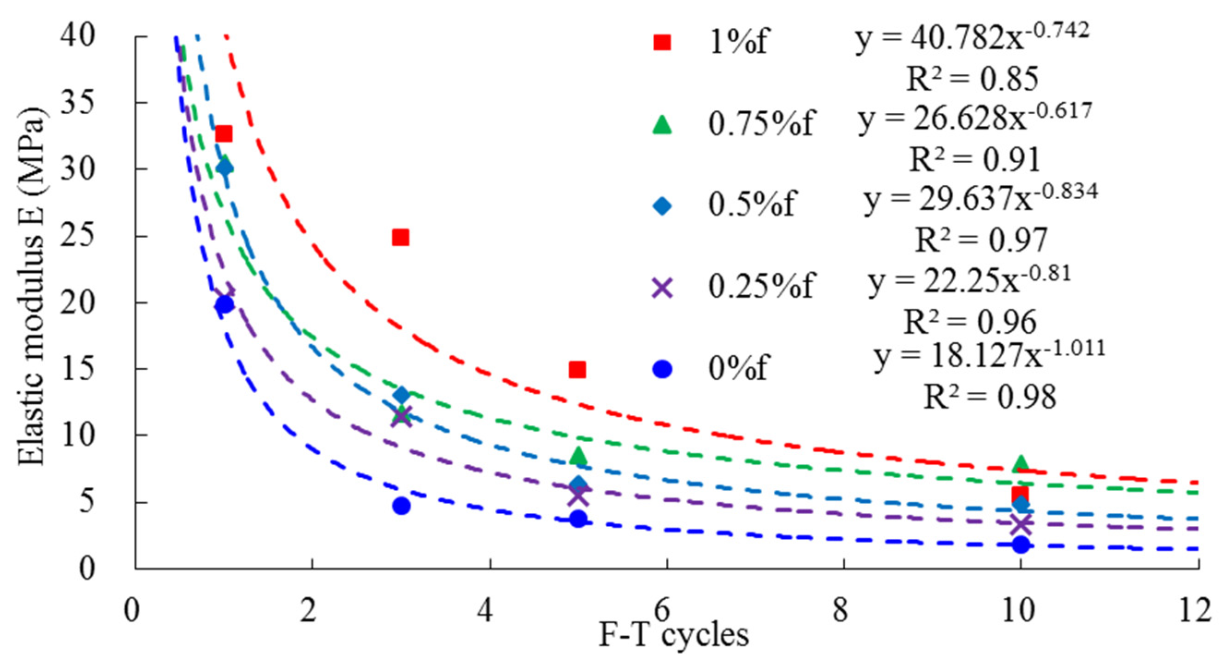
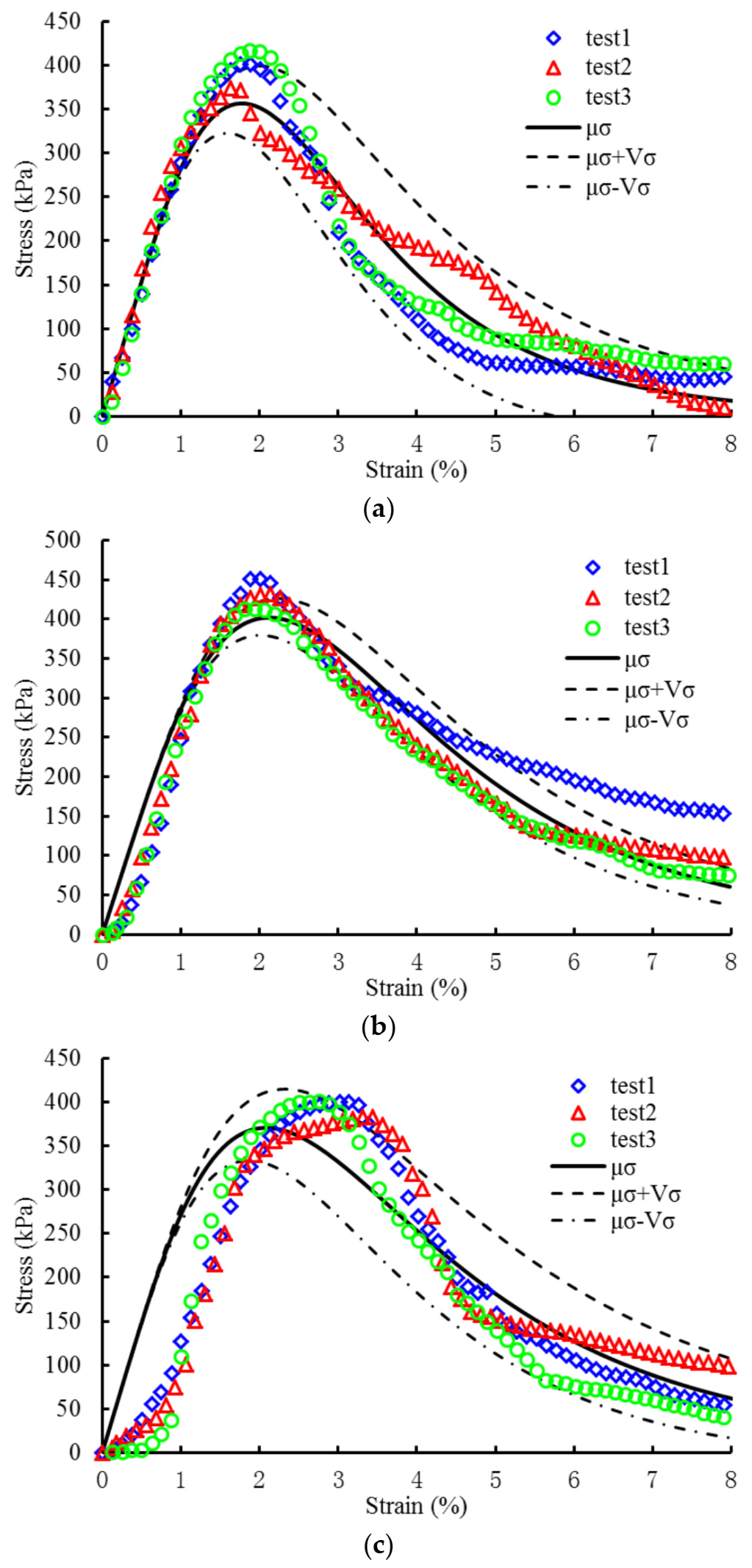
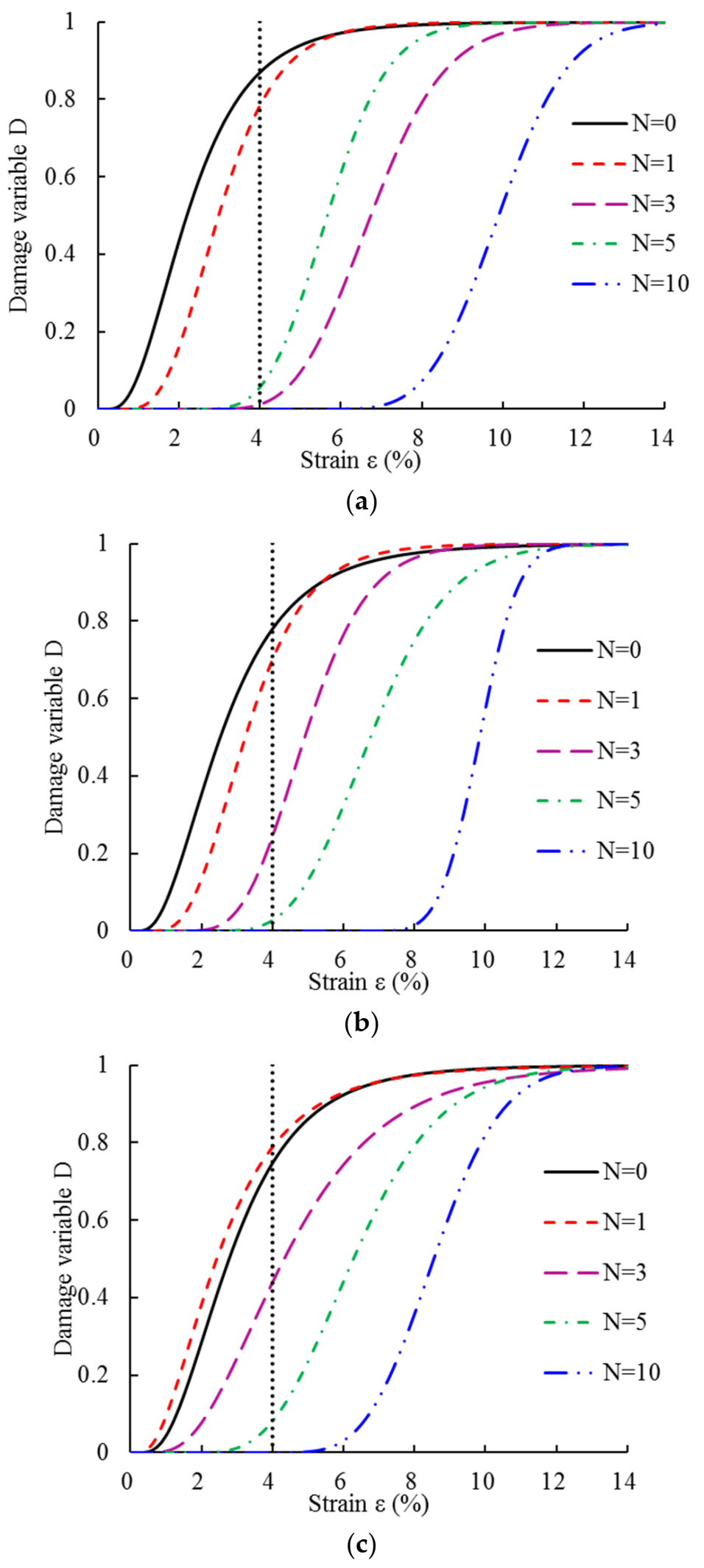
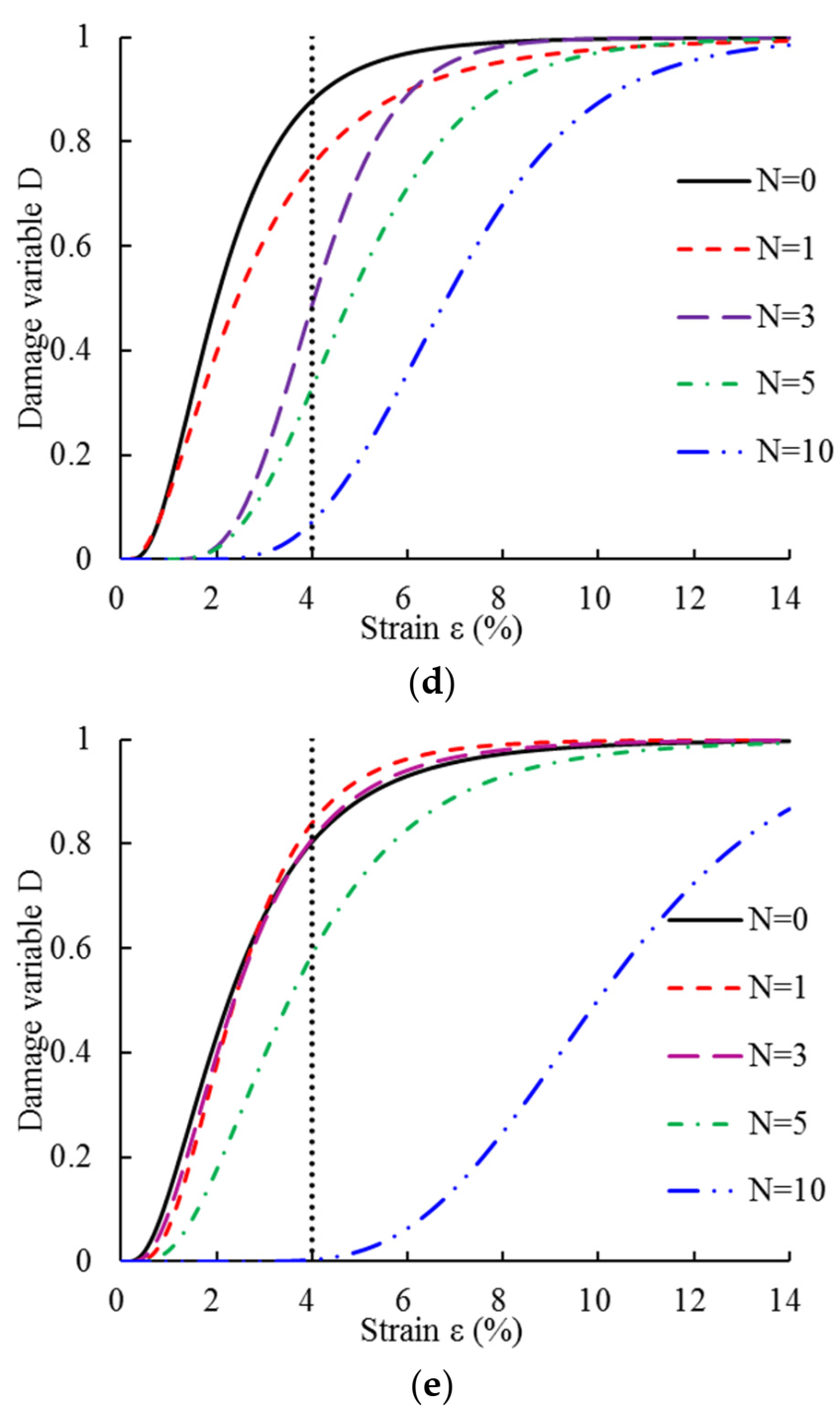
- With the increase of F–T cycles, the elastic modulus of the FCMS gradually decreased and satisfied the power function. The parameters of the meso random damage model were then obtained using the PSO algorithm to establish the stress–strain relationship of the FCMS. Compared with the test results, the mean value of the experimental stress could be in the range of plus and minus one times the variance of the fitting curve. These results show that the two-stage damage model proposed in this paper can better characterize the stress–strain characteristics of the FCMS uniaxial compression F–T damage.
- (3)
- The damage variable of the FCMS with the same fiber content decreased with the increase of F–T cycles. The addition of fiber can improve the frost resistance of the FCMS. When the content of fiber is 0.75%, frost resistance was highest.
- (1)
- PSO was successfully used to identify parameters of the meso random damage model for the FCMS during F–T cycles, retaining wall design [27], concrete frame design [28] and bridge engineering [29,30]. However, civil engineering materials are polyphase materials [37,38,39] and are based on the no free lunch theorem [31]. Whether PSO theory is suitable for other fields of civil engineering remains to be studied.
- (2)
- In addition to PSO, other algorithms exist, such as the genetic algorithm [40], simulated annealing algorithm [41] and ant colony algorithm [42], which can identify model parameters. Although PSO can produce satisfactory results, the parameter identification algorithm used to investigate the most suitable meso random damage model of the FCMS during F–T cycles needs further study.
- (3)
- This study discusses only the mechanical properties of the FCMS during F–T cycles with water content of construction slurry at 100%. Additional research on the water content of construction slurry, such as optimal water content, plastic limit and liquid limit need further study.
- (4)
Author Contributions
Funding
Conflicts of Interest
References
- Biswal, D.R.; Sahoo, U.C.; Dash, S.R. Durability and shrinkage studies of cement stabilized granular lateritic soils. Int. J. Pavement Eng. 2019, 20, 1451–1462. [Google Scholar] [CrossRef]
- Abdellatif, E.; Mostafa, B.; Bruno, B.; Thomas, G. In situ effectiveness of alkaline and cementitious amendments to stabilize oxidized acid-generating tailings. Minerals 2019, 9, 314. [Google Scholar]
- Ke, R.; Wang, H.X.; Tan, Y.Z.; Wang, L.H. Solidification of high organic matter content sludge by cement, lime and metakaolin. Period. Polytech. Civ. 2019, 63, 53–62. [Google Scholar]
- Tobias, D.; Ulla, H.J.; Mette, R.G. Mineralogical sequence of self-healing products in cracked marine concrete. Minerals. 2019, 9, 284. [Google Scholar]
- Liu, Y.; Jiang, Y.; Xiao, H.; Lee, F.H. Determination of representative strength of deep cement-mixed clay from core strength data. Géotechnique 2017, 67, 350–364. [Google Scholar] [CrossRef]
- Yao, K.; Chen, Q.S.; Ho, J.H.; Xiao, H.W.; Lee, F.H. Strain-dependent shear stiffness of cement-treated marine clay. J. Mater. Civ. Eng. 2018, 30, 04018255. [Google Scholar] [CrossRef]
- Jiang, P.; Qiu, L.Q.; Li, N.; Wang, W.; Zhou, A.Z.; Xiao, J.P. Shearing performance of lime reinforced iron tailing powder based on energy dissipationl. Adv. Civ. Eng. 2018, 2018, 4748526. [Google Scholar]
- Wang, W.; Li, N.; Zhang, F.; Zhou, A.Z.; Chi, S. Experimental and mathematical investigations on unconfined compressive behavior of coastal soft soil under complicated freezing processes. Pol. Marit. Res. 2016, 23, 112–116. [Google Scholar] [CrossRef] [Green Version]
- Yao, K.; Li, N.; Chen, D.H.; Wang, W. Generalized hyperbolic formula capturing curing period effect on strength and stiffness of cemented clay. Constr. Build. Mater. 2019, 199, 63–71. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, C.; Li, N.; Tao, F.F.; Yao, K. Characterisation of nano magnesia-cement-reinforced seashore soft soil by direct-shear test. Mar. Georesour. Geotec. 2019, 37, 989–998. [Google Scholar] [CrossRef]
- Wang, Y.X.; Guo, P.P.; Li, X.; Lin, H.; Liu, Y.; Yuan, H.P. Behavior of fiber-reinforced and lime-stabilized clayey soil in triaxial tests. Appl. Sci. 2019, 9, 900. [Google Scholar] [CrossRef] [Green Version]
- Ma, Q.Y.; Gao, C.H. Effect of basalt fiber on the dynamic mechanical properties of cement-soil in SHPB test. J. Mater. Civ. Eng. 2018, 30, 04018185. [Google Scholar] [CrossRef]
- Tran, K.Q.; Satomi, T.; Takahashi, H. Effect of waste cornsilk fiber reinforcement on mechanical properties of soft soils. Transp. Geotech. 2018, 16, 76–84. [Google Scholar] [CrossRef]
- Tajdini, M.; Bonab, M.H.; Golmohamadi, S. An experimental investigation on effect of adding natural and synthetic fibres on mechanical and behavioural parameters of soil-cement materials. Int. J. Civ. Eng. 2018, 16, 353–370. [Google Scholar] [CrossRef]
- Liu, J.K.; Wang, T.L.; Tian, Y.H. Experimental study of the dynamic properties of cement- and lime-modified clay soils subjected to freeze-thaw cycles. Cold Reg. Sci. Technol. 2010, 61, 29–33. [Google Scholar] [CrossRef]
- Jahandari, S.; Saberian, M.; Tao, Z.; Mojtahedi, S.F.; Li, J.; Ghasemi, M.; Li, W.G. Effects of saturation degrees, freezing-thawing, and curing on geotechnical properties of lime and lime-cement concretes. Cold Reg. Sci. Technol. 2019, 160, 242–251. [Google Scholar] [CrossRef]
- Shihata, S.A.; Baghdadi, Z.A. Simplified method to asses freeze-thaw durability of soil cement. J. Mater. Civ. Eng. 2001, 13, 243–247. [Google Scholar] [CrossRef]
- Boz, A.; Sezer, A. Influence of fiber type and content on freeze-thaw resistance of fiber reinforced lime stabilized clay. Cold Reg. Sci. Technol. 2018, 151, 359–366. [Google Scholar] [CrossRef]
- Ding, M.T.; Zhang, F.; Ling, X.Z.; Lin, B. Effects of freeze-thaw cycles on mechanical properties of polypropylene Fiber and cement stabilized clay. Cold Reg. Sci. Technol. 2018, 154, 155–165. [Google Scholar] [CrossRef]
- Kachanov, L.M. Time of the rupture process under creep conditions, Izv Akad. Nauk USS R Otd Techn Nauk. 1958, 8, 26–31. [Google Scholar]
- Rabotnov, Y.N. On the equations of state for creep. Prog. Appl. Mech. 1963, 178, 307–315. [Google Scholar]
- Engelbrecht-Wiggans, A.; Phoenix, S.L. A stochastic model based on fiber breakage and matrix creep for the stress-rupture failure of unidirectional continuous fiber composites. Int. J. Fract. 2019, 217, 1–34. [Google Scholar] [CrossRef] [Green Version]
- Magri, M.; Lemoine, G.; Adam, L.; Segurado, J. A coupled model of diffusional creep of polycrystalline solids based on climb of dislocations at grain boundaries. J. Mech. Phys. Solids 2020, 135, 103786. [Google Scholar] [CrossRef] [Green Version]
- Lemaitre, J. Application of damage concepts to predict creep-fatigue failure. J. Eng. Mater. Technol. 1979, 101, 202–209. [Google Scholar] [CrossRef]
- Kajcinovic, D. Continuum damage theory of brittlematerials. J. Appl. Mech. 1981, 48, 809–824. [Google Scholar]
- Zheng, Y.; Liao, Y. Parameter identification of nonlinear dynamic systems using an improved particle swarm optimization. Optik 2016, 127, 7865–7874. [Google Scholar] [CrossRef]
- Khajehzadeh, M.; Raihan, T.M.; El-Shafie, A.; Eslami, M. Modified particle swarm optimization for optimum design of spread footing and retaining wall. J. Zhejiang Univ. Sci. A 2011, 6, 3–15. [Google Scholar] [CrossRef]
- Kaveh, A.; Sabzi, O.A. Comparative study of two meta-heuristic algorithms for optimum design of reinforced concrete frames. Int. J. Civ. Eng. 2011, 9, 193–206. [Google Scholar]
- Galvan-Nunez, S.; Attoh-Okine, N. Hybrid particle swarm optimization and K-Means analysis for bridge clustering based on national bridge inventory data. J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2017, 3, F4016001. [Google Scholar] [CrossRef]
- You, T.; Jin, H.; Li, P. Optimal placement of wireless sensor nodes for bridge dynamic monitoring based on improved particle swarm algorithm. Int. J. Distrib. Sens. Netw. 2013, 9, 390936. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef] [Green Version]
- Chinese Code. Standard for Geotechnical Testing Method (GB/T 50123-2019); China Planning Press: Beijing, China, 2019. [Google Scholar]
- Li, J. A review on the constitutive model for static and dynamic damage of concrete. Adv. Mech. 2010, 40, 284–297. [Google Scholar]
- Kandarpa, S.; Kirkner, D.J.; Spencer, B.F. Stochastic damage model for brittle materials subjected to monotonic loading. J. Eng. Mech. ASCE 1996, 8, 788–795. [Google Scholar] [CrossRef]
- Li, J.; Ren, X. Recent developments on stochastic damage mechanics for concrete. J. Build. Struct. 2014, 35, 20–29. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks (IEEE 2002), Perth, WA, Australia, 27 November–1 December 1995. [Google Scholar] [CrossRef]
- Paya-Zaforteza, I.; Yepes, V.; Gonzalez-Vidosa, F.; Hospitaler, A. On the Weibull cost estimation of building frames designed by simulated annealing. Meccanica 2010, 45, 693–704. [Google Scholar] [CrossRef]
- Li, K.Q.; Li, D.Q.; Liu, Y. Meso-scale investigations on the effective thermal conductivity of multi-phase materials using the finite element method. Int. J. Heat Mass Tran. 2020, 151, 119383. [Google Scholar] [CrossRef]
- Yao, K.; An, D.L.; Wang, W.; Li, N.; Zhang, C.; Zhou, A.Z. Effect of nano-mgo on mechanical performance of cement stabilized silty clay. Mar. Georesour. Geotec. 2020, 20, 250–255. [Google Scholar] [CrossRef]
- Phutthananon, C.; Jongpradist, P.; Jongpradist, P.; Dias, D.; Baroth, J. Parametric analysis and optimization of T-shaped and conventional deep cement mixing column-supported embankments. Comput. Geotech. 2020, 122, 103555. [Google Scholar] [CrossRef]
- Wang, L.; Liu, Y.Q. Application of simulated annealing particle swarm optimization based on correlation in parameter identification of induction motor. Math. Probl. Eng. 2018, 2018, 1869232. [Google Scholar] [CrossRef]
- Koopialipoor, M.; Murlidhar, B.R.; Hedayat, A.; Armaghani, D.J.; Gordan, B.; Mohamad, E.T. The use of new intelligent techniques in designing retaining walls. Eng. Comput. 2020, 36, 283–294. [Google Scholar] [CrossRef]
- Li, N.; Lv, S.W.; Wang, W.; Guo, J.; Jiang, P.; Liu, Y. Experimental investigations on the mechanical behavior of iron tailings powder with compound admixture of cement and nano-clay. Constr. Build. Mater. 2020, 254, 119259. [Google Scholar] [CrossRef]
- Wang, W.; Li, Y.; Yao, K.; Li, N.; Zhou, A.Z.; Zhang, C. Strength properties of nano-MgO and cement stabilized coastal silty clay subjected to sulfuric acid attack. Mar. Georesour. Geotec. 2019. [Google Scholar] [CrossRef]








| Cement Content (%) | Fiber Content (%) | Curing Age (Days) | F–T Cycles |
|---|---|---|---|
| 20 | 0, 0.25, 0.5, 0.75, 1 | 28 | 0, 1, 3, 5, 10 |
| F–T Cycles | Fiber Content (%) | ||||
|---|---|---|---|---|---|
| 0 | 0.25 | 0.5 | 0.75 | 1 | |
| 0 | 31 | 31 | 32 | 44 | 48 |
| 1 | 20 | 20 | 30 | 30 | 33 |
| 3 | 4.8 | 12 | 13 | 12 | 25 |
| 5 | 3.8 | 5.5 | 6.3 | 8.4 | 15 |
| 10 | 1.9 | 3.3 | 4.8 | 7.8 | 5.6 |
| Population Size | Evolution Times | Particle Velocity Vmax | Particle Velocity Vmin | C1 | C2 |
|---|---|---|---|---|---|
| 100 | 200 | 1 | −1 | 1.5 | 1.5 |
| Fiber Content (%) | F–T Cycles | λ | ζ | ω | Average Error (kPa) |
|---|---|---|---|---|---|
| 0 | 0 | −3.76 | 0.56 | 50 | 22 |
| 1 | −3.40 | 0.39 | 200 | 17 | |
| 3 | −2.53 | 0.22 | 50 | 25 | |
| 5 | −2.7 | 0.21 | 5 | 13 | |
| 10 | −2.12 | 0.14 | 10 | 13 | |
| 0.25 | 0 | −3.64 | 0.62 | 260 | 30 |
| 1 | −3.33 | 0.42 | 125 | 33 | |
| 3 | −2.87 | 0.29 | 15 | 54 | |
| 5 | −2.54 | 0.26 | 8.5 | 35 | |
| 10 | −2.11 | 0.09 | 18 | 10 | |
| 0.5 | 0 | −3.53 | 0.57 | 165 | 18 |
| 1 | −3.69 | 0.65 | 75 | 35 | |
| 3 | −3.07 | 0.52 | 150 | 21 | |
| 5 | −2.63 | 0.31 | 100 | 27 | |
| 10 | −2.28 | 0.18 | 10 | 29 | |
| 0.75 | 0 | −3.87 | 0.62 | 500 | 39 |
| 1 | −3.72 | 0.75 | 425 | 25 | |
| 3 | −3.08 | 0.34 | 55 | 30 | |
| 5 | −2.93 | 0.41 | 20 | 23 | |
| 10 | −2.56 | 0.35 | 25 | 38 | |
| 1 | 0 | −3.78 | 0.7 | 188 | 29 |
| 1 | −3.68 | 0.55 | 60 | 38 | |
| 3 | −3.71 | 0.63 | 190 | 40 | |
| 5 | −3.3 | 0.59 | 150 | 31 | |
| 10 | −2.17 | 0.32 | 27 | 51 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, P.; Zhou, L.; Wang, Y.; Qian, B.; Wang, W.; Li, N.; Zhang, F. Freeze–Thaw Damage Model of Polypropylene Fiber Reinforced Cement Stabilized Waste Construction Slurry under Uniaxial Action. Minerals 2021, 11, 743. https://doi.org/10.3390/min11070743
Jiang P, Zhou L, Wang Y, Qian B, Wang W, Li N, Zhang F. Freeze–Thaw Damage Model of Polypropylene Fiber Reinforced Cement Stabilized Waste Construction Slurry under Uniaxial Action. Minerals. 2021; 11(7):743. https://doi.org/10.3390/min11070743
Chicago/Turabian StyleJiang, Ping, Lin Zhou, Yue Wang, Biao Qian, Wei Wang, Na Li, and Fang Zhang. 2021. "Freeze–Thaw Damage Model of Polypropylene Fiber Reinforced Cement Stabilized Waste Construction Slurry under Uniaxial Action" Minerals 11, no. 7: 743. https://doi.org/10.3390/min11070743
APA StyleJiang, P., Zhou, L., Wang, Y., Qian, B., Wang, W., Li, N., & Zhang, F. (2021). Freeze–Thaw Damage Model of Polypropylene Fiber Reinforced Cement Stabilized Waste Construction Slurry under Uniaxial Action. Minerals, 11(7), 743. https://doi.org/10.3390/min11070743








