Dynamic Mechanics and Energy Dissipation of Saturated Layered Phyllite
Abstract
:1. Introduction
2. SHPB Test Scheme
2.1. Pattern Preparation
2.2. Experimental Process
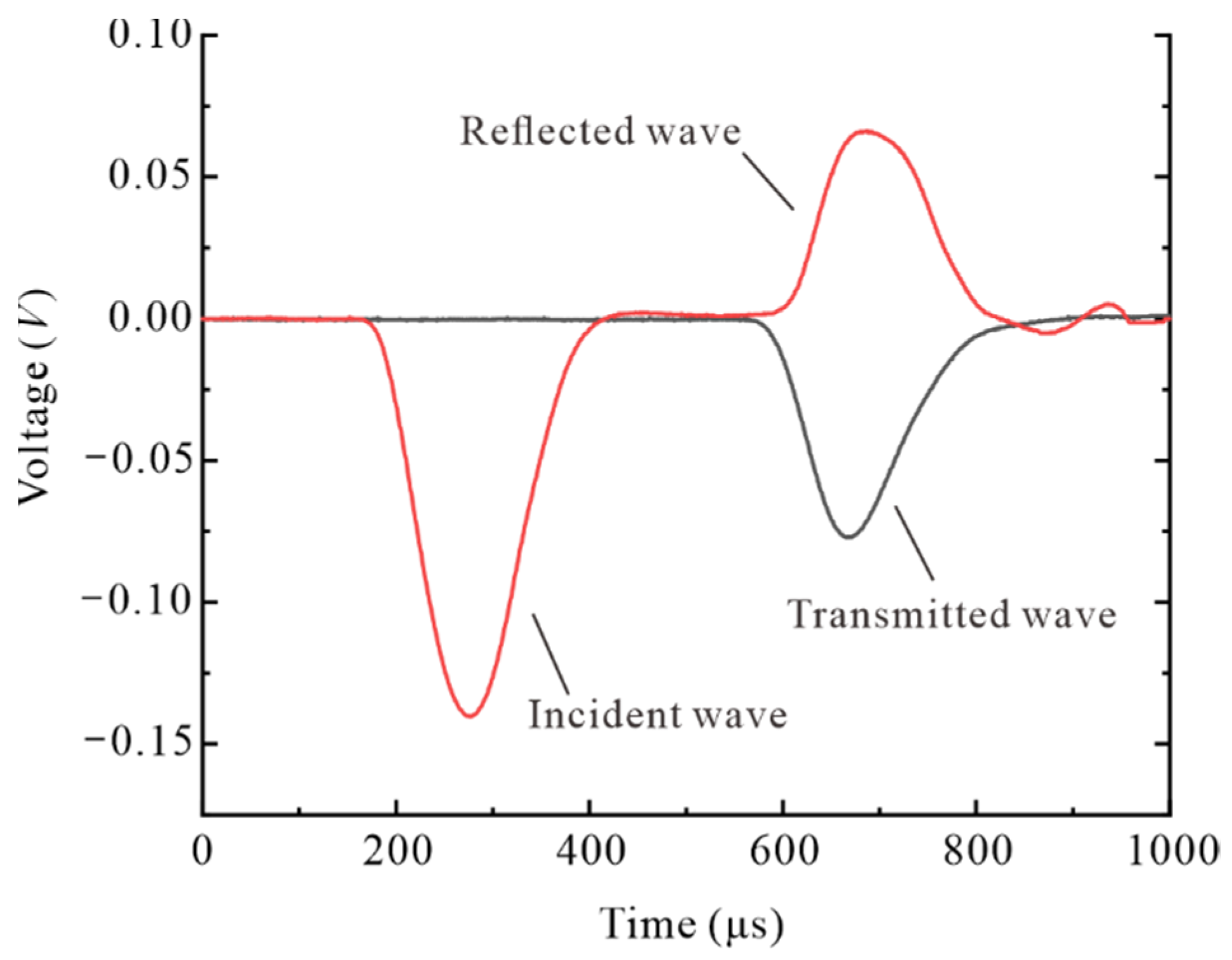
2.3. Stress Equalization
2.4. Calculation of Mechanical Parameters
3. Dynamic Mechanical Properties of Saturated Phyllite
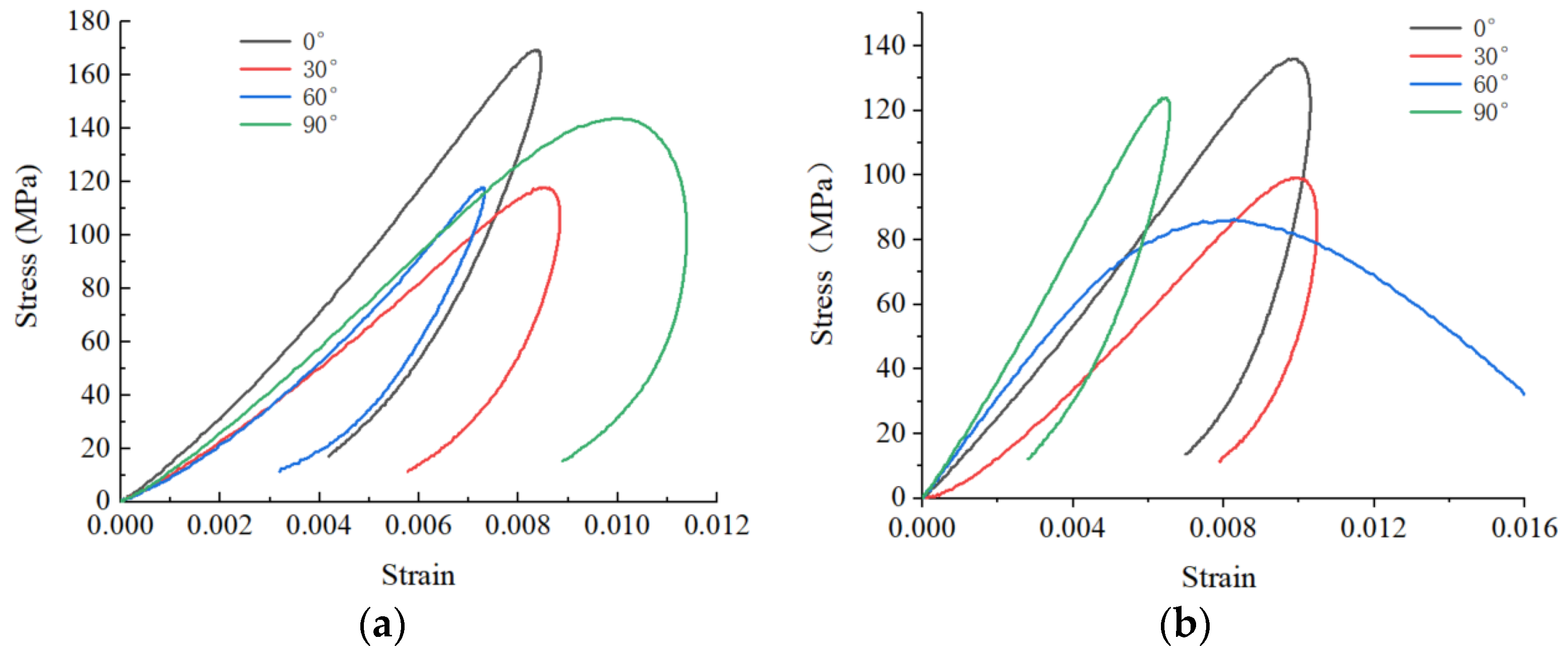
3.1. Characteristics of Stress-Strain Curve
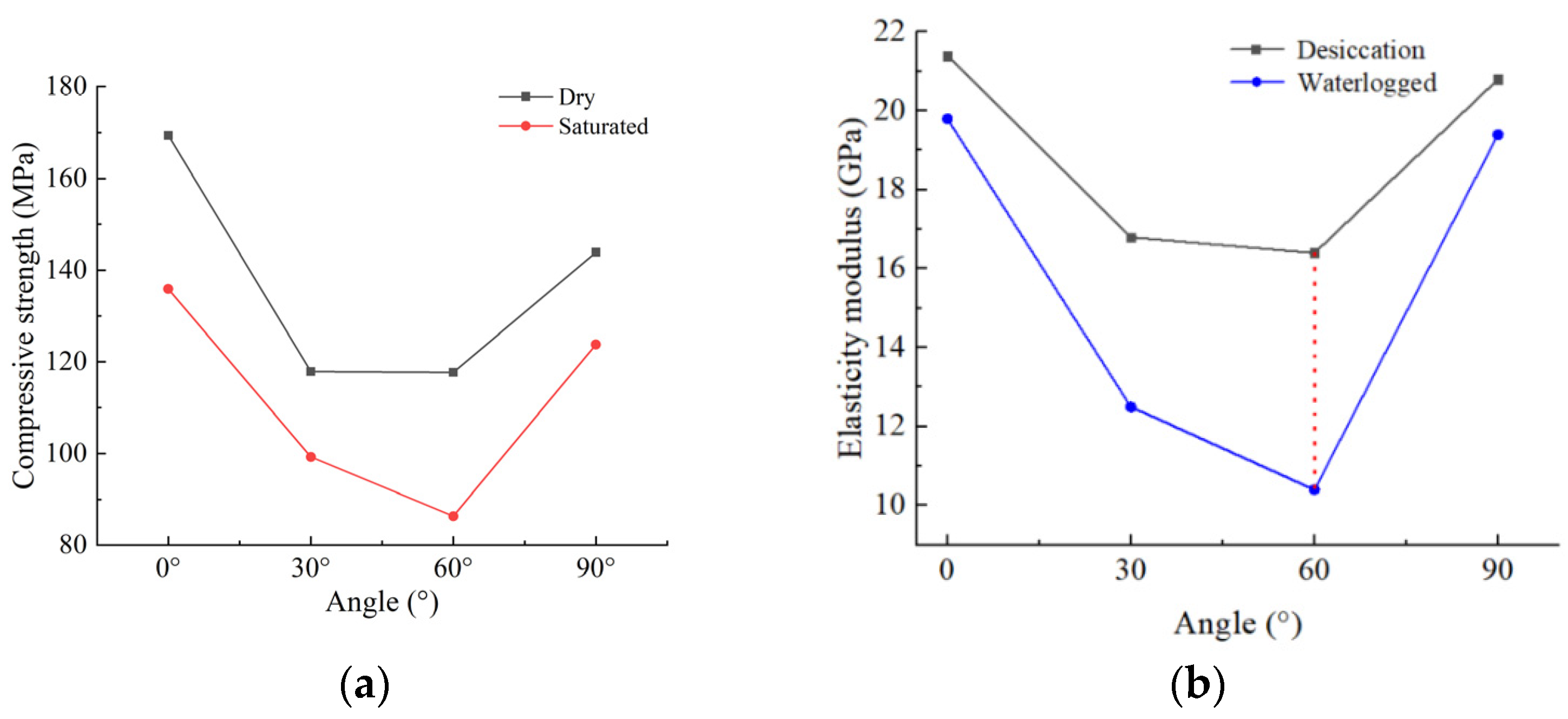
3.2. Compressive Strength and Modulus of Elasticity Parameter Curves
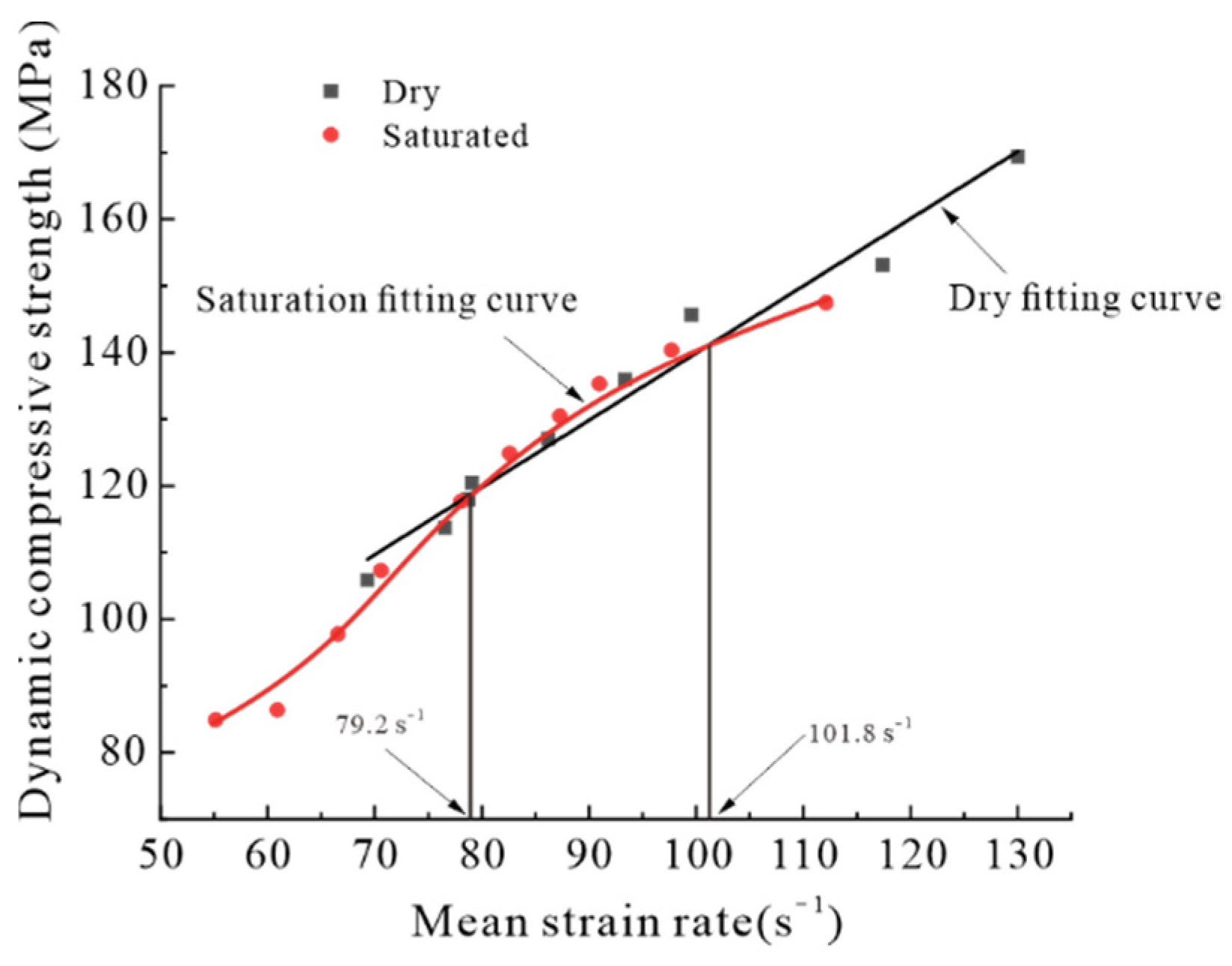
3.3. Compressive Strength and Average Strain Rate of Specimens
3.4. Failure Patterns
4. Energy Dissipation Law of Saturated Phyllite under Impact Load
4.1. Calculation of Energy Dissipation
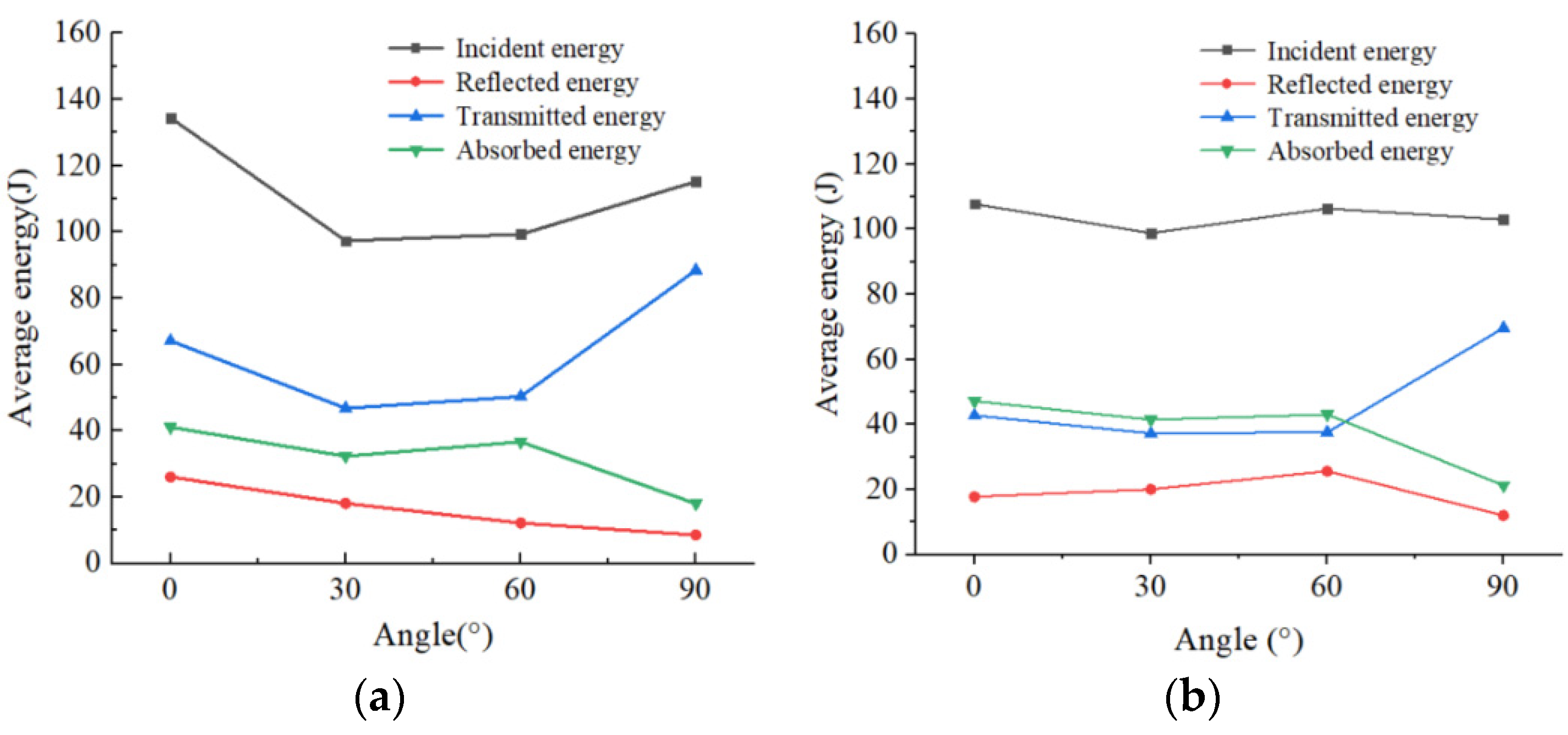
4.2. Energy Distribution Curves for Different Stratification Angles
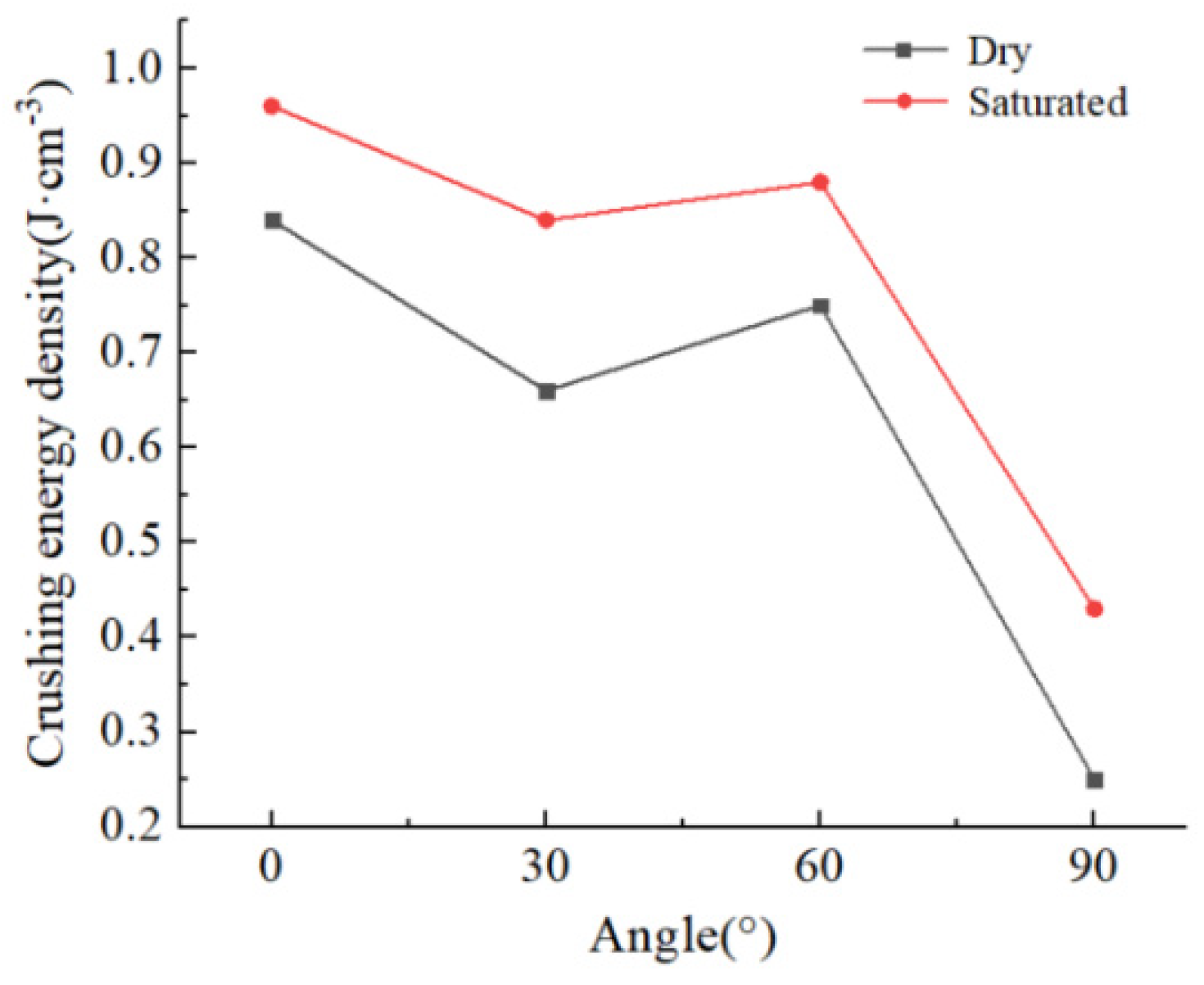
4.3. Stratification Angle and Crushing Energy Consumption Density
4.4. Crushing Energy Consumption Density and Average Strain Rate
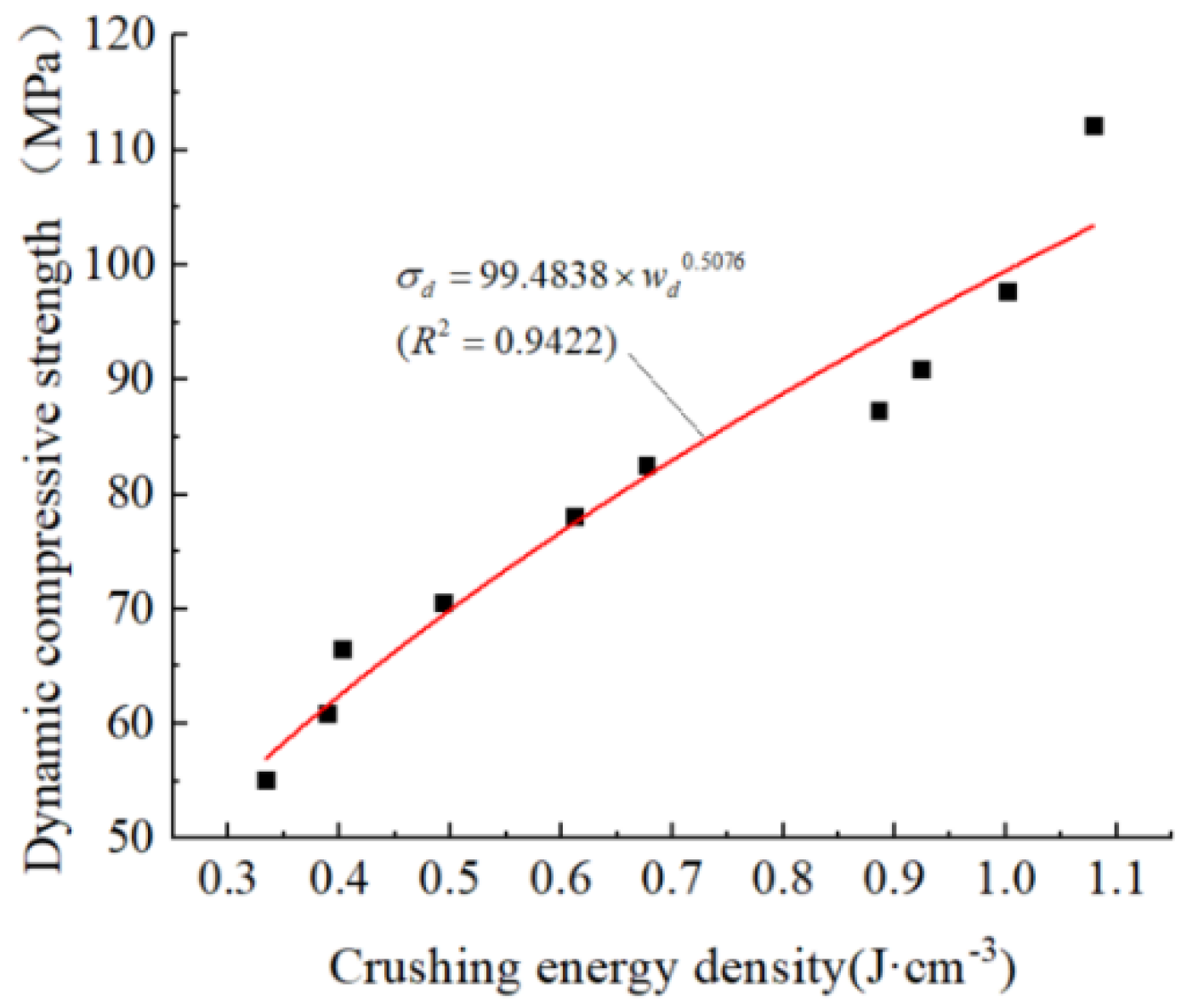
4.5. Dynamic Strength of Samples and Crushing Energy Consumption Density
5. Analysis of Mechanical Properties and Energy Dissipation of Layered Phyllite
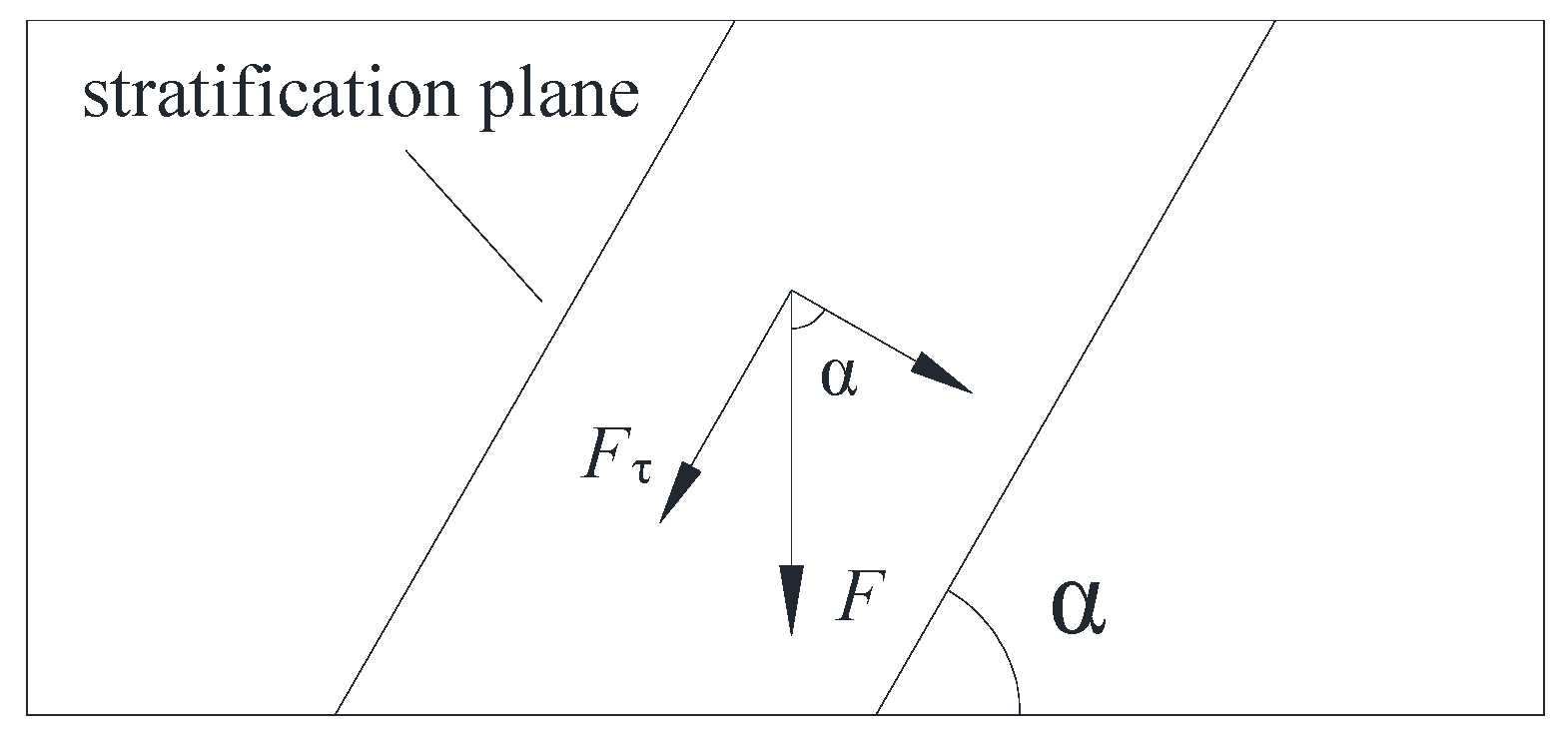
5.1. Analysis Stratification Angle and Crushing Energy Consumption
5.2. Water Sensitivity Analysis
5.3. Influence of Stratification Angle and Mechanism of Water-Sensitive Joint Action
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, Y.; Zhao, B.; Yang, J.; Sun, J.; Huang, W.; Li, Z.; Wang, B. Experimental Study on the Influence of Confining Pressure and Bedding Angles on Mechanical Properties in Coal. Minerals 2022, 12, 345. [Google Scholar] [CrossRef]
- Shi, Z.; Zhao, Y.; Danesh, N.N.; Zhang, X.; Tang, T. Role of bedding plane in the relationship between Mode-I fracture toughness and tensile strength of shale. Bull. Eng. Geol. Environ. 2022, 81, 81. [Google Scholar] [CrossRef]
- Ramamurthy, T. Strength and modulus responses of anisotropic rocks. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1994, 31, 313–329. [Google Scholar]
- Tien, Y.M.; Kuo, M.C. A failure criterion for transversely isotropic rocks. Int. J. Rock Mech. Min. Sci. 2001, 38, 399–412. [Google Scholar] [CrossRef]
- Zaid, M. Three-dimensional finite element analysis of urban rock tunnel under static loading condition: Effect of the rock weathering. Geomech. Eng. 2021, 25, 99–109. [Google Scholar]
- Zaid, M. Dynamic stability analysis of rock tunnels subjected to impact loading with varying UCS. Geomech. Eng. 2021, 24, 505–518. [Google Scholar]
- Zaid, M. Preliminary Study to Understand the Effect of Impact Loading and Rock Weathering in Tunnel Constructed in Quartzite. Geotech. Geol. Eng. 2021, 1–29. [Google Scholar] [CrossRef]
- Zaid, M.; Mishra, S. Numerical Analysis of Shallow Tunnels Under Static Loading: A Finite Element Approach. Geotech. Geol. Eng. 2021, 39, 2581–2607. [Google Scholar] [CrossRef]
- Zaid, M.; Sadique, R.; Alam, M.M. Blast Resistant Analysis of Rock Tunnel Using Abaqus: Effect of Weathering. Geotech. Geol. Eng. 2021, 40, 809–832. [Google Scholar] [CrossRef]
- Zaid, M.; Shah, I.A. Numerical Analysis of Himalayan Rock Tunnels under Static and Blast Loading. Geotech. Geol. Eng. 2021, 39, 5063–5083. [Google Scholar]
- Sadique, R.; Zaid, M.; Alam, M.M. Rock Tunnel Performance Under Blast Loading through Finite Element Analysis. Geotech. Geol. Eng. 2021, 40, 35–56. [Google Scholar] [CrossRef]
- Fan, X.; Luo, N.; Liang, H.; Sun, X.; Zhai, C.; Xie, L. Dynamic Breakage Characteristics of Shale with Different Bedding Angles under the Different Ambient Temperatures. Rock Mech. Rock Eng. 2021, 54, 3245–3261. [Google Scholar] [CrossRef]
- Shuang, G.; Zhen, W.; Lei, Z. Dynamic fracture mechanics and energy distribution rate response characteristics of coal containing bedding structure. PLoS ONE 2021, 16, e0247908. [Google Scholar]
- Zhao, Y.; Liu, S.; Jiang, Y.; Wang, K.; Huang, Y. Dynamic Tensile Strength of Coal under Dry and Saturated Conditions. Rock Mech. Rock Eng. 2015, 49, 1709–1720. [Google Scholar] [CrossRef]
- Zhang, X.; Ou, X.; Gong, F.; Yang, J. Effects of Bedding on The Dynamic Compressive Properties of Low Anisotropy Slate. Rock Mech. Rock Eng. 2018, 52, 981–990. [Google Scholar] [CrossRef]
- Xie, H.; Ju, Y.; Li, L. Rock strength and overall damage criterion based on the principle of energy dissipation and release. J. Rock Mech. Eng. 2005, 1, 3003–3010. [Google Scholar]
- Xie, H.; Peng, R.D.; Ju, Y. Analysis of energy dissipation during rock deformation and damage. J. Rock Mech. Eng. 2004, 21, 3565–3570. [Google Scholar]
- Deng, Y.; Chen, M.; Jin, Y.; Zou, D. Theoretical analysis and experimental research on the energy dissipation of rock crushing based on fractal theory. J. Nat. Gas Sci. Eng. 2016, 33, 231–239. [Google Scholar] [CrossRef]
- Feng, J.; Wang, E.; Chen, X.; Ding, H. Energy dissipation rate: An indicator of coal deformation and failure under static and dynamic compressive loads. Int. J. Min. Sci. Technol. 2018, 28, 397–406. [Google Scholar] [CrossRef]
- Ramamurthy, T.; Venkatappa, R.; Singh, J. Engineering behaviour of phyllites. Eng. Geol. 1993, 33, 209–225. [Google Scholar] [CrossRef]
- Amour, F.; Christensen, H.F.; Hajiabadi, M.R.; Nick, H.M. Effects of Porosity and Water Saturation on the Yield Surface of Upper Cretaceous Reservoir Chalks From the Danish North Sea. J. Geophys. Res. Solid Earth 2021, 126, e2020JB020608. [Google Scholar] [CrossRef]
- Si, X.-F.; Huang, L.-Q.; Li, Z.-B.; Gong, F.-Q.; Liu, X.-L. Mechanical properties and rockburst proneness of phyllite under uniaxial compression. Trans. Nonferrous Met. Soc. China 2021, 31, 3862–3878. [Google Scholar] [CrossRef]
- Villalobos, F.A.; Rodriguez, P.A.; Vera, M. Study of the anisotropic tensile and compressive strength of a foliated phyllite. Proc. Inst. Civ. Eng. Geotech. Eng. 2021, 1–12. [Google Scholar] [CrossRef]
- Yang, Z.; Su, S.; Peng, L. Mechanical Behavior, Energy Release, and Crack Distribution Characteristics of Water-Saturated Phyllite under Triaxial Cyclic Loading. Adv. Civ. Eng. 2021, 2021, 3681439. [Google Scholar]
- Ma, L.H.; Chen, J.; Zhao, Y.F.; Zhang, C.; Liu, R.; Ren, S. Water Content and Bedding Angle Effects on the Mechanical Properties and Micro-/Macro-Failure Mechanism of Phyllite. Arab. J. Sci. Eng. 2022, 1–19. [Google Scholar] [CrossRef]
- Qiu, J.; Li, D.; Li, X. Dynamic failure of a phyllite with a low degree of metamorphism under impact Brazilian test. Int. J. Rock Mech. Min. Sci. 2017, 94, 10–17. [Google Scholar] [CrossRef]
- Xu, J.; Li, X. The dynamical loading on rock with different loading wave shapes conventional SHPB. J. Cent. South Univ. Technol. 1998, 5, 57–59. [Google Scholar] [CrossRef]
- Hong, L.; Li, X.; Liu, X.; Zhou, Z.; Ye, Z.; Yin, T. Stress uniformity process of specimens in SHPB test under different loading conditions of rectangular and half-sine input waves. Trans. Tianjin Univ. 2008, 14, 450–456. [Google Scholar] [CrossRef]
- Yang, G.; Bi, J.; Li, X.; Liu, J.; Feng, Y. SHPB Testing and Analysis of Bedded Shale under Active Confining Pressure. J. Eng. 2020, 2020, 5034902. [Google Scholar] [CrossRef]
- Xie, B.; Ai, D.; Yang, Y. An automatic pixel-level crack identification method for coals experiencing SHPB impact tests. J. Geophys. Eng. 2019, 16, 297–308. [Google Scholar] [CrossRef]
- Chen, R.; Nie, Z.Y.; Peng, Y.; Xu, Y.; Yao, W. A Dynamic Hydraulic Fracturing Test Technology Based on Split Hopkinson Pressure Bar System. Exp. Mech. 2022, 62, 813–822. [Google Scholar] [CrossRef]
- Li, B.; Ye, X.; Dou, Z.; Zhao, Z.; Li, Y.; Yang, Q. Shear Strength of Rock Fractures Under Dry, Surface Wet and Saturated Conditions. Rock Mech. Rock Eng. 2020, 53, 2605–2622. [Google Scholar] [CrossRef]
- Bauer, S.J.; Song, B.; Sanborn, B. Dynamic compressive strength of rock salts. Int. J. Rock Mech. Min. Sci. 2019, 113, 112–120. [Google Scholar] [CrossRef]
- Braunagel, M.J.; Griffith, W.A. The Effect of Dynamic Stress Cycling on the Compressive Strength of Rocks. Geophys. Res. Lett. 2019, 46, 6479–6486. [Google Scholar] [CrossRef]
- Liu, S.; Xu, J. Experimental and Numerical Analysis of Qinling Mountain Engineered Rocks during Pulse-Shaped SHPB Test. Int. J. Nonlinear Sci. Numer. Simul. 2015, 16, 165–171. [Google Scholar] [CrossRef]
- Feng, P.; Liu, B.; Tang, R.; Wei, M.; Zhang, Y.; Li, H. Dynamic Fracture Behaviors and Fragment Characteristics of Pre-compressed Flawed Sandstones. Int. J. Mech. Sci. 2022, 220, 107162. [Google Scholar] [CrossRef]
- Xie, H.; Li, L.; Ju, Y.; Peng, R.; Yang, Y. Energy analysis for damage and catastrophic failure of rocks. Sci. China Technol. Sci. 2011, 54, 199–209. [Google Scholar] [CrossRef]
- Shan, P.; Lai, X.; Liu, X. Correlational Analytical Characterization of Energy Dissipation-Liberation and Acoustic Emission during Coal and Rock Fracture Inducing by Underground Coal Excavation. Energies 2019, 12, 2382. [Google Scholar] [CrossRef] [Green Version]





| State | Number | Sample Volume/cm3 | Incident Energy WI/J | Crushing Energy Consumption WS/J | Energy Consumption Density wd/J∙cm−3 | Average Strain Rate | Dynamic Compressive Strength | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Test Value | Average Value | Test Value | Average Value | Test Value | Average Value | |||||
| Dry | 0°-1 | 49.09 | 105.56 | 115.83 | 40.00 | 41.23 | 0.81 | 0.84 | 117.44 | 153.08 |
| 0°-2 | 49.09 | 126.11 | 42.45 | 0.86 | 130.03 | 169.37 | ||||
| 30°-1 | 49.10 | 95.70 | 97.36 | 47.15 | 32.39 | 0.96 | 0.66 | 69.31 | 105.88 | |
| 30°-2 | 49.17 | 99.03 | 17.63 | 0.36 | 76.56 | 113.70 | ||||
| 60°-1 | 49.13 | 101.83 | 99.32 | 43.46 | 36.73 | 0.89 | 0.75 | 78.78 | 117.95 | |
| 60°-2 | 49.09 | 96.81 | 30.00 | 0.61 | 79.09 | 120.44 | ||||
| 90°-1 | 49.11 | 106.82 | 115.21 | 16.39 | 18.07 | 0.33 | 0.25 | 86.20 | 127.05 | |
| 90°-2 | 49.09 | 123.60 | 19.76 | 0.40 | 93.36 | 135.90 | ||||
| Saturation | 0°-1 | 49.08 | 107.71 | 107.79 | 49.16 | 47.24 | 1.00 | 0.96 | 97.71 | 140.37 |
| 0°-2 | 49.03 | 107.87 | 45.31 | 0.92 | 112.11 | 147.47 | ||||
| 30°-1 | 49.06 | 100.10 | 98.83 | 33.44 | 41.47 | 0.68 | 0.84 | 78.06 | 117.71 | |
| 30°-2 | 49.14 | 97.56 | 49.50 | 1.01 | 82.60 | 124.85 | ||||
| 60°-1 | 49.20 | 106.12 | 106.38 | 33.19 | 43.08 | 0.68 | 0.88 | 66.58 | 97.79 | |
| 60°-2 | 49.09 | 106.64 | 52.97 | 1.08 | 70.61 | 107.29 | ||||
| 90°-1 | 49.10 | 102.84 | 103.01 | 18.35 | 21.30 | 0.37 | 0.43 | 87.31 | 130.43 | |
| 90°-2 | 49.10 | 103.18 | 24.24 | 0.49 | 90.96 | 135.30 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, G.; Peng, Y.; Zuo, Q.; Su, Y.; Wu, L. Dynamic Mechanics and Energy Dissipation of Saturated Layered Phyllite. Minerals 2022, 12, 1246. https://doi.org/10.3390/min12101246
Liu G, Peng Y, Zuo Q, Su Y, Wu L. Dynamic Mechanics and Energy Dissipation of Saturated Layered Phyllite. Minerals. 2022; 12(10):1246. https://doi.org/10.3390/min12101246
Chicago/Turabian StyleLiu, Guangjin, Yaxiong Peng, Qingjun Zuo, Ying Su, and Li Wu. 2022. "Dynamic Mechanics and Energy Dissipation of Saturated Layered Phyllite" Minerals 12, no. 10: 1246. https://doi.org/10.3390/min12101246






