Analysis and Optimization of Grinding Performance of Vertical Roller Mill Based on Experimental Method
Abstract
:1. Introduction
2. Material and Methods
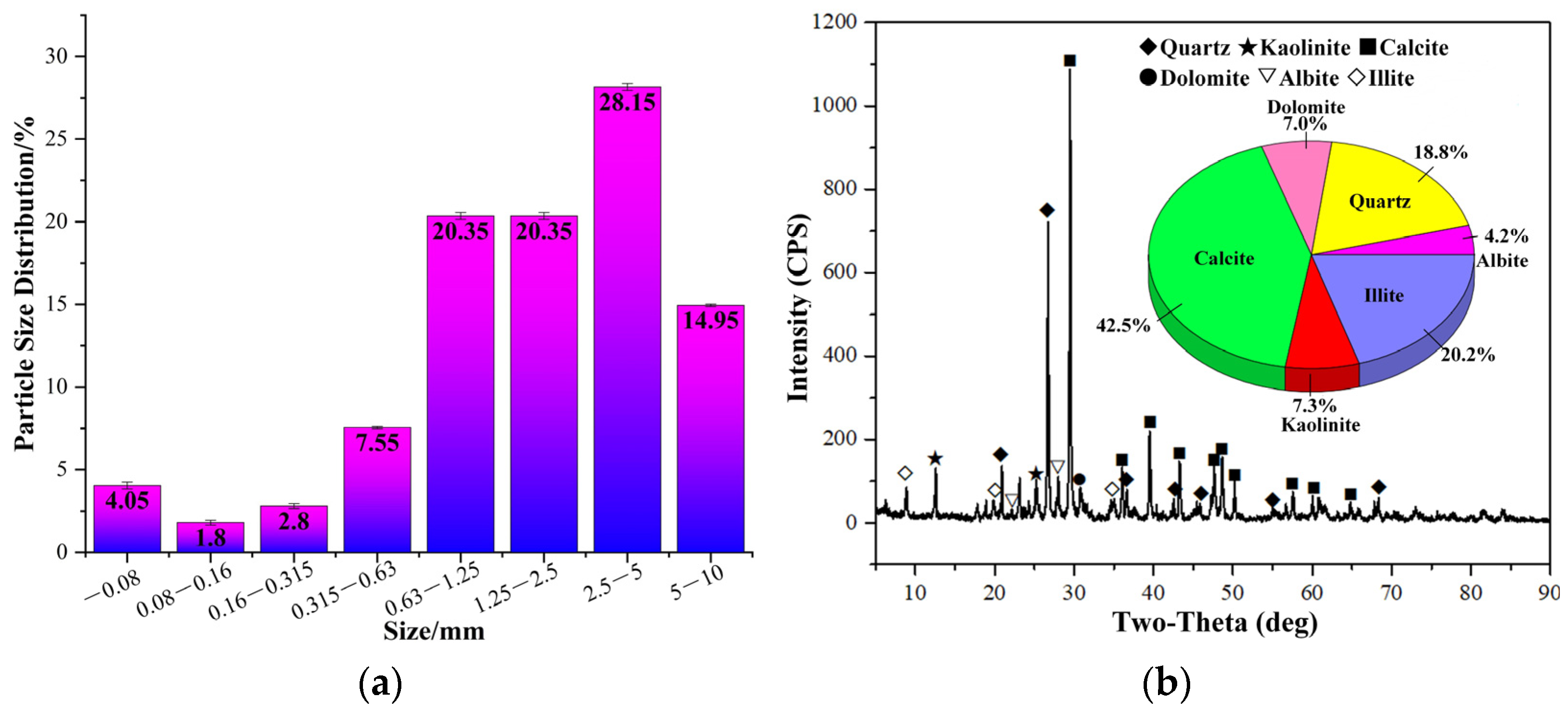
2.1. Material Properties
2.2. Experimental Setup
2.3. Grinding Performance Indexes
3. Response Surface Models and Parametric Study
3.1. Design of Experimental (DOE)
3.2. Response Surface Models
3.3. Analysis of Variance (ANOVA)
3.3.1. Analysis of Variance of Energy Consumption () Responses
3.3.2. Analysis of Variance of Grinding Energy Efficiency (η) Responses
3.4. Validation of the RS Models
3.5. Parametric Study
3.5.1. Effect of Operating Parameters on Response
3.5.2. Effect of Operating Parameters on Response
4. Multi-Objective Optimization Design (MOD)
4.1. Description of the Optimization Problem
4.2. Desirability Function Approach
4.3. Design Optimization Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Curry, J.A.; Ismay, M.J.L.; Jameson, G.J. Mine operating costs and the potential impacts of energy and crushing. Miner. Eng. 2014, 56, 70–80. [Google Scholar] [CrossRef]
- Napier-Munn, T. Is progress in energy-efficient comminution doomed? Miner. Eng. 2015, 73, 1–6. [Google Scholar] [CrossRef]
- Johansson, M.; Bengtsson, M.; Evertsson, M.; Hulthen, E. A fundamental model of an industrial-scale jaw crusher. Miner. Eng. 2017, 105, 69–78. [Google Scholar] [CrossRef]
- Liu, R.Y.; Shi, B.Q.; Li, G.G.; Yu, H. Influence of operating conditions and crushing chamber on energy consumption of cone crusher. Energies 2018, 11, 1102. [Google Scholar] [CrossRef] [Green Version]
- Altun, D.; Gerold, C.; Benzer, H.; Altun, O.; Aydogan, N. Copper ore grinding in a mobile vertical roller mill pilot plant. Int. J. Miner. Process. 2015, 136, 32–36. [Google Scholar] [CrossRef]
- Gao, C.M. History, present situation and development of vertical grinding of cement at home and abroad. Cem. Guide New Epoch. 2017, 3, 22–26. [Google Scholar]
- Schaefer, H.U. Loesche vertical roller mills for the comminution of ores and minerals. Miner. Eng. 2001, 14, 1155–1160. [Google Scholar] [CrossRef]
- Tamashige, T.; Obana, H.; Hamaguchi, M. Operational results of OK series roller mill. In Proceedings of the IEEE Cement Industry Technical Conference, Tarpon Springs, FL, USA, 22–24 May 1990. [Google Scholar] [CrossRef]
- Ito, M.; Sato, K.; Naoi, Y. Productivity increase of the vertical roller mill for cement grinding. In Proceedings of the IEEE Cement Industry Technical Conference, Hershey, PA, USA, 20–24 April 1997. [Google Scholar]
- Roy, G.R. Increasing cement grinding capacity with vertical roller mill technology. In Proceedings of the IEEE Cement Industry Technical Conference, Jacksonville, FL, USA, 5–9 May 2002. [Google Scholar]
- Simmons, M.; Gorby, L.; Terembula, J. Operational experience from the United States’ first vertical roller mill for cement grinding. In Proceedings of the IEEE Cement Industry Technical Conference, Kansas City, MO, USA, 15–20 May 2005. [Google Scholar]
- Jorgensen, S.W. Cement grinding-a comparison between vertical roller mill and ball mill. Cem. Int. 2005, 3, 54–63. [Google Scholar]
- Gerold, C.; Schmitz, C.; Stapelmann, M.; Dardemann, F. Recent installations and developments of loesche vertical roller mills in the ore industry. In Proceedings of the Comminution’12, Cape Town, South Africa, 14–15 November 2012; pp. 1–22. [Google Scholar]
- Gerold, C.; Schmitz, C.; Stapelmann, M.; Dardemann, F. Recent installations and developments of loesche vertical roller mills in the ore industry. In Proceedings of the XXVI International Mineral Processing Congress (IMPC), New Delhi, India, 24–28 September 2012; pp. 18–29. [Google Scholar]
- Brundiek, H.; Poesch, F. A roller mill for cement and blast furnace slag in theory and practice. In Proceedings of the IEEE Cement Industry Technical Conference, San Juan, PR, USA, 4–9 June 1995. [Google Scholar]
- Lian, D.; Xiaoli, L.; Kang, W.; Yang, L. Research on slag grinding process control. In Proceedings of the 34th Chinese Control Conference (CCC), Hangzhou, China, 28–30 July 2015. [Google Scholar]
- He, Y.Q.; Xie, W.N.; Zhao, Y.M.; Li, H.; Wang, S. Triboelectrostatic separation of pulverized fuel of coal power plant based on mineralogical analyses. Int. J. Miner. Process. 2017, 166, 7–12. [Google Scholar] [CrossRef]
- Xie, W.N.; He, Y.Q.; Zhang, Y.H.; Huang, Y.; Li, H.; Wei, H.; Wang, H.F. Simulation study of the energy-size reduction of MPS vertical spindle pulverizer. Fuel 2015, 139, 180–189. [Google Scholar] [CrossRef]
- Xie, W.N.; He, Y.Q.; Shi, F.N.; Huang, Y.; Zuo, W.; Wang, S.; Li, B.; Wei, H.; Zhou, N. Comparison of energy efficiency between E and MPS type vertical spindle pulverizer based on the experimental and industrial sampling tests. Energy 2017, 130, 174–181. [Google Scholar] [CrossRef] [Green Version]
- Shi, F.N.; Xie, W.G. A specific energy-based size reduction model for batch grinding ball mill. Miner. Eng. 2015, 70, 130–140. [Google Scholar] [CrossRef]
- Nadolski, S.; Klein, B.; Kumar, A.; Davaanyam, Z. An energy benchmarking model for mineral comminution. Miner. Eng. 2014, 65, 178–186. [Google Scholar] [CrossRef]
- Touil, D.; Belaadi, S.; Frances, C. The specific selection function effect on clinker grinding efficiency in a dry batch ball mill. Int. J. Miner. Process. 2008, 87, 141–145. [Google Scholar] [CrossRef] [Green Version]
- Boeham, A.; Meissner, P.; Plochberger, T. An energy based comparison of vertical roller mills and tumbling mills. Int. J. Miner. Process. 2015, 136, 37–41. [Google Scholar] [CrossRef]
- Altun, D.; Benzer, H.; Aydogan, N.; Gerold, C. Operational parameters affecting the vertical roller mill performance. Miner. Eng. 2016, 103, 67–71. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments, 8th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2013; pp. 478–479. [Google Scholar]
- Chen, Z.R.; Wang, G.Q.; Xue, D.M.; Bi, Q. Simulation and optimization of gyratory crusher performance based on the discrete element method. Powder Technol. 2020, 376, 93–103. [Google Scholar] [CrossRef]
- Chen, Z.R.; Wang, G.Q.; Xue, D.M.; Cui, D. Simulation and optimization of crushing chamber of gyratory crusher based on the DEM and GA. Powder Technol. 2021, 384, 36–50. [Google Scholar] [CrossRef]
- Pasandideh, S.H.R.; Niaki, S.T.A. Multi-response simulation optimization using genetic algorithm within desirability function framework. Appl. Math. Comput. 2006, 175, 366–382. [Google Scholar] [CrossRef]





| Parameters | Code | −1 | 0 | 1 |
|---|---|---|---|---|
| Loading pressure (MPa) | P | 6 | 7 | 8 |
| Rotation speed (rpm) | n | 350 | 450 | 550 |
| Moisture content (%) | ω | 0 | 1 | 2 |
| No. | P (MPa) | n (rpm) | ω (%) | (kWh/kg) | (kg/kWh) |
|---|---|---|---|---|---|
| 1 | 7.00 | 450.00 | 1.00 | 0.03 | 0.834 |
| 2 | 6.00 | 550.00 | 1.00 | 0.028 | 0.856 |
| 3 | 8.00 | 450.00 | 2.00 | 0.04 | 0.756 |
| 4 | 8.00 | 450.00 | 0.00 | 0.038 | 0.962 |
| 5 | 7.00 | 350.00 | 2.00 | 0.028 | 0.756 |
| 6 | 8.00 | 550.00 | 1.00 | 0.043 | 0.751 |
| 7 | 6.00 | 450.00 | 0.00 | 0.024 | 1.021 |
| 8 | 7.00 | 450.00 | 1.00 | 0.03 | 0.834 |
| 9 | 6.00 | 350.00 | 1.00 | 0.025 | 1.042 |
| 10 | 7.00 | 550.00 | 2.00 | 0.035 | 0.426 |
| 11 | 7.00 | 450.00 | 1.00 | 0.03 | 0.834 |
| 12 | 6.00 | 450.00 | 2.00 | 0.027 | 0.812 |
| 13 | 7.00 | 450.00 | 1.00 | 0.03 | 0.834 |
| 14 | 7.00 | 550.00 | 0.00 | 0.029 | 0.654 |
| 15 | 7.00 | 350.00 | 0.00 | 0.026 | 0.994 |
| 16 | 7.00 | 450.00 | 1.00 | 0.028 | 0.834 |
| 17 | 8.00 | 350.00 | 1.00 | 0.038 | 0.942 |
| Source | Sum of Squares | Df | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 4.948 × 10−4 | 9 | 5.498 × 10−5 | 77.75 | <0.0001 |
| P | 3.781 × 10−4 | 1 | 3.781 × 10−4 | 534.72 | <0.0001 |
| n | 4.050 × 10−5 | 1 | 4.050 × 10−5 | 57.27 | 0.0001 |
| ω | 2.113 × 10−5 | 1 | 2.113 × 10−5 | 29.87 | 0.0009 |
| Pn | 1.000 × 10−6 | 1 | 1.000 × 10−6 | 1.41 | 0.2731 |
| Pω | 2.500 × 10−7 | 1 | 2.500 × 10−7 | 0.35 | 0.5708 |
| nω | 4.000 × 10−6 | 1 | 4.000 × 10−6 | 5.66 | 0.0490 |
| P2 | 4.655 × 10−5 | 1 | 4.655 × 10−5 | 65.83 | <0.0001 |
| n2 | 1.392 × 10−6 | 1 | 1.392 × 10−6 | 1.97 | 0.2034 |
| ω2 | 1.918 × 10−6 | 1 | 1.918 × 10−6 | 2.71 | 0.1435 |
| Residual | 4.950 × 10−6 | 7 | 7.071 × 10−7 | ||
| Lack of Fit | 1.750 × 10−6 | 3 | 5.833 × 10−7 | 0.73 | 0.5860 |
| Pure Error | 3.200 × 10−6 | 4 | 8.000 × 10−7 | ||
| Cor Total | 4.998 × 10−4 | 16 | |||
| R2 | Adjusted R2 | Predicted R2 | Adequate precision | ||
| 0.9901 | 0.9774 | 0.934 | 30.429 | ||
| Source | Sum of Squares | Df | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 0.34 | 9 | 0.038 | 21.82 | 0.0003 |
| P | 0.013 | 1 | 0.013 | 7.42 | 0.0296 |
| n | 0.14 | 1 | 0.14 | 79.48 | <0.0001 |
| ω | 0.097 | 1 | 0.097 | 56.27 | 0.0001 |
| Pn | 6.250 × 10−6 | 1 | 6.250 × 10−6 | 3.625 × 10−3 | 0.9537 |
| Pω | 2.250 × 10−6 | 1 | 2.250 × 10−6 | 1.305 × 10−3 | 0.9722 |
| nω | 2.500 × 10−5 | 1 | 2.500 × 10−5 | 0.015 | 0.9075 |
| P2 | 0.063 | 1 | 0.063 | 36.35 | 0.0005 |
| n2 | 0.014 | 1 | 0.014 | 8.29 | 0.0237 |
| ω2 | 0.020 | 1 | 0.020 | 11.38 | 0.0119 |
| Residual | 0.012 | 7 | 1.724 × 10−3 | ||
| Lack of Fit | 0.012 | 3 | 4.023 × 10−3 | ||
| Pure Error | 0.000 | 4 | 0.000 | ||
| Cor Total | 0.35 | 16 | |||
| R2 | Adjusted R2 | Predicted R2 | Adequate precision | ||
| 0.9656 | 0.9213 | 0.854 | 18.79 | ||
| Parameter | (MPa) | (rpm) | (%) | Desirability | ||
|---|---|---|---|---|---|---|
| Example | 7 | 450 | 1 | 0.03 | 0.834 | / |
| Optimzed | 6 | 350 | 2 | 0.02314 | 1.11343 | 0.449 |
| Parameter | (kWh/kg) | (kg/kWh) |
|---|---|---|
| Predicted | 0.02314 | 1.11343 |
| Experimental | 0.02135 | 1.02981 |
| Error | 7.7% | 9.2% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Chen, Z.; Mao, Y.; Yao, Z.; Zhang, W.; Ye, W.; Duan, Y.; Xie, Q. Analysis and Optimization of Grinding Performance of Vertical Roller Mill Based on Experimental Method. Minerals 2022, 12, 133. https://doi.org/10.3390/min12020133
Liu C, Chen Z, Mao Y, Yao Z, Zhang W, Ye W, Duan Y, Xie Q. Analysis and Optimization of Grinding Performance of Vertical Roller Mill Based on Experimental Method. Minerals. 2022; 12(2):133. https://doi.org/10.3390/min12020133
Chicago/Turabian StyleLiu, Chang, Zuobing Chen, Ya Mao, Zhiming Yao, Weili Zhang, Weidong Ye, Yuanyuan Duan, and Qiang Xie. 2022. "Analysis and Optimization of Grinding Performance of Vertical Roller Mill Based on Experimental Method" Minerals 12, no. 2: 133. https://doi.org/10.3390/min12020133
APA StyleLiu, C., Chen, Z., Mao, Y., Yao, Z., Zhang, W., Ye, W., Duan, Y., & Xie, Q. (2022). Analysis and Optimization of Grinding Performance of Vertical Roller Mill Based on Experimental Method. Minerals, 12(2), 133. https://doi.org/10.3390/min12020133






