A Joint Experiment and Discussion for Strength Characteristics of Cemented Paste Backfill Considering Curing Conditions
Abstract
:1. Introduction
2. Experimental Materials and Methods
2.1. Materials
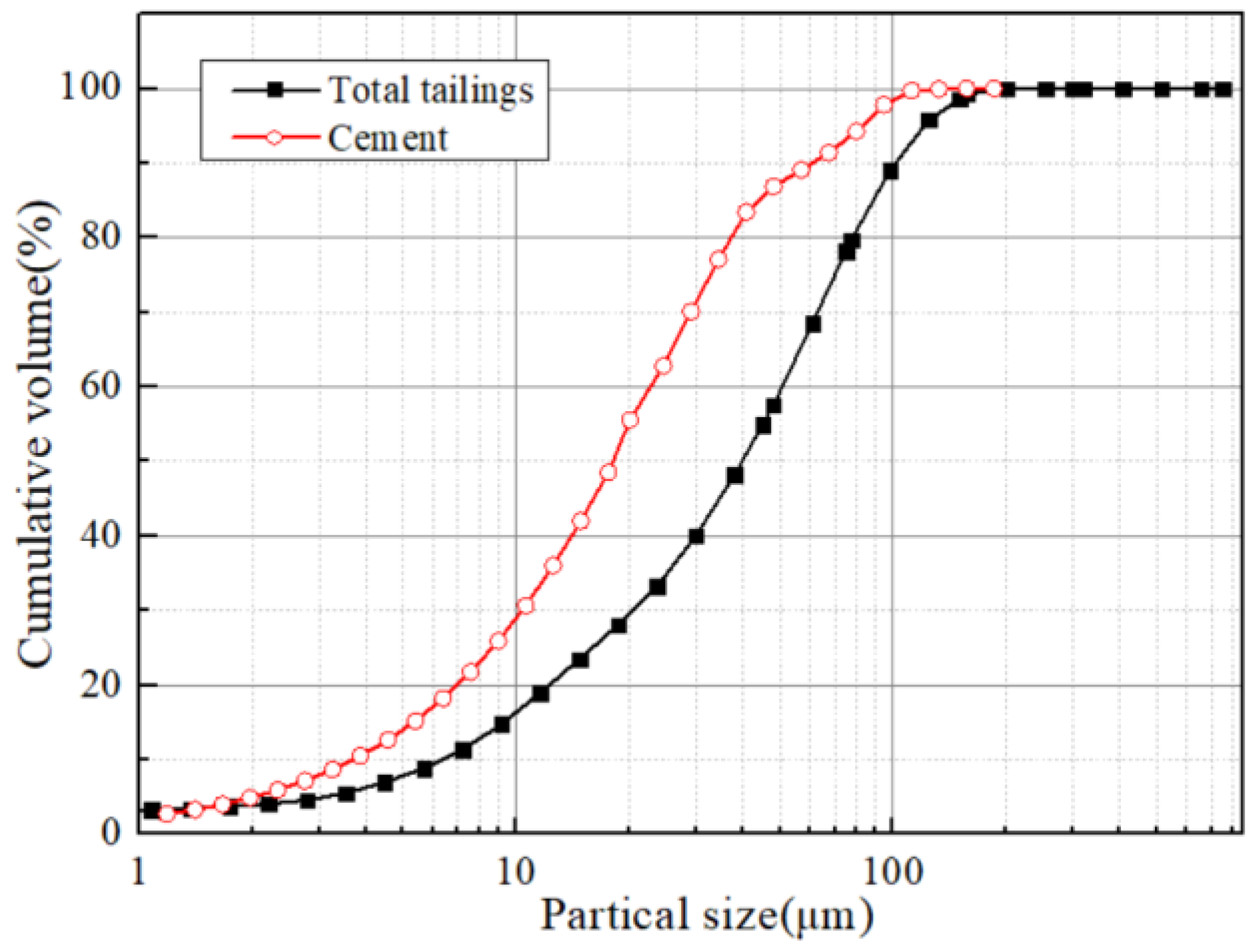
2.1.1. Tailings
2.1.2. Binders
2.1.3. Water
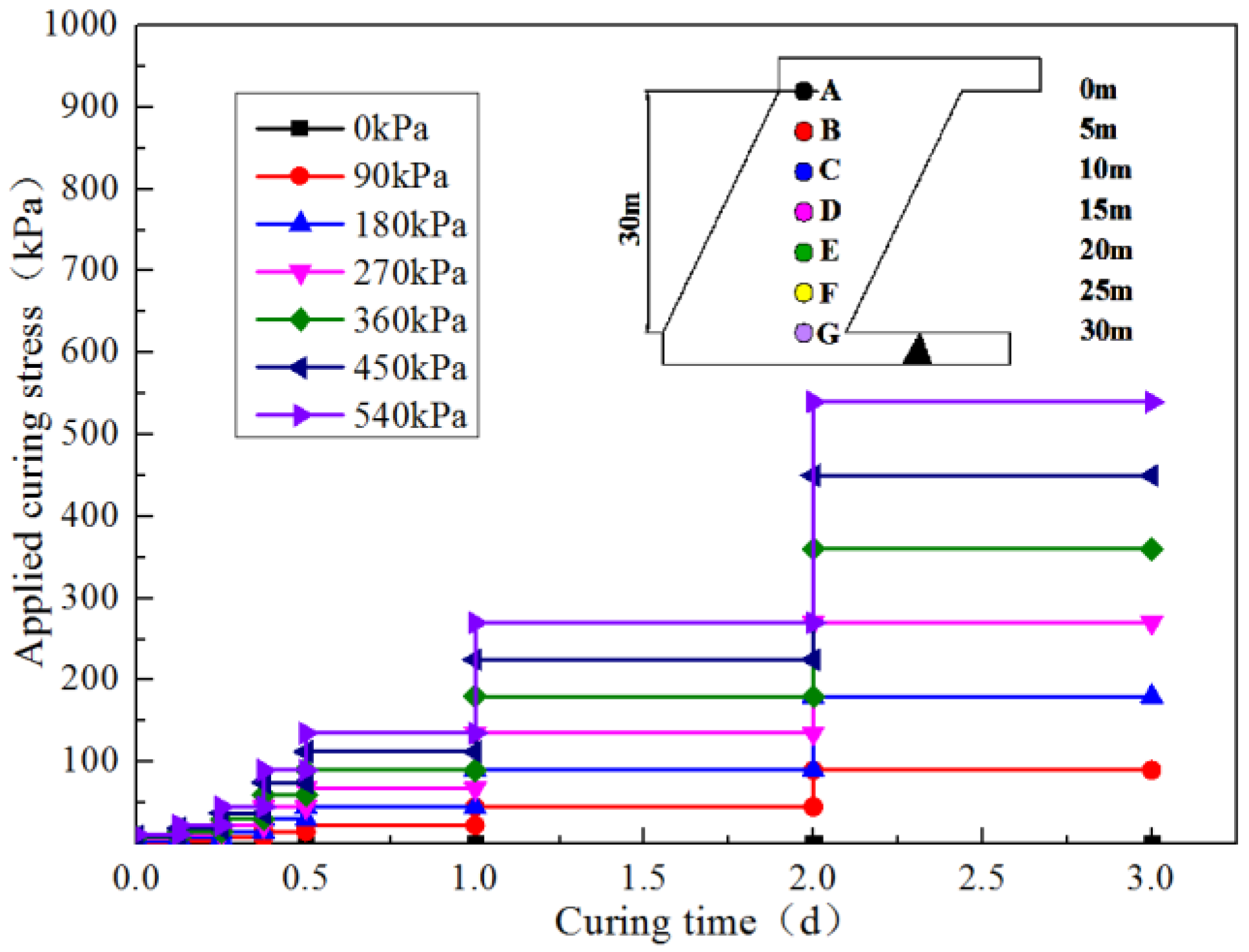
2.2. Preparation and Mix Proportion of CPB
2.3. UCS Tests
3. Results and Discussion
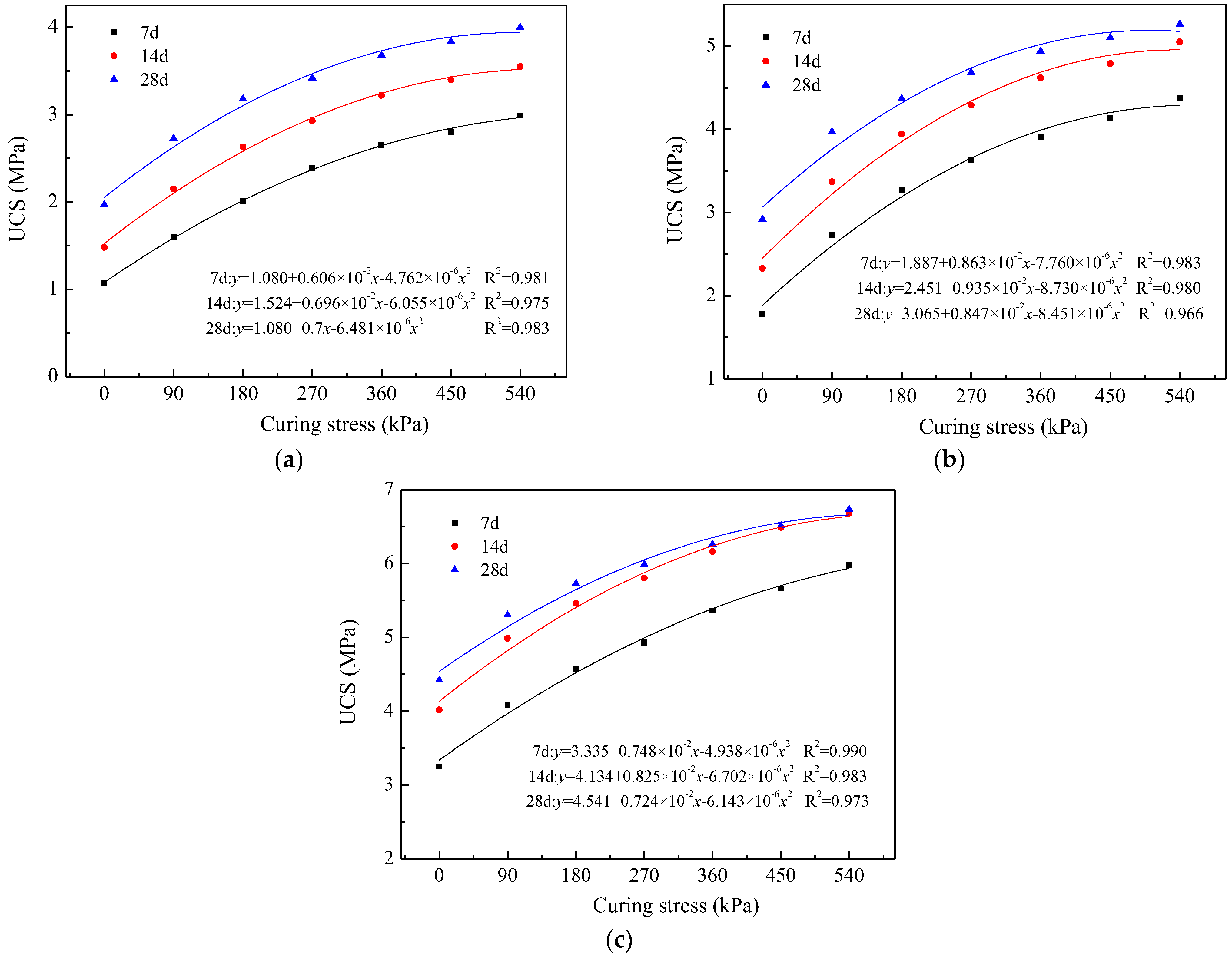
3.1. Influence of Curing Stress on UCS
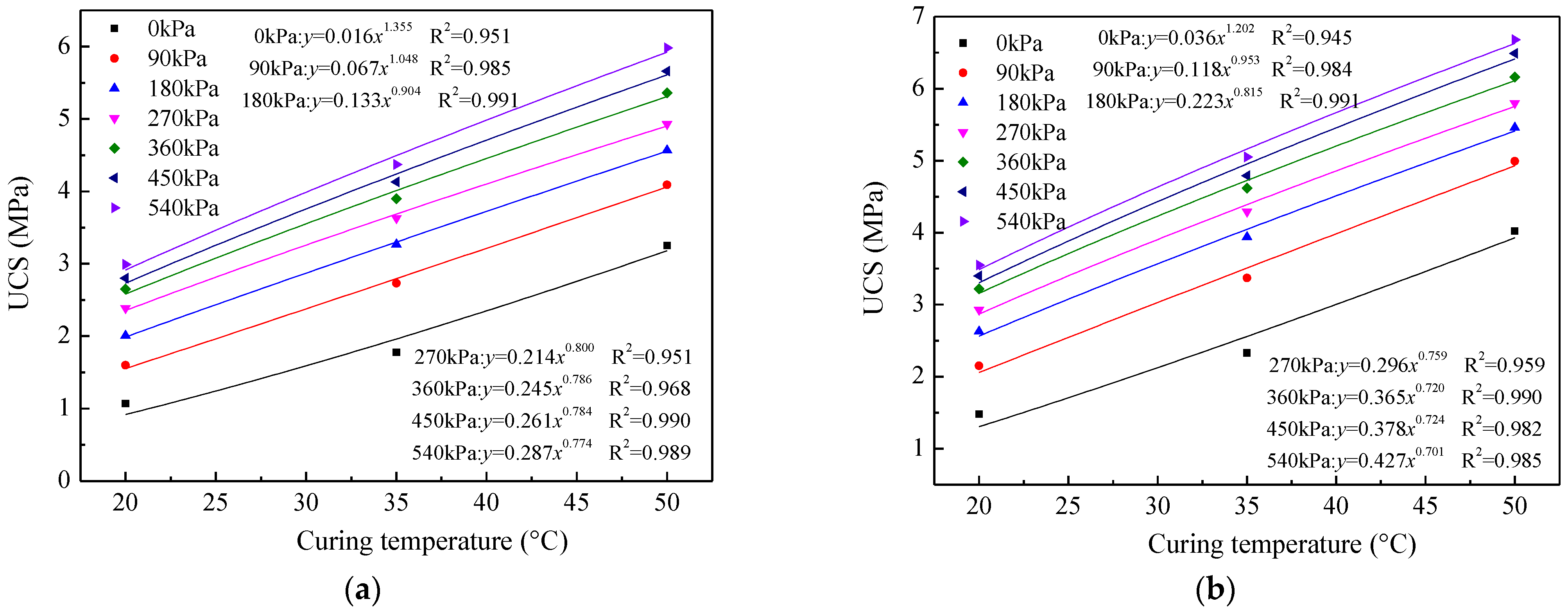
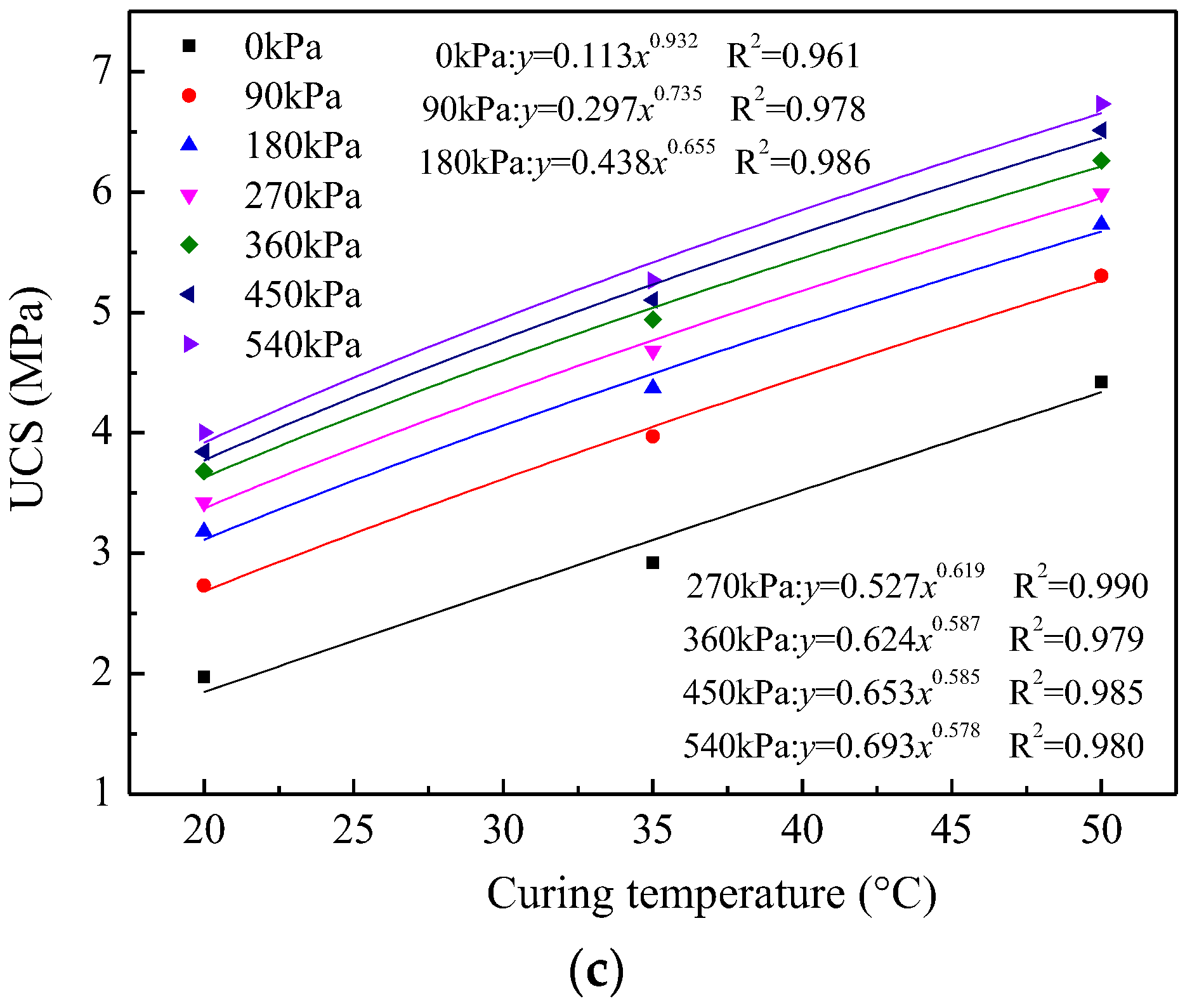
3.2. Influence of Curing Temperature on UCS
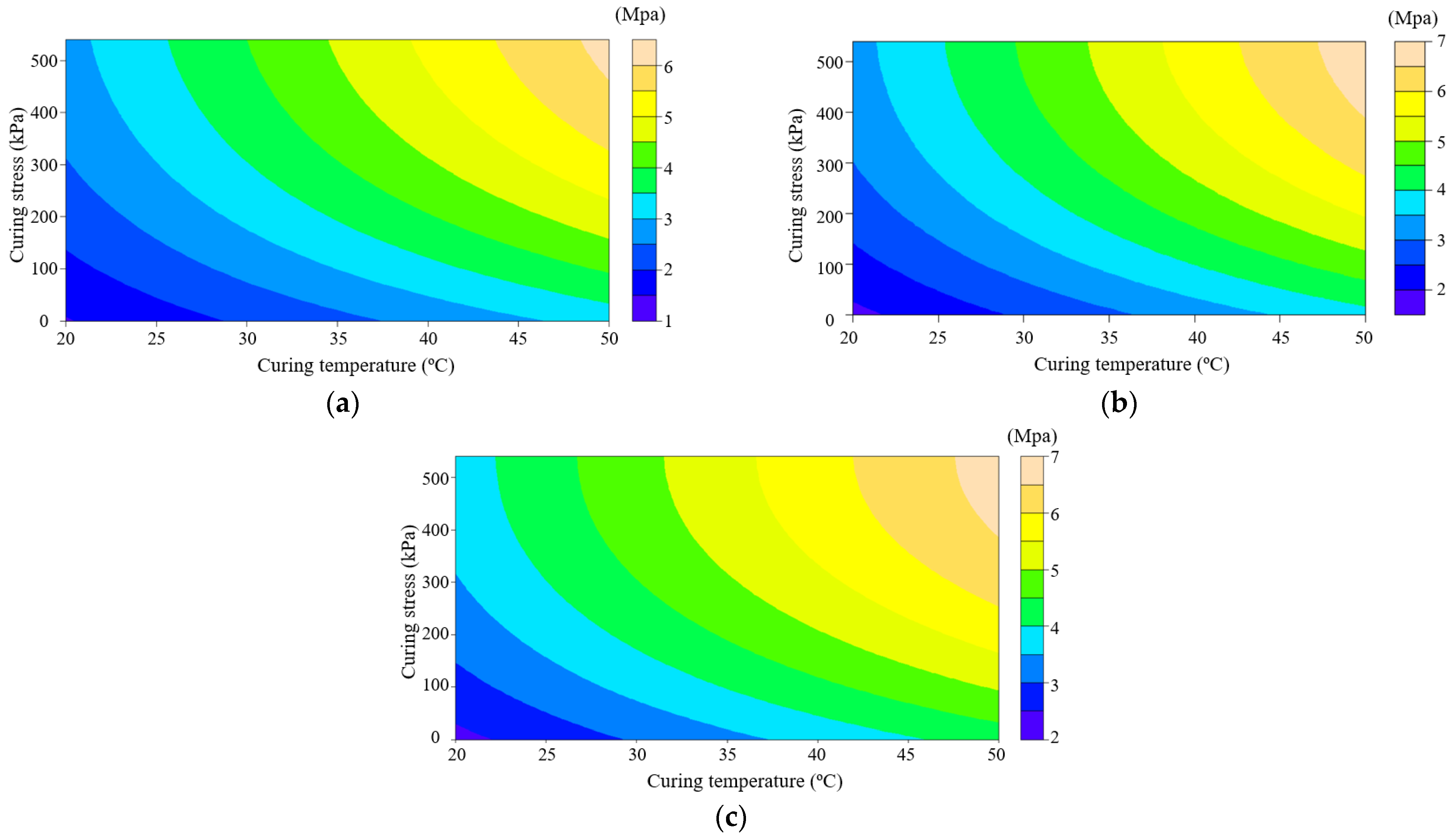
3.3. Coupled Effects of Curing Conditions on UCS
4. Mathematical Strength Model
4.1. Establish of the Mathematical Strength Model
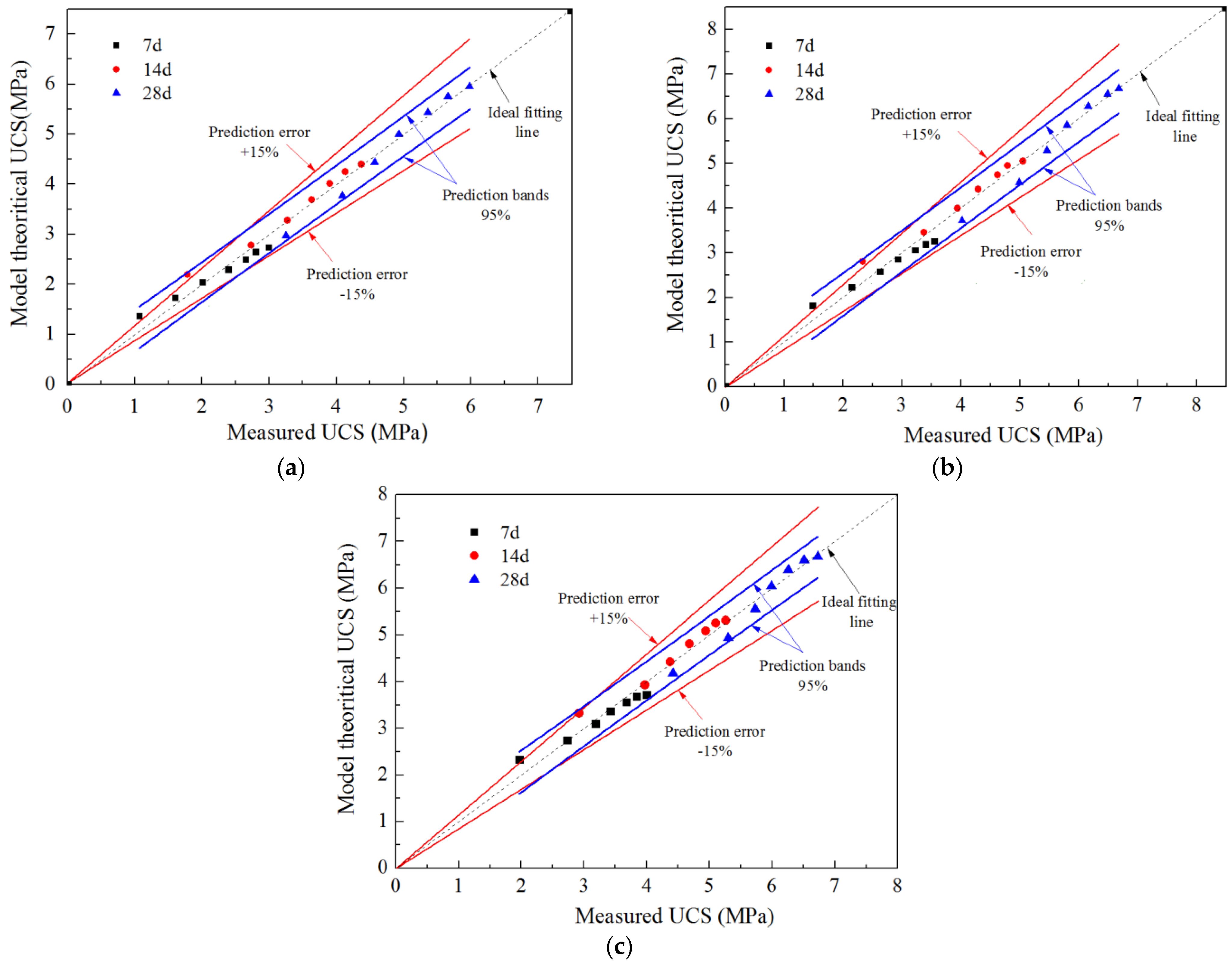
4.2. Comparison of Experimental Results and Theoretical Model for UCS
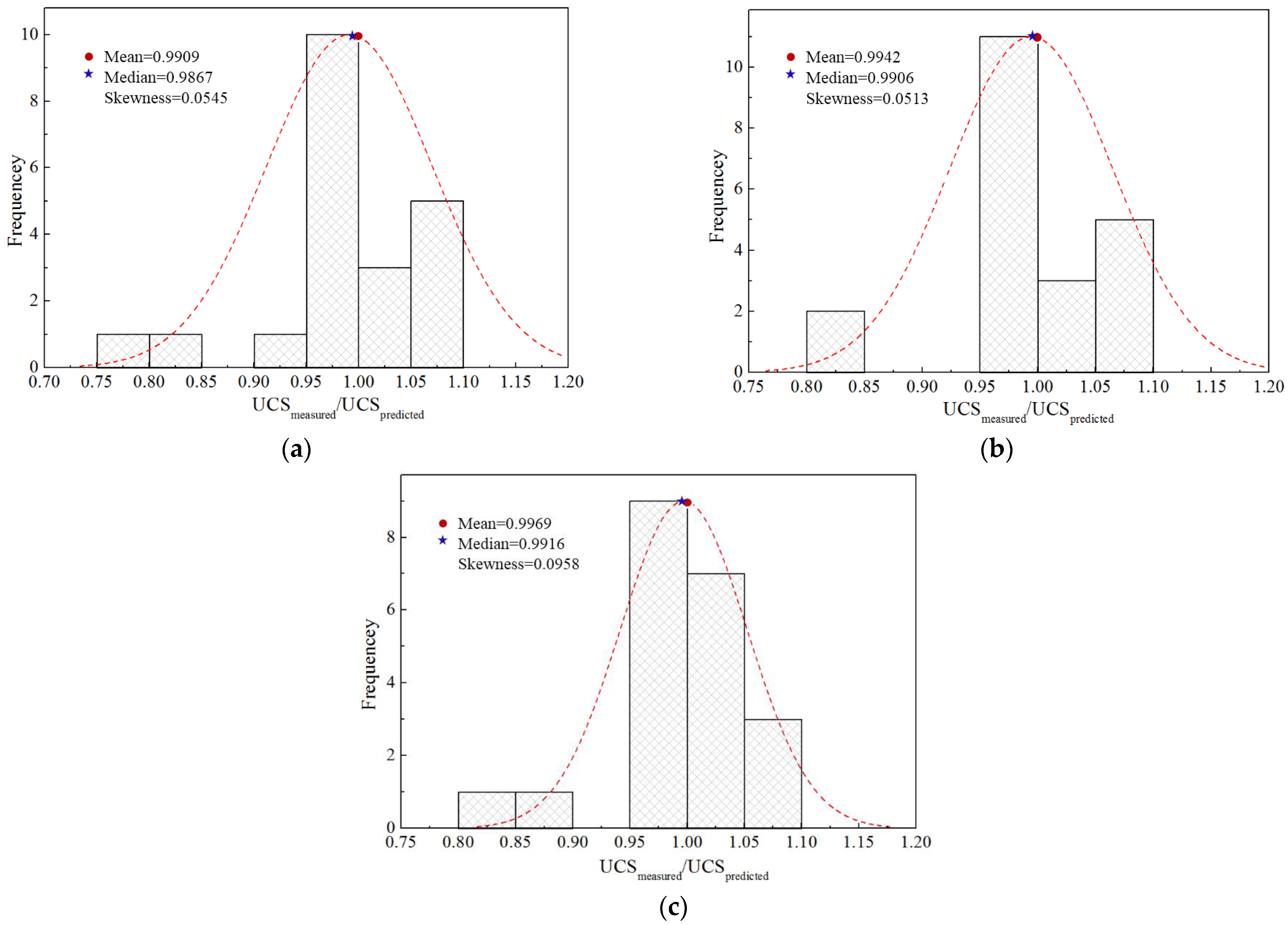
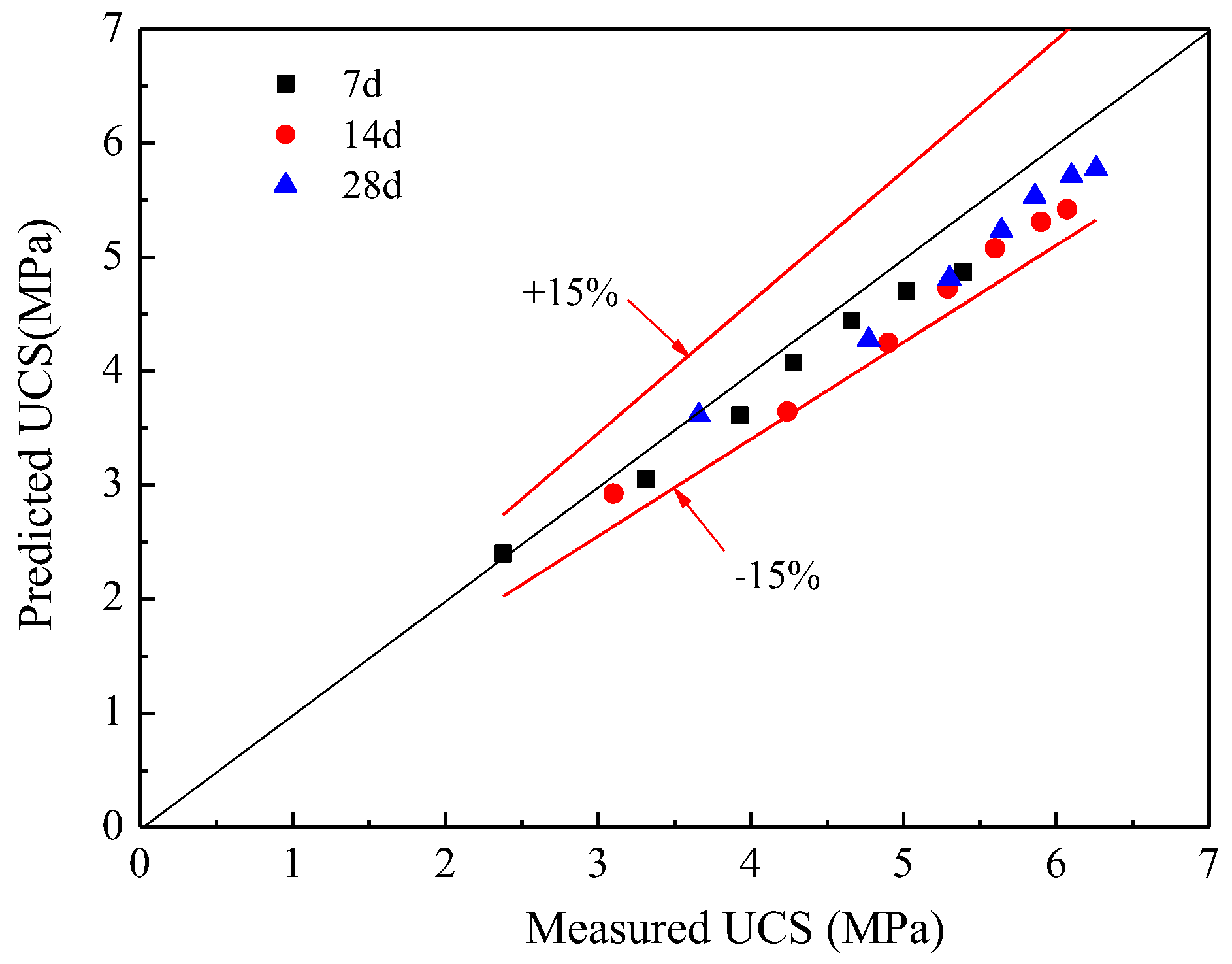
4.3. Verification of the Mathematical Strength Model
5. Conclusions
- (1)
- The results show that the function of quadratic polynomial with one variable can represent the correlation between the UCS and the curing stress well. Moreover, the correlation between the UCS and curing temperature shows the power function.
- (2)
- It is found that the trend of the three curves under different curing ages for the UCS are extremely similar, indicating that there exists a regular rule for the UCS with different curing conditions. The established mathematical strength model for CPB considering the curing conditions is developed.
- (3)
- The established mathematical strength model is verified by the engineering data, the prediction error between the measured UCS and the prediction UCS is less than 15%, all of the specimen points are in the range of prediction bands for 95%, indicating that the prediction results are in agreement with the experiment results under different curing ages, therefore, the established mathematical strength model is rational, which can provide some technical support for the mix proportion design of CPB.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Qi, C.; Fourie, A. Cemented paste backfill for mineral tailings management: Review and future perspectives. Miner. Eng. 2019, 144, 106025. [Google Scholar] [CrossRef]
- Sun, Q.; Li, X.L.; Wei, X.; Mu, Q.W. Experimental study on the influence of mine water corrosion over filling paste strength. Bull. Chin. Ceram. Soc. 2015, 34, 1246–1251. [Google Scholar]
- Wang, Q.; Shi, M.; Wang, D. Influence of elevated curing temperature on the properties of cement paste and concrete at the same hydration degree. J. Wuhan Uni. Technol. Mater. Sci. Ed. 2017, 32, 1344–1351. [Google Scholar] [CrossRef]
- Wu, D.; Zhang, Y.; Liu, Y. Mechanical performance and ultrasonic properties of cemented gangue backfill with admixture of fly ash. Ultrason 2016, 64, 89–96. [Google Scholar] [CrossRef]
- Hasan, E.; Atac, B. Influence of silica fume on mechanical property of cemented paste backfill. Constr. Build. Mater. 2022, 317, 1–9. [Google Scholar]
- Lu, G.D.; Fall, M.; Cui, L. A multiphysics-viscoplastic cap model for simulating blast response of cemented tailings backfill. J. Rock Mech. Geotech. Eng. 2017, 9, 551–564. [Google Scholar] [CrossRef]
- Kashani, A.; Nicolas, S.R.; Qiao, G.G.; Deventer, J.S.J.; Provis, J.L. Modelling the yield stress of ternary cement-slag-fly ash pastes based on particle size distribution. Powder Technol. 2014, 266, 203–209. [Google Scholar] [CrossRef]
- Dong, Q.; Liang, B.; Jia, L.F.; Jiang, L.G. Effect of sulfide on the long-term strength of lead-zinc tailings cemented paste backfill. Constr. Build. Mater. 2019, 200, 436–446. [Google Scholar] [CrossRef]
- Xiu, Z.G.; Wang, S.H.; Ji, Y.C.; Wang, F.L.; Ren, F.Y.; Wang, P.Y. An analytical model for the triaxial compressive Stress-strain relationships of Cemented Pasted Backfill (CPB) with different curing time. Constr. Build. Mater. 2021, 313, 1087–1102. [Google Scholar] [CrossRef]
- Yilmaz, E.; Belem, T.; Benzaazoua, M.; Kesimal, A.; Ercikdi, B. Evaluation of the strength properties of deslimed tailings paste backfill. Miner. Resour. Eng. 2013, 12, 129–144. [Google Scholar]
- Bull, A.J.; Fall, M. Curing temperature dependency of the release of arsenic from cemented paste backfill made with Portland cement. J. Environ. Manag. 2020, 269, 110772. [Google Scholar] [CrossRef] [PubMed]
- Fall, M.; Samb, S.S. Influence of curing temperature on strength, deformation behaviour and pore structure of cemented paste backfill at early ages. Constr. Build. Mater. 2006, 305, 125–135. [Google Scholar] [CrossRef]
- Jiang, H.Q.; Fall, M.; Yilmaz, E.; Li, Y.H.; Yang, L. Effect of mineral admixtures on flow properties of fresh cemented paste backfill: Assessment of time dependency and thixotropy. Powder Technol. 2020, 372, 258–266. [Google Scholar] [CrossRef]
- Liu, L.; Xin, J.; Huan, C.; Qi, C.; Song, K.L. Pore and strength characteristics of cemented paste backfill using sulphide tailings: Effect of sulphur content. Constr. Build. Mater. 2020, 237, 117452. [Google Scholar] [CrossRef]
- Tian, X.C.; Fall, M. Non-isothermal evolution of mechanical properties, pore structure and self-desiccation of cemented paste backfill. Constr. Build. Mater. 2021, 297, 123657. [Google Scholar] [CrossRef]
- Yang, L.H.; Wang, H.J.; Wu, A.X.; Li, H.; Bruno, T.A.; Zhou, X.; Wang, X.T. Effect of mixing time on hydration kinetics and mechanical property of cemented paste backfill. Constr. Build. Mater. 2020, 247, 118516. [Google Scholar] [CrossRef]
- Zhao, Y.; Taheri, A.; Karakus, M.; Chen, Z.W.; Deng, A. Effects of water content, water type and temperature on the rheological behaviour of slag-cement and fly ash-cement paste backfill. Int. J. Min. Sci. Technol. 2020, 30, 271–278. [Google Scholar] [CrossRef]
- Libos, I.L.S.; Cui, L. Effects of curing time, cement content, and saturation state on mode-I fracture toughness of cemented paste backfill. Eng. Fract. Mech. 2020, 235, 107174. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, C.; Fu, J.X.; Song, W.D.; Zhang, Y.F. Effect of water saturation on mechanical characteristics and damage behavior of cemented paste backfill. J. Mater. Res. Technol. 2021, 15, 6624–6639. [Google Scholar] [CrossRef]
- Yilmaz, E.; Belem, T.; Bussière, B.; Mbonimpa, M.; Benzaazoua, M. Curing time effect on consolidation behaviour of cemented paste backfill containing different cement types and contents. Constr. Build. Mater. 2015, 75, 99–111. [Google Scholar] [CrossRef]
- Zhou, Y.B.; Fall, M.; Haruna, S. Flow ability of cemented paste backfill with chloride-free antifreeze additives in sub-zero environments. Cem. Concr. Compos. 2022, 126, 104359. [Google Scholar] [CrossRef]
- Ghirian, A. Coupled Thermo-Hydro-Mechanical-Chemical (THMC) Processes in Cemented Tailings Backfill Structures and Implications for Their Engineering Design. Ph.D. Thesis, University of Ottawa, Ottawa, ON, Canada, 2016. [Google Scholar]
- Ouyang, S.Y.; Huang, Y.L.; Zhou, N. Experiment on hydration exothermic characteristics and hydration mechanism of sand-based cemented paste backfill materials. Constr. Build. Mater. 2022, 318, 125870. [Google Scholar] [CrossRef]
- Fall, M.; Benzaazoua, M.; Ouellet, S. Experimental characterization of the influence of tailings fineness and density on the quality of cemented paste backfill. Miner. Eng. 2005, 18, 41–44. [Google Scholar] [CrossRef]
- Zhang, Q.L.; Li, X.P.; Yang, W. Optimization of filling slurry ratio in a mine based on back-propagation neural network. J. Cent. South Univ. (Sci. Tech.) 2013, 44, 2867–2874. [Google Scholar]
- Huang, S.; Xia, K.W.; Qiao, L. Dynamic tests of cemented paste backfill: Effects of strain rate, curing time, and cement content on compressive strength. J. Mater. Sci. 2011, 46, 5165–5170. [Google Scholar] [CrossRef]
- Ehsan, S.; Hakan, B.; Luo, G.H.; Ali, K.; Richard, D.; Andy, F.; Mohamed, E. Multi-objective mixture design of cemented paste backfill using particle swarm optimisation algorithm. Miner. Eng. 2020, 153, 106385. [Google Scholar]
- Li, D.; Feng, G.R.; Guo, Y.X.; Qi, T.Y.; Jia, X.Q.; Feng, J.R.; Li, Z. Analysis on the strength increase law of filling material based on response surface method. J. China Coal Soc. 2016, 41, 392–398. [Google Scholar]
- Zhao, G.Y.; Ma, J.; Peng, K.; Yang, Q.; Zhou, L. Mix ratio optimization of alpine mine backfill based on the response surface method. Chin. J. Eng. 2013, 35, 559–565. [Google Scholar]
- Xu, M.F.; Gao, Y.T.; Jin, A.B.; Zhou, Y.; Guo, L.J.; Liu, G.S. Prediction of cemented backfill strength by ultrasonic pulse velocity and BP neural network. Chin. J. Eng. 2016, 38, 1059–1068. [Google Scholar]
- Wei, W.; Gao, Q. Strength prediction of backfilling body based on modified BP neural network. J. Harbin Inst. Technol. 2013, 45, 90–95. [Google Scholar]
- Qi, C.; Chen, Q.; Fourie, A.; Zhang, Q. An intelligent modelling framework for mechanical properties of cemented paste backfill. Miner. Eng. 2018, 123, 16–27. [Google Scholar] [CrossRef]
- Mitchell, R.J.; Olsen, R.S.; Smith, J.D. Model studies on cemented tailings used in mine backfill. Can. Geotech. J. 2011, 19, 14–28. [Google Scholar] [CrossRef]
- Fu, Z.G.; Qiao, D.P.; Guo, Z.L.; Li, K.G.; Xie, J.C.; Wang, J.X. A model for calculating strength of ultra-fine tailings cemented hydraulic fill and its application. Rock Soil Mech. 2018, 39, 3147–3156. [Google Scholar]
- Qi, C.C.; Chen, Q.S.; Kim, S.S. Integrated and intelligent design framework for cemented paste backfill: A combination of robust machine learning modelling and multi-objective optimization. Miner. Eng. 2020, 155, 106422. [Google Scholar] [CrossRef]
- Wei, X.; Li, C.; Zhang, L.; Zhou, X.; Hu, B. Strength prediction model of cemented backfill and inversion calculation of cement consumption. Geotech. Geol. Eng. 2018, 36, 649–656. [Google Scholar] [CrossRef]
- Orejarena, L.; Fall, M. Artificial neural network based modeling of the coupled effect of sulphate and temperature on the strength of cemented paste backfill. Can. J. Civ. Eng. 2011, 38, 100–109. [Google Scholar] [CrossRef]
- Cui, L.; Fall, M. Mathematical modelling of cemented tailings backfill: A review. Int. J. Mining, Reclam. Environ. 2018, 33, 389–408. [Google Scholar] [CrossRef]
- Zhao, Y.L.; Wu, P.Q.; Qiu, J.P.; Guo, Z.B.; Tian, Y.S.; Sun, X.G.; Gu, X.W. Recycling hazardous steel slag after thermal treatment to produce a binder for cemented paste backfill. Powder Technol. 2022, 395, 652–662. [Google Scholar] [CrossRef]
- Klein, K.; Simon, D. Effect of specimen composition on the strength development in cemented paste backfill. Can. Geotech. J. 2006, 43, 310–324. [Google Scholar] [CrossRef]
- Cao, S.; Yilmaz, E.; Song, W.D. Fiber type effect on strength, toughness and microstructure of early age cemented tailings backfill. Constr. Build. Mater. 2019, 223, 44–54. [Google Scholar] [CrossRef]
- Chen, S.J.; Du, Z.W.; Zhang, Z.; Zhang, H.W.; Xia, Z.G.; Feng, F. Effects of chloride on the early mechanical properties and microstructure of gangue-cemented paste backfill. Constr. Build. Mater. 2020, 235, 117504. [Google Scholar] [CrossRef]
- Li, W.C.; Fall, M. Strength and self-desiccation of slag-cemented paste backfill at early ages: Link to initial sulphate concentration. Cem. Concr. Compos. 2018, 89, 160–168. [Google Scholar] [CrossRef]
- Fahey, M.; Helinski, M.; Fourie, A. Development of specimen curing procedures that account for the influence of effective stress during curing on the strength of cemented mine backfill. Geotech. Geol. Eng. 2011, 29, 709–723. [Google Scholar] [CrossRef]
- Ghirian, A.; Fall, M. Strength evolution and deformation behaviour of cemented paste backfill at early ages: Effect of curing stress, filling strategy and drainage. Int. J. Min. Sci. Technol. 2016, 26, 809–817. [Google Scholar] [CrossRef]
- Qiu, J.P.; Guo, Z.B.; Yang, L.; Jiang, H.Q.; Zhao, Y.L. Effect of tailings fineness on flow, strength, ultrasonic and microstructure characteristics of cemented paste backfill. Constr. Build. Mater. 2020, 263, 120645. [Google Scholar] [CrossRef]
- Zisi, C.; Pappa-Louisi, A.; Nikitas, P. Separation optimization in HPLC analysis implemented in R programming language. J. Chromatogr. A. 2020, 1617, 460823. [Google Scholar] [CrossRef] [PubMed]

| Parameter | Al2O3 (%) | CaO (%) | FeO3 (%) | MgO (%) | P2O5 (%) | SiO2 (%) | TiO2 (%) | Na2O (%) | K2O (%) |
|---|---|---|---|---|---|---|---|---|---|
| Tailings | 1.04 | 44.05 | 2.89 | 5.02 | 0.18 | 43.55 | 0.35 | 0.10 | 2.82 |
| OPC | 5.37 | 66.18 | 3.36 | 3.01 | 0.11 | 21.12 | 0.20 | 0.2 | 0.45 |
| Curing Time (d) | Curing Temperature (°C) | UCS Growth Rate (%) | ||||||
|---|---|---|---|---|---|---|---|---|
| 0 kPa | 90 kPa | 180 kPa | 270 kPa | 360 kPa | 450 kPa | 540 kPa | ||
| 7 | 20 | 0 | 49.53 | 25.63 | 18.91 | 10.88 | 5.66 | 6.79 |
| 35 | 0 | 53.37 | 19.78 | 11.01 | 7.44 | 5.90 | 5.81 | |
| 50 | 0 | 25.85 | 11.74 | 7.88 | 8.72 | 5.60 | 5.65 | |
| 14 | 20 | 0 | 45.27 | 22.33 | 11.41 | 9.90 | 5.59 | 4.41 |
| 35 | 0 | 44.64 | 16.91 | 8.88 | 7.69 | 3.68 | 5.43 | |
| 50 | 0 | 24.13 | 9.42 | 6.23 | 6.21 | 5.36 | 2.93 | |
| 28 | 20 | 0 | 38.58 | 16.48 | 7.55 | 7.60 | 4.35 | 4.17 |
| 35 | 0 | 35.96 | 10.08 | 7.09 | 5.56 | 3.24 | 3.14 | |
| 50 | 0 | 19.91 | 8.11 | 4.54 | 4.51 | 3.99 | 3.38 | |
| Curing Time (d) | Curing Temperature (°C) | UCS Growth Rate (%) | ||||||
|---|---|---|---|---|---|---|---|---|
| 0 kPa | 90 kPa | 180 kPa | 270 kPa | 360 kPa | 450 kPa | 540 kPa | ||
| 7 | 20 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 35 | 66.36 | 70.63 | 62.69 | 51.88 | 47.17 | 47.50 | 46.15 | |
| 50 | 82.58 | 49.82 | 39.76 | 35.81 | 37.44 | 37.05 | 36.84 | |
| 14 | 20 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 35 | 57.43 | 56.74 | 49.81 | 46.42 | 43.48 | 40.88 | 42.25 | |
| 50 | 72.53 | 48.07 | 38.58 | 35.20 | 33.33 | 35.49 | 32.28 | |
| 28 | 20 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 35 | 48.22 | 45.42 | 37.42 | 36.84 | 34.24 | 32.81 | 31.50 | |
| 50 | 51.37 | 33.50 | 31.12 | 27.99 | 26.72 | 27.65 | 27.95 | |
| Curing Time (d) | Parameters | R2 | |||
|---|---|---|---|---|---|
| e | |||||
| 7 | 0.108 | 3.446 × 10−4 | −2.663 × 10−7 | 0.847 | 0.977 |
| 14 | 0.175 | 4.854 × 10−4 | −7.603 × 10−7 | 0.782 | 0.972 |
| 28 | 0.345 | 7.009 × 10−4 | −7.009 × 10−7 | 0.637 | 0.970 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Wang, W.; Yan, R.; Wu, A.; Wang, Y.; Yilmaz, E. A Joint Experiment and Discussion for Strength Characteristics of Cemented Paste Backfill Considering Curing Conditions. Minerals 2022, 12, 211. https://doi.org/10.3390/min12020211
Chen S, Wang W, Yan R, Wu A, Wang Y, Yilmaz E. A Joint Experiment and Discussion for Strength Characteristics of Cemented Paste Backfill Considering Curing Conditions. Minerals. 2022; 12(2):211. https://doi.org/10.3390/min12020211
Chicago/Turabian StyleChen, Shunman, Wei Wang, Rongfu Yan, Aixiang Wu, Yiming Wang, and Erol Yilmaz. 2022. "A Joint Experiment and Discussion for Strength Characteristics of Cemented Paste Backfill Considering Curing Conditions" Minerals 12, no. 2: 211. https://doi.org/10.3390/min12020211
APA StyleChen, S., Wang, W., Yan, R., Wu, A., Wang, Y., & Yilmaz, E. (2022). A Joint Experiment and Discussion for Strength Characteristics of Cemented Paste Backfill Considering Curing Conditions. Minerals, 12(2), 211. https://doi.org/10.3390/min12020211







