An Improved Capacity Model of the Cone Crushers Based on the Motion Characteristics of Particles Considering the Influence of the Spatial Compound Motion of the Mantle
Abstract
:1. Introduction
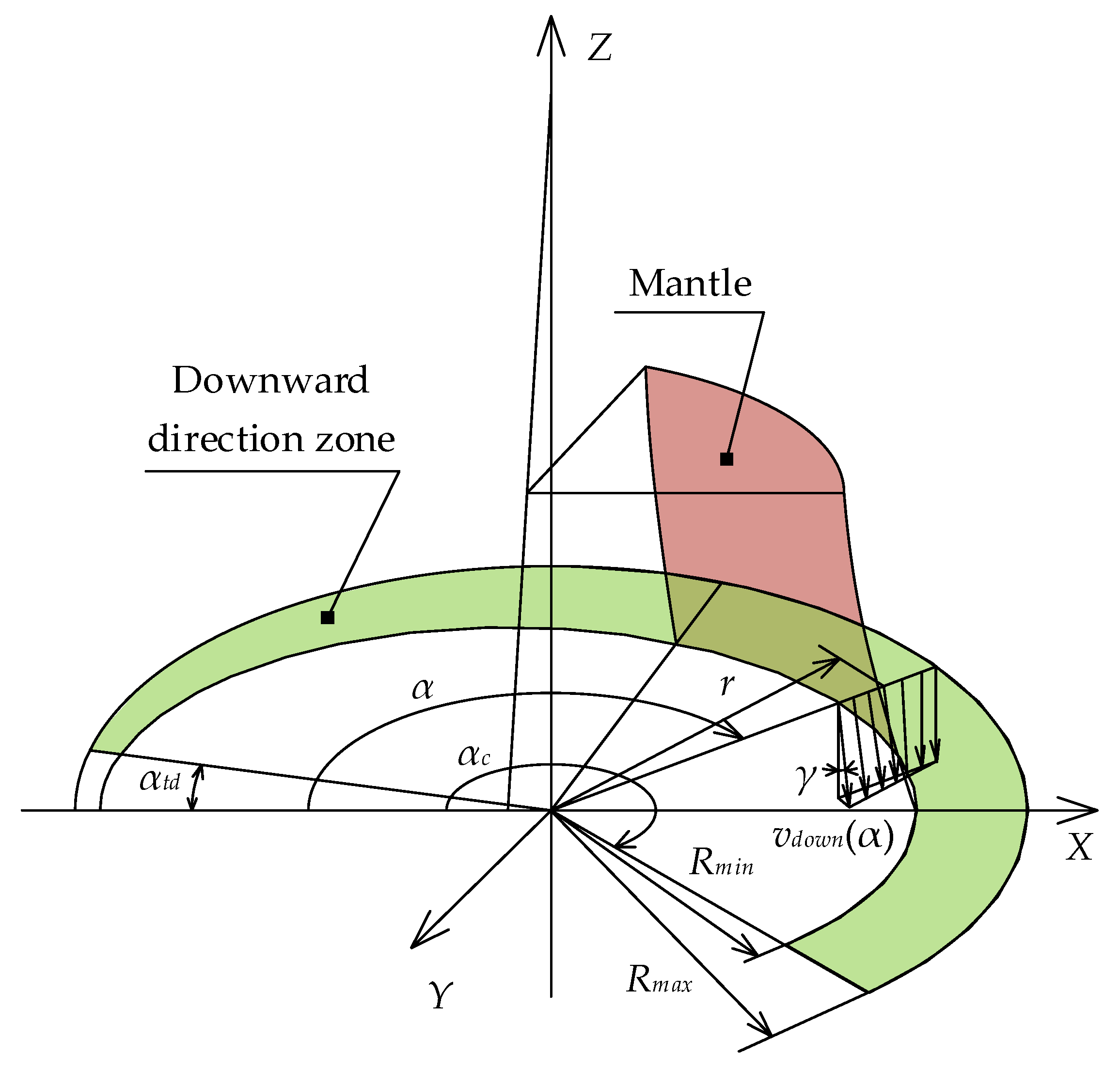
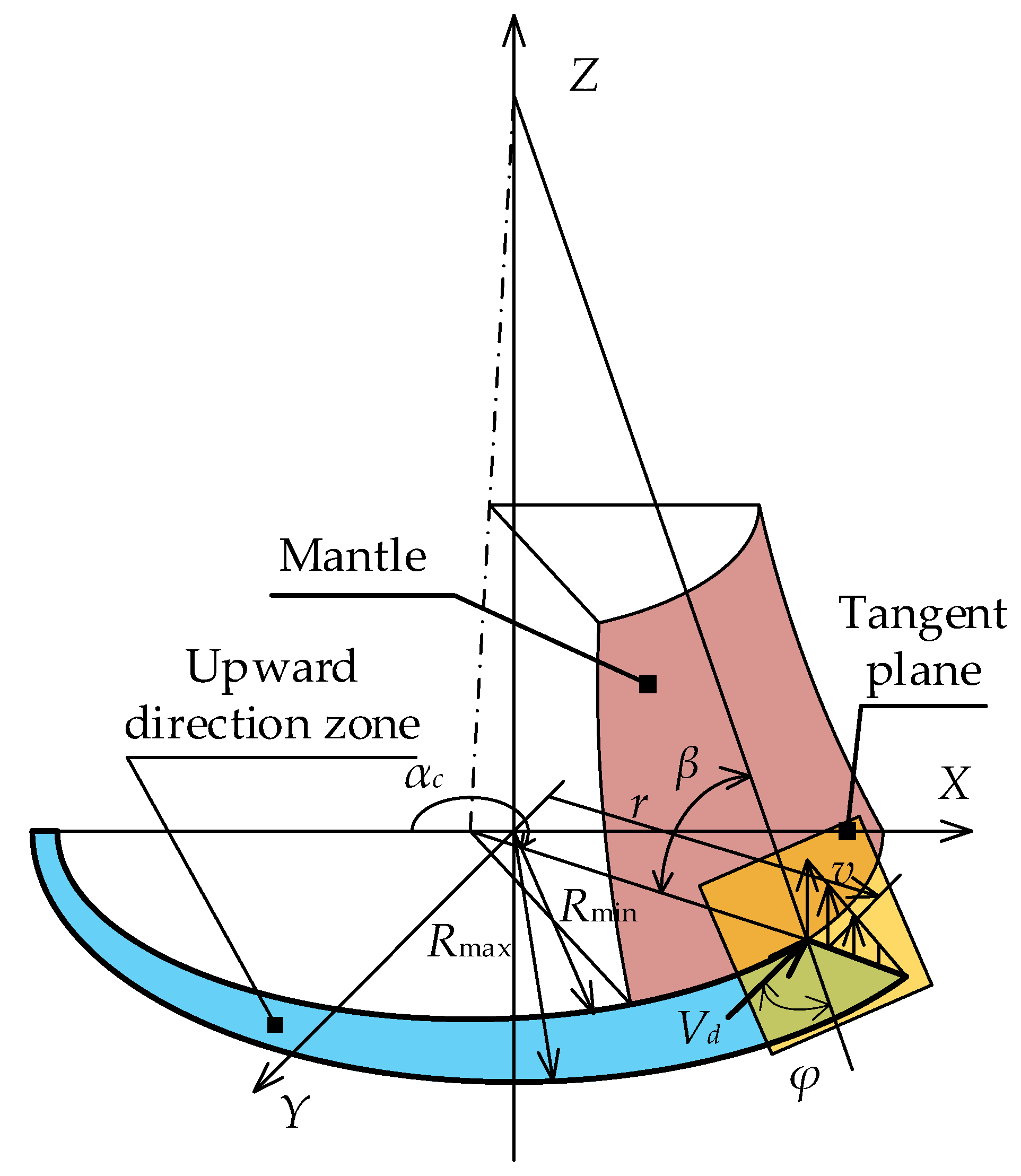
2. Motion Characteristics of Particles Affected by Spatial Compound Motion of the Mantle
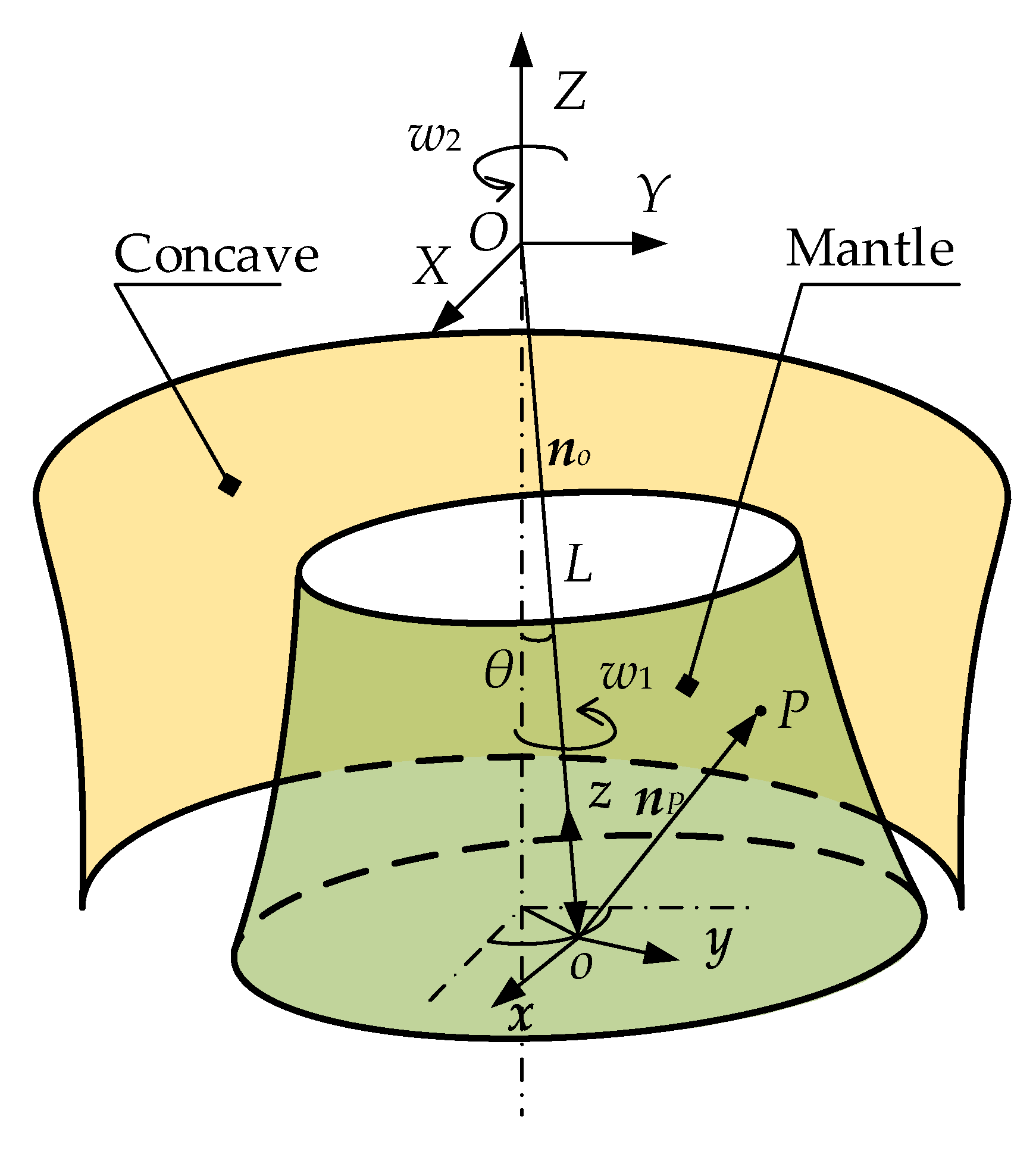
2.1. Spatial Compound Motion of the Mantle
2.2. Motion Characteristics of Particles in the Crushing Chamber
2.2.1. Coordinate System Transformation Matrix
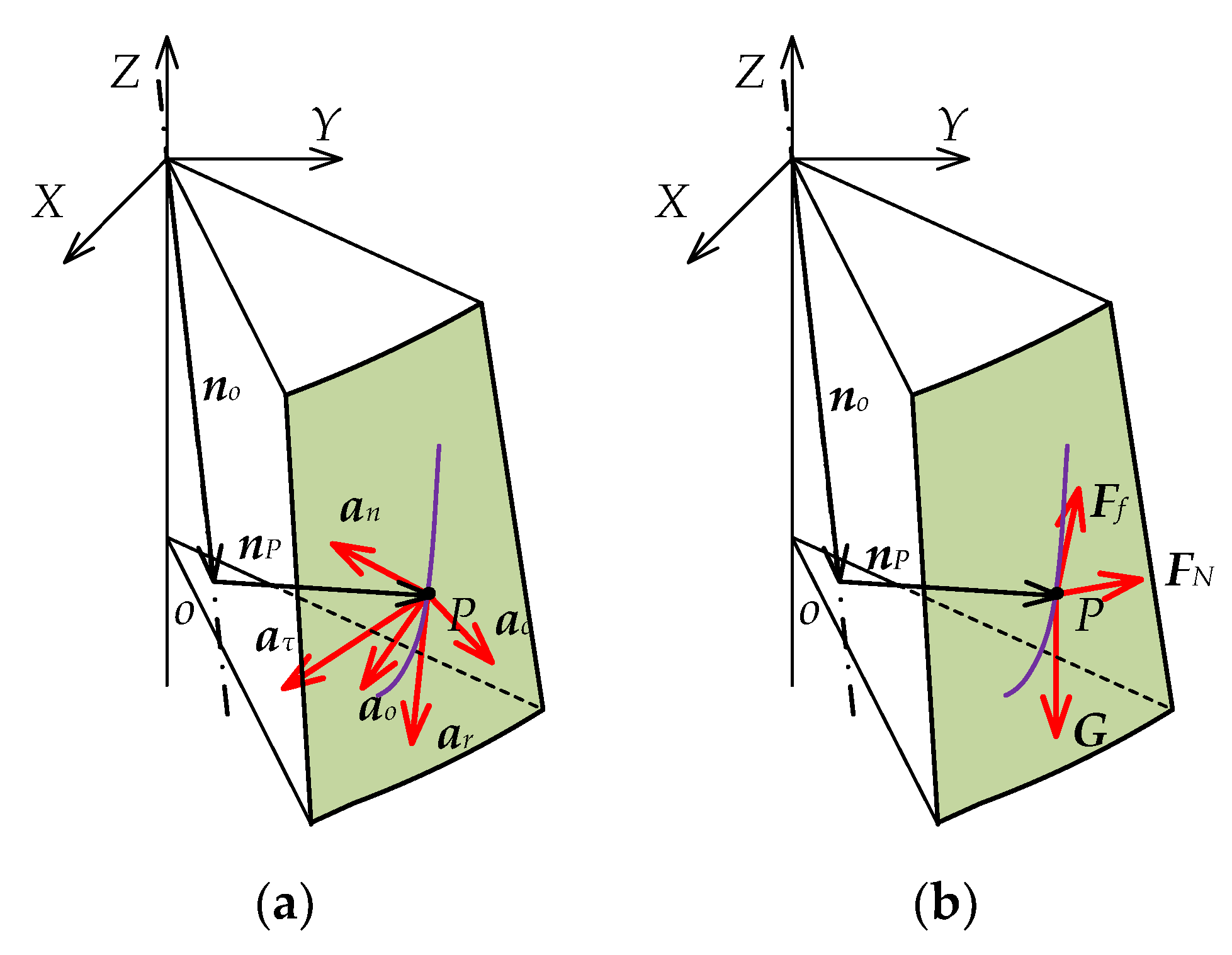
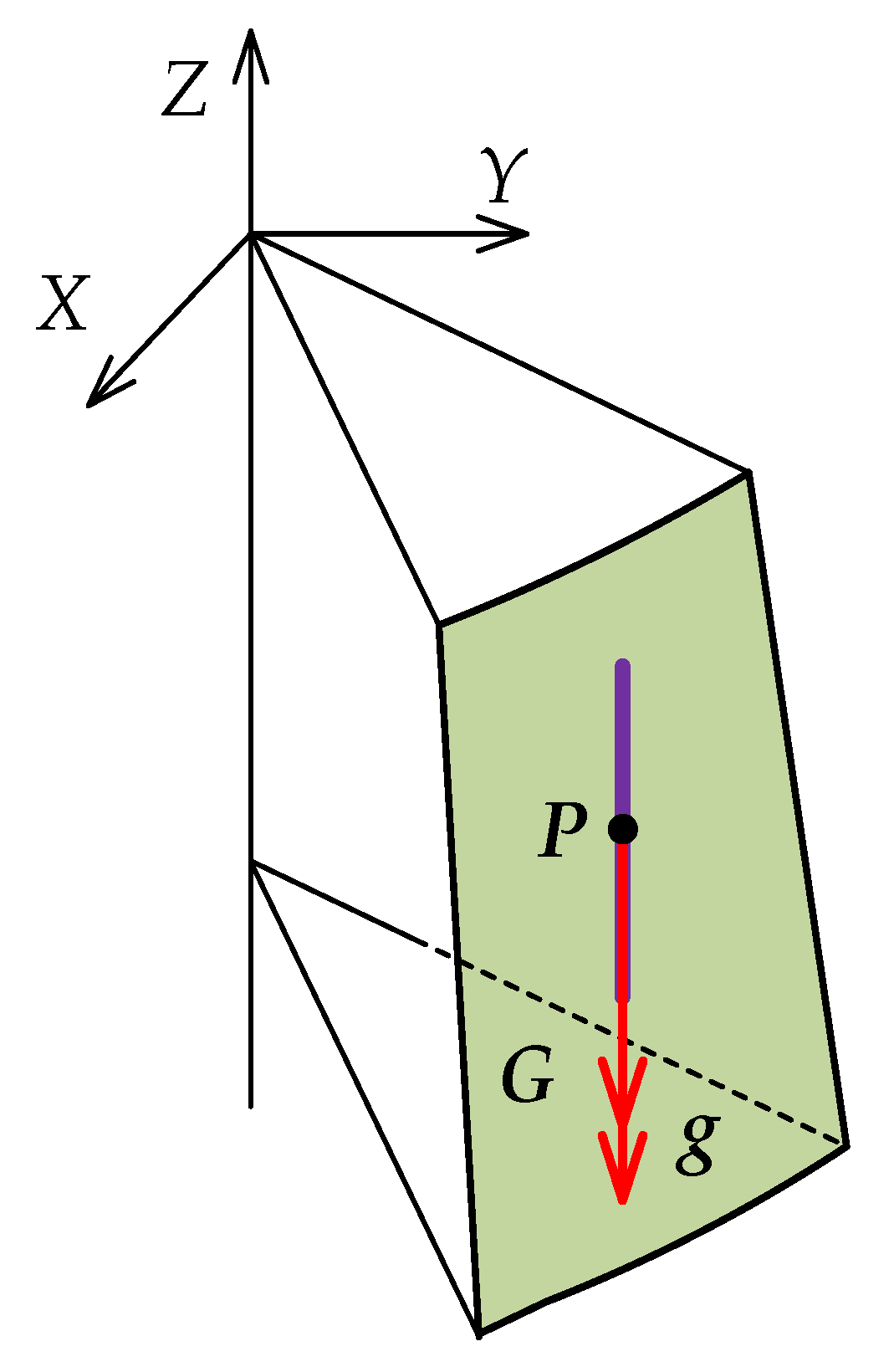
2.2.2. Motion Characteristic Equations of the Particles
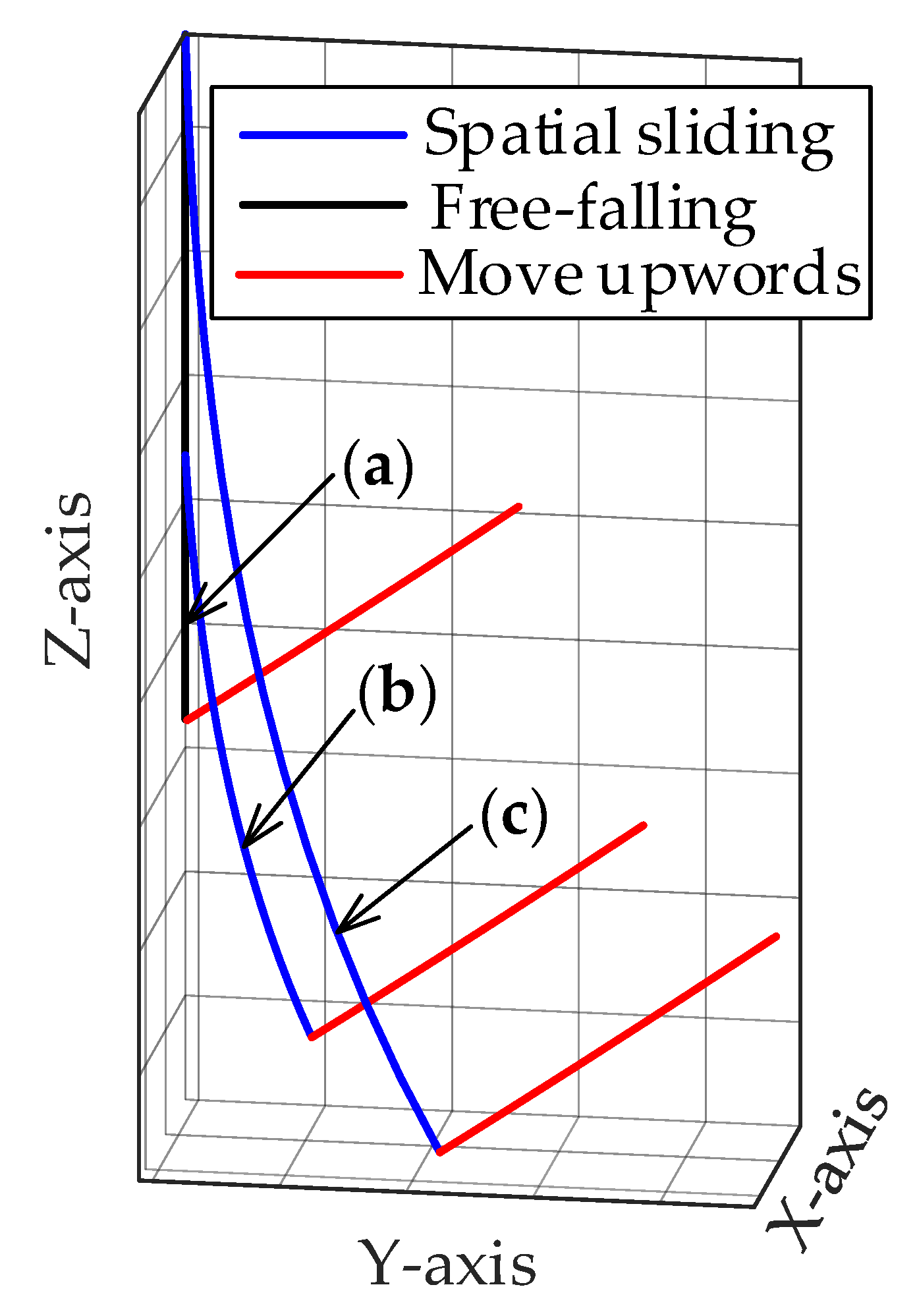
Motion Characteristic Equation of the Particle with Spatial Sliding
Motion Characteristic Equation of the Particle with Free-Falling
Motion Characteristic Equation of the Particle with Spatial Compound Falling
2.2.3. Path of Particle Affected by the Spatial Compound Motion of the Mantle
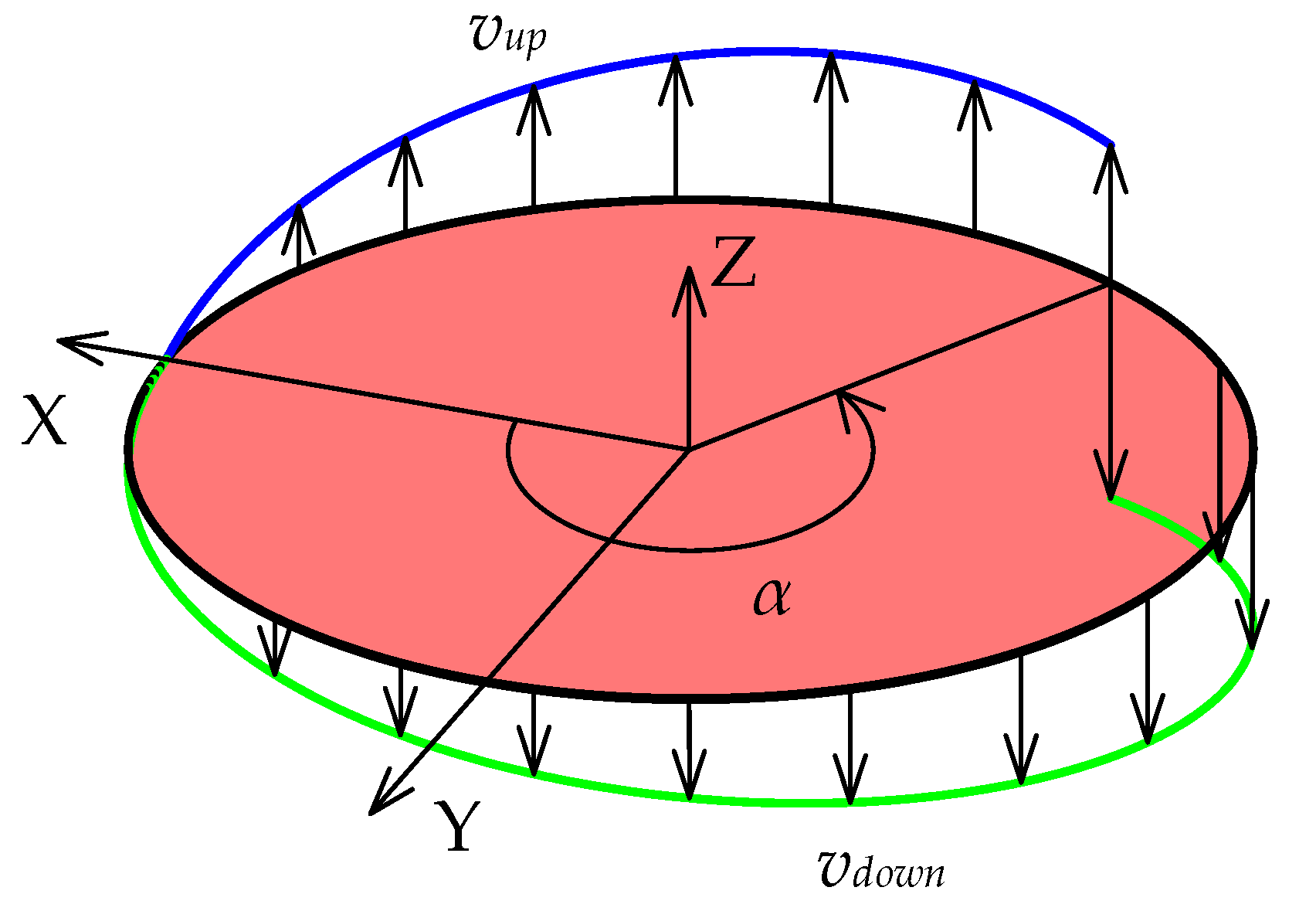
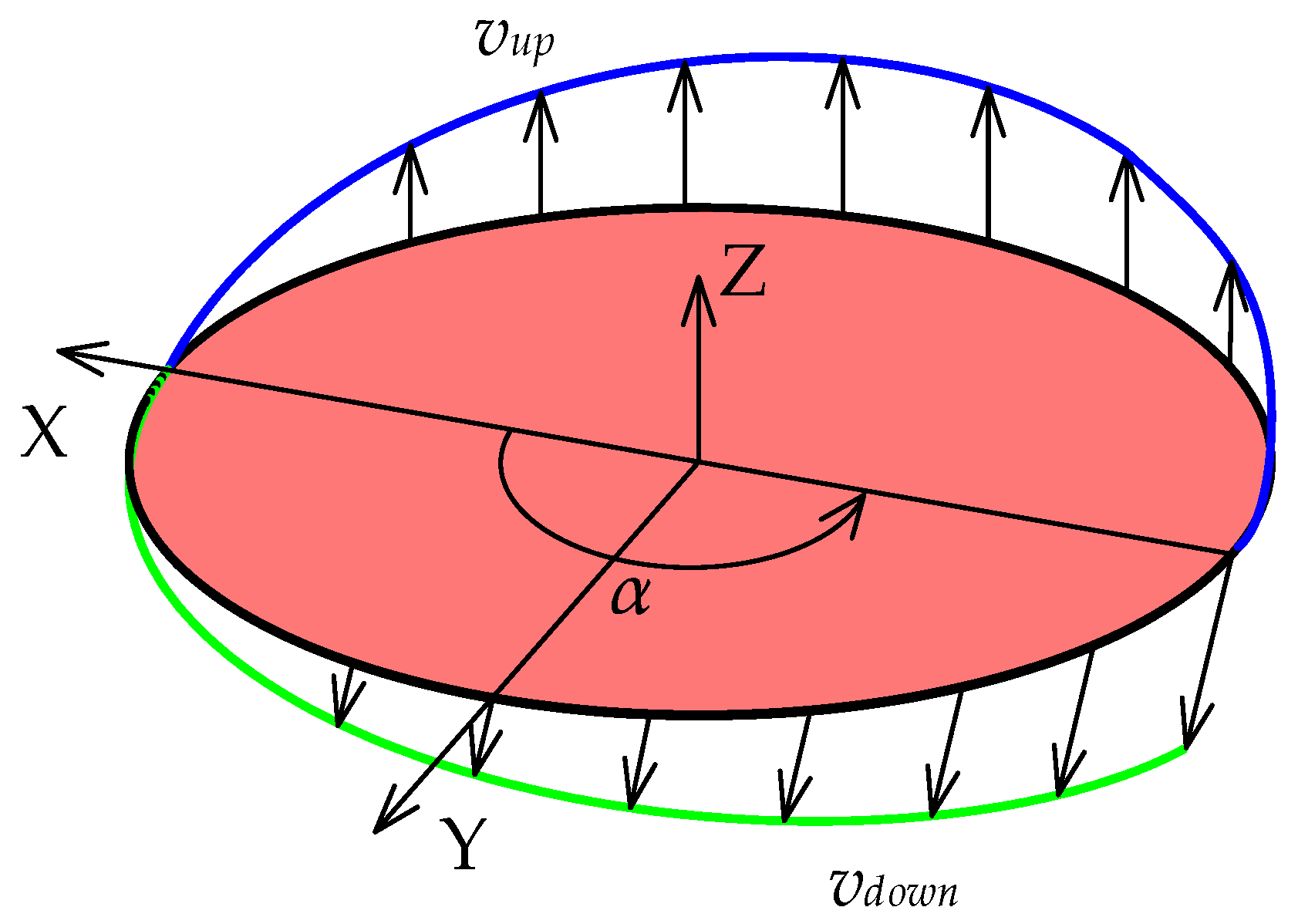
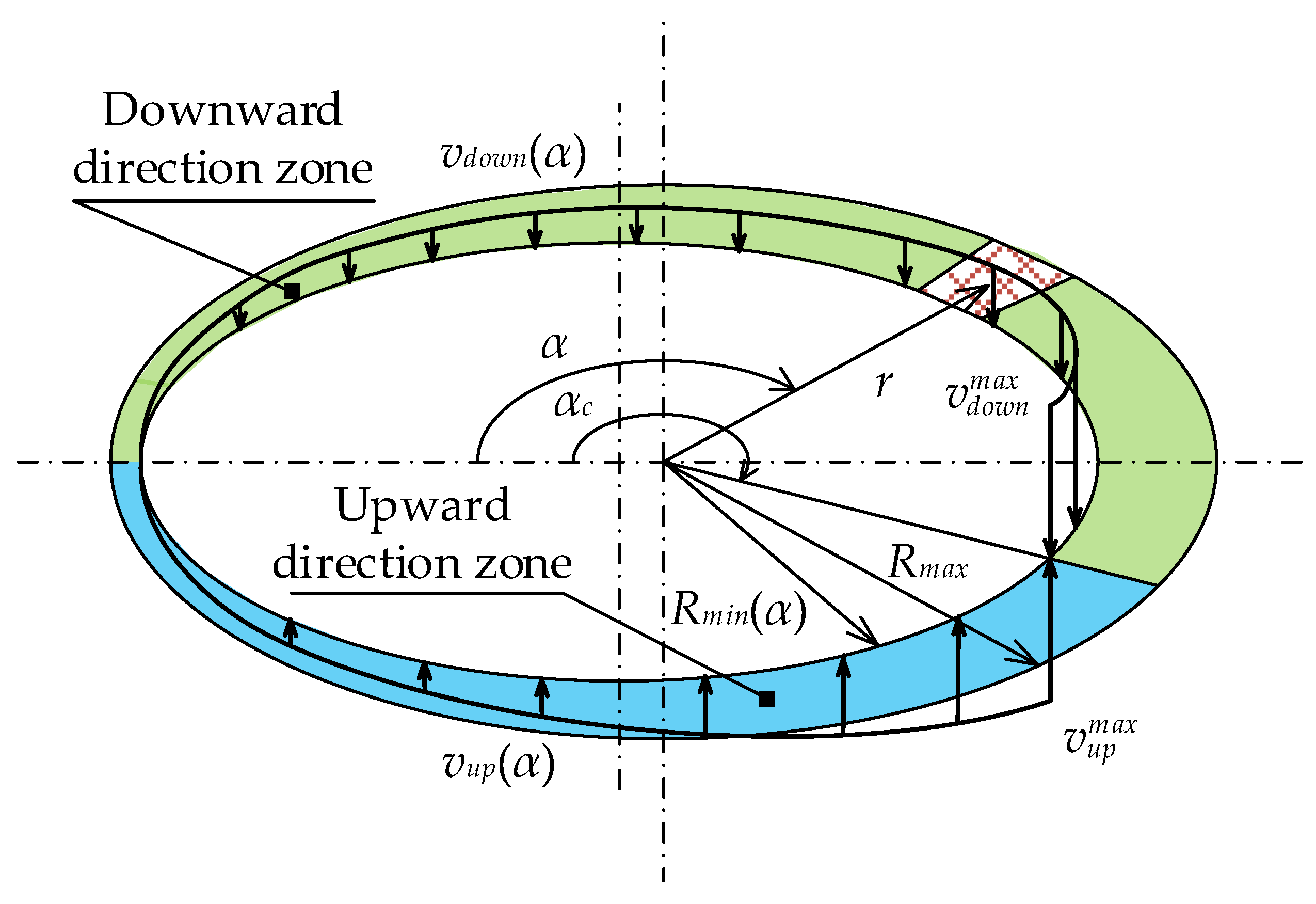
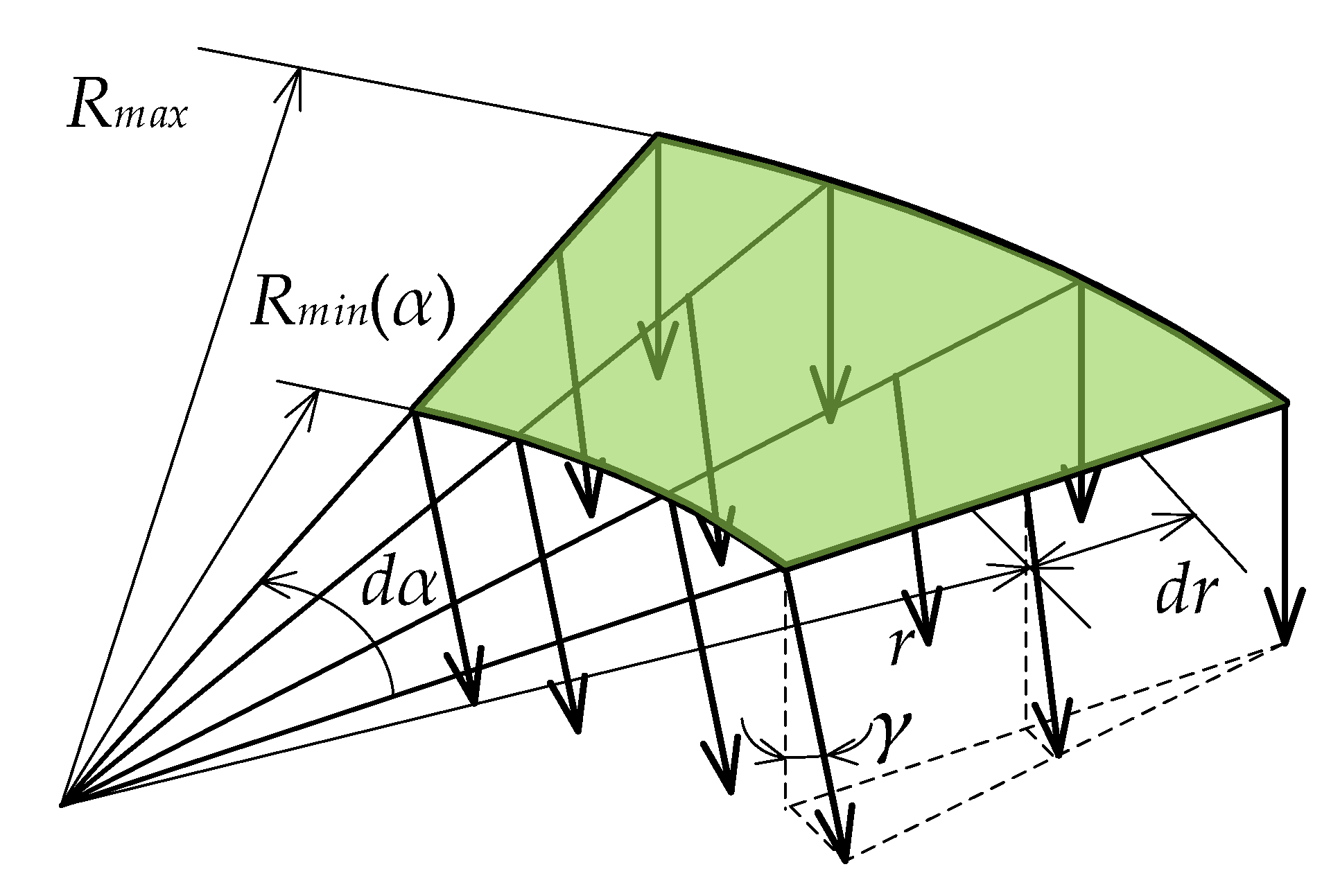
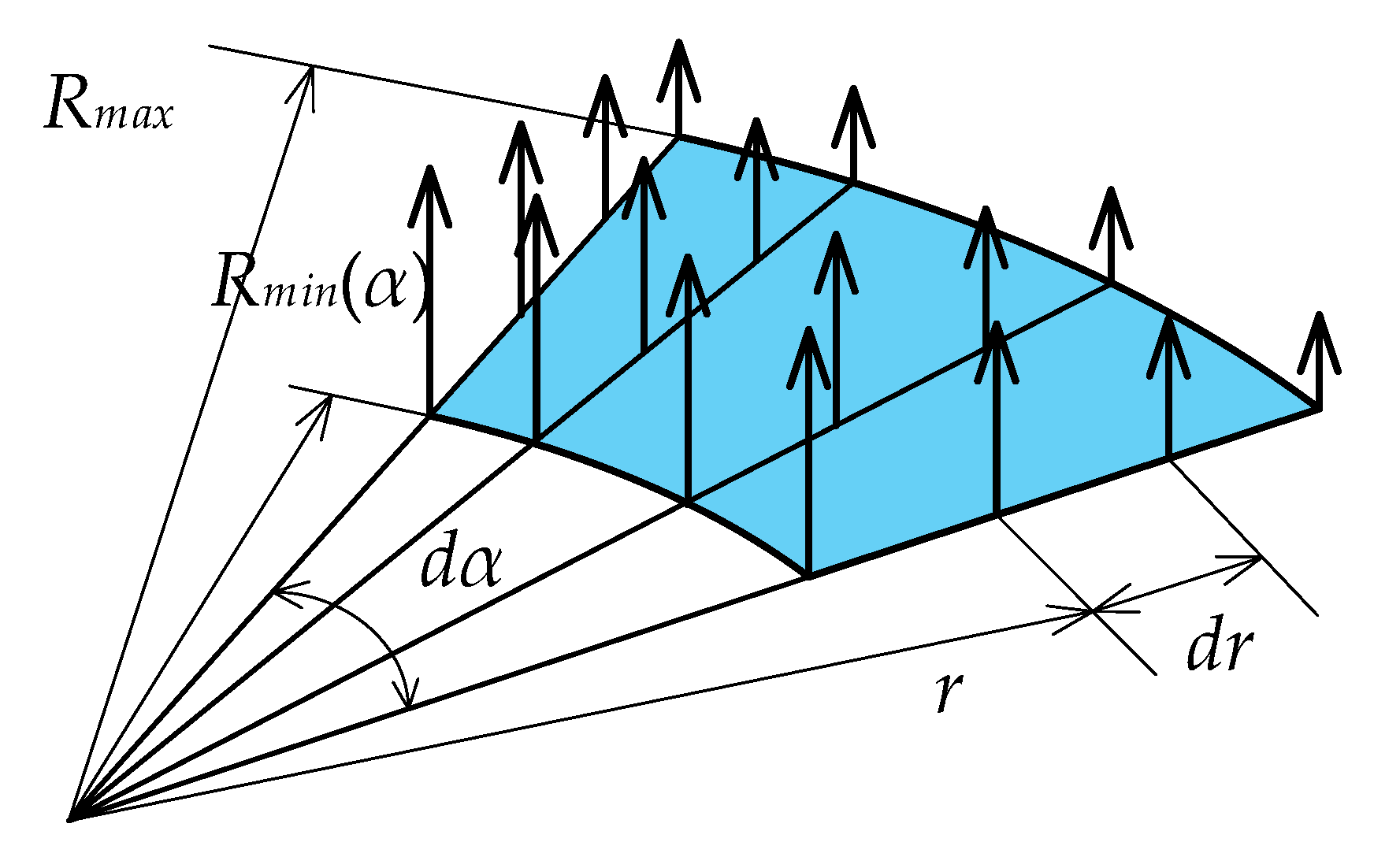
2.2.4. Velocity Distributions of Particles around the Mantle Surface
3. Improved Capacity Model of Cone Crusher
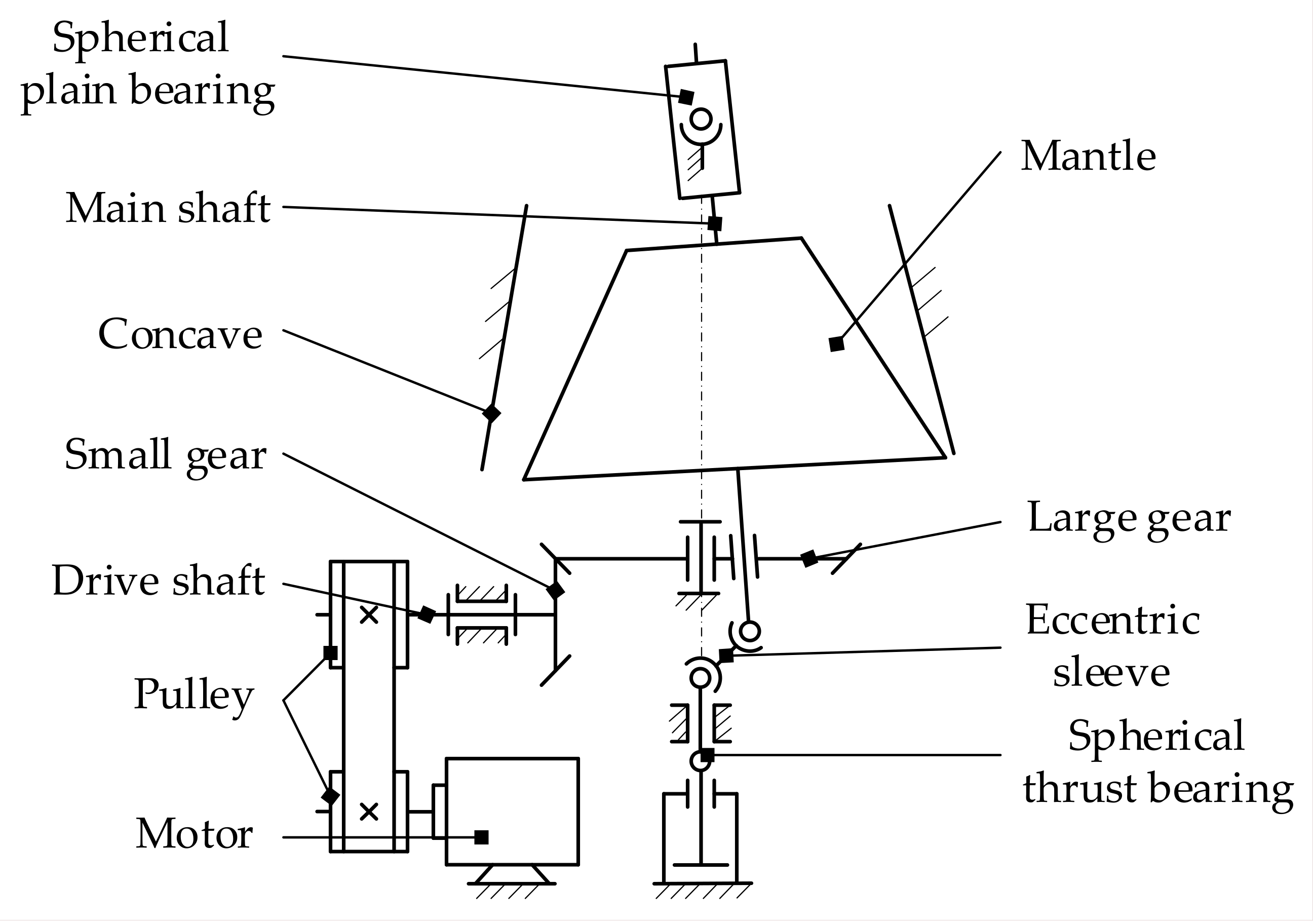
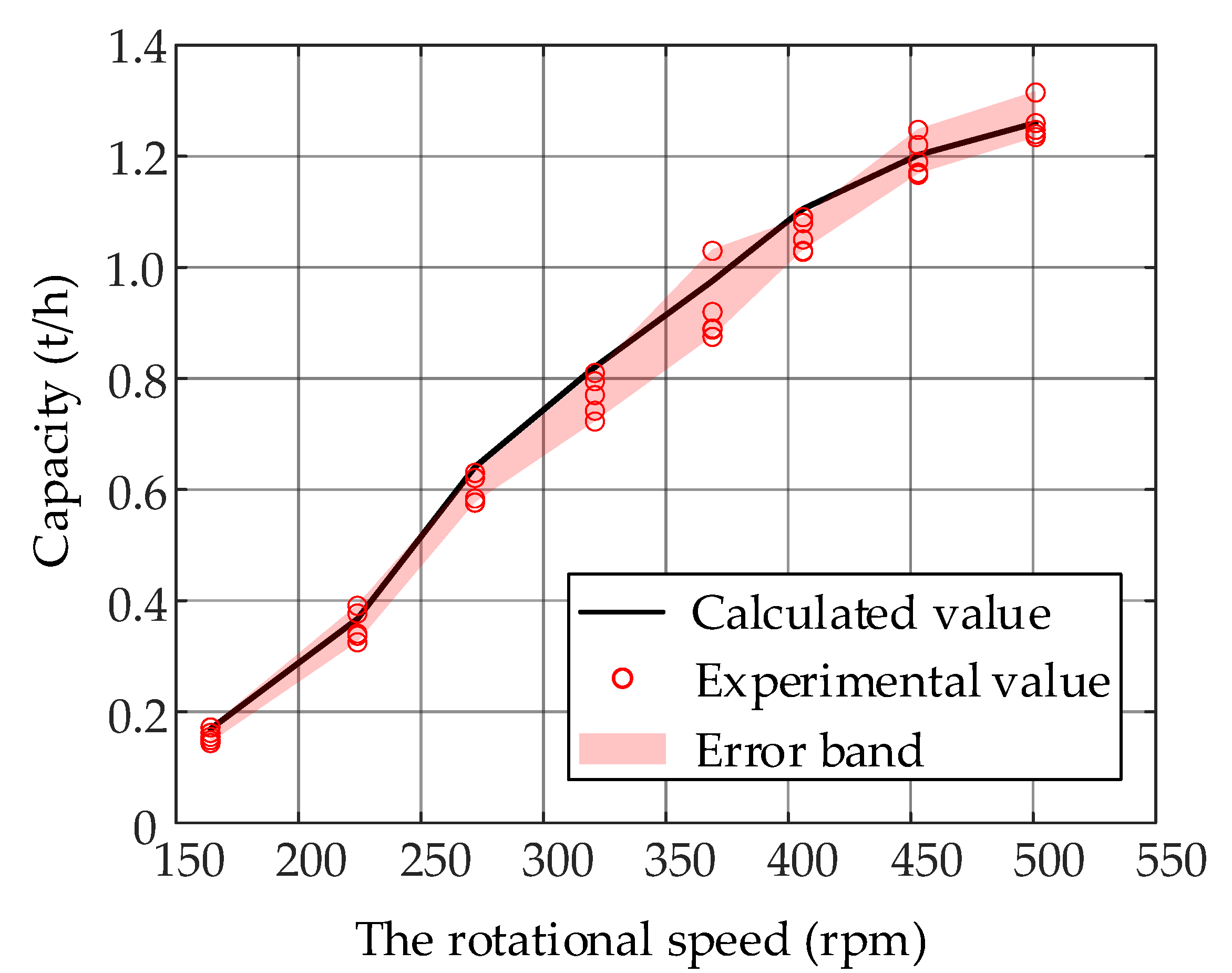
4. Capacity Experiment Using Reduced-Scale Cone Crusher
- Step 1
- The power is turned on for the reduced-scale cone crusher, and the rotational speed of the main shaft is adjusted to 164 rpm using the power inverter.
- Step 2
- Ensure that the reduced-scale cone crusher operates smoothly. The particles with mass of 5 kg and size of 10–15 mm are fed into the crushing chamber, and the time is initiated immediately.
- Step 3
- The crushing process of the particles in the crushing chamber is continuously observed through the observation holes of the reduced-scale cone crusher, and the residual number of particles in the crushing chamber is constantly monitored.
- Step 4
- The time is stopped as soon as the particles are found to be completely crushed and discharged from the crushing chamber through the observation hole.
- Step 5
- Turn off the power and record the required time for the particles to be crushed fully and discharged from the crushing chamber in Table 3.
- Step 6
- Repeat the experimental steps 1–5 and set the rotational speed of the main shaft to 224 rpm, 272 rpm, 321 rpm, 369 rpm, 406 rpm, 453 rpm, and 501 rpm respectively. The experimental data of the required time that the particles with different motion characteristics are crushed in the crushing chamber of the reduced-scale cone crusher is obtained.
5. Improved Capacity Model Applied to Capacity Calculation of ZS200MF Cone Crusher
6. Discussion
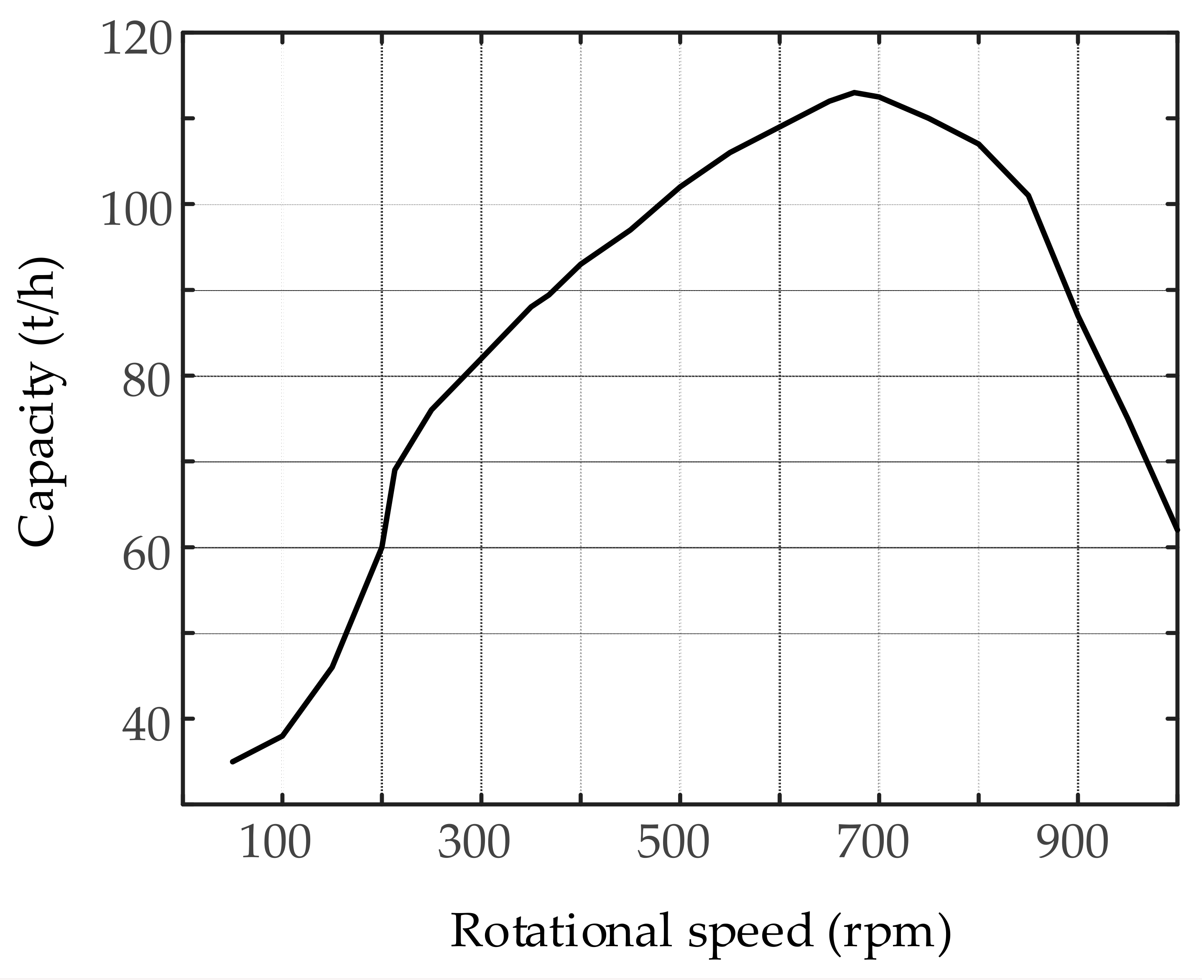
6.1. Rotational Speed of the Main Shaft
6.2. Size of the Closed Side Setting
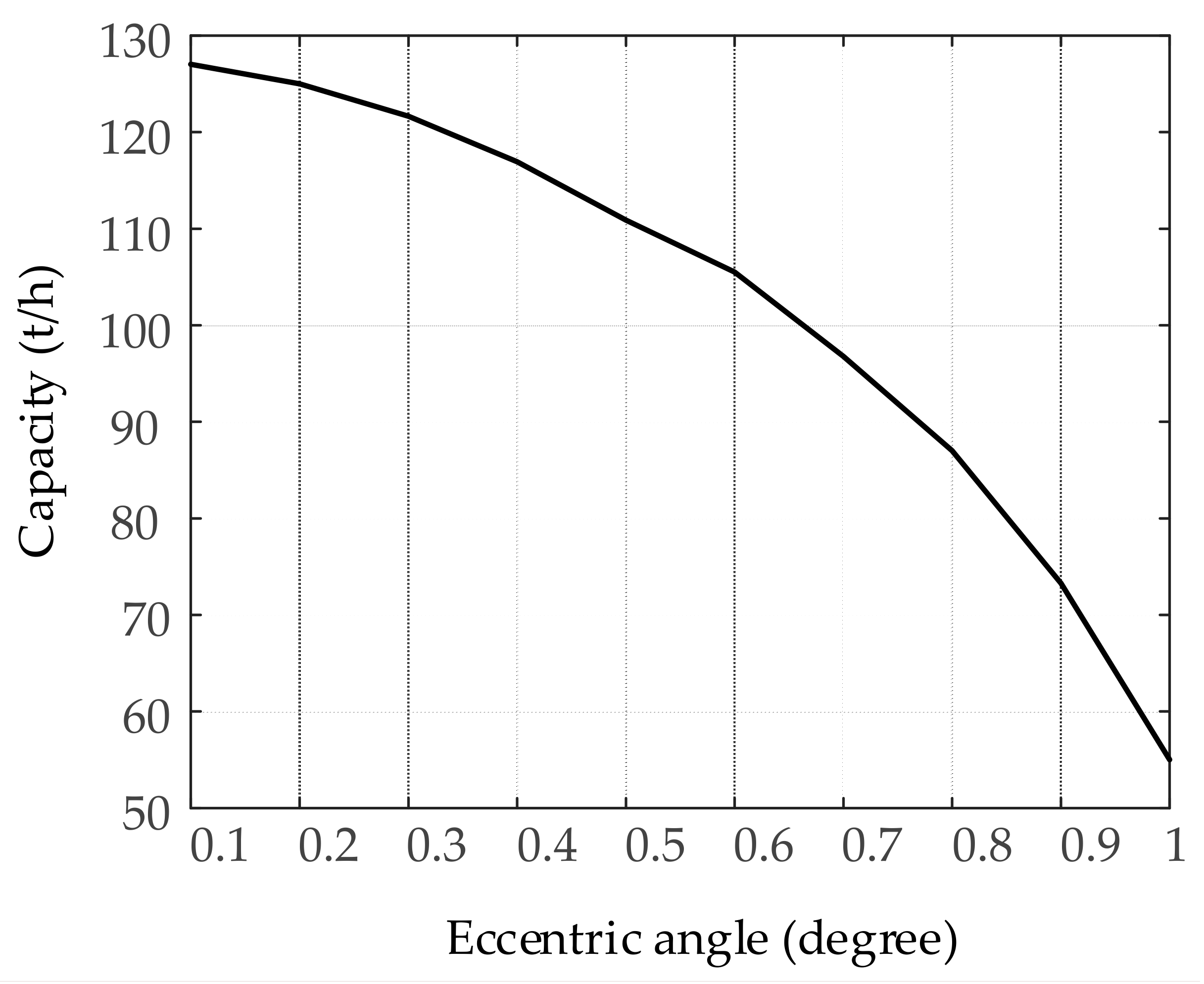
6.3. Eccentric Angle of the Main Shaft
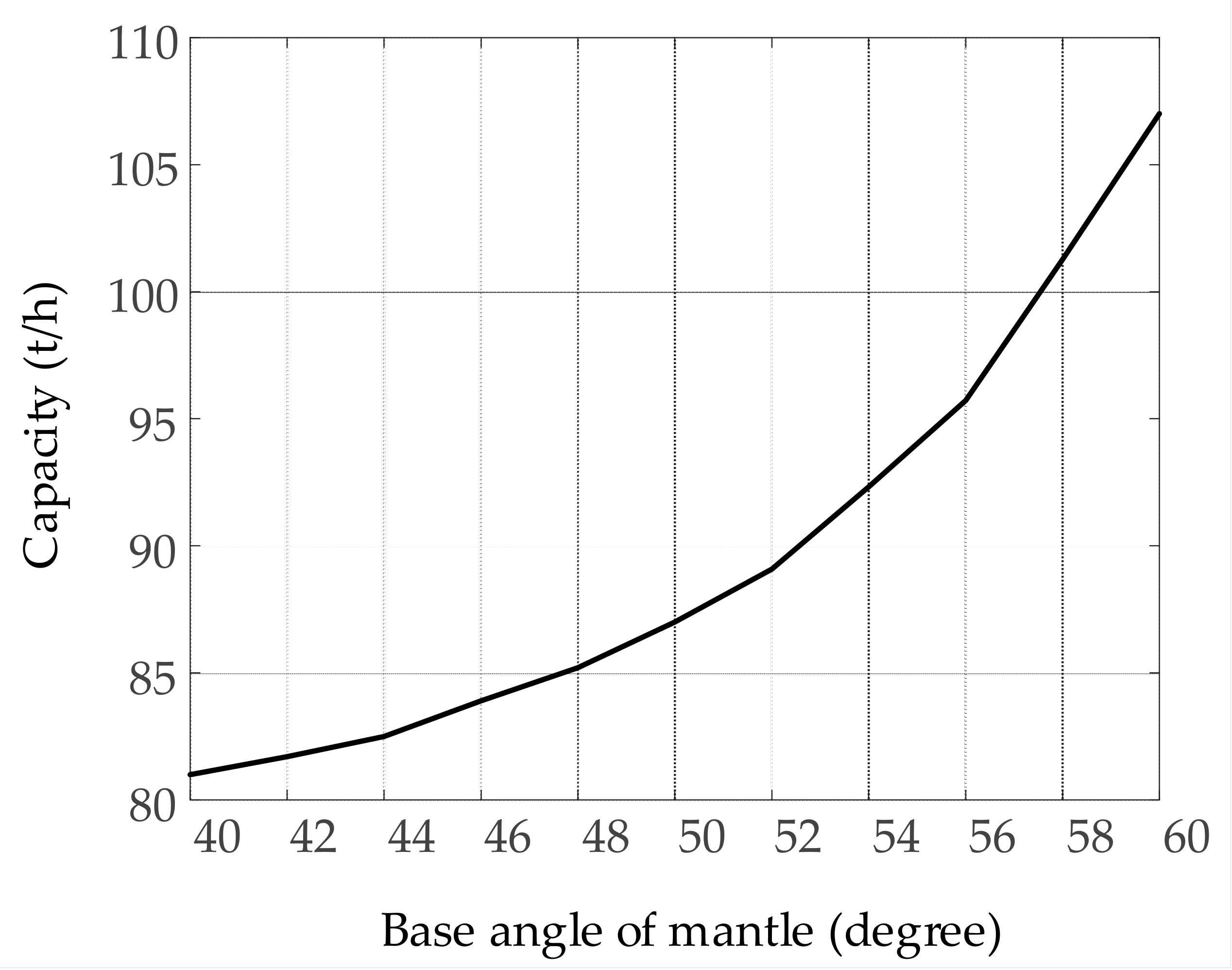
6.4. Base Angle of Mantle
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Evertsson, C.M. Cone Crusher Performance. Ph.D. Thesis, Chalmers University of Technology, Gothenburg, Sweden, 2000. [Google Scholar]
- Gauldie, K. Performance of jaw crushers. Engineering 1953, 10, 456–458. [Google Scholar]
- Gauldie, K. The output of gyratory crushers. Engineering 1954, 4, 557–559. [Google Scholar]
- Briggs, C.A.; Bearman, R.A. An investigation of rock breakage and damage in comminution equipment. Miner. Eng. 1996, 9, 489–497. [Google Scholar] [CrossRef]
- Briggs, C.A. Fundamental Model of a Cone Crusher. Ph.D. Thesis, University of Queensland, Queensland, Australia, 1997. [Google Scholar]
- Bearman, R.A.; Briggs, C.A.; Kojovic, T. The application of rock mechanics parameters to the prediction of comminution behavior. Miner. Eng. 1997, 10, 255–264. [Google Scholar] [CrossRef]
- Evertsson, C.M. Output prediction of cone crushers. Miner. Eng. 1998, 11, 215–231. [Google Scholar] [CrossRef]
- Evertsson, C.M. Modelling of Flow in Cone Crushers. Miner. Eng. 1999, 12, 1479–1499. [Google Scholar] [CrossRef]
- Lindqvist, M.; Evertsson, C.M. Improved flow and pressure model for cone crushers. Miner. Eng. 2004, 17, 1217–1225. [Google Scholar] [CrossRef]
- Lindqvist, M. Energy considerations in compressive and impact crushing of rock. Miner. Eng. 2008, 21, 631–641. [Google Scholar] [CrossRef]
- Pierre, J.; Yoël, F.; Olivier, P. A constitutive law for dense granular flows. Nature 2006, 441, 727–730. [Google Scholar]
- Oliver, B.; John, B.; Paul, H.; Ian, L. Flows of granular material in two-dimensional channels. J. Eng. Math. 2016, 98, 49–70. [Google Scholar]
- Zhang, Z.; Ren, T.; Cheng, J. The improved motion model of particles in the cone crusher considering the spatial com-pound motion of the mantle. Minerals 2022, 12, 16. [Google Scholar] [CrossRef]
- Weerasekara, N.S.; Powell, M.S.; Cleary, P.W.; Tavares, L.M.; Evertsson, C.M.; Morrison, R.D.; Quist, J.; Carvalho, R.M. The contribution of DEM to the science of comminution. Powder Technol. 2013, 248, 3–24. [Google Scholar] [CrossRef]
- Cleary, P.W.; Sinnott, M.D. Simulation of particle flows and breakage in crushers using DEM: Part 1–Compression crushers. Miner. Eng. 2015, 74, 178–197. [Google Scholar] [CrossRef]
- Cleary, P.W.; Delaney, G.W.; Sinnott, M.D.; Cummins, S.J.; Morrison, R.D. Advanced comminution modelling: Part 1–crushers. Appl. Math. Model. 2020, 88, 238–265. [Google Scholar] [CrossRef]
- Herbst, J.A.; Potapov, A.V. Making a discrete grain breakage model practical for comminution equipment performance simulation. Powder Technol. 2004, 143, 144–150. [Google Scholar] [CrossRef]
- Lichter, J.; Lim, K.; Potapov, A.; Kaja, D. New developments in cone crusher performance optimization. Miner. Eng. 2009, 22, 613–617. [Google Scholar] [CrossRef]
- Li, H.; McDowell, G.R.; Lowndes, I.S. A laboratory investigation and discrete element modeling of rock flow in a chute. Powder Technol. 2012, 229, 199–205. [Google Scholar] [CrossRef]
- Johansson, M.; Quist, J.; Evertsson, C.M.; Hulthén, E. Cone crusher performance evaluation using DEM simulations and laboratory experiments for model validation. Miner. Eng. 2017, 103, 93–101. [Google Scholar] [CrossRef]
- Delaney, W.G.; Morrison, D.R.; Sinnott, D.M.; Cummins, S.; Cleary, W.P. DEM modelling of non-spherical particle breakage and flow in an industrial scale cone crusher. Miner. Eng. 2015, 74, 112–122. [Google Scholar] [CrossRef]
- Cleary, P.W.; Sinnott, M.D.; Morrison, R.D.; Cummins, S.; Delaney, W.G. Analysis of cone crusher performance with changes in material properties and operating conditions using DEM. Miner. Eng. 2017, 100, 49–70. [Google Scholar] [CrossRef]
- Flávio, P.A.; Luís, M.T. Simulating a laboratory-scale cone crusher in DEM using polyhedral particles. Powder Technol. 2020, 372, 362–371. [Google Scholar]
- Chen, Z.; Wang, G.; Xue, D.; Cui, D. Simulation and optimization of crushing chamber of gyratory crusher based on the DEM and GA. Powder Technol. 2021, 384, 36–50. [Google Scholar] [CrossRef]
- Cheng, J.; Ren, T.; Zhang, Z.; Liu, D.; Jin, X. A Dynamic Model of Inertia Cone Crusher Using the Discrete Element Method and Multi-Body Dynamics Coupling. Minerals 2020, 10, 862. [Google Scholar] [CrossRef]
- Meriam, J.L.; Kraige, L.G. Engineering Mechanics, Dynamics; John Wiley and Sons: New York, NY, USA, 1987; pp. 154–196. [Google Scholar]





| Parameter | Value | Unit | |
|---|---|---|---|
| Size of feed port | df | 52 | mm |
| Particles size | d | 10–15 | mm |
| Size of output port | do | 11 | mm |
| Stroke | s | 9 | mm |
| Eccentric angle | θ | 0.81 | deg |
| Rotational speed | n | 30–500 | rpm |
| Parameter | Value | Unit | |
|---|---|---|---|
| Particles material | - | Hematite | - |
| Particles composition | - | Fe2O3 | - |
| Mohs hardness | HM | 5.6 | - |
| Compressive strength | σ | 115 | Mpa |
| Tap density | ρT | 3.9 | t/m3 |
| Pack density | ρP | 2.6 | t/m3 |
| Rotational Speed | Crushing Times | ||||
|---|---|---|---|---|---|
| Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ | |
| n | t1 | t2 | t3 | t4 | t5 |
| 164 rpm | 104.65 s | 111.11 s | 116.13 s | 120.81 s | 125.16 s |
| 224 rpm | 46.04 s | 47.74 s | 52.79 s | 53.41 s | 55.33 s |
| 272 rpm | 28.57 s | 28.99 s | 30.82 s | 31.22 s | 31.21 s |
| 321 rpm | 22.22 s | 22.64 s | 23.37 s | 24.26 s | 24.91 s |
| 369 rpm | 17.48 s | 19.57 s | 20.57 s | 20.22 s | 20.27 s |
| 406 rpm | 16.51 s | 16.67 s | 17.14 s | 17.48 s | 17.51 s |
| 453 rpm | 14.43 s | 14.75 s | 15.13 s | 15.38 s | 15.43 s |
| 501 rpm | 13.69 s | 14.29 s | 14.43 s | 14.52 s | 14.58 s |
| Parameter | Value | Unit | |
|---|---|---|---|
| Particles material | - | Magnetite | - |
| Particles composition | - | Fe3O4 | - |
| Mohs hardness | HM | 5.9 | - |
| Tap density | ρT | 4.9 | t/m3 |
| Pack density | ρP | 2.8 | t/m3 |
| Moisture content | w | 3.6 | % |
| Parameter | Value | Unit | |
|---|---|---|---|
| Rotational speed | n | 368 | rpm |
| Top diameter of mantle | dT | 1035 | mm |
| Bottom diameter of mantle | dB | 404 | mm |
| Base angle of mantle | β | 52 | degree |
| Size of feed port | df | 120 | mm |
| Size of output port | do | 22 | mm |
| Nip angle | αn | 31 | degree |
| Length of parallel strip | lp | 80 | mm |
| Stroke | s | 25 | mm |
| Eccentric distance | e | 12 | mm |
| Eccentric angle | θ | 0.8 | degree |
| Variables | Value | Unit | |
|---|---|---|---|
| Motion characteristic | - | Free-falling | - |
| Delayed time | td | 0.010 | s |
| Falling time | tαc | 0.107 | s |
| Circumferential angle | αc | 237.651 | degree |
| Radius of concave | Rmax | 0.480 | m |
| Radius of mantle | Rmin | 0.528 | m |
| Velocity in downward direction zone | vdown | m/s | |
| Velocity in upward direction zone | vup | m/s | |
| Filling rate | ηc | 0.375 | - |
| Density | ρ | 2.67 | t/m3 |
| Capacity | Q | 87.9 | t/h |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Ren, T.; Cheng, J.; Zhu, J. An Improved Capacity Model of the Cone Crushers Based on the Motion Characteristics of Particles Considering the Influence of the Spatial Compound Motion of the Mantle. Minerals 2022, 12, 235. https://doi.org/10.3390/min12020235
Zhang Z, Ren T, Cheng J, Zhu J. An Improved Capacity Model of the Cone Crushers Based on the Motion Characteristics of Particles Considering the Influence of the Spatial Compound Motion of the Mantle. Minerals. 2022; 12(2):235. https://doi.org/10.3390/min12020235
Chicago/Turabian StyleZhang, Zilong, Tingzhi Ren, Jiayuan Cheng, and Jianxu Zhu. 2022. "An Improved Capacity Model of the Cone Crushers Based on the Motion Characteristics of Particles Considering the Influence of the Spatial Compound Motion of the Mantle" Minerals 12, no. 2: 235. https://doi.org/10.3390/min12020235
APA StyleZhang, Z., Ren, T., Cheng, J., & Zhu, J. (2022). An Improved Capacity Model of the Cone Crushers Based on the Motion Characteristics of Particles Considering the Influence of the Spatial Compound Motion of the Mantle. Minerals, 12(2), 235. https://doi.org/10.3390/min12020235





