An Evaluation on the Impact of Ore Fragmented by Blasting on Mining Performance
Abstract
:1. Introduction
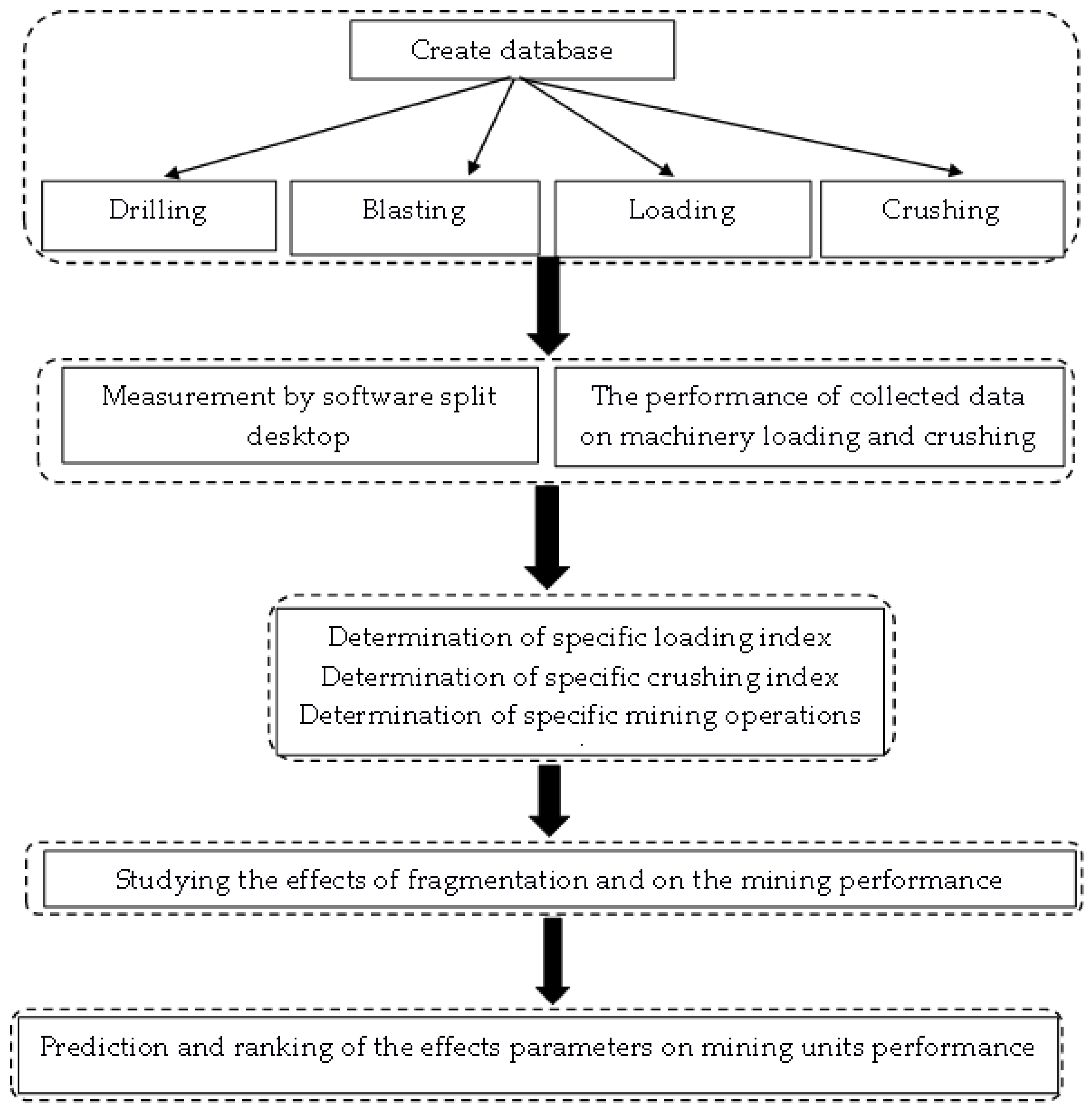
2. Materials and Methods
2.1. Mining Performance
2.2. Structure of the Database
2.3. Specific Unit Operation Index
2.4. Sarcheshmeh Copper Mine
2.5. Database from Unit Operation
2.6. Measurement of Blast Fragmentation
2.6.1. Stages of Image Analysis
2.6.2. Working Algorithm of This Project
2.7. Evaluation of Fragmentation
2.8. Data Analysis
3. Results and Discussion
3.1. Blasting and Mining Performance
3.2. Statistical Analysis
3.2.1. Relation of and with Production Performance
3.2.2. Loading and Production Performance
3.2.3. Specific Loading and Specific Mine Unit Operation Index
3.2.4. Ranking the Most Effective Parameters for Mining Performance
4. Conclusions
5. Future Works
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| No. | Rock Type | Zone | Alteration | Ucs (MPa) | Hardness Level | D (mm) | B (m) | S (m) | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | SP+ Dike | Hypogene | QS and Clay | 38.25 | Medium hard to hard | 152.4 | 5 | 6 | 0.054 |
| 2 | Dike +AN | Hypogene | QS and Clay | 41.13 | Medium hard to hard | 241.3 | 7 | 9.5 | 0.018 |
| 3 | GR | Hypogene | SQ and Clay | 38.63 | Medium hard to hard | 152.4 | 6 | 7 | 0.029 |
| 4 | Dike +SP | Hypogene | QS and Clay | 44.75 | Medium hard to hard | 152.4 | 7 | 9.5 | 0.04 |
| 5 | AN+ Dike | Hypogene | QS and Clay | 46.25 | Medium hard to hard | 152.4 | 5 | 6 | 0.041 |
| 6 | QI | Hypogene | QS, Bio, and Clay | 39.88 | Medium hard to hard | 152.4 | 5 | 6 | 0.04 |
| 7 | AN | Hypogene | QS and Clay | 35.38 | Medium hard to hard | 152.4 | 5 | 6 | 0.037 |
| 8 | LF+ Dike | Hypogene & supergene | QS, Bio, and Clay | 38.88 | Medium hard to hard | 152.4 | 5 | 6 | 0.04 |
| 9 | AN | Hypogene | QS and K-Feldspar | 39.13 | Medium hard to hard | 152.4 | 7 | 9 | 0.019 |
| 10 | LF+ Dike | Hypogene | QS, Bio, and Clay | 43.88 | Medium hard to hard | 152.4 | 5 | 6 | 0.04 |
| 11 | SP+ Dike +BD | Hypogene | QS, K-Feldspar, and Clay | 45.00 | Medium hard to hard | 25.4 | 7 | 9 | 0.019 |
| 12 | AN+ Dike | Hypogene | QS and Clay | 43.25 | Medium hard to hard | 241.3 | 7 | 9 | 0.019 |
| 13 | LF+ Dike | Hypogene | SQ and Clay | 43.38 | Medium hard to hard | 228.6 | 7 | 9 | 0.019 |
| 14 | SP+BD+ Dike | Hypogene | QS, Bio, and Clay | 43.38 | Medium hard to hard | 25.4 | 7 | 9 | 0.019 |
| 15 | AN+ Dike | Hypogene | SQ and Clay | 39.75 | Medium hard to hard | 24.13 | 7 | 9 | 0.019 |
| 16 | SP+ Dike | Hypogene | SQ and Clay | 38.63 | Medium hard to hard | 152.4 | 5 | 6 | 0.024 |
| 17 | SP+ Dike | Hypogene | QS, Bio, and Clay | 41.13 | Medium hard to hard | 241.3 | 7 | 9 | 0.04 |
| 18 | SP+ Dike | Hypogene | QS and Clay | 41.25 | Medium hard to hard | 241.3 | 7 | 9 | 0.019 |
| 19 | SP+ Dike | Hypogene | QS and Clay | 39.75 | Medium hard to hard | 241.3 | 7 | 9 | 0.019 |
| 20 | LF+ Dike | Hypogene | QS, K-Feldspar, and Clay | 45.00 | Medium hard to hard | 241.3 | 7 | 9 | 0.019 |
| VI | V | IV | III | II | I | Class |
|---|---|---|---|---|---|---|
| >50 | 50–65 | 65–75 | 75–85 | 85–95 | <95 | Efficiency (%) |
| Very poor | Unsuitable | Moderate | Good | Very good | Excellent | Qualitative |
| Rock Type | Explosive Type | Fine Fragmentation (%) | Fragmentation Efficiency (%) | ||||
|---|---|---|---|---|---|---|---|
| SP+ Dike | * Emulan | 5.28 | 0.352 | 12.69 | 20.64 | 25 | 92.50 |
| Dike +AN | Emulan | 1.36 | 0.322 | 4.68 | 8.59 | 70 | 79 |
| GR | ANFO | 2.65 | 0.293 | 3.62 | 7.31 | 75 | 77.50 |
| Dike +SP | Emulan | 3.74 | 0.308 | 8.1 | 13.6 | 75 | 77.50 |
| AN+ Dike | Emulan | 3.36 | 0.457 | 7.52 | 12.42 | 42 | 86.50 |
| QI | Emulan | 0.96 | 0.399 | 2.2 | 4.56 | 90 | 73 |
| AN | EM and AN | 2.34 | 0.256 | 2.6 | 6.2 | 82.5 | 75.25 |
| LF+ Dike | ANFO | 2.96 | 0.256 | 3.02 | 6.69 | 80 | 76 |
| AN | Emulan | 3.25 | 0.317 | 6.34 | 10.77 | 55 | 83.50 |
| LF+ Dike | ANFO | 5.28 | 0.424 | 4.52 | 11.21 | 65 | 80.50 |
| SP+ Dike +BD | Emulan | 6.39 | 0.369 | 6.55 | 11.85 | 53 | 84.10 |
| AN+ Dike | Emulan | 4.72 | 0.343 | 6.72 | 14.13 | 46.5 | 86.05 |
| LF+ Dike | EM and ANFO | 1.39 | 0.334 | 3.82 | 6.28 | 80 | 76 |
| SP+BD+ Dike | Emulan | 6.07 | 0.398 | 5.68 | 9.62 | 60 | 82 |
| AN+ Dike | Emulan | 3.00 | 0.469 | 9.39 | 23.32 | 40 | 88 |
| SP+ Dike | ANFO | 1.20 | 0.381 | 10.46 | 25.73 | 35 | 78.5 |
| SP+ Dike | ANFO | 4.89 | 0.457 | 5.51 | 9.08 | 62.5 | 81.25 |
| SP+ Dike | Emulan | 7.04 | 0.436 | 10.39 | 24.49 | 35 | 89.50 |
| SP+ Dike | Emulan | 5.14 | 0.453 | 9.11 | 20.58 | 40 | 88 |
| LF+ Dike | Emulan | 2.07 | 0.329 | 6.72 | 14.13 | 50 | 85 |
| Type Shovel Loading | Bucket Volume () | Fuel Shovel | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Hydraulic | 16.5 | Diesel | 33.0 | 2.07 | 0.005 | 0.353 | 0.180 | 0.009 | 476.34 | 0.008 |
| Hydraulic | 4.5 | Diesel | 48.23 | 3.04 | 0.005 | 0.038 | 0.050 | 0.005 | 556.3 | 0.005 |
| Hydraulic | 16.5 | Diesel | 18.40 | 3.08 | 0.005 | 0.061 | 0.097 | 0.015 | 533.6 | 0.006 |
| Rope | 12 | Electricity | 30.91 | 1.87 | 0.002 | 0.004 | 0.047 | 0.004 | 1552.35 | 0.003 |
| Rope | 12 | Electricity | 32.1 | 1.94 | 0.001 | 0.009 | 0.035 | 0.004 | 2179.1 | 0.001 |
| Hydraulic | 4.5 | Diesel | 20.8 | 2.73 | 0.004 | 0.024 | 0.071 | 0.013 | 602.8 | 0.005 |
| Rope | 18 | Electricity | 32.92 | 1.71 | 0.002 | 0.012 | 0.059 | 0.003 | 1663.86 | 0.002 |
| Hydraulic | 2.15 | Diesel | 14.38 | 5.25 | 0.005 | 0.079 | 0.204 | 0.008 | 471.2 | 0.009 |
| Rope | 12 | Electricity | 39.50 | 2.08 | 0.002 | 0.011 | 0.034 | 0.003 | 1480.15 | 0.002 |
| Rope | 12 | Electricity | 35.38 | 1.90 | 0.002 | 0.041 | 0.054 | 0.004 | 1197.88 | 0.003 |
| Rope | 12 | Electricity | 33.0 | 1.67 | 0.002 | 0.014 | 0.058 | 0.005 | 1563.6 | 0.003 |
| Hydraulic | 15 | Diesel | 48.2 | 2.61 | 0.005 | 0.324 | 0.177 | 0.011 | 566.0 | 0.007 |
| Rope | 12 | Electricity | 35.29 | 2.00 | 0.002 | 0.021 | 0.067 | 0.004 | 1185.02 | 0.003 |
| Rope | 12 | Electricity | 39.19 | 3.15 | 0.004 | 0.031 | 0.056 | 0.005 | 703.6 | 0.005 |
| Hydraulic | 11 | Diesel | 45.67 | 1.78 | 0.006 | 0.212 | 0.114 | 0.020 | 451.7 | 0.008 |
| Hydraulic | 18 | Electricity | 30.30 | 1.79 | 0.007 | 0.044 | 0.218 | 0.005 | 394.7 | 0.006 |
| Rope | 12 | Electricity | 33.0 | 1.69 | 0.001 | 0.015 | 0.056 | 0.002 | 1744.7 | 0.002 |
| Hydraulic | 16.5 | Diesel | 51.5 | 3.16 | 0.004 | 0.014 | 0.093 | 0.005 | 653.3 | 0.005 |
| Hydraulic | 16.5 | Diesel | 43.80 | 2.64 | 0.004 | 0.000 | 0.084 | 0.006 | 620.3 | 0.005 |
| Rope | 12 | Electricity | 37.15 | 1.86 | 0.001 | 0.004 | 0.022 | 0.001 | 1982.29 | 0.002 |
| Rock Type | Fine Fragmentation (%) | Boulder (%) | Efficiency (%) |
|---|---|---|---|
| Ore | 58.23 | 0.55 | 81.98 |
| Total Energy Consumption Blast Block (kw) | |||||
|---|---|---|---|---|---|
| 3.74 | 0.33 | 1516.05 | 1384.34 | 0.171 | 2.60 |
| 68.89 | 1.45 | 1531.79 | 25,221.60 | 0.167 | 0.49 |
| 13.97 | 0.32 | 1465.65 | 4999.00 | 0.171 | 0.87 |
| 13.31 | 0.3 | 1465.06 | 4760.93 | 0.171 | 0.63 |
| 17.92 | 0.4 | 1464.85 | 6408.98 | 0.171 | 0.32 |
| 12.8 | 0.29 | 1462.73 | 4577.86 | 0.171 | 1.36 |
| 24.22 | 0.51 | 1499.15 | 8864.29 | 0.167 | 0.32 |
| 29.27 | 0.9 | 1537.41 | 10,408.50 | 0.162 | 1.49 |
| 31.8 | 0.98 | 1535.37 | 11293.2 | 0.162 | 0.20 |
| 11.51 | 0.79 | 1433.54 | 4198.09 | 0.178 | 0.91 |
| 42.27 | 3.21 | 1602.20 | 17,231.25 | 0.178 | 0.37 |
| 20.89 | 1.42 | 1432.50 | 7613.79 | 0.178 | 0.81 |
| 30.23 | 2.05 | 1432.76 | 11,019.98 | 0.178 | 0.34 |
| 45.62 | 3.1 | 1432.76 | 16,630.22 | 0.178 | 0.67 |
| 12.64 | 0.86 | 1432.95 | 4608.35 | 0.178 | 1.27 |
| 9.16 | 0.62 | 859.72 | 3339.37 | 0.178 | 0.98 |
| 9.89 | 0.67 | 1327.09 | 3606.57 | 0.178 | 0.65 |
| 30.78 | 2.09 | 1432.75 | 11,220.36 | 0.178 | 0.74 |
| 19.79 | 1.35 | 1432.54 | 7213.09 | 0.178 | 0.77 |
| 14.84 | 1.01 | 1432.79 | 5409.86 | 0.178 | 0.22 |
References
- Roy, M.P.; Singh, P. Blast Design and Fragmentation Control–Key to Productivity; CSIR-Central Institute of Mining and Fuel Research: Dhanbad, India, 2012; pp. 1–18. [Google Scholar]
- Janković, A.; Valery, W. Mine to mill optimisation for conventional grinding circuits: A scoping study. J. Min. Metall. A 2002, 38, 49–66. [Google Scholar]
- Adel, G.; Kojovic, T.; Thornton, D. Mine-to-Mill Optimization of Aggregate Production; Virginia Polytechnic Inst. and State Univ. (Virginia Tech): Blacksburg, VA, USA, 2006. [Google Scholar]
- Taji, M.; Ataei, M.; Goshtasbi, A.; Osanloo, M. ODM: A new approach for open pit mine blasting evaluation. J. Vib. Control 2013, 19, 1738–1752. [Google Scholar] [CrossRef]
- Osanloo, M.; Hekmat, A. Prediction of shovel productivity in the Gol-e-Gohar iron mine. J. Min. Sci. 2005, 41, 177–184. [Google Scholar] [CrossRef]
- Lopez Jimeno, C.; Lopez Jimeno, A.; Ayala Carcedo, F.J.; Visser de Ramiro, Y. Drilling and Blasting of Rocks; Balkema, A.A., Ed.; Brookfield: Rotterdam, The Netherlands, 1995. [Google Scholar]
- Blanco, J.A.S.; Singh, A.K. Measurement and Analysis of Blast Fragmentation; CRC Press: London, UK, 2012. [Google Scholar]
- Tatiya, R.R. Surface and Underground Excavations: Methods, Techniques and Equipment; CRC Press: London, UK, 2005. [Google Scholar]
- Gokhale, B.V. Rotary Drilling and Blasting in Large Surface Mines; CRC Press: London, UK, 2010. [Google Scholar]
- Bise, C.J. Mining Engineering Analysis; SME: Littleton, CO, USA, 2003. [Google Scholar]
- Frimpong, M.; Kabongo, K.; Davies, C.-W. Diggability, a Measure of Dragline Effectiveness and Productivity; International Society of Explosives Engineers: Cleveland, OH, USA, 1996. [Google Scholar]
- Singh, S.; Yalcin, T.; Glogger, M.; Narendrula, M. Interaction between the size distribution of the muck and the loading equipment. In Proceedings of the 4th International Conference on Computer Applications in Mineral Industries, Calgary, AB, Canada, 8–10 September 2003. [Google Scholar]
- Afeni, T.B. Optimization of drilling and blasting operations in an open pit mine—The SOMAIR experience. Min. Sci. Technol. 2009, 19, 736–739. [Google Scholar] [CrossRef]
- Bowa, V.M. Optimization of blasting design parameters on open pit bench a case study of Nchanga open pits. Int. J. Sci. Technol. Res. 2015, 4, 45–51. [Google Scholar]
- Mackenzie, A.S. Optimum blasting. In Proceedings of the 28th Annual Minnesota Mining Symposium, Duluth, MN, USA, 14–16 January 1967. [Google Scholar]
- Eloranta, J. The efficiency of blasting versus crushing and grinding. In Proceedings of the 23rd Conference of Explosives and Blasting Technique, Orlando, FA, USA, 19–23 January 1997. [Google Scholar]
- Fuerstenau, M.; Chi, G.; Bradt, R. Optimization of Energy Utilization and Production Costs in Mining and Ore Preparation Processes; Society for Mining, Metallurgy and Exploration: Littleton, CO, USA, 1995. [Google Scholar]
- Eloranta, J. Downstream costs and their relationship to blasting. In Proceedings of the Mineblast 99, Duluth, MN, USA, 7–11 June 1999. [Google Scholar]
- Morin, M.A.; Ficarazzo, F. Monte Carlo simulation as a tool to predict blasting fragmentation based on the Kuz–Ram model. Comput. Geosci. 2006, 32, 352–359. [Google Scholar] [CrossRef]
- Bremer, D.; Ethier, R.; Lilly, D. Factors driving continuous blasting improvement at the Lafarge Ravena Plant. In Proceedings of the 33rd Conference on Explosives and Blasting Technique, Nashville, TN, USA, 28–31 January 2007. [Google Scholar]
- Kanchibotla, S.S. Optimum blasting? Is it minimum cost per broken rock or maximum value per broken rock? Fragblast 2003, 7, 35–48. [Google Scholar] [CrossRef]
- Eshun, P.; Affum, B.; Boakye, A. Drill and Blast Performance Evaluation at the Obra Pit of Chirano Gold Mines Ltd, Ghana. Ghana Min. J. 2016, 16, 28–35. [Google Scholar] [CrossRef]
- Bilim, N.; Çelik, A.; Kekeç, B. A study in cost analysis of aggregate production as depending on drilling and blasting design. J. Afr. Earth Sci. 2017, 134, 564–572. [Google Scholar] [CrossRef]
- Sun, X.; Wang, L.; Lu, Y.; Jiang, B.; Li, Z.; Zhang, J. A yielding bolt-grouting support design for a soft-rock roadway under high stress: A case study of the Yuandian No. 2 coal mine in China. J. S. Afr. Inst. Min. Metall. 2018, 118, 71–82. [Google Scholar] [CrossRef] [Green Version]
- Abbaspour, H.; Drebenstedt, C.; Badroddin, M.; Maghaminik, A. Optimized design of drilling and blasting operations in open pit mines under technical and economic uncertainties by system dynamic modelling. Int. J. Min. Sci. Technol. 2018, 28, 839–848. [Google Scholar] [CrossRef]
- Rocha Gil, M.; Flores, D.; Cebrian, D. Digitization for Optimization: Easier and Cheaper. In Proceedings of the 10th World Conference on Explosives and Blasting, Helsinki, Finland, 15–17 September 2019. [Google Scholar]
- Dinis da Gama, C.; Lopez Jimeno, C. Rock fragmentation control for blasting cost minimization and environmental impact abatement. In Proceedings of the International Symposium on Rock Fragmentation by Blasting, Vienna, Austria, 5–8 July 1993. [Google Scholar]
- Nielsen, K.; Malvik, T. Grindability enhancement by blast-induced microcracks. Powder Technol. 1999, 105, 52–56. [Google Scholar] [CrossRef]
- Taqieddin, S.A. Evaluation of the efficiency of a blasting operation designed for a dragline strip mining process. Min. Sci. Technol. 1989, 8, 59–64. [Google Scholar] [CrossRef]
- Aler, J.; Du Mouza, J.; Arnould, M. Measurement of the fragmentation efficiency of rock mass blasting and its mining applications. Int. J. Rock Mech. Min. 1996, 33, 125–139. [Google Scholar] [CrossRef]
- Schleifer, J.; Tessier, B. Fragmentation assessment using the FragScan system: Quality of a blast. Fragblast 2002, 6, 321–331. [Google Scholar] [CrossRef]
- Shim, H.-J.; Ryu, D.-W.; Chung, S.-K.; Synn, J.-H.; Song, J.-J. Optimized blasting design for large-scale quarrying based on a 3-D spatial distribution of rock factor. Int. J. Rock Mech. Min. Sci. 2009, 46, 326–332. [Google Scholar] [CrossRef]
- Jahani, M.; Taji, M. Comparison of empirical fragmentation models at the Gol-Gohar iron ore mine. In Proceedings of the 11th International Symposium on Rock Fragmentation by Blasting, Sydney, Australia, 24–26 August 2015. [Google Scholar]
- Gaunt, J.; Symonds, D.; McNamara, G.; Adiyansyah, B.; Kennelly, L.; Sellers, E.A.J.A.; Kanchibotla, S.S. Optimisation of drill and blast for mill throughput improvement at Ban Houayxai Mine. In Proceedings of the 11th International Symposium on Rock Fragmentation by Blasting, Sydney, Australia, 24–26 August 2015. [Google Scholar]
- Hakami, A.; Mansouri, H.; Farsangi, E.; Dehghan, M.R.; Faramarzi, F. Study of the effect of blast pattern design on autogenous and semi-autogenous mill throughput at gol-e-gohar iron ore mine. In Proceedings of the 11th International Symposium on Rock Fragmentation by Blasting, Sydney, Australia, 24–26 August 2015. [Google Scholar]
- Nikkhah, A.; Taji, M. Investigating the impacts of fragmentation due to blasting operation on machinary efficiency of Sarcheshmeh Copper Mine. J. Miner. Res. Eng. 2017, 2, 25–36. [Google Scholar]
- La Rosa, D.; Caron, K.; Valery, W.; Diaz, R.; Mamani, H. Blast fragmentation impacts on downstream processing at Goldfields Cerro Corona. In Proceedings of the 11th International Symposium on Rock Fragmentation by Blasting, Sydney, Australia, 24–26 August 2015. [Google Scholar]
- Silva, A.C.; Martins, P.A.A.; Silva, E.M.S.; Fonseca, A.L.S.; Ferrari, A.J.D.; Cunha, E.B.; Silva, V.M.; Matthew, V.O.; Vilela, D.R.T. Fragmentation optimisation–adopting mine to mill for reducing costs and increasing productivity. In Proceedings of the 11th International Symposium on Rock Fragmentation by Blasting, Sydney, Australia, 24–26 August 2015. [Google Scholar]
- Kanchibotla, S.S.; Valery, W.; Morrell, S. Modelling fines in blast fragmentation and its impact on crushing and grinding. In Proceedings of the Explo ‘99–A conference on rock breaking, The Australasian Institute of Mining and Metallurgy, Kalgoorlie, Australia, 7–11 November 1999. [Google Scholar]
- Janković, A.; Grundstrom, C.; Kanchibotla, S.; Thornton, D. Blast fragmentation for maximising the sag mill throughput at Porgera Gold Mine. In Proceedings of the Annual Conference on Explosives and Blasting Technique, Orlando, FL, USA, 28–31 January 2001. [Google Scholar]
- Workman, L.; Eloranta, J. The effects of blasting on crushing and grinding efficiency and energy consumption. In Proceedings of the 29th Conference on Explosives and Blasting Techniques, Nashville, TN, USA, 2–5 February 2003. [Google Scholar]
- Khademian, A.; Bagherpour, R. Alteration of grindability of minerals due to applying different explosives in blasting operation. Miner. Eng. 2017, 111, 174–181. [Google Scholar] [CrossRef]
- Beyglou, A.H. Improvement of Blast-Induced Fragmentation and Crusher Efficiency by Means of Optimized Drilling and Blasting in Aitik. Master’s Thesis, Lulea University of Technology, Luleå, Sweden, 2012. [Google Scholar]
- Stagg, M.; Ottemess, R.; Siskind, D. Effects of blasting practices on fragmentation. In Proceedings of the 33rd US Symposium on Rock Mechanics (USRMS), Santa Fe, NM, USA, 3–5 June 1992. [Google Scholar]
- Strelec, S.; Gazdek, M.; Mesec, J. Blasting design for obtaining desired fragmentation. Teh. Vjesn. 2011, 18, 79–96. [Google Scholar]
- Kim, K. Blasting Design Using Fracture Toughness and Image Analysis of the Bench Face and Muckpile. Master’s Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2006. [Google Scholar]
- Sharma, A.; Mishra, A.K.; Choudhary, B.S. Impact of blast design parameters on blasted muckpile profile in building stone quarries. Ann. Chim.-Sci. Mater. 2019, 43, 29–36. [Google Scholar] [CrossRef] [Green Version]
- Esen, S.; Nagarajan, M. Muck pile shaping for draglines and dozers at surface coalmines. In Proceedings of the 11th International Symposium on Rock Fragmentation by Blasting Sydney, Sydney, Australia, 24–26 August 2015. [Google Scholar]
- Tittarelli, F.; Mobili, A.; Bellezze, T. The use of a Phosphate-based migrating corrosion inhibitor to repair reinforced concrete elements contaminated by chlorides. IOP Conf. Ser: Mater. Sci. Eng. 2017, 225, 012106. [Google Scholar] [CrossRef]
- Rafeeian, N.; Taji, M.; Nikkhah, A. Mine to mill optimisation in Sarcheshmeh copper mine. In Proceedings of the 10th World Conference on Explosives and Blasting, Helsinki, Finland, 15–17 September 2019. [Google Scholar]
- Hamdi, E.; Du Mouza, J. A methodology for rock mass characterisation and classification to improve blast results. Int. J. Rock Mech. Min. Sci. 2005, 42, 177–194. [Google Scholar] [CrossRef]
- Singh, S.; Yalcin, T. Effects of muck size distribution on scooping operations. In Proceedings of the Annual Conference on Explosives and Blasting Technique, Las Vegas, NV, USA, 10–13 February 2002. [Google Scholar]
- Singh, S.; Narendrula, R. Factors affecting the productivity of loaders in surface mines. Int. J. Surf. Min. Reclam. Environ. 2006, 20, 20–32. [Google Scholar] [CrossRef]
- Mosher, J. Comminution circuits for gold ore processing. In Gold Ore Processing; Adams, M., Ed.; Elsevier: Amsterdam, The Netherlands, 2016; pp. 259–277. [Google Scholar]
- Kojovic, T. Influence of aggregate stemming in blasting on the SAG mill performance. Miner. Eng. 2005, 18, 1398–1404. [Google Scholar] [CrossRef]
- Cunningham, C. The Kuz-Ram fragmentation model–20 years on. In Proceedings of the European Federation of Explosives Engineers Brighton Conference Proceedings, Brighton, UK, 13–16 September 2005. [Google Scholar]
- Moodley, L.; Cunningham, C.; Lourens, H. Measuring the effect of blasting fragmentation on hard rock quarrying operations. In Rock Fragmentation by Blasting; Mohanty, B., Ed.; CRC Press: London, UK, 1996; pp. 353–359. [Google Scholar]
- Babanouri, N.; Mansouri, H.; Nasab, S.K.; Bahaadini, M. A coupled method to study blast wave propagation in fractured rock masses and estimate unknown properties. Comput. Geotech. 2013, 49, 134–142. [Google Scholar] [CrossRef]
- Sołtys, A.; Pyra, J.; Winzer, J. Analysis of blast-induced vibration structure in open-cast mines. J. Vibroeng. 2017, 19, 409–418. [Google Scholar]
- Sołtys, A. Assessment of the impact of blasting works on buildings located in the vicinity of open-pit mines using matching pursuit algorithm. Arch. Min. Sci. 2020, 65, 199–212. [Google Scholar]
- Sołtys, A. Firing explosive charges with millisecond delay in surface mining—Historical outline. Inz. Miner. 2018, 20, 177–190. [Google Scholar]
- Pyra, J.; Sołtys, A. Method for studying the structure of blast-induced vibrations in open-cast mines. J. Vibroeng. 2016, 18, 3829–3840. [Google Scholar] [CrossRef]
- Miao, Y.; Zhang, Y.; Wu, D.; Li, K.; Yan, X.; Lin, J. Rock fragmentation size distribution prediction and blasting parameter optimization based on the muck-pile model. Min. Metall. Explor. 2021, 38, 1071–1080. [Google Scholar] [CrossRef]
- Kirsanov, A.K.; Vokhmin, S.A.; Kurchin, G.S.; Zaitseva, E.V.; Volkov, E.P. Grain-size composition predicting models after explosion in open-pit mining. J. Degrade. Min. Land. Manage. 2019, 7, 1915–1919. [Google Scholar] [CrossRef]
- Man, K.; Liu, X.; Song, Z. Blasting vibration monitoring scheme and its application. J. Vibroeng. 2021, 23, 1640–1651. [Google Scholar]
- Nikkhah, A.; Taji, M. The effect of the underground water on production costs and mining operation in open-pit mines, case study: Sarcheshmeh copper mine. J. Geosci. 2019, 28, 267–272. [Google Scholar]
- National Iranian Copper Industies Company, NICICo., Tehran, Iran. Technical reports of Sarcheshmeh Copper Complex—Computer and technical services department of Sarcheshmeh Copper Mine. 2021; (not published work). [Google Scholar]
- National Iranian Copper Industies Company, NICICo., Tehran, Iran. Blasting reports of Sarcheshmeh Copper Complex—The drilling and blasting department of Sarcheshmeh Copper Mine. 2021; (not published work). [Google Scholar]


| Parameter | Refs |
|---|---|
| EC | [4,15,16,17,18,19,20,21,22,23,24,25,26] |
| OC | [4,15,16,17,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38] |
| El.Cs | [17,18,21,23,24,31,36,39,40,41,42] |
| En.Cs | [17,24,31,39,41,42,43] |
| TC | [15,23,24,26] |
| Sc | [4,16,18,19,20,21,22,23,24,25,26,27,28,30,33,34,35,36,37,38,39,40,42,43,44,45,46,47,48,49,50] |
| Sd | [4,20,22,23,24,25,26,33,42,43,45,49,50,51] |
| DL | [4,11,12,16,17,29,33,48,51,52,53] |
| Pe | [33] |
| LP | [4,11,12,17,21,28,29,30,33,48,50,51,53] |
| Cr.P | [18,24,28,32,33,36,37,38,39,41,42,43,50,54] |
| MT | [18,24,34,35,36,37,38,39,40,41,42,55] |
| Mu | [4,22,29,33,46,47,48,52,53] |
| DF | [4,11,12,15,16,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,54,55,56,57] |
| E.Co | [4,27,33] |
| SB | [4,22,26,27,32,33] |
| Di | [26,33,39] |
| RLW | [36,58] |
| DBB | [36,58] |
| Parameter (Unit) | Symbol | Explanation | Average | Std. Deviation |
|---|---|---|---|---|
| Diameter (inch) | D | Hole diameter of blast blocks | 8 | 1.8 |
| Burden (m) | B | Row spacing of blast blocks | 26 | 0.9 |
| Spacing (m) | S | Hole spacing in a row of blocks | 7.3 | 1.3 |
| Uniaxial compressive strength (MPa) | UCS | Mechanical properties of rocks | 28 | 11 |
| Ratio of length to width of blast block | Division of length of blast block by width of blast block | 6.05 | 2.75 | |
| Volume of blast block (m3) | Non situ volume of blast blocks | 17,798.36 | 23,609.78 | |
| Division of area of blast block on non situ volume | 0.029 | 0.011 | ||
| Division of consumption charge of blast block on non situ volume | 0.198 | 0.07 | ||
| 50% Input dimensions (cm) | 50% Input dimensions of rock caused by blasting operation | 3.26 | 2.11 | |
| 80% Input dimensions (cm) | 80% Input dimensions of rock caused by blasting operation | 9.41 | 6.36 | |
| Fragmentation efficiency index | FE | - | 36.3 | 18.1 |
| over-fragment rock | F | - | 70.7 | 5.26 |
| A loading cycle of machine’s bucket(s) | Including a round cycle of bucket of loading machine | 58.34 | 9.507 | |
| Operation of machine | Operation of loading machine for loading 1 cubic meter | 17.623 | 0.002 | |
| When loading machine is in loading blast block is out of order | 0.027 | 0.102 | ||
| When the loading machine is ready for loading operation of blast block | 0.067 | 0.058 | ||
| Movement machine | Length and width handling time of loading machine in block | 0.045 | 0.004 | |
| Tonnage of loading per hour (ton/h) | Division of total tonnage of blast block on the hour of operation | 1058.02 | 574.202 | |
| Specific loading (h/m3) | Division of total available time of loading machineries’ blast block according to hour to total volume | 0.005 | 0.002 | |
| Operation of crusher (h) | Operation of crusher for grading in blast block | 12.102 | 15.132 | |
| Operation of crusher (h) | Failure of crusher for grading in blast block | 12.687 | 0.853 | |
| Production of crusher in blast block | 1245.158 | 143.99 | ||
| Division of total consumption energy of blast block according to KW on total tonnage of input rock | 0.135 | 0.006 | ||
| Specific mine unit operation index (kg.h.kW/m2) | Multiplication of specific drilling, specific charge, specific loading, and specific crushing | 0.439 | 0.549 |
| Fragmentation Efficiency | Boulder (%) | Loading Efficiency in Muck Pile [24] | Digging Conditions in Muck Pile [24] | Overall Blast Result | Capacity | |||
|---|---|---|---|---|---|---|---|---|
| Condition | Shovel | Truck (ton) | ||||||
| Very good | 0 | Moderate | Difficult | 47 | Good | 16.5 | 100 | 476.34 |
| Good | 0 | Relatively good | Easy | 61 | Moderate | 4.5 | 136 | 556.31 |
| Good | 0 | Relatively good | Easy | 30 | Good | 16.5 | 100 | 533.59 |
| Good | 0 | Very good | Very good | 40 | Good | 12 | 100 | 1552.35 |
| Good | 0 | Excellent | Excellent | 41 | Good | 12 | 136 | 2179.15 |
| Moderate | 0 | Excellent | Excellent | 34 | Good | 4.5 | 136 | 602.79 |
| Good | 0 | Excellent | Excellent | 42 | Good | 18 | 136 | 1663.86 |
| Good | 0 | Excellent | Excellent | 44 | Good | 2.15 | 100 | 471.18 |
| Good | 0 | Excellent | Very good | 35 | Good | 12 | 136 | 1480.15 |
| Good | 0 | Good | Excellent | 55 | Good | 12 | 136 | 1197.88 |
| Good | 0 | Excellent | Very good | 55 | Good | 12 | 136 | 1563.58 |
| Very good | 0 | Excellent | Difficult | 36 | Good | 15 | 100 | 565.98 |
| Good | 0 | Relatively good | Easy | 33 | Good | 12 | 136 | 1185.02 |
| Good | 0 | Relatively good | Difficult | 32 | Good | 12 | 136 | 703.56 |
| Very good | 0 | Moderate | Moderate | 37 | Good | 11 | 136 | 451.71 |
| Good | 11 | Low | Difficult | 30 | Good | 18 | 100 | 394.71 |
| Good | 0 | Excellent | Excellent | 30 | Good | 12 | 136 | 1744.71 |
| Very good | 0 | Relatively good | Relatively difficult | 33 | Good | 16.5 | 100 | 653.33 |
| Very good | 0 | Relatively good | Relatively difficult | 35 | Good | 16.5 | 100 | 620.26 |
| Good | 0 | Excellent | Excellent | 25 | Good | 12 | 136 | 1982.29 |
| V | IV | III | II | I | Class |
|---|---|---|---|---|---|
| >100 | 75–100 | 50–75 | 25–50 | <25 | ξj |
| Very weak | Weak | Moderate | Good | Very good | Condition |
| Blasting No. | Possible Reasons for Low Production Levels of Loading Machine |
|---|---|
| 1 | (1) Blast used to create new horizon on the floor of the mine and lack of suitable design of pattern for blast to create new benches. (2) Insufficient efficiency of loading device in muck pile due to lack of free surface of the blast and lack of displacement of the block after blasting. (3) Penetration and carving of crushed piles caused by blasting operation and by loading machine with more time. (4) Disproportionate capacity of loading bucket with the hauling machine. (5) Wear and depreciation of the hauling devices. |
| 2 | (1) Inappropriate efficiency of loading device in muck pile due to lack of free surface of the blast and lack of displacement of the block after blasting. (2) Too much time wasted penetrating and digging out the muck piles by loading machine. (3) Disproportionate capacity of loading bucket to the hauling machine. (4) Wear and depreciation of the hauling devices. |
| 3 | (1) Disproportionate capacity of loading bucket with the hauling machine. (2) Wear and depreciation of the hauling devices. |
| 6 | (1) Disproportionate capacity of loading bucket to the hauling machine. (2) Depreciation of the hauling devices. |
| 8 | (1) Disproportionate capacity of loading bucket to the hauling machine. |
| 12 | (1) Inappropriate efficiency of loading device in muck pile due to lack of free surface of the blast and lack of displacement of the block after blasting. (2) Too much time wasted penetrating and digging out the muck piles by loading machine. (3) Disproportionate capacity of the loading bucket to the hauling machine. (4) Wear and depreciation of the loading devices. |
| 14 | (1) Disproportionate capacity of loading bucket to the hauling machine. (2) Depreciation of the loading devices. |
| 15 | (1) Inappropriate efficiency of loading device in muck pile due to lack of free surface for the blast and lack of displacement of the block after blasting. (2) Too much time wasted penetrating and digging out the muck piles by loading machine. (3) Wear and depreciation of the loading devices. |
| 16 | (1) Inappropriate efficiency of loading device in muck pile due to lack of free surface for the blast and lack of displacement of the block after blasting. (2) Disproportionate capacity of loading bucket to the hauling machine. (3) Wear and depreciation of the loading devices. |
| 18 | (1) Inappropriate efficiency of loading device in muck pile due to lack of free surface for the blast and lack of displacement of the block after blasting. (2) Too much time wasted penetrating and digging out the muck piles by loading machine. (3) Disproportionate capacity of loading bucket with the hauling machine. (4) Wear and depreciation of the loading devices. |
| 19 | (1) Inappropriate efficiency of loading device in muck pile due to lack of free surface of the blast and lack of displacement of the block after blasting. (2) Too much time wasted penetrating and digging out the muck piles by loading machine. (3) Disproportionate capacity of loading bucket with the hauling machine. (4) Wear and depreciation of the loading devices. |
| Predict Model | ||||||
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | ||||||
| Model No. | Analysis of variance (ANOVA) | |||||
| R | Adj. | Std. error | F change | p Value | ||
| 1 | 0.803 | 0.646 | 0.579 | 1.872 | 9.714 | 0.001 |
| 2 | 0.762 | 0.581 | 0.469 | 4.759 | 5.19 | 0.003 |
| Predict Model | ||||||
|---|---|---|---|---|---|---|
| 3 | ||||||
| 4 | ||||||
| 5 | ||||||
| 6 | ||||||
| 7 | ||||||
| Model No. | Analysis of variance (ANOVA) | |||||
| R | Adj. | Std. error | F change | p Value | ||
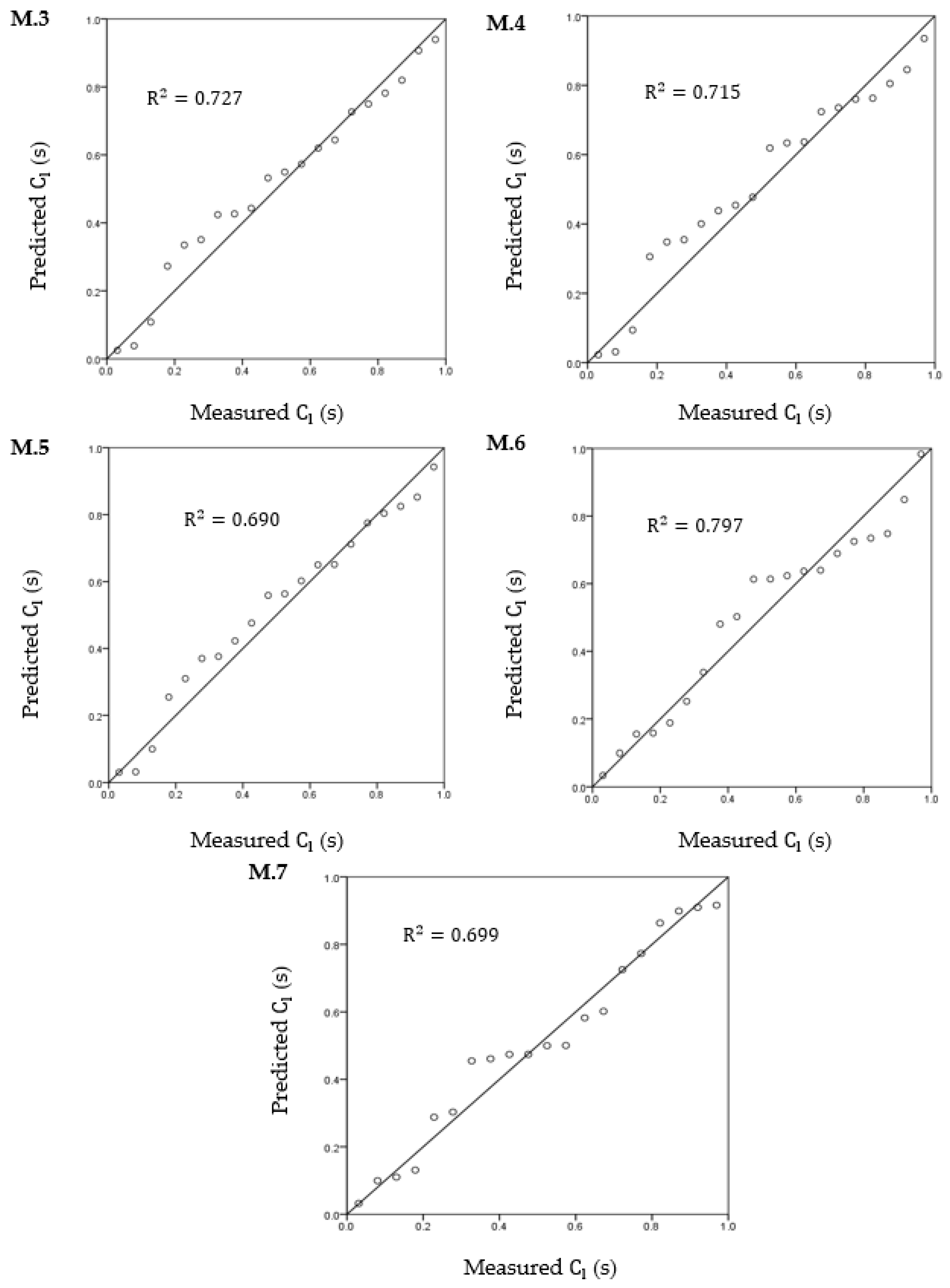
| 3 | 0.853 | 0.727 | 0.676 | 5.549 | 14.235 | 0.001 |
| 4 | 0.845 | 0.715 | 0.661 | 5.676 | 13.365 | 0.001 |
| 5 | 0.831 | 0.69 | 0.632 | 5.917 | 11.876 | 0.004 |
| 6 | 0.893 | 0.797 | 0.759 | 4.791 | 20.917 | 0.001 |
| 7 | 0.836 | 0.699 | 0.642 | 5.832 | 12.382 | 0.007 |
| Predict Model | ||||||
|---|---|---|---|---|---|---|
| 8 | ||||||
| 9 | ||||||
| 10 | ||||||
| Model No. | Analysis of variance (ANOVA) | |||||
| R | Adj. | Std. error | F change | p Value | ||
| 8 | 0.895 | 0.8 | 0.777 | 0.001 | 34.04 | 0.001 |
| 9 | 0.811 | 0.658 | 0.567 | 0.371 | 7.215 | 0.002 |
| 10 | 0.801 | 0.642 | 0.600 | 0.356 | 15.229 | 0.008 |
| Model No. | Independent Variables | Unstandardized Coefficients | Standardized Coefficients | t Values | 95% Confidence Interval for B | Collinearity Statistics | |||
|---|---|---|---|---|---|---|---|---|---|
| B | Std. Error | Beta | Lower Bound | Upper Bound | Tolerance | VIF | |||
| 1 | Constant | 29.544 | 6.326 | 4.670 | 16.132 | 42.955 | |||
| D | 17.161 | 5.243 | 0.625 | 3.273 | 6.047 | 28.275 | 0.608 | 1.645 | |
| 4.235 | 1.692 | 0.412 | 2.503 | 0.648 | 7.823 | 0.817 | 1.223 | ||
| −9.135 | 1.785 | −0.993 | –5.117 | −12.919 | −5.350 | 0.588 | 1.7 | ||
| 2 | Constant | 44.508 | 26.4 | 1.697 | −11.465 | 101.075 | |||
| D | 43.026 | 13.352 | 0.692 | 3.222 | 14.566 | 71.486 | 0.606 | 1.651 | |
| H | 19.726 | 28.591 | 0.15 | 0.690 | –41.215 | 80.666 | 0.593 | 1.687 | |
| 7.531 | 4.744 | 0.324 | 1.587 | –2.644 | 17.706 | 0.664 | 1.506 | ||
| –21.822 | 5.553 | –1.048 | –3.930 | –33.658 | –9.986 | 0.393 | 2.545 | ||
| 3 | Constant | 1.843 | 5.687 | 0.324 | −10.213 | 13.9 | |||
| D | 2.75 | 0.755 | 0.524 | 3.644 | 1.15 | 4.35 | 0.823 | 1.215 | |
| 1.112 | 0.488 | 0.322 | 2.281 | 0.079 | 2.146 | 0.855 | 1.175 | ||
| 0.543 | 0.199 | 0.364 | 2.73 | 0.121 | 0.965 | 0.96 | 1.042 | ||
| 4 | Constant | –30.092 | 11.795 | 2.551 | −55.096 | −5.088 | |||
| D | 50.498 | 13.528 | 0.544 | 3.733 | 21.819 | 79.176 | 0.84 | 1.191 | |
| 8.936 | 5.075 | 0.257 | 1.761 | −1.821 | 19.693 | 0.836 | 1.196 | ||
| 14.921 | 6.293 | 0.334 | 2.371 | 1.58 | 28.262 | 0.899 | 1.112 | ||
| 5 | Constant | −25.107 | 11.786 | –2.130 | −50.091 | –0.123 | |||
| D | 51.265 | 14.101 | 0.552 | 3.636 | 21.373 | 81.158 | 0.84 | 1.191 | |
| 8.425 | 5.383 | 0.242 | 1.565 | −2.986 | 19.837 | 0.807 | 1.239 | ||
| 13.705 | 6.941 | 0.297 | 1.975 | −1.008 | 28.419 | 0.857 | 1.167 | ||
| 6 | Constant | 16.462 | 2.776 | 5.93 | 10.577 | 22.347 | |||
| D | 0.291 | 0.044 | 0.871 | 6.59 | 0.198 | 0.385 | 0.728 | 1.374 | |
| 0.296 | 0.062 | 1.219 | 4.762 | 0.164 | 0.428 | 0.194 | 5.161 | ||
| 0 | −1.172 | −4.263 | 0 | 0 | 0.168 | 5.957 | |||
| 7 | Constant | 2.756 | 6.008 | 0.459 | –9.980 | 15.492 | |||
| 0 | 0.257 | 1.788 | 0 | 0 | 0.91 | 1.099 | |||
| D | 3.053 | 0.76 | 0.582 | 4.019 | 1.442 | 4.663 | 0.897 | 1.115 | |
| 0.613 | 0.214 | 0.41 | 2.864 | 0.159 | 1.067 | 0.917 | 1.091 | ||
| 8 | Constant | 0.017 | 0.002 | 8.604 | 0.013 | 0.021 | |||
| 0.005 | 0.001 | 0.622 | 4.221 | 0.003 | 0.008 | 0.541 | 1.848 | ||
| 0.003 | 0.001 | 0.347 | 2.355 | 0 | 0.005 | 0.541 | 1.848 | ||
| 9 | Constant | 3.444 | 0.634 | 5.433 | 2.093 | 4.795 | |||
| D | −0.005 | 0.003 | −0.278 | −1.628 | −0.012 | 0.002 | 0.784 | 1.275 | |
| H | 0.011- | 0.003 | −0.636 | −3.887 | −0.017 | −0.005 | 0.851 | 1.175 | |
| 0.002 | −0.002 | −0.010 | −0.005 | 0.005 | 0.862 | 1.161 | |||
| 0.001 | 0 | 0.212 | 1.312 | 0 | 0.002 | 0.874 | 1.144 | ||
| 10 | Constant | 0.811 | 0.118 | 6.862 | 0 | 0.562 | |||
| D | 0 | −0.241 | −1.626 | 0.122 | 0 | 0.955 | 1.046 | ||
| 0 | 0.715 | 4.814 | 0 | 0 | 0.956 | 1.046 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nikkhah, A.; Vakylabad, A.B.; Hassanzadeh, A.; Niedoba, T.; Surowiak, A. An Evaluation on the Impact of Ore Fragmented by Blasting on Mining Performance. Minerals 2022, 12, 258. https://doi.org/10.3390/min12020258
Nikkhah A, Vakylabad AB, Hassanzadeh A, Niedoba T, Surowiak A. An Evaluation on the Impact of Ore Fragmented by Blasting on Mining Performance. Minerals. 2022; 12(2):258. https://doi.org/10.3390/min12020258
Chicago/Turabian StyleNikkhah, Ayyub, Ali Behrad Vakylabad, Ahmad Hassanzadeh, Tomasz Niedoba, and Agnieszka Surowiak. 2022. "An Evaluation on the Impact of Ore Fragmented by Blasting on Mining Performance" Minerals 12, no. 2: 258. https://doi.org/10.3390/min12020258
APA StyleNikkhah, A., Vakylabad, A. B., Hassanzadeh, A., Niedoba, T., & Surowiak, A. (2022). An Evaluation on the Impact of Ore Fragmented by Blasting on Mining Performance. Minerals, 12(2), 258. https://doi.org/10.3390/min12020258








