Abstract
The deep-seabed mining system for mining resources consists of a mining vessel, lifting riser, lifting pump, buffer system, flexible riser, and mining robot. Because this system is exposed to extreme environments such as fluid resistance, high water pressure, and deep water, a considerable amount of time and cost is consumed in the design and test evaluation of equipment. To tackle these problems, the deep-seabed mining system in an extreme environment requires simulation-based technology. In particular, due to the large movement caused by marine energy, vibration caused by the operation of the mechanical system, and driving resistance of mining robot by the subsea soft soil, it is very important in the mining system design to analyze the dynamic effects of the various elements that constitute the deep-seabed mining system in a single integrated environment. This paper introduces the development of an integrated dynamic simulation method for deep-seabed mining systems and discusses the results.
1. Introduction
Due to the importance of deep-seabed resources, a number of concepts for commercial production of deep-seabed resources have been studied since the 1970s [1,2,3,4,5,6]. Since the deep-seabed resources are located in soft ground with a high water content 2000 m below sea level, it is very important to develop a method of collecting resources and transferring them to the surface. To tackle these problems, various mining technologies and methods have recently been proposed based on advanced technology. A novel underwater mining technique for extracting inland mineral deposits in flooded open-cut mines has been developed through the project Viable Alternative Mine Operating System (VAMOS) [7]. In addition, China (COMRA) and India (NOIT) have developed and tested pump and pipe-based transport systems, nodule collector travel and artificial nodule collection, and nodule collector travel [8].
However, the development of a deep-sea mining system composed of several mechanical systems and performance tests in the real sea takes a lot of time and money. Simulation technologies [9] and model test methods [10] are being used to tackle these problems. In particular, the use of dynamic simulation-based design and virtual test evaluation technologies that can reflect the dynamic characteristics of the ocean mechanical system is increasing because model tests performed with small similar models can derive response characteristics different from those of real-scale systems [10,11,12].
In Korea, Hong [13] developed mining technology using an underwater mining robot to collect manganese nodules in deep-seabed resources and conducted research on buffer systems, riser systems, and mining vessels to safely transfer collected resources to vessels. Since it is almost impossible to transport manganese nodules to the collection system in deep-seabed soft soils with high moisture content, a continuous mining system (as shown in Figure 1) was developed. It continuously transfers the resources collected from the mining robot through the riser system to the mining vessel on the sea.
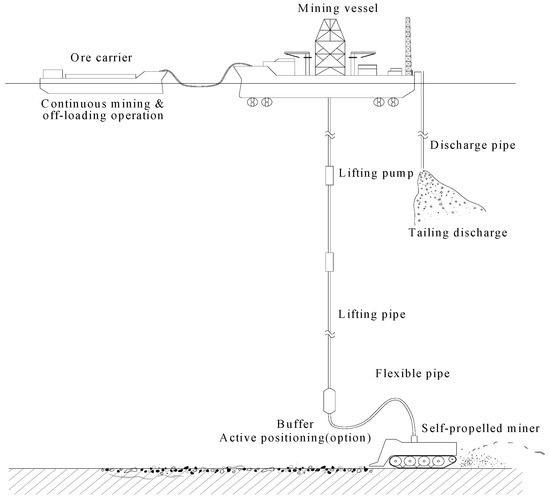
Figure 1.
Continuous system concept for deep-seabed resources mining [11].
This continuous mining system is composed of a mining vessel, lifting pump, lifting risers, buffer system, flexible risers, and underwater mining robot as shown in Figure 1. However, this continuous system has weak points as follows. First, the state and the behavior of the flexible riser connecting the intermediate buffer and the self-propelled mining robot have a great influence on the driving performance of the mining robot. Second, the 5000 m-long lifting riser and the intermediate buffer’s behavior also affect the driving performance of the mining robot. Third, hydrodynamics occurs in the system due to the elements of the marine environment such as ocean currents and waves. Hydrodynamics affects the system performance by affecting the system behavior. Therefore, the analysis of the dynamic behavior of a continuous mining system depending on environmental and mechanical factors is an important core technology [11,14].
In particular, an underwater mining robot that drives on soft ground is a vehicle with a driving system composed of infinite four-row tracks. Therefore, to analyze the driving and mining characteristics, an analysis technique considering the interaction between the soil ground and the driving system of the vehicle is important. In addition, the deep-seabed mining system composed of various mechanical systems, including mining robots, has a vast degree of freedom when using the fully developed model, and it takes enormous computation time. Due to this problem, the integrated modeling and simulation method and the reduced-order modeling and simulation method that can analyze the integrated behavior of the system in a short time are also very important. So far, most studies have focused on the development of a single analysis technique for elemental equipment, such as three-dimensional flow response analysis of subsea risers [15] and dynamic analysis of risers by vortex discharge excitation [16].
In this study, two “modeling and simulation techniques” were developed based on multibody dynamics. One is a mechanical modeling and simulation technique that enables integrated dynamic behavior analysis of “components of a deep-seabed mining system and a mining robot” with vast degrees of freedom. The other is an environmental modeling and simulation technique that can apply “marine environmental factors and soft ground characteristics”. The developed modeling and simulation technology was compared and verified with previously verified S/Ws. In this paper, we will discuss the results of technology development.
2. Multibody Dynamics
Multibody dynamics has kinematic relationships, kinematic equations, and solution steps as follows. As shown in Figure 2, the coordinate system is the inertial reference frame, and the coordinate system is the body reference frame.

Figure 2.
Kinematic relationships among mining system bodies [17].
The position of the -point in the body i is defined as [17,18,19].
where and are position vector and orientation matrix, respectively. represents a constant vector to -point in body reference frame as . The superscript T denotes a transpose matrix.
The velocities of the body i are defined in the body reference frame in this paper as
where and are translational velocity and rotational velocity vectors, respectively.
The accelerations of the body i are obtained by taking the time derivative of Equation (2) as follows [17].
where “~” is a tilde operation, which is the cross-product of a standard vector such as .
The variational form of Newton-Euler equations of motion for body i can be expressed as follows [17].
where and are the mass of body i and the external force vector, respectively. and are the moment of inertia of the body i and the external torque, respectively.
Through the matrix form in Equation (4), the augmented equation of motion for a multibody system that satisfies the constraints equation can be written as follows [17,18,19].
where is the total mass matrix, is the generalized acceleration vector, is the generalized force vector, is the constrained force to which the Lagrange multiplier theory (Haug, 1989) is applied. is the constraints equation for a joint, and is the lambda of the Lagrange multiplier. Subscript nbd is the number of total bodies in the system.
The equations of motion, the constraint equations, and the second-order Euler implicit integrations comprise the combined equations of H as follows.
where , and are the generalized coordinate, velocity, and acceleration vectors. and are the time and time step size. The Newton–Raphson method can be applied to solving the unknown variable as follows.
where is the Jacobian matrix for . In Equation (8), superscript i represents a number that is repeatedly calculated to converge to the residual .
The linear equation of Equation (7) can be simplified as follows using the decoupling method [20].
where , is the system Jacobian matrix related to , and is the residual of the equations of motion and constraint equations.
3. Development of Environmental Modeling Technologies
3.1. Formulations of Hydrodynamics
Objects present in fluid are more affected by acceleration and velocity than those in gas. The influence on acceleration and velocity can be explained by the concept of added mass, drag force, and so on. Acceleration around the fluid requires more force than just accelerating just the object. A relatively simple way to describe the mass of a fluid that is accelerated is to add an additional mass to the mass of the object [21]. The hydrodynamics and moment for the body in the fluid are as follows [22,23,24]. In Equation (11), the first and the second terms represent the effects of added mass.
where represents an added mass matrix of size 6 × 6. is the Coriolis force matrix by fluid. is the fluid damping matrix. In this paper, the fluid damping matrix is assumed to be the sum of the linear and secondary damping matrices. They might be measured from an experimental method. is the relative velocity between body i and ocean current in the fluid velocity field. The fluid Coriolis force matrix can be calculated as follows.
where the tilde operator of arbitrary vector is . , , , and are the 3 × 3 size sub-matrices that make up the matrix.
The third term in Equation (11) represents the effect of fluid damping. The fluid damping force can be expressed with the Morrison equation, which is a semi-experimental formula for calculating the working load in a fluid wave, and it is mainly used to obtain the load acting on the offshore platform. Since the volume of the object does not change in the fluid, the inertia component is omitted and only the drag component can be represented as in Equation (14) [22].
where is the fluid density. is the drag coefficient. is the area matrix of the object in contact with the fluid, and is the relative velocity between body i and ocean current.
The surface area of the body in contact with the fluid can be obtained by the area projected onto the inertial reference frame. The orientation of the body i existing on the initial reference frame can be calculated in Equation (15) using the Euler angle [17,25].
where is the algebraic vector. By inverse calculating the Euler angle rotation, the area of the object projected on the inertial reference frame can be calculated as shown in Equation (16).
where is the cross-sectional area vector in three-direction in the body reference frame. The area of the block projected in the X-direction of the inertial reference frame can be expressed as shown in Figure 3.
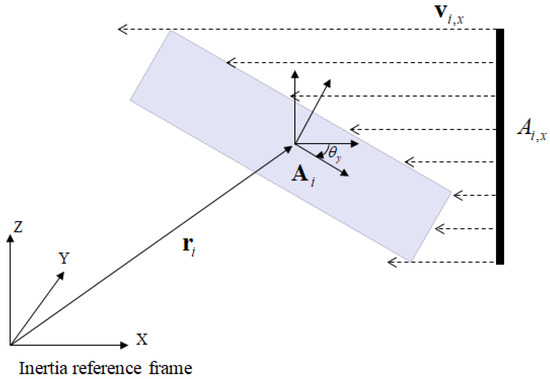
Figure 3.
Calculation method of the area of drag force acting on a single body.
3.2. Formulation of Buoyancy Force
As shown in Figure 4, buoyancy force is an upward force exerted by a fluid that opposes the weight of an immersed object (Body). Force of equal effect which is in the fluid can be represented by vector force. Buoyancy represents a single component force acting between ground and bodies. Additionally, force is acting on the action body in the opposite direction to gravity. The buoyancy acting between the ground and the body i can be expressed as [21].
where is the volume of body i. is the gravity vector.

Figure 4.
Buoyancy kinematic relationship between a body i and ground.
3.3. Formulations of Ocean Current
Similar to the gravitational field, ocean current represents the velocity field in the inertial reference frame. As shown in Figure 5, there are three types of currents. This type exists as constant, linear, and parabolic, respectively. In the inertial reference frame, the sea level is defined as z = 0, and there is no current at z > 0. The velocity of the current is defined by Equations (18)–(20), respectively.
where and are current height and current velocity at sea level, respectively.
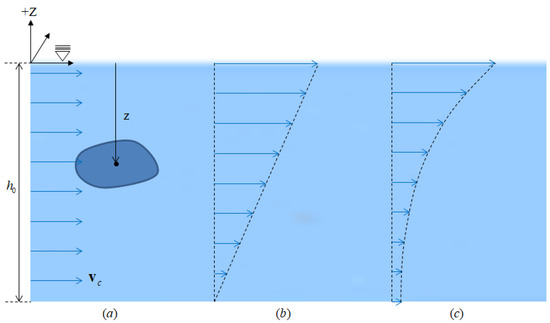
Figure 5.
Three types of ocean current: (a) a constant, (b) a linear, (c) a parabolic.
4. Development of Mechanical System Modeling Technologies
4.1. Riser System
Formulations of Beam Elastic Theory
The riser system installed in the deep sea is a structure with a large slenderness ratio and can be mathematically expressed using beam elastic theory. The mathematically simulated riser model consists of a rigid beam element representing the body of the riser and the hydrodynamics, fluid resistance force, and buoyancy force acting as an external force on the riser. The beam model used in the riser model is a beam elastic model to which Euler and Timoshenko beam theory is applied. The stiffness matrix of the beam is symmetric, and the components of each stiffness matrix K11 to K66 represent the stiffnesses for the cross-sectional shape and direction. The cross-sectional shape of the riser is typically defined as a cylinder and a hollow circle (pipe). The beam stiffness formula is as shown in Equation (21) [26,27].
where , , ,, , , , and . E is Young’s modulus, G is the shear modulus, A is the cross-sectional area, L is the length, I is the area moment of inertia, and P is the coefficient by shear force. Commonly, P’s value is zero when the beam stiffness is calculated [26].
To apply the beam stiffness to the dynamics model, it is converted into a beam elastic force and applied. The beam elastic force is expressed as Equation (22).
where is the damping matrix. and are the deformation and deformation velocity of the beam, respectively.
As shown in Figure 6, the riser represented by the beam consists of n concentrated mass bodies and n−1 elements. Between the bodies of riser and ground, hydrodynamics and drag forces are applied as shown in Equations (23) and (24), respectively.
where subscript j is the sequence of the concentrated mass bodies that make up the riser. , , , , and are the added mass matrix, the Coriolis force matrix, the relative velocity between bodies and current, the drag coefficient, and the area of the drag force acting on body corresponding to each of the j th bodies of the riser. The area of the drag force acting on the riser that is rotated in the Y-direction in the initial reference frame can be expressed as shown in Figure 7.
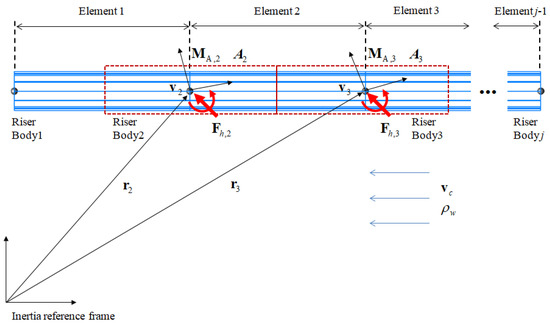
Figure 6.
Hydrodynamics and kinematic relationship in riser system.

Figure 7.
A method of calculating the area of drag force acting on a riser.
As shown in Figure 8, the developed buoyancy is also applied to the riser in the same method as the hydrodynamic. Buoyancy forces between each body of the riser and the ground are applied as shown in Equation (25).
where subscript j is the sequence of the riser body. is the volume of the j th body of the riser.

Figure 8.
Buoyancy and kinematic relationships in the riser system.
4.2. Formulations of Buoyancy Modules
The buoyancy modules are attached to the riser as a device to maintain the installation shape in the deep-seabed of the riser by generating positive buoyancy through the combination of material properties and size [27]. As shown in Figure 9, the buoyancy module is hollow shaped in the cross-section and L length and fixed to the riser bodies. As shown in Figure 10, n buoyancy modules are attached to the riser, and the fluid forces are applied to the buoyancy module in the same method as Equations (23)–(25). The parameters used here are the added mass, Coriolis, and drag coefficients for the buoyant segment.
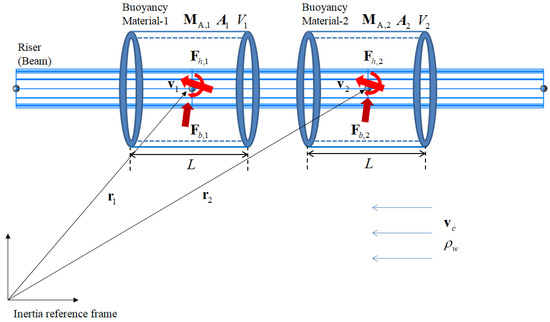
Figure 9.
Kinematic relationships of hydrodynamics and buoyancy in buoyancy modules.

Figure 10.
Buoyancy modules attached to riser system.
4.3. Formulations of Mining Vessel
As shown in Figure 11, the six-directions motion (surge, sway, heave, roll, pitch, and yaw) of the mining vessel by ocean current (wave) can be represented by joint motions. The combination of three translational constraints and three rotational constraints makes the joint motion of a mining vessel possible. Translational and rotational constraint equations are given by Equations (26) and (27), respectively [17,19].
where , , and are spherical, parallel-1, parallel-2 and dot-1 constraint equations.
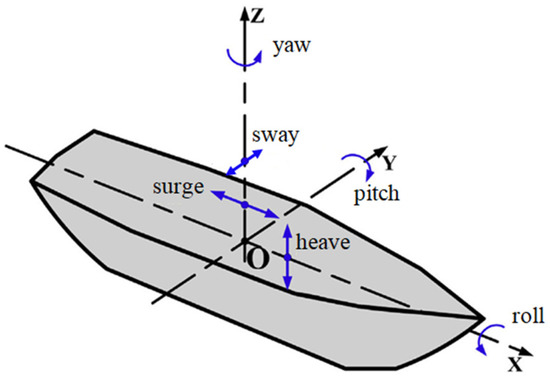
Figure 11.
Six-directional vessel motions related with kinematic constraints.
The six-way motion of the mining vessel is in the form of a sine wave in each direction. Sine waves are defined as in Equation (28).
where , and are magnitude, period and phase of the sine wave.
4.4. Formulations of Mining Robot
The mining robot is a tracked vehicle composed of four rows of the track. As shown in Figure 12, there are two types of mining robots depending on the track composition of the bottom of the robot.

Figure 12.
Mining robot models: (a) concept of a single-body track model, (b) concept of a multibody track model.
One is as shown in Figure 12a, A single-body track model is a method that simplifies a multibody track by summating soil contact forces acting on track links and applying them to a single rigid body with six degrees of freedom. The other method is the multibody track model with multiple track links applied. As shown in Figure 12b, a mining robot using a multibody model consists of sprockets, idlers, rollers, and multiple track links.
A multibody track model can predict the dynamic behavior of each element based on detailed modeling of each element of the vehicle, which is very useful for detailed design. However, by using a large number of rigid bodies, constraints, and numerous contact relationships of links, the system degree of freedom and the amount of calculation due to contact increase greatly. As the degree of freedom increases, the number of equations to be solved increases, and numerical analysis requires a great deal of time because it uses implicit integration. In contrast, the single-body track model is simplified, which solves the numerical analysis time problem of the multibody track model. However, by simplifying the interactions between the track links, there are constraints on the results of the analysis, and it can lead to low reliability
4.4.1. Formulations of Single-Body Track Model for Mining Robot
Kim [28,29] proposed a single-body track method for mining robot models. As shown in Figure 12a, the single-body track method applies the soil contact force to a single rigid body, which is the main body of a tracked robot, to analyze the dynamic behavior of the robot on soft ground. This is a method that does not constitute track links (bodies) as in the multi-body method but assumes that the links are in contact with the ground. After meshing for a single track row, sinkage and shear displacements are obtained between the center point of each element (contact surface of the track link) and the soft ground. This kinematic relationship also yields the normal and shear stresses that occur in a single track. The soil contact force and moment acting on the robot can be obtained by integration of the normal and shear stresses as the contact area of the track mesh. Since this method assumes a track body as one rigid body, the tension caused by the flexibility between track links cannot be taken into account. Further, as there are no track links and rollers, the motion by contact between them cannot be taken into account, either. However, it is possible to quickly analyze the mining robot’s straight and steering driving performance on the soft ground.
When the mining robot moves, a slip occurs from the relative velocity between the robot’s body and the track. The slip velocity at the track mesh point of a moving robot can be expressed as follows.
where superscript j represents the track row number. and are translational and rotational velocities of track robot. is the track velocity and is the longitudinal direction of the robot. Shear displacement of the track by soil can be obtained through the time integration of slip velocity as shown in Equation (30).
where subscript n is the previous value. h is the time step size.
When the mining robot moves, additional dynamic sinkage occurs due to shear deformation. Dynamic sinkage has the following relationship with shear displacement and ground pressure.
where is the dynamic sinkage coefficient. is the normal pressure. is the critical pressure coefficient. and are shear displacements in each direction. ms is a dynamic sinkage coefficient and 1 is usually used. The dynamic sinkage coefficients and ms are obtained through an experiment. The total sinkage of the track can be represented by the sum of the static sinkage and the dynamic sinkage as follows.
where the total sinkage i can be obtained by the track mesh point sunk from the ground. Static sinkage can be obtained from Equation (32), and soil contact force can be obtained through static sinkage and shear displacement. This soil contact force is obtained from each track mesh, summed with respect to a single track row, and transferred to the robot body. The kinematic algorithm of a single-body track model is shown in Figure 13a, and the soil contact force between the soft ground and the track is described in the next chapter.

Figure 13.
Algorithm for single-body track model: (a) the kinematic relationship of the soil contact force acting on the track, (b) the soil contact force acting on the track.
4.4.2. Formulations of Multibody Track Model for Mining Robot
In the multibody track model constructed as shown in Figure 12b, the tension between track links, the contact force between track links and rollers, and soil contact force between track links and soft ground are applied. The tension acting between the track links is applied to a compliant track model that exhibits rubber bushing characteristics between the pin and the track link. This bushing force and torque are expressed as follows [30].
where and are the 3 × 3 diagonal matrices that contain the stiffness matrix. and are the 3 × 3 diagonal matrices that contain the damping coefficient matrix. is translational force vector and is the vector of translational deformations between two track links. Similarly, is the rotational force vector and is the vector of relative rotational deformations between two track links
The contact force acting between track links and rollers such as sprockets, idlers, support rollers, and guide rollers can be obtained using Equation (34) using the Hertz contact theory [31].
where and are the stiffness and damping coefficient of the contact. is the penetration vector which is the relative distance between contact points. is the vector of penetration velocity. The soil contact between the track links and the soft ground is the same as the soil contact force mechanism used in the single-body model and is described in the next chapter.
5. Development of Soil Contact Mechanism
5.1. Formulations of Soil Contact Force
Soft cohesion soil (soft ground) has a very large nonlinear characteristic that causes the ground to collapse rapidly if a certain amount of shear displacement occurs. It is very difficult to apply a general linear contact model. Therefore, soil models that can take large nonlinearities into account should be used. The ground reactions can be divided into the normal and shear stresses of the soil. Normal stress is expressed with the ground pressure corresponding to the static sinkage of the track and is obtained by the relationship between pressure and sinkage. Shear stress can be obtained through the shear displacement caused by track and ground contact, generating traction force and moment.
For the normal stress acting between the mining robot and the ground, as shown in Figure 14a, the Bode model, which is a non-linear experimental formula with the relationship between pressure and sinkage was used [32]. This normal stress is expressed as a function of static sinkage and can be expressed as Equation (35).
where represents the pressure in Figure 14a where the asymptote of the slope meets the y-axis (pressure). and are coefficients representing a linear slope. For the shear stress, the Wong model with the shear stress-shear displacement relationship was used as shown in Figure 14b [33]. The maximum shear stress of the soft soil is given by Equation (36).
where c is the cohesion. p is the ground pressure. is the internal friction angle. Shear stress of cohesive soil is given by Equation (37).
where is the sensitivity, which is the ratio of the maximum shear stress to residual stress in Figure 14b. is the shear displacement at the point where the maximum shear stress occurs. is the shear displacement. The soil contact force algorithm is shown in Figure 13b.
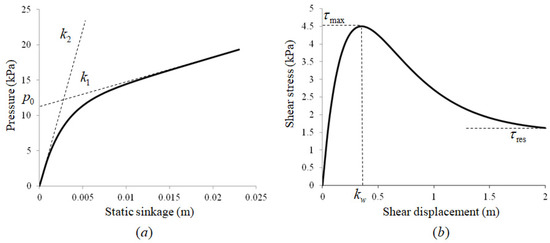
Figure 14.
Models for soft soil: (a) Bode model for the pressure–sinkage relationship, (b) Wong model for shear stress-shear displacement relationship.
5.2. Formulations for Three-Dimensional Ground
The proposed 3D ground can express the three-dimensional geometry of the ground and is an efficient method to find track elements in contact with the ground in order to calculate the sinkage between the mining robot and the ground. As shown in Figure 15a, the three-dimensional ground consists of many triangular elements. As shown in Figure 15b, each element has three points of connectivity information and soil property information, and all points have x, y, and z positions in the inertial reference frame. As shown in Figure 16, the concept of the shell is introduced to divide the length and width of the ground and classify the elements included in each shell.
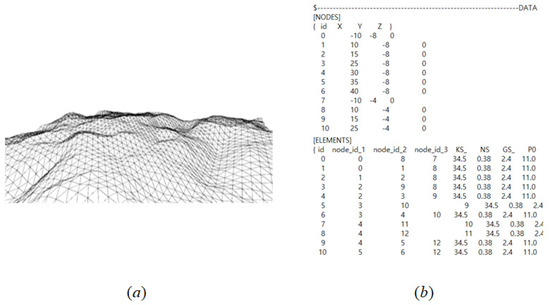
Figure 15.
Three-dimensional ground models: (a) ground geometry composed of triangular elements, (b) configuration data (position information of nodes, information for connectivity of elements, and properties of soil) of the ground geometry.

Figure 16.
Shell concepts to efficiently contact search between 3D ground and track.
The length and width of the 3D ground are defined by the x-y plane, and the height of the ground is defined by the z position. The length and width of the ground can be obtained as in Equations (38) and (39), respectively.
where and are the end and start positions of the ground in the length direction, respectively. The total number of shells can be expressed as in Equation (40).
where and the number of shells in the length and width directions of the ground, respectively. The length and width resolutions of the ground are equal to Equations (41) and (42) when the ground is divided by the number of shells in each direction.
The length and the width of all the points on the ground are calculated in the same method as in Equations (38) and (39) and the quotient is taken by dividing each length by the resolution. The number of each element containing these points is contained in a two-dimensional array of shells by quotient. That is, it is possible to figure out the number of elements in the shell. This process for the ground is calculated only once in the initial state. Track located on the ground can find the shell number in the same processor. This process can significantly reduce the amount of computation because it does not search among all elements of the ground and the track, but only within the shell number. As shown in Figure 17, the points within the triangle can be determined by the sum of the internal angle, as follows.
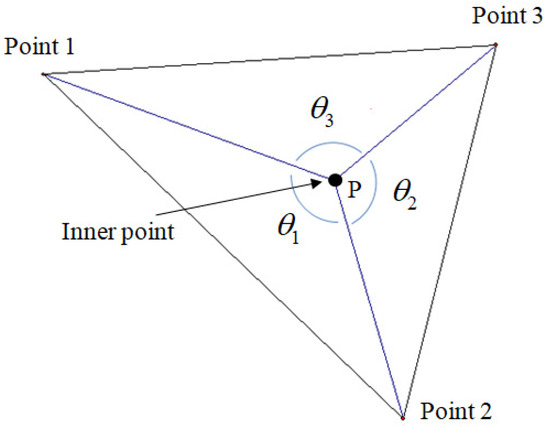
Figure 17.
Existence determining method for arbitrary point in a triangular element.
Each internal angle can be obtained from the second law of cosine.
where and are two lines between the vertex of the triangular element and the inside point. is the angle between two lines and . As shown in Figure 18, if the element number including the track mesh point of the mining robot is found, the sinkage can be obtained by the equation of the plane. The normal distance from the plane to an arbitrary point can be expressed as [34].
where , and are the elements of the normal vector on the plane. Since the normal vector has direction, if the distance value is positive, the track mesh is above ground, If negative, it is below ground. An algorithm for efficient contact calculation between the three-dimensional ground and the track mesh is shown in Figure 19.
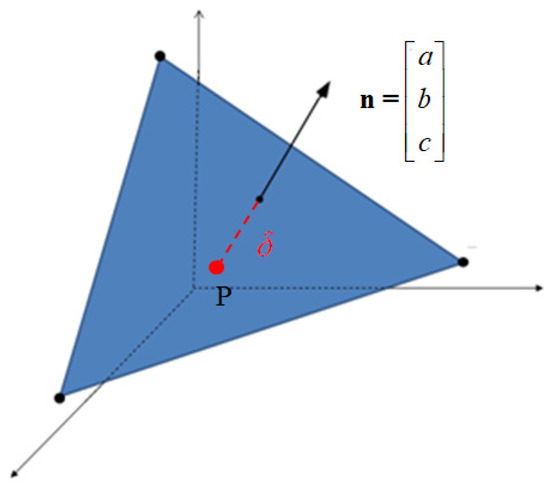
Figure 18.
Calculation methods for sinkage to an arbitrary point from a plane.
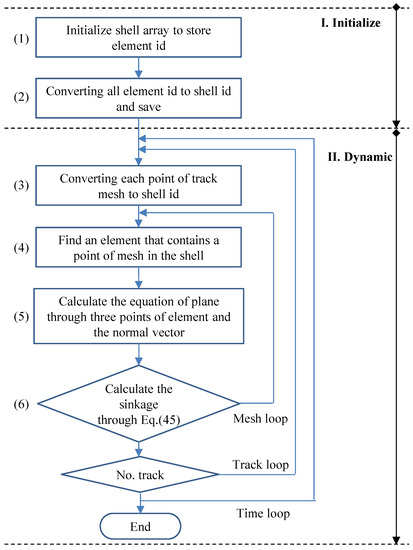
Figure 19.
Algorithm for efficient contact calculation between 3D ground and mining robot.
6. Structure and User Interface of Modelers
The developed program has the structure shown in Figure 20. There are user interfaces for each of the four environment modelers. It has user interfaces for each of the four mechanical modelers. The user interface is made in the C# language.

Figure 20.
Structure and user interface of the developed program.
6.1. User Interface of Environmental Modelers
As shown in Figure 21a, the hydrodynamic user interface may input a 6 × 6 matrix for each tap. The constant input for the user interface is shown in Figure 21b and applied as the diagonal value of the 6 × 6 matrix. The buoyancy user interface is shown in Figure 21c, and the volume of the object is obtained by CAD geometry and density. The user interface of the current is shown in Figure 21d. The velocity of current is represented as a spline and current density is applied to the entire system in the same way as gravitational acceleration.

Figure 21.
User interface of environment modeler: (a) matrix input dialog for hydrodynamics, (b) constant input dialog for hydrodynamics, (c) input dialog for buoyancy, (d) input dialog for ocean current.
6.2. User Interface of Mechanical System Modelers
The user interface of the riser is shown in Figure 22. The geometry information of the beam is shown in Figure 22a. The properties of the beam are shown in Figure 22b. The tap in the middle of the dialog has a user interface for beam properties and hydrodynamic, respectively. The buoyancy module user interface is shown in Figure 23a. It indicates the beam id to which the buoyancy module is attached, and inputs the outer diameter and inner diameter value of the beam cross-sectional area. The user interface of the mining vessel is shown in Figure 23b and the sine wave information is entered in the six directions of the vessel motion. The user interface for the soil contact force is shown in Figure 23c. The parameters of soil contact force are the same for the single-body track robot.
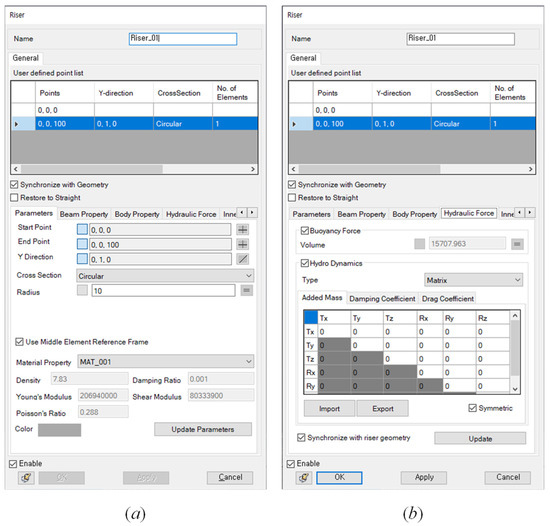
Figure 22.
User interface of the mechanical system modeler: (a) definition dialog for the shape of the riser, (b) input dialog for the hydraulic properties of the riser.
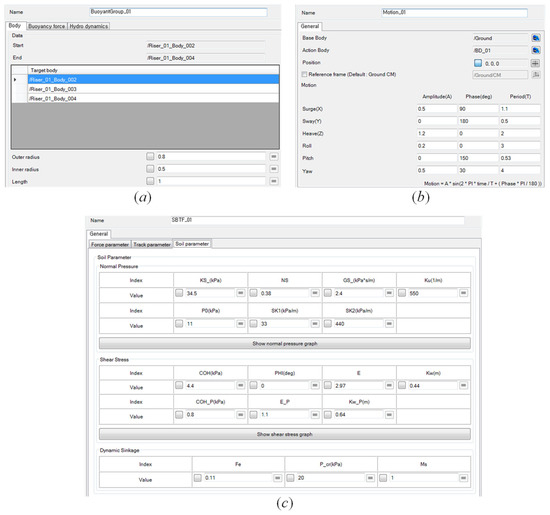
Figure 23.
User interface of mechanical system modeler: (a) definition dialog for the shape of buoyancy module, (b) definition dialog for the motion of mining vessel, (c) input dialog for parameters of the soil model.
7. Verification
Using the results of OrcaFlex, commercial software for ocean riser analysis, the developed simulation methods were compared and verified as the hydrodynamics and riser models. The soil mechanism was compared and verified through the analysis result of seabed vehicles using Tracsim [9,28,29], an analysis tool developed for the performance analysis of tracked vehicles in a soil environment.
7.1. Offshore Riser System
The model applied for the verification of the developed riser simulation method is the deep-seabed riser model (as shown in Figure 24a) presented by [35]. The specifications of this riser are shown in Table 1. Ruan’s deep-sea riser model is a deep-seabed riser model used to compare OrcaFlex and the developed riser analysis technique. This is a general SLWR model cited in recent papers [36] for verification of development analysis techniques.
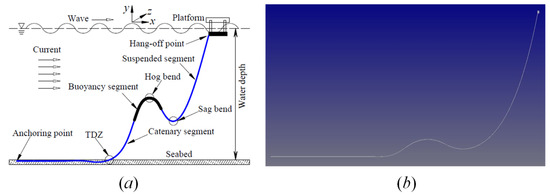
Figure 24.
Riser analysis model: (a) schematic diagram of riser model [35], (b) riser dynamic model using the developed method.

Table 1.
Steel lazy wave riser properties [35].
As shown in Figure 24b, the riser dynamic model using the developed simulation method is equipped with the catenary region and buoyancy modules attached to the seafloor, and it consists of a buoyancy region shaped into an S shape, and a suspended region connected vertically from the vessel. The total length of the SLWR is 3170 m assembled by 1200 m catenary, 370 m buoyancy, and 1600 m suspended risers.
The result of the analysis of the riser dynamic model was compared with that of OrcaFlex and Ruan. As shown in Figure 25, a configuration result with little error was derived. Additionally, as shown in Table 2, it was confirmed that the error was within 0.5% in the main response of riser analysis such as touchdown position, top tension, and bottom tension.
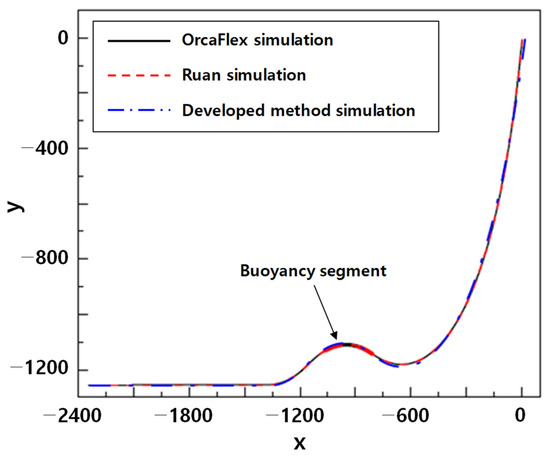
Figure 25.
Riser configuration results using OrcaFlex, Ruan’s method, and the developed method.

Table 2.
Comparison of the dynamic analysis of the SLWR.
The reason for the error is due to the difference in the method of expressing the stiffness of the submarine ground model. In OrcaFlex and Ruan’s thesis, the seabed is used with the simple stiffness method, but the developed method uses Bode’s soil interaction method. As a result, the calculation result of the ground reaction force is different and the load error occurs in addition to the configuration error.
7.2. Soil Contact Mechanism
The developed soil contact mechanism was compared with Tracsim’s undersea vehicle analysis. In general, the driving performance of a seabed vehicle is evaluated according to straight and steering. Therefore, the results of the dynamic behavior analysis of the vehicle and the soil contact forces generated at this time were compared.
The mining robot model [12] used for verification has four track rows, and the model information and soil properties are shown in Table 3 and Table 4. In the case of a straight drive, the velocity of each track row is as shown in Figure 26a and has a steering ratio [12] of 1.0 as shown in Figure 26b. In the case of a steering drive, the velocity of each track row is as shown in Figure 27a and has a steering ratio of 1.4 as shown in Figure 27b.

Table 3.
Model information of mining robot.

Table 4.
Properties of soft soil.
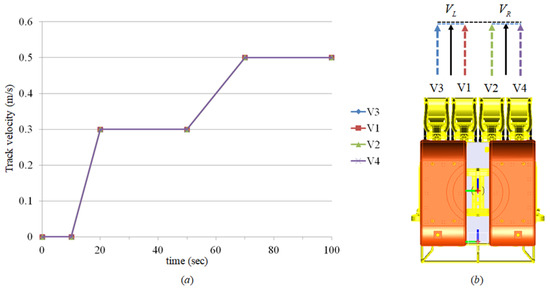
Figure 26.
Track input speed and steering ratio of a mining robot for straight driving: (a) input speed of each track row, (b) definition of track row ID and steering ratio calculation method (Top view of mining robot).

Figure 27.
Track input speed and steering ratio of a mining robot for steering driving: (a) input speed of each track row, (b) definition of track row ID and steering ratio calculation method (Top view of mining robot).
Figure 28 shows the results for a straight drive and compares and verifies the position of the vehicle, velocity of the vehicle, and soil contact force acting on the vehicle. The responses of the vehicle behavior are defined as shown in Figure 11. Figure 28a,b show the surge and heave responses of the vehicle. Figure 28c,d show longitudinal and transverse velocities of the vehicle. Figure 28e,f show the traction and normal forces acting on the vehicle. The results of the developed method are almost similar to the results of the Tracsim. As shown in Figure 28f, the normal soil contact force during initial contact is more vibrating than the result of the Tracsim, and the damping effect is weaker. This vibration causes the contact force to be about 60 kgf larger than that of the Tracsim, resulting in 2 cm more sinking as shown in Figure 28b. The difference comes from the integrator. Since the two programs use different integrators, studies of numerical conditions and integrator coefficients are necessary for the same result.
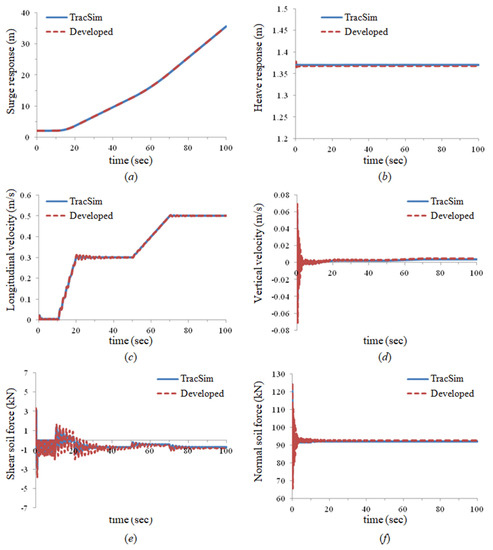
Figure 28.
Comparison of the straight drive dynamic analysis results between the developed method and Tracsim: (a) surge response of the mining robot, (b) heave response of the mining robot, (c) longitudinal velocity of the mining robot, (d) transverse velocity of the mining robot, (e) shear soil contact force acting on mining robot, (f) normal soil contact force acting on mining robot.
Figure 29 and Figure 30 show the results for a steering drive. Figure 29 compares the position and velocity of the vehicle, and Figure 30 compares the soil contact forces acting on the vehicle and steering radius. Figure 29a–c show the surge, sway and heave responses of the vehicle. Figure 29d–f show the longitudinal, lateral, and transverse velocities of the vehicle. Figure 30a,b show the traction and normal forces acting on a vehicle. Figure 30c shows the steering radius of the vehicle.
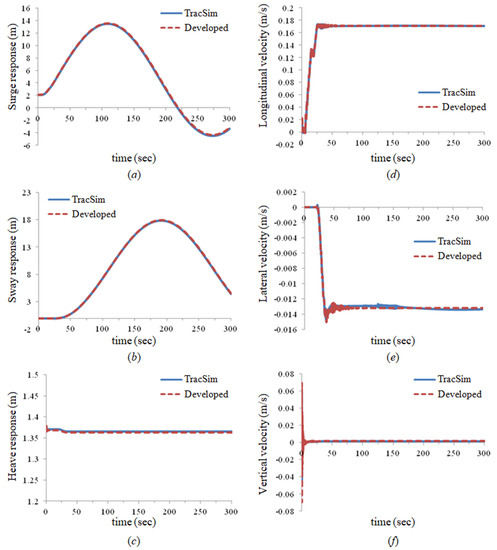
Figure 29.
Comparison of the steering drive dynamic analysis results between the developed method and Tracsim: (a) surge response of the mining robot, (b) sway response of the mining robot, (c) heave response of the mining robot, (d) longitudinal velocity of the mining robot, (e) lateral velocity of the mining robot, (f) transverse velocity of the mining robot.

Figure 30.
Comparison of the steering drive dynamic analysis results between the developed method and Tracsim: (a) shear soil contact force acting on mining robot, (b) normal soil contact force acting on mining robot, (c) steering radius of the mining robot.
7.3. Three-Dimensional Ground Mechanism for Soil Contact
As shown in Figure 31, a plane composed of triangular elements is applied to verify the proposed three-dimensional ground method. Figure 31a is the ground shape used for the straight drive, and Figure 31b is the ground shape used for the steering drive.
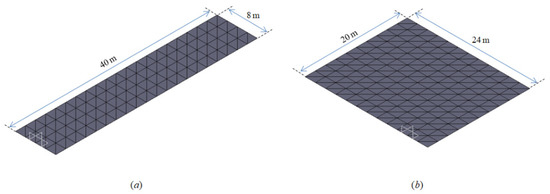
Figure 31.
Geometry of developed three-dimensional ground: (a) geometry of ground for straight driving, (b) geometry of ground for steering driving.
In the three-dimensional ground method verification, the same simulation conditions and driving scenarios were applied to the developed method and the comparison of Tracsim results. The simulation environment is Inter (R) Xeon (R) CPU E3-1230 v3 3.30 GHz. As shown in Figure 32, Figure 33 and Figure 34, the results of the 3D ground method are compared with the results of the developed method. The results of applying the 3D ground are similar to those of the developed method.
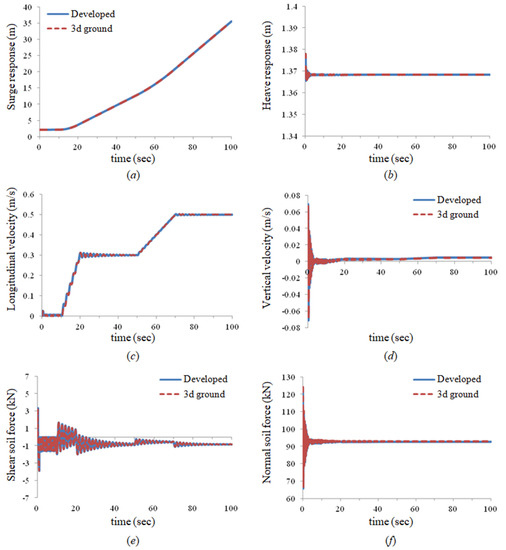
Figure 32.
Comparison of the straight drive dynamic analysis results between the developed method and 3D ground model: (a) surge response of the mining robot, (b) heave response of the mining robot, (c) longitudinal velocity of the mining robot, (d) transverse velocity of the mining robot, (e) shear soil contact force acting on mining robot, (f) normal soil contact force acting on mining robot.
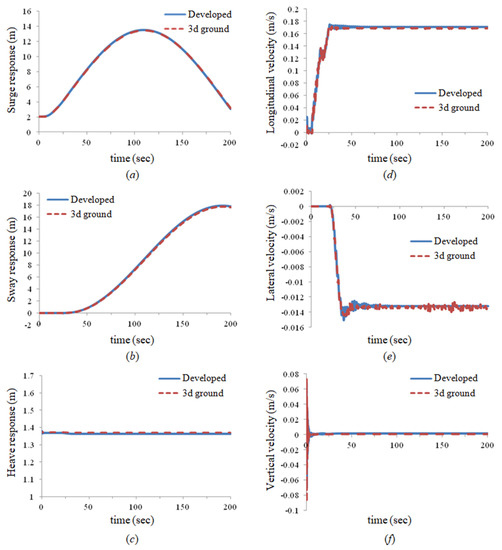
Figure 33.
Comparison of the steering drive dynamic analysis results between the developed method and 3D ground model: (a) surge response of the mining robot, (b) sway response of the mining robot, (c) heave response of the mining robot, (d) longitudinal velocity of the mining robot, (e) lateral velocity of the mining robot, (f) transverse velocity of the mining robot.
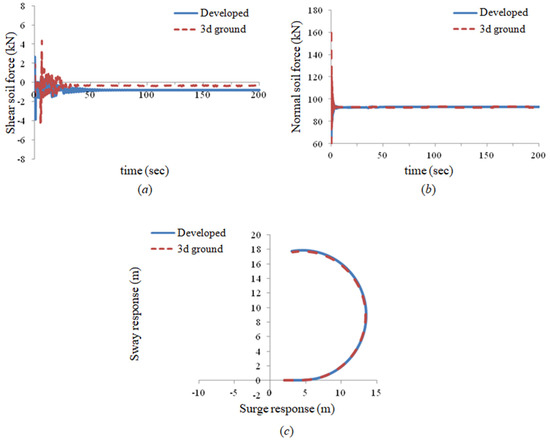
Figure 34.
Comparison of the steering drive dynamic analysis results between the developed method and 3D ground model: (a) shear soil contact force acting on mining robot, (b) normal soil contact force acting on mining robot, (c) steering radius of the mining robot.
The simulation time and memory differences between the developed method and the three-dimensional ground method are shown in Table 5. More simulation time is required by algorithmic computation to find elements on the ground that contact the track. There is no difference in the memory used.

Table 5.
Comparison of the dynamic analysis results between the original method of developed program and 3D ground.
Figure 35 shows an example of a bumper-shaped three-dimensional ground. As shown in Figure 35a, the geometry of the bumper where the track rows 3 and 1 contact is flat, and the place where the 2nd and 4th rows contact rises 0.2 m. Figure 35b shows the heave response in each track row.
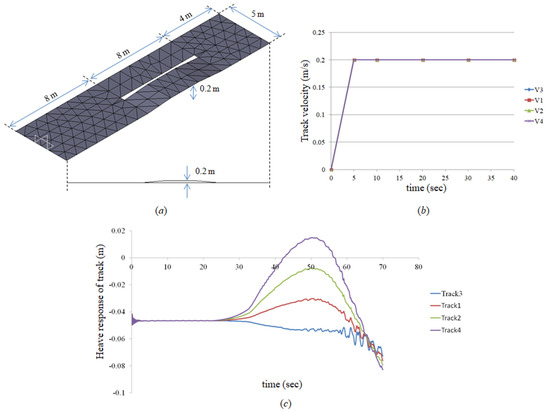
Figure 35.
Three-dimensional ground application example: (a) bumper geometry of 3D ground, (b) input velocity of each track row, (c) Heave response of each track row.
8. Conclusions
In this study, a novel integrated simulation technology was developed based on multibody dynamics for the comprehensive dynamic behavior analysis of a deep-sea mining system and mining robot with vast degrees of freedom. Many existing studies were unable to analyze the behavior of the entire deep-seabed mining system because the analysis was mainly performed on an element-by-element basis. However, the developed method makes it possible to analyze the entire dynamic behavior of a continuous mining system in one integrated environment.
The developed method consists of mechanical system modeling techniques, environmental modeling techniques, and soil contact mechanisms for mining system analysis in this one integrated environment. Especially, a single-body track model that can express and interpret the mining robot as a single object for real-time analysis for simulation of the mining robot running on the deep-seabed soft ground, and a multibody model and soil contact mechanism on 3D ground to consider the 3D ground driving environment were developed through this study.
A developed single-body track model for the mining robot is a simplified model that analyzes the dynamic behavior of the mining robot by applying the soil contact mechanism to the meshed track. A multi-body mining robot model composed of multiple track links and rollers was introduced. In the multi-body track model, the bushing force between the track links, the contact force between the track link and the roller, and the soft ground mechanism between the track link and the ground are applied. The normal stress of the Bode model and the shear stress of the Wong model were used for the soil contact mechanism.
The soil mechanism developed in the existing commercial tools can only use the two-dimensional shape of the ground. The two-dimensional shape as a spline has only height information in the length direction. That is, it is difficult to consider the geometry of the width direction. To deal with this problem, an extended soil mechanism that can apply a three-dimensional shape of the ground was developed. This extended mechanism is a technology that can efficiently find a track in contact with elements on a three-dimensional surface. In addition, the 3D ground has location information of points, point connection information of elements, and soil property information. As a result, soil characteristics for each area on the ground can be reflected. Therefore, this technique allows for various seabed topography to be taken into account.
The developed technology was verified by comparing the analysis results of OrcaFlex and Tracsim, which are commercial tools. The developed hydrodynamics and riser system were compared with the analysis results of OrcaFlex for the offshore riser model and showed the same results. The developed soil contact mechanism was compared with the results of Tracsim’s submarine vehicle analysis and showed similar results. The straight and steering driving of the mining robot were compared on flat and soft ground, and the sinkage was 2 cm larger in the developed model. This can be seen as a difference in the numerical conditions of the integrator, and it is meaningless in terms of the scale of a 27-ton mining robot. In addition, the developed three-dimensional ground in soil contact mechanism was compared with the previously verified soil contact mechanism analysis results and the same results were shown. There was a difference of 1.4 times in the computation time of 3D ground and 2D spline to which efficient contact search algorism was applied.
In future research, it is necessary to study the following four points. First, it is necessary to study the numerical condition of the integrator or the integrator coefficient for the developed soil mechanism method. Second, we will study the relationship between computation time and accuracy compared to the size of the ground mesh. Third, the 3D ground model is a reliable study of various ground surface geometries. Finally, to ensure the accuracy of the 3D ground, a study on the development of an improved single-body track model considering the flexibility between track links is needed.
Author Contributions
Conceptualization, J.-H.L. and J.-W.O.; methodology, J.-H.L., J.-W.O., H.-W.K. and D.-S.B.; software, J.-H.L. and D.-S.B.; validation, J.-H.L. and J.-W.O.; formal analysis, H.-W.K. and S.H.; investigation, J.-H.L. and S.H.; data curation, J.-W.O. and H.-W.K.; writing—original draft preparation, J.-H.L. and J.-W.O.; writing—review and editing, J.-W.O., D.-S.B. and H.-W.K.; visualization, J.-H.L., J.-W.O., D.-S.B. and H.-W.K.; supervision, J.-W.O.; project administration, S.H. and H.-W.K.; funding acquisition, S.H. and J.-W.O. All authors have read and agreed to the published version of the manuscript.
Funding
The authors are grateful for the full support shown for this research work. This study was initiated from R&D Projects, “Technology Development of Deep-seabed Mining System for Manganese Nodules” sponsored by the Ministry of Ocean and Fishers of Korea (PMS3090), and “Technology development of digital twin in oscillating water column type for smart operation and maintenance service” funded by Korea Research Institute of Ships and Ocean Engineering (PES4410).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Brink, A.W.; Chung, J.S. Automatic Position Control of a 300,000-Ton Ship Ocean Mining System. J. Energy Resour. Technol. 1982, 104, 285–293. [Google Scholar] [CrossRef]
- Amann, H.; Oebius, H.U.; Gehbauer, F.; Schwarz, W.; Weber, R. Soft Ocean Mining. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 6–9 May 1991. [Google Scholar]
- Chung, J.S. Deep-ocean Mining: Technologies for Manganese Nodules and Crusts. Int. J. Offshore Polar Eng. 1996, 6, 244–254. [Google Scholar]
- Hong, S.; Kim, K. Proposed Technologies for Mining Deep-Seabed Polymetallic Nodules—Chap 12 Research and Development of Deep Seabed Mining Technologies for Polymetallic Nodules in Korea. In Proceedings of the International Seabed Authority’s Workshop, Kingston, Jamaica, 3–6 August 1999. [Google Scholar]
- Deepak, C.R.; Shajahan, M.A.; Atmanand, M.A.; Annamalai, K. Development Tests on the Underwater Mining System Using Flexible Riser Concept. In Proceedings of the 4th ISOPE Ocean Mining Symposium, Szczecin, Poland, 23–27 September 2001. [Google Scholar]
- Leng, D.; Shao, S.; Xie, Y.; Wang, H.; Liu, G. A brief review of recent progress on deep sea mining vehicle. Ocean Eng. 2021, 228, 108565. [Google Scholar] [CrossRef]
- Bleier, M.; Almeida, C.; Ferreira, A.; Pereira, R.; Matias, B.; Almeida, J.; Pidgeon, J.; Lucht, J.V.D.; Schilling, K.; Martins, A.; et al. 3D Underwater Mine Modelling in the Vamos Project. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Limassol, Cyprus, 2–3 May 2019. [Google Scholar]
- Kang, Y.; Liu, S. The Development History and Latest Progress of Deep-Sea Polymetallic Nodule Mining Technology. Minerals 2021, 11, 1132. [Google Scholar] [CrossRef]
- Raja, V.; Solaiappan, S.K.; Kumar, L.; Marimuthu, A.; Gnanasekaran, R.K.; Choi, Y. Design and Computational Analyses of Nature Inspired Unmanned Amphibious Vehicle for Deep Sea Mining. Minerals 2022, 12, 342. [Google Scholar] [CrossRef]
- Wu, Q.; Yang, J.; Guo, X.; Liu, L.; Lu, W.; Lu, H. Experimental study on dynamic responses of a deep-sea mining system. Ocean Eng. 2022, 248, 110675. [Google Scholar] [CrossRef]
- Oh, J.-W.; Lee, C.-H.; Hong, S.; Bae, D.-S.; Cho, H.-J.; Kim, H.-W. A study of the kinematic characteristic of a coupling device between the buffer system and the flexible pipe of a deep-seabed mining system. Int. J. Nav. Arch. Ocean Eng. 2014, 6, 652–669. [Google Scholar] [CrossRef][Green Version]
- Oh, J.-W.; Lee, C.-H.; Hong, S.; Bae, D.-S.; Lim, J.-H.; Kim, H.-W. Study on Optimum Curve Driving of Four-row Tracked Vehicle in Soft Ground using Multi-body Dynamics (in Korean). J. Ocean Eng. Technol. 2014, 28, 167–176. [Google Scholar] [CrossRef]
- Hong, S.; Choi, J.; Yeu, T.; Kim, H.; Kim, S.; Min, C.; Lee, M.; Seong, K.; Lee, C.; Oh, J. Development of buffer station for safe and eco-friendly mining of seabed mineral resources. In Proceedings of the Underwater Mining Institute, Lisbon, Portugal, 21–28 September 2014. [Google Scholar]
- Park, S.J.; Yeu, T.K.; Yoon, S.M.; Hong, S.; Kim, H.W. Development of Operating S/W and DBMS for Deep-sea Manganese Nodule Miner. J. Korean Soc. Oceanogr. 2008, 13, 229–236. [Google Scholar]
- Hong, S. Dynamic Analysis of Riser with Vortex Excitation by Coupled Wake Oscillator Model. J. Korean Soc. Oceanogr. 2000, 13, 237–245. [Google Scholar]
- Hwang, S.; Choi, J.; Yeu, T.; Kim, H.; Kim, S.; Min, C.; Lee, M.; Seong, K.; Lee, C.; Oh, J. Three-Dimensional flow response analysis of subsea riser transporting deep ocean water. In Proceedings of the Underwater Mining Institute, Lisbon, Portugal, 21–28 September 2014. [Google Scholar]
- Haug, E.J. Computer Aided Kinematics and Dynamics of Mechanical Systems Volume I: Basic Methods; Allyn & Bacon: Boston, MA, USA, 1989. [Google Scholar]
- Lee, J.K.; Kang, J.S.; Bae, D.S. An Efficient Real-time Vehicle Simulation Method Using a Chassis-based Kinematic Formulation. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2014, 228, 272–284. [Google Scholar] [CrossRef]
- Lim, J.-H.; Jo, S.-C.; Bae, D.-S.; Cho, H.-J. A Jacobian formulation for efficient simulation of multibody chain dynamics. J. Mech. Sci. Technol. 2018, 32, 3745–3754. [Google Scholar] [CrossRef]
- Bae, D.S.; Kim, H.W.; Yoo, H.H.; Suh, M.S. A Decoupling Solution Method for Implicit Numerical Integration of Constrained Mechanical Systems. Mech. Struct. Mach. 1999, 27, 129–141. [Google Scholar] [CrossRef]
- Potter, M.C. Mechanics of Fluids; 3/E: SI Ver.; Cengage Learning: Boston, MA, USA, 2008. [Google Scholar]
- Fossen, T.I. Marine Control System: Guidance, Navigation and Control of Ships, Rigs and Underwater Vehicles; Marine Cybernetics: Trondheim, Norway, 2002. [Google Scholar]
- Kim, H.W.; Hong, S. Hydrodynamic Effects on Dynamics of Test Miner on Soft Deep Seafloor. J. Korean Soc. Precis. Eng. 2007, 24, 19–25. [Google Scholar]
- Hong, S.; Kim, H.W. Coupled Dynamic Analyses of Underwater Tracked Vehicle and Long Flexible Pipe. J. Korean Soc. Oceanogr. 2008, 13, 237–245. [Google Scholar]
- Diebel, J. Representing Attitude: Euler Angles, Unit Quarterions, and Rotation Vectors; Stanford University: Stanford, CA, USA, 2006. [Google Scholar]
- Crandall, S.H. An Introduction to Mechanics of Solids: In SI Units, 3rd ed.; McGrawHill: New York, NY, USA, 2012. [Google Scholar]
- Oh, J.-W.; Min, C.-H.; Lee, C.-H.; Hong, S.; Bae, D.-S.; Lim, J.-H.; Kim, H.-W. Arrangement Plan of Buoyancy Modules for the Stable Operation of the Flexible Riser in a Deep-Seabed Mining System. Ocean Polar Res. 2015, 37, 119–125. [Google Scholar] [CrossRef][Green Version]
- Kim, H.-W.; Lee, C.-H.; Hong, S.; Choi, J.-S.; Yeu, T.-K.; Min, C.-H. Study on Steering Ratio of Four-Row Rigid Tracked Vehicle on Extremely Cohesive Soft Soil Using Numerical Simulation. J. Ocean Eng. Technol. 2013, 27, 81–89. [Google Scholar] [CrossRef]
- Kim, H.-W.; Min, C.-H.; Lee, C.-H.; Hong, S.; Bae, D.-S.; Oh, J.-W. Dynamic Analysis of Tracked Vehicle by Buoy Characteristics. Ocean Polar Res. 2014, 36, 495–503. [Google Scholar] [CrossRef]
- Ryu, H.S.; Bae, D.S.; Choi, J.H.; Shabana, A.A. A compliant track link model for high-speed, high-mobility tracked vehicles. Int. J. Numer. Methods Eng. 2000, 48, 1481–1502. [Google Scholar] [CrossRef]
- Machado, M.; Moreira, P.; Flores, P.; Lankarani, H.M. Compliant contact force models in multibody dynamics: Evolution of the Hertz contact theory. Mech. Mach. Theory 2012, 53, 99–121. [Google Scholar] [CrossRef]
- Bode, O. Simulation der Fahrt von Raupen-fahrwerken auf Teefseeböden. Ph.D. Thesis, University of Hannover, Hannover, Germany, 1991. [Google Scholar]
- Wong, J.Y. Theory of Ground Vehicles, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Kreyszig, E. Advanced Engineering Mathematics, 9th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Ruan, W.; Liu, S.; Li, Y.; Bai, Y.; Yuan, S. Nonlinear Dynamic Analysis of Deepwater Steel Lazy Wave Riser Subjected to Imposed Top-End Excitations. In Proceedings of the ASME 2016 35th International Conference on Ocean, Offshore and Arctic Engineering, Busan, Korea, 19–24 June 2016. [Google Scholar]
- Oh, J.; Jung, D.; Kim, H.; Min, C.; Cho, S. A study on the simulation-based installation shape design method of steel lazy wave riser (SLWR) in ultra deepwater depth. Ocean Eng. 2020, 197, 106902. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).