1. Introduction
Deep-sea mining involves extracting minerals from the ocean bed, including sulphide deposits, polymetallic nodules and cobalt-rich crusts [
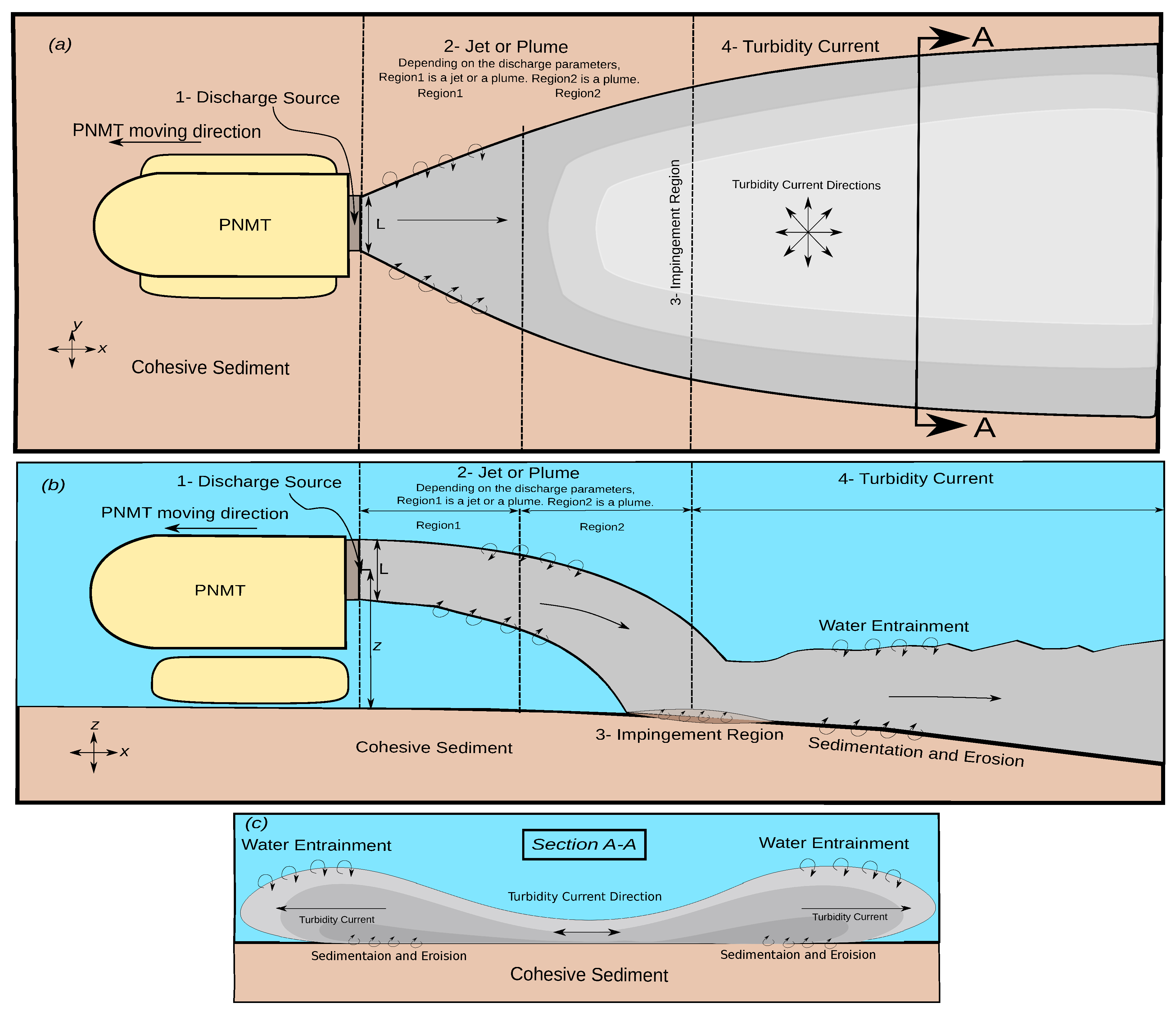
1]. In case of polymetallic nodules, a Polymetallic Nodule Mining Tool (PNMT) collects the potato-shaped ore from the ocean bed, after which a primary separation process separates the ore from the excess water–sediment mixture (
Figure 1). At the end of the process, the mixture is discharged from the back of the mining tool. The discharged mixture ends up triggering turbidity currents [
2], that can significantly alter deep-sea turbidity levels. Keep in mind that not only the discharged mixture affects the surrounding environment but also the disturbances resulting from driving gears such as the wake generated behind the PNMT. According to [
3], the negative impact of the generated turbidity current on the environment will result in a change in fauna behaviour and increase the mortality rate of benthic organisms. For that reason, and for the sake of minimizing the affected area by optimizing discharge properties, the present paper focuses on characterizing the different physical parameters (e.g., propagation speed and concentration distribution) that describe a generated current. Moreover, we present our numerical modeling approach that can accurately predict the current.
Overall, gravity currents are characterized by a heavier fluid flowing underneath a lighter fluid, creating a mixing zone in between [
4]. Turbidity currents are sediment-laden gravity currents, with forward motion being caused by gravity acting on the density difference between the denser water–sediment mixture and the lighter ambient fluid. Note that the concentration of the suspended sediment within the current is subject to changes throughout the propagation of the current, i.e., sediment deposition, sediment (re-)suspension (erosion) and entrainment of the ambient water.
Generally speaking, turbidity currents are challenging to investigate in the field [
5] because of the high cost of the field experiments, and the same applies to mining-generated turbidity currents. However, scaled laboratory experiments are an alternative and widely used option for investigating turbidity currents, with lock-exchange experiments being a particularly simple and useful experimental technique to study turbidity currents [
6,
7,
8,
9]. This type of experiments involves suddenly releasing a higher density fluid into a slightly lower density fluid.
Employing lock-exchange experiments, a two-layer shallow-water model including the effect of water entrainment is developed by [
10]. Moreover, using an image analysis technique the propagation velocity of the current and concentration profiles are quantified by [
11]. Lock-exchange experiments are carried out by [
12] to study the effect of bottom roughness on current hydrodynamics. Furthermore, unconfined lock-exchange experiments are also used to study the effect of the lock width on the dynamics of the current by [
13].
The effect of particle size on the propagation of turbidity currents is also discussed in literature. The effect of poorly sorted sediments (i.e., wide range of grain sizes) on the deposition behaviour of a turbidity current is investigated by [
9,
14]. Lock-exchange techniques are also utilized by [
6] to examine the effect of bi- and poly-disperse particle mixtures (silicon carbide particles with a particle density of
kg/m
3) on the propagation of turbidity currents with a fixed initial volumetric concentration of 0.349% at the lock.
Mathematical and numerical models are also employed to investigate turbidity currents [
2,
15,
16,
17,
18], but with consideration of a proper validation against field or laboratory experiments. Many numerical studies have been carried out to investigate the characteristics of turbidity currents. Direct numerical simulations are performed for lock-exchange experiments to analyse the structure of the head [
16]. The work of [
17] presents the effect of the sedimentation on the propagation of the current. Moreover, two- and three-dimensional CFD simulations are used by [
18] to investigate the effect of the turbulence vortices on the breakdown of turbidity currents into different sections, i.e., body and tail. Two-dimensional Large Eddy Simulations are performed by [
17] to simulate a lock-exchange experiment. Eulerian-Eulerian approach is also used to investigate the effect of particle inertia on current propagation [
19]. Additionally, turbidity currents generated in lock-exchange experiments are studied by [
20] through LES simulations, comparing the results to an older DNS simulation to assess the quality of this approach.
The well-known Euler–Euler model approaches the turbidity current as separate phases of fluid and solids which are considered interpenetrating continua. From this perspective, the model consists of fluid and solid momentum equations. These equations are coupled by means of source terms [
21], which are obtained from the application of the kinetic theory. Mixture models such as the drift–flux model, on the other hand, approach turbidity currents as a single continuum. In other words, the model requires that a single momentum equation to be solved for the mixture as a whole [
22,
23]. Note that so-called drift velocities are a correction of the “drift” of particles relative to mixture momentum. Many researchers have worked on developing the two-phase drift–flux model, i.e., liquid and single solid phases [
22,
23,
24,
25,
26]. Recently, a clear mathematical framework for a multiple-phase drift–flux model was presented, where each particle size represents a phase. In this respect, he reported a closure to the relative velocity of the different phases (see
Section 4). The main assumptions of drift–flux model are [
27]:
- (i)
Settling velocity of particles is small compared with the bulk velocity of the mixture;
- (ii)
Particles react instantaneously to velocity changes.
The propagation of bi-disperse currents (i.e., two particle sizes are present in the mixture) is investigated by [
5], where the lock-exchange experiments done by [
6] are simulated and validated by [
5] using an Euler–Euler modelling approach.
Beyond the impingement region, the generated turbidity current is directed towards all directions, as shown in the top view in
Figure 1. As mentioned before, it is challenging to investigate full-scale generated turbidity currents due to the high costs of the field experiment involved. In order to simplify the process of investigating such a complicated current, we hypothesize that the full-scale turbidity current consists of many small currents next to each other. Taking a small section from a developed mining-generated current such as section A-A in
Figure 1, we find that a current generated in a lock-exchange experiment is representative of these small currents in terms of front velocities. In this regard, lock-exchange experiments can be a valuable tool to investigate the effect of different parameters on the propagation behaviour of the current, e.g., initial concentration and particle size. However, it is important to note that the lock-exchange generated currents are not scaled to those generated in mining contexts due to various limitations, such as the free surface area in the lock-exchange experiment and a moving discharge source. We believe that the conclusions drawn from this study will improve approaches to designing the discharge process.
In the present study, we use lock-exchange experiments to investigate the effect of particle size and initial concentration on the behaviour of turbidity currents. We test different initial concentrations for three sediment types with particle densities of
kg/m
3 to 2650 kg/m
3 which is similar to sediment densities in abyssal plains (see
Section 2 for the methodology of the lock-exchange experiments). Moreover, we model the turbidity current by taking multiple fractions into account. Supported by our experimental study, using minimal computational efforts, we aim to demonstrate that the drift–flux model is capable of predicting the main physical parameters (e.g., forward velocity, concentration profiles) associated with turbidity currents. The findings of this paper contribute to defining a discharge framework for mining technology to minimize environmental impact. We present our lock-exchange experimental methodology in
Section 2. In
Section 3, the experimental results, such as front speed and concentration profiles, are discussed. In
Section 4, we describe the numerical methodology based on the drift–flux modelling approach. The numerical results are compared with the laboratory experiments in
Section 5. Finally, conclusions are drawn in
Section 6.
4. Numerical Model Description
In this section, we present a drift–flux model that is used in turbidity current simulations. The drift–flux model is a mixture model where one momentum equation for the whole mixture is required. In this modelling approach, the particles follow the surrounding flow motion but also have a deposition behaviour. In order to justify our choice of drift–flux modeling approach, first, we have to ensure that the particles follow the flow and do not have their own trajectories. Fortunately, Stokes number (
) can be used to determine this criterion, where a particle’s Stokes number is the ratio between particle response time
to the flow characteristic time scale
of the flow:
where
is particle concentration,
is particle diameter,
is the liquid phase dynamic viscosity,
L is the characteristic length scale and
U is the velocity of the flow at the length scale. In our case,
L and
U are taken to be the thickness of the current and the front speed of the current, respectively. In case of
, this means that the particle response time is much lower than the shortest eddy time scale, which means the particles remain within the flow eddies. If
, on the other hand, the particle’s response time is much longer. Consequently, the particle does not follow the eddy. Coarse particles have a high Stokes number. Accordingly, following the experimental results mentioned in
Section 3, using the diameter sizes of 60 and 105 μm for runs 6,14 and 22, which the highest front velocity,
is calculated to be
,
and
, respectively. As such, the drift–flux model is appropriate for this study.
The main assumption of the drift–flux model is that the momentum of solid phases (i.e., each particle size represents a phase) rapidly adapts to the momentum of the liquid phase in a planar direction while continuing to move relative to the liquid phase in the gravitational direction [
28]. To put it differently, there is little or no momentum exchange between the solid and liquid phases [
27]. This study uses the mathematical multiple-fractions-drift–flux model that was recently reported by [
27]. Furthermore, this model is extended in OpenFOAM (an open-source CFD tool). OpenFOAM solves the governing equations sequentially using the Finite-Volume Method (FVM). Accordingly, the equations are integrated at each computational cell, yielding discretized equations for each quantity.
4.1. Governing Equations
The drift–flux model is composed mainly of one mixture momentum equation, one mixture continuity equation and one phase transport equation for each particle size fraction. The mixture continuity equation is defined by the following relationship:
and the mixture momentum equation can be described as follows:
where the subscripts
k and
m denote the phase
k and mixture
m,
is the mixture pressure gradient,
is the volume fraction phase
k,
is the mixture kinematic viscosity,
is the eddy viscosity,
is external source term,
is the mixture density,
is the relative velocity of the phase
k to the mixture
m,
is the phase velocity and
is the mixture velocity and is calculated as follows:
Interestingly, the third term on the right-hand side of equation
4,
, is the advection term resulting from the existence of the solid particles. The phase transport equation is given as follows:
The right-hand side represents the particle turbulence diffusion.
is the turbulence diffusion coefficient, which is defined as the ratio between the eddy viscosity
and turbulent Schmidt number
. In this study,
is taken to be 1. Note that we solve the phase transport equation only for the solid phases. To calculate the liquid phase, we use the following:
Based on that, , where is the volumetric concentration of the liquid phase and is the volumetric concentration of total solid phases.
Following Equations (
4) and (
6),
,
, and
require closure. Starting with
, we employ the following equation using the relative velocity approach [
27]:
where
,
is the relative velocity of the phase
k to the liquid phase
c, which is also known as the terminal settling velocity, and
is the mass fraction of phase
k. The terminal settling velocity
is calculated for each solid phase using the following equation [
29]:
where
is the kinematic viscosity of the liquid phase,
g is the gravitational acceleration,
,
is the particle density,
is the liquid phase density, and
and
are presented in
Table 4.
The effect of hindered settling is also taken into account, by using the [
30] formula for hindered settling.
where
e is the so-called Richardson and Zaki index, which depends on a particle’s Reynolds number that can be defined as the ratio between the particle inertial and viscous forces. We use the empirical equation of [
31] to calculate the value of
e as follows:
where
and
d are experimental coefficients and are taken to be
and
, respectively.
The presence of the particles will influence the viscosity. Noting that the mixture is considered in the Newtonian regime, we use the formula of [
32] that describes the mixture viscosity as a function of the volume concentration of solids as follows:
where
A and
B are empirical factors that are taken to be
and
, respectively [
27].
Finally, to calculate
in Equation
4, we use the buoyant
model as a closure for turbulence, where
k accounts for the turbulence kinetic energy and
for the turbulence energy dissipation rate. The Buoyant
model can be described by the following equations [
26]:
where
,
are the turbulent Prandtl numbers,
,
, and
are turbulence model constants.
is the generation of turbulence kinetic energy due to mean velocity gradients, and
is the generation of turbulence kinetic energy due to buoyancy. It is important to emphasize that, for non-stratified flows, the buoyancy term vanishes where
, while
in the case of stable stratification. After solving the
model, eddy viscosity
can be calculated following this relation:
where
is a turbulence constant.
4.2. Application of the Numerical Model
Two-dimensional (2D) computational mesh representing the experimental set-up is shown in
Figure 2. A 2D mesh is used further to reduce the computational efforts required.
Figure 10 also shows the used Boundary Conditions (B.C); see
Section 4.2.1. Two cell zones are defined, with first cell zone 1 representing clear water, i.e.,
,
and cell zone 2 representing the lock region where
has a value depending on the initial condition of the numerical run and
. The 2D mesh consists of 8000 mesh cells. Furthermore, in both zones, cell dimensions increase in the positive
Z direction with a growth rate of 1.02, for the purpose of capturing the dynamics of the current near the bottom in greater detail. The cell dimensions are kept constant in the
x-direction (see
Figure 10).
4.2.1. Boundary Conditions
In this section, we summarize the general aspects and characteristics of the B.C used in the numerical runs presented here. Boundary conditions are specified for quantities .
For the velocities (), at the free ambient water surface, a slip boundary condition is used. Thus, there are neither convective nor diffusive fluxes present at the top surface, but velocity values are calculated at the boundary. A no-slip condition, i.e., zero velocities at the boundaries, is applied to all solid boundaries of the tank domain. For the pressure , a value of 1.013 bar is used at the top surface of the tank to simulate the effect of atmospheric pressure, while zero gradient is used at all tank walls. In addition, the zero gradient for volume fractions is assigned to all boundaries of the domain, including the free surface. A zero-gradient boundary condition guarantees that the volume fractions do not escape the domain, and that a bed builds up at the bottom boundary. The presence of walls affects the turbulent flow significantly. In the region near the wall, viscous damping and kinematic blocking reduce normal and tangential velocity fluctuations. Far from the near-wall region, turbulence increases rapidly because of the production of turbulent kinetic energy k. In the current study, wall functions are used for solid boundaries in order to link the viscosity-affected sub-layers between the fully turbulent and near-wall regions. For the free top surface, a zero- gradient BC is used for k and .
4.2.2. Grid Dependency
To investigate the influence of the mesh sizes, front position versus time is depicted for four different computational meshes. Three 2D meshes with 4800, 8000 and 16,800 cells and one three-dimensional (3D)mesh with 60,000 cells are selected to represent coarse, used, fine and 3D meshes, respectively. Experimental run7 is reproduced numerically, using the four proposed computational meshes, and the resulting distance–time figures are plotted in
Figure 11. An adjustable time step is used, which means that a new time step is calculated at the end of the previous time step based on the Courant number
. The Courant number represents how quickly information travels along the mesh cells. To have steady numerical runs, we keep
C below 1.
The resulting distance–time curves for the four meshes compare very well, which means that the numerical solution can be considered mesh independent. To ascertain the mesh-independence of the solution in more detail, we also calculated the error in two cases: between used/fine meshes and used/3D meshes. Comparing the results of the used and fine meshes, we found that doubling the cell number yields an average difference of 1% in the values of time with respect to distance, while the average difference between the 3D and used meshes is found to be 6.43%. Both are in an acceptable range.
4.3. Number of Used Fractions Sensitivity Analysis
The number of the used fractions in the numerical runs is also a critical factor that can affect the simulation’s accuracy in predicting the parameters associated with a turbidity current. Therefore, we must carry out a number-of-fractions sensitivity analysis to investigate the effect of the used fractions number on the forward velocity of the currents. Run15 is reproduced numerically using number of fractions of 1, 12 and 24. The resulting distance–time curves for the numerical runs and the experimental run are plotted in
Figure 12.
The potential energy that the mixture possesses before the gate is removed and the buoyancy forces resulting from the presence of solid particles are the main driving forces of a current. After removing the gate, the potential energy of a mixture transforms directly into kinetic energy. The effect of the kinetic energy on the driving force of the current decreases with time, and buoyancy forces become dominant. Following this understanding, in the first 60 s on the
x-axis in
Figure 12, front velocity compares well with experimental results because the driving forces were equal in all numerical runs. However, when the effect of the potential energy reduces and buoyancy forces become dominant, a degree of deviation is observed. As a result, beyond 60 s on the
x-axis in
Figure 12, in the case of 1 and 12 fractions used, a deviation from the experimental result can be observed. This deviation can be attributed to the change in buoyancy forces, since the number of fractions used significantly influences the buoyancy forces. As a result, the 24-fractions run compares well during the whole propagation time of the current, unlike the 1- and 12-fraction runs. Therefore, using a more representable number of fractions of a sediment type in a numerical run will increase the accuracy of a simulated result.
5. Comparison of Numerical Simulations with Experiments
The predictions of the multi-phase drift–flux model are validated in this section. We compare the experimental results to the corresponding numerical results. Runs 1, 7 and 15 are reproduced numerically using the same initial conditions as in the experimental runs. Particle sizes were analysed through PSD testing for each sediment type in order to identify the quantities of each particle size present in the sediment. In addition, 14,12 and 24 fractions are used for Type1, Type2 and Type3, respectively. This information is used to set up the initial conditions of each numerical run.
Figure 13 compares the observed and simulated front position of the current versus time for runs 1, 7 and 15. The numerical model predicts the observed front position very well. This means that the simulations are capable of predicting the three phases of the current, i.e., the slumping, self-similar and viscous phases mentioned in the experimental results,
Section 3.
Since it is also important to compare concentration distribution, two snapshots are taken at the same time frame and same front position in both the simulations and the experiments. The first snapshot is taken when the front of the current is almost at the middle of the tank, while the second snapshot is taken when the current reaches the end of the visualized region (see
Figure 2). Two concentration profiles are taken per snapshot. For the first snapshot, the first profile is taken at the front of the current, at
m from the lock gate, while the second profile is taken at the body region of the current at a distance of
m from the lock gate. For the second snapshot, the front is taken to be at the end of the visualized region, which is
m from the lock gate and the second profile is at
m from the lock gate. In run 1, only the first snapshot is taken at 24.5 s because the current is unquantifiable when it reaches the last third of the tank. For runs 7 and 15, the first snapshot is taken at 69.5 s and 73.1 s, while the second snapshot is taken at 113 s and 130 s, respectively.
Figure 14,
Figure 15 and
Figure 16, show the experimental concentration profiles versus the simulated concentration profiles for runs 1, 7 and 15. Generally speaking, the numerical simulations show good agreement with the experimental data. Looking in more detail, a minor degree of divergence is observed between the experiments and simulations in all validation cases, which can be explained by two main factors:
The use of buoyant turbulence modelling, as this model introduces a degree of inaccuracy to the turbulence calculations.
The accuracy of the concentration calibration process in the experiments.
Various processes contribute to the turbulence process. One of the most important turbulence damping mechanisms in turbidity currents is damping by buoyancy forces, where solid-particle gravity forces oppose the upward flow fluctuations. This will result in a reduction in kinetic turbulence energy [
33]. This mechanism could have a significant effect on the turbulence calculations even in low-concentration currents. Another damping mechanism is the reduction in turbulence kinetic energy due to the change in the effective viscosity, which is why the presence of particles increases the bulk viscosity of the mixture [
33].
The standard
model was originally developed on the basis of isotropic eddy viscosity and eddy diffusivity models. Accordingly, this model produces good estimations of turbulence calculations in non-stratified flows [
34]. With stratified flows (e.g., turbidity currents), the model needs to be tweaked to account for the presence of sediment particles [
34]. One of these modifications involves adding a buoyancy damping function term
to account for damped turbulence flux resulting from particle buoyancy. Note that this modification was made in the present study (see Equations (
16) and (
17)). However, our approach still lacks two other damping processes: the turbulence flux of momentum in the vertical direction and the extra vertical mixing between the flow layers due to the particles, i.e., turbulent wake resulting from particle deposition in the vertical direction. These two processes must be modelled in the
model. In addition, an accurate estimation of the Schmidt number
is needed, where
is the damping function for momentum,
is the damping function for the mixing and
is the neutral Schmidt number. Normally, the
and
are calculated as a function of the Richardson number, which is defined as the ratio between buoyancy flux and flow shear (for more on estimating damping functions, see [
33]). In addition to damping processes, another possible reason for the observed divergence is the wave at the tank surface caused by removing the lock gate, which is not taken into consideration. Moreover, there is a miss-estimation of the bed formed in the experiments because of the limitations of the calibration process (
Section 2.2,
Table 3). Keeping this in mind, the deviation between the experimental and numerical calculated concentration distribution at the bottom of the tank, i.e., first 2 cm on the
y-axis
Figure 14,
Figure 15 and
Figure 16, can be attributed to the inaccuracy of the measured concentration distribution in the experiments.
To conclude, the damping processes mentioned here and the wave are the reasons for the minor degree of divergence observed in the vertical concentration profiles. However, for the sake of minimizing computational efforts and capturing the general trend of the current without extra costs, we consider that the multiple fractions drift–flux modelling approach can effectively predict the behaviour of a current in a good manner.
6. Conclusions
Particle size plays a major role in turbidity current propagation. In order to quantify turbidity currents generated by mining, this paper investigated the effect of particle size and initial concentration on the propagation of turbidity currents experimentally and numerically. In the following context, the low-concentration turbidity currents and high-concentration turbidity currents are denoted to the currents of and of the initial concentration, respectively. Note that these conclusions are limited by the tested run-out distance of the current, i.e., the tank length.
Increasing initial concentrations inside the lock yields high front velocities independent of sediment type. In other words, the transition time to the self-similar phase increases when increasing the initial concentration.
Increasing particle size leads to low front velocities. With coarse-particle, low-concentration currents, the turbidity current transitions to the self-similar phase more quickly, unlike fine-particle currents that take much longer to transition.
Increasing initial concentrations neutralizes the particle size effect on current propagation.
With high-concentration currents, coarse particles have little/no effect on the motion of the current compared to fine-particle currents with the same initial concentration, while in low-concentration currents, coarse particles settle and affect the forward velocity of the current.
In case of fine-particle, low-concentration currents, low local concentration distribution values are observed during the propagation of the current.
The new multiple fractions drift–flux model can satisfactorily predict how turbidity currents develop. It is important to remember that the number of fractions used is critical to the accuracy of the predictions, with a greater degree of accuracy being achieved when using a large number of fractions.
These findings can contribute to our understanding of the discharge process from a PNMT. Increasing particle size through flocculation and decreasing the initial concentration at the source might be beneficial in order to minimize environmental impact. Another key point is that the drift–flux model can be utilized to predict the behaviour of turbidity flows behind mining tools. Furthermore, the drift–flux model can be an acceptable choice to optimize the momentum, volume and buoyancy fluxes at the discharge source.
The aggregation-breakup processes that occur between sediment particles during the discharge process and during turbidity current propagation is a matter of importance in any discharge process assessment. However, despite the fact that there are some studies about flocculation processes for deep-sea mininig applications [
1,
35], a comprehensive understanding of flocculation is still lacking. Moreover, a properly validated numerical model that can predict particle size in the near-field region is still needed.