Role of Defects and Radiation Damage on He Diffusion in Magnetite: Implication for (U-Th)/He Thermochronology
Abstract
:1. Introduction
2. Materials and Methods
2.1. Theoretical Multiscale He Diffusion Modeling
2.1.1. Theoretical Computational Details
2.1.2. Atomic Scale
2.1.3. Macroscopic Scale
2.2. Theoretical Damage Quantification
3. Results
3.1. Defect-Free Magnetite Structure
3.2. Magnetite Structure Containing Crystallographic Defect or Radiation Damage
4. Discussion
4.1. He Diffusion in Magnetite Structure
4.1.1. Theoretical Investigation of He Diffusion
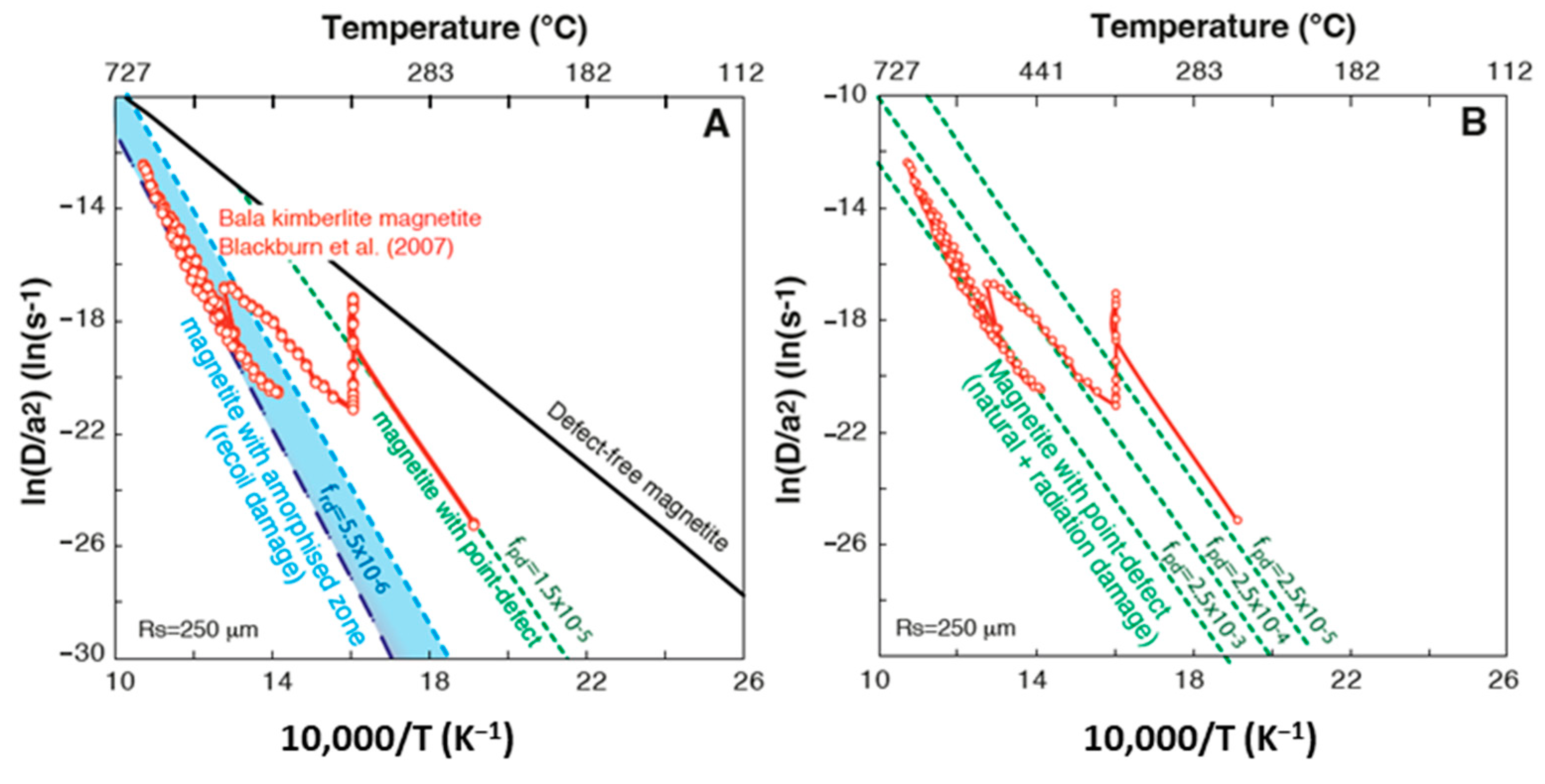
4.1.2. Defect and Damage Impact on He Diffusion
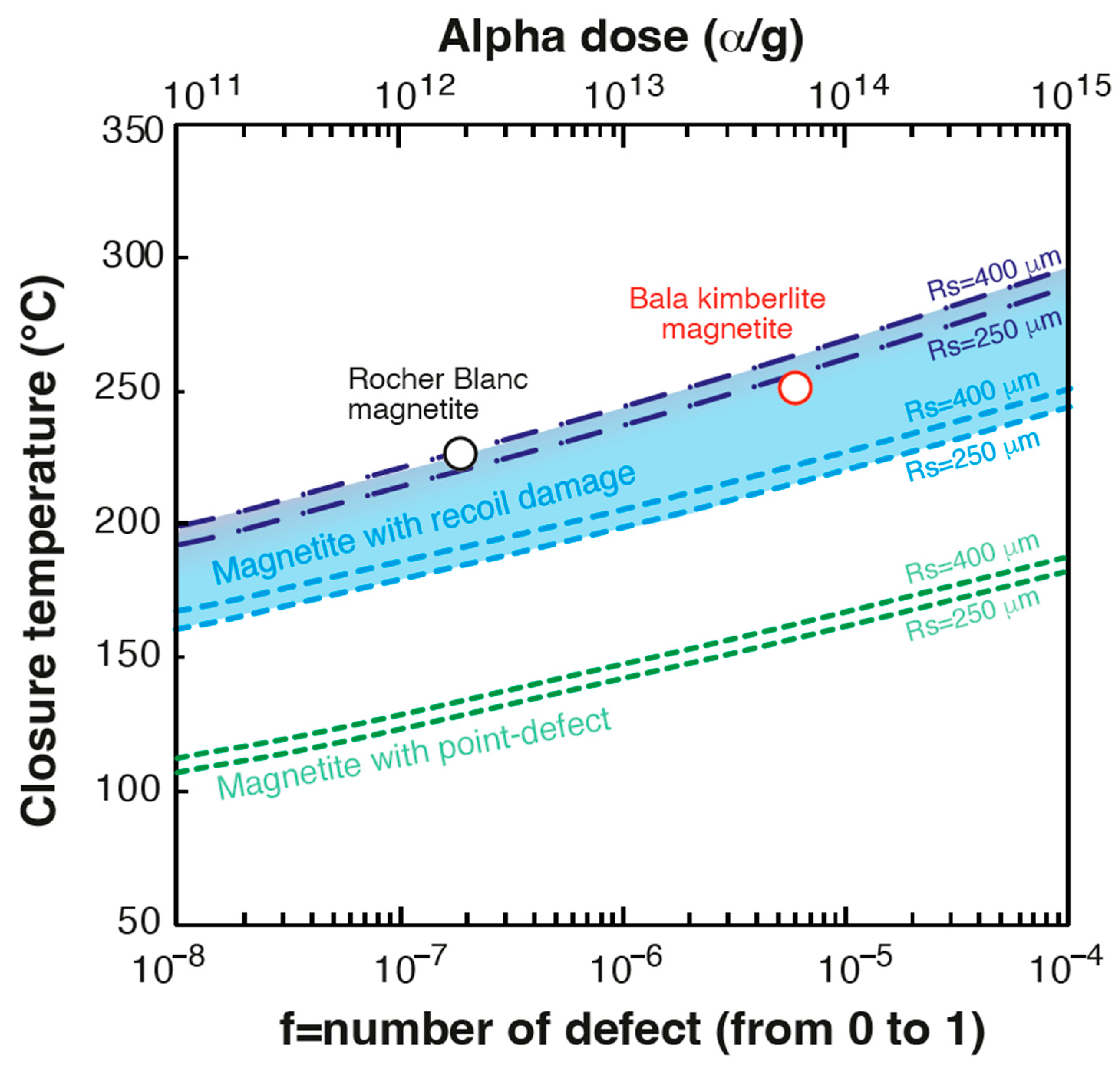
4.2. Implication for Magnetite (U-Th)/He Thermo-Geo-Chronometer
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Miller, D.N.; Folk, R.L. Occurrence of detrital magnetite and ilmenite in red sediments: New approach to significance of redbeds: Geological notes. AAPG Bull. 1995, 39, 338–345. [Google Scholar]
- Phillips, S.C.; Johnson, J.E.; Clyde, W.C.; Setera, J.; Maxbauer, D.P.; Severmann, S.; Riedinger, N. Rock magnetic and geochemical evidence for authigenic magnetite formation via iron reduction in coal-bearing sediments offshore Shimokita Peninsula, Japan (IODP Site C0020): Authigenic magnetite offshore Shimokita. Geochem. Geophys. Geosystems 2017, 18, 2076–2098. [Google Scholar] [CrossRef]
- Boutroy, E.; Dare, S.A.; Beaudoin, G.; Barnes, S.-J.; Lightfoot, P.C. Magnetite composition in Ni-Cu-PGE deposits worldwide: Application to mineral exploration. J. Geochem. Explor. 2014, 145, 64–81. [Google Scholar] [CrossRef]
- Ward, L.A.; Holwell, D.A.; Barry, T.L.; Blanks, D.E.; Graham, S.D. The use of magnetite as a geochemical indicator in the exploration for magmatic Ni-Cu-PGE sulfide deposits: A case study from Munali, Zambia. J. Geochem. Explor. 2018, 188, 172–184. [Google Scholar] [CrossRef] [Green Version]
- Canil, D.; Grondahl, C.; Lacourse, T.; Pisiak, L.K. Trace elements in magnetite from porphyry Cu–Mo–Au deposits in British Columbia, Canada. Ore Geol. Rev. 2016, 72, 1116–1128. [Google Scholar] [CrossRef] [Green Version]
- Nadoll, P.; Angerer, T.; Mauk, J.; French, D.; Walshe, J. The chemistry of hydrothermal magnetite: A review. Ore Geol. Rev. 2014, 61, 1–32. [Google Scholar] [CrossRef]
- Knipping, J.L.; Bilenker, L.D.; Simon, A.; Reich, M.; Barra, F.; Deditius, A.; Wӓlle, M.; Heinrich, C.; Holtz, F.; Munizaga, R. Trace elements in magnetite from massive iron oxide-apatite deposits indicate a combined formation by igneous and magmatic-hydrothermal processes. Geochim. Cosmoch. Acta 2015, 171, 15–38. [Google Scholar] [CrossRef] [Green Version]
- Nyström, J.O.; Billström, K.; Henríquez, F.; Fallick, A.E.; Naslund, H.R. Oxygen isotope composition of magnetite in iron ores of the Kiruna type in Chile and Sweden. GFF 2008, 130, 177–188. [Google Scholar] [CrossRef]
- Dare, S.A.S.; Barnes, S.-J.; Beaudoin, G.; Méric, J.; Boutroy, E.; Potvin-Doucet, C. Trace elements in magnetite as petrogenetic indicators. Miner. Depos. 2014, 49, 785–796. [Google Scholar] [CrossRef]
- Huang, X.-W.; Sappin, A.-A.; Boutroy, E.; Beaudoin, G.; Makvandi, S. Trace Element Composition of Igneous and Hydrothermal Magnetite from Porphyry Deposits: Relationship to Deposit Subtypes and Magmatic Affinity. Econ. Geol. 2019, 114, 917–952. [Google Scholar] [CrossRef]
- Maffione, M.; Morris, A.; Plümper, O.; Van Hinsbergen, D.J.J. Magnetic properties of variably serpentinized peridotites and their implication for the evolution of oceanic core complexes. Geochem. Geophys. Geosystems 2014, 15, 923–944. [Google Scholar] [CrossRef] [Green Version]
- Oufi, O. Magnetic properties of variably serpentinized abyssal peridotites. J. Geophys. Res. 2002, 107, 2095. [Google Scholar] [CrossRef]
- Brunet, F. Hydrothermal Production of H2 and Magnetite From Steel Slags: A Geo-Inspired Approach Based on Olivine Serpentinization. Front. Earth Sci. 2019, 7, 17. [Google Scholar] [CrossRef] [Green Version]
- Klein, F.; Bach, W.; McCollom, T.M. Compositional controls on hydrogen generation during serpentinization of ultramafic rocks. Lithos 2013, 178, 55–69. [Google Scholar] [CrossRef]
- Klein, F.; Bach, W.; Humphris, S.E.; Kahl, W.-A.; Jöns, N.; Moskowitz, B.; Berquó, T.S. Magnetite in seafloor serpentinite—Some like it hot. Geology 2014, 42, 135–138. [Google Scholar] [CrossRef]
- McCollom, T.M.; Seewald, J.S. Serpentinites, Hydrogen, and Life. Elements 2013, 9, 129–134. [Google Scholar] [CrossRef]
- Blackburn, T.J.; Stockli, D.F.; Walker, J.D. Magnetite (U-Th)/He dating and its application to the geochronology of intermediate to mafic volcanic rocks. Earth Planet Sci. Lett. 2007, 259, 360–371. [Google Scholar] [CrossRef]
- Blackburn, T.J.; Stockli, D.F.; Carlson, R.W.; Berendsen, P. (U–Th)/He dating of kimberlites—A case study from north-eastern Kansas. Earth Planet. Sci. Lett. 2008, 275, 111–120. [Google Scholar] [CrossRef]
- Cooperdock, E.H.; Stockli, D.F. Unraveling alteration histories in serpentinites and associated ultramafic rocks with magnetite (U–Th)/He geochronology. Geology 2016, 44, 967–970. [Google Scholar] [CrossRef] [Green Version]
- Cooperdock, E.H.G.; Stockli, D.F.; Kelemen, P.B.; de Obeso, J.C. Timing of magnetite growth associated with peridotite-hosted carbonate veins in the SE Samail ophiolite, Wadi fins, Oman. J. Geophys. Res. Solid Earth 2020, 125, e2019JB018632. [Google Scholar] [CrossRef]
- Schwartz, S.; Gautheron, C.; Ketcham, R.; Brunet, F.; Corre, M.; Agranier, A.; Pinna-Jamme, R.; Haurine, F.; Monvoin, G.; Riel, N. Unraveling the exhumation history of high-pressure ophiolites using magnetite (U-Th-Sm)/He thermochronometry. Earth Planet. Sci. Lett. 2020, 543, 116359. [Google Scholar] [CrossRef]
- Lazar, C.; Cooperdock, E.H.G.; Seymour, B.H.T. A continental forearc serpentinite diapir with deep origins: Elemental signatures of slab-derived fluids and a mantle wedge protolith at New Idria, California. Lithos 2021, 398–399, 106252. [Google Scholar] [CrossRef]
- Hofmann, F.; Cooperdock, E.H.G.; West, A.J.; Hildebrandt, D.; Strößner, K.; Farley, K.A. Exposure dating of detrital magnetite using 3He enabled by microCT and calibration of the cosmogenic 3He production rate in magnetite. Geochronol. Discuss. 2021, 3, 395–414. [Google Scholar] [CrossRef]
- Gerin, C.; Gautheron, C.; Oliviero, E.; Bachelet, C.; Djimbi, D.M.; Seydoux-Guillaume, A.-M.; Tassan-Got, L.; Sarda, P.; Roques, J.; Garrido, F. Influence of vacancy damage on He diffusion in apatite investigated at atomic to mineralogical scales. Geochim. Cosmoch. Acta 2017, 197, 87–103. [Google Scholar] [CrossRef]
- Gautheron, C.; Djimbi, D.M.; Roques, J.; Balout, H.; Ketcham, R.A.; Simoni, E.; Pik, R.; Seydoux-Guillaume, A.-M.; Tassan-Got, L. A multi-method, multi-scale theoretical study of He and Ne diffusion in zircon. Geochim. Cosmoch. Acta 2020, 268, 348–367. [Google Scholar] [CrossRef]
- Djimbi, D.M.; Gautheron, C.; Roques, J.; Tassan-Got, L.; Gerin, C.; Simoni, E. Impact of apatite chemical composition on (U-Th)/He thermochronometry: An atomistic point of view. Geochim. Et Cosmochim. Acta 2015, 167, 162–176. [Google Scholar] [CrossRef]
- Bassal, F.; Roques, J.; Gautheron, C. Neon diffusion in goethite, α-FeO(OH): A theoretical multi-scale study. Phys. Chem. Miner. 2020, 47, 14. [Google Scholar] [CrossRef]
- Balout, H.; Roques, J.; Gautheron, C.; Tassan-Got, L.; Mbongo-Djimbi, D. Helium diffusion in pure hematite (α-Fe2O3) for thermochronometric applications: A theoretical multi-scale study. Comput. Theor. Chem. 2017, 1099, 21–28. [Google Scholar] [CrossRef]
- Balout, H.; Roques, J.; Gautheron, C.; Tassan-Got, L. Computational investigation of the interstitial neon diffusion in pure hematite, α-Fe2O3. Comput. Mater. Sci. 2017, 128, 67–74. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef] [Green Version]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef] [Green Version]
- Mills, G.; Jónsson, H.; Schenter, G.K. Reversible work transition state theory: Application to dissociative adsorption of hydrogen. Surf. Sci. 1995, 324, 305–337. [Google Scholar] [CrossRef] [Green Version]
- Jónsson, H.; Mills, G.; Jacobsen, K.W. Nudged Elastic Band Method for Finding Minimum Energy Paths of Transitions. In Classical and Quantum Dynamics in Condensed Phase Simulations; Berne, J.B., Ciccotti, C., Coker, D.F., Eds.; World Scientific: Singapore, 1998; p. 385. [Google Scholar]
- Fleet, M.E. The structure of magnetite. Acta Crystallogr. Sect. B 1981, 37, 917–920. [Google Scholar] [CrossRef]
- Cornell, R.M.; Schwertmann, U. The Iron Oxides: Structure, Properties, Reactions, Occurences and Uses, Second Edition; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Wright, J.P.; Attfield, J.P.; Radaelli, P.G. Charge ordered structure of magnetite Fe3O4 below the Verwey transition. Phys. Rev. B 2002, 66, 214422. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for open-shell transition metals. Phys. Rev. B 1994, 48, 13115. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Guo, H.; Barnard, A.S. Thermodynamic modelling of nanomorphologies of hematite and goethite. J. Mater. Chem. 2011, 21, 11566–11577. [Google Scholar] [CrossRef]
- Rohrbach, A.; Hafner, J.; Kresse, G. Electronic correlation effects in transition-metal sulfides. J. Phys. Condens. Matter 2003, 15, 979. [Google Scholar] [CrossRef]
- Rollmann, G.; Rohrbach, A.; Entel, P.; Hafner, J. First-principles calculation of the structure and magnetic phases of hematite. Physical Review B 2004, 69, 165107. [Google Scholar] [CrossRef] [Green Version]
- Yin, S.; Ellis, D.E. DFT studies of Cr(VI) complex adsorption on hydroxylated hematite (1102) surfaces. Surf. Sci. 2009, 603, 736–746. [Google Scholar] [CrossRef]
- Dudarev, S.L.; Liechtenstein, A.I.; Castell, M.R.; Briggs, G.A.D.; Sutton, A.P. Surface states on NiO (100) and the origin of the contrast reversal in atomically resolved scanning tunneling microscope images. Phys. Rev. B 1997, 56, 4900–4908. [Google Scholar] [CrossRef]
- Roldan, A.; Santos-Carballal, D.; de Leeuw, N.H. A comparative DFT study of the mechanical and electronic properties of greigite Fe3S4 and magnetite Fe3O4. J. Chem. Phys. 2013, 138, 204712. [Google Scholar] [CrossRef] [PubMed]
- Santos-Carballal, D.; Roldan, A.; Grau-Crespo, R.; de Leeuw, N.H. A DFT study of the structures, stabilities and redox behaviour of the major surfaces of magnetite Fe3O4. Chem. Phys. 2014, 16, 21082–21097. [Google Scholar] [CrossRef] [Green Version]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Bortz, A.B.; Kalos, M.H.; Lebowitz, J.L. A new algorithm for Monte Carlo simulation of Ising spin systems. J. Comput. Phys. 1975, 17, 10–18. [Google Scholar] [CrossRef]
- Einstein, A. Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Ann. Phys. 1905, 322, 549–560. [Google Scholar] [CrossRef] [Green Version]
- Ziegler, J.F. Helium Stopping Powers and Ranges in All Elements; Pergamon Press: Oxford, UK, 1977; Volume 4. [Google Scholar]
- Ziegler, J.F. SRIM-2008 The Stopping Range of Ions in Matter; United States Naval Academy: Annapolis, MD, USA, 2008. [Google Scholar]
- Dodson, M.H. Closure temperature in cooling geochronological and petrological systems. Contrib. Mineral. Petrol. 1973, 40, 259–274. [Google Scholar] [CrossRef]
- Recanati, A.; Gautheron, C.; Barbarand, J.; Missenard, B.; Pinna-Jamme, R.; Tassan-Got, L.; Carter, A.; Douville, E.; Bordier, L.; Pagel, M.; et al. Helium trapping in apatite damage: Insights from (U-Th-Sm)/He dating of different granitoid lithologies. Chem. Geol. 2017, 470, 116–131. [Google Scholar] [CrossRef] [Green Version]
- Shuster, D.; Flowers, R.; Farley, K.A. The influence of natural radiation damage on helium diffusion kinetics in apatite. Earth Planet. Sci. Lett. 2006, 249, 148–161. [Google Scholar] [CrossRef]
- Farley, K.A. Helium diffusion from apatite: General behavior as illustrated by Durango fluorapatite. J. Geophys. Res. 2000, 105, 2903–2914. [Google Scholar] [CrossRef] [Green Version]
- Hallström, S.; Höglund, L.; Ågrena, J. Modeling of iron diffusion in the iron oxides magnetite and hematite with variable stoichiometry. Acta Mater. 2011, 59, 53–60. [Google Scholar] [CrossRef]
- Sundman, B. An assessment of the Fe-O system. J. Phase Equilibria 1991, 12, 127–140. [Google Scholar] [CrossRef]
- Dieckmann, R. Defects and Cation Diffusion in Magnetite (IV): Nonstoichiometry and Point Defect Structure of Magnetite (Fe3-δO4). Ber. Der Bunsenges. Für Phys. Chem. 1982, 86, 112–118. [Google Scholar] [CrossRef]
- Arras, R.; Warot-Fonrose, B.; Calmels, L. Electronic structure near cationic defects in magnetite. J. Phys. Condens. Matter 2013, 25, 256002. [Google Scholar] [CrossRef]
- Xu, H.; Shen, Z.; Konishi, H. Si-magnetite nano-precipitates in silician magnetite from banded iron formation: Z-contrast imaging and ab initio study. Am. Mineral. 2014, 99, 2196–2202. [Google Scholar] [CrossRef]
- Bender, W.M.; Becker, U. Quantum-Mechanical Investigation of the Structures and Energetics of Uranium and Plutonium Incorporated into the Magnetite (Fe3O4) Lattice. ACS Earth Space Chem. 2019, 3, 637–651. [Google Scholar] [CrossRef]



| Defect-Free Crystal | a (Å) | b (Å) | c (Å) | Einsertion (eV) | ||
|---|---|---|---|---|---|---|
| 16c | 8b | 48f | ||||
| Cubic cell ( × × ) | 8.49 | 8.49 | 8.49 | 1.13 | 3.96 | unstable |
| Cubic cell ( × × ) | 16.98 | 8.49 | 8.49 | 1.10 | - | - |
| Einsertion (eV) | Emig (eV) | Ea (eV) | Do (cm2/s) | Tc (°C) * Rs = 250 µm | Tc (°C) * Rs = 500 µm | |
|---|---|---|---|---|---|---|
| Theoretical study | ||||||
| Defect-free crystal ( ) | 1.13 | 0.97 | 0.97 | 3.07 × 10−3 | 35 | 47 |
| Defect-free crystal ( ) | 1.10 | 0.99 | 0.99 | 3.07 × 10−3 | - | - |
| Crystallographic Fe3+ point defect ** | 0.50 | 1.78 | - | - | - | - |
| Recoil damage | 0 | 2.1 to 2.28 | - | - | - | - |
| Experimental study | ||||||
| Cubic cell ( ) | 16.98 | 8.49 | 8.49 | 250 | 262 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bassal, F.; Roques, J.; Corre, M.; Brunet, F.; Ketcham, R.; Schwartz, S.; Tassan-Got, L.; Gautheron, C. Role of Defects and Radiation Damage on He Diffusion in Magnetite: Implication for (U-Th)/He Thermochronology. Minerals 2022, 12, 590. https://doi.org/10.3390/min12050590
Bassal F, Roques J, Corre M, Brunet F, Ketcham R, Schwartz S, Tassan-Got L, Gautheron C. Role of Defects and Radiation Damage on He Diffusion in Magnetite: Implication for (U-Th)/He Thermochronology. Minerals. 2022; 12(5):590. https://doi.org/10.3390/min12050590
Chicago/Turabian StyleBassal, Fadel, Jérôme Roques, Marianna Corre, Fabrice Brunet, Richard Ketcham, Stéphane Schwartz, Laurent Tassan-Got, and Cécile Gautheron. 2022. "Role of Defects and Radiation Damage on He Diffusion in Magnetite: Implication for (U-Th)/He Thermochronology" Minerals 12, no. 5: 590. https://doi.org/10.3390/min12050590
APA StyleBassal, F., Roques, J., Corre, M., Brunet, F., Ketcham, R., Schwartz, S., Tassan-Got, L., & Gautheron, C. (2022). Role of Defects and Radiation Damage on He Diffusion in Magnetite: Implication for (U-Th)/He Thermochronology. Minerals, 12(5), 590. https://doi.org/10.3390/min12050590







