Long- and Short-Term Strategies for Estimation of Hydraulic Fracturing Cost Using Fuzzy Logic
Abstract
:1. Introduction
2. Fuzzy Logic Applications into the Mining and Cost Estimation
3. Fuzzy Inference System Development
3.1. Fuzzy Set
3.1.1. Fuzzy Arithmetic Operation
3.1.2. Fuzzy Inferences System
3.2. Cost Optimisation in Mining
3.3. Cost Variables of Hydraulic Fracturing Costs
3.3.1. Drilling Related Costs
3.3.2. Frack Pumping Costs
3.3.3. Fluid and Proppant Costs
3.4. Cavability
3.4.1. Cavability Index
Natural Factor
Induced Factor
4. Cost Estimation with a Strategic View
4.1. Long- and Short-Term Strategy for Estimation of HF Cost Using Fuzzy Logic
4.2. Short-Term Strategy for HF Operation
4.3. Long-Term Strategy for HF Estimation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Brown, E.T. Block Caving Geo Mechanics, 2nd ed.; Julius Kruttschnitt Mineral Research Centre: Brisbane, Australia, 2007; p. 696. [Google Scholar]
- Manca, L.; Dunstan, G. Cadia East—A case study in applied innovative design. In Proceedings of the 3rd International Seminar on Mine Planning; GECAMIN: Santiago, Chile, 2013; pp. 181–190. [Google Scholar]
- Luhandjula, M.; Joubert, J. On some optimisation models in a fuzzy-stochastic environment. Eur. J. Oper. Res. 2010, 207, 1433–1441. [Google Scholar] [CrossRef] [Green Version]
- Van As, A.; Jeffrey, R.G. Hydraulic fracturing as a cave inducement technique at North parkes Mines. In Proceedings MassMin 2000, Brisbane; Chitombo, G., Ed.; Australasian Institute of Mining & Metallurgy: Melbourne, Australia, 2000; pp. 165–172. [Google Scholar]
- Mills, K.; Jeffrey, R.; Karzulovic, A.; Alfaro, M. Remote high resolution stress change monitoring for hydraulic fractures. In Proceedings of the MassMin: Proud to be Miners, Santiago, Chile, 22–25 August 2004. [Google Scholar]
- Jeffrey, R.G.; Bunger, A.; Lecampion, B.; Zhang, X.; Chen, Z.; van As, A.; Allison, D.P.; De Beer, W.; Dudley, J.W.; Siebrits, E.; et al. Measuring Hydraulic Fracture Growth in Naturally Fractured Rock. In Proceedings of the SPE annual technical conference and exhibition, New Orleans, LA, USA, 4–7 October 2009. [Google Scholar]
- Catalan, A.; Onederra, I.; Chitombo, G. A proposed methodology for evaluation of the preconditioning by blasting at the Cadia East Pannel cave mine. In Proceedings of the MassMin 2012: 6th International Conference and Exhibition on Mass Mining, Sudbury, ON, Canada, 10–14 June 2012; Canadian Institute of Mining, Metallurgy and Petroleum: Westmount, QC, Canada, 2012. [Google Scholar]
- Chacón, E.; Barrera, V.; van As, J.R. Hydraulic fracturing used to preconditioning ore and reduce fragment size for block caving. In Proceedings of the MassMin 2004 Proceedings, Santiago, Chile, 22–25 August 2004. [Google Scholar]
- Castro, C.; Baez, F.; Arancibia, E.; Barrera, V. Study of the impact of rock mass preconditioning on a block caving mine operation. In Proceedings of the 3rd International Symposium on Block and Sublevel Caving: Caving 2014, Santiago, Chile, 5–6 June 2004. [Google Scholar]
- Board, M.; Rorke, T.; Williams, G.; Gay, N. Fluid injection for rockburst control in deep mining. In Proceedings of the 33rd US Symposium on Rock Mechanics (USRMS), Santa Fe, New Mexico, 3–5 June 1992. [Google Scholar]
- Lyu, S.; Wang, S.; Li, J.; Chen, X.; Chen, L.; Dong, Q.; Zhang, X.; Huang, P. Massive Hydraulic Fracturing to Control Gas Outbursts in Soft Coal Seams. Rock Mech. Rock Eng. 2022, 55, 1759–1776. [Google Scholar] [CrossRef]
- Lyu, S.; Wang, S.; Chen, X.; Wang, S.; Wang, T.; Shi, X.; Dong, Q.; Li, J. Natural fractures in soft coal seams and their effect on hydraulic fracture propagation: A field study. J. Pet. Sci. Eng. 2020, 192, 107255. [Google Scholar] [CrossRef]
- Galetakis, M.; Vasiliou, A.; Steiakakis, E.; Soultana, A.; Deligiorgis, V. Applications of fuzzy inference systems in mineral industry-an overview. MATEC Web Conf. 2021, 342, 05006. [Google Scholar] [CrossRef]
- Bandopadhyay, S. Fuzzy algorithm for decision making in mining engineering. Geotech. Geol. Eng. 1987, 5, 149–154. [Google Scholar] [CrossRef]
- Hartog, M.D.; Babuska, R.; Deketh, H.; Grima, M.A.; Verhoef, P.; Verbruggen, H. Knowledge-based fuzzy model for performance prediction of a rock-cutting trencher. Int. J. Approx. Reason. 1997, 16, 43–66. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Y.M.; Park, D.W.; Deb, D.; Sanford, R. Application of fuzzy set theory in the evaluation of roof categories in longwall mining. Min. Eng. 1997, 49, 53–57. Available online: https://www.osti.gov/etdeweb/biblio/469432 (accessed on 16 March 2022).
- Cebesoy, T. Surface mining equipment selection based on multi criteria fuzzy dominant algorithms. In Proceedings of the 15th mining congress of Turkey, Antalya, Turkey, 6–9 May 1997; pp. 79–87. [Google Scholar]
- Bascetin, A. Optimal Equipment Selection in Open-Pit Mines. Ph.D. Thesis, Istanbul Technical University, Istanbul, Turkey, 1999. [Google Scholar]
- Yao, Y.; Li, X.; Yuan, Z. Tool wear detection with fuzzy classification and wavelet fuzzy neural network. Int. J. Mach. Tools Manuf. 1999, 39, 1525–1538. [Google Scholar] [CrossRef] [Green Version]
- Wei, X.; Wang, C.; Zhou, Z. Study on the fuzzy ranking of granite sawability. J. Mater. Process. Technol. 2003, 139, 277–280. [Google Scholar] [CrossRef]
- Li, W.; Mei, S.; Zai, S.; Zhao, S.; Liang, X. Fuzzy models for analysis of rock mass displacements due to underground mining in mountainous areas. Int. J. Rock Mech. Min. Sci. 2005, 43, 503–511. [Google Scholar] [CrossRef]
- Iphar, M.; Goktan, R. An application of fuzzy sets to the Diggability Index Rating Method for surface mine equipment selection. Int. J. Rock Mech. Min. Sci. 2006, 43, 253–266. [Google Scholar] [CrossRef]
- Ghasemi, E.; Ataei, M. Application of fuzzy logic for predicting roof fall rate in coal mines. Neural Comput. Appl. 2012, 22, 311–321. [Google Scholar] [CrossRef]
- Dong, L.-J.; Zhou, Y.; Deng, S.-J.; Wang, M.; Sun, D.-Y. Evaluation methods of man-machine-environment system for clean and safe production in phosphorus mines: A case study. J. Central South Univ. 2021, 28, 3856–3870. [Google Scholar] [CrossRef]
- Muñoz, M.; Miranda, E. A fuzzy system for estimating premium cost of option exchange using mamdani inference: Derivates market of Mexico. In Proceedings of the 2016 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Vancouver, BC, Canada, 24–29 July 2016. [Google Scholar] [CrossRef]
- Kasie, F.M.; Bright, G.; Walker, A. An intelligent decision support system for on-demand fixture retrieval, adaptation and manufacture. J. Manuf. Technol. Manag. 2017, 28, 189–211. [Google Scholar] [CrossRef]
- Fayek, A.R.; Flores, J.R.R. Application of fuzzy logic to quality assessment of infrastructure projects at conceptual cost estimating stage. Can. J. Civ. Eng. 2010, 37, 1137–1147. [Google Scholar] [CrossRef]
- Alshibani, A.; Hassanain, M.A. Estimating facilities maintenance cost using post-occupancy evaluation and fuzzy set theory. J. Qual. Maint. Eng. 2018, 24, 449–467. [Google Scholar] [CrossRef]
- Chen, T. Estimating unit cost using agent-based fuzzy collaborative intelligence approach with entropy-consensus. Appl. Soft Comput. 2018, 73, 884–897. [Google Scholar] [CrossRef]
- Mason, A.K.; Kahn, D.J., Sr. Estimating costs with fuzzy logic. AACE Int. Trans. 1997, p. 122. Available online: https://www.proquest.com/scholarly-journals/estimating-costs-with-fuzzy-logic/docview/208181169/se-2?accountid=10382 (accessed on 16 March 2022).
- Petley, G.; Edwards, D. Further developments in chemical plant cost estimating using fuzzy matching. Comput. Chem. Eng. 1995, 19, 675–680. [Google Scholar] [CrossRef]
- Zima, K. The use of fuzzy case-based reasoning in estimating costs in the early phase of the construction project. AIP Conf. Proc. 2015, 1648, 600010. [Google Scholar] [CrossRef]
- Shaheen, A.; Fayek, A.R.; Abourizk, S.M. Fuzzy Numbers in Cost Range Estimating. J. Constr. Eng. Manag. 2007, 133, 325–334. [Google Scholar] [CrossRef]
- Plebankiewicz, E.; Meszek, W.; Zima, K.; Wieczorek, D. Probabilistic and Fuzzy Approaches for Estimating the Life Cycle Costs of Buildings under Conditions of Exposure to Risk. Sustainability 2020, 12, 226. [Google Scholar] [CrossRef] [Green Version]
- Cocodia, E. Risk Based Fuzzy Modeling of Cost Estimating Relationships for Floating Structures. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Estoril, Portugal, 15–20 June 2008; Volume 48180, pp. 129–142. [Google Scholar] [CrossRef]
- Kahraman, C.; Sarı, İ.U.; Onar, S.C.; Oztaysi, B. Fuzzy economic analysis methods for environmental economics. In Intelligence Systems in Environmental Management: Theory and Applications; Springer: Cham, Switzerland, 2017; pp. 315–346. [Google Scholar] [CrossRef]
- Kaino, T.; Hirota, K.; Pedrycz, W. Fuzzy Sensitivity Analysis and Its Application. In Fuzzy Engineering Economics with Applications; Springer: Berlin, Germany, 2008; pp. 183–216. [Google Scholar] [CrossRef]
- Çoban, V.; Onar, S.Ç. Pythagorean fuzzy engineering economic analysis of solar power plants. Soft Comput. 2018, 22, 5007–5020. [Google Scholar] [CrossRef]
- Dimitrovski, A.; Matos, M. Fuzzy engineering economic analysis [of electric utilities]. IEEE Trans. Power Syst. 2000, 15, 283–289. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef] [Green Version]
- He, Q.; Suorineni, F.T.; Oh, J. Strategies for Creating Prescribed Hydraulic Fractures in Cave Mining. Rock Mech. Rock Eng. 2016, 50, 967–993. [Google Scholar] [CrossRef]
- Trends in U.S. Oil and Natural Gas Upstream Costs. 2016. Available online: https://www.eia.gov/analysis/studies/drilling/pdf/upstream.pdf (accessed on 16 March 2022).
- Bunger, A.P.; Jeffrey, R.G.; Kear, J.; Zhang, X.; Morgan, M. Experimental investigation of the interaction among closely spaced hydraulic fractures. In Proceedings of the 45th US Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 26–29 June 2011. [Google Scholar]
- Adams, J.; Rowe, C. Differentiating applications of hydraulic fracturing. In Proceedings of the ISRM International Conference for Effective and Sustainable Hydraulic Fracturing, Brisbane, Australia, 20–22 May 2013. [Google Scholar]
- Rafiee, R.; Ataei, M.; KhalooKakaie, R.; Rafiee, R.; Ataei, M.; KhalooKakaie, R. A new cavability index in block caving mines using fuzzy rock engineering system. Int. J. Rock Mech. Min. Sci. 2015, 77, 68–76. [Google Scholar] [CrossRef]
- Bieniawski, Z.T. Engineering Rock Mass Classifications: A Complete Manual for Engineers and Geologists in Mining, Civil, and Petroleum Engineering; John Wiley & Sons: Hoboken, NJ, USA, 1989. [Google Scholar]
- Laubscher, D.H. Cave Mining Handbook; De Beers: Johannesburg, South Africa, 2003; 138p. [Google Scholar]
- Lorig, L.; Board, M.P.; Potyondy, D.; Coetzee, M.J. Numerical modeling of caving using continuum and micro-mechanical models. In Proceedings of the CAMI’95 Canadian Conference on Computer Applications in the Mining Industry, Montreal, QC, Kanada, 22 October 1995; pp. 416–424. [Google Scholar]
- Mawdesley, C.A. Predicting Rock Mass Cavability in Block Caving Mines. Ph.D. Thesis, The University of Queensland, Brisbane, Australia, 2002. [Google Scholar]
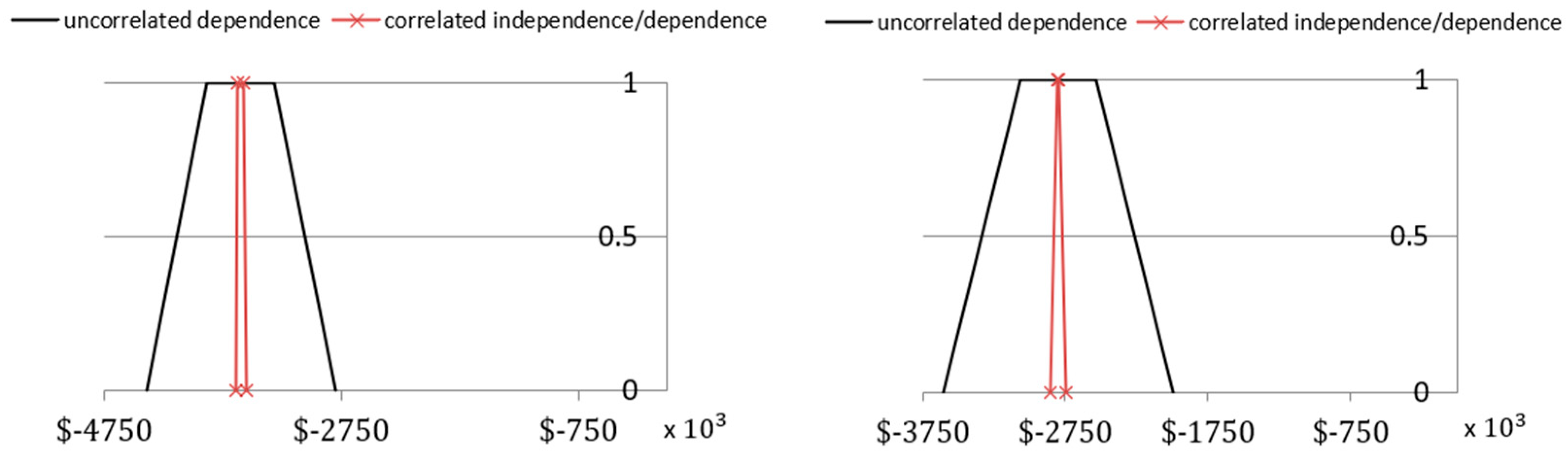
- Dimitrovski, A.; Matos, M. Fuzzy present worth analysis with correlated and uncorrelated cash flows. In Fuzzy Engineering Economics with Applications; Springer: Berlin, Germany, 2008; pp. 11–41. [Google Scholar] [CrossRef]
- RP18R-97. Available online: https://online.aacei.org/aacessa/ecssashop.show_category?p_category_id=RP&p_cust_id=&p_order_serno=&p_promo_cd=&p_price_cd=&p_session_serno=&p_trans_ty= (accessed on 16 March 2022).
- Hollmann, J.K. Improve your contingency estimates for more realistic project budgets: Reliable risk-analysis and contingency-estimation practices help to better manage costs in CPI projects of all sizes. Chem. Eng. 2014, 121, 36–44. [Google Scholar]

| Application | HF Size | Injection Rate (L/s) | Addictive | Proppant | Distances between Fractures (m) | Orientation | |
|---|---|---|---|---|---|---|---|
| Cave mining industry | About 30 m in radius | 8–20 | 5–10 | No | Some | 1.25 | Mostly vertical in Australia |
| Shale gas industry | Hundreds of meters in half-length | 135–1000 | 75–250 | Yes | Yes | About 100 | Mostly horizontal |
| HF Cost Component | Items | P10 | P50 | P90 |
|---|---|---|---|---|
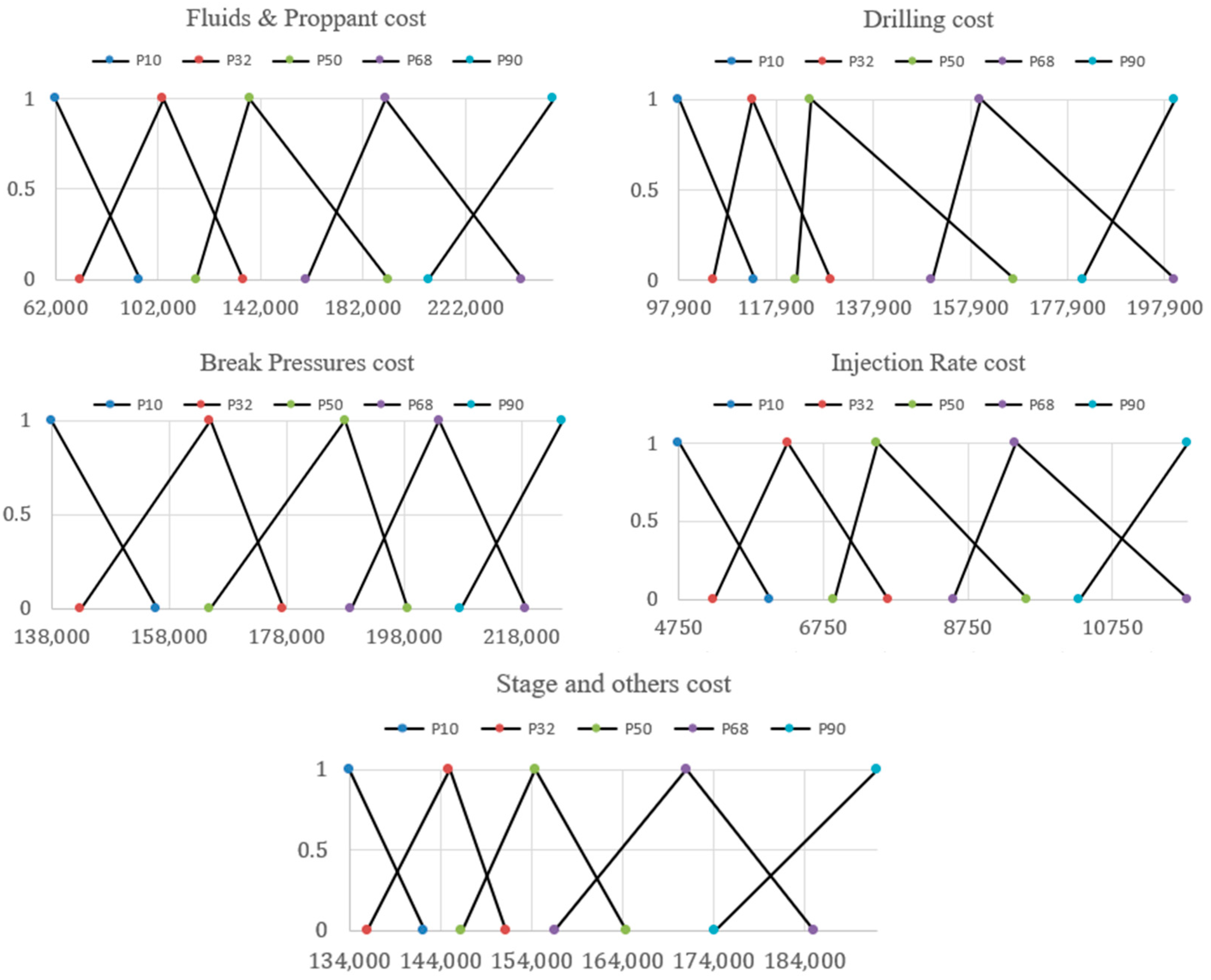
| Frack cost | Fluid cost | $31,250 | $68,750 | $125,000 |
| Proppant cost | Water and sand cost | $31,250 | $68,750 | $131,250 |
| Drilling cost | $97,500 | $125,000 | $200,000 | |
| Frack pumping cost | Stage cost | $15,000 | $16,250 | $16,875 |
| Break pressures cost | $137,500 | $187,500 | $225,000 | |
| Injection rate cost | $4750 | $7500 | $11,750 | |
| Others | $118,750 | $137,500 | $175,000 |
| Rating | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| Scenario A | |||||
| Hydraulic radius | 18.5 m | ||||
| Fragmentation | 512 | ||||
| Block height | 125 m | ||||
| Undercut direction | Fair | ||||
| Scenario B | |||||
| Hydraulic radius | 50 m | ||||
| Fragmentation | 0.2 | ||||
| Block height | 180 m | ||||
| Undercut direction | Fair | ||||
| Scenario C | |||||
| Hydraulic radius | 25 | ||||
| Fragmentation | 10 | ||||
| Block height | 225 m | ||||
| Undercut direction | Fair | ||||
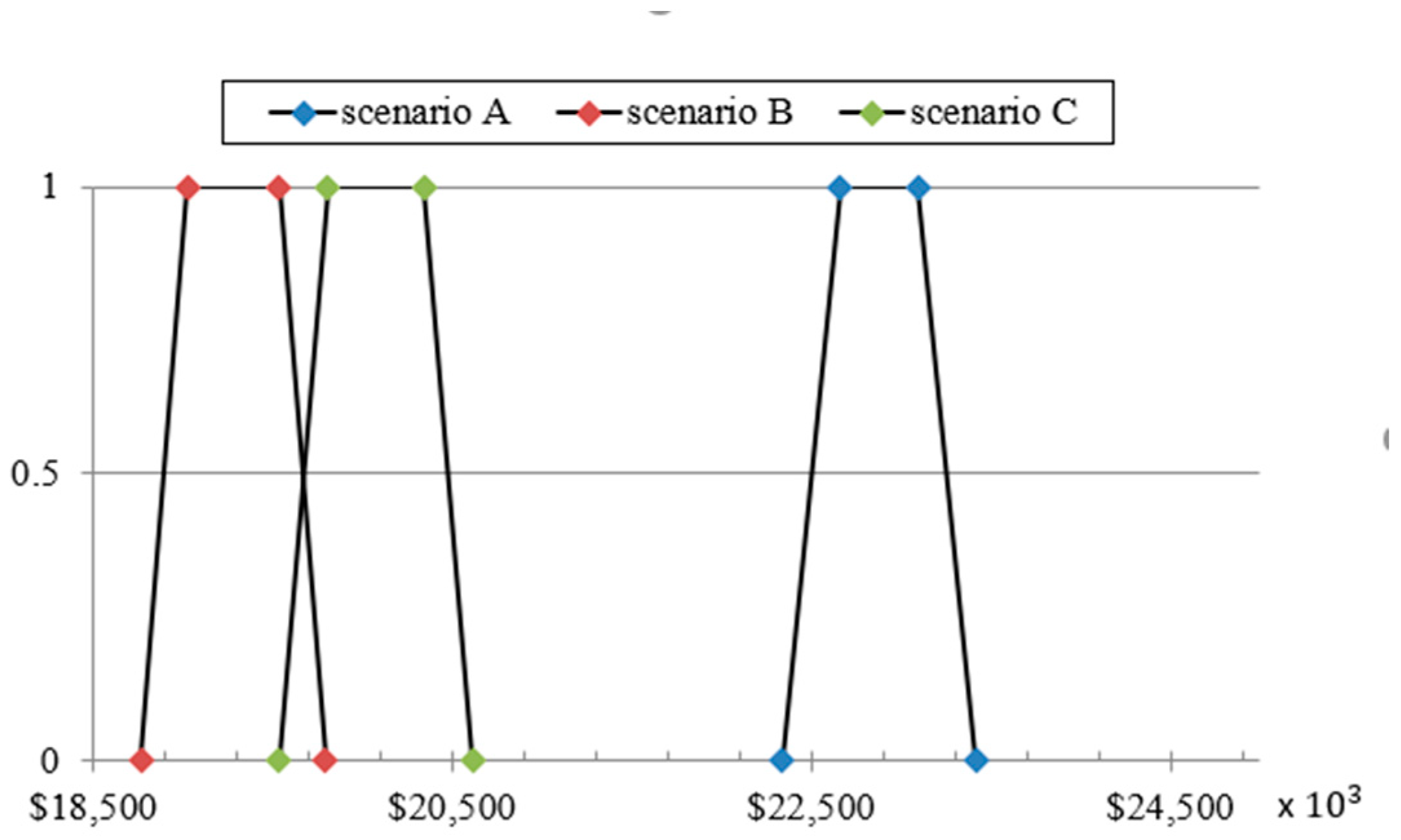
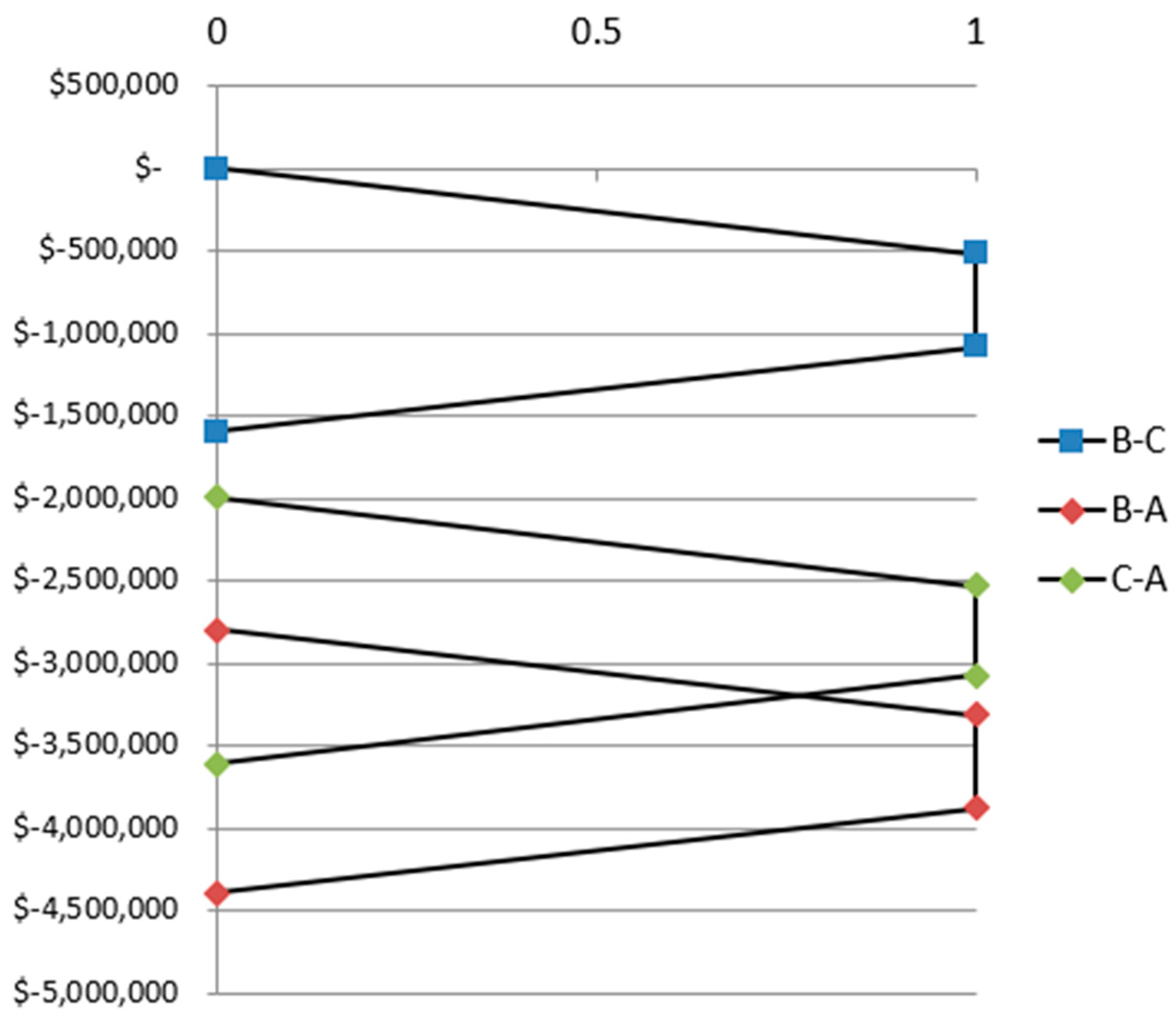
| Scenarios/Cost | Others and Stage Cost | Fluid and Proppants Costs | Drilling Costs Costs | Break Pressures Costs | Injection Rate Costs |
|---|---|---|---|---|---|
| scenario A | $4,950,000 | $5,780,000 | $4,770,000 | $5,800,000 | $280,000 |
| scenario B | $4,380,000 | $3,900,000 | $3,810,000 | $4,840,000 | $208,000 |
| scenario C | $4,460,000 | $4,290,000 | $3,870,000 | $5,160,000 | $225,000 |
| Estimate Class | Primary Characteristic | Secondary Characteristic |
|---|---|---|
| Maturity level of project definition deliverables | Expected Accuracy range | |
| Class5 | Key deliverables and target status: block flow diagram by key stakeholders | P10: −20% to −50% P90: +30% to +100% |
| Class 4 | Key deliverables and target status: process flow diagrams (PFDS) issued for design. | P10: −15% to −30% P90: +20% to +50% |
| Class 3 | Key deliverables and target status: piping and instrumentation diagrams (P& IDs) issued for design. | P10: −10% to −20% P90: 10% to +30% |
| Class 2 | Key deliverables and target status: All specifications and datasheet complete including for instrumentation. | P10: −5% to −15% P90: +5% to +20% |
| Class 1 | Key deliverables and target status: All deliverables in the maturity matrix complete. | P10: −3% to −10% P90: +3% to +15% |
| Systemic Contingency as a Percentage of the Unexpended Base Estimate | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Scope Definition | Class 3 | Class 4 | Class 5 | |||||||
| Complexity | Low | Medium | High | Low | Medium | High | Low | Medium | High | |
| Tech. | Low | 3% | 8% | 12% | 10% | 15% | 20% | 19% | 24% | 29% |
| Medium | 6% | 11% | 15% | 13% | 18% | 23% | 22% | 27% | 32% | |
| High | 15% | 20% | 25% | 22% | 27% | 32% | 32% | 47% | 42% | |
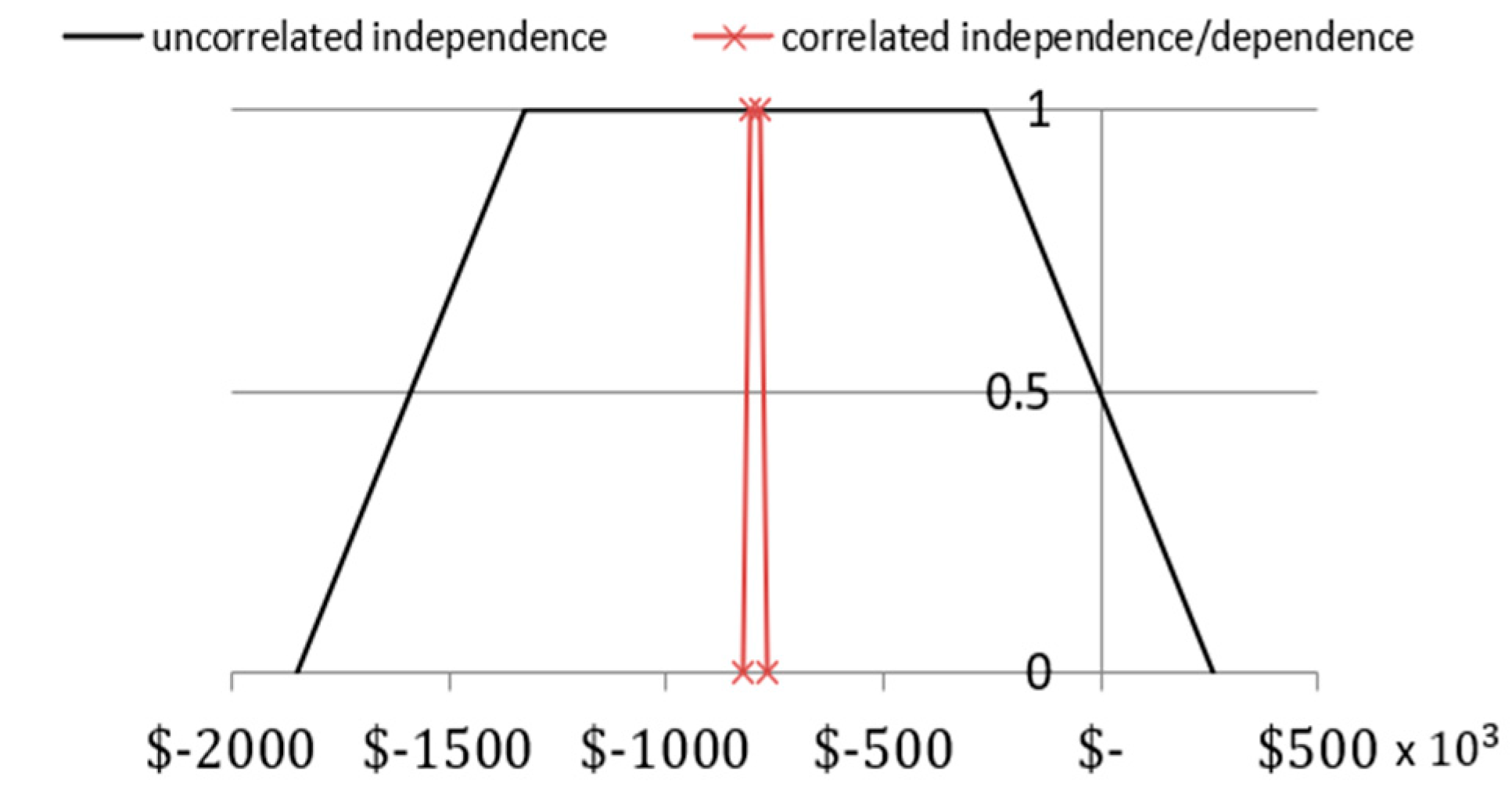
| Contingency Rate/α Cut Intervals | α = 0 | α = 1 | α = 1 | α = 0 |
|---|---|---|---|---|
| Scenario A | 3.5% | 5% | 7% | 8.5% |
| Scenario B | 9.5% | 11% | 14% | 15.5% |
| Scenario C | 8.5% | 10% | 13% | 14.5% |
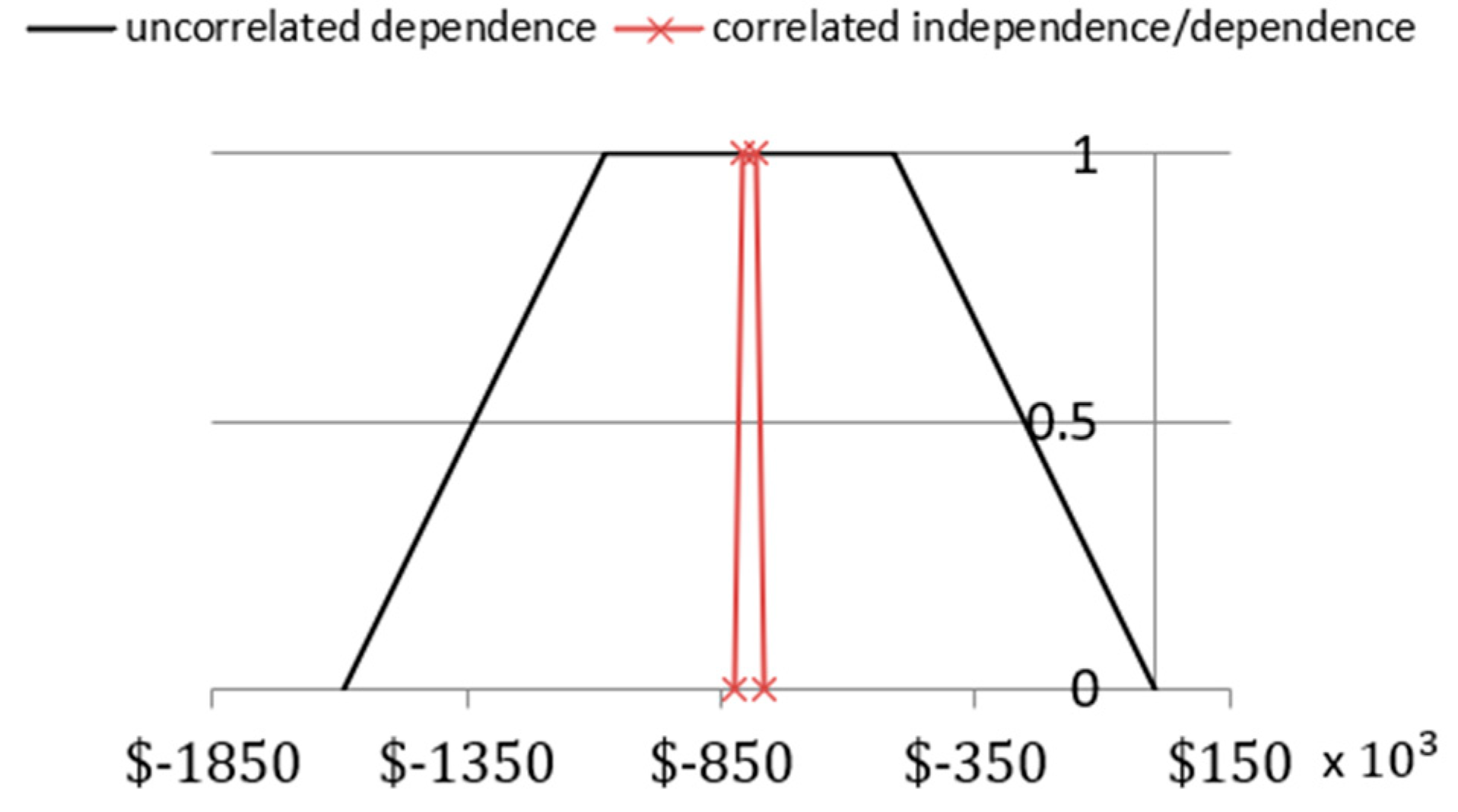
| Scenarios/Cost Estimation as per Contingency Rate | α = 0 | α = 1 | α = 1 | α = 0 |
|---|---|---|---|---|
| A | 3.5% | 5% | 7% | 8.5% |
| $22,335,300 | $22,659,000 | $23,090,600 | $23,414,300 | |
| B | 9.5% | 11% | 14% | 15.5% |
| $18,766,110 | $19,023,180 | $19,537,320 | $19,794,390 | |
| C | 8.5% | 10% | 13% | 14.5% |
| $19,535,425 | $19,805,500 | $20,345,650 | $20,615,725 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Im, H.; Jang, H.; Topal, E.; Nehring, M. Long- and Short-Term Strategies for Estimation of Hydraulic Fracturing Cost Using Fuzzy Logic. Minerals 2022, 12, 715. https://doi.org/10.3390/min12060715
Im H, Jang H, Topal E, Nehring M. Long- and Short-Term Strategies for Estimation of Hydraulic Fracturing Cost Using Fuzzy Logic. Minerals. 2022; 12(6):715. https://doi.org/10.3390/min12060715
Chicago/Turabian StyleIm, Hyunjun, Hyongdoo Jang, Erkan Topal, and Micah Nehring. 2022. "Long- and Short-Term Strategies for Estimation of Hydraulic Fracturing Cost Using Fuzzy Logic" Minerals 12, no. 6: 715. https://doi.org/10.3390/min12060715
APA StyleIm, H., Jang, H., Topal, E., & Nehring, M. (2022). Long- and Short-Term Strategies for Estimation of Hydraulic Fracturing Cost Using Fuzzy Logic. Minerals, 12(6), 715. https://doi.org/10.3390/min12060715








