Control Structure Design Using Global Sensitivity Analysis for Mineral Processes under Uncertainties
Abstract
:1. Introduction
2. Materials and Methods
2.1. Uncertainty Analysis (UA)
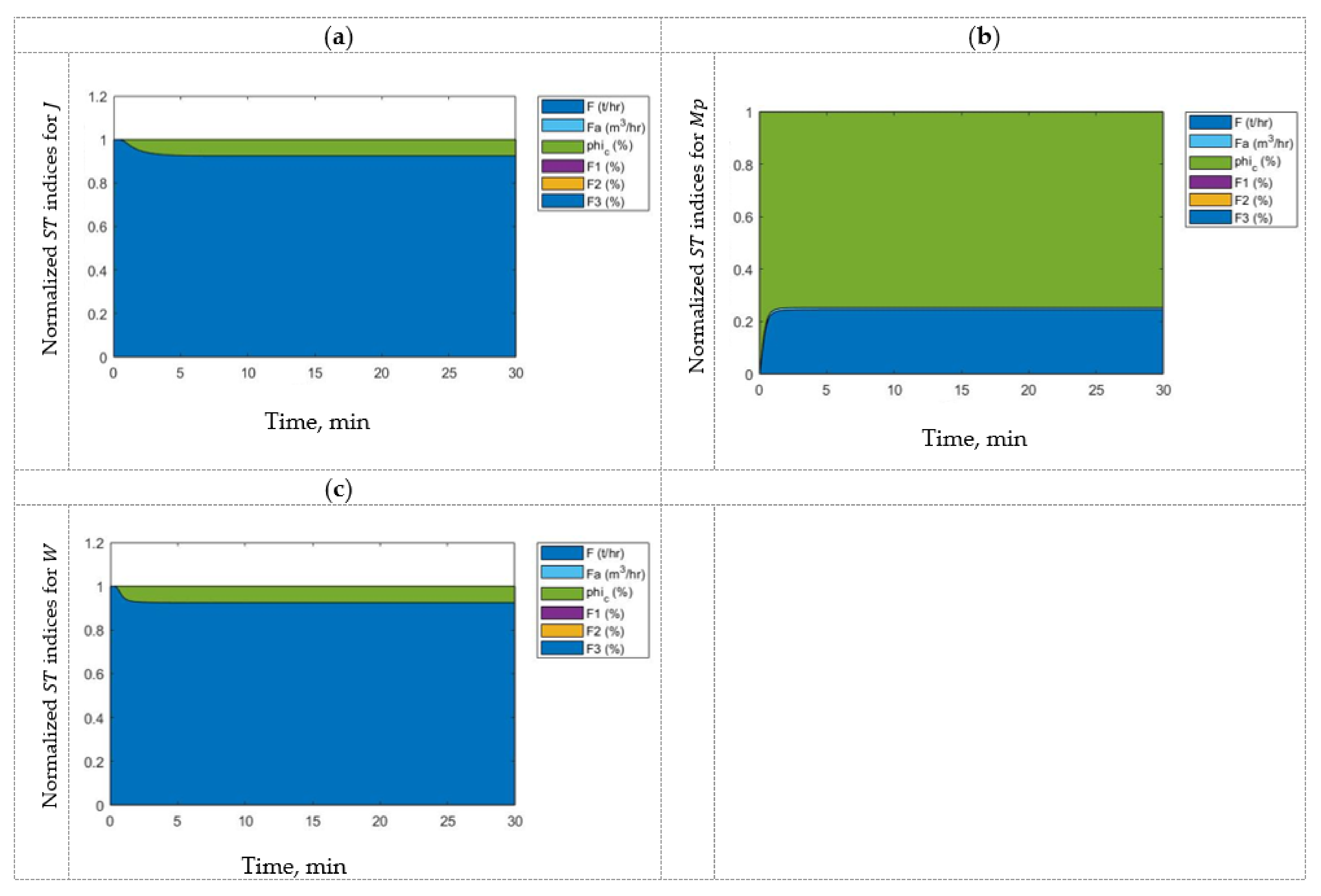
2.2. Sensitivity Analysis (SA)
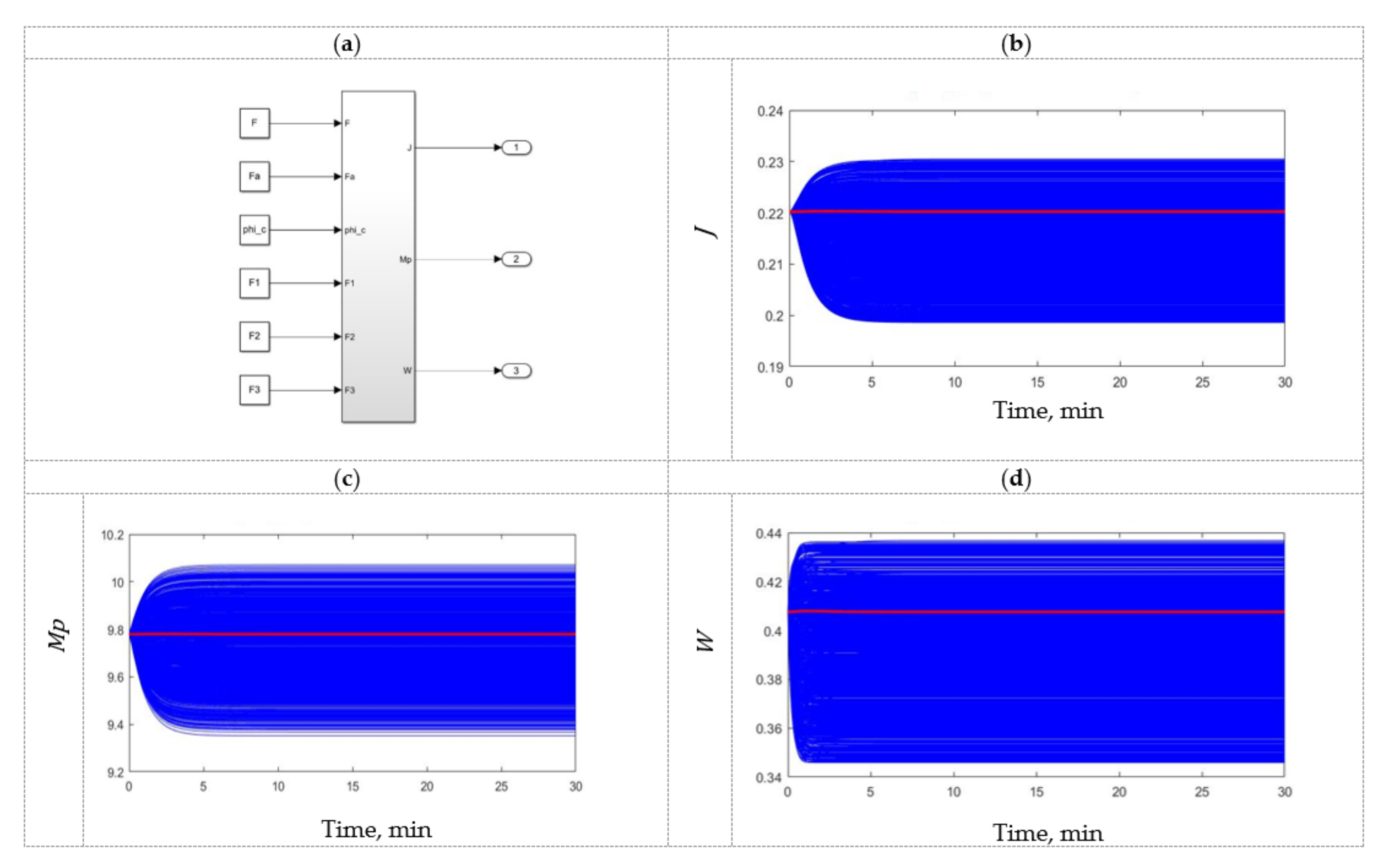
2.3. Solving the Model in MATLAB–Simulink
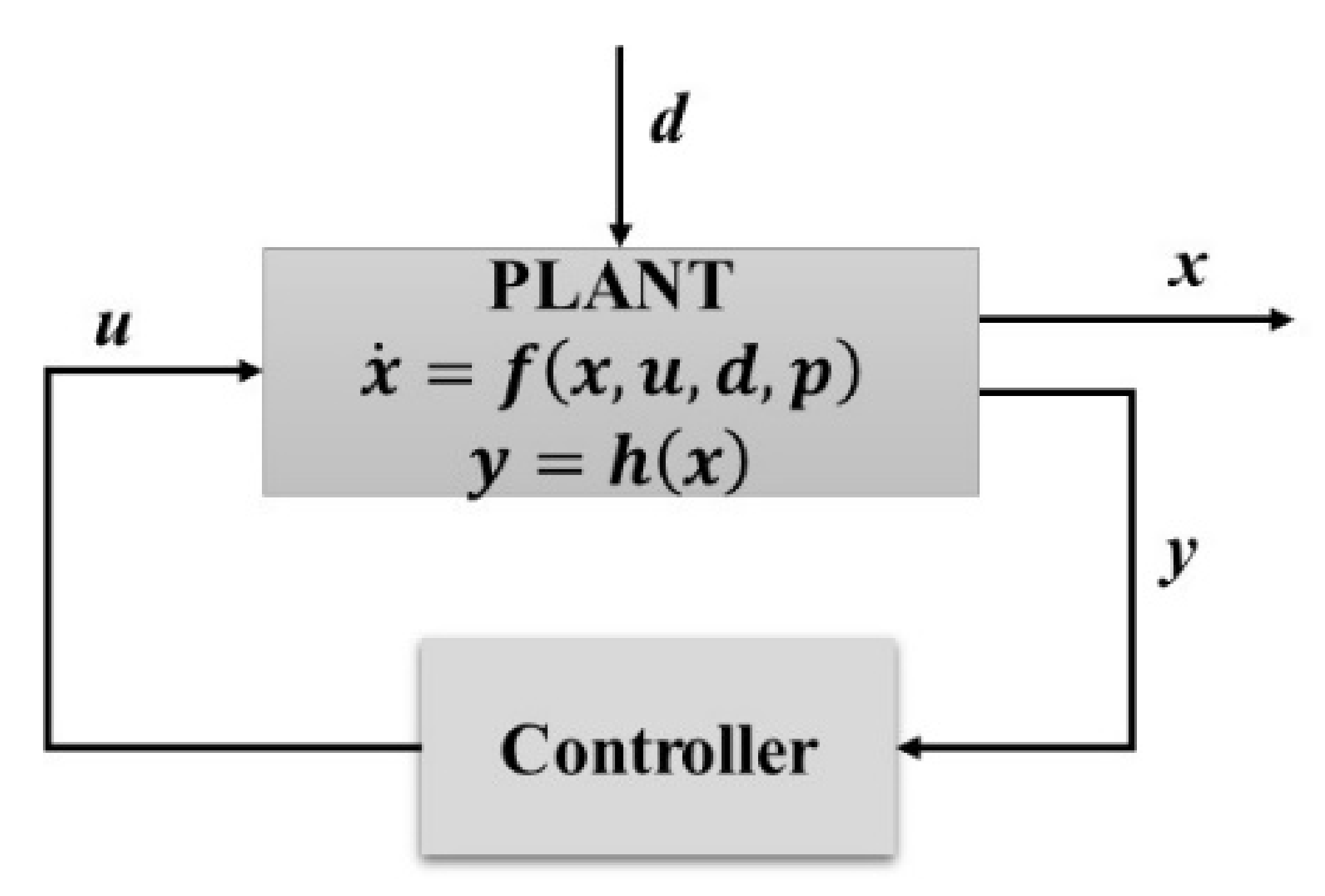
2.4. Methodology for Control Structure Design (CSD)
3. Results
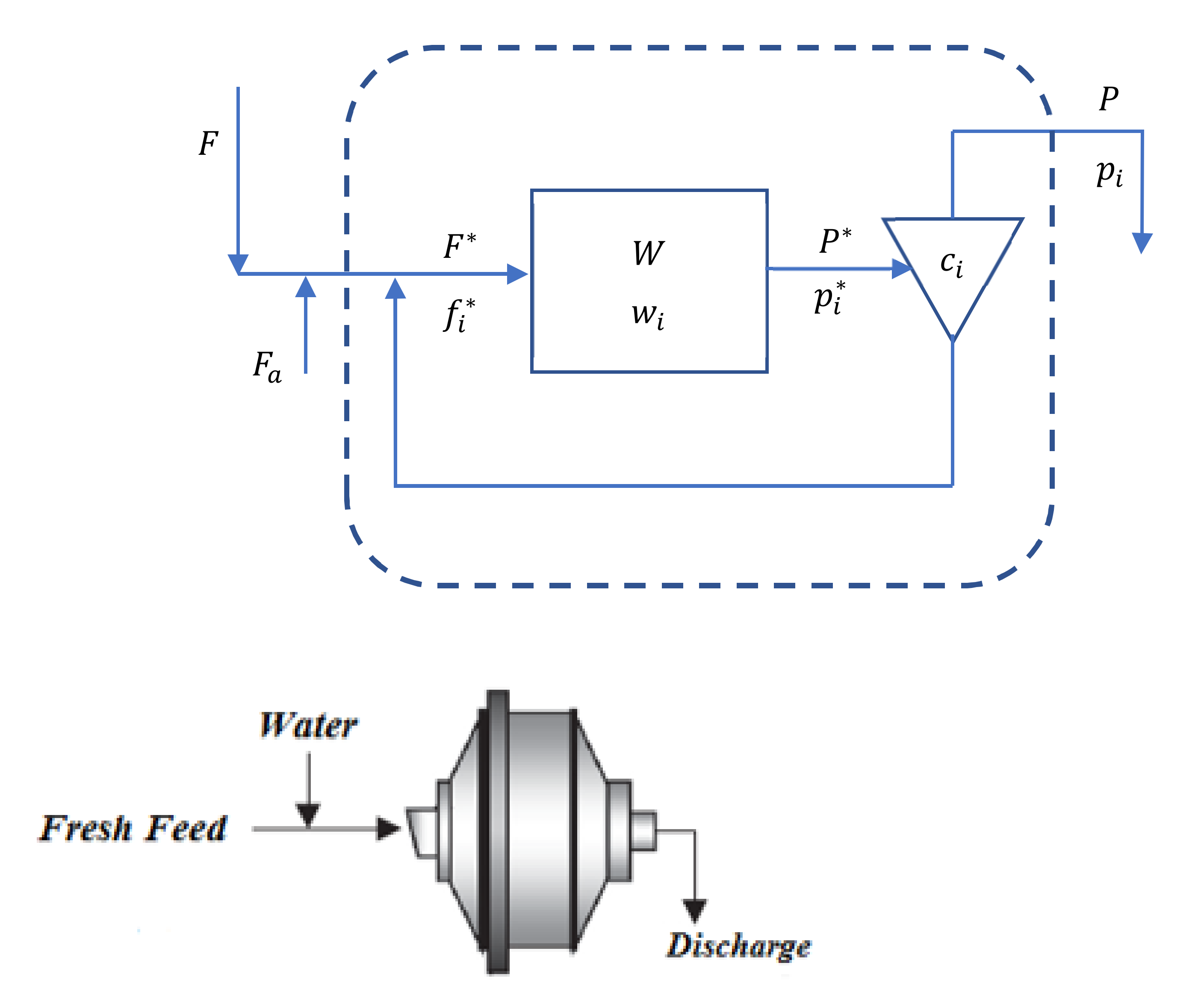
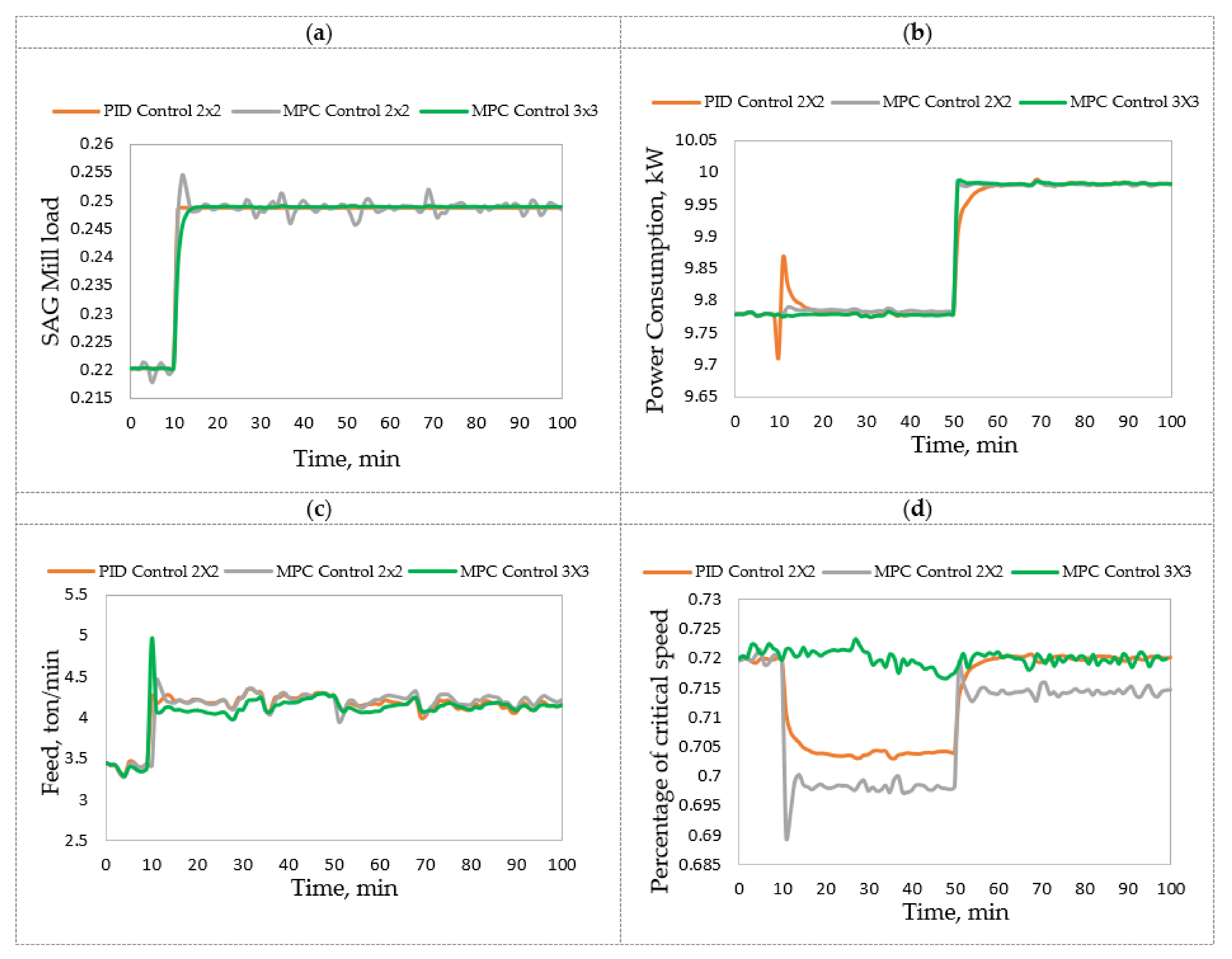
3.1. Semi-Autogenous Grinding (SAG)
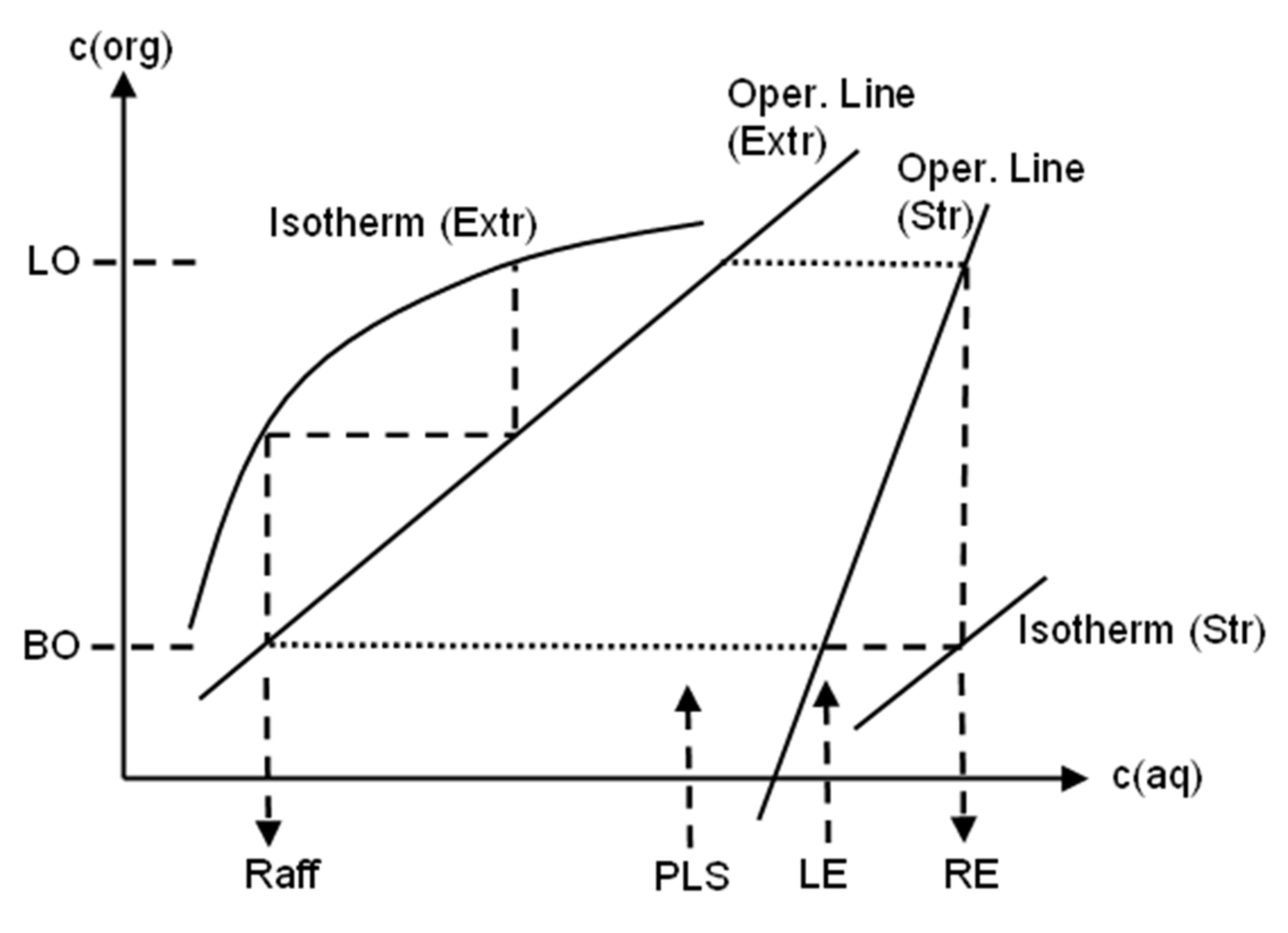
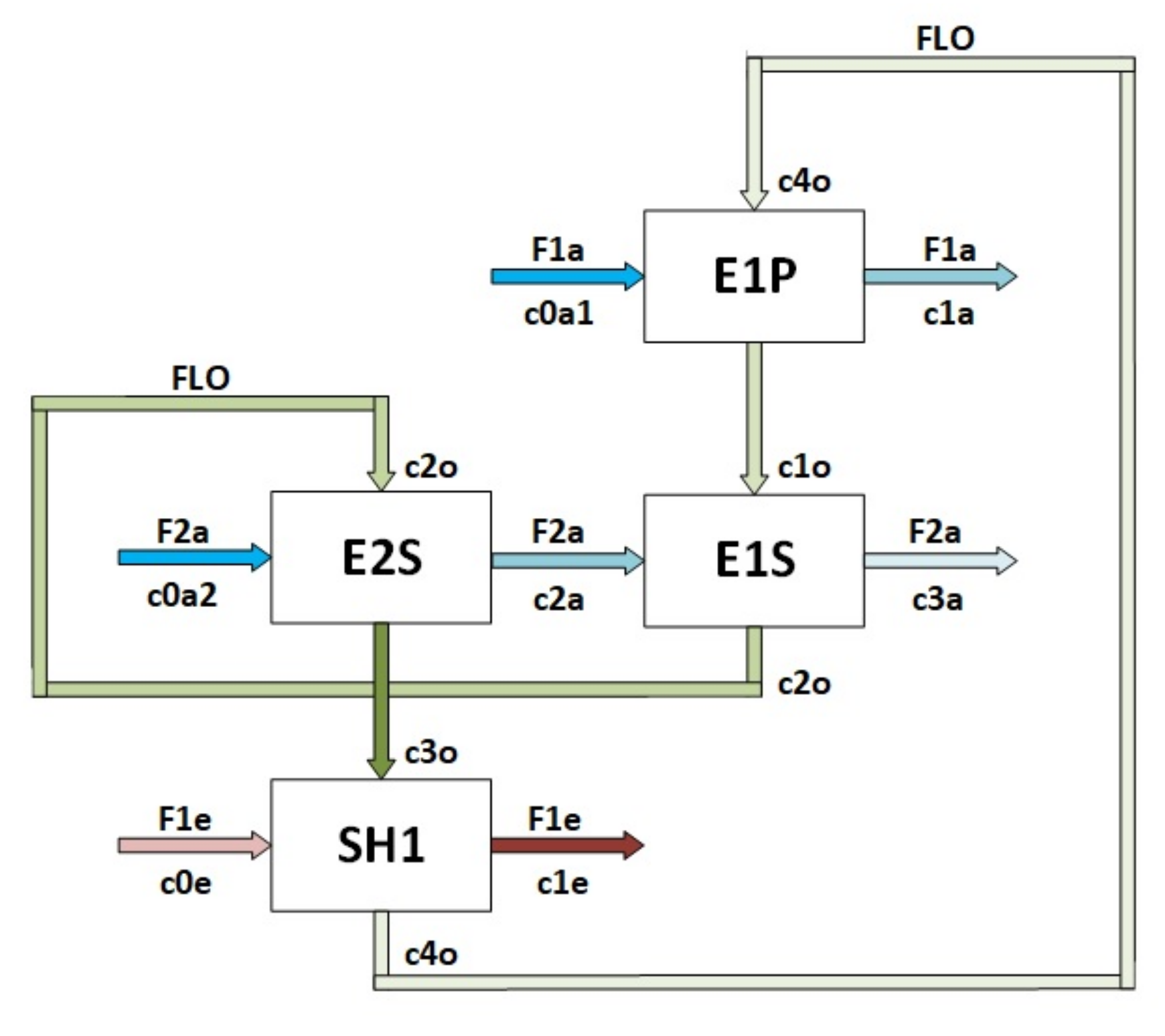
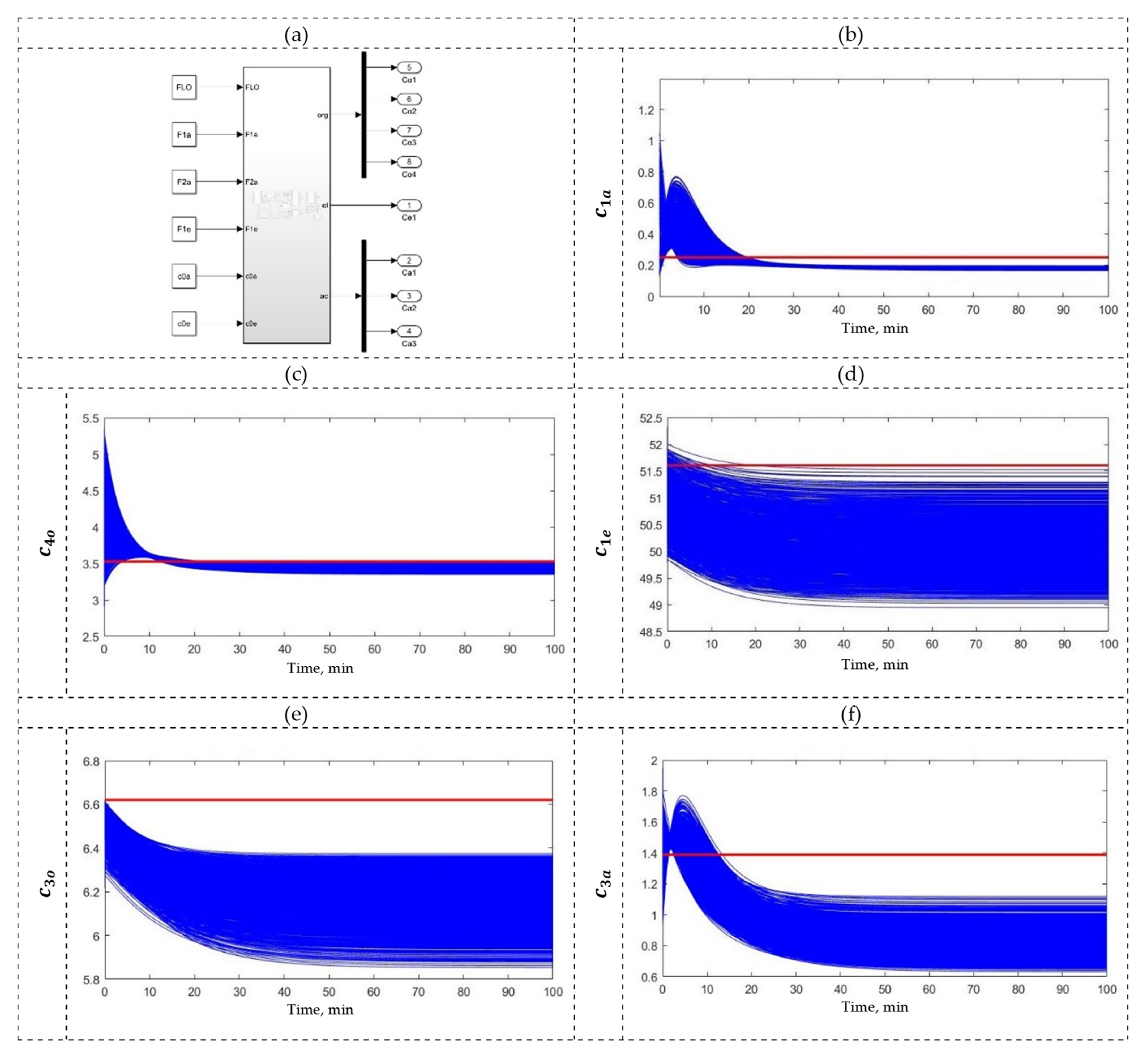
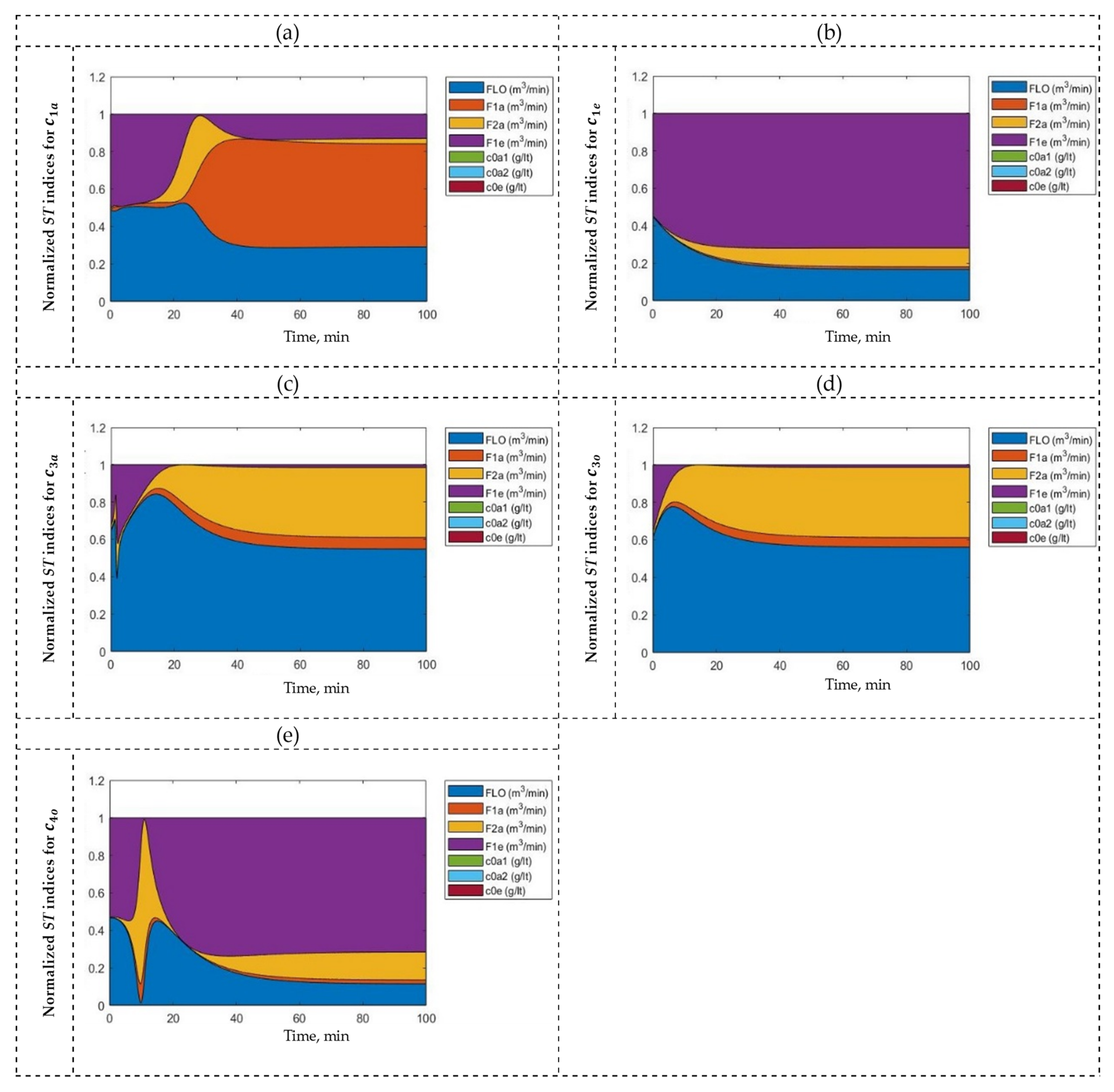
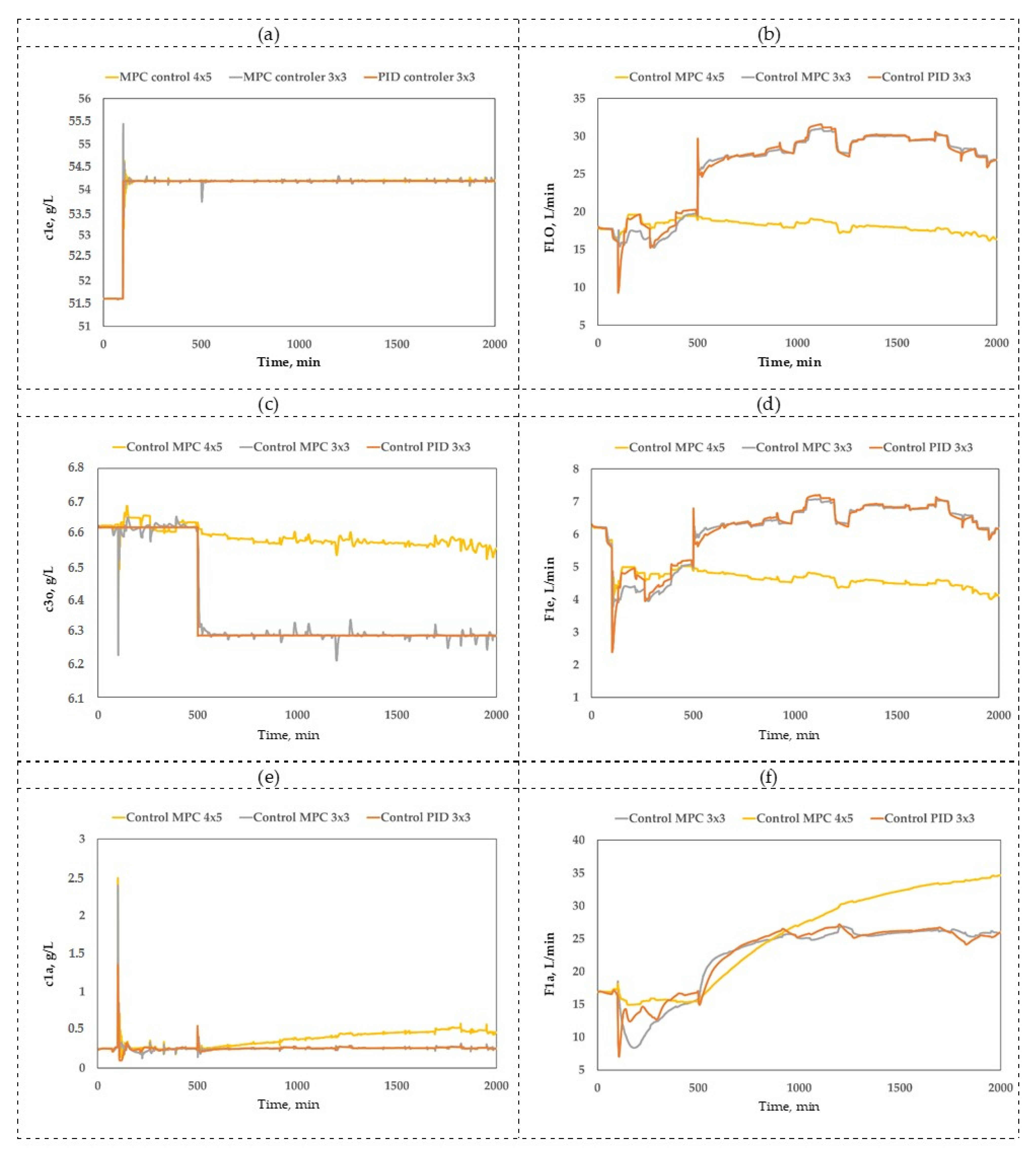
3.2. Solvent Extraction (SX) Process
- (a)
- A traditional structure (4 × 5) reported previously [24], with = 4 and = 5:
- (b)
- A reduced structure (3 × 3) obtained in step 2, with = = 3:
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| For SAG model: | |
| ore impact breakage parameter | |
| parameter of specific breakage rate model | |
| parameter of specific breakage rate model | |
| cumulative breakage distribution function | |
| values of input variables that provide desired behavior of output milling model | |
| values of input variables that provide unwanted behavior of output milling model | |
| ore impact breakage parameter | |
| breakage distribution function | |
| number of species present in fresh feed | |
| mass flow recirculated internally by grill | |
| classification efficiency of internal grid mill | |
| solid weight percentage in mill charge | |
| mill diameter | |
| comminution specific energy (kWh/t) | |
| fresh ore flux fed to mill, t/h | |
| fraction of fresh ore flux fed to mill | |
| fraction of mill filling | |
| percentage of mill volume occupied by steel balls | |
| specific breakage rate | |
| mill length | |
| parameter of classification efficiency model | |
| mill power consumption | |
| total number of input variables in model | |
| total number of simulations | |
| first-order sensitivity index for input variable | |
| total sensitivity index for input variable | |
| mill volume | |
| total number of simulations | |
| variance of model | |
| mass retained in mill | |
| water in mill charge | |
| ratio between ore mass and water mass retained inside mill | |
| weight fraction of retained mass in mill | |
| percentage of solids in discharge mill | |
| parameter of specific breakage rate model | |
| particle size of species present in fresh feed | |
| parameter of classification efficiency model | |
| parameter of classification efficiency model | |
| characteristic parameter of material | |
| parameter of specific breakage rate model | |
| parameter of specific breakage rate model | |
| fraction of fines produced in a single fracture event | |
| parameter of classification efficiency model | |
| parameter of cumulative breakage distribution function | |
| parameter of specific breakage rate model | |
| parameter of specific breakage rate model | |
| parameter of cumulative breakage distribution function | |
| percentage of critical speed | |
| parameter of classification efficiency model | |
| For SX model: | |
| flow inputs to process, pregnant leach solution (PLS) | |
| flow inputs to process, pregnant leach solutions (PLS) | |
| solution with a copper concentration | |
| poor electrolyte flow | |
Appendix A. SAG Model
Appendix B. SX Model
References
- Liu, G.; Wang, Z.; Mei, C.; Ding, Y. A Review of Decoupling Control Based on Multiple Models. In Proceedings of the 2012 24th Chinese Control and Decision Conference (CCDC), Taiyuan, China, 23–25 May 2012; pp. 1077–1081. [Google Scholar]
- Xiong, Q.; Cai, W.J.; He, M.J. A Practical Loop Pairing Criterion for Multivariable Processes. J. Process Control 2005, 15, 741–747. [Google Scholar] [CrossRef]
- Vaes, D.; Swevers, J.; Sas, P. Optimal Static Decoupling to Simplify and Improve Multivariable Control Design. Mediterr. J. Meas. Control 2006, 2, 48–62. [Google Scholar]
- Liu, L.; Tian, S.; Xue, D.; Zhang, T.; Chen, Y.Q.; Zhang, S. A Review of Industrial MIMO Decoupling Control. Int. J. Control Autom. Syst. 2019, 17, 1246–1254. [Google Scholar] [CrossRef]
- Hanuma, R.; Ashok, D.; Anjaneyulu, K. Control Configuration Selection and Controller Design for Multivariable Processes Using Normalized Gain. Int. J. Electr. Comput. Eng. 2014, 8, 1–5. [Google Scholar] [CrossRef]
- Castaño Arranz, M.; Birk, W.; Nikolakopoulos, G. A Survey on Control Configuration Selection and New Challenges in Relation to Wireless Sensor and Actuator Networks. In Proceedings of the IFAC-PapersOnLine, Touluse, France, 10–14 July 2017; Volume 50, pp. 8810–8825. [Google Scholar]
- Jain, A.; Babu, B.V. Relative Response Array: A New Tool for Control Configuration Selection. Int. J. Chem. Eng. Appl. 2015, 6, 356–362. [Google Scholar] [CrossRef] [Green Version]
- Niederlinski, A. A Heuristic Approach to the Design of Linear Multivariable Interacting Control Systems. Automatica 1971, 7, 691–701. [Google Scholar] [CrossRef]
- Zhu, Z.X. Variable Pairing Selection Based on Individual and Overall Interaction Measures. Ind. Eng. Chem. Res. 1996, 35, 4091–4099. [Google Scholar] [CrossRef]
- Kinnaert, M. Interaction Measures and Pairing of Controlled and Manipulated Variables for Multiple-Input Multiple-Output Systems: A Survey. Journal A 1995, 16, 15–23. [Google Scholar]
- Mc Avoy, T.; Arkun, Y.; Chen, R.; Robinson, D.; Schnelle, P.D. A New Approach to Defining a Dynamic Relative Gain. Control Eng. Pract. 2003, 11, 907–914. [Google Scholar] [CrossRef]
- Salgado, M.E.; Conley, A. MIMO Interaction Measure and Controller Structure Selection. Int. J. Control 2004, 77, 367–383. [Google Scholar] [CrossRef]
- Wittenmark, B.; Salgado, M.E. Hankel-Norm Based Interaction Measure for Input-Output Pairing. In Proceedings of the IFAC Proceedings Volumes (IFAC-PapersOnline), Barcelona, Spain, 21–26 July 2002; Volume 15, pp. 429–434. [Google Scholar]
- Hanzon, B. The Area Enclosed by the (Oriented) Nyquist Diagram and the Hilbert-Schmidt-Hankel Norm of a Linear System. IEEE Trans. Autom. Control 1992, 37, 835–839. [Google Scholar] [CrossRef]
- Birk, W.; Medvedev, A. A Note on Gramian-Based Interaction Measures. In Proceedings of the European Control Conference (ECC), Cambridge, UK, 1–4 September 2003; pp. 2625–2630. [Google Scholar]
- Halvarsson, B.; Carlsson, B.; Wik, T. A New Input/Output Pairing Strategy Based on Linear Quadratic Gaussian Control. In Proceedings of the 2009 IEEE International Conference on Control and Automation (ICCA), Christchurch, New Zealand, 9–11 December 2009; pp. 978–982. [Google Scholar]
- Jain, A.; Babu, B.V. Sensitivity of Relative Gain Array for Processes with Uncertain Gains and Residence Times. In Proceedings of the IFAC-PapersOnLine, Tiruchirappalli, India, 1–5 February 2016; Volume 49, pp. 486–491. [Google Scholar]
- Coetzee, L.C.; Craig, I.K.; Kerrigan, E.C. Robust Nonlinear Model Predictive Control of a Run-of-Mine Ore Milling Circuit. IEEE Trans. Control Syst. Technol. 2010, 18, 1–86. [Google Scholar] [CrossRef] [Green Version]
- Craig, I.K.; MacLeod, I.M. Specification Framework for Robust Control of a Run-of-Mine Ore Milling Circuit. Control Eng. Pract. 1995, 3, 621–630. [Google Scholar] [CrossRef]
- Olivier, L.E.; Craig, I.K. Model-Plant Mismatch Detection and Model Update for a Run-of-Mine Ore Milling Circuit under Model Predictive Control. In Proceedings of the Journal of Process Control, Cape Town, South Africa, 24–29 August 2014; Volume 23, pp. 100–107. [Google Scholar]
- Olivier, L.E.; Huang, B.; Craig, I.K. Dual Particle Filters for State and Parameter Estimation with Application to a Run-of-Mine Ore Mill. J. Process Control 2012, 22, 710–717. [Google Scholar] [CrossRef] [Green Version]
- Karelovic, P.; Putz, E.; Cipriano, A. Dynamic Hybrid Modeling and Simulation of Grinding-Flotation Circuits for the Development of Control Strategies. Miner. Eng. 2016, 93, 65–79. [Google Scholar] [CrossRef]
- Bauer, M.; Brooks, K.; Burchell, J.; Coetzee, L.; le Roux, D.; McCoy, J.; Miskin, J.; Winter, D. The Use of a Semi-Rigorous SAG Mill Model for a Hands-on Workshop. In Proceedings of the IFAC-PapersOnLine, Berlin, Germany, 11–17 July 2020; Volume 53. [Google Scholar]
- Komulainen, T.; Doyle III, F.J.; Rantala, A.; Jämsä-Jounela, S.-L. Control of an Industrial Copper Solvent Extraction Process. J. Process Control 2009, 19, 2–15. [Google Scholar] [CrossRef] [Green Version]
- Maldonado, M.; Desbiens, A.; Villar, D.R. Decentralized Control of a Pilot Flotation Column: A 3×3 System. Can. Metall. Q. 2008, 47, 377–385. [Google Scholar] [CrossRef]
- Guo, N.; Zheng, H.; Zou, T.; Jia, Y. Integration of Numerical Simulation and Control Scheme for Energy Conservation of Aluminum Melting Furnaces. IEEE Access 2019, 7, 114659–114669. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis. The Primer; John Wiley & Sons, Ltd.: Chichester, UK, 2007; ISBN 9780470725184. [Google Scholar]
- Saltelli, A.; Annoni, P.; Azzini, I.; Campolongo, F.; Ratto, M.; Tarantola, S. Variance Based Sensitivity Analysis of Model Output. Design and Estimator for the Total Sensitivity Index. Comput. Phys. Commun. 2010, 181, 259–270. [Google Scholar] [CrossRef]
- Homma, T.; Saltelli, A. Importance Measures in Global Sensitivity Analysis of Nonlinear Models. Reliab. Eng. Syst. Saf. 1996, 52, 1–17. [Google Scholar] [CrossRef]
- Lucay, F.A.; Gálvez, E.D.; Salez-Cruz, M.; Cisternas, L.A. Improving Milling Operation Using Uncertainty and Global Sensitivity Analyses. Miner. Eng. 2019, 131, 249–261. [Google Scholar] [CrossRef]
- Mellado, M.; Cisternas, L.; Lucay, F.; Gálvez, E.; Sepúlveda, F. A Posteriori Analysis of Analytical Models for Heap Leaching Using Uncertainty and Global Sensitivity Analyses. Minerals 2018, 8, 44. [Google Scholar] [CrossRef] [Green Version]
- Helton, J.C.; Burmaster, D.E. Treatment of Aleatory and Epistemic Uncertainty in Performance Assesments for Complex Systems. Reliab. Eng. Syst. Saf. 1996, 54, 91–94. [Google Scholar] [CrossRef]
- Zio, E.; Pedroni, N. Methods for Representing Uncertainty—A Literature Review. Found. Ind. Saf. Cult. (FonCSI) 2013, 5, 77–88. [Google Scholar]
- Saltelli, A. Sensitivity Analysis for Importance Assessment. Risk Anal. 2002, 22, 579–590. [Google Scholar] [CrossRef]
- Reuter, U.; Liebscher, M. Global Sensitivity Analysis in View of Nonlinear Structural Behavior. LS-Dyna Users Conf. 2008, 56, 903–915. [Google Scholar]
- Lilburne, L.; Tarantola, S. Sensitivity Analysis of Spatial Models. Int. J. Geogr. Inf. Sci. 2009, 23, 151–168. [Google Scholar] [CrossRef] [Green Version]
- Sepúlveda, F.D.; Lucay, F.; González, J.F.; Cisternas, L.A.; Gálvez, E.D. A Methodology for the Conceptual Design of Flotation Circuits by Combining Group Contribution, Local/Global Sensitivity Analysis, and Reverse Simulation. Int. J. Miner. Process. 2017, 164, 56–66. [Google Scholar] [CrossRef]
- Lucay, F.A.; Cisternas, L.A.; Gálvez, E.D. An LS-SVM Classifier Based Methodology for Avoiding Unwanted Responses in Processes under Uncertainties. Comput. Chem. Eng. 2020, 138, 106860. [Google Scholar] [CrossRef]
- Calisaya-Azpilcueta, D.; Herrera-Leon, S.; Lucay, F.A.; Cisternas, L.A. Assessment of the Supply Chain under Uncertainty: The Case of Lithium. Minerals 2020, 10, 604. [Google Scholar] [CrossRef]
- Lucay, F.A.; Lopez-Arenas, T.; Sales-Cruz, M.; Gálvez, E.D.; Cisternas, L.A. Performance Profiles for Benchmarking of Global Sensitivity Analysis Algorithms. Rev. Mex. Ing. Quim. 2020, 19, 423–444. [Google Scholar] [CrossRef] [Green Version]
- Saltelli, A.; Aleksankina, K.; Becker, W.; Fennell, P.; Ferretti, F.; Holst, N.; Li, S.; Wu, Q. Why so Many Published Sensitivity Analyses Are False: A Systematic Review of Sensitivity Analysis Practices. Environ. Model. Softw. 2019, 114, 29–39. [Google Scholar] [CrossRef]
- Velez, C. Global Sensitivity and Uncertainty Analysis (GSUA). Available online: https://www.mathworks.com/matlabcentral/fileexchange/47758-global-sensitivity-and-uncertainty-analysis-gsua (accessed on 5 May 2022).
- Pianosi, F.; Beven, K.; Freer, J.; Hall, J.W.; Rougier, J.; Stephenson, D.B.; Wagener, T. Sensitivity Analysis of Environmental Models: A Systematic Review with Practical Workflow. Environ. Model. Softw. 2016, 79, 214–232. [Google Scholar] [CrossRef]
- Austin, L.G.; Barahona, C.A.; Weymont, N.P.; Suryanarayanan, K. An Improved Simulation Model for Semi-Autogenous Grinding. Powder Technol. 1986, 47, 265–283. [Google Scholar] [CrossRef]
- Austin, L.G.; Menacho, J.M.; Pearcy, F. A General Model for Semi-Autogenous and Autogenous Milling. In Proceedings of the Twentieth International Symposium on the Application of Computers and Mathematics in the Mineral Industries APCOM 87, Johannesburg, South Africa, 19–23 October 1987; pp. 107–126. [Google Scholar]
- Barani, K.; Balochi, H. First-Order and Second-Order Breakage Rate of Coarse Particles in Ball Mill Grinding. Physicochem. Probl. Miner. Process. 2016, 52, 268–278. [Google Scholar] [CrossRef]
- Fuerstenau, D.W.; De, A.; Kapur, P.C. Linear and Nonlinear Particle Breakage Processes in Comminution Systems. Int. J. Miner. Process. 2004, 74, S317–S327. [Google Scholar] [CrossRef]
- Magne, L.; Améstica, R.; Barría, J.; Menacho, J. Modelización Dinámica de Molienda Semiautógena Basada En Un Modelo Fenomenológico Simplificado. Rev. Metal. 1995, 31, 97–105. [Google Scholar] [CrossRef]
- Magne, L.; Barría, J.; Améstica, R.; Menacho, J. Evaluación de Variables de Operación En Molienda Semiautógena. In Proceedings of the Segundo Congreso en Metalurgia e Ingeniería de Materiales, IBEROMET II, Ciudad de Mexico, Mexico, 8–14 November 1992; Available online: https://www.revistas.usach.cl/ojs/index.php/remetallica/article/view/1701/1581 (accessed on 5 May 2022).
- Tripathy, S.K.; Murthy, Y.R.; Singh, V.; Srinivasulu, A.; Ranjan, A.; Satija, P.K. Performance Optimization of an Industrial Ball Mill for Chromite Processing. J. S. Afr. Inst. Min. Met. 2017, 117, 75–81. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y. The Fractal Evolution of Particle Fragmentation under Different Fracture Energy. Powder Technol. 2018, 323, 337–345. [Google Scholar] [CrossRef]
- Helton, J.C.; Oberkampf, W.L. Alternative Representations of Epistemic Uncertainty. Engineering and System Safety. Reliab. Eng. Syst. Saf. 2004, 85, 1–10. Available online: https://www.sciencedirect.com/science/article/abs/pii/S0951832004000481?via%3Dihub (accessed on 5 May 2022). [CrossRef]
- Salazar, J.L.; Valdés-González, H.; Vyhmesiter, E.; Cubillos, F. Model Predictive Control of Semiautogenous Mills (Sag). Miner. Eng. 2014, 64, 92–96. [Google Scholar] [CrossRef]
- César, G.Q.; Daniel, S.H. Multivariable Model Predictive Control of a Simulated SAG Plant. IFAC Proc. Vol. 2009, 42, 37–42. [Google Scholar] [CrossRef]
- Kämpjärvi, P.; Jämsä-Jounela, S.L. Level Control Strategies for Flotation Cells. Miner. Eng. 2003, 16, 1061–1068. [Google Scholar] [CrossRef] [Green Version]
- Komulainen, T.; Pekkala, P.; Rantala, A.; Jämsä-Jounela, S.L. Dynamic Modelling of an Industrial Copper Solvent Extraction Process. Hydrometallurgy 2006, 81, 52–61. [Google Scholar] [CrossRef] [Green Version]



| Control | Controlled Variables | Manipulated Variables | |||
|---|---|---|---|---|---|
| IAE | |||||
| High performance | PID 2 × 2 | MPC 3 × 3 | PID 2 × 2 | PID 2 × 2 | |
| 0.001 | 0.111 | 6.437 | 0.793 | ||
| Good performance | MPC 3 × 3 | MPC 2 × 2 | MPC 3 × 3 | MPC 3 × 3 | |
| 0.020 | 0.299 | 6.081 | 0.240 | ||
| Sufficient performance | MPC 2 × 2 | PID 2 × 2 | MPC 2 × 2 | MPC 2 × 2 | |
| 0.075 | 0.630 | 9.594 | 0.995 | ||
| Reference | Open-loop | ||||
| 0.255 | 11.536 | ||||
| Control | Controlled Variables | Manipulated Variables | |||||
|---|---|---|---|---|---|---|---|
| High performance | PID 3 × 3 | PID 3 × 3 | PID 3 × 3 | MPC 3 × 3 | MPC 3 × 3 | MPC 3 × 3 | |
| 0.008 | 0.072 | 0.001 | 2.300 | 9.088 | 9.365 | ||
| Good performance | MPC 3 × 3 | MPC 3 × 3 | MPC 3 × 3 | PID 3 × 3 | PID 3 × 3 | PID 3 × 3 | |
| 0.096 | 0.090 | 0.060 | 2.545 | 10.230 | 10.660 | ||
| Sufficient performance | MPC 4 × 5 | MPC 4 × 5 | MPC 4 × 5 | MPC 4 × 5 | MPC 4 × 5 | MPC 4 × 5 | |
| 0.112 | 2.234 | 2.636 | 21.598 | 85.689 | 110.112 | ||
| Reference | Open-loop | ||||||
| 2.180 | 0.099 | 0.605 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mamani-Quiñonez, O.; Cisternas, L.A.; Lopez-Arenas, T.; Lucay, F.A. Control Structure Design Using Global Sensitivity Analysis for Mineral Processes under Uncertainties. Minerals 2022, 12, 736. https://doi.org/10.3390/min12060736
Mamani-Quiñonez O, Cisternas LA, Lopez-Arenas T, Lucay FA. Control Structure Design Using Global Sensitivity Analysis for Mineral Processes under Uncertainties. Minerals. 2022; 12(6):736. https://doi.org/10.3390/min12060736
Chicago/Turabian StyleMamani-Quiñonez, Oscar, Luis A. Cisternas, Teresa Lopez-Arenas, and Freddy A. Lucay. 2022. "Control Structure Design Using Global Sensitivity Analysis for Mineral Processes under Uncertainties" Minerals 12, no. 6: 736. https://doi.org/10.3390/min12060736







