The Numerical Simulation and Characterization of Complex Fracture Network Propagation in Multistage Fracturing with Fractal Theory
Abstract
:1. Introduction
2. Description of Natural Joints with Fractal Theory
3. The Fracture Propagation Model of Fracture Network Expansion in Fractured Reservoirs
3.1. The Fluid–Structure Interaction and Global Cohesive Zone Model
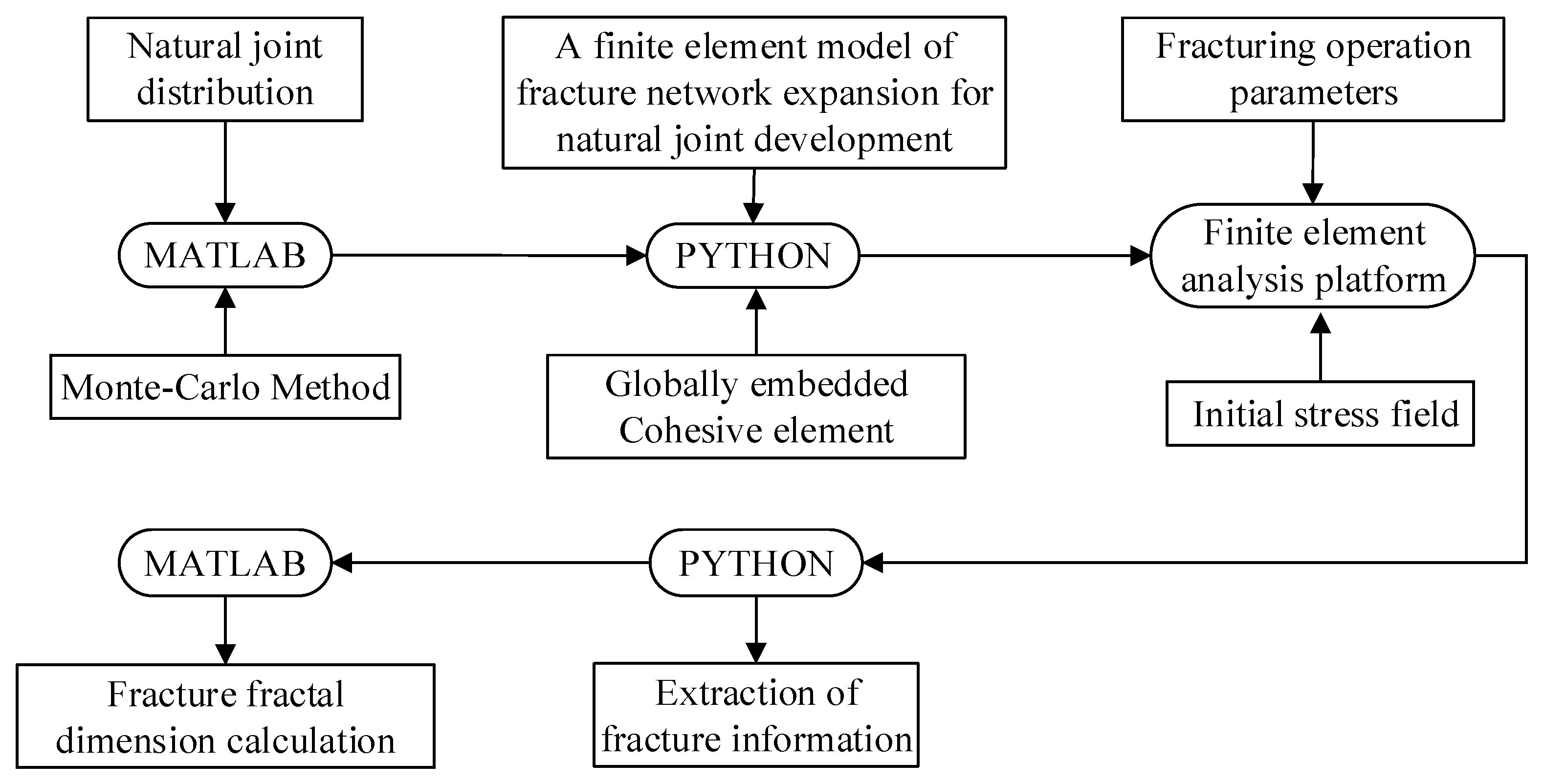
3.2. Model Construction
3.3. Characteristic Analysis of Rock Mechanics Parameters
4. Numerical Simulation Results
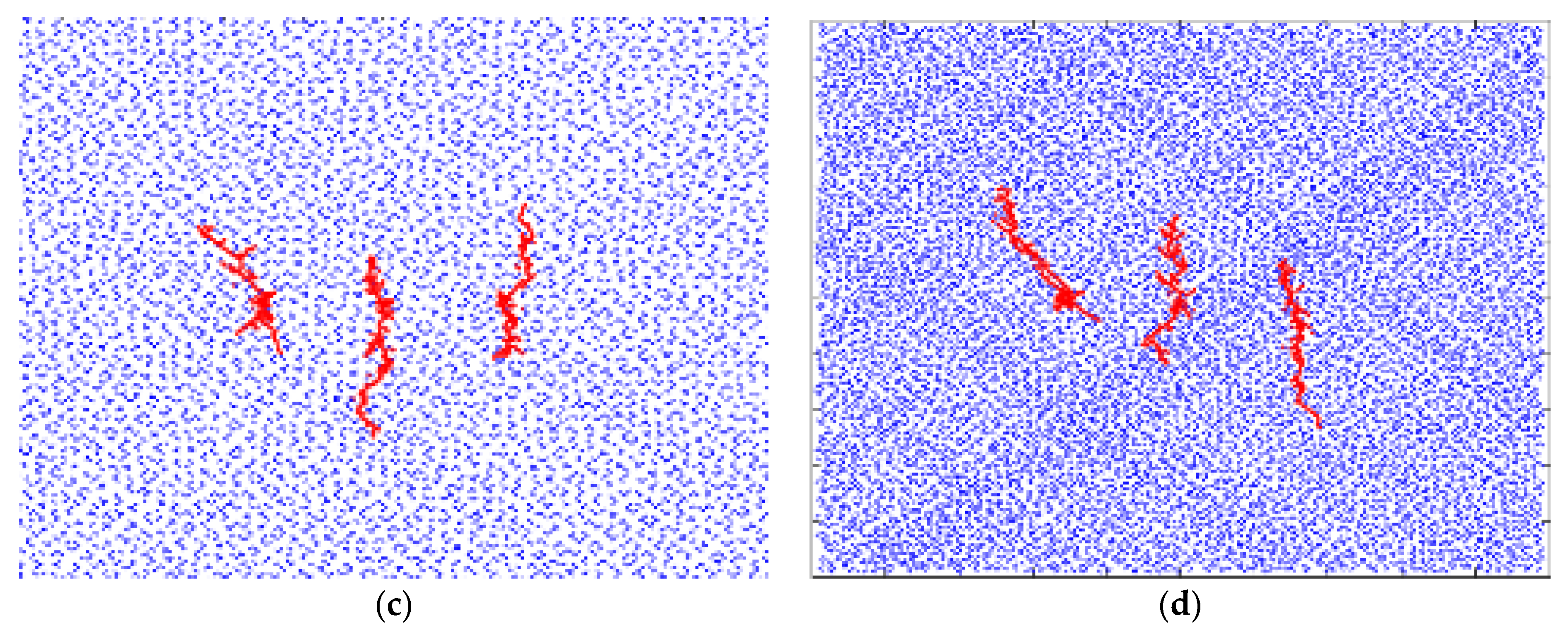
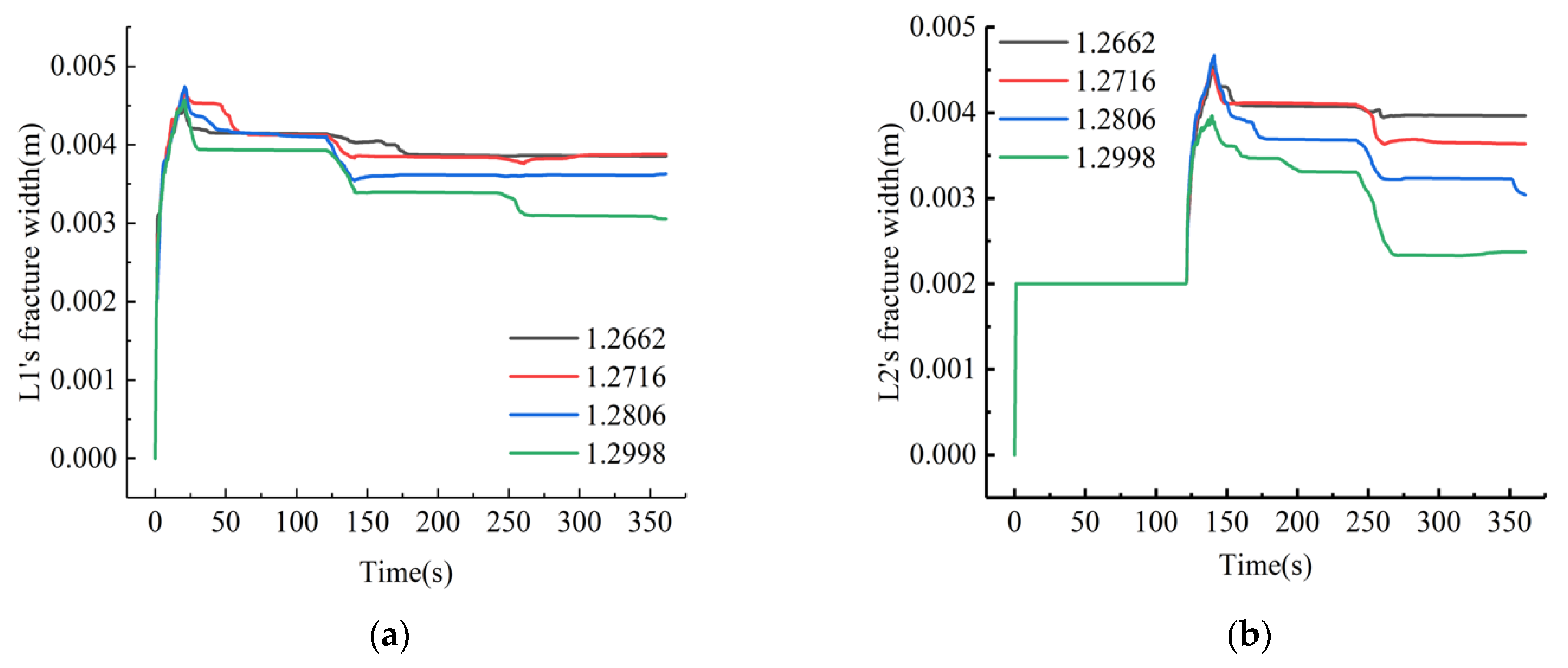
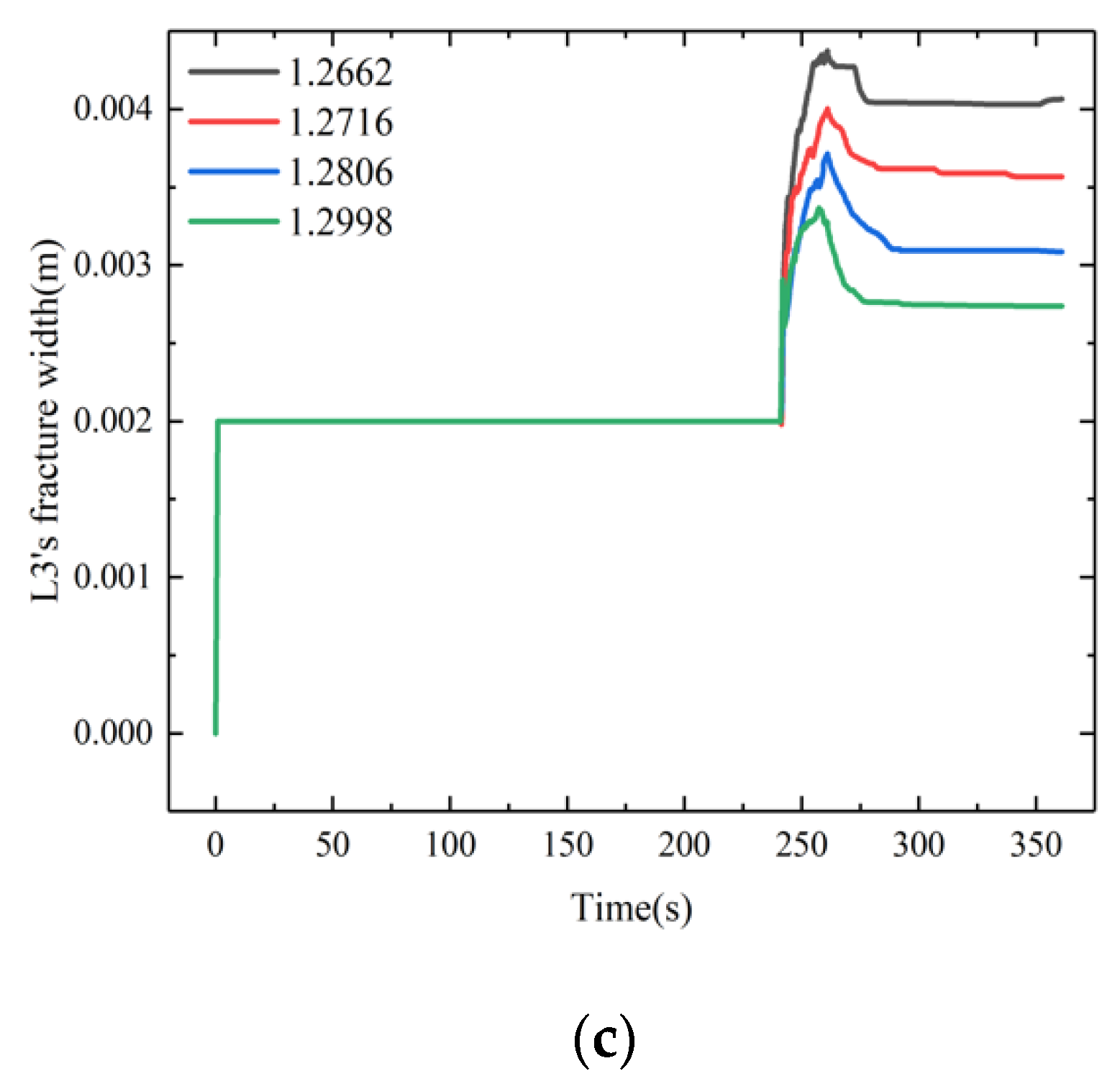
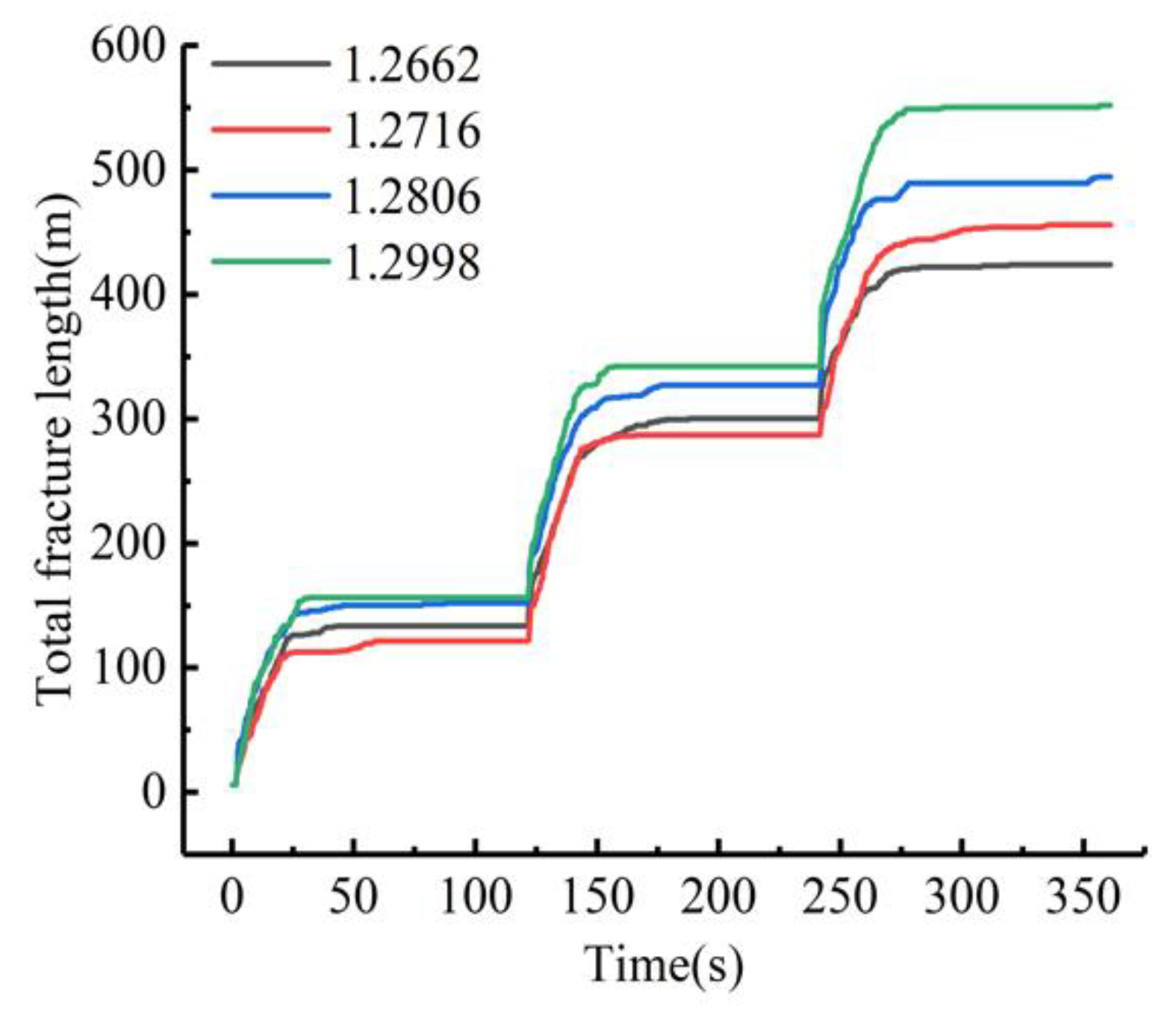
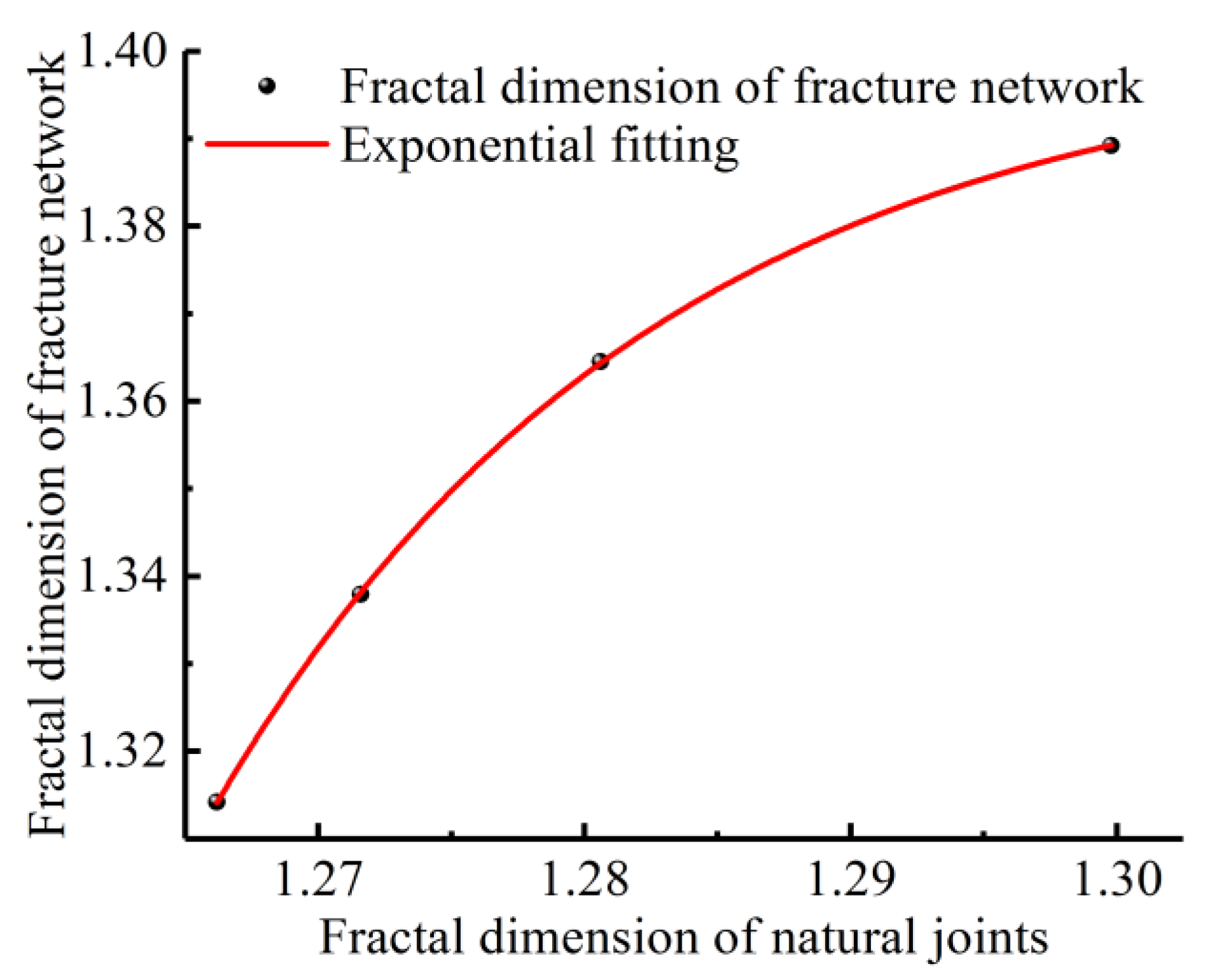
4.1. Influence of the Fractal Dimensions of Natural Joints on the Fractal Propagation of Fractures
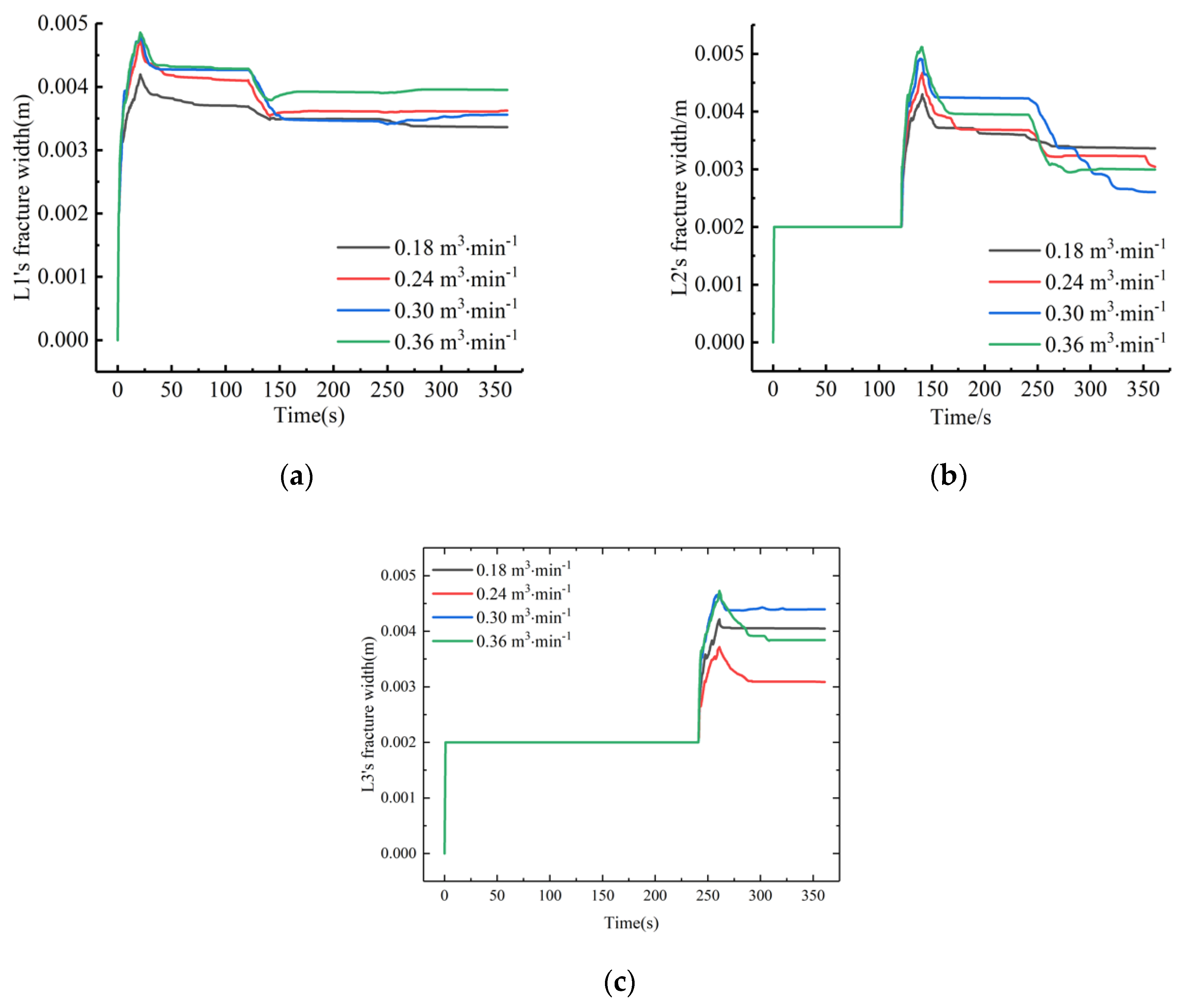
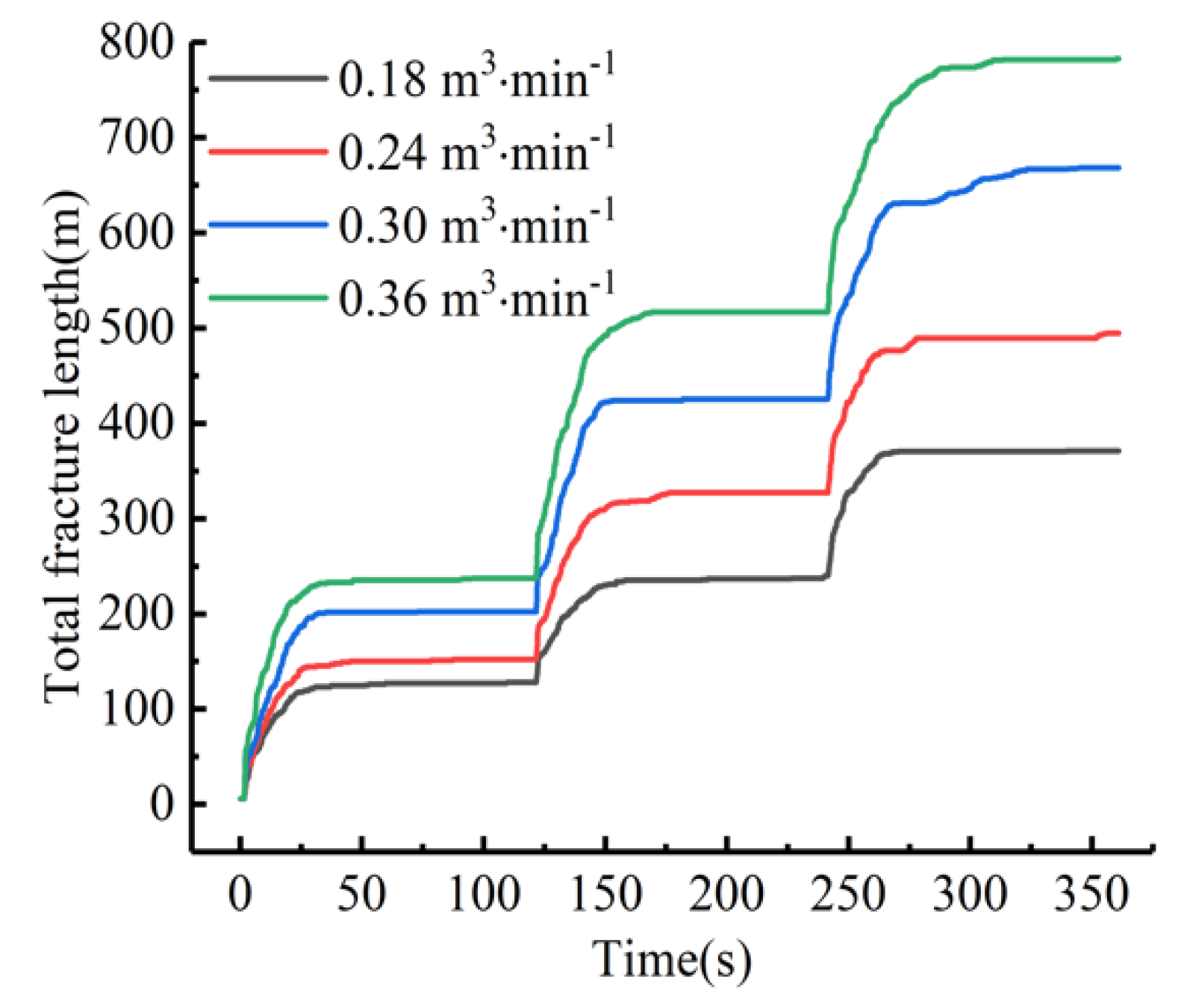
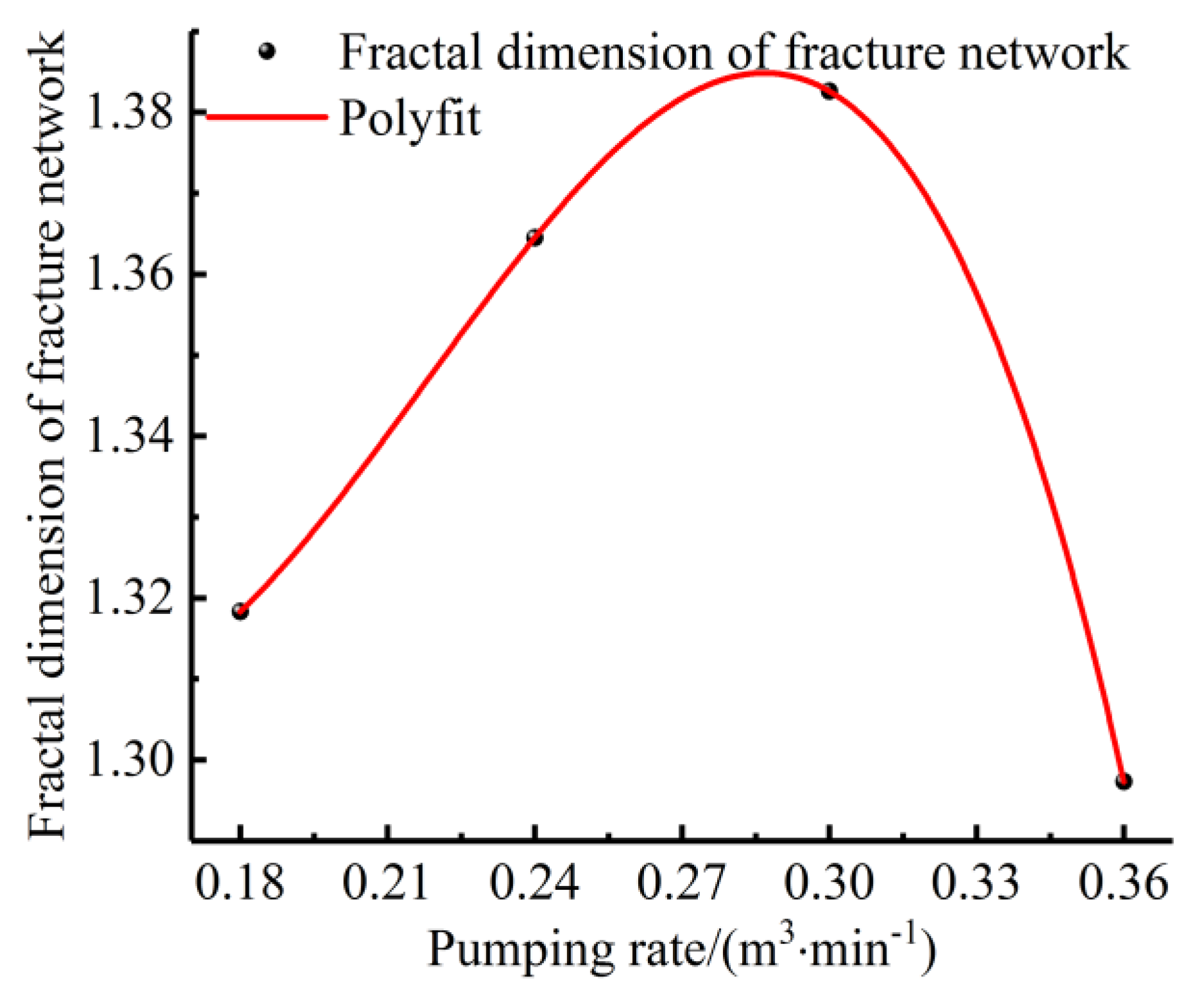
4.2. Influence of the Fracturing Fluid Pumping Rate on Fracture Fractal Propagation
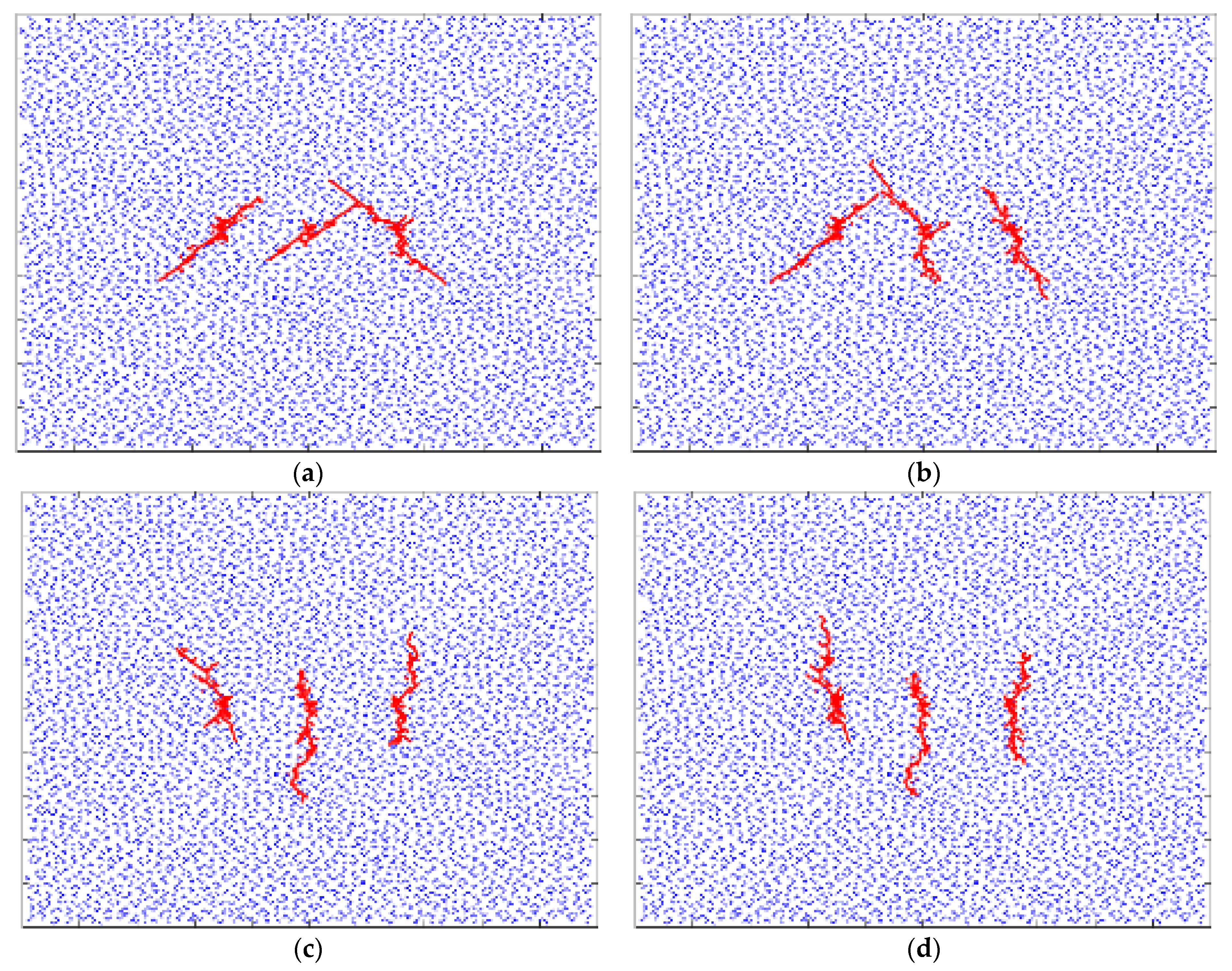
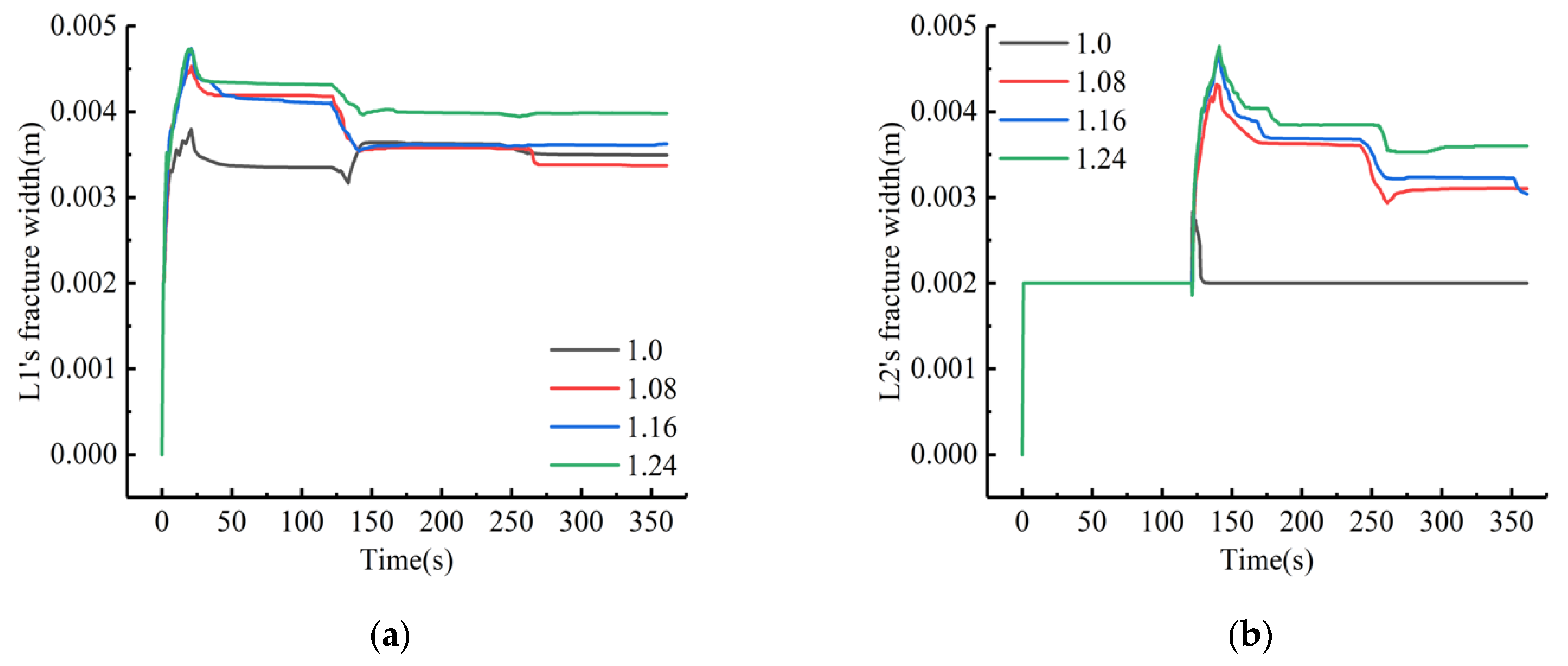
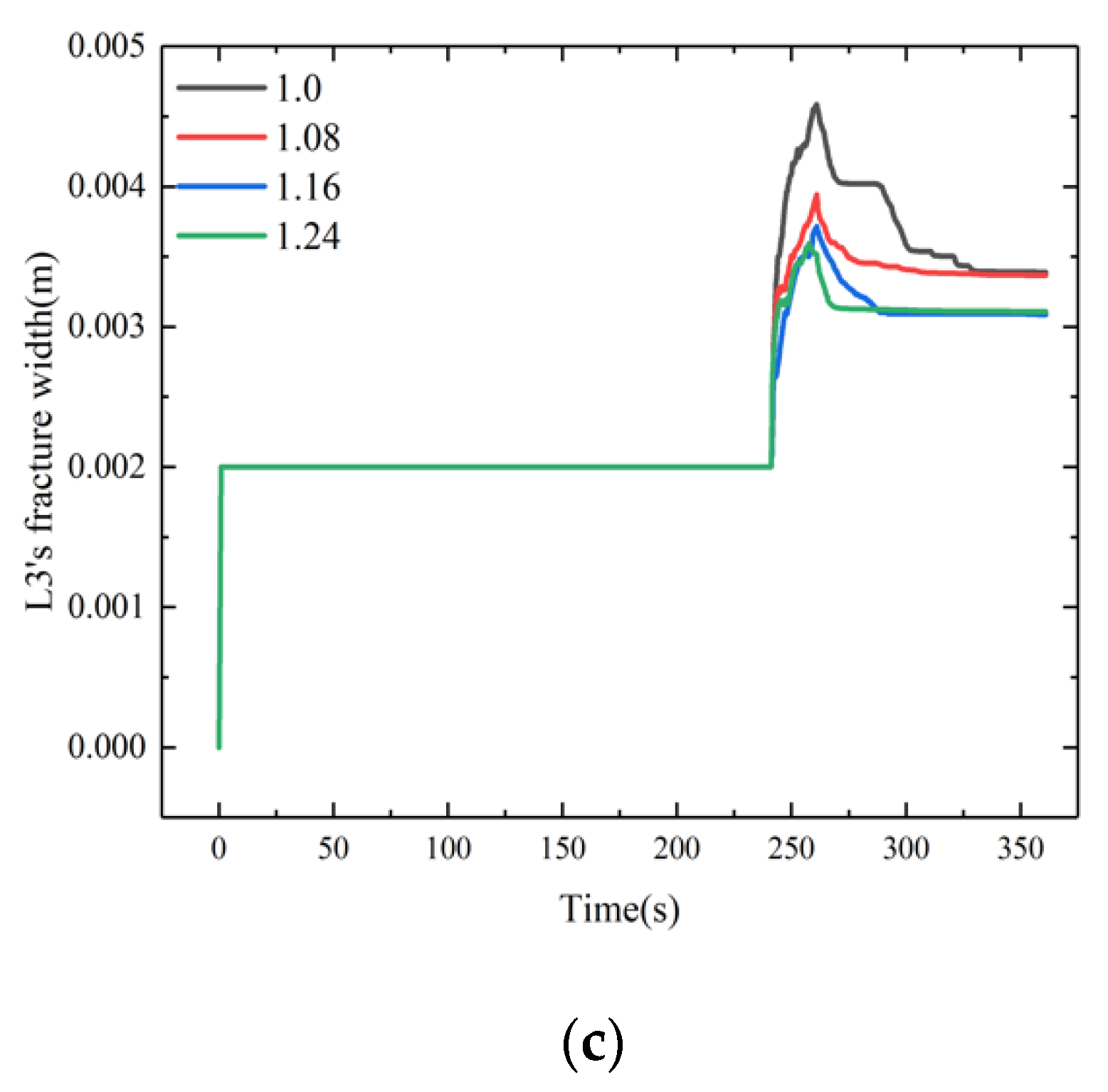
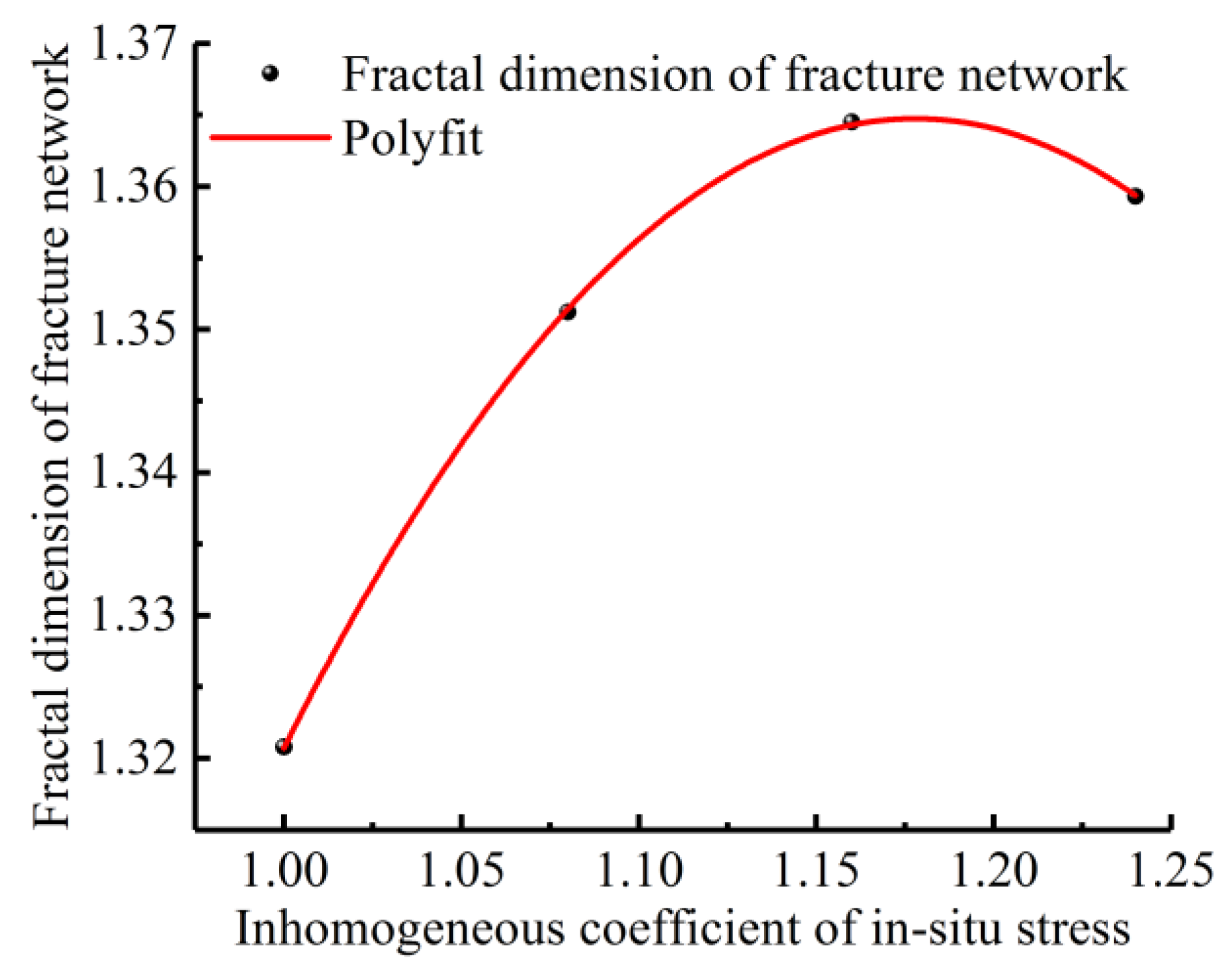
4.3. Influence of the Inhomogeneity Coefficient of the In Situ Stress on Fracture Fractal Propagation
4.4. The Influence of Fracturing Interval Spacing on Fracture Fractal Propagation
5. Conclusions
- (1)
- The two fracture surfaces were considered the dislocation boundary surfaces in the formation, and a displacement parameter control model of fracture propagation was established. The displacement and stress expressions of fracture propagation of the model were obtained. The numerical solution of fracture propagation of the horizontal well was established, which provides a more accurate theoretical and numerical model for subsequent analysis.
- (2)
- Using the calculation formula of stress interference for reference and derivation, the composite stress field under homologous stress interference was established, and the interactive development environment of the MATLAB-PYTHON-FEM platform was used to complete the construction and calculation of the model of the fracture network expansion in fractured reservoirs under homologous stress interference conditions with staged fracturing. The complexity of the fracture network was characterized by the fractal dimension, with the assumption of a random distribution of natural joints. The factors that affected the fractal expansion of the fracture were analyzed.
- (3)
- The interfracture stress interference effect in CBM reservoirs with developed natural joints was more obvious, and the intensity of the interfracture stress interference effect was positively correlated with the fractal dimensions of natural joints and negatively correlated with the in situ stress nonuniformity coefficient and fracture interval spacing. The intensity of stress interference between fractures first increased and then decreased with an increasing fracturing fluid pumping rate.
- (4)
- The fractal dimension of the fracture network that was formed by fracturing reconstruction satisfied the negative exponential increase rule with an increasing fractal dimension of the natural joints, and it first increased and then decreased with an increasing fracturing fluid pumping rate and in situ stress heterogeneity. With the increase in the interval between fracturing sections, the rule of positive exponential increase was satisfied.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Blanton, T.L. An experimental study of interaction between hydraulically induced and pre-existing fractures. In Proceedings of the SPE Unconventional Gas Recovery Symposium, Pittsburgh, PA, USA, 16–18 May 1982. [Google Scholar]
- Warpinski, N.R.; Teufel, L.W. Influence of geologic discontinuities on hydraulic fracture propagation. J. Pet. Technol. 1987, 39, 209–220. [Google Scholar] [CrossRef]
- Olson, J.E. Multi-fracture propagation modeling: Applications to hydraulic in shales and tight gas sands. In Proceedings of the 42nd U.S. Rock Mechanics Symposium (USRMS), San Francisco, CA, USA, 29 June–2 July 2008. [Google Scholar]
- Olson, J.E.; Taleghani, A.D. Modeling simultaneous growth of multiple hydraulic fractures and their interaction with natural fractures. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 19–21 January 2009. [Google Scholar]
- Olson, J.E. Predicting fracture swarms—The influence of subcritical crack growth and the crack-tip process zone on joint spacing in rock. Geol. Soc. Lond. Spec. Publ. 2004, 231, 73–88. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Y.-W.; Li, W.; Chen, Z.-J.; Zhao, Y.; Yu, F.-H.; Zheng, Y. Study on Propagation Behaviors of Hydraulic Fracture Network in Tight Sandstone Formation with Closed Cemented Natural Fractures. Geofluids 2020, 2020, 8833324. [Google Scholar] [CrossRef]
- Cipolla, C.L.; Williams, M.J.; Weng, X.; Mack, M.; Maxwell, S. Hydraulic fracture monitoring to reservoir simulation: Maximizing value. In Proceedings of the Second EAGE Middle East Tight Gas Reservoirs Workshop, Manama, Bahrain, 12–15 December 2010. [Google Scholar]
- Peirce, A.P.; Bunger, A.P. Interference fracturing: Nonuniform distributions of perforation clusters that promote simultaneous growth of multiple hydraulic fractures. SPE J. 2013, 20, 384–395. [Google Scholar] [CrossRef] [Green Version]
- Gordeliy, E.; Peirce, A. Coupling schemes for modeling hydraulic fracture propagation using the XFEM. Comput. Methods Appl. Mech. Eng. 2013, 253, 305–322. [Google Scholar] [CrossRef]
- Kresse, O.; Weng, X.; Wu, R.; Gu, H. Numerical modeling of hydraulic fractures interaction in complex naturally fractured formations. Rock Mech. Rock Eng. 2013, 46, 555–568. [Google Scholar] [CrossRef]
- Kresse, O.; Cohen, C.; Weng, X.; Wu, R.; Gu, H. Numerical modeling of hydraulic fracturing in naturally fractured formations. Rock Mech. 2011, 15, 516–535. [Google Scholar]
- Morrill, J.; Miskimins, J.L. Optimization of hydraulic fracture spacing in unconventional shales. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 6–8 February 2012. [Google Scholar]
- Nagel, N.B.; Sanchez-Nagel, M. Stress shadowing and microseismic events: A numerical evaluation. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 30 October–2 November 2011. [Google Scholar]
- Yan, X.Z.; Li, X.Y. Development and application of unconventional oil and gas well fracturing optimization design software based on fracture interference model. J. China Univ. Pet. Ed. Nat. Sci. 2013, 37, 120–128. (In Chinese) [Google Scholar]
- Li, Y.; Jia, D.; Liu, J.; Fu, C.; Ai, C. The calculation method based on the equivalent continuum for the fracture initiation pressure of fracturing of coalbed methane well. J. Pet. Sci. Eng. 2016, 146, 909–920. [Google Scholar] [CrossRef]
- Li, Y.; Long, M.; Zuo, L.; Li, W.; Zhao, W. Brittleness evaluation of coal based on statistical damage and energy evolution theory. J. Pet. Sci. Eng. 2019, 172, 753–763. [Google Scholar] [CrossRef]
- Li, Y.; Rui, Z.; Zhao, W.; Bo, Y.; Fu, C.; Chen, G.; Patil, S. Study on the mechanism of rupture and propagation of T-type fractures in coal fracturing. J. Nat. Gas Sci. Eng. 2018, 52, 379–389. [Google Scholar] [CrossRef]
- Cong, Z.; Li, Y.; Liu, Y.; Xiao, Y. A new method for calculating the direction of fracture propagation by stress numerical search based on the displacement discontinuity method. Comput. Geotech. 2021, 140, 104482. [Google Scholar] [CrossRef]
- Cong, Z.; Li, Y.; Pan, Y.; Liu, B.; Shi, Y.; Wei, J.; Li, W. Study on CO2 foam fracturing model and fracture propagation simulation. Energy 2022, 238, 121778. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Wheeler, J.A. The Fractal Geometry of Nature; Gulf Professional Publishing House: Houston, TX, USA, 1982. [Google Scholar]
- Sarkar, N.; Chaudhuri, B.B. An efficient differential box-counting approach to compute fractal dimension of image. IEEE Trans. Syst. Man Cybern. 1994, 24, 115–120. [Google Scholar] [CrossRef] [Green Version]
- Xie, H.P.; Chen, Z.D. Fractal geometry and rock fracture. Acta Mech. Sin. 1988, 20, 264–271, 290. (In Chinese) [Google Scholar]
- Zhao, X.; Wang, X.Y. An approach to compute fractal dimension of color images Fractals-complex. Geom. Patt. Scal. Nat. Soc. 2017, 25, 149–163. [Google Scholar]
- Farhidzadeh, A.; Dehghan-Niri, E.; Moustafa, A.; Salamone, S.; Whittaker, A. Damage assessment of reinforced concrete structures using fractal analysis of residual crack patterns. Exp. Mech. 2013, 53, 1607–1619. [Google Scholar] [CrossRef]
- Korvin, G. Fraetal Modeling the Earth Seience; Elsevier Publishing: Amsterdam, The Netherlands, 1992. [Google Scholar]
- Wang, S.; Wang, X.; Bao, L.; Feng, Q.; Wang, X.; Xu, S. Characterization of hydraulic fracture propagation in tight formations: A fractal perspective. J. Pet. Sci. Eng. 2020, 195, 107871. [Google Scholar] [CrossRef]
- Liu, J.; Jiang, L.; Liu, T.; Yang, D. Characterization of Fractal-like Fracture Network Using Tracer Flowback Tests for a Multifractured Horizontal Well in a Tight Formation. Fractals 2022. [Google Scholar] [CrossRef]
- Li, Y.M.; Chen, X.Y.; Zhao, J.Z.; Shen, F.; Qiao, H.J. Interference between segmented multi-clustered fractures in horizontal wells. J. Southwest Pet. Univ. 2016, 38, 76–83. (In Chinese) [Google Scholar]
- Shojaei, A.K.; Shao, J.F. Porous Rock Fracture Mechanics with Application to Hydraulic Fracturing, Drilling and Structural Engineering; Woodhead Publishing Series in Civil and Structural Engineering: Cambridgeshire, UK, 2017. [Google Scholar]
- Barenblatt, G.I. The mathematical theory of equilibrium cracks in Brittle fracture. Adv. Appl. Mech. 1962, 7, 55–129. [Google Scholar]
- Shi, X.; Qin, Y.; Xu, H.; Feng, Q.; Wang, S.; Xu, P.; Han, S. Numerical simulation of hydraulic fracture propagation in conglomerate reservoirs. Eng. Fract. Mech. 2021, 248, 107738. [Google Scholar] [CrossRef]
- Zhang, H.; Sheng, J.J. Numerical simulation and optimization study of the complex fracture network in naturally fractured reservoirs. J. Pet. Sci. Eng. 2020, 195, 107726. [Google Scholar] [CrossRef]
- Wang, H.Y. Hydraulic fracture propagation in naturally fractured reservoirs: Complex fracture or fracture networks. J. Nat. Gas Sci. Eng. 2019, 68, 102911. [Google Scholar] [CrossRef] [Green Version]
- Belyadi, H.; Fathi, E.; Belyadi, F. Hydraulic Fracturing in Unconventional Reservoirs; Elsevier Publishing: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Kanninen, M.F.; Popelar, C.H. Advanced Fracture Mechanics: Oxford Engineering Science Series; Oxford University Press: Oxford, UK, 1985. [Google Scholar]
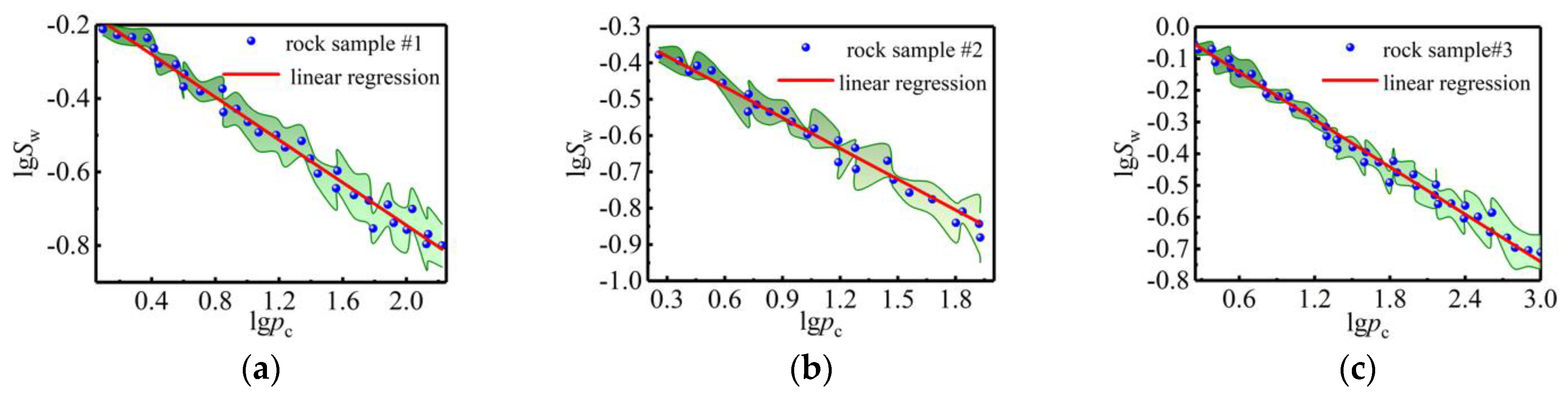


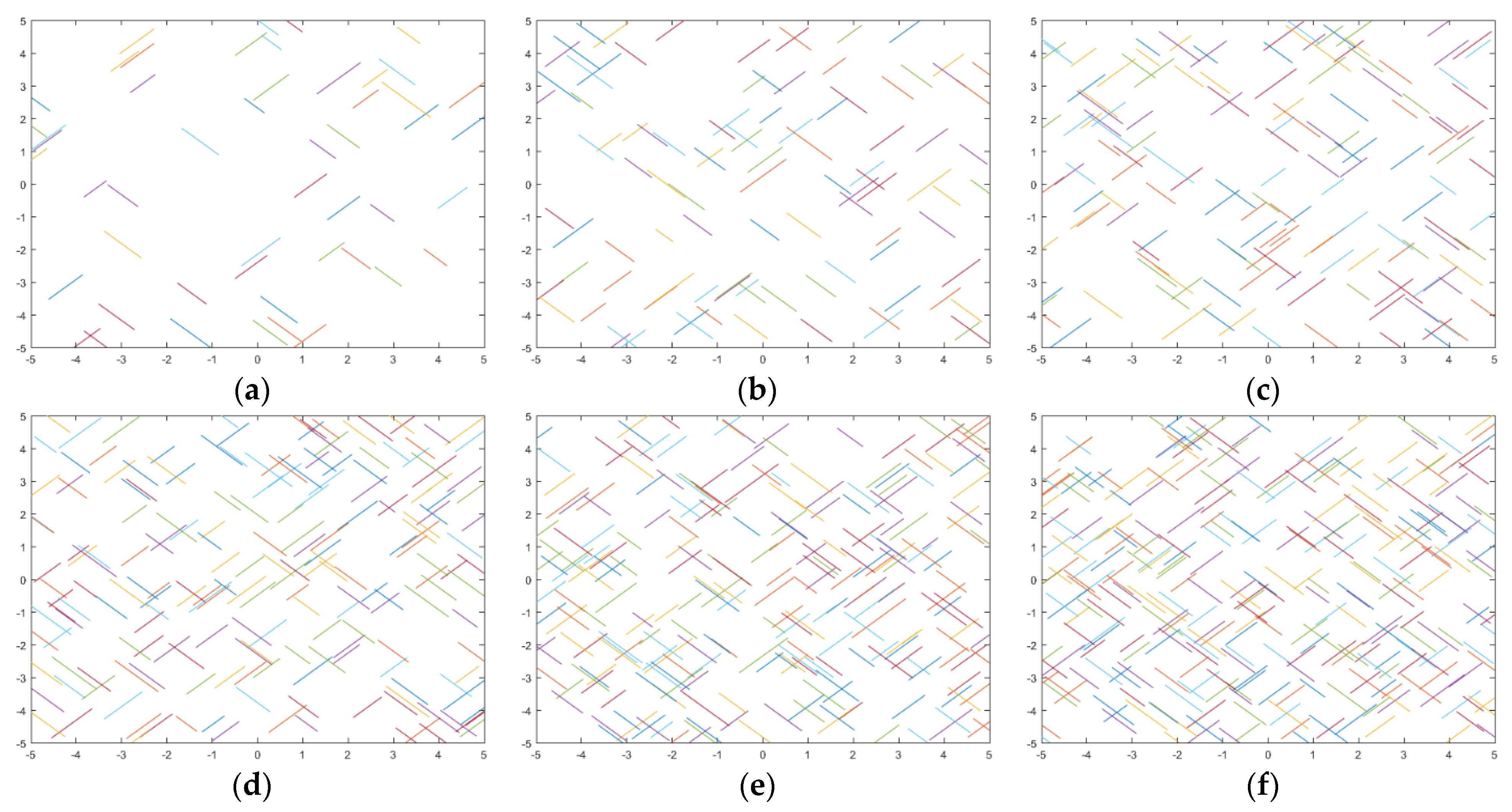
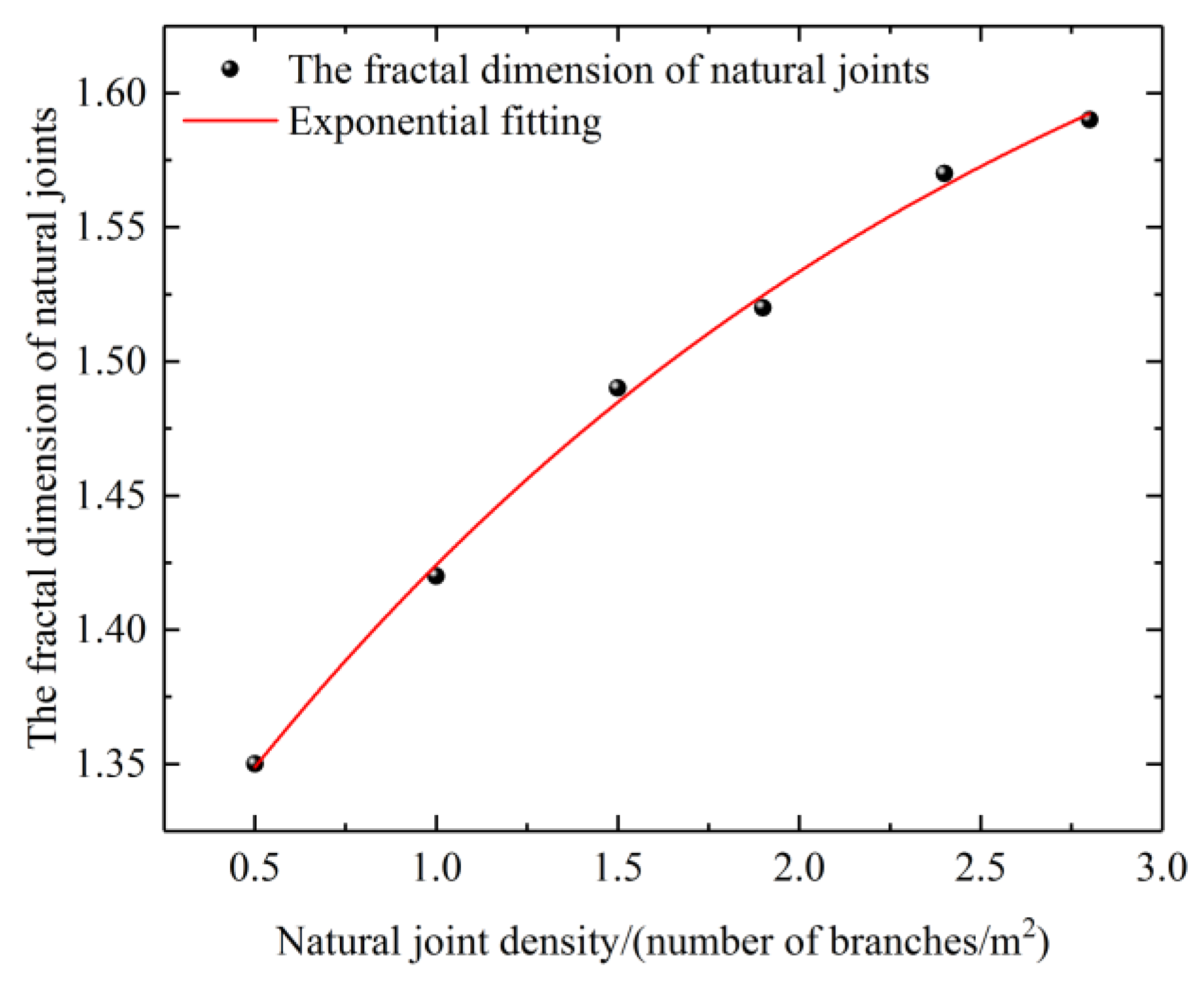
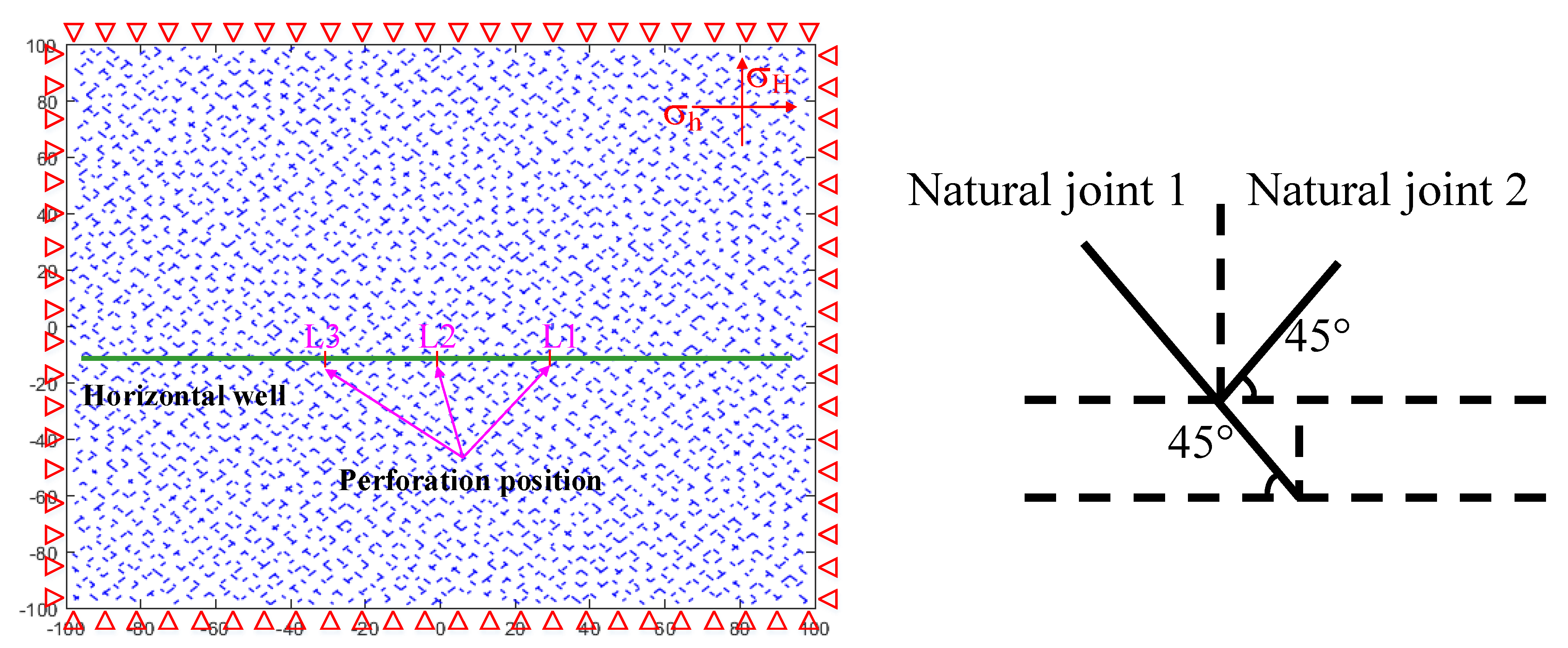
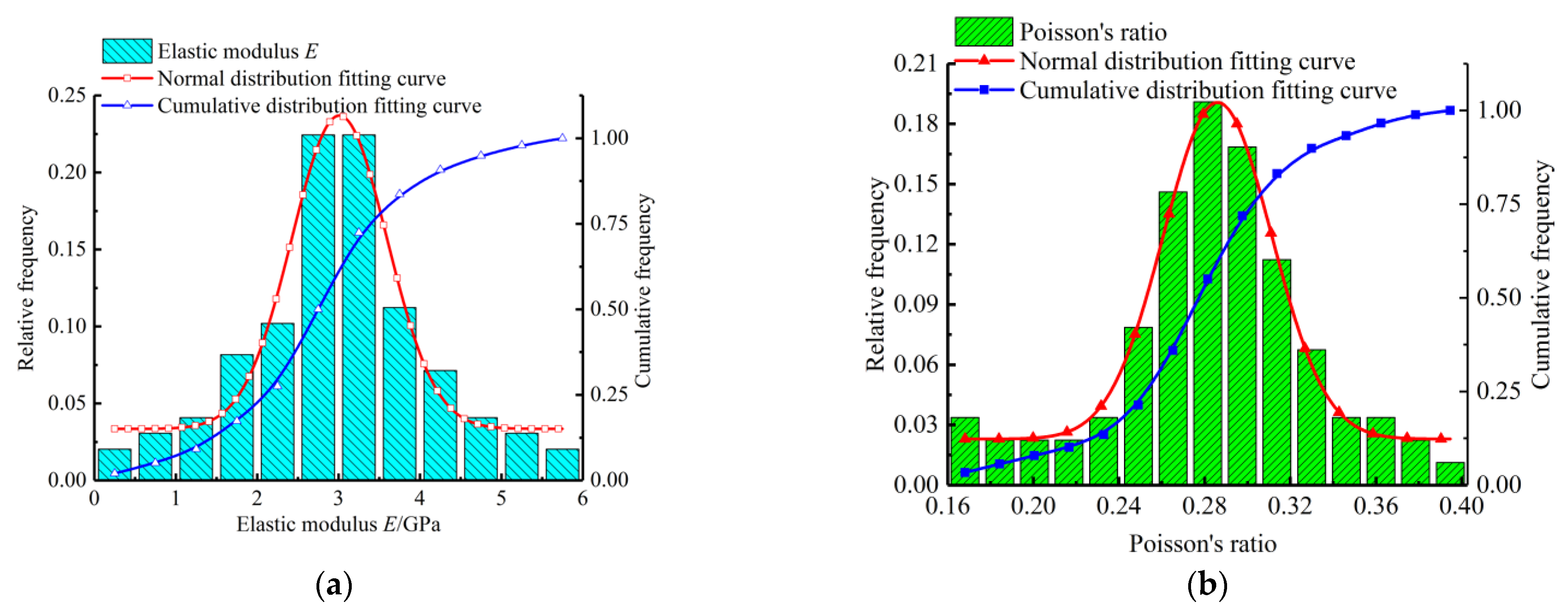
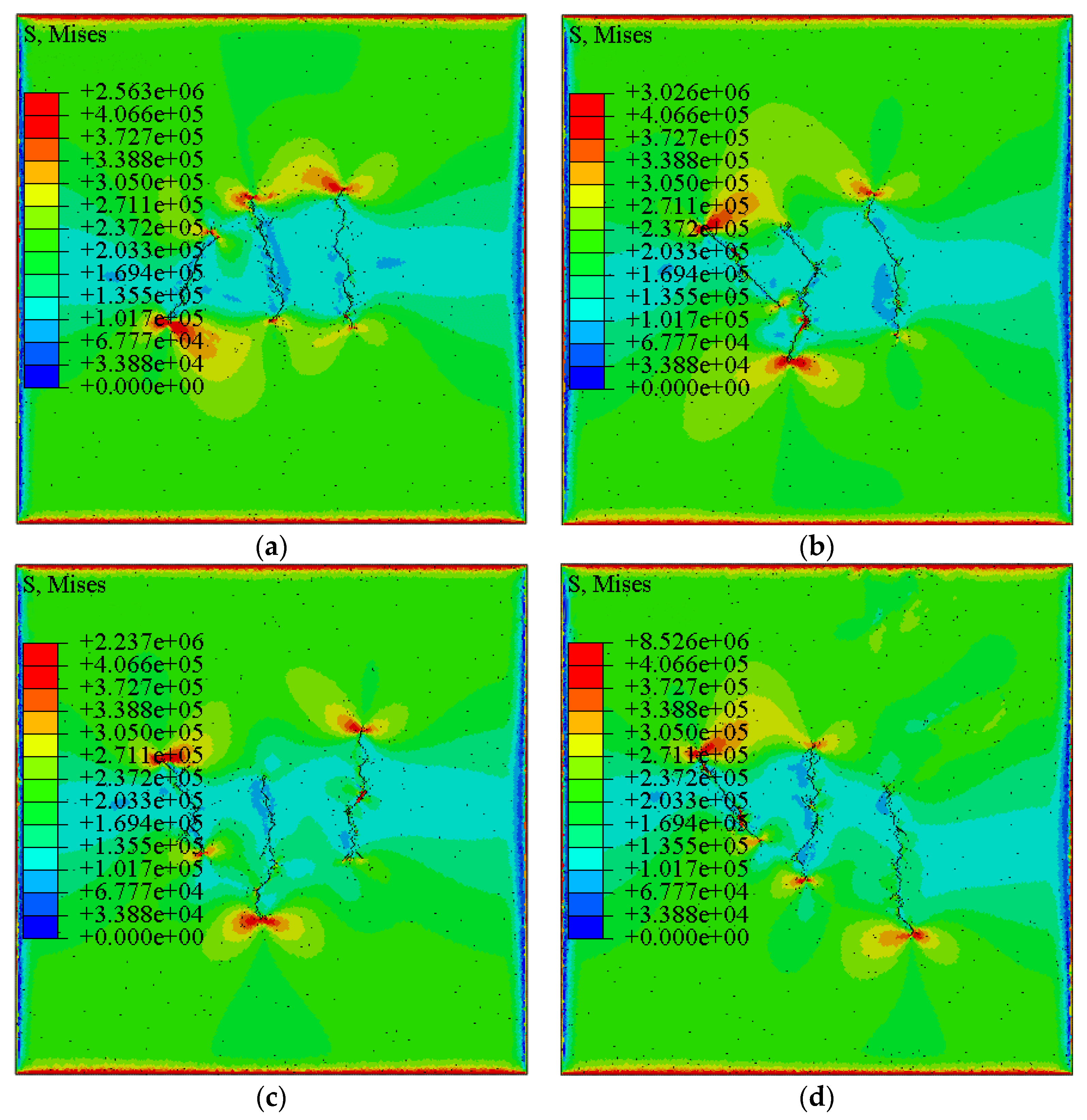
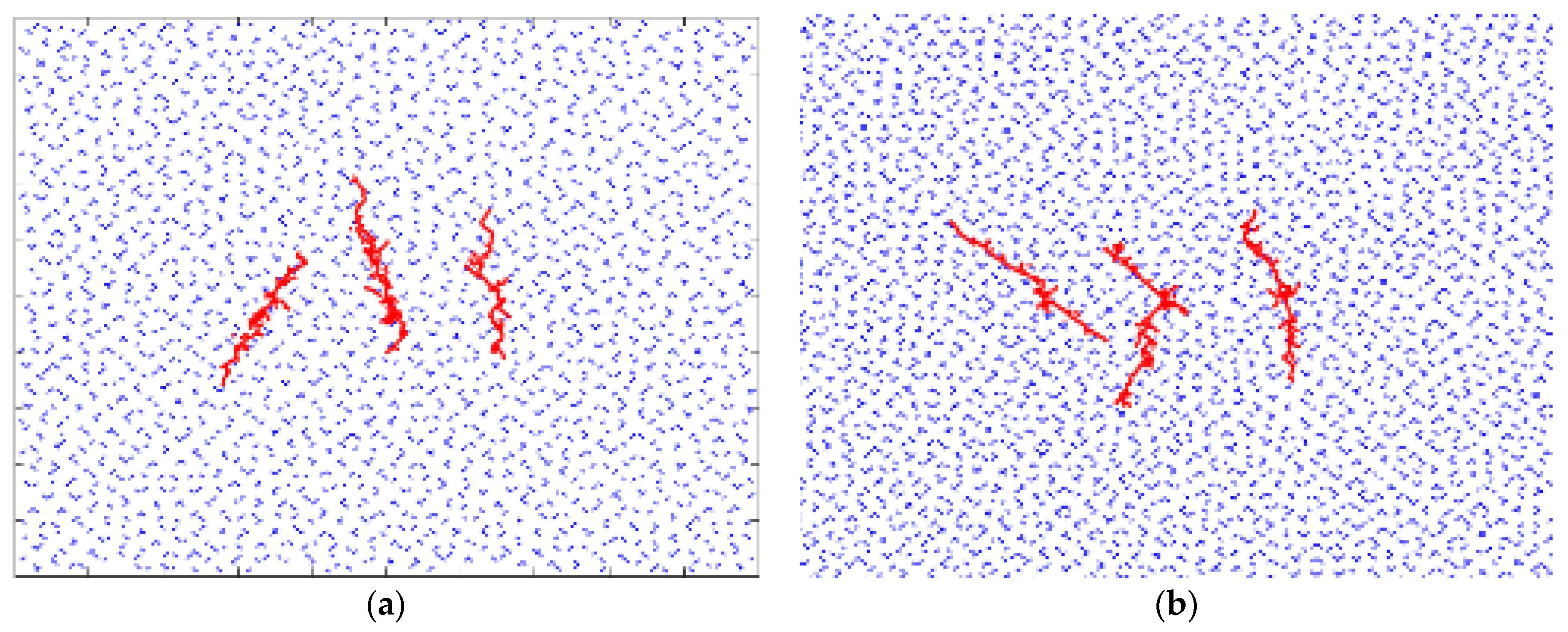


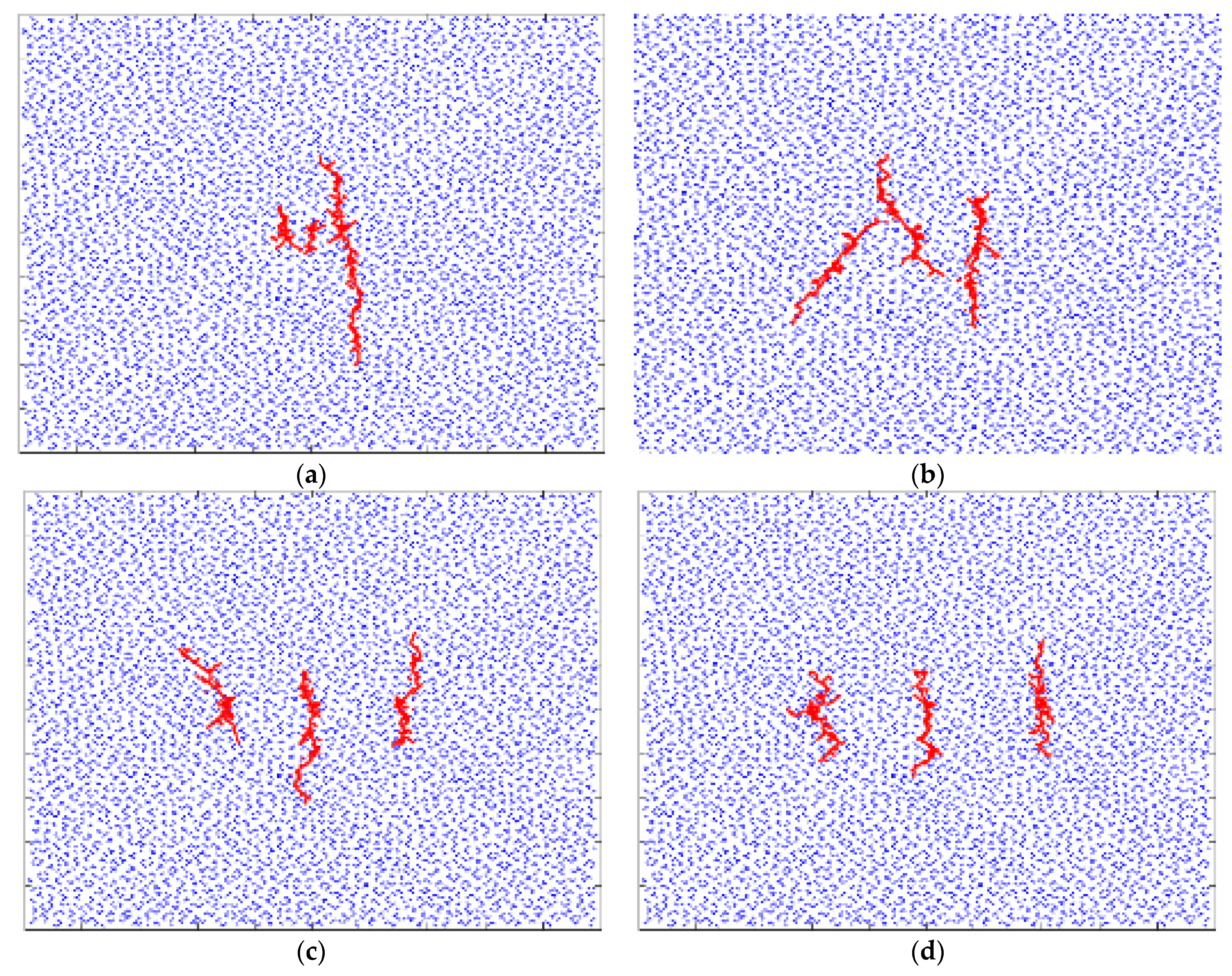
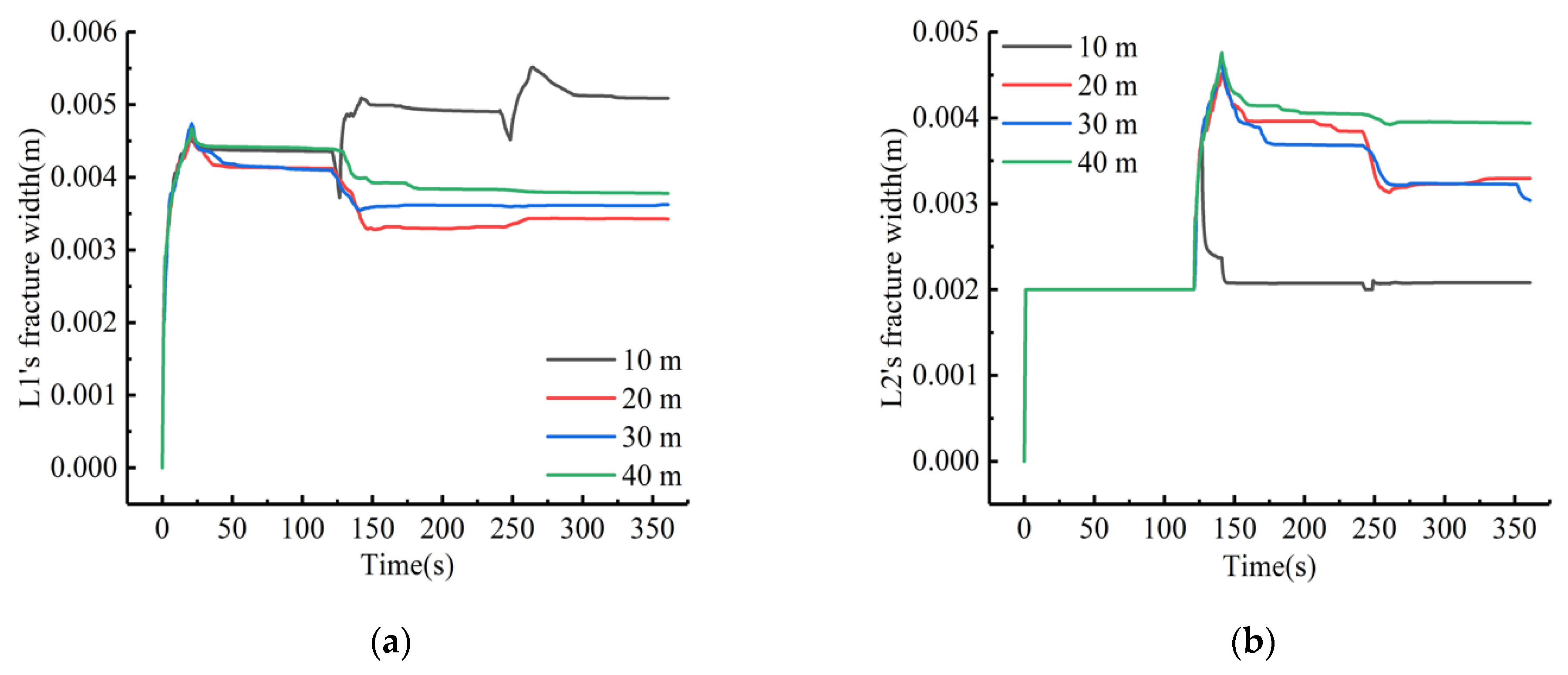
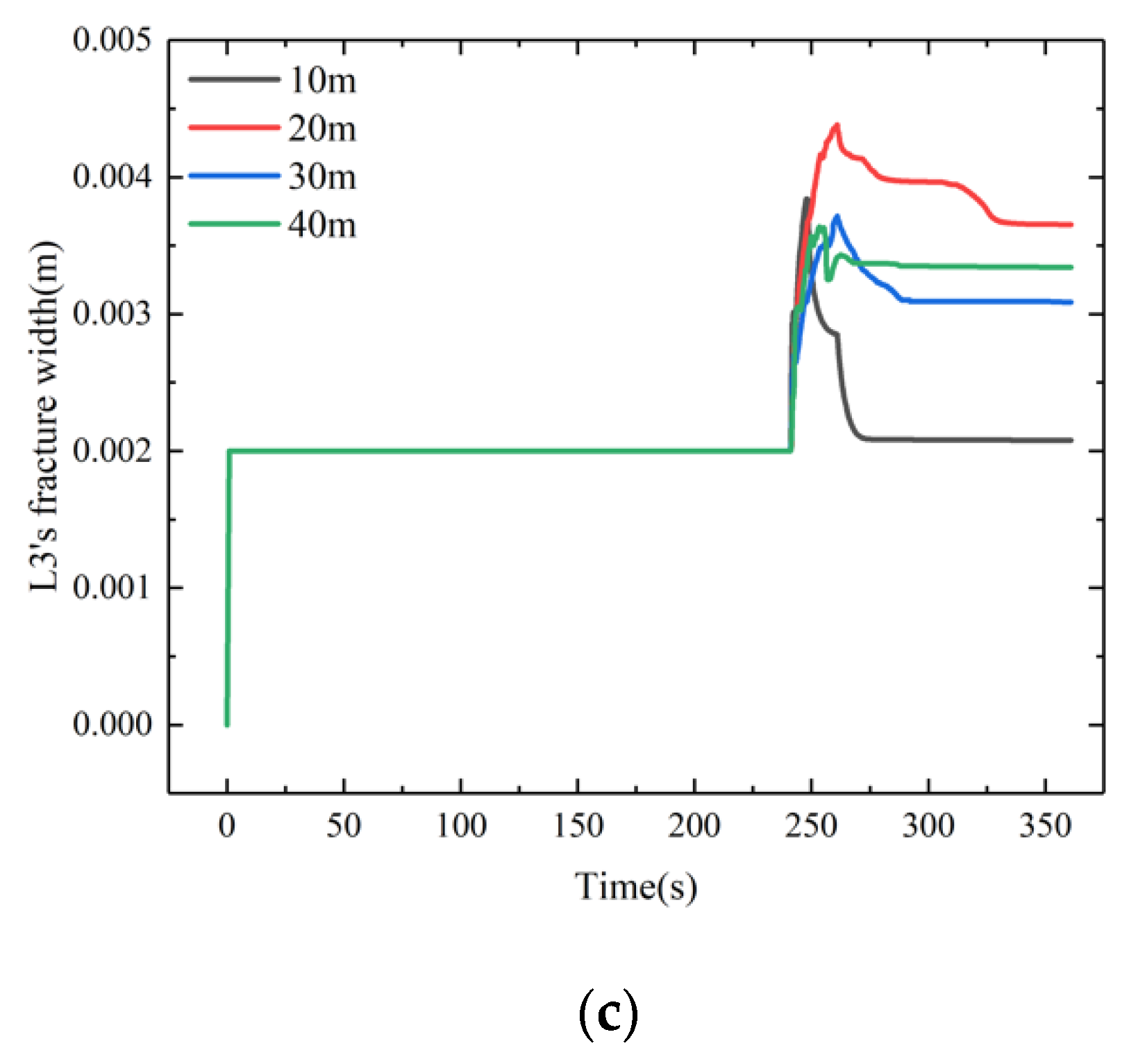

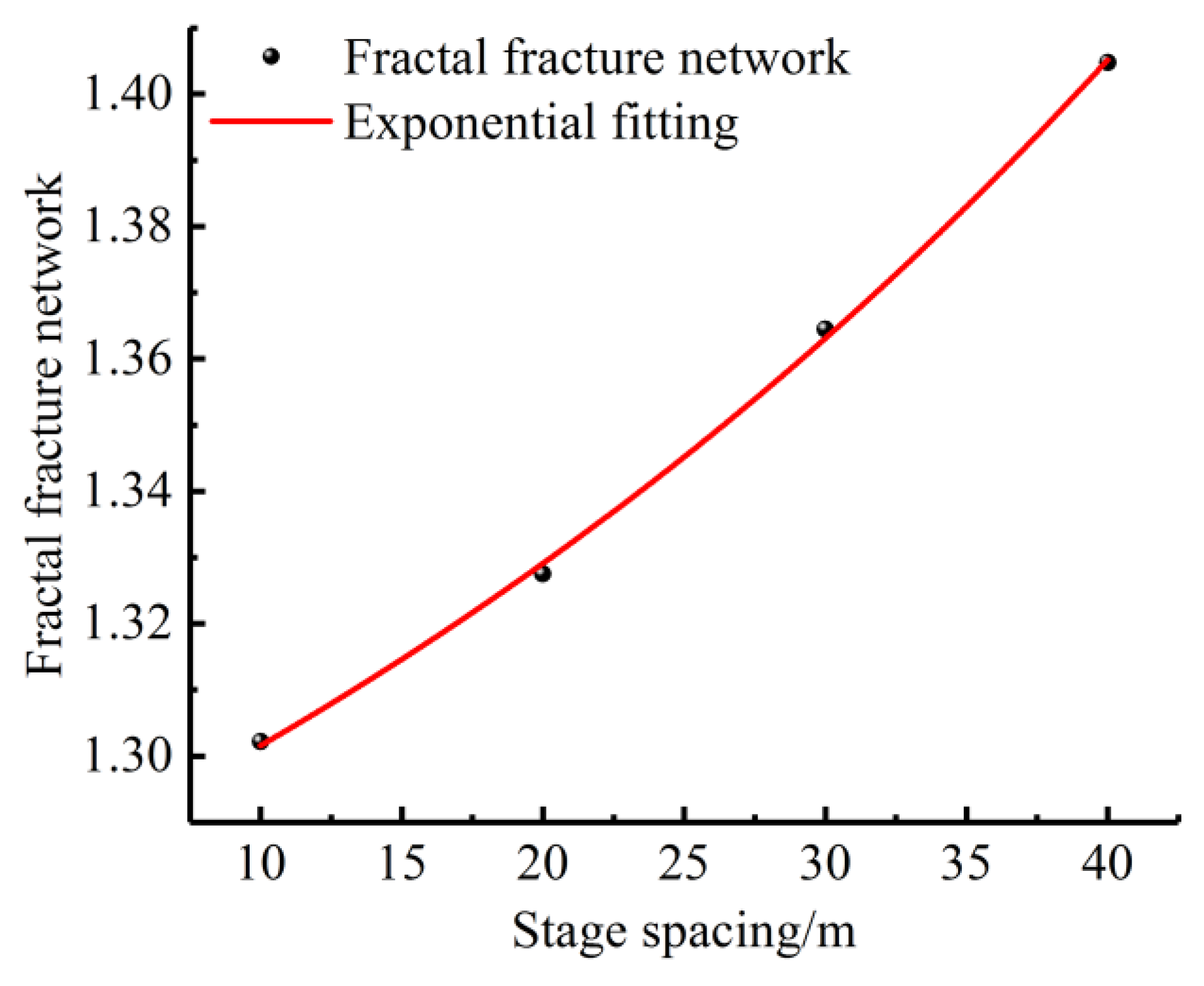
| Rock Parameter | Min (GPa) | Max (GPa) | Average (GPa) | Standard Deviation (GPa) | Lower 95% Confidence Interval of the Mean (GPa) | Upper 95% Confidence Interval of the Mean (GPa) |
|---|---|---|---|---|---|---|
| Elastic modulus | 0.24 | 5.7 | 2.98 | 1.126 | 2.75 | 3.20 |
| Poisson’s ratio | 0.16 | 0.43 | 0.29 | 0.0658 | 0.276 | 0.303 |
| Model Parameter | Numerical Value |
|---|---|
| Young’s modulus (GPa) | 4.36 |
| Poisson’s ratio/dimensionless | 0.28 |
| Rock permeability coefficient (m·s−1) | 3.89 × 10−8 |
| Rock tensile strength (MPa) | 0.43 |
| Rock fracture toughness (J·m−2) | 215 |
| Joint tensile strength (MPa) | 0.22 |
| Joint fracture toughness (J·m−2) | 55 |
| Fracturing fluid viscosity (Pa·s) | 0.001 |
| Filtration coefficient (m3·Pa−1·s−1) | 1 × 10−13 |
| Fracturing fluid pumping rate (m3·min−1) | 0.24 |
| Pumping injection time (s) | 20 |
| Length of perforation section (m) | 1 |
| Minimum horizontal in situ stress (MPa) | 18 |
| In situ stress inhomogeneity coefficients | 1.0, 1.08, 1.16, and 1.24 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Pu, C.; Shi, X.; Xu, Z.; Ye, Z. The Numerical Simulation and Characterization of Complex Fracture Network Propagation in Multistage Fracturing with Fractal Theory. Minerals 2022, 12, 955. https://doi.org/10.3390/min12080955
Zhang P, Pu C, Shi X, Xu Z, Ye Z. The Numerical Simulation and Characterization of Complex Fracture Network Propagation in Multistage Fracturing with Fractal Theory. Minerals. 2022; 12(8):955. https://doi.org/10.3390/min12080955
Chicago/Turabian StyleZhang, Peng, Chunsheng Pu, Xian Shi, Zhiqian Xu, and Zhengqin Ye. 2022. "The Numerical Simulation and Characterization of Complex Fracture Network Propagation in Multistage Fracturing with Fractal Theory" Minerals 12, no. 8: 955. https://doi.org/10.3390/min12080955
APA StyleZhang, P., Pu, C., Shi, X., Xu, Z., & Ye, Z. (2022). The Numerical Simulation and Characterization of Complex Fracture Network Propagation in Multistage Fracturing with Fractal Theory. Minerals, 12(8), 955. https://doi.org/10.3390/min12080955






