Impact of Stimulated Fractures on Tree-Type Borehole Methane Drainage from Low-Permeability Coal Reservoirs
Abstract
:1. Introduction
2. Computational Model
2.1. Governing Equation of Methane Flow in the Stimulated Fractures
2.2. Governing Equation of Methane Flow in Coal Matrix and Cleats
2.3. Governing Equations of Coal Deformation
2.4. Governing Equations of Heat Transfer in Stimulated Coal Seam by TTHF
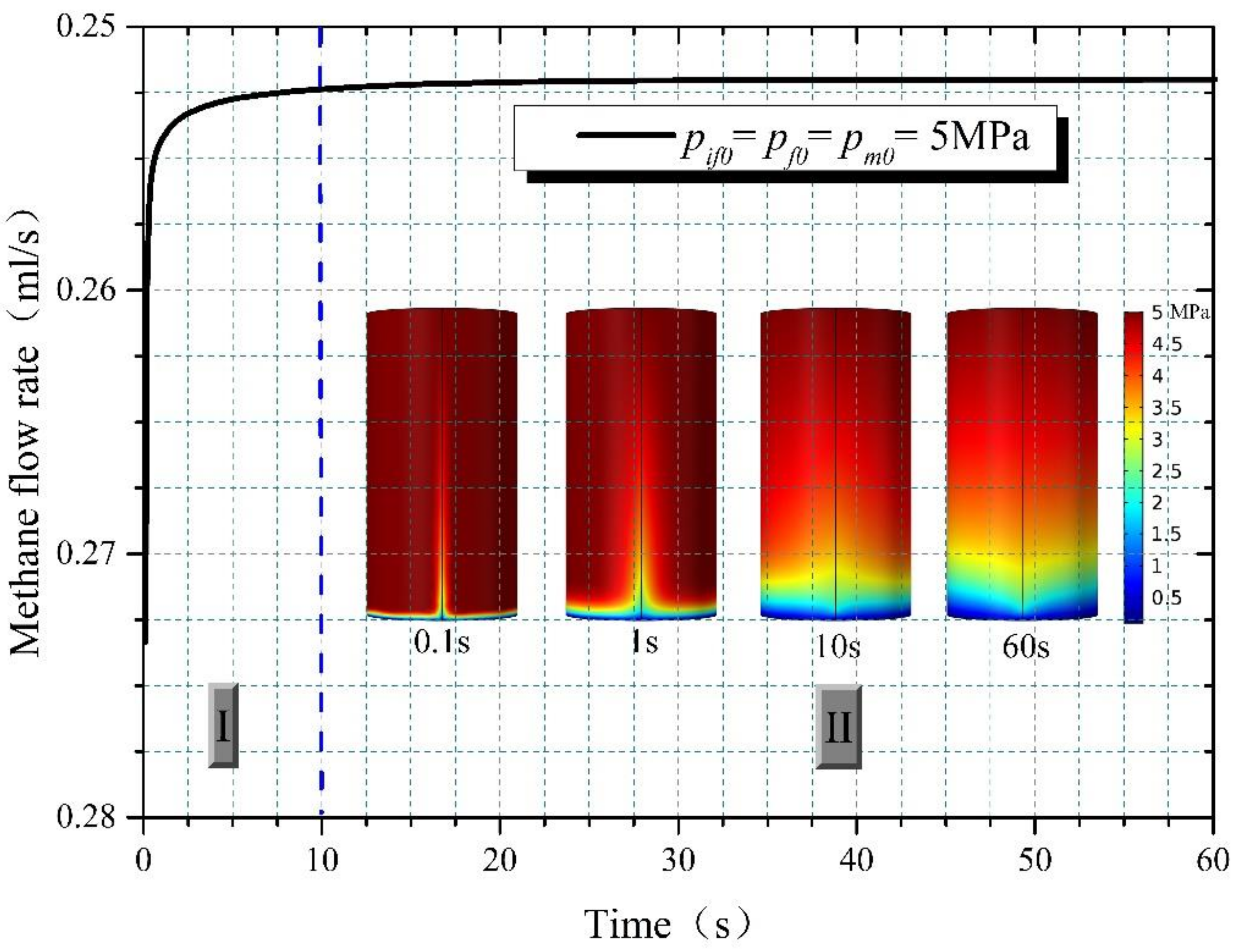
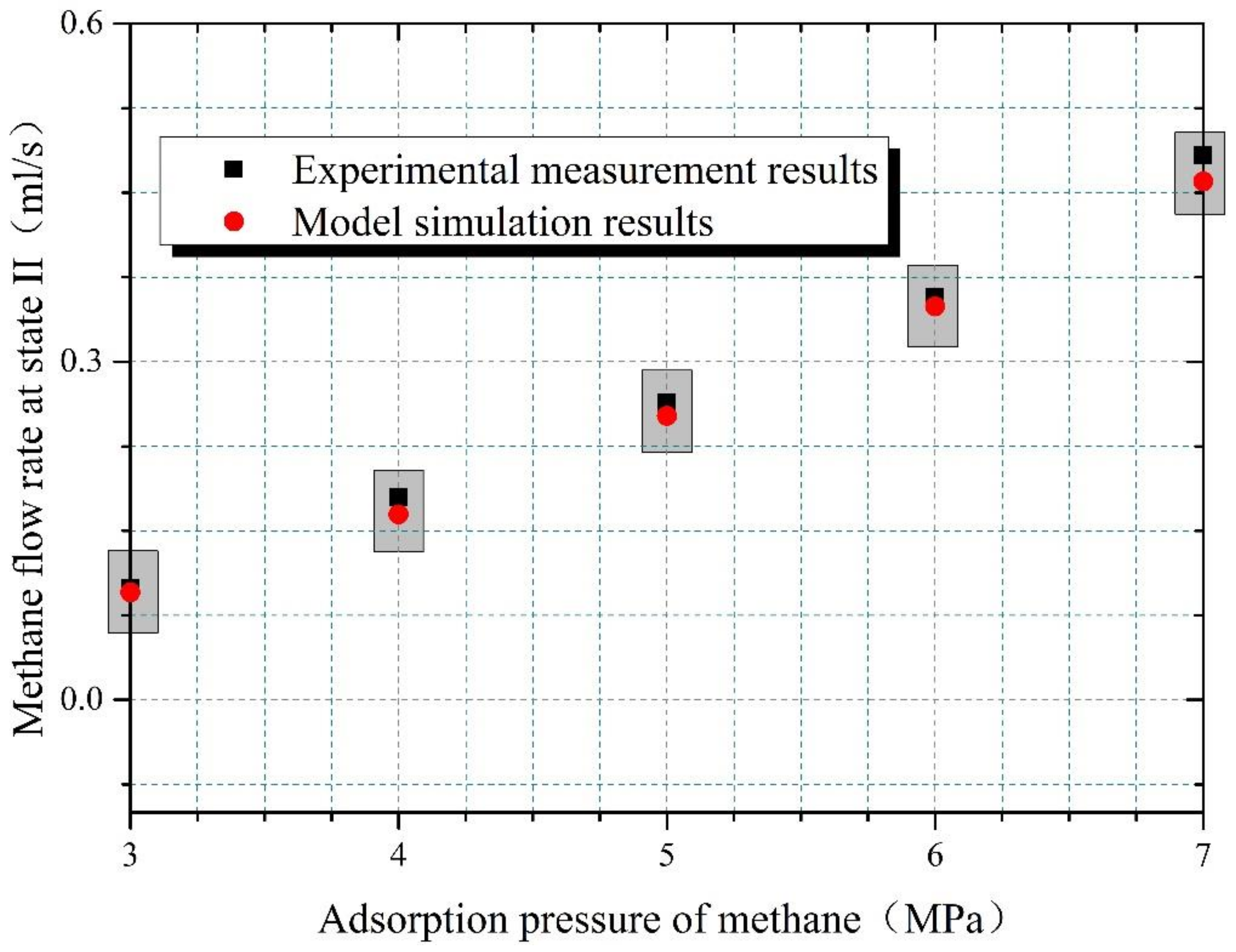
3. Validation of the Multi-Scale THM Model
4. Numerical Simulation of Methane Drainage from a Coal Seam Subjected to TTHF and Discussion
4.1. Model Generation and Description
4.2. Simulation and Discussion
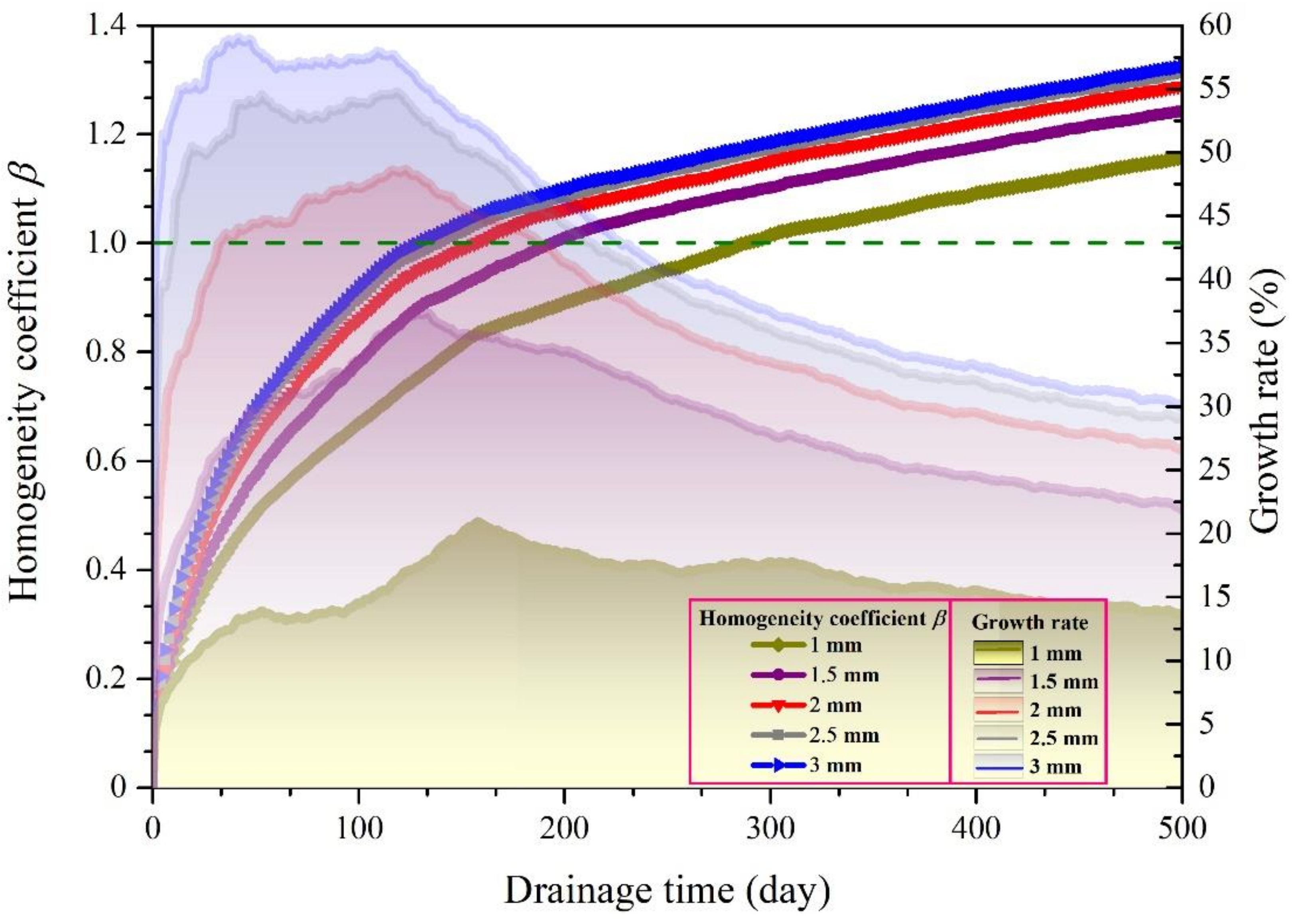
4.2.1. Effect of Stimulated Fracture Aperture
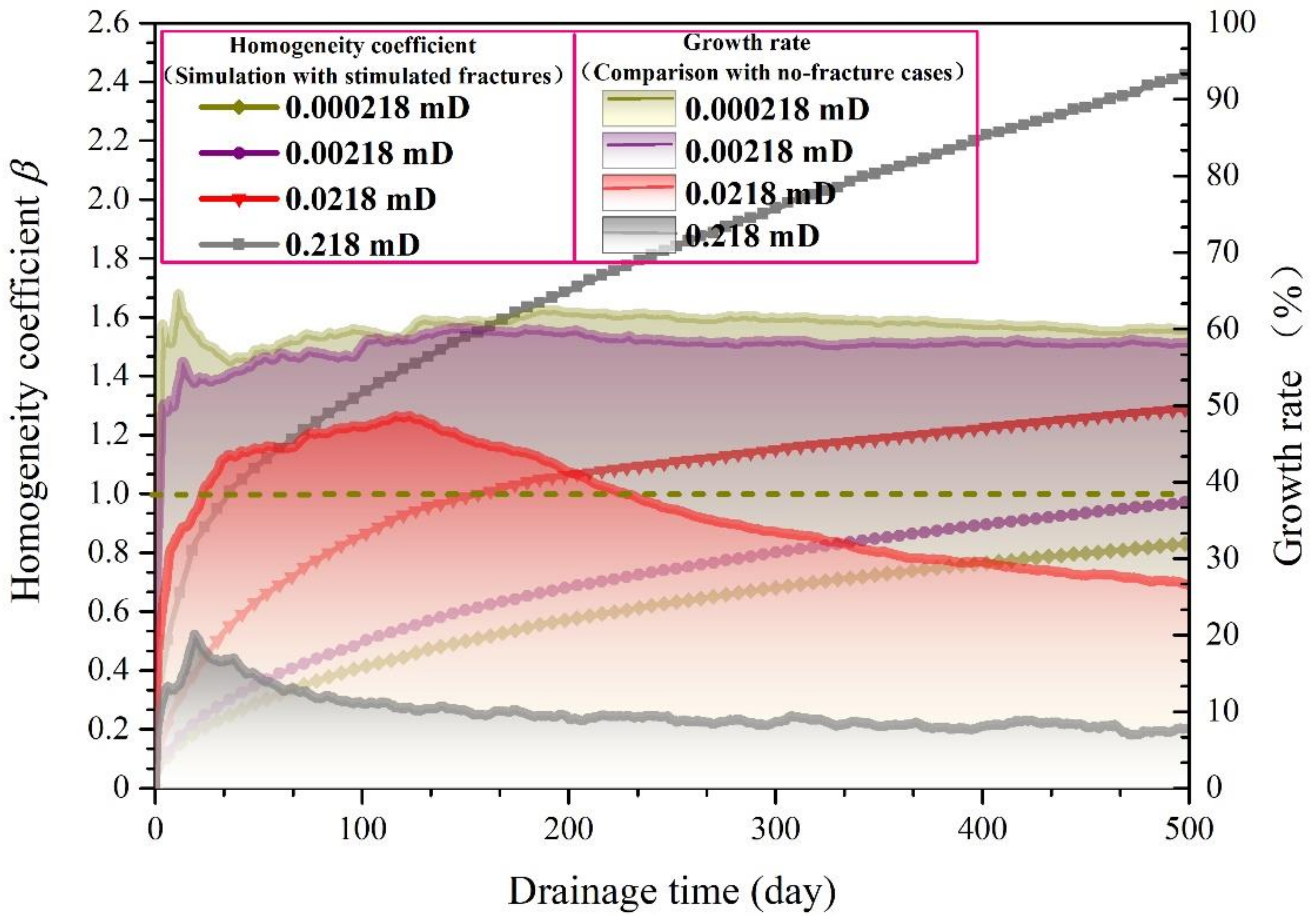
4.2.2. Effect of Initial Permeability of the Cleat System
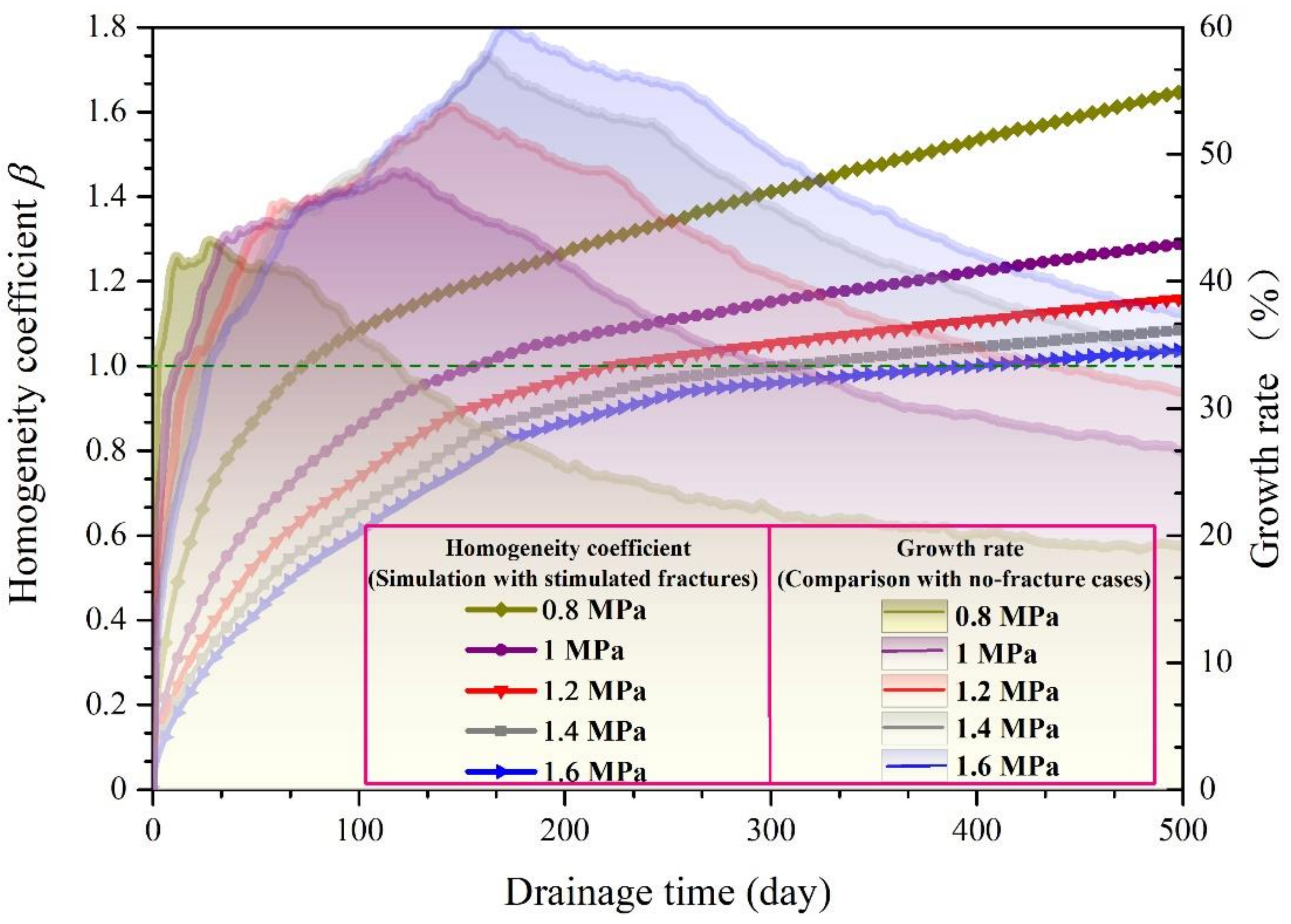
4.2.3. Effect of Remnant CSM Pressure
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sheng, J.; Tunnicliffe, R.; Ganesan, A.L.; Maasakkers, J.D.; Shen, L.; Prinn, R.G.; Song, S.; Zhang, Y.; Scarpelli, T.; Anthony Bloom, A.; et al. Sustained methane emissions from China after 2012 despite declining coal production and rice-cultivated area. Environ. Res. Lett. 2021, 16, 104018. [Google Scholar] [CrossRef]
- Adedoyin, F.F.; Gumede, M.I.; Bekun, F.V.; Etokakpan, M.U.; Balsalobre-Lorente, D. Modelling coal rent, economic growth and CO2 emissions: Does regulatory quality matter in BRICS economies? Sci. Total Environ. 2020, 710, 136284. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.; Fridley, D.; Lu, H.; Price, L.; Zhou, N. Has coal use peaked in China: Near-term trends in China’s coal consumption. Energy Policy 2018, 123, 208–214. [Google Scholar] [CrossRef]
- Garcia, E.; Liu, H. Ilmenite as alternative bed material for the combustion of coal and biomass blends in a fluidised bed combustor to improve combustion performance and reduce agglomeration tendency. Energy 2022, 239, 121913. [Google Scholar] [CrossRef]
- Nandimandalam, H.; Gude, V.G.; Marufuzzaman, M. Environmental impact assessment of biomass supported electricity generation for sustainable rural energy systems—A case study of Grenada County, Mississippi, USA. Sci. Total Environ. 2021, 802, 149716. [Google Scholar] [CrossRef] [PubMed]
- BP. Statistical Review of World Energy. Available online: https://www.bp.com/content/dam/bp/business-sites/en/global/corporate/pdfs/energy-economics/statistical-review/bp-stats-review-2021-full-report.pdf?utm_source=BP_Global_GroupCommunications_UK_external&utm_medium=email&utm_campaign=11599394_Statistical%20Review%202020%20-%20on%20the%20day%20reminder&dm_i=1PGC%2C6WM5E%2COV0LQ4%2CRQW75%2C1 (accessed on 26 October 2021).
- Neininger, B.G.; Kelly, B.F.J.; Hacker, J.M.; Lu, X.; Schwietzke, S. Coal seam gas industry methane emissions in the Surat Basin, Australia: Comparing airborne measurements with inventories. Philos Trans. A Math. Phys. Eng. Sci. 2021, 379, 20200458. [Google Scholar] [CrossRef]
- Hendel, J.; Lukanko, L.; Macuda, J.; Kosakowski, P.; Loboziak, K. Surface geochemical survey in the vicinity of decommissioned coal mine shafts. Sci. Total Environ. 2021, 779, 146385. [Google Scholar] [CrossRef]
- Jia, L.; Peng, S.; Xu, J.; Yan, F. Interlayer interference during coalbed methane coproduction in multilayer superimposed gas-bearing system by 3D monitoring of reservoir pressure: An experimental study. Fuel 2021, 304, 121472. [Google Scholar] [CrossRef]
- Ge, Z.; Cao, S.; Lu, Y.; Gao, F. Fracture mechanism and damage characteristics of coal subjected to a water jet under different triaxial stress conditions. J. Pet. Sci. Eng. 2022, 208, 109157. [Google Scholar] [CrossRef]
- Zhang, L.; Ge, Z.; Lu, Y.; Zhou, Z.; Xiao, S.; Zuo, S. Permeability Enhancement and Methane Drainage Capacity of Tree-type Boreholes to Stimulate Low-permeability Coal Seams. Arab. J. Sci. Eng. 2020, 46, 573–586. [Google Scholar] [CrossRef]
- Ge, Z.; Lu, Y.; Zhou, D.; Zuo, W.; Xia, B. Study on regular and mechanism of coal bed methane desorption experiment under sonic vibrating of cavitation water jets. Meitan Xuebao/J. China Coal Soc. 2011, 36, 1150–1155. [Google Scholar]
- Bo, L.; Liu, M.; Liu, Y.; Wang, N.; Guo, X. Research on pressure relief scope of hydraulic flushing bore hole. Procedia Eng. 2011, 26, 382–387. [Google Scholar] [CrossRef] [Green Version]
- Kong, X.; Wang, E.; Liu, X.; Li, N.; Chen, L.; Feng, J.; Kong, B.; Li, D.; Liu, Q. Coupled analysis about multi-factors to the effective influence radius of hydraulic flushing: Application of response surface methodology. J. Nat. Gas Sci. Eng. 2016, 32, 538–548. [Google Scholar] [CrossRef]
- Liu, Q.; Cheng, Y.; Dong, J.; Liu, Z.; Zhang, K.; Wang, L. Non-Darcy Flow in Hydraulic Flushing Hole Enlargement-Enhanced Gas Drainage: Does It Really Matter? Geofluids 2018, 2018, 1–15. [Google Scholar] [CrossRef]
- Zhang, H.; Cheng, Y.; Yuan, L.; Wang, L.; Pan, Z. Hydraulic flushing in soft coal sublayer: Gas extraction enhancement mechanism and field application. Energy Sci. Eng. 2019, 7, 1970–1993. [Google Scholar] [CrossRef] [Green Version]
- Fan, Y.; Shu, L.; Huo, Z.; Hao, J.; Li, Y. Numerical simulation of sectional hydraulic reaming for methane extraction from coal seams. J. Nat. Gas Sci. Eng. 2021, 95, 104180. [Google Scholar] [CrossRef]
- Lu, Y.; Liu, Y.; Li, X.; Kang, Y. A new method of drilling long boreholes in low permeability coal by improving its permeability. Int. J. Coal Geol. 2010, 84, 94–102. [Google Scholar] [CrossRef]
- Lu, Y.; Ge, Z.; Yang, F.; Xia, B.; Tang, J. Progress on the hydraulic measures for grid slotting and fracking to enhance coal seam permeability. Int. J. Min. Sci. Technol. 2017, 27, 867–871. [Google Scholar] [CrossRef]
- Shen, C.; Lin, B.; Sun, C.; Zhang, Q.; Li, Q. Analysis of the stress–permeability coupling property in water jet slotting coal and its impact on methane drainage. J. Pet. Sci. Eng. 2015, 126, 231–241. [Google Scholar] [CrossRef]
- Gao, F.; Xue, Y.; Gao, Y.A.; Zhang, Z.Z.; Teng, T.; Liang, X. Fully coupled thermo-hydro-mechanical model for extraction of coal seam gas with slotted boreholes. J. Nat. Gas Sci. Eng. 2016, 31, 226–235. [Google Scholar] [CrossRef]
- Zhao, Y.; Lin, B.; Liu, T.; Kong, J.; Zheng, Y. Gas flow in hydraulic slotting-disturbed coal seam considering stress relief induced damage. J. Nat. Gas Sci. Eng. 2020, 75, 103160. [Google Scholar] [CrossRef]
- Szott, W.; Słota-Valim, M.; Gołąbek, A.; Sowiżdżał, K.; Łętkowski, P. Numerical studies of improved methane drainage technologies by stimulating coal seams in multi-seam mining layouts. Int. J. Rock Mech. Min. Sci. 2018, 108, 157–168. [Google Scholar] [CrossRef]
- Fan, C.; Li, S.; Luo, M.; Yang, Z.; Lan, T. Numerical simulation of hydraulic fracturing in coal seam for enhancing underground gas drainage. Energy Explor. Exploit. 2018, 37, 166–193. [Google Scholar] [CrossRef] [Green Version]
- Xiao, S.; Ge, Z.; Cheng, L.; Zhou, Z.; Zhao, H.; Chen, J. Gas migration mechanism and enrichment law under hydraulic fracturing in soft coal seams: A case study in Songzao coalfield. Energy Sources Part A Recovery Util. Environ. Eff. 2019, 43, 1897–1911. [Google Scholar] [CrossRef]
- Gong, M.; Xiong, B.; Wang, C.; Wang, H. Discussion on distribution of dynamic stress and gas draining efficiency in coal seams by blasting through layers of coal-rock. Chin. J. Rock Mech. Eng. 2012, 31, 2989–2996. [Google Scholar]
- Zhu, W.C.; Wei, C.H.; Li, S.; Wei, J.; Zhang, M.S. Numerical modeling on destress blasting in coal seam for enhancing gas drainage. Int. J. Rock Mech. Min. Sci. 2013, 59, 179–190. [Google Scholar] [CrossRef]
- Xie, Z.; Zhang, D.; Song, Z.; Li, M.; Liu, C.; Sun, D. Optimization of Drilling Layouts Based on Controlled Presplitting Blasting through Strata for Gas Drainage in Coal Roadway Strips. Energies 2017, 10, 1228. [Google Scholar] [CrossRef] [Green Version]
- Zuo, S.; Ge, Z.; Deng, K.; Zheng, J.; Wang, H. Fracture initiation pressure and failure modes of tree-type hydraulic fracturing in gas-bearing coal seams. J. Nat. Gas Sci. Eng. 2020, 77, 103260. [Google Scholar] [CrossRef]
- Li, Q.; Lu, Y.; Ge, Z.; Zhou, Z.; Zheng, J.; Xiao, S. A New Tree-Type Fracturing Method for Stimulating Coal Seam Gas Reservoirs. Energies 2017, 10, 1388. [Google Scholar] [CrossRef] [Green Version]
- Zuo, S.; Ge, Z.; Lu, Y.; Cao, S.; Zhang, L. Analytical and Experimental Investigation of Perforation Layout Parameters on Hydraulic Fracture Propagation. J. Energy Resour. Technol. 2021, 143, 013005. [Google Scholar] [CrossRef]
- Cao, P.; Liu, J.; Leong, Y.-K. A multiscale-multiphase simulation model for the evaluation of shale gas recovery coupled the effect of water flowback. Fuel 2017, 199, 191–205. [Google Scholar] [CrossRef]
- Chen, M.; Hosking, L.J.; Sandford, R.J.; Thomas, H.R. Numerical Analysis of Improvements to CO2 Injectivity in Coal Seams Through Stimulated Fracture Connection to the Injection Well. Rock Mech. Rock Eng. 2020, 53, 2887–2906. [Google Scholar] [CrossRef]
- Ge, Z.L.; Zhang, L.; Sun, J.Z.; Hu, J.H. Fully Coupled Multi-Scale Model for Gas Extraction from Coal Seam Stimulated by Directional Hydraulic Fracturing. Appl. Sci. 2019, 9, 4720. [Google Scholar] [CrossRef] [Green Version]
- Witherspoon, P.A.; Wang, J.S.Y.; Iwai, K.; Gale, J.E. Validity of Cubic Law for fluid flow in a deformable rock fracture. Water Resour. Res. 1980, 16, 1016–1024. [Google Scholar] [CrossRef] [Green Version]
- Zhou, L.; Su, X.; Hou, Z.; Lu, Y.; Gou, Y. Numerical investigation of the hydromechanical response of a natural fracture during fluid injection using an efficient sequential coupling model. Environ. Earth Sci. 2016, 75, 1263. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, J.; Elsworth, D.; Chen, Z.; Connell, L.; Pan, Z. Dual poroelastic response of a coal seam to CO2 injection. Int. J. Greenh. Gas Control 2010, 4, 668–678. [Google Scholar] [CrossRef]
- Zhang, L.; Qi, Q.; Deng, K.; Zuo, S.; Liu, Y. Optimum Layout of Multiple Tree-type Boreholes in Low-Permeability Coal Seams to Improve Methane Drainage Performance. Front. Energy Res. 2021, 9, 732827. [Google Scholar] [CrossRef]
- Lim, K.T.; Aziz, K. Matrix-fracture transfer shape factors for dual-porosity simulators. J. Pet. Sci. Eng. 1995, 13, 169–178. [Google Scholar] [CrossRef]
- Liu, J.; Chen, Z.; Elsworth, D.; Miao, X.; Mao, X. Linking gas-sorption induced changes in coal permeability to directional strains through a modulus reduction ratio. Int. J. Coal Geol. 2010, 83, 21–30. [Google Scholar] [CrossRef]
- Zheng, C.; Chen, Z.; Kizil, M.; Aminossadati, S.; Zou, Q.; Gao, P. Characterisation of mechanics and flow fields around in-seam methane gas drainage borehole for preventing ventilation air leakage: A case study. Int. J. Coal Geol. 2016, 162, 123–138. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Fan, C.; Han, J.; Luo, M.; Yang, Z. A fully coupled thermal-hydraulic-mechanical model with two-phase flow for coalbed methane extraction. J. Nat. Gas Sci. Eng. 2016, 33, 324–336. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Tang, D.; Pan, Z.; Xu, H.; Tao, S.; Liu, Y.; Ren, P. Geological Conditions of Deep Coalbed Methane in the Eastern Margin of the Ordos Basin, China: Implications for Coalbed Methane Development. J. Nat. Gas Sci. Eng. 2018, 53, 394–402. [Google Scholar] [CrossRef]
- Liu, T.; Lin, B.; Fu, X.; Zhao, Y.; Gao, Y.; Yang, W. Modeling coupled gas flow and geomechanics process in stimulated coal seam by hydraulic flushing. Int. J. Rock Mech. Min. Sci. 2021, 142, 104769. [Google Scholar] [CrossRef]
- Feng, Q.; Jin, J.; Zhang, S.; Liu, W.; Yang, X.; Li, W. Study on a Damage Model and Uniaxial Compression Simulation Method of Frozen–Thawed Rock. Rock Mech. Rock Eng. 2021, 55, 187–211. [Google Scholar] [CrossRef]
- Ge, Z.; Zhang, D.; Lu, Y.; Liu, W.; Xiao, S.; Cao, S. Propagation of Stress Wave and Fragmentation Characteristics of Gangue-Containing Coal Subjected to Water Jets. J. Nat. Gas Sci. Eng. 2021, 95, 104137. [Google Scholar] [CrossRef]
- Shen, Z.; Zhou, L.; Li, H.; Lu, Z.; Cai, J. Experimental and Numerical Study on the Anisotropic and Nonlinear Gas Flow Behavior of a Single Coal Fracture under Loading. Energy Fuels 2020, 34, 4230–4242. [Google Scholar] [CrossRef]
- Li, W.-S.; Jiang, B.-Y.; Gu, S.-T.; Yang, X.-X.; Shaikh, F.U.A. Experimental study on the shear behavior of grout-infilled specimens and micromechanical properties of grout-rock interface. J. Cent. South Univ. 2022, 29, 1686–1700. [Google Scholar] [CrossRef]
- Ge, Z.; Li, S.; Zhou, Z.; Lu, Y.; Xia, B.; Tang, J. Modeling and Experiment on Permeability of Coal with Hydraulic Fracturing by Stimulated Reservoir Volume. Rock Mech. Rock Eng. 2018, 52, 2605–2615. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, L.; Ge, Z.; Zhou, Z.; Deng, K.; Zuo, S. Fracture and pore structure dynamic evolution of coals during hydraulic fracturing. Fuel 2020, 259, 116272. [Google Scholar] [CrossRef]
- Zhu, W.C.; Wei, C.H.; Liu, J.; Qu, H.Y.; Elsworth, D. A Model of Coal–Gas Interaction under Variable Temperatures. Int. J. Coal Geol. 2011, 86, 213–221. [Google Scholar] [CrossRef]
- Zhang, C.; Xu, J.; Peng, S.; Li, Q.; Yan, F. Experimental study of drainage radius considering borehole interaction based on 3D monitoring of gas pressure in coal. Fuel 2019, 239, 955–963. [Google Scholar] [CrossRef]
- Zhang, L.; Ge, Z.; Lu, Y.; Zhou, Z.; Xiao, S.; Deng, K. Tree-Type Boreholes in Coal Mines for Enhancing Permeability and Methane Drainage: Theory and an Industrial-Scale Field Trial. Nat. Resour. Res. 2020, 29, 3197–3213. [Google Scholar] [CrossRef]
- Kumar, H.; Elsworth, D.; Liu, J.; Pone, D.; Jonathan, P. Mathews. Permeability Evolution of Propped Artificial Fractures in Coal on Injection of CO2. J. Pet. Sci. Eng. 2015, 133, 695–704. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, L.; Tu, S.; Hao, D.; Teng, T. Experimental and Numerical Study of the Influence of Gas Pressure on Gas Permeability in Pressure Relief Gas Drainage. Transp. Porous Media 2018, 124, 995–1015. [Google Scholar] [CrossRef]






| Parameters | Value | Unit |
|---|---|---|
| Size of cylindrical coal sample (-) | Φ100 × 200 | M × m |
| Inject pressure (pin) | [3,4,5,6,7] | MPa |
| Elastic modulus of coal (E) | 1850 | MPa |
| Poisson’s ratio (υ) | 0.28 | -- |
| ) | 1444 | kg/m3 |
| Ash content of coal (A) | 16.43 | % |
| Water content of coal (W) | 1.32 | % |
| ) | 0.0287 | m3/kg |
| Langmuir pressure constant () | 0.756 | MPa |
| CH4′s dynamic viscosity (μ) | 1.84 × 10−5 | Pa·s |
| Initial fracture aperture at the stress-free state (b0) | 0.002 | m |
| Intrinsic permeability of the cleat system (kf0) | 0.0077 | mD |
| Initial temperature (T) | 323 | K |
| ) | 0.025 | -- |
| Fracture compressibility (cf) | 0.21 | MPa−1 |
| -- | Measured Value | Simulated Value | Relative Error |
|---|---|---|---|
| Total volume of methane within 60 s | 15.9 ml | 15.132 mL | 4.83% |
| Methane flow rate at stage II | 0.264 mL/s | 0.252 mL/s | 4.55% |
| Parameters | Value | Unit |
|---|---|---|
| Model dimension | 50 × 50 | m × m |
| Maximum horizontal stress, σH | 19.5 | MPa |
| Minimum horizontal stress, σh | 12.5 | MPa |
| Initial angle of tree-type fracturing borehole, θ | 10 | ° |
| Initial ratio of adjacent sub-borehole, ri | 0.9 | -- |
| Elastic modulus of coal, E | 2000 | MPa |
| Elastic modulus of coal grains, Em | 8469 | MPa |
| Tensile strength of coal, σt | 0.58 | MPa |
| Poisson’s ratio, υ | 0.23 | -- |
| CH4′s dynamic viscosity, μ | 1.84 × 10−5 | Pa·s |
| Ash content in coal, A | 0.243 | % |
| Water content in coal, W | 0.035 | % |
| Coal’s density, ρc | 1400 | kg/m3 |
| Standard atmospheric pressure, pa | 0.1013 | MPa |
| Coal seam methane pressure, p0 | 1 | MPa |
| Initial coal seam temperature, T0 | 323 | K |
| Thermal expansion coefficient of coal, αT | 2.4 × 10−5 | K−1 |
| Specific heat constant of coal skeleton, Cs | 1250 | |
| Specific heat capacity of methane, Cg | 1625 | |
| Thermal conductivity of coal skeleton, λs | 0.2 | J/(m∙s∙K) |
| Langmuir volume constant, VL | 21 × 10−3 | m3/kg |
| Langmuir pressure constant, PL | 1.729 | MPa |
| Initial permeability of the cleat system, kf0 | 0.0218 | mD |
| Intrinsic permeability of the coal matrix, km0 | 1 × 10−18 | m2 |
| Intrinsic porosity of the coal matrix, ϕm0 | 0.07 | -- |
| Initial aperture of stimulated fractures, b0 | 2 | mm |
| Stimulated fractures’ compressibility, cf | 0.21 | MPa−1 |
| Langmuir volume strain, εL | 0.025 | -- |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Qi, Q.; Chen, X.; Zuo, S.; Deng, K.; Bi, R.; Chai, J. Impact of Stimulated Fractures on Tree-Type Borehole Methane Drainage from Low-Permeability Coal Reservoirs. Minerals 2022, 12, 940. https://doi.org/10.3390/min12080940
Zhang L, Qi Q, Chen X, Zuo S, Deng K, Bi R, Chai J. Impact of Stimulated Fractures on Tree-Type Borehole Methane Drainage from Low-Permeability Coal Reservoirs. Minerals. 2022; 12(8):940. https://doi.org/10.3390/min12080940
Chicago/Turabian StyleZhang, Liang, Qingjie Qi, Xuexi Chen, Shaojie Zuo, Kai Deng, Ruiqing Bi, and Jiamei Chai. 2022. "Impact of Stimulated Fractures on Tree-Type Borehole Methane Drainage from Low-Permeability Coal Reservoirs" Minerals 12, no. 8: 940. https://doi.org/10.3390/min12080940
APA StyleZhang, L., Qi, Q., Chen, X., Zuo, S., Deng, K., Bi, R., & Chai, J. (2022). Impact of Stimulated Fractures on Tree-Type Borehole Methane Drainage from Low-Permeability Coal Reservoirs. Minerals, 12(8), 940. https://doi.org/10.3390/min12080940








