Effect of Heat Transfer Driving Force and Ice Seed Loading on the Production of Ice and Salt from a Dilute Brine Treated Using Eutectic Freeze Crystallization
Abstract
:1. Introduction
2. Background
3. Materials and Methods
3.1. Experimental Design
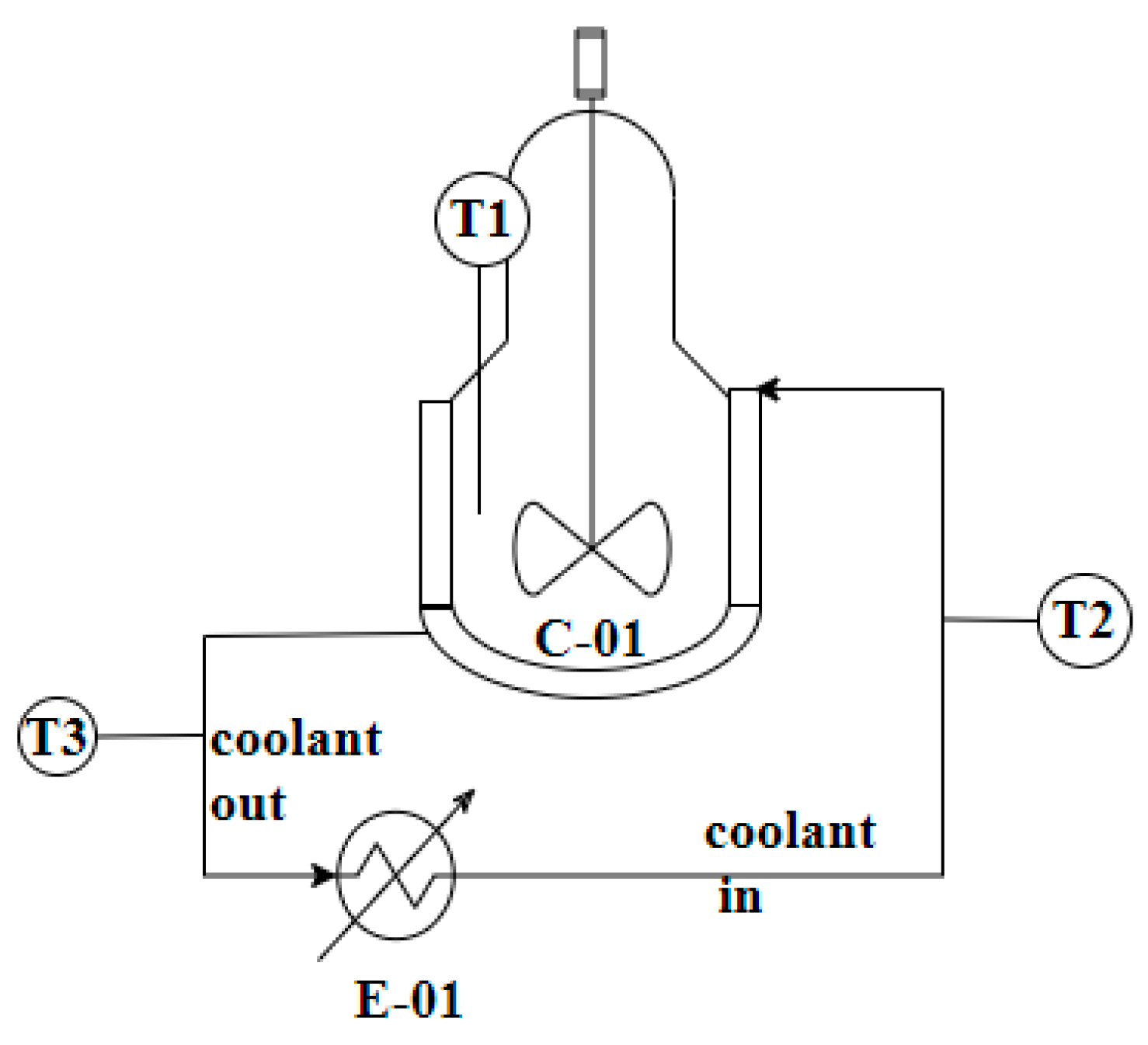
3.2. Experimental Set Up
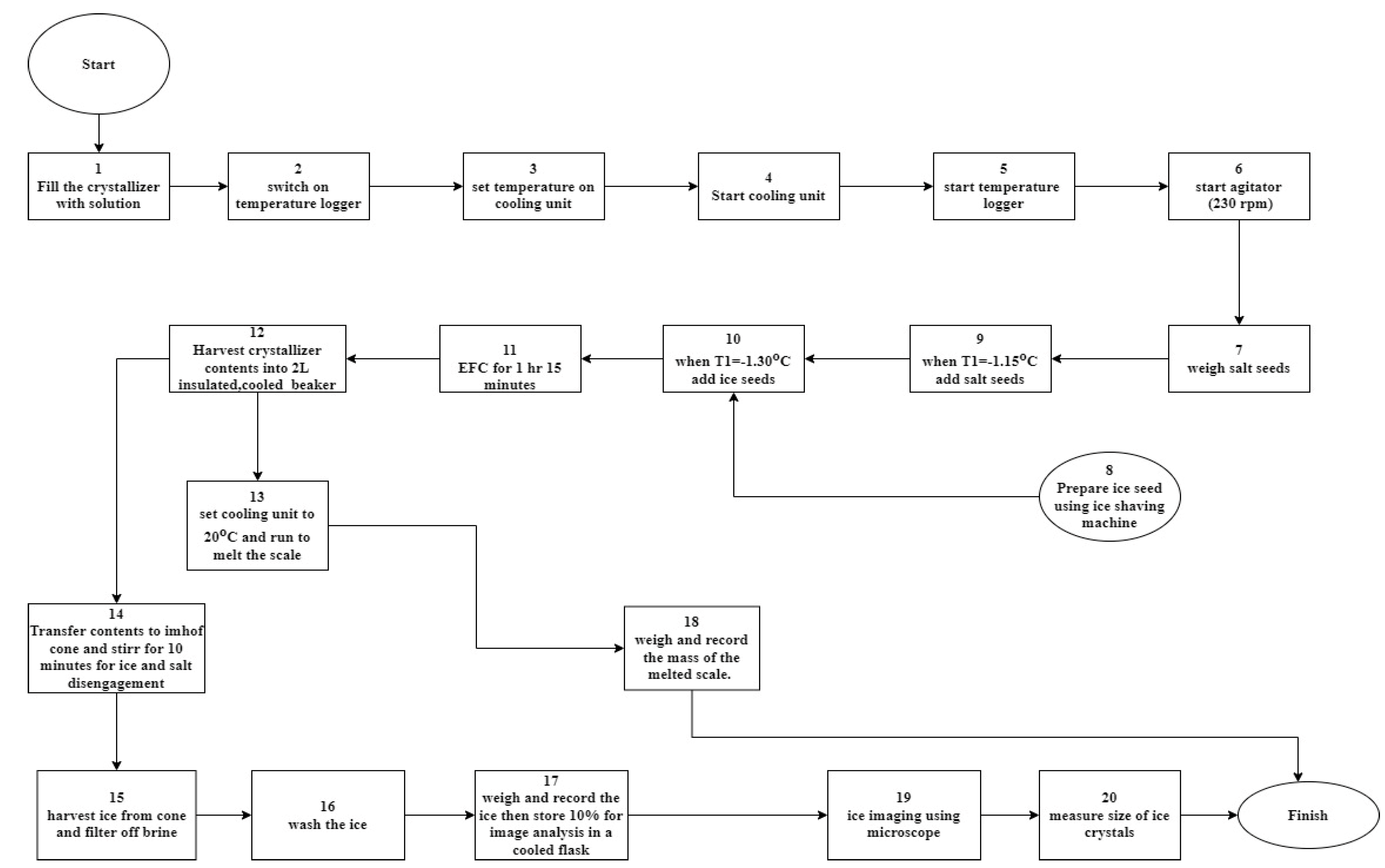
3.3. Experimental Procedure
4. Results and Discussion
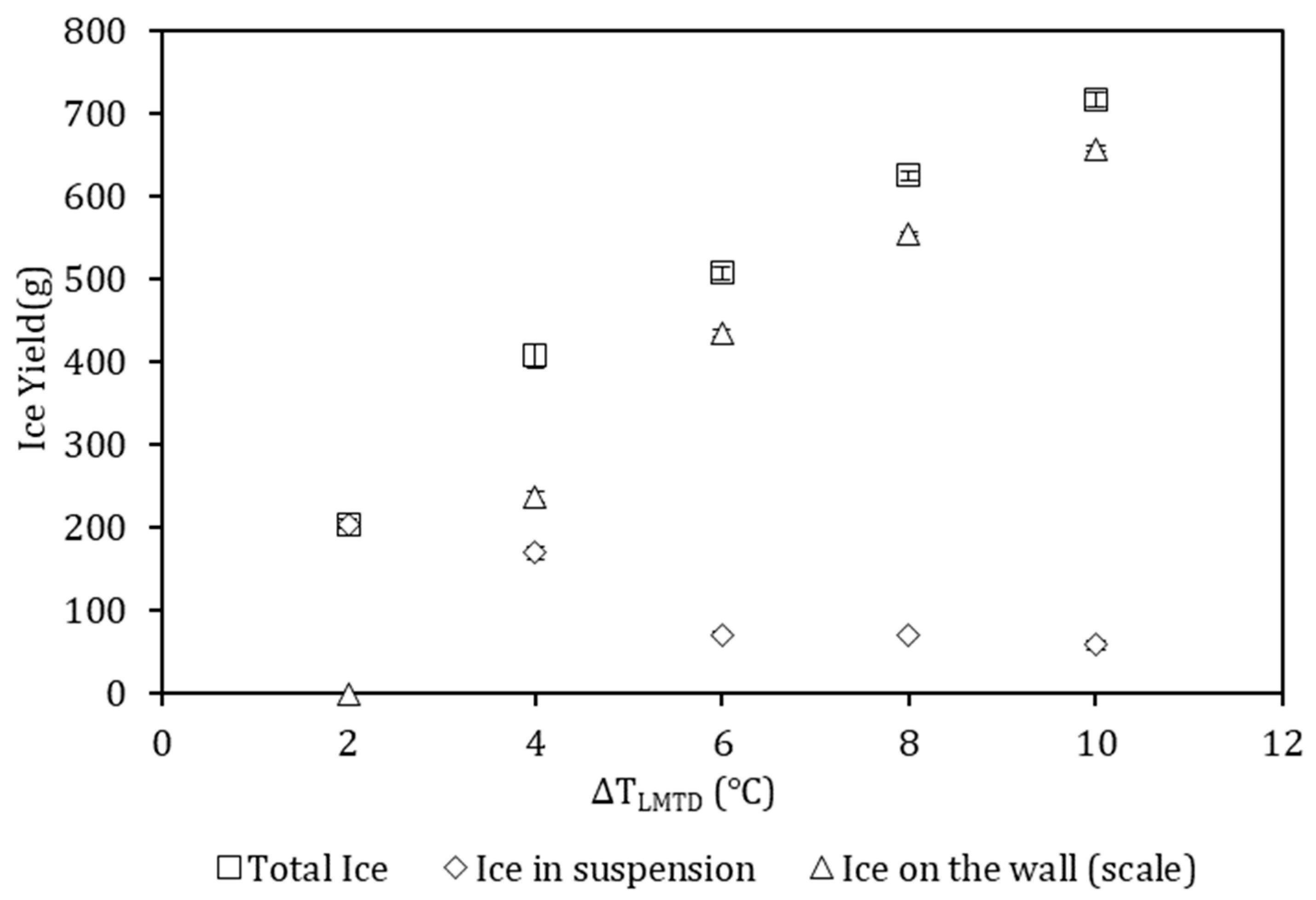
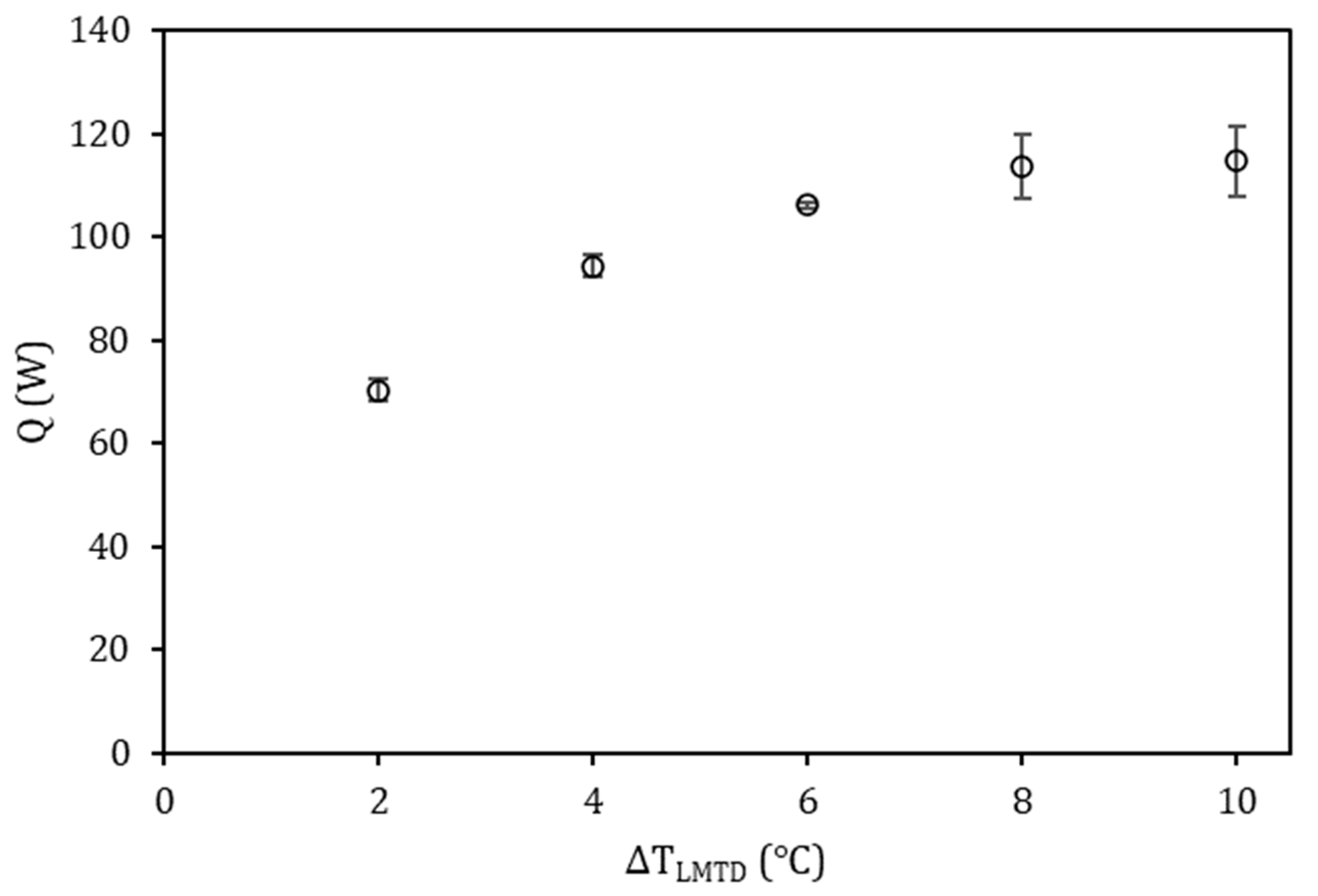
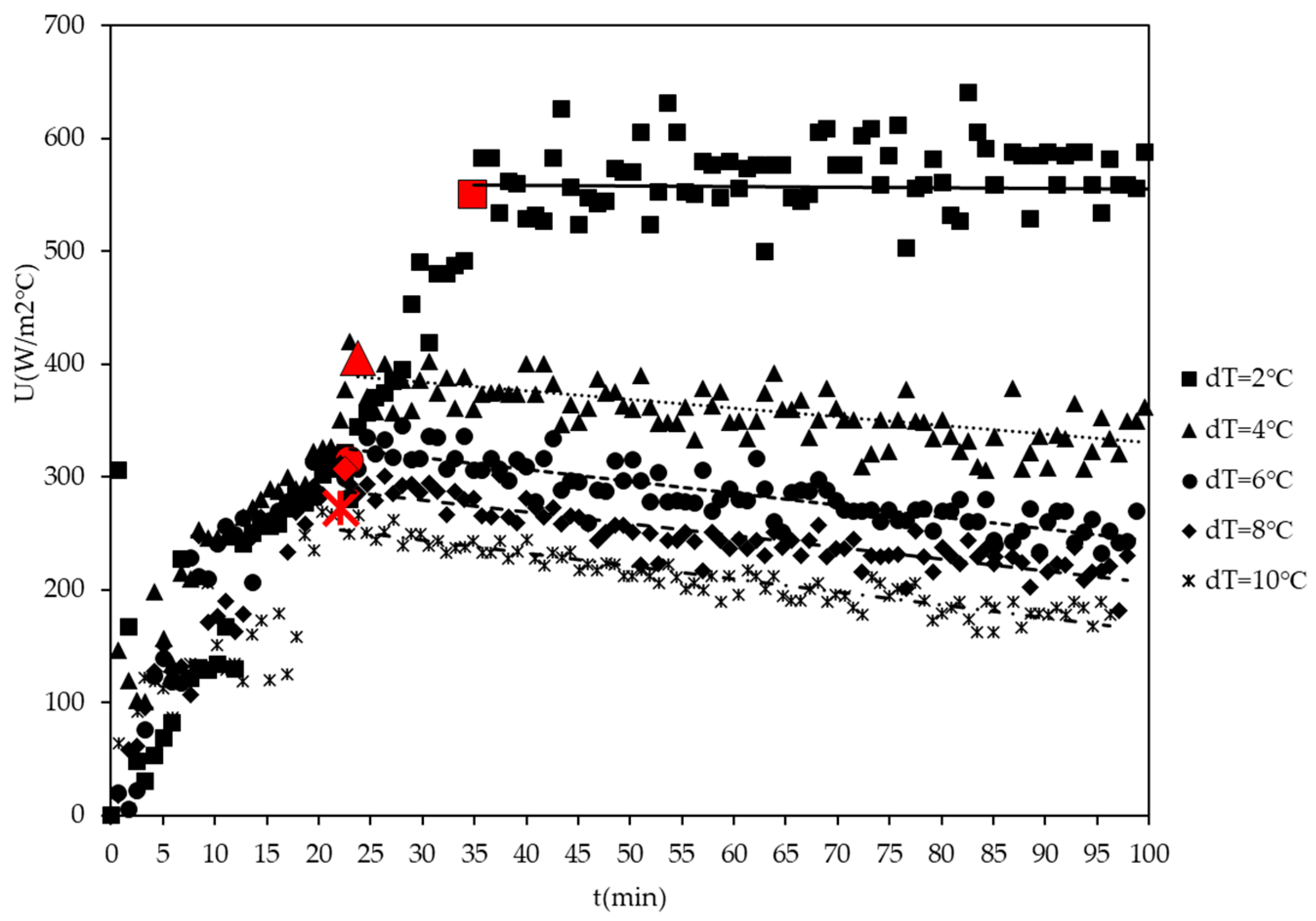
4.1. Effect of ΔTLMTD on Ice Yield
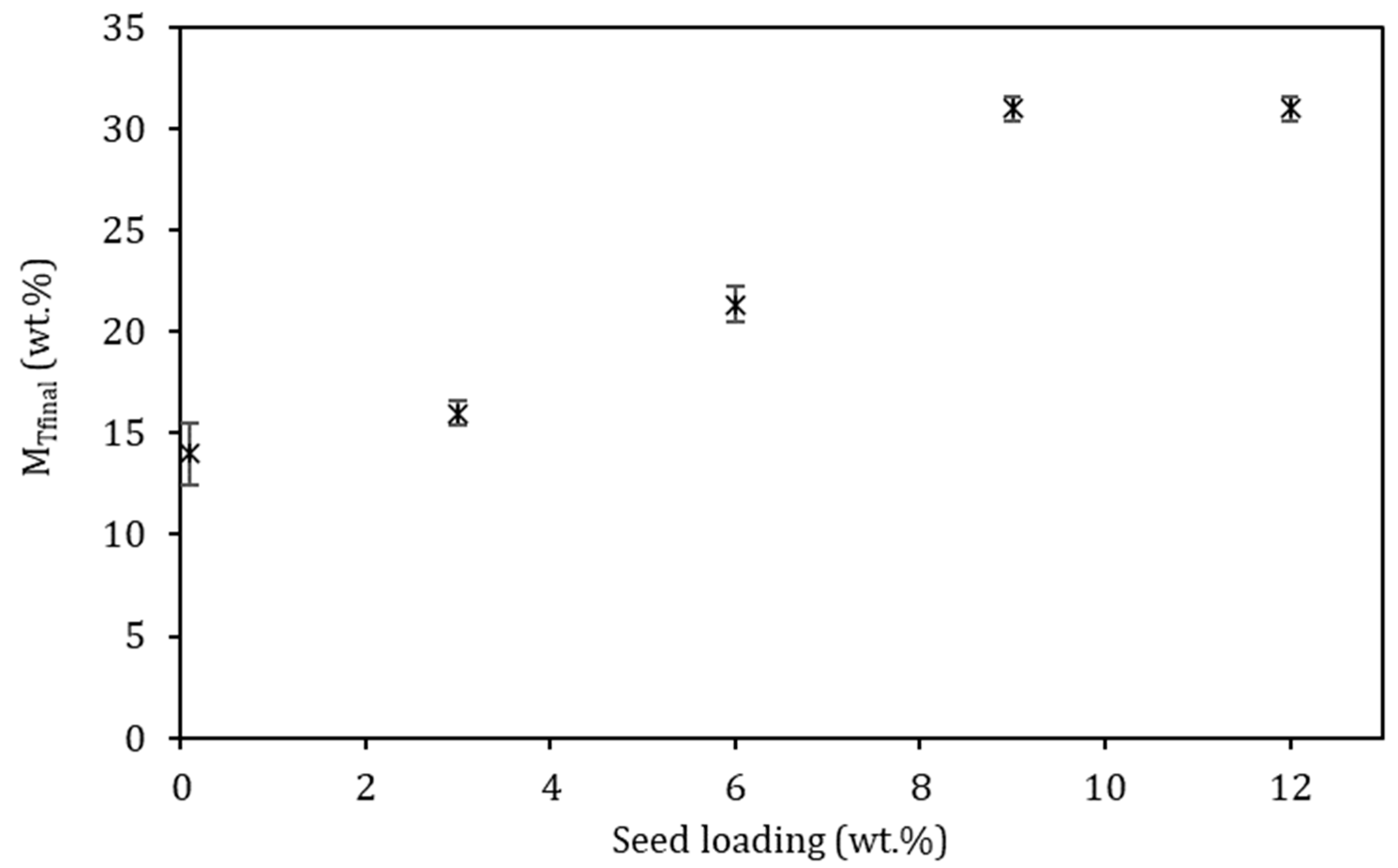
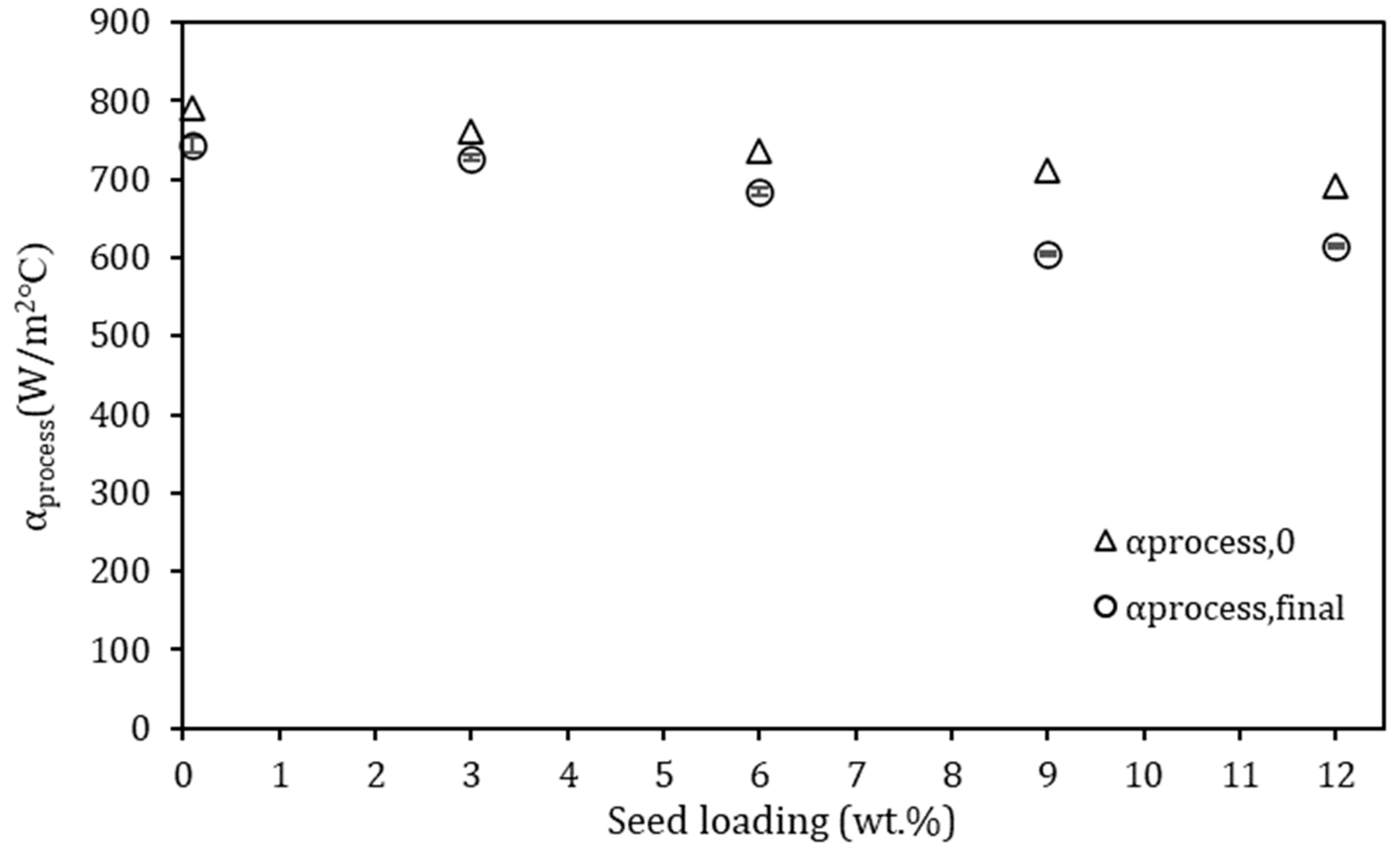
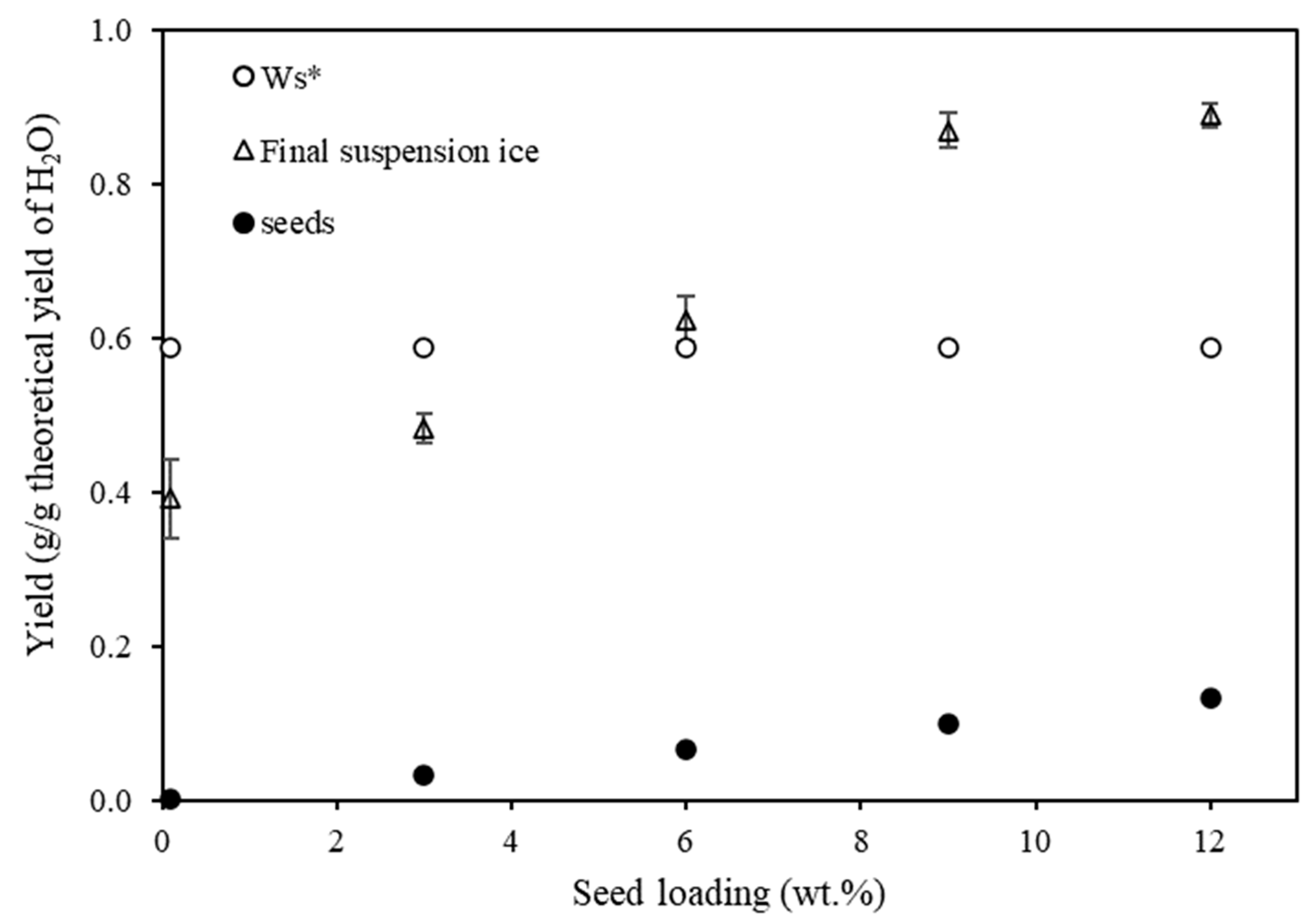
4.2. Effect of Ice Seed Loading on Ice Yield
5. Conclusions
- The ice on the wall (scale layer) made up an increasing amount of the ice yield as ΔTLMTD increased, with the scale contributing ≥91% of the total yield at the highest ΔTLMTD of 10°C.
- The ice on the wall caused a significant reduction of up to 67% in the heat transfer rate between the coolant and the bulk, demonstrating the significance of avoiding scale formation in EFC.
- The amount of ice formed in suspension gradually increased as the seed loading increased while the amount of ice formed on the wall remained relatively constant across the full range of seed loadings. A maximum in the amount of ice in suspension and a minimum in the amount of ice on the wall were observed when a seed loading of 9 wt.% was used. At this seed loading, there was 50% more ice in the bulk than on the wall.
- The observed reduction in scaling as the seed loading increased was attributed to the provision of more surface area at higher seed loading, which enhanced ice crystallization in the bulk and suppressed heterogeneous nucleation at the wall.
- Although the yield of ice in suspension increased as seed loading increased, the final particle size distribution of the ice was found to be unimodal and independent of the initial seed loading. It was concluded that both nucleation and growth/size enlargement of ice crystals occurred during the crystallization period.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| SL (wt.%) | Suspension Ice | Scale | Total Ice |
|---|---|---|---|
| g/g Theoretical Yield | |||
| 0.1 | 0.12 | 0.18 | 0.30 |
| 3 | 0.11 | 0.19 | 0.30 |
| 6 | 0.13 | 0.19 | 0.32 |
| 9 | 0.22 | 0.15 | 0.37 |
| 12 | 0.19 | 0.17 | 0.36 |
Appendix B
References
- Bello, A.S.; Zouari, N.; Da’Ana, D.A.; Hahladakis, J.N.; Al-Ghouti, M.A. An overview of brine management: Emerging desalination technologies, life cycle assessment, and metal recovery methodologies. J. Environ. Manag. 2021, 288, 112358. [Google Scholar] [CrossRef] [PubMed]
- Ogunbiyi, O.; Saththasivam, J.; Al-Masri, D.; Manawi, Y.; Lawler, J.; Zhang, X.; Liu, Z. Sustainable brine management from the perspectives of water, energy and mineral recovery: A comprehensive review. Desalination 2021, 513, 115055. [Google Scholar] [CrossRef]
- Lewis, A.E.; Nathoo, J.; Thomsen, K.; Kramer, H.J.; Witkamp, G.J.; Reddy, S.T.; Randall, D.G. Design of a Eutectic Freeze Crystallization process for multicomponent wastewater stream. Chem. Eng. Res. Des. 2010, 88, 1290–1296. [Google Scholar] [CrossRef]
- Rodriguez Pascual, M.; Genceli, F.; Trambitas, D.; Evers, H.; Van Spronsen, J.; Witkamp, G. A novel scraped cooled wall crystallizer: Recovery of sodium carbonate and ice from an industrial aqueous solution by eutectic freeze crystallization. Chem. Eng. Res. Des. 2010, 88, 1252–1258. [Google Scholar] [CrossRef]
- Van der Ham, F.; Witkamp, G.J.; de Graauw, J.; Rosmalen, G.M. Eutectic freeze crystallization: Application to process streams and wastewater purification. Chem. Eng. Processing Process Intensif. 1998, 37, 207–213. [Google Scholar] [CrossRef]
- Chivavava, J.; Jooste, D.; Aspeling, B.; Peters, E.; Ndoro, D.; Heydenrych, H.; Pascual, M.R.; Lewis, A. CHAPTER 14 Continuous Eutectic Freeze Crystallization; The Handbook of Continuous Crystallization; The Royal Society of Chemistry: London, UK, 2020; pp. 508–541. [Google Scholar]
- Chivavava, J.; Aspeling, B.; Jooste, D.; Peters, E.; Ndoro, D.; Heydenrych, H.; Rodriguez Pascual, M.; Lewis, A.E. Continuous Eutectic Freeze Crystallization; Water Research Commission Report K5/2229; Water Research Commission: Pretoria, South Africa, 2017. [Google Scholar]
- van der Ham, F.; Seckler, M.M.; Witkamp, G.J. Eutectic freeze crystallization in a new apparatus: The cooled disk column crystallizer. Chem. Eng. Processing Process Intensif. 2004, 43, 161–167. [Google Scholar] [CrossRef]
- Vaessen, R.J.C.; Himawan, C.; Seckler, M.M.; Witkamp, G.J. Evaluation of a newly developed eutectic freeze crystallizer: Scraped cooled wall crystallizer. In Proceedings of the 15th International Symposium on Industrial Crystallization, Sorrento, Italy, 15–18 September 2002. [Google Scholar]
- Genceli, F.; Gärtner, R.; Witkamp, G. Eutectic freeze crystallization in a 2nd generation cooled disk column crystallizer for MgSO4·H2O system. J. Cryst. Growth 2005, 275, e1369–e1372. [Google Scholar] [CrossRef]
- Himawan, C.; Kramer, H.; Witkamp, G. Study on the recovery of purified MgSO4·7H2O crystals from industrial solution by eutectic freezing. Sep. Purif. Technol. 2006, 50, 240–248. [Google Scholar] [CrossRef]
- Genceli, F.E.; Popescu, D.; Gärtner, R.; Rodriguez, M.; Witkamp, G.-J. 3rd generation cooled disk column crystallizer and a skid mounted unit for eutectic freeze crystallization. In Proceedings of the 16th Annual Symposium on Industrial Crystallization, Dresden Germany, 11–14 September 2005; VDI Berichte: Dresden Germany, 2005; pp. 855–860. [Google Scholar]
- Vaessen, R.; Seckler, M.; Witkamp, G. Heat transfer in scraped eutectic crystallizers. Int. J. Heat Mass Transf. 2004, 47, 717–728. [Google Scholar] [CrossRef]
- Genceli, F.E. Scalling up Eutectic Freeze Crystallization. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2008. [Google Scholar]
- Lewis, A.E.; Seckler, M.M.; Kramer, H.; van Rosmalen, G.M. Industrial Crystallization: Fundamentals and Applications; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Doki, N.; Kubota, N.; Sato, A.; Yokota, M.; Hamada, O.; Masumi, F. Scaleup experiments on seeded batch cooling crystallization of potassium alum. AIChE J. 1999, 45, 2527–2533. [Google Scholar] [CrossRef]
- Doki, N.; Kubota, N.; Yokota, M.; Chianese, A. Determination of Critical Seed Loading Ratio for the Production of Crystals of Uni-Modal Size Distribution in Batch Cooling Crystallization of Potassium Alum. J. Chem. Eng. Jpn. 2002, 35, 670–676. [Google Scholar] [CrossRef]
- Leyland, D.; Chivavava, J.; Lewis, A.E. Investigations into ice scaling during eutectic freeze crystallization of brine streams at low scraper speeds and high supersaturation. Sep. Purif. Technol. 2019, 220, 33–41. [Google Scholar] [CrossRef]
- OLI-Systems-Inc. OLI Studio 10.0 Morris Plains; OLI Systems Inc.: Parsippany, NJ, USA, 2020. [Google Scholar]
- Kaboyashi, A.; Shirai, Y. A method for making large, agglomerated ice crystals for freeze crystallization. J. Food En-Gineering 1996, 27, 1–15. [Google Scholar] [CrossRef]
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. NIH Image to ImageJ: 25 Years of image analysis. Nat. Methods 2012, 9, 671–675. [Google Scholar] [CrossRef] [PubMed]
- Beckmann, W. Crystallization: Basic Concepts and Industrial Applications; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Vaessen, R.J.C.; Janse, B.J.H.; Seckler, M.M.; Witkamp, G.J. Evaluation of the Performance of a Newly Developed Eutectic Freeze Crystallizer: Scraped Cooled Wall CrystalIizer. Chem. Eng. Res. Des. 2003, 81, 1363–1372. [Google Scholar] [CrossRef]
- Mardles, E.W.J. Viscosity of Suspensions and the Einstein Equation. Nature 1940, 145, 970. [Google Scholar] [CrossRef]
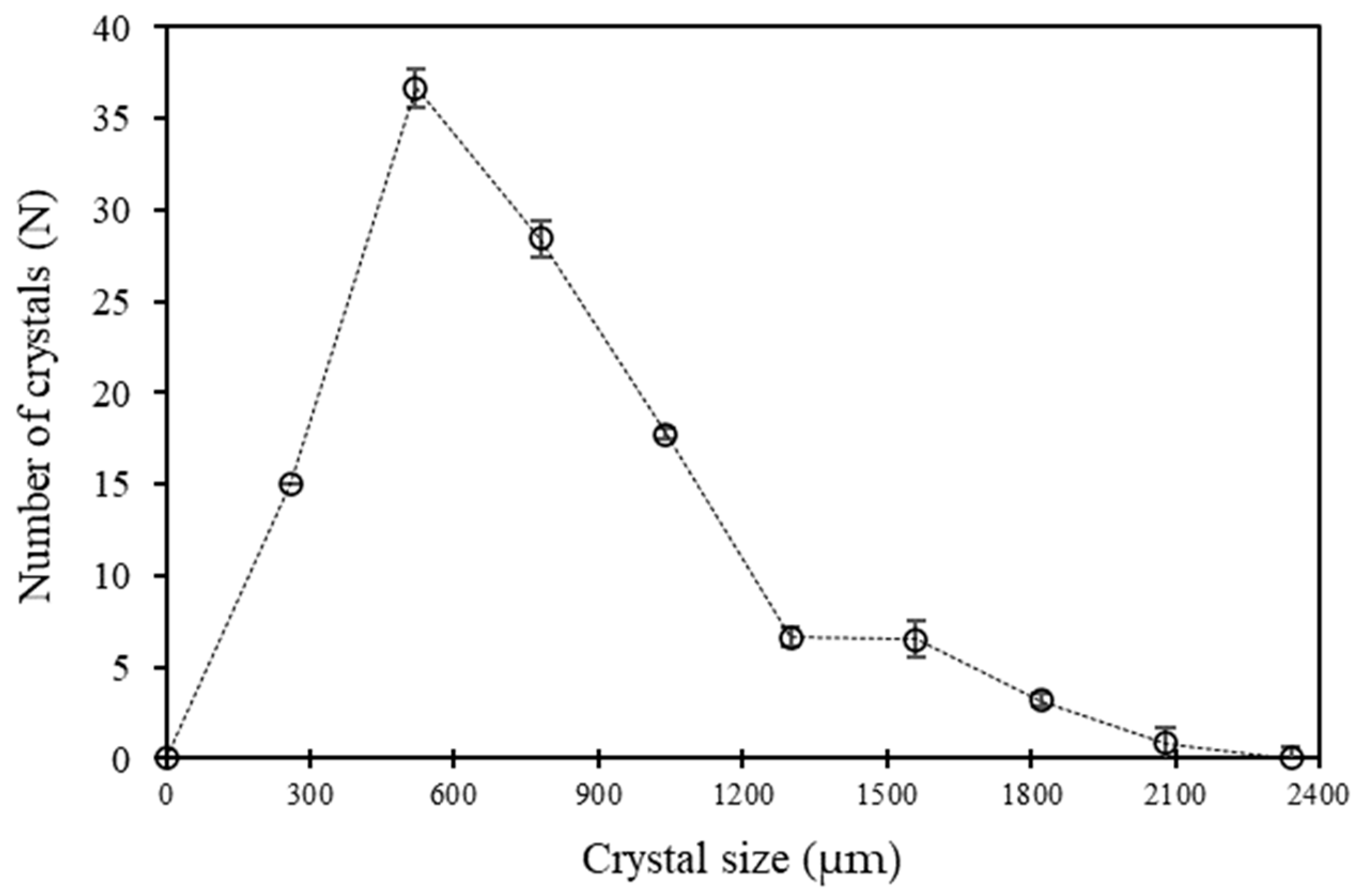







| Seed Loading (wt.%) | Seeds | Ice Product Sizes | ||||
|---|---|---|---|---|---|---|
| d10 (μm) | d50 (μm) | d90 (μm) | d10 (μm) | d50 (μm) | d90 (μm) | |
| 0.1 | 260 | 573 | 1261 | 1200 | 1786 | 2375 |
| 3 | 1075 | 1636 | 2233 | |||
| 6 | 1051 | 1560 | 2020 | |||
| 9 | 1188 | 1744 | 2309 | |||
| 12 | 1112 | 1663 | 2275 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Spencer, A.; Chivavava, J.; Lewis, A.E. Effect of Heat Transfer Driving Force and Ice Seed Loading on the Production of Ice and Salt from a Dilute Brine Treated Using Eutectic Freeze Crystallization. Minerals 2022, 12, 1094. https://doi.org/10.3390/min12091094
Spencer A, Chivavava J, Lewis AE. Effect of Heat Transfer Driving Force and Ice Seed Loading on the Production of Ice and Salt from a Dilute Brine Treated Using Eutectic Freeze Crystallization. Minerals. 2022; 12(9):1094. https://doi.org/10.3390/min12091094
Chicago/Turabian StyleSpencer, Anotidaishe, Jemitias Chivavava, and Alison Emslie Lewis. 2022. "Effect of Heat Transfer Driving Force and Ice Seed Loading on the Production of Ice and Salt from a Dilute Brine Treated Using Eutectic Freeze Crystallization" Minerals 12, no. 9: 1094. https://doi.org/10.3390/min12091094
APA StyleSpencer, A., Chivavava, J., & Lewis, A. E. (2022). Effect of Heat Transfer Driving Force and Ice Seed Loading on the Production of Ice and Salt from a Dilute Brine Treated Using Eutectic Freeze Crystallization. Minerals, 12(9), 1094. https://doi.org/10.3390/min12091094







