A Multi-Objective Approach for Optimizing the Layout of Additional Boreholes in Mineral Exploration

Abstract

Accurate subsurface exploration requires an optimal network of boreholes. This paper proposes a multi-objective approach to optimize the layout of additional exploratory boreholes. In order to illustrate this approach, geochemical analyses of core samples at the eastern part of the Kahang copper deposit, Central Iran, were used. A measure of the grade uncertainty (kriging standard deviation) and a confidence measure on the ore/waste classification were first calculated by implementing ordinary and indicator kriging. An ore value function was then determined to measure the total value of each block by considering the grades of all the effective variables and their ore membership degree derived from a fuzzy treatment of the grades. Finally, a misclassification cost is defined for each block based on the expected economic effects of ore loss and waste dilution. As a result, an index for the selection of additional boreholes was introduced in order to maximize the kriging standard deviation, the ore misclassification cost, and the ore value and to minimize the confidence measure. Applied to the Kahang copper deposit, this index allowed the prioritization of areas for infill sampling, leading to the recommendation for eight vertical and two directional additional boreholes.

1. Introduction

The spatial sampling design describes the sample number and its spatial pattern in a selected area [1]. In the additional sampling stage, we focus on the questions of where to locate additional samples and how many samples are needed to end this stage when spatial data are collected. This situation occurs in various disciplines, including mineral and oil exploration, environmental studies, oceanography, agriculture, meteorology, hydrology, and forestry [2,3]. Optimal additional samples must include valuable information and significantly improve the spatial distribution modeling of the regionalized variables under study [4]. In case of sampling shortage, there is a lack of sufficient knowledge about the target; in the reverse situation, sampling redundancy leads to increased exploration costs [3,4,5]. Borehole drilling is a common tool for the purpose of core sampling for subsurface investigation, in particular, in mineral exploration [5,6,7]. The amount of boreholes and the accuracy of subsequent mineral resource estimations increase during mineral exploration steps.

One of the first attempts to optimize spatial sampling designs is associated with a probabilistic geometry approach [8,9]. The probability of intersection between the target and the exploration network was calculated as a function of the target geometry and its relative orientation concerning the directional and dimensional properties of the exploration network. The target assumed ellipses because the shape of the surface projection of many natural resource targets can be approximated by an ellipse [9,10,11,12]. The optimum spacing of exploratory boreholes was evaluated by maximizing the expected gross drilling return (GDR) [13].

A second solution for optimal sampling design is geostatistical error management. Originally, the foundation of this approach is the reduction of the estimation error measured by a kriging variance or a kriging standard deviation, which can be either a global error [14,15] or an average or a maximum local error [16,17,18]. The samples are either ranked one at a time or as a set of samples are selected (e.g., via the definition of a regular sampling design and a sampling mesh) based on minimizing the kriging variance or kriging standard deviation and the number of samples. These methods have been extended by the use of simulation and optimization algorithms [19,20,21,22,23,24,25].

In the past decades, many other geostatistical objective functions have been proposed as an alternative to the kriging variance for optimal sampling design, such as the weighted kriging variance [26,27,28], interpolation variance [29,30,31], combined variance [31,32,33], conditional variance [34], information entropy [31,35], value of information [36], efficacy of information [37], GET (grade-estimation error-thickness) function [10,38], cross-validation error [39], interquartile range [40], probability interval widths [34,41], probability of classification error [42], probability of threshold exceedance [43], expected ore value [44], expected cost of classification errors [45], or increase of indicated and measured mineral resource categories [46]. These objective functions account for local ore grade variability, expected grade, expected productivity, expected profit, and/or reduction of uncertainty, unlike the kriging variance that only depends on the spatial correlation (variogram) and geometric configuration of the data. However, most of them focus on a single objective for optimizing a spatial sampling design in circumstances where this design should account for a multiplicity of factors.

Geologists, engineers, and investors are not only interested in reducing the uncertainty on the unknown ore grade values but also in how much the additional samples increase the confidence in the ore-waste classification, given some cut-off grades on the main products and by-products, how much they reduce the cost of ore loss (ore material wrongly sent to dump) or of waste dilution (waste material wrongly sent to the processing plant), or how much they increase the potential economic value of the ore material. This is the main motivation of this paper, which proposes a simple and meaningful multi-objective approach for infill-sampling design.

The paper is outlined as follows: Section 2 presents the eastern Kahang porphyry deposit, which is selected for the study, and the available data. The proposed methodology, which mixes statistical, geostatistical, and fuzzy logic considerations, is then described in Section 3 (as summarized in Figure 1), and the results are illustrated and discussed in Section 4. Conclusions follow in Section 5.

2. Case Study: Eastern Kahang Deposit

Deposit

The Kahang porphyry copper deposit is located 73 km NE of Isfahan in Central Iran. This porphyry system is situated on the Urumieh-Dokhtar magmatic arc, which extends from NW to SE and contains the main copper-bearing regions in Iran, such as Sarcheshmeh, Sungun, Meiduk, Darehzar, Sarkuh, and Daralu [47,48,49]. The Kahang ore consists of three main parts: eastern, central, and western; the eastern body has been drilled for a detailed exploration. It mainly consists of andesite, andesite porphyry, dacite porphyry, quartz monzonite, diorite, andesitic breccia, and quartz veins with iron oxide fillings. Andesitic lavas and Eocene volcanic breccias with propylitic alteration as the oldest igneous unit have a high potential for copper–molybdenum mineralization. Dacitic units with porphyry texture are accompanied by quartz-sericite, argillic, and quartz–goethite alterations intruded into andesite rocks. Semi-deep sections of andesite porphyry are intruded by quartz monzonite and diorite stocks with phyllic and propylitic alterations leading to mineralization. The alteration zoning from center to margin includes silicification, phyllic, argillic, and propylitic, respectively. In this porphyry system, the ore minerals comprise chalcocite, covelite, chalcopyrite, pyrite, malachite, chalcantite, magnetite, hematite, jarosite, and goethite; these Fe-hydroxides are concerned with the central part of alteration. The studied area is affected by two fault systems with NE–SW and NW–SE orientations [50,51,52]. In Figure 2, the geological map with the location of the eastern part of the Kahang deposit is depicted.

In the eastern region of Kahang, 32 vertical and directional boreholes were drilled in the various mineral exploration phases, totaling about 15,550 m of drilling. The depth of these boreholes varies from 100 to 700 m, and their dip fluctuates within a range of 60 to 90 degrees. Cores samples were assayed for Cu, Mo, Ag, and Au and were composited to a length of 2 m, which corresponds to the mode of the assayed core lengths. Most often (>95% of the time), the original core length was in the range of 1 to 3 m; core samples larger than 3 m had negligible grades for all the geochemical elements, so their decomposition into 2 m composites was not an issue.

The Kahang deposit has a significant value with copper and molybdenum, which constitute the main products of interest. Their three-dimensional distribution in the composite samples is illustrated in Figure 3. Gold and silver anomalies were also detected in limited areas that are reasonable prospects for eventual economic extraction and may, therefore, be considered by-products. The statistical parameters of Cu, Mo, Ag, and Au are shown in

Table 1. Descriptive statistics of copper, molybdenum, silver, and gold grades in the composite samples.

Parameter	Cu (ppm)	Mo (ppm)	Ag (ppm)	Au (ppm)
Number of data	6205	5760	5169	4657
Minimum	0.000	0.000	0.000	0.000
Maximum	49,200	1479	31.8	0.789
Mean	1800.9	33.76	1.173	0.013
Mode	0.000	1.5	0.6	0.005
Quartile 1	340	3.3	0.36	0.005
Median	890.5	10.8	0.6	0.005
Quartile 3	1988	26.38	1.3	0.015
St. deviation	3209.5	88.73	1.751	0.028

. The mean values are 1800, 34, 1.17, and 0.01 ppm, respectively.

Geologists and engineers of Kahang’s project defined thresholds (cut-offs) for copper (1500 ppm), molybdenum (400 ppm), silver (20 ppm), and gold (0.5 ppm), which have been applied to codify the geochemical grades into indicators. These thresholds are considered in the definition of the recoverable mineral resources subject to an eventual economic extraction by open pit mining.

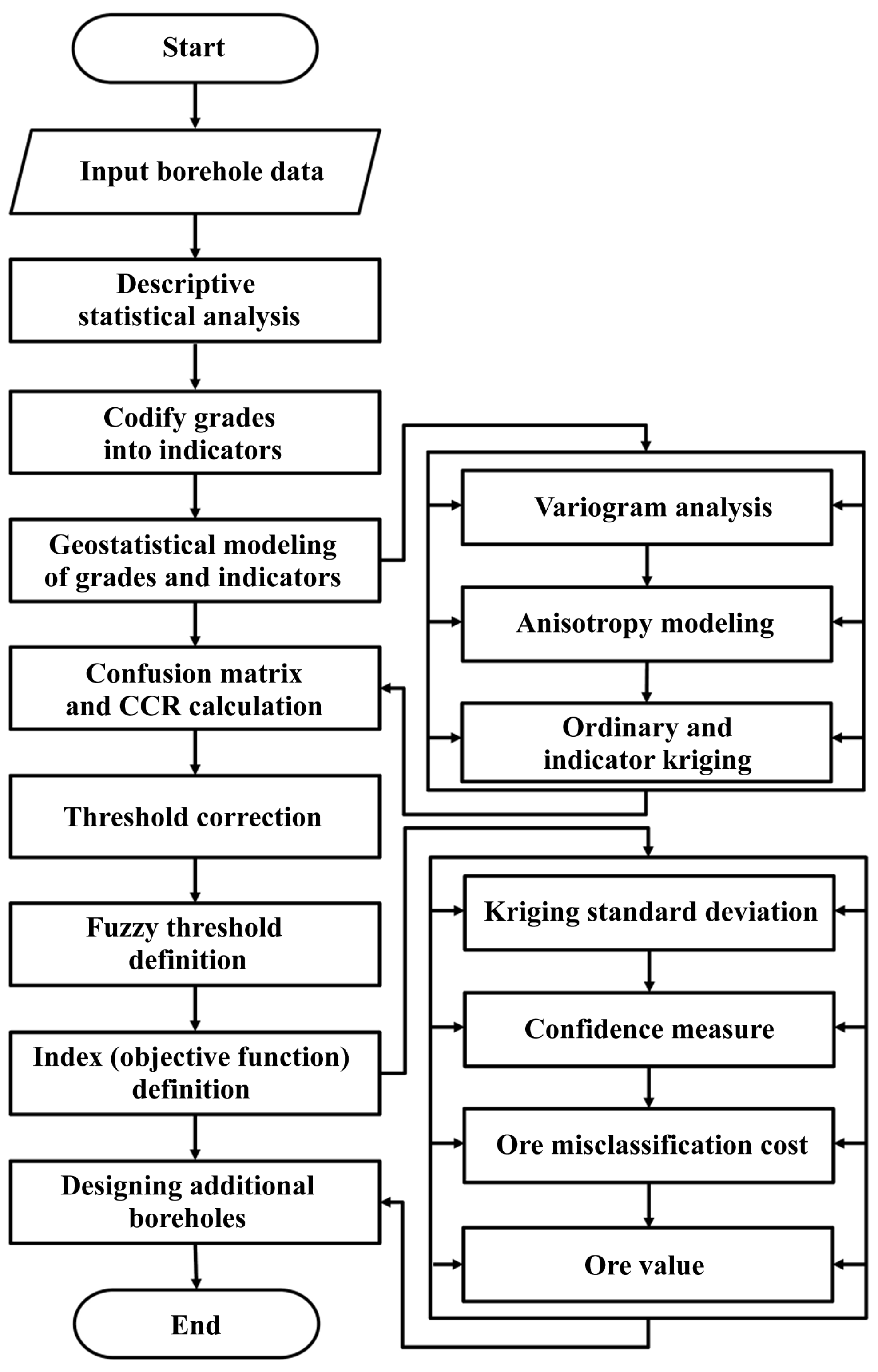
3. Methodology

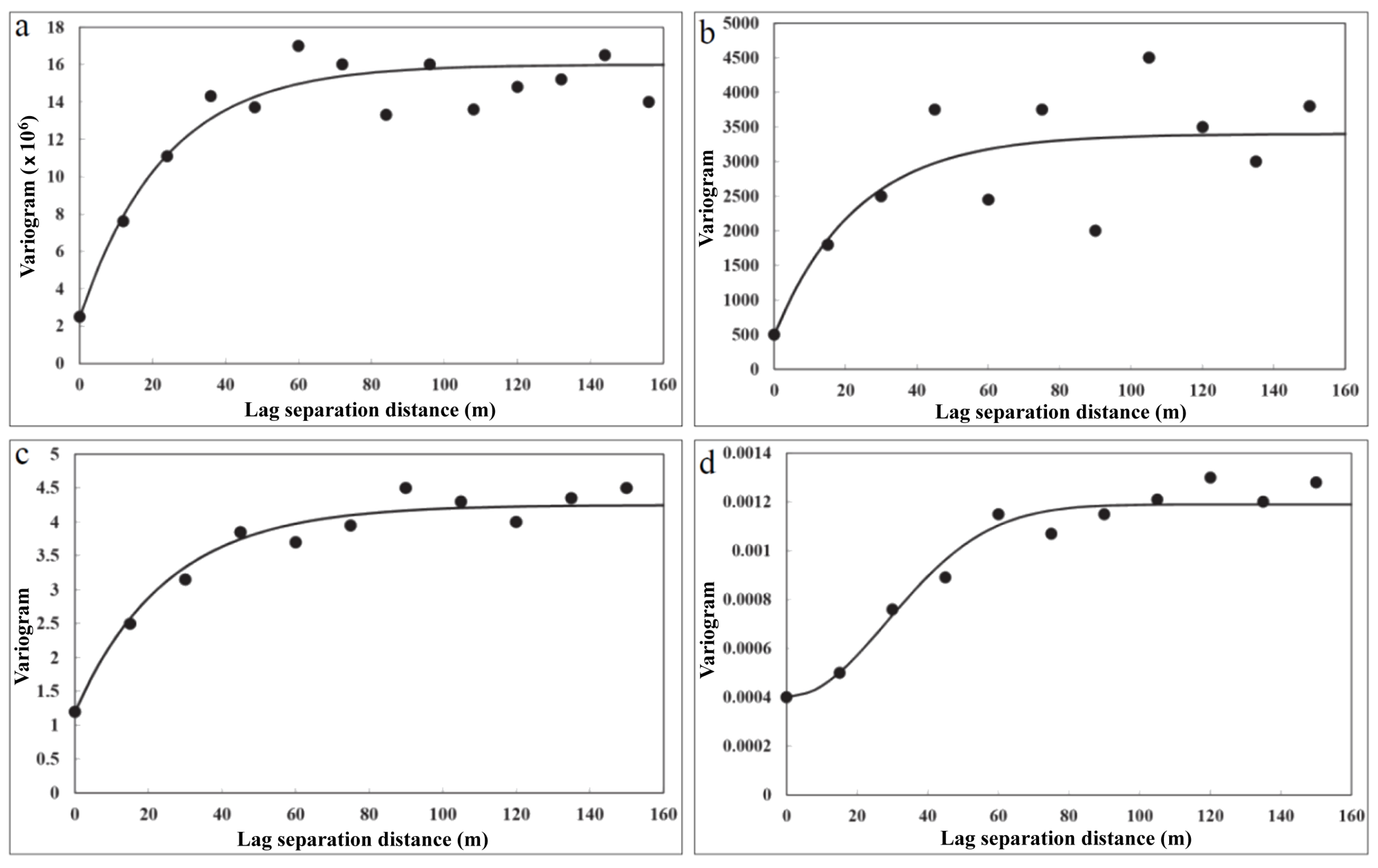
3.1. Directional Variogram Analysis

The composite samples are used for variogram analysis. Three-dimensional experimental variograms are first computed to analyze the spatial distributions of Cu, Mo, Ag, and Au for 24 directions with varying azimuths and inclinations. In the first instance, theoretical variogram models are fitted to the directional experimental variograms in the identified main direction of continuity, which depends on the variable under consideration, with a range of approximately 70 m. The models consider a nugget effect and an exponential structure for Cu, Mo, and Ag or a Gaussian structure for Au. As shown in Figure 4, the relative nugget effect for Cu and Mo is approximately $15\%$, and for Ag and Au, it increases to $30\%$. The fitting of variogram models in the directions of lower continuity will be explained in the next subsection.

In the same way, indicator variograms are calculated based on the indicator data of Cu, Mo, Ag, and Au in the same 24 directions, and theoretical models are fitted in the direction of maximum continuity, involving a nugget effect and an exponential structure for Cu or a spherical structure for Mo, Ag, and Au. The correlation ranges of these models vary from 55 to 100 m. The relative nugget effect of the Ag model is larger than its continuous structure, yet for Cu, Mo, and Au, the spatial structure is considerable (Figure 5).

3.2. Spatial Anisotropy Modeling

Anisotropy can affect the geostatistical estimation procedure and should, therefore, be modeled as accurately as possible [38,53]. In the Kahang deposit, structural features and geological formations with various rock units cause anisotropy of grade distributions. The characteristics of the direction and dimensions of geostatistical anisotropy ellipsoids are the basis for interpreting spatial changes and identifying geological controls. In this research, as explained in the previous subsection, variograms were computed for 24 directions. The anisotropy parameters, which consist of two anisotropy factors (ratio of major axis range to semi-major axis range and of the major axis range to minor axis range) and three rotation angles (azimuth, plunge, and dip) were determined for the four variables based on the experimental directional variograms of the original grades and indicators (

Table 2. Anisotropy parameters of Cu, Mo, Ag, and Au for original grades and indicators.

Case	Variable	Anisotropy Factor (Major/Semimajor)	Anisotropy Factor (Major/Minor)	Azimuth (${}^{\circ }$)	Plunge (${}^{\circ }$)	Dip (${}^{\circ }$)
Original	Cu	1.17	1.32	266.9	47.4	40.5
data	Mo	1.35	1.78	260.3	70.0	0.74
	Ag	1.31	1.93	264.0	60.1	56.6
	Au	1.27	1.45	263.8	61.1	29.7
Indicator	Cu	1.16	1.42	31.1	42.6	62.3
data	Mo	1.27	1.65	52.6	20.6	19.3
	Ag	1.12	1.22	91.6	80.0	46.9
	Au	1.15	1.27	58.6	19.3	28.5

).

3.3. Ordinary Kriging

Ordinary kriging was applied to estimate the three-dimensional spatial distribution of the ore grades (Cu, Mo, Ag, and Au), based on the variogram analysis results. The horizontal dimensions of the grid were determined by considering the anisotropy modeling and the borehole layout. The size of the elementary blocks was set to 25 m × 25 m × 12.5 m. The block height was associated with mine excavation planning and with the vertical distribution of the ore and waste thicknesses [54,55].

The kriging variance can be used as a criterion for choosing additional samples [17,18,25,56,57,58]. Additional samples are commonly designed away from observation locations or where the kriging variance is maximized [22,55]. Here, the ordinary block kriging standard deviation (${\sigma }_{obk}$) was calculated and normalized (${\widehat{\sigma }}_{obk}$) within a range of [0; 1] for each ore variable:

$${\widehat{\sigma }}_{obk}=\frac{{\sigma }_{obk}-\min \left({\sigma }_{obk}\right)}{\max \left({\sigma }_{obk}\right)-\min \left({\sigma }_{obk}\right)},$$

(1)

where $\min \left({\sigma }_{obk}\right)$ and $\max \left({\sigma }_{obk}\right)$ stand for the minimal and maximal kriging standard deviations calculated over all the blocks, respectively. Then, an average of ${\widehat{\sigma }}_{obk}$ for the ore variables (denoted as KSD, the acronym for kriging standard deviation, hereinafter) is calculated in each block (Equation (2)):

$$KSD=\frac{{\left({\widehat{\sigma }}_{obk}\right)}_{Cu}+{\left({\widehat{\sigma }}_{obk}\right)}_{Mo}+{\left({\widehat{\sigma }}_{obk}\right)}_{Ag}+{\left({\widehat{\sigma }}_{obk}\right)}_{Au}}{4}.$$

(2)

Drilling in areas where KSD reaches high values will be selected as one of the objectives to plan the configuration of additional boreholes.

3.4. Indicator Kriging

The output of indicator kriging represents an estimate of the probability for the indicator variable to be equal to 1 at the designated point. In other words, it approximates the probability that the point has a grade greater than the threshold. One application of indicator kriging is ore-waste classification [59]. The confidence of the classification result can be measured by the relative difference between the ore and waste probabilities (denoted as $P_o$ and $P_w$):

$$\mathit{Confidence} \mathit{measure}\left(\mathit{CM}\right)=\left\{\begin{array}{c}\frac{P_o-P_w}{P_o}\mathrm{if}{P}_o>P_w\hfill \\ \frac{P_w-P_o}{P_w}\mathrm{if}{P}_w>P_o\hfill \\ 0\mathrm{if}{P}_o=P_w.\hfill \end{array}\right.$$

(3)

Such a confidence measure ranges between 0 and 1. It is 0 when the probabilities of ore and waste are equal, and the sample or the block cannot be specifically assigned to ore or waste. In contrast, when the two probabilities are completely discriminated against each other, i.e., when $P_o\to 1$ and $P_w\to 0$ or when $P_o\to 0$ and $P_w\to 1$, the confidence measure is equal to 1.

The confidence measure provides an approach to making decisions about the uncertainty of assigning blocks to the ore or waste classes. In a detailed exploration stage, additional boreholes can be realized in areas where the confidence measure reaches low values. In a multi-element deposit such as eastern Kahang, this measure is computed for each ore element and then averaged in each block.

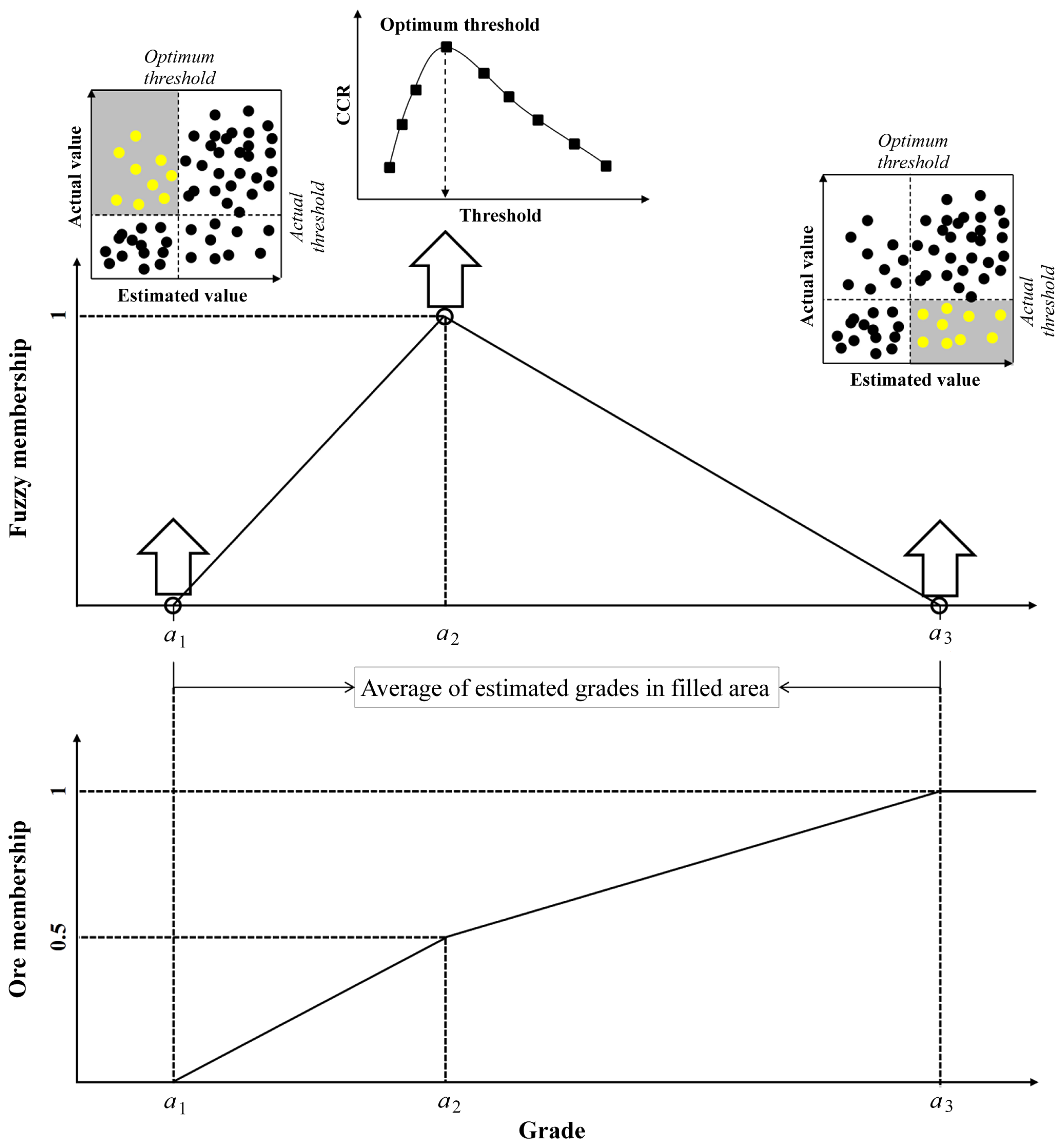
3.5. Introducing Fuzzy Thresholds and the Ore Membership Degree

A sharp threshold categorizes data into two classes. To reflect uncertainty, one can define a fuzzy threshold instead of a sharp one. The triangular fuzzy number (TFN) is a proper choice for designing a fuzzy threshold due to its simplicity and its membership being one of the most commonly applied in different scientific disciplines [44,56,60,61,62,63]. It defines a ‘fuzzy membership function’ ${\mu }_{f,e}$ for each ore element e (e = Cu, Mo, Ag, or Au):

$${\mu }_{f,e}\left(g_e\right)=\left\{\begin{array}{c}0\mathrm{if}{g}_e<a_1\hfill \\ \frac{g_e-a_1}{a_2-a_1}\mathrm{if}{a}_1\le g_e<a_2\hfill \\ \frac{a_3-g_e}{a_3-a_2}\mathrm{if}{a}_2\le g_e<a_3\hfill \\ 0\mathrm{if}{g}_e\ge a_3,\hfill \end{array}\right.$$

(4)

where $g_e$ stands for the estimated grade of element e, and $a_1$, $a_2$, and $a_3$ are thresholds (that vary from one element to another) such that $a_1\le a_2\le a_3$.

In the usual approach to defining this fuzzy membership function, the most promising value, $a_2$, is equal to the sharp threshold, and the limiting thresholds ($a_1$ and $a_3$) are determined based on equal data frequency on both sides of $a_2$. In this work, a different approach is proposed, in which the most promising value, the lower, and the upper thresholds are calculated by comparing the classification of actual and estimated values obtained by leave-one-out cross-validation.

Considering the indicator threshold when plotting the scatter of actual values against their estimates creates four combinations of sub-areas as follows: true positive (TP), false negative (FN), true negative (TN), and false positive (FP) [64]. True positive refers to ore data that were correctly labeled by a classifier, and a true negative is the set of waste data that was correctly labeled by the classifier. In the false positive category, the output of estimation is ore, while the data are, in fact, waste. False negative refers to ore data that were misclassified as waste [59,65]. A useful ranking tool for analyzing the performance of a classifier is the confusion matrix, where each row corresponds to the data in an estimated class, while each column corresponds to the data in an actual class [66,67]. The correct classification rate (CCR) can be calculated by summing the correct decisions in the diagonal of the confusion matrix and dividing this sum by the total number of tests [68]:

$$\mathit{CCR}=\frac{\mathit{Count}(\mathit{TP}+\mathit{TN})}{\mathit{Count}(\mathit{TP}+\mathit{TN}+\mathit{FP}+\mathit{FN})}.$$

(5)

For defining the most promising value of the fuzzy membership function, different modes of classification are considered based on a constant sharp threshold for the actual value and dynamic thresholds for the estimated value chosen in a tolerance interval around the sharp threshold. The CCR is calculated for each dynamic threshold to find the maximum CCR and corresponding threshold for allocating a promising value ($a_2$) to the fuzzy membership function. The lower and upper thresholds ($a_1$ and $a_3$) are computed by averaging the estimated values in the FN and FP categories, respectively (Figure 6).

Finally, the ‘ore membership function’ (${\mu }_{o,e}$) of element e (e = Cu, Mo, Ag, or Au) is introduced based on the thresholds of the fuzzy membership function ${\mu }_{f,e}$ so defined:

$${\mu }_{o,e}\left(g_e\right)=\left\{\begin{array}{c}0\mathrm{if}{g}_e<a_1\hfill \\ \frac{g_e-a_1}{2(a_2-a_1)}\mathrm{if}{a}_1\le g_e<a_2\hfill \\ \frac{g_e+a_3-2a_2}{2(a_3-a_2)}\mathrm{if}{a}_2\le g_e<a_3\hfill \\ 1\mathrm{if}{g}_e\ge a_3,\hfill \end{array}\right.$$

(6)

with $g_e$ standing for the estimated grade of element e. The ore membership function equals 0 for an estimated grade less than or equal to $a_1$. It reaches $0.5$ for an estimated grade equal to $a_2$ and increases to 1 for an estimated grade greater than or equal to $a_3$ (Figure 6).

As a result of this procedure, the promising values of Cu, Mo, Ag, and Au are found to be 1600, 390, 20, and $0.5$ ppm, respectively. In the fuzzy membership function of Cu, the right side is larger than the other side: the average estimated grade of the false positives differs more from the promising value than the average estimated grade of the false negatives. The reverse situation occurs for Ag and Au, for which the left side of the fuzzy membership function is larger than its right side, whereas the fuzzy membership function of Mo is described by a symmetric TFN. Accordingly, the lower threshold $a_1$, most promising value $a_2$, and upper threshold $a_3$ of Cu, Mo, Ag, and Au (expressed in ppm) are determined as: $(1124,1600,2342)$, $(256,390,538)$, $(9,20,20)$, and $(0.03,0.5,0.5)$, respectively (Figure 7).

3.6. Ore Value Modeling

The ‘ore value’ function is applied to transform the estimated grade into a relative value of ore variables such as Cu, Mo, Ag, and Au based on the different thresholds. This function determines the total value of each block by considering all the effective variables. It is calculated by the sum of a weight factor ($w_e$) times the ore membership degree (${\mu }_{o,e}\left(g_e\right)$) times the estimated grade in ppm ($g_e$) for all the ore elements (e = Cu, Mo, Ag, or Au) in each block. The weight factor for each variable depends on the expected recovery and selling price of the element [44]:

$$\mathit{Ore} \mathit{value}\left(\mathit{OV}\right)=\sum _{e=1}^4{w}_e\times {\mu }_{o,e}\left(g_e\right)\times g_e,$$

(7)

with $w_{Cu}=0.155$, $w_{Mo}=0.493$, $w_{Ag}=18.8$, and $w_{Au}=1030$.

3.7. Misclassification Cost

A misclassification cost can be introduced when there are different types of classification errors and the costs they bring are different [69]. In the assessment of mineral resources and mineral reserves, errors have an impact on the metal recovery and production tonnage: if ore blocks are inadvertently classified as waste, the ore is lost; conversely, if waste blocks are included in ore, the total tonnage increases but the average grade decreases [57,70]. The economic impact of ore loss is the income lost when the ore is sent to the waste dumps and never recovered. This is calculated using the ore value (Equation (7)). The dilution economic effect is imposed on the extra cost of mining and processing waste that is treated as ore [71].

According to the previous statements, the ‘misclassification cost’ (MC) can be defined as follows:

$$\begin{array}{cc}\hfill \mathit{Misclassification} \mathit{cost} \left(\mathit{MC}\right)& =\sum _{e=1}^{4}w(1-{\mu }_{o,e}\left(g_e\right))\times \mathbb{I}(g_e,t_e)\hfill \\ \hfill & +\sum _{e=1}^4{w}_e\times {\mu }_{o,e}\left(g_e\right)\times g_e\times (1-\mathbb{I}(g_e,t_e)),\hfill \end{array}$$

(8)

where w is a weight factor that depends on the mining and processing cost per block (in the present case, $w=180$), $t_e$ is the cut-off for element e ($t_{Cu}=1500$ ppm, $t_{Mo}=400$ ppm, $t_{Ag}=20$ ppm, and $t_{Au}=0.5$ ppm), $g_e$ is the estimated grade of element e, and $\mathbb{I}$ is an indicator function that determines whether a block is classified as ore or as waste: $\mathbb{I}(g_e,t_e)=1$ if $g_e\ge t_e$, 0 otherwise. One goal of detailed exploration is to reduce such a misclassification cost.

3.8. Our Proposal: Multi-Objective Function Index

To design the additional boreholes, an index is introduced to detect locations with a high potential [44,72]. This index has four sub-objectives to identify new boreholes that can improve the accuracy of classification and estimation of mineral resources and reserves:

• maximize the kriging standard deviation (KSD), reflecting a high uncertainty in the true unknown grades;
• minimize confidence measure (CM), reflecting a high uncertainty in the ore-waste classification;
• maximize ore value (OV), reflecting a high potential economic value;
• maximize misclassification cost (MC), reflecting a high impact of ore loss and waste dilution.

The 3D block models of these four sub-objectives are illustrated in Figure 8a–d, while Figure 8e depicts a 2D map of the average ore value along the vertical column of blocks.

It is common to standardize each term in the same range for a simultaneous application of these objectives in the index. In the present study, to introduce and maximize the index in terms of a fraction, its numerator includes parameters to be maximized (kriging standard deviation, ore value, and misclassification cost), while the confidence measure is situated in the denominator:

$$\mathit{Index}=\frac{\mathit{KSD}\times \mathit{OV}\times \mathit{MC}}{\mathit{CM}}.$$

(9)

4. Results and Discussion

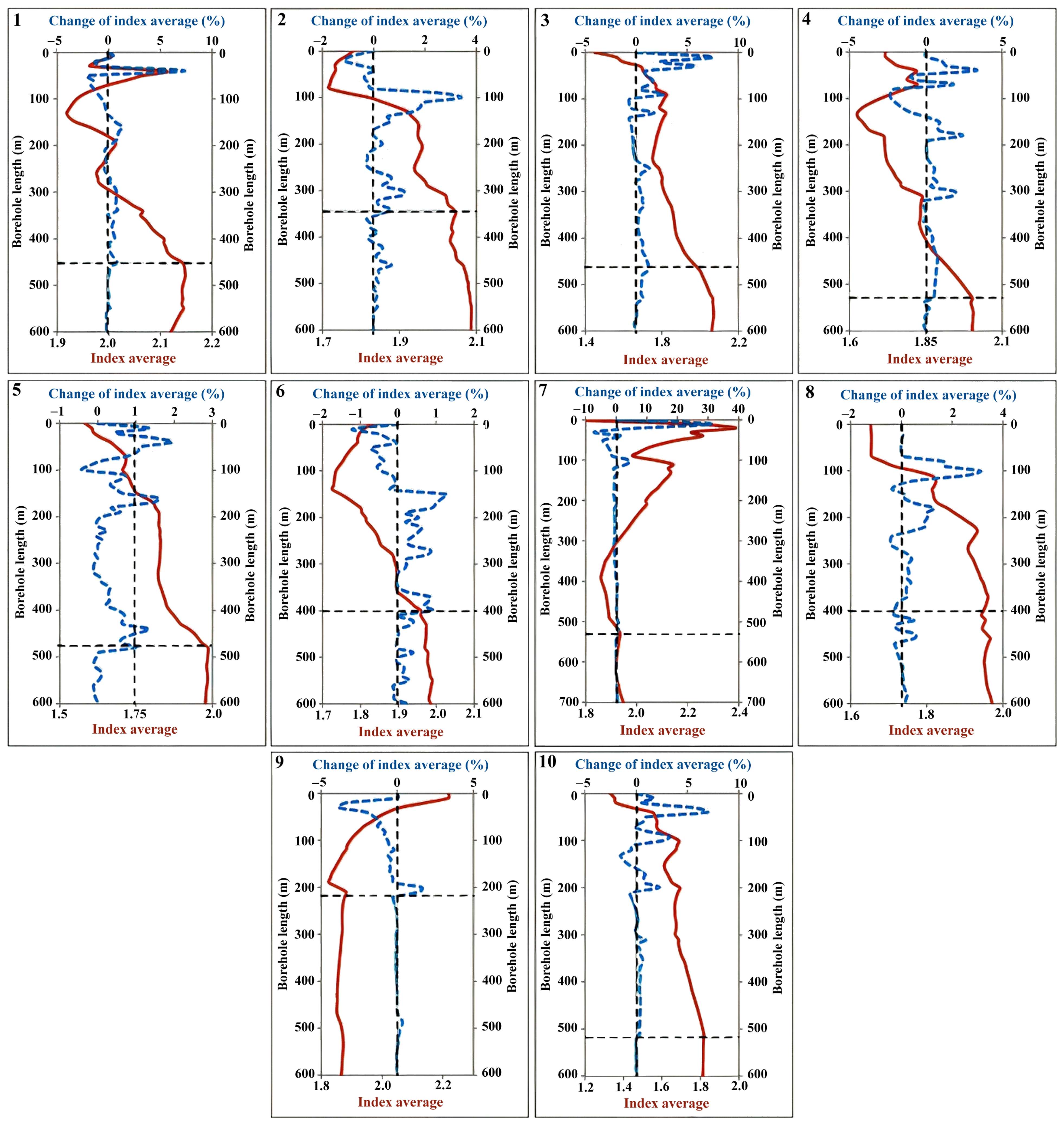
4.1. Application of the Index to Define Additional Boreholes

Figure 9a displays the 3D spatial distribution of the index within the block model. The index values are averaged along a vertical column of blocks assigned to the block centers’ longitude and latitude and plotted on a 2D map. Then, eight vertical boreholes are located based on large amounts of the index values in the 2D map (Figure 9c). Two potential directional boreholes are also candidates based on the fact that they intersect areas exhibiting large index values that are not located along the same vertical line. The locations and directions of these boreholes are shown in Figure 9b.

The index average and its variations are surveyed along the imaginary axis of the boreholes to determine the length and priority of each additional borehole. A change in the index average tending to zero or becoming negative, indicating that the index value remains constant or trends downward, is the main criterion to calculate the length of the borehole. The priority of boreholes is defined based on comparing the index average value in the calculated length. In Figure 10, the index average and change of index average are shown with a solid smooth line and dash line, respectively, and the crossed dash line (black) represents the borehole length.

Finally, the dimensional and directional properties, such as the header coordinates (x, y, z), length, azimuth, and dip of ten proposed additional boreholes with their priorities, are presented in

Table 3. Dimensional and directional properties of proposed boreholes with higher priority.

Priority	Collar X (m)	Collar Y (m)	Collar Z (m)	Azimuth (${}^{\circ }$)	Dip (${}^{\circ }$)	Length (m)	Average Index Value
1	638,484.9	3,644,905	2269	0	90	460	2.146
2	638,511.8	3,644,872	2269	0	90	340	2.046
3	638,638.7	3,644,784	2272.4	0	90	480	2.011
4	638,680.2	3,644,745	2275.7	0	90	530	2.002
5	638,610.7	3,644,708	2272.1	0	90	480	1.985
6	638,437.3	3,644,861	2269	0	90	400	1.960
7	638,604.9	3,644,599	2283.1	29.5	75.7	520	1.928
8	638,437.3	3,644,563	2287	0	90	400	1.925
9	638,106.5	3,644,911	2274.8	0	90	210	1.881
10	638,694.3	3,644,788	2284.4	296.1	69.2	510	1.818

.

4.2. Discussion

One focus for discussion relates to the simultaneous selection of additional boreholes, which may introduce some interference effects due to possible information redundancy between these boreholes: drilling ‘twinned’ holes (i.e., two or more holes next to each other) may decrease the target index just a little more than drilling a single hole. Therefore, an extra criterion to select the additional borehole should be a minimal spacing between them. In the present case, the boreholes with priorities 1 and 2 are distant $42.6$ m from each other, while the borehole with priority 10 is distant $45.9$ m from borehole 4 near the collar (elevation 2275 m) and 28 m from borehole 3 near elevation 2157 m. The remaining additional boreholes are distant more than 55 m from each other, a distance for which the grade variograms (Figure 4) and the indicator variograms (Figure 5) reach more than $90\%$ of their sills (or $80\%$ of the sill in the case of the Mo indicator); this means that, except for the twinned holes 1-2, 3-10, and 4-10, there is practically no interference between the selected boreholes. Concerning these twinned holes, their locations may be adjusted, e.g., by moving borehole 2 slightly (say, 10 m) to the south-east in order to decrease its redundancy with borehole 1 while still drilling an area with a large index value (Figure 9c). Moving borehole 10 may not be desirable, as the interest for this borehole mainly lies in its deepest part (Figure 9b), for which the distance with boreholes 3 and 4 is greater than 55 m; hence, the information redundancy is minimal.

As a second focus for discussion, it is seen that the proposed index (Equation (9)) gives the same importance to the four parameters KSD, CM, OV, and MC: an increase of, say, $10\%$ of KSD has the same effect on the index as an increase of $10\%$ of OV or MC, or a decrease of $10\%$ of CM. One could generalize this index to weight these parameters differently, at the cost of greater complexity, in the following fashion:

$$\mathit{Index}=\frac{{\mathit{KSD}}^{\alpha }\times {\mathit{OV}}^{\beta }\times {\mathit{MC}}^{\gamma }}{{\mathit{CM}}^{\delta }},$$

(10)

with $\alpha ,\beta ,\gamma ,\delta >0$. Equivalently, $ln\left(\mathit{Index}\right)=\alpha ln\left(\mathit{KSD}\right)+\beta ln\left(\mathit{OV}\right)+\gamma ln\left(\mathit{MC}\right)-\delta ln\left(\mathit{CM}\right)$. This way, one can assign more importance to one parameter to the detriment of another, depending on the decision-makers’ experience and risk preferences.

The indices (9) and (10) may also be extended to incorporate more sub-objectives in order to account for auxiliary geoscientific information of the subsurface, if available. In particular, lithological, structural, alteration and topographical maps, hyperspectral imaging, as well as ground or airborne magnetic, electrical, gravimetric, and seismic surveys, are often used for mineral potential mapping and are therefore good candidates for the definition of a ‘geological potential’ parameter relevant to the definition of exploratory boreholes (in addition to KSD, CM, OV, and MC). The reader is referred to [73,74,75,76,77,78] for applications of geophysical surveys to the exploration of volcanogenic massive sulfide, iron oxide copper gold, and porphyry ore deposits and to the sampling design problem.

However, it should be noted that the geological and geophysical layers are subject to some degree of subjectivity and to possible cognitive biases, as they result from human decisions (e.g., the choice of a conceptual model of the mineral deposit) or from indirect, incomplete and imperfect information (e.g., geophysical inversion, or interpolated information due to incomplete spatial coverage), which raises the question of the confidence to place in these layers [79,80]. This is the reason why they are used in the prospective stage to propose the primary boreholes in and around the detected anomalies, and their weight is often reduced against existing drilling data when designing the layout of infill boreholes for detailed exploration. According to the level of exploration studies of the eastern Kahang deposit, the geological and geophysical layers cannot play a significant role, and the existing drilling network is more prominent in the design of complementary boreholes.

5. Conclusions

A new approach has been presented to determine the layout of additional boreholes in mineral exploration projects. The proposed method was applied to the eastern part of the Kahang copper deposit in Central Iran. The locations and lengths of eight vertical and two directional complementary drillings were suggested for further exploration of this area. These complementary drillings were selected using the following steps:

• The average kriging standard deviation quantifies the uncertainty in the true grades and was obtained based on ordinary kriging results.
• The confidence measure expresses the certainty of the decision to assign blocks to the ore or waste classes. This measure was calculated by a discrimination rate between ore and waste probabilities, which were obtained based on indicator kriging results.
• Fuzzy thresholds were recommended instead of a sharp threshold. The actual and kriging estimated grades were classified to calculate a confusion matrix and correct classification rate (CCR), which were applied to define fuzzy thresholds for Cu, Mo, Ag, and Au. The center of the triangular fuzzy number (TFN) was determined by maximizing CCR, and the lower and upper limits of the TFN were determined by the average of estimated grades in the false positive (FP) and false negative (FN) categories, respectively. The TFNs of Cu, Mo, Ag, and Au were obtained as $(1124,1600,2342)$; $(256,390,538)$; $(9,20,20)$; and $(0.03,0.5,0.5)$. The ore membership function was then modeled by a quasi-trapezoidal membership function based on the TFN center and limits.
• The ore value function represents the total value of each block by calculating the sum of a weight factor times the ore membership degree times the estimated grade for all the ore elements. It measures the economic potential of the block.
• The misclassification cost includes the ore loss and dilution economic impact computed by the income lost when sending ore to the dump and the extra cost of mining and processing waste material.
• An index for the selection of additional boreholes was finally defined by multiplying the kriging standard deviation, ore value, and misclassification cost and dividing by the confidence measure. By surveying the index average and its change along the axis of the additional boreholes, the properties of eight vertical and two directional additional boreholes were proposed together with their priorities.