CFD Numerical Simulation on the Mode of Ligament Disintegration during Centrifugal Granulation of Molten Slag by Using a Spinning Cup
Abstract
:1. Introduction
2. CFD Model Formulation
2.1. Model Assumptions and Computation Domain
2.2. Governing Equations and Computation Scheme
3. Results and Discussion
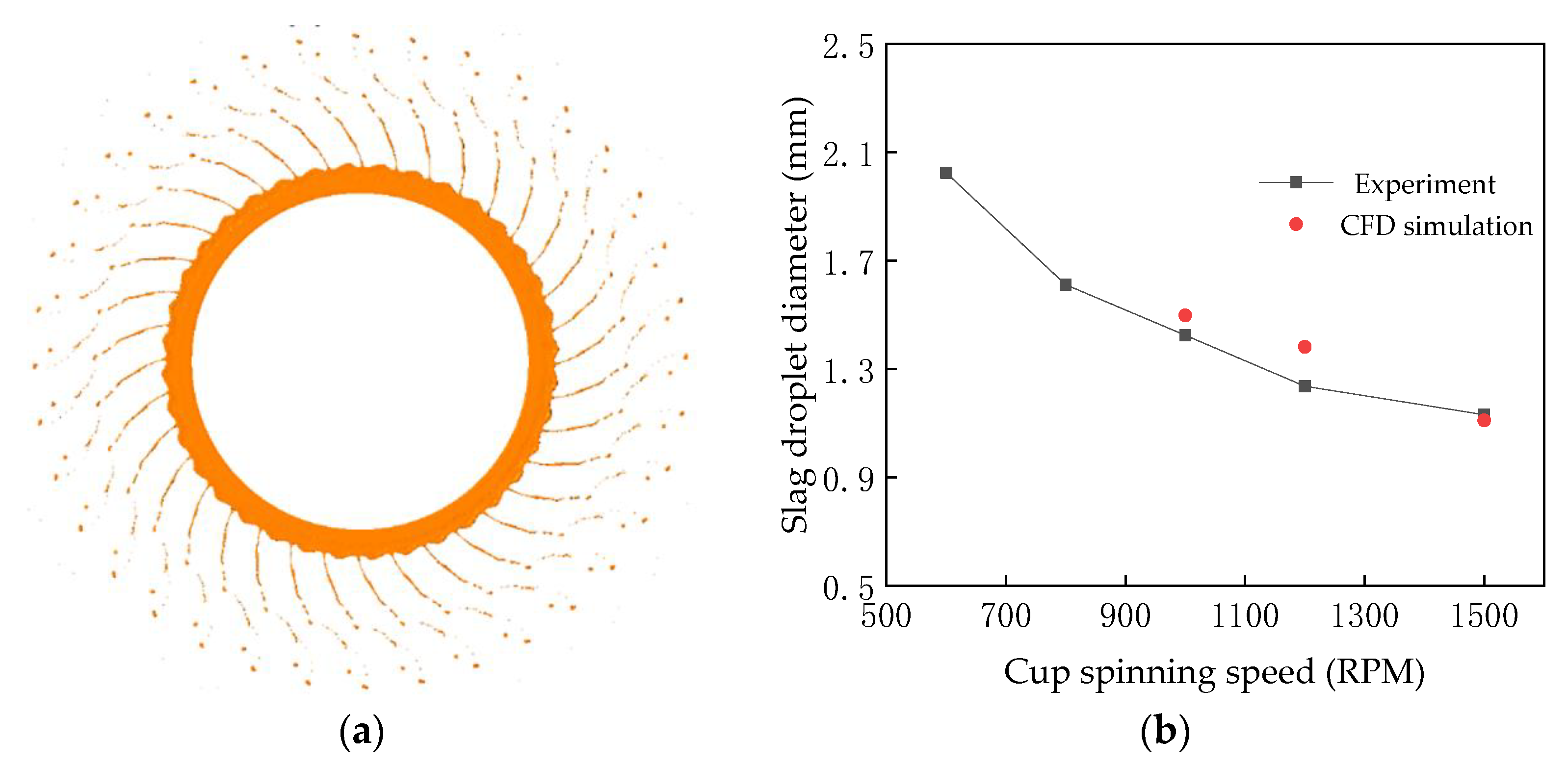
3.1. CFD Model Validity
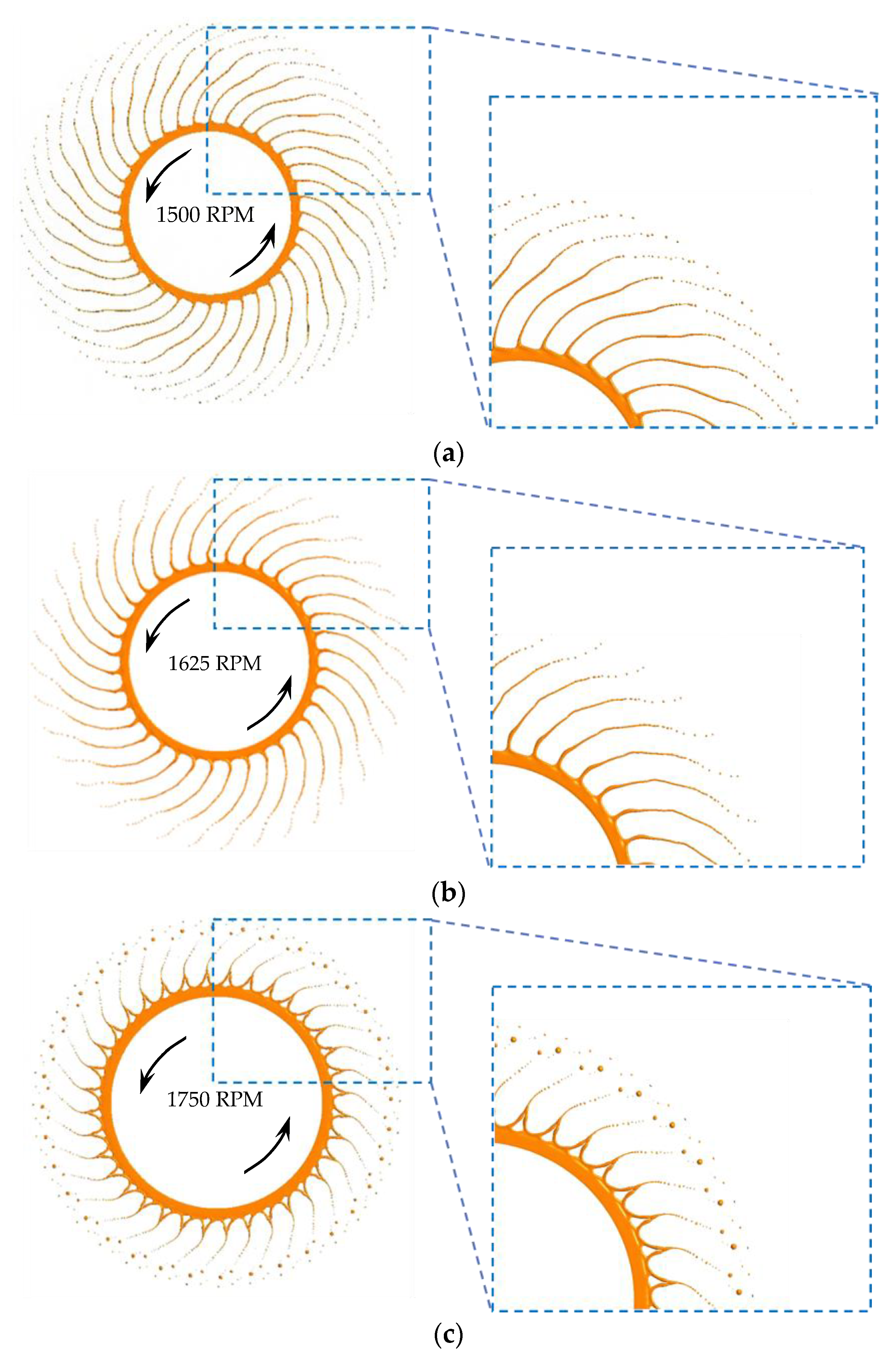
3.2. Breakup of Molten Slag Ligament in the Spinning Cup Centrifugal Granulation Process
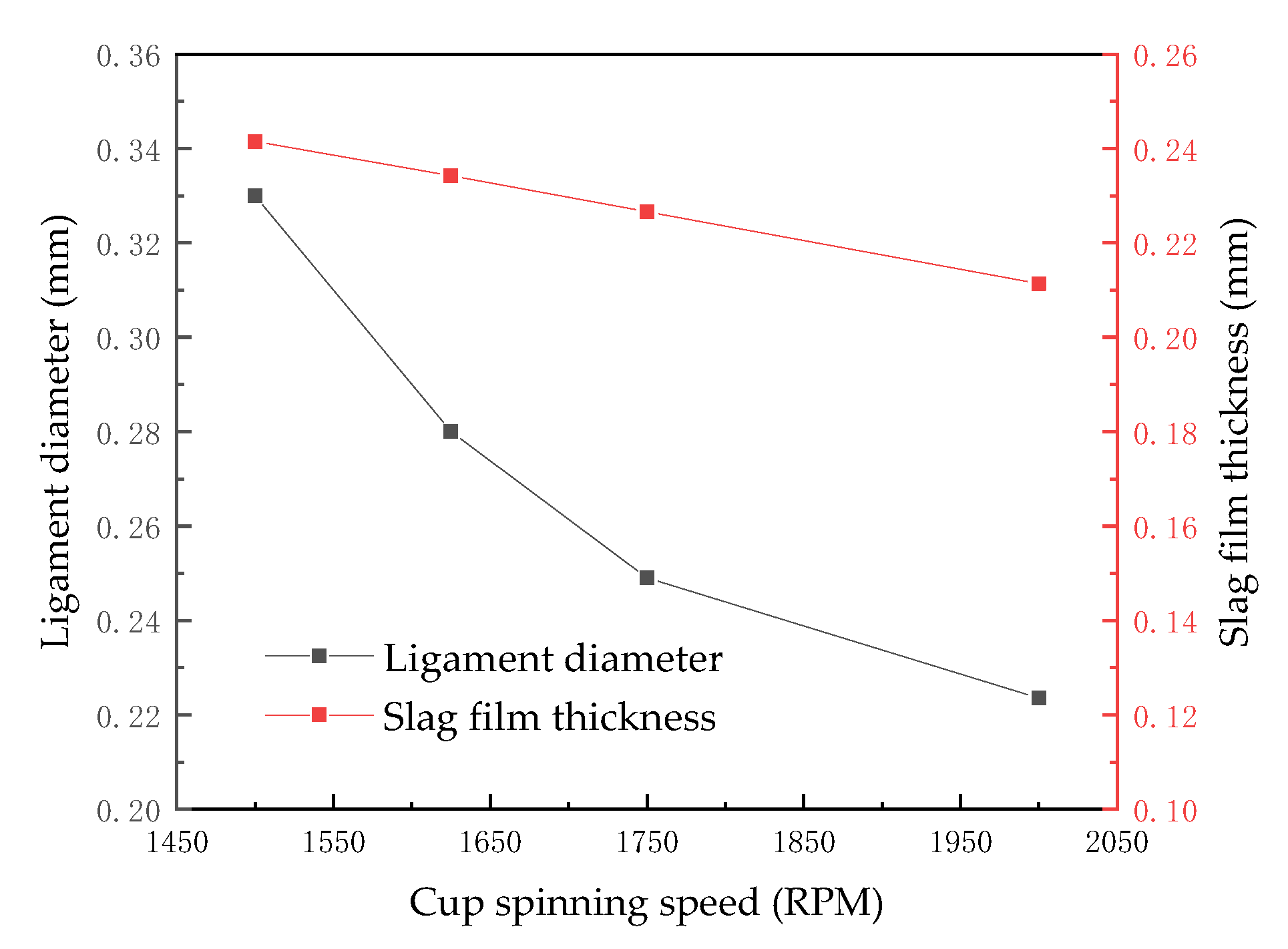
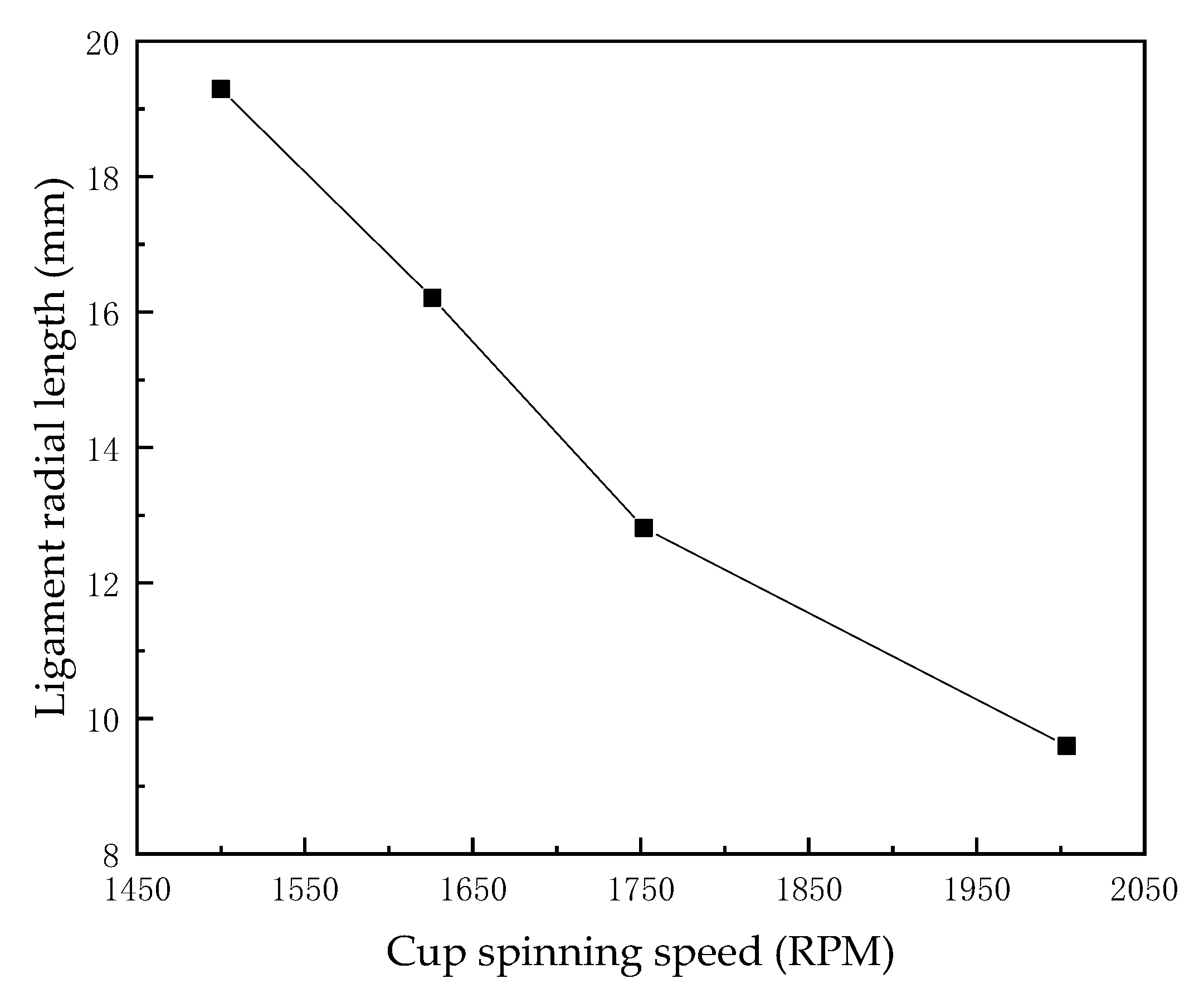
3.3. Effect of Cup Spinning Speed on the Granulation Process
3.4. Mechanism of Molten Slag Ligament Breakup in the Spinning Cup Centrifugal Granulation Process
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, Y.; Feng, J.; Xie, Z.; Zhu, Y. Exergy analysis and system optimization design of sensible heat recovery of blast furnace slag in fixed-bed. J. North China Electr. Power Univ. 2012, 39, 97–102. [Google Scholar]
- Liu, J.; Yu, Q.; Li, P. Cold experiments on ligament formation for blast furnace slag granulation. Appl. Therm. Eng. 2012, 40, 351–357. [Google Scholar] [CrossRef]
- Liu, J. Experimental study on heat transfer characteristics of blast furnace slag waste heat recovery device. Master’s Thesis, Northeastern University, Shenyang, China, 2009. [Google Scholar]
- Liu, J.; Yu, Q.; Qin, Q. System for Recovering Waste Heat from High Temperature Molten Blast Furnace Slag; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2011. [Google Scholar]
- Wu, J.; Tan, Y.; Li, P.; Wang, H.; Zhu, X.; Liao, Q. Centrifugal-Granulation-Assisted thermal energy recovery towards low-carbon blast furnace slag treatment: State of the art and future challenges. Appl. Energy 2022, 325, 119835. [Google Scholar] [CrossRef]
- Feng, Y.; Zhang, Z.; Gao, J.; Feng, G.P.; Qiu, L. Research status of centrifugal granulation, physical heat recovery and resource utilization of blast furnace slags. J. Anal. Appl. Pyrolysis 2021, 157, 105220. [Google Scholar] [CrossRef]
- Yu, P.; Wang, S. Current and future of dry centrifugal granulation process. Key Eng. Mater. 2016, 719, 92–97. [Google Scholar] [CrossRef]
- Dombrowski, N.; Lloyd, T. Atomisation of liquids by spinning cups. Chem. Eng. J. 1974, 8, 63–81. [Google Scholar] [CrossRef]
- Liu, J.; Yu, Q.; Guo, Q. Experimental investigation of liquid disintegration by rotary cups. Chem. Eng. Sci. 2012, 73, 44–50. [Google Scholar] [CrossRef]
- Wu, J.; Wang, H.; Zhu, X.; Liao, Q.; Li, K. Cold experiment of slag centrifugal granulation by rotary atomizer: Effect of atomizer configuration. Appl. Therm. Eng. 2017, 111, 1557–1564. [Google Scholar] [CrossRef]
- Mizuochi, T.; Akiyama, T.; Shimada, T.; Kasai, E.; Yagi, J. Feasibility of rotary cup atomizer for slag granulation. Isij Int. 2001, 41, 1423–1428. [Google Scholar] [CrossRef] [Green Version]
- Wegener, M.; Muhmood, L.; Sun, S.; Deev, A. The formation and breakup of molten oxide jets. Chem. Eng. Sci. 2014, 105, 143–154. [Google Scholar] [CrossRef]
- Purwanto, H.; Mizuochi, T.; Akiyama, T. Prediction of granulated slag properties produced from spinning disk atomizer by mathematical model. Mater. Trans. 2005, 46, 1324–1330. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Ling, X.; Peng, H. Theoretical analysis of free-surface film flow on the rotary granulating disk in waste heat recovery process of molten slag. Appl. Therm. Eng. 2014, 63, 387–395. [Google Scholar] [CrossRef]
- Wang, D.; Ling, X.; Peng, H. Simulation of ligament mode breakup of molten slag by spinning disk in the dry granulation process. Appl. Therm. Eng. 2015, 84, 437–447. [Google Scholar] [CrossRef]
- Cheng, R.; Zhang, H.; Li, Y.; Fang, Q.; Wang, B. Effect of process parameters on dry centrifugal granulation of molten slag by a rotary disk atomizer. J. Iron Steel Res. Int. 2021, 28, 263–271. [Google Scholar] [CrossRef]
- Liu, Y. Study on Droplet solidification characteristics of blast furnace slag granulation. Master’s Thesis, North China University of Science and Technology, Qinhuangdao, China, 2019. [Google Scholar]
- Lord Rayleigh, F.R.S. On the instability of jets. Proc. Lond. Math. Soc. 1878, 10, 4–13. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Zhao, M.; Ma, P.; Pan, Y.; Meng, F. Numerical modeling of centrifugal granulation of molten blast furnace slag using spinning cups. Iron Steel 2020, 55, 127–133. [Google Scholar]
- Inaba, S.; Kimura, Y.; Shibata, H.; Ohta, H. Measurement of physical properties of slag formed around the raceway in the working blast furnace. ISIJ Int. 2004, 44, 2120–2126. [Google Scholar] [CrossRef] [Green Version]
- ANSYS Inc. ANSYS CFX User’s Manual, Release 18.0; ANSYS Inc.: Canonsburg, PA, USA, 2017. [Google Scholar]
- Hirt, C.; Nichols, B. Volume of Fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Menter, F. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Brackbill, J.; Kothe, D.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Liu, J.; Yu, Q.; Dou, C.; Hu, X. Experimental study on rotary cup granulation of blast furnace slag. In Proceedings of the National Energy and Thermal Engineering Annual Conference, Guiyang, China, 5 November 2008. [Google Scholar]
- Wang, G.; Ning, Z.; Lv, M.; Jiang, Z. Break process and surface wave of annular swirling viscous jet. Veh. Engine 2018, 5, 1–7. [Google Scholar]
- Zhao, M.; Pan, Y.; Zhao, A.; Zhang, S.; Ma, P.; Feng, X. CFD modeling and cold physical model simulation on single molten slag ligament disintegration into droplets. Miner. Spec. Issue Granulation Heat Recovery Metall. Slags 2023, 13, 139. [Google Scholar] [CrossRef]








| Material | Density (kg·m−3) | Dynamic Viscosity (Pa·s) | Surface Tension (N·m−1) |
|---|---|---|---|
| Liquid blast furnace slag | 2590 | 0.5 | 0.478 |
| Air (at 25 °C) | 1.185 | 1.831 × 10−5 | - |
| Simulation Case Number | Cup Spinning Speed (RPM) | Slag Film Thickness at the Cup Edge (mm) | Other Conditions |
|---|---|---|---|
| 1 2 3 4 | 1500 | 0.2415 | The slag flowrate is 3 kg min−1; the inner height of the cup wall is 5 mm; the inclination angle of the cup wall is 5°; and the diameter of the cup edge is 60 mm. |
| 1625 | 0.2343 | ||
| 1750 | 0.2266 | ||
| 2000 | 0.2114 | ||
| Literature case [25] | 1000 | 0.3440 | The slag flowrate is 6.667 kg min−1; the inner height of the cup wall is 20 mm; the inclination angle of the cup wall is 45°; and the diameter of the cup edge is 100 mm. |
| Study Method/ Liquid Ligament | Ligament Diameter dl (mm) | Droplet Diameter dp (mm) | dp/dl |
|---|---|---|---|
| 0.22 | 0.41 | 1.85 | |
| CFD/Molten slag | 0.25 | 0.45 | 1.80 |
| 0.28 | 0.53 | 1.89 | |
| 0.33 | 0.60 | 1.82 | |
| Average | 1.84 | ||
| 0.45 | 1.13 | 2.51 | |
| 0.60 | 1.25 | 2.08 | |
| 0.85 | 1.60 | 1.88 | |
| Experiment/Liquid paraffin [27] | 1.00 | 1.73 | 1.73 |
| 1.25 | 2.05 | 1.64 | |
| 1.45 | 2.25 | 1.55 | |
| Average | 1.90 | ||
| 1.00 | 1.70 | 1.70 | |
| Experiment/Water [27] | 1.00 | 1.90 | 1.90 |
| 1.00 | 1.98 | 1.98 | |
| Average | 1.86 | ||
| Rayleigh disintegration mechanism (Equation (3)) [18] | - | - | 1.89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, A.; Pan, Y.; Zhao, M.; Zhang, S.; Ma, P.; Feng, X. CFD Numerical Simulation on the Mode of Ligament Disintegration during Centrifugal Granulation of Molten Slag by Using a Spinning Cup. Minerals 2023, 13, 316. https://doi.org/10.3390/min13030316
Zhao A, Pan Y, Zhao M, Zhang S, Ma P, Feng X. CFD Numerical Simulation on the Mode of Ligament Disintegration during Centrifugal Granulation of Molten Slag by Using a Spinning Cup. Minerals. 2023; 13(3):316. https://doi.org/10.3390/min13030316
Chicago/Turabian StyleZhao, Aifu, Yuhua Pan, Ming Zhao, Shili Zhang, Ping Ma, and Xin Feng. 2023. "CFD Numerical Simulation on the Mode of Ligament Disintegration during Centrifugal Granulation of Molten Slag by Using a Spinning Cup" Minerals 13, no. 3: 316. https://doi.org/10.3390/min13030316




