Geostatistical Evaluation of a Porphyry Copper Deposit Using Copulas
Abstract
:1. Introduction
2. Materials and Methods
2.1. Copula
2.2. Spatial Copula
2.3. Copula Modeling
2.4. Combination of Archimedean Copulas
2.5. Steps of Prediction
- (i)
- Transform the variable into uniform distribution through .
- (ii)
- Choose lag distances and lag tolerance for calculating empirical copulas for them.
- (iii)
- For each lag, estimate the best copula parameters and find their best combination.
- (iv)
- To calculate copula density at distances other than lag distances, model copula parameters and weights given to them.
- (v)
- For each conditioning sample, put its distance from the prediction point into the fitted models of the previous step to get its density at the prediction point.
- (vi)
- Compute conditional cumulative distribution function at the prediction point in order to get weights given to the samples. Multiply sample values by their weights, sum up the multiplication results and back-transform them into original data space.
3. Case Study
3.1. Geology

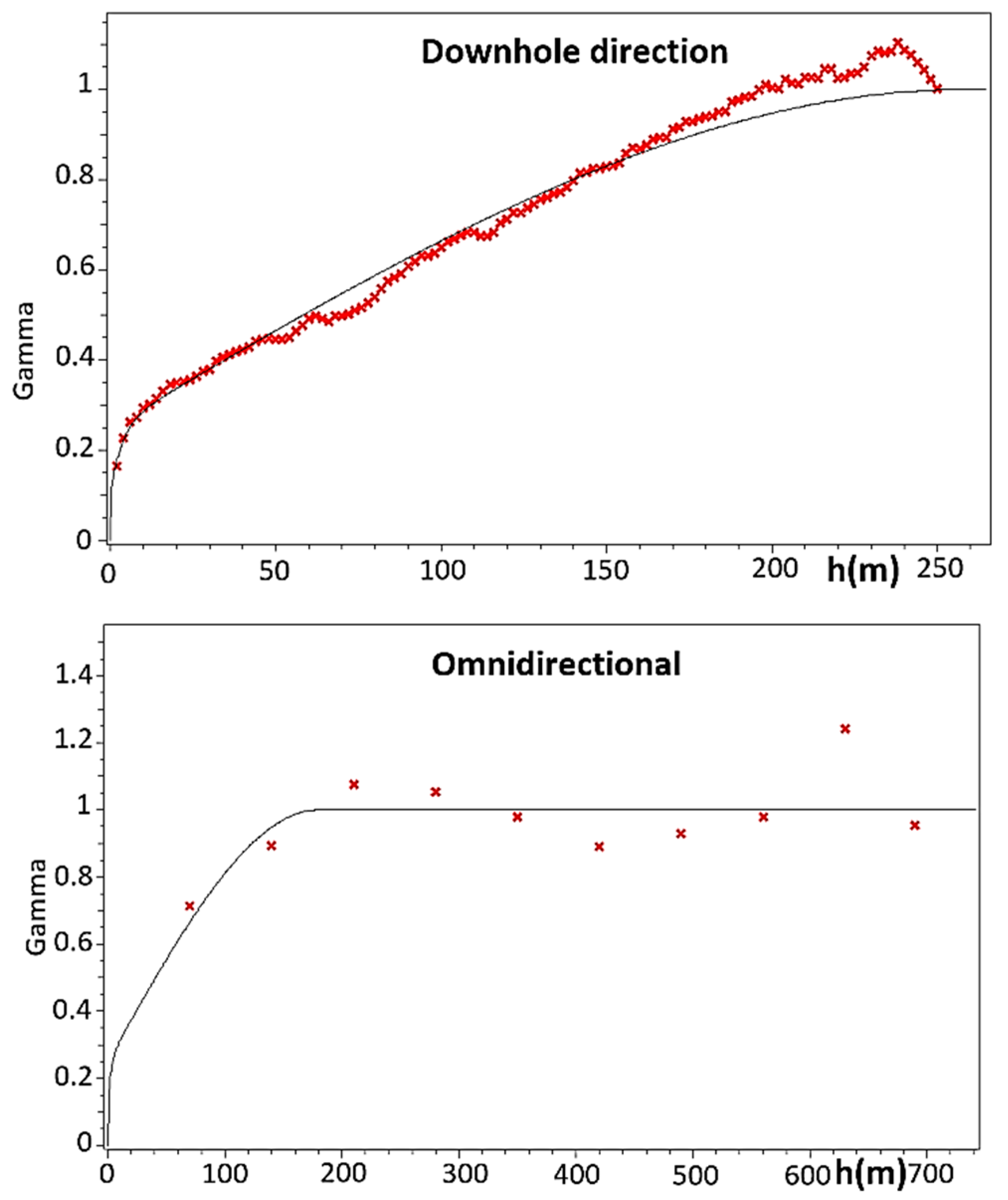
3.2. Data Description
3.3. Split-Sample Cross-Validation
3.4. Estimation and Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sohrabian, B.; Tercan, A.E. Introducing minimum spatial cross-correlation kriging as a new estimation method of heavy metal contents in soils. Geoderma 2014, 226, 317–331. [Google Scholar] [CrossRef]
- Rossi, M.E.; Deutsch, C.V. Mineral Resource Estimation; Springer: Dordrecht, The Netherlands, 2014; ISBN 978-1-4020-5716-8. [Google Scholar]
- Sohrabian, B.; Ozcelik, Y.; Hasanpour, R. Estimating major elemental oxides of an andesite quarry using compositional kriging. Int. J. Min. Reclam. Environ. 2016, 31, 475–487. [Google Scholar] [CrossRef]
- Rahimi, H.; Asghari, O.; Afshar, A. A geostatistical investigation of 3D magnetic inversion results using multi-Gaussian kriging and sequential Gaussian co-simulation. J. Appl. Geophys. 2018, 154, 136–149. [Google Scholar] [CrossRef]
- Jeuken, R.; Xu, C.; Dowd, P. Improving Coal Quality Estimations with Geostatistics and Geophysical Logs. Nat. Resour. Res. 2020, 29, 2529–2546. [Google Scholar] [CrossRef]
- Lloyd, C.; Atkinson, P. Assessing uncertainty in estimates with ordinary and indicator kriging. Comput. Geosci. 2001, 27, 929–937. [Google Scholar] [CrossRef]
- Wackernagel, H. Multivariate Geostatistics; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Gräler, B.; Pebesma, E. The pair-copula construction for spatial data: A new approach to model spatial dependency. Procedia Environ. Sci. 2011, 7, 206–211. [Google Scholar] [CrossRef]
- Monteiro da Rocha, M.; Yamamoto, J.K. Comparison Between Kriging Variance and Interpolation Variance as Uncertainty Measurements in the Capanema Iron Mine, State of Minas Gerais—Brazil. Nat. Resour. Res. 2000, 9, 223–235. [Google Scholar] [CrossRef]
- Gräler, B. Modelling skewed spatial random fields through the spatial vine copula. Spat. Stat. 2014, 10, 87–102. [Google Scholar] [CrossRef]
- Sklar, A. Fonctions de Répartition à n Dimensions et Leurs Marges; Publications de l’Institut Statistique de l’Université de Paris: Paris, France, 1959; Volume 8, pp. 229–231. [Google Scholar]
- Joe, H. Multivariate Models and Multivariate Dependence Concepts; C&H/CRC Monographs on Statistics & Applied Probability; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Frahm, G.; Junker, M.; Szimayer, A. Elliptical copulas: Applicability and limitations. Stat. Probab. Lett. 2003, 63, 275–286. [Google Scholar] [CrossRef]
- Nelsen, R.B. An introduction to Copulas; Springer: New York, NY, USA, 2006. [Google Scholar]
- Li, D.; Peng, L. Goodness-of-fit test for tail copulas modeled by elliptical copulas. Stat. Probab. Lett. 2009, 79, 1097–1104. [Google Scholar] [CrossRef]
- Choe, G.H.; Jang, H.J. Efficient Algorithms for Basket Default Swap Pricing with Multivariate Archimedean Copulas. Insur. Math. Econ. 2011, 48, 205–213. [Google Scholar] [CrossRef]
- Li, C.; Huang, Y.; Zhu, L. Color texture image retrieval based on Gaussian copula models of Gabor wavelets. Pattern Recognit. 2017, 64, 118–129. [Google Scholar] [CrossRef]
- Dinda, K.; Samanta, B. Non-Gaussian Copula Simulation for Estimation of Recoverable Reserve in an Indian Copper Deposit. Nat. Resour. Res. 2020, 30, 57–76. [Google Scholar] [CrossRef]
- Xu, D.; Zhu, Y. A Copula–Hubbert Model for Co(By)-Product Minerals. Nat. Resour. Res. 2020, 29, 3069–3078. [Google Scholar] [CrossRef]
- Bárdossy, A. Copula-based geostatistical models for groundwater quality parameters. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Van de Vyver, H.; Van den Bergh, J. The Gaussian copula model for the joint deficit index for droughts. J. Hydrol. 2018, 561, 987–999. [Google Scholar] [CrossRef]
- Li, F.; Zhou, J.; Liu, C. Statistical modelling of extreme storms using copulas: A comparison study. Coast. Eng. 2018, 142, 52–61. [Google Scholar] [CrossRef]
- Lourme, A.; Maurer, F. Testing the Gaussian and Student’s t copulas in a risk management framework. Econ. Model. 2017, 67, 203–214. [Google Scholar] [CrossRef]
- Bárdossy, A.; Li, J. Geostatistical interpolation using copulas. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Marchant, B.P.; Saby, N.P.A.; Jolivet, C.C.; Arrouays, D.; Lark, R.M. Spatial prediction of soil properties with copulas. Geoderma 2011, 162, 327–334. [Google Scholar] [CrossRef]
- Quessy, J.-F.; Rivest, L.-P.; Toupin, M.-H. Goodness-of-fit tests for the family of multivariate chi-square copulas. Comput. Stat. Data Anal. 2019, 140, 21–40. [Google Scholar] [CrossRef]
- Quessy, J.F.; Rivest, L.P.; Toupin, M.H. On the family of multivariate chi-square copulas. J. Multivar. Anal. 2016, 152, 40–60. [Google Scholar] [CrossRef]
- Egozcue, M.; Fuentes García, L.; Wong, W.K.; Zitikis, R. Convex combinations of quadrant dependent copulas. Appl. Math. Lett. 2013, 26, 249–251. [Google Scholar] [CrossRef]
- Helbin, P.; Baczyński, M.; Grzegorzewski, P.; Niemyska, W. Some properties of fuzzy implications based on copulas. Inf. Sci. 2019, 502, 1–17. [Google Scholar] [CrossRef]
- Sohrabian, B. Geostatistical prediction through convex combination of Archimedean copulas. Spat. Stat. 2021, 41, 100488. [Google Scholar] [CrossRef]
- Bedford, T.; Cooke, R.M. Vines—A new graphical model for dependent random variables. Ann. Stat. 2002, 30, 1031–1068. [Google Scholar] [CrossRef]
- Aas, K.; Czado, C.; Frigessi, A.; Bakken, H. Pair-copula constructions of multiple dependence. Insur. Math. Econ. 2009, 44, 182–198. [Google Scholar] [CrossRef]
- Musafer, G.N.; Thompson, M.H.; Kozan, E.; Wolff, R.C. Spatial Pair-Copula Modeling of Grade in Ore Bodies: A Case Study. Nat. Resour. Res. 2016, 26, 223–236. [Google Scholar] [CrossRef]
- Musafer, G.N.; Thompson, M.H.; Wolff, R.C.; Kozan, E. Nonlinear Multivariate Spatial Modeling Using NLPCA and Pair-Copulas. Geogr. Anal. 2017, 49, 409–432. [Google Scholar] [CrossRef]
- Matheron, G. The Internal Consistency of Models in Geostatistics. In Geostatistics; Armstrong, M., Ed.; Kluwer: Deventer, The Netherlands, 1989; pp. 21–38. [Google Scholar]
- Cherubini, U.; Luciano, E. Value-at-risk Trade-off and Capital Allocation with Copulas. Econ. Notes 2001, 30, 235–256. [Google Scholar] [CrossRef]
- Genest, C.; Favre, A.C. Everything You Always Wanted to Know about Copula Modeling but Were Afraid to Ask. J. Hydrol. Eng. 2007, 12, 347–368. [Google Scholar] [CrossRef]
- Genest, C.; Gendron, M.; Bourdeau-Brien, M. The Advent of Copulas in Finance. Eur. J. Financ. 2009, 15, 609–618. [Google Scholar] [CrossRef]
- Bacigál, T.; Juránová, M.; Mesiar, R. On some new constructions of Archimedean copulas and applications to fitting problems. Neural Netw. World Int. J. Neural Mass Parallel Comput. Inf. Syst. 2010, 20, 81–90. [Google Scholar]
- Bacigál, T.; Mesiar, R.; Najjari, V. Generators of copulas and aggregation. Inf. Sci. 2015, 306, 81–87. [Google Scholar] [CrossRef]
- Berberian, M.; King, G.C.P. Towards a paleogeography and tectonic evolution of Iran. Can. J. Earth Sci. 1981, 18, 210–265. [Google Scholar] [CrossRef]
- Tangestani, M.H.; Moore, F. Mapping porphyry copper potential with a fuzzy model, northern Shahr-e-Babak, Iran. Aust. J. Earth Sci. 2003, 50, 311–317. [Google Scholar] [CrossRef]
- Safari, H.O.; Bagas, L.; Shafiei Bafti, B. Structural controls on the localization of Cu deposits in the Kerman Cu metallogenic province of Iran using geoinformatic techniques. Ore Geol. Rev. 2015, 67, 43–56. [Google Scholar] [CrossRef]
- Mirnejad, H.; Raeisi, D.; Heidari, F. Geochemistry and petrogenesis of tonalite from Iju area, northwest of Shahr-e Babak (Kerman province), with emphasis on adakitic magmatism. Petrology 2016, 6, 197–210. [Google Scholar]
- Mirnejad, H.; Mathur, R.; Hassanzadeh, J.; Shafie, B.; Nourali, S. Linking cu mineralization to host porphyry emplacement: Re-os ages of molybdenites versus u-pb ages of zircons and sulfur isotope compositions of pyrite and chalcopyrite from the iju and sarkuh porphyry deposits in southeast Iran. Econ. Geol. 2013, 108, 861–870. [Google Scholar] [CrossRef]
- Asadin Karam, O.; Qishlaqi, A. Concentration and speciation of heavy elements in soils and plants around Ijo porphyry copper mine (NW Share-Babak, Kerman province). J. New Find. Appl. Geol. 2019, 13, 109–123. [Google Scholar]
- Godoy, M. The Effective Management of Geological Risk in Long-Term Production Scheduling of Open Pit mines. Ph.D. Thesis, University of Queensland, Brisbane, Australia, 2002; 354p. [Google Scholar]
- Sohrabian, B.; Hosseinzadeh Gharehgheshlagh, H.; Soltani-Mohammadi, S.; Abdollahi Sharif, J. Evaluation of Tailings from a Porphyry Copper Mine based on Joint Simulation of Contaminants. Nat. Resour. Res. 2020, 29, 983–1005. [Google Scholar] [CrossRef]
- Sohrabian, B.; Soltani-Mohammadi, S.; Bakhtavar, E.; Taherinia, A. Joint simulation through orthogonal factors generated by the L-SHADE optimization method. Spat. Stat. 2021, 43, 100521. [Google Scholar] [CrossRef]










| Copula Name | Generator | Parameter Range | |||
|---|---|---|---|---|---|
| Gumbel | 0 | ||||
| Clayton | 0 | ||||
| Frank | 0 | 0 |
| Variable | Number | Mean | Variance | Skewness | Minimum | Maximum |
|---|---|---|---|---|---|---|
| Cu | 5458 | 0.1680 | 0.0250 | 2.37 | 0.0006 | 1.3884 |
| Variogram | Nugget | Structure #1 | Structure #2 | C1 | C2 | Range 1 (m) | Range 2 (m) |
|---|---|---|---|---|---|---|---|
| Horizontal | 0.1 | Exp | Sph | 0.15 | 0.75 | 7 | 175 |
| Downhole | 10 | 260 |
| Estimation Method | Measured Mean | Estimated Mean | Mean Squared Error (Perfect Value Is 0) | Correlation (Perfect Value Is 1) |
|---|---|---|---|---|
| Kriging | 0.1218 | 0.1369 | 0.0162 | 0.42 |
| Copula | 0.1278 | 0.0143 | 0.51 |
| Mean | First Quartile | Median | Third Quartile | Variance | Min | Max | |
|---|---|---|---|---|---|---|---|
| Data | 0.168 | 0.060 | 0.125 | 0.222 | 0.025 | 0.0006 | 1.388 |
| Kriging | 0.134 | 0.052 | 0.102 | 0.191 | 0.011 | 0.008 | 0.913 |
| Copula | 0.144 | 0.047 | 0.104 | 0.200 | 0.019 | 0.006 | 1.099 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sohrabian, B.; Soltani-Mohammadi, S.; Pourmirzaee, R.; Carranza, E.J.M. Geostatistical Evaluation of a Porphyry Copper Deposit Using Copulas. Minerals 2023, 13, 732. https://doi.org/10.3390/min13060732
Sohrabian B, Soltani-Mohammadi S, Pourmirzaee R, Carranza EJM. Geostatistical Evaluation of a Porphyry Copper Deposit Using Copulas. Minerals. 2023; 13(6):732. https://doi.org/10.3390/min13060732
Chicago/Turabian StyleSohrabian, Babak, Saeed Soltani-Mohammadi, Rashed Pourmirzaee, and Emmanuel John M. Carranza. 2023. "Geostatistical Evaluation of a Porphyry Copper Deposit Using Copulas" Minerals 13, no. 6: 732. https://doi.org/10.3390/min13060732





