A New Anisotropic Singularity Algorithm to Characterize Geo-Chemical Anomalies in the Duolong Mineral District, Tibet, China
Abstract
:1. Introduction
2. Study Area and Datasets

3. Methods
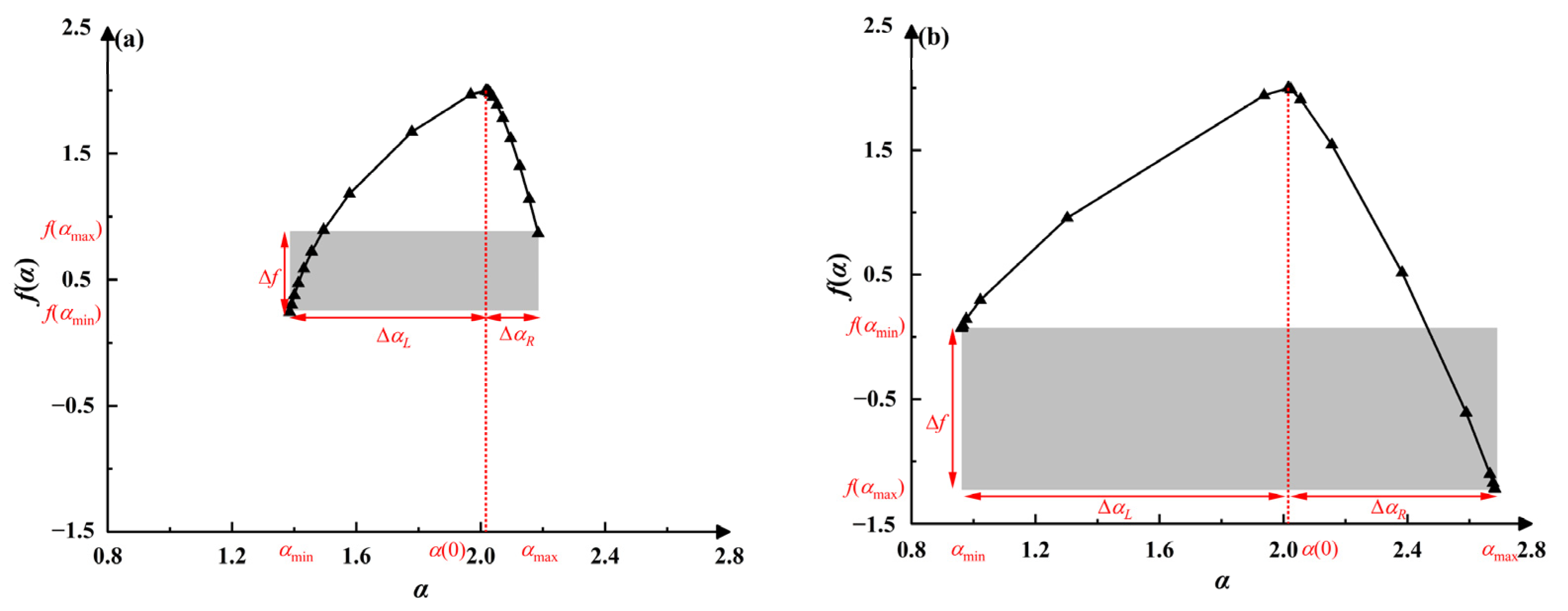
3.1. Fractal/Multifractal Theory
3.2. Local Singularity Analysis
3.3. Anisotropic Singularity Algorithm
- (1)
- Select a representative sample as the centroid and designate the initial rectangular window as A1 (A = ε1 × ε1, where ε1 can be any length depending on scales of analyzed exploratory data). Subsequently, generate a sequence of rectangular windows extending northward from the original window with sizes of ε1 × εi (where εi can be defined by practical application scenarios);
- (2)
- At each scale εi, firstly orient the rectangular window in the north direction (0°), and then rotate the azimuth at an interval. The interval (0°–360°) is predefined depending on the scales of analyzed data as well. Calculate average elemental concentrations within each directional windows C[A(εi)].
- (3)
- As geochemical behaviors such as accumulation and depletion cannot be predetermined prior to analysis, both the maximum and minimum element concentrations within their corresponding rotation window and azimuths at each scale are selected. This results in two (i.e., maximum and minimum) sets of determined element concentrations.
- (4)
- At each scale, plot the concentrations C[A(εi)] and window sizes εi corresponding to the sets of maximum and minimum on a log–log plot, respectively. The slopes k on the log–log graph can be estimated by the least squares method. Among the slopes at all scales, the one with the largest absolute value is chosen to estimate the anisotropic singularity index, k = α − 1.
- (5)
- In contrast to the isotropic singularity estimation algorithm, the new method represents the azimuths of selected windows at each scale as vectors with arrows (from low to high concentration), effectively illustrating multi-scale migration trends of elements. Additionally, these vectors at each scale can be summed to comprehensively depict anisotropic geochemical behaviors of geochemical distributions.
- (6)
- Similar to the square window-based algorithm, the aforementioned steps are executed for every location within the entire study area, thereby generating a spatial distribution of the singularity index across the space.
4. A Case Study in the Duolong Mineral District
4.1. Geochemical Distributions of Ore Elements
4.2. Multifractal Analysis
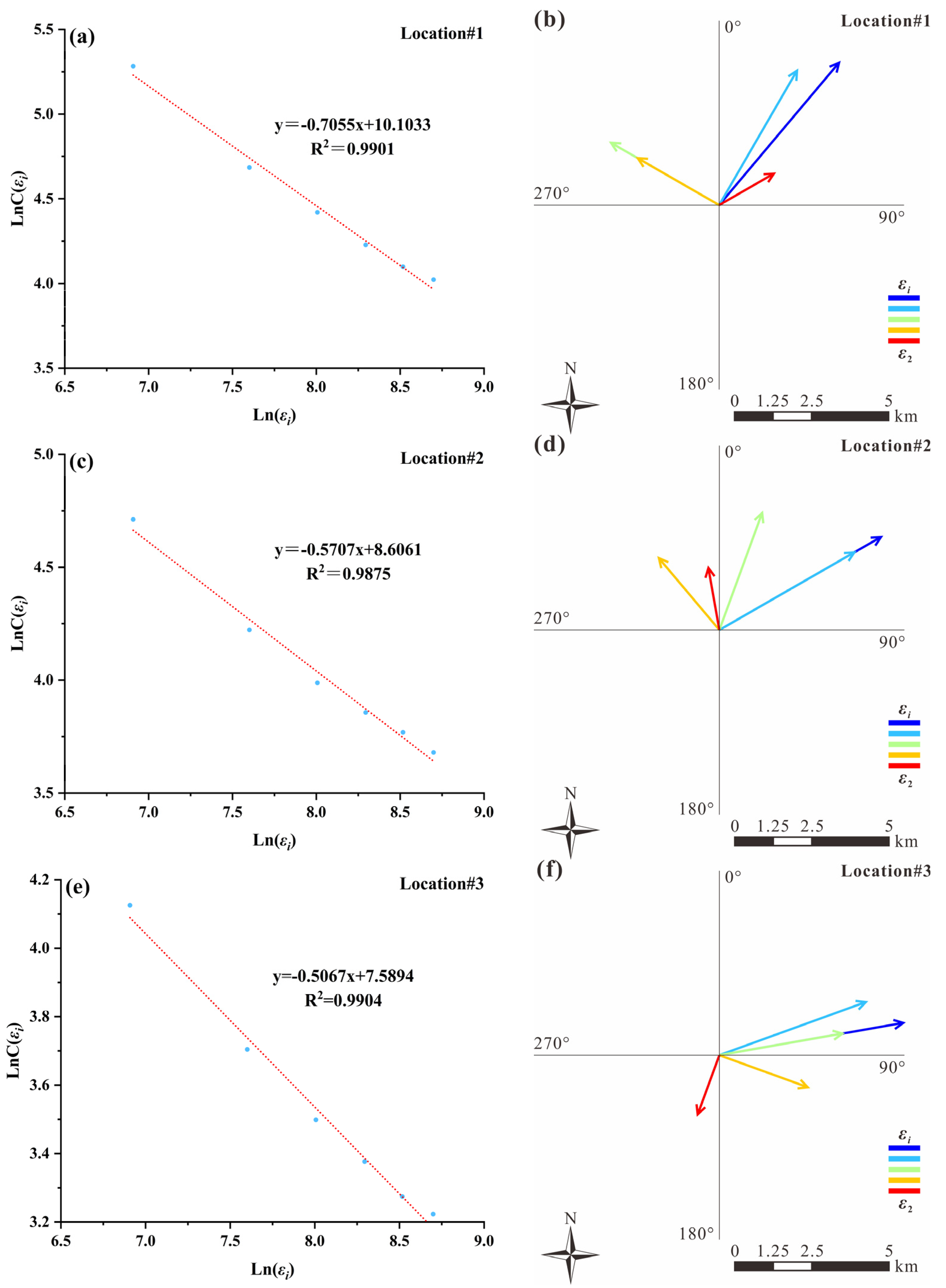
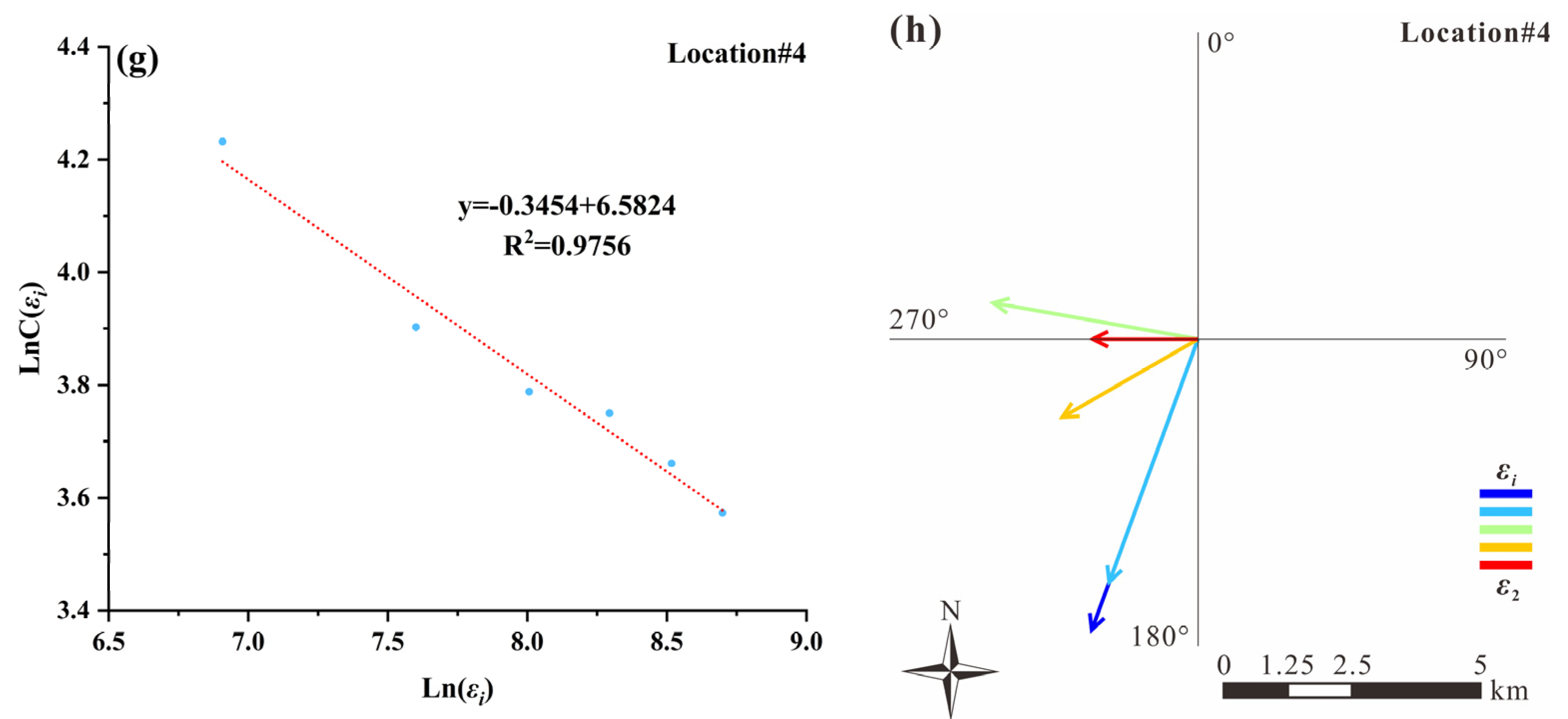
4.3. Anisotropic Singularity
- (1)
- By selecting a geochemical sampling location, the initial rectangular window is designated as A1 (A = ε1 × ε1, ε1 = 1 km). Subsequently, a series of northward trending rectangular windows are defined with dimensions of ε1 × εi (εi = 1 km, 2 km, 3 km, 4 km, 5 km, and 6 km) (where εi ranges from 1 to 6 km);
- (2)
- At each scale εi, a window rotation interval of 10° is defined to count the average elemental concentrations within directional windows C[A(εi)];
- (3)
- The maximum and minimum sets of element concentrations can be determined from all directional windows;
- (4)
- The anisotropic singularity index can be estimated in a similar manner as the aforementioned steps;
- (5)
- Vectors with arrows are used to mark all azimuths of selected windows at each scale, which are then summed up to represent the anisotropic migration and/or distributions of ore elements;
- (6)
- By implementing these steps at all sampling locations, the anisotropic nature of ore elements can be depicted in both grid and vector forms, revealing spatial variations.
4.4. Results and Discussion
5. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, H.Y.; Zhang, J.L. What is the Future Road for Mineral Exploration in the 21st Century? J. Earth Sci. 2022, 33, 1328–1329. [Google Scholar] [CrossRef]
- Agterberg, F.P. Aspects of Regional and Worldwide Mineral Resource Prediction. J. Earth Sci. 2021, 32, 279–287. [Google Scholar] [CrossRef]
- Zhao, P.D.; Chen, Y.Q. Digital Geosciences and Quantitative Mineral Exploration. J. Earth Sci. 2021, 32, 269–275. [Google Scholar] [CrossRef]
- Chen, H.Y.; Cheng, J.M.; Zhang, J.L. Multidimensional study of ore deposits: Current status and future prospects. Bull. Geol. Sci. Technol. 2022, 41, 1–4. [Google Scholar]
- Carranza, E.J.M. Geochemical anomaly and mineral prospectivity mapping in GIS. Handbook of Exploration and Environmental Geochemistry; Elsevier: Amsterdam, The Netherlands, 2008; Volume 11, 351p. [Google Scholar]
- Cheng, Q.M.; Agterberg, F.P.; Ballantyne, S.B. The separation of geochemical anomalies from background by fractal methods. J. Geochem. Explor. 1994, 51, 109–130. [Google Scholar] [CrossRef]
- Wang, W.L.; Zhao, J.; Cheng, Q.M. Analysis and integration of geo-information to identify granitic intrusions as exploration targets in southeastern Yunnan District, China. Comput. Geosci. 2011, 37, 1946–1957. [Google Scholar] [CrossRef]
- Cheng, Q.M. Mapping singularities with stream sediment geochemical data for prediction of undiscovered mineral deposits in Gejiu, Yunnan Province, China. Ore Geol. Rev. 2007, 32, 314–324. [Google Scholar] [CrossRef]
- Cheng, Q.M.; Zhao, P.D. Singularity theories and methods for characterizing mineralization processes and mapping geo-anomalies for mineral deposit prediction. Geosci. Front. 2011, 2, 67–79. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.L.; Zhao, J.; Cheng, Q.M.; Zhang, S.Y. Spatially quantitative characterization of geological processes associated with polymetallic Sn-W mineralization in the Malipo mineral district, Southeastern Yunnan, China. Ore Geol. Rev. 2017, 91, 1147–1161. [Google Scholar] [CrossRef]
- Wang, W.L.; Zhao, J.; Cheng, Q.M.; Carranza, E.J.M. GIS-based mineral potential modeling by advanced spatial analytical methods in the southeastern Yunnan mineral district, China. Ore Geol. Rev. 2015, 71, 735–748. [Google Scholar] [CrossRef]
- Wang, W.L.; Zhao, J.; Cheng, Q.M. Fault trace-oriented singularity mapping technique to characterize anisotropic geochemical signatures in Gejiu mineral district, China. J. Geochem. Explor. 2013, 134, 27–37. [Google Scholar] [CrossRef]
- Wang, W.L.; Zhao, J.; Cheng, Q.M.; Liu, J.T. Tectonic-geochemical exploration modeling for characterizing geo-anomalies in southeastern Yunnan district, China. J. Geochem. Explor. 2012, 122, 71–80. [Google Scholar] [CrossRef]
- Zhao, P.D. Theory and Practice of Geoanomaly in Mineral Exploration; China University of Geosciences Press: Wuhan, China, 1999. [Google Scholar]
- Eklundh, L.; Singh, A. A comparative analysis of standardized and unstandardized principal components analysis in remote sensing. Int. J. Remote Sens. 1993, 14, 1359–1370. [Google Scholar] [CrossRef]
- Tobler, W.R. A Computer Movie Simulating Urban Growth in the Detroit Region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Lam, N.S.N. Spatial interpolation methods: A review. Am. Cartogr. 1983, 10, 129–149. [Google Scholar] [CrossRef]
- Wei, J.H. Preliminary discussion on the theory of ore-forming field and its significant role for mineral exploration. Bull. Geol. Sci. Technol. 2020, 39, 114–129. [Google Scholar]
- Mandelbrot, B.B. How long is the coast of britain? Statistical self-similarity and fractional dimension. Science 1967, 156, 636–638. [Google Scholar] [CrossRef] [Green Version]
- Schertzer, D.; Lovejoy, S.; Schmitt, F.; Chigirinskaya, Y.; Marsan, D. Multifractal cascade dynamics and turbulent intermittency. Fractals-Interdiscip. J. Complex Geom. Nat. 1997, 5, 427–471. [Google Scholar] [CrossRef]
- Veneziano, D.; Furcolo, P. Multifractality of rainfall and scaling of intensity-duration-frequency curves. Water Resour. Res. 2002, 38, 42-1–42-12. [Google Scholar] [CrossRef]
- Malamud, B.D.; Turcotte, D.L.; BARTON, C.C. The 1993 Mississippi River Flood: A One Hundred or a One Thousand Year Event? Environ. Eng. Geosci. 1996, 2, 479–486. [Google Scholar] [CrossRef]
- Malamud, B.D.; Turcotte, D.L.; Guzzetti, F.; Reichenbach, P. Landslide inventories and their statistical properties. Earth Surf. Process. Landf. 2004, 29, 687–711. [Google Scholar] [CrossRef]
- Turcotte, D.L. Fractals and Chaos in Geology and Geophysics; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Wang, W.L.; Zhao, J.; Cheng, Q.M. Nonlinearity. In Encyclopedia of Mathematical Geosciences; Daya Sagar, B.S., Cheng, Q., McKinley, J., Agterberg, F., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 1–6. [Google Scholar]
- Agterberg, F.P. Multifractal modeling of the sizes and grades of giant and supergiant deposits. Int. Geol. Rev. 1995, 37, 1–8. [Google Scholar] [CrossRef]
- Cheng, Q.M. Multifractal imaging filtering and decomposition methods in space, Fourier frequency, and eigen domains. Nonlinear Process. Geophys. 2007, 14, 293–303. [Google Scholar] [CrossRef] [Green Version]
- Cheng, Q.M.; Agterberg, F.P. Multifractal modeling and spatial statistics. Math. Geol. 1996, 28, 1–16. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Multifractal measures, especially for the geophysicist. Pure Appl. Geophys. 1989, 131, 5–42. [Google Scholar] [CrossRef]
- Cheng, Q.M.; Agterberg, F.P. Singularity analysis of ore-mineral and toxic trace elements in stream sediments. Comput. Geosci. 2009, 35, 234–244. [Google Scholar] [CrossRef]
- Turcotte, D.L. Fractals in petrology. Lithos 2002, 65, 261–271. [Google Scholar] [CrossRef]
- Bonham-Carter, G.F. Geographic Information Systems for Geoscientists: Modelling with GIS, Computer Methods in the Geosciences, 1st ed; Pergamon: New York, NY, USA, 1994. [Google Scholar]
- Agterberg, F.P. Multifractals and geostatistics. J. Geochem. Explor. 2012, 122, 113–122. [Google Scholar] [CrossRef]
- Cheng, Q.M. Multifractality and spatial statistics. Comput. Geosci. 1999, 25, 949–961. [Google Scholar] [CrossRef]
- Carranza, E.J.M. Geocomputation of mineral exploration targets. Comput. Geosci. 2011, 37, 1907–1916. [Google Scholar] [CrossRef]
- Porwal, A.; Carranza, E.J.M. Introduction to the Special Issue: GIS-based mineral potential modelling and geological data analyses for mineral exploration. Ore Geol. Rev. 2015, 71, 477–483. [Google Scholar] [CrossRef]
- Cheng, Q.M.; Xu, Y.; Grunsky, E. Multifractal power spectrum–area method for geochemical anomaly separation. Nat. Resour. Res 2000, 9, 43–51. [Google Scholar] [CrossRef]
- Cheng, Q.M. Singularity theory and methods for mapping geochemical anomalies caused by buried sources and for predicting undiscovered mineral deposits in covered areas. J. Geochem. Explor. 2012, 122, 55–70. [Google Scholar] [CrossRef]
- Zhang, D.J.; Cheng, Q.M.; Agterberg, F.P.; Chen, Z.J. An improved solution of local window parameters setting for local singularity analysis based on Excel VBA batch processing technology. Comput. Geosci. 2016, 88, 54–66. [Google Scholar] [CrossRef]
- Zuo, R.G.; Wang, J.L. ArcFractal: An ArcGIS Add-In for Processing Geoscience Data Using Fractal/Multifractal Models. Nat. Resour. Res. 2020, 29, 3–12. [Google Scholar] [CrossRef]
- Chen, G.X.; Huang, N.; Wu, G.P.; Luo, L.; Wang, D.T.; Cheng, Q.M. Mineral prospectivity mapping based on wavelet neural network and Monte Carlo simulations in the Nanling W-Sn metallogenic province. Ore Geol. Rev. 2022, 143, 104765. [Google Scholar] [CrossRef]
- Chen, G.X.; Cheng, Q.M.; Puetz, S. Special Issue: Data-Driven Discovery in Geosciences: Opportunities and Challenges. Math. Geosci. 2023, 55, 287–293. [Google Scholar] [CrossRef]
- Cheng, Q.M. Fractal Calculus and Analysis for Characterizing Geoanomalies Caused by Singular Geological Processes. J. Earth Sci. 2021, 32, 276–278. [Google Scholar] [CrossRef]
- Cheng, Q.M.; Chen, Y.Q.; Zuo, R.G. Preface to the Special Issue on Digital Geosciences and Quantitative Exploration of Mineral Resources. J. Earth Sci. 2021, 32, 267–268. [Google Scholar] [CrossRef]
- Zhang, Z.J.; Kusky, T.; Gao, M.; Cheng, Q.M. Spatio-temporal analysis of big data sets of detrital zircon U-Pb geochronology and Hf isotope data: Tests of tectonic models for the Precambrian evolution of the North China Craton. Earth-Sci. Rev. 2023, 239, 104372. [Google Scholar] [CrossRef]
- Xiao, F.; Chen, J.G.; Hou, W.S.; Wang, Z.H.; Zhou, Y.Z.; Erten, O. A spatially weighted singularity mapping method applied to identify epithermal Ag and Pb-Zn polymetallic mineralization associated geochemical anomaly in Northwest Zhejiang, China. J. Geochem. Explor. 2018, 189, 122–137. [Google Scholar] [CrossRef]
- Li, Q.M.; Liu, S.H.; Liang, G.H. Anisotropic singularity and application for mineral potential mapping in GIS environments. Prog. Geophys. 2005, 20, 1015–1020. [Google Scholar]
- Wang, W.L.; Cheng, Q.M.; Zhang, S.Y.; Zhao, J. Anisotropic singularity: A novel way to characterize controlling effects of geological processes on mineralization. J. Geochem. Explor. 2018, 189, 32–41. [Google Scholar] [CrossRef]
- Cheng, Q.M. Spatial and scaling modelling for geochemical anomaly separation. J. Geochem. Explor. 1999, 65, 175–194. [Google Scholar] [CrossRef]
- Wang, W.L.; Zhu, M.Q. Anisotropy of geochemical distributions characterized by irregular window-based local singularity analysis. Geochem.-Explor. Environ. Anal. 2022, 22. [Google Scholar] [CrossRef]
- Wang, W.L.; Zhu, M.Q.; Zhao, J.; Chen, Z.J.; Cheng, Q.M. Joint Modeling Based on Singularity Mapping and U-statistical Methods for Geo-Anomaly Characterization. Nat. Resour. Res. 2022, 31, 1909–1923. [Google Scholar] [CrossRef]
- Li, J.X.; Qin, K.Z.; Li, G.M.; Richards, J.P.; Zhao, J.X.; Cao, M.J. Geochronology, geochemistry, and zircon Hf isotopic compositions of Mesozoic intermediate-felsic intrusions in central Tibet: Petrogenetic and tectonic implications. Lithos 2014, 198, 77–91. [Google Scholar] [CrossRef]
- Zhu, D.C.; Li, S.M.; Cawood, P.A.; Wang, Q.; Zhao, Z.D.; Liu, S.A.; Wang, L.Q. Assembly of the Lhasa and Qiangtang terranes in central Tibet by divergent double subduction. Lithos 2016, 245, 7–17. [Google Scholar] [CrossRef] [Green Version]
- Metcalfe, L. Gondwana dispersion and Asian accretion: Tectonic and palaeogeographic evolution of eastern Tethys. J. Asian Earth Sci. 2013, 66, 1–33. [Google Scholar] [CrossRef]
- Zhu, D.C.; Zhao, Z.D.; Niu, Y.L.; Dilek, Y.; Hou, Z.Q.; Mo, X.X. The origin and pre-Cenozoic evolution of the Tibetan Plateau. Gondwana Res. 2013, 23, 1429–1454. [Google Scholar] [CrossRef]
- Fan, J.J.; Li, C.; Xie, C.M.; Wang, M. Petrology, geochemistry, and geochronology of the Zhonggang ocean island, northern Tibet: Implications for the evolution of the Banggongco-Nujiang oceanic arm of the Neo-Tethys. Int. Geol. Rev. 2014, 56, 1504–1520. [Google Scholar] [CrossRef]
- Shi, R.D. SHRIMP dating of the Bangong Lake SSZ-type ophiolite: Constraints on the closure time of ocean in the Bangong Lake-Nujiang River, northwestern Tibet. Chin. Sci. Bull. 2007, 52, 936–941. [Google Scholar] [CrossRef]
- Pan, G.T.; Wang, L.Q.; Li, R.S.; Yuan, S.H.; Ji, W.H.; Yin, F.G.; Zhang, W.P.; Wang, B.D. Tectonic evolution of the Qinghai-Tibet Plateau. J. Asian Earth Sci. 2012, 53, 3–14. [Google Scholar] [CrossRef]
- Wang, B.D.; Wang, L.Q.; Chung, S.L.; Chen, J.L.; Yin, F.G.; Liu, H.; Li, X.B.; Chen, L.K. Evolution of the Bangong-Nujiang Tethyan ocean: Insights from the geochronology and geochemistry of mafic rocks within ophiolites. Lithos 2016, 245, 18–33. [Google Scholar] [CrossRef]
- Baxter, A.T.; Aitchison, J.C.; Zyabrev, S.V. Radiolarian age constraints on Mesotethyan ocean evolution, and their implications for development of the Bangong-Nujiang suture, Tibet. J. Geol. Soc. 2009, 166, 689–694. [Google Scholar] [CrossRef]
- Liu, W.L.; Xia, B.; Zhong, Y.; Cai, J.X.; Li, J.F.; Liu, H.F.; Cai, Z.R.; Sun, Z.L. Age and composition of the Rebang Co and Julu ophiolites, central Tibet: Implications for the evolution of the Bangong Meso-Tethys. Int. Geol. Rev. 2014, 56, 430–447. [Google Scholar] [CrossRef]
- Zhang, K.J.; Zhang, Y.X.; Tang, X.C.; Xia, B. Late Mesozoic tectonic evolution and growth of the Tibetan plateau prior to the Indo-Asian collision. Earth-Sci. Rev. 2012, 114, 236–249. [Google Scholar] [CrossRef]
- Tang, J.X.; Song, Y.; Wang, Q.; Lin, B.; Yang, C.; Guo, N.; Fang, X.; Yang, H.H.; Wang, Y.Y.; Gao, K.; et al. Geological Characteristics and Exploration Model of the Tiegelongnan Cu (Au-Ag) Deposit: The First Ten Million Tons Metal Resources of a Porphyry-epithermal Deposit in Tibet. Acta Geosci. Sin. 2016, 37, 663–690. [Google Scholar]
- Zhang, T.Y.; Deng, J.H.; Wang, M.; Li, C.; Zhang, L.P.; Sun, W.D. Geochemistry and genesis of the Nadun Nb-enriched arc basalt in the Duolong mineral district, western Tibet: Indication of ridge subduction. Geosci. Front. 2022, 13, 101283. [Google Scholar] [CrossRef]
- Wang, M.; Xie, C.M.; Fan, J.J. 1:50000 Regional Surveys in Duobuza, Gaize County, Tibet; Geological Survey and Research Institute of Jilin University: Changchun, China, 2016. [Google Scholar]
- Li, G.M.; Duan, Z.M.; Liu, B.; Zhang, H.; Dong, S.L.; Zhang, L.J. The discovery of Jurassic accretionary complexes in Duolong area, northern Bangong Co -Nujiang suture zone, Tibet, and its geologic significance. Geol. Bull. China 2011, 30, 1256–1260. [Google Scholar]
- Gao, K.; Tang, J.X.; Fang, X.; Zhang, Z.; Wang, Q.; Yang, H.H.; Wang, Y.Y.; Feng, J. Geological and Geochemical Characteristics and Significance of the Sena Cu-Au Deposit from Duolong Ore-concentration Area, Tibet, China. Acta Mineral. Sin. 2016, 36, 199–207. [Google Scholar]
- Li, Y.B.; Zhong, W.T.; Guo, J.C.; Qin, Z.P.; Zhang, Z.; Li, J.L.; Deng, S.Q.; Li, Y.C. Petrogenesis of igneous rocks and ore_forming material source of the Nating porphyry Cu (Au) deposit in the western section of the Bangong Co-Nujiang metallogenic belt, Tibet. Acta Petrol. Sin. 2019, 35, 1717–1737. [Google Scholar]
- Li, J.; Qin, K.; Li, G.; Xiao, B.; Zhao, J.; Chen, L. Magmatic-hydrothermal evolution of the Cretaceous Duolong gold-rich porphyry copper deposit in the Bangongco metallogenic belt, Tibet: Evidence from U-Pb and 40Ar/39Ar geochronology. J. Asian Earth Sci. 2011, 41, 525–536. [Google Scholar] [CrossRef]
- Wang, Q.; Tang, J.X.; Chen, Y.C.; Hou, J.F.; Li, Y.B. The metallogenic model and prospecting direction for the Duolong super large copper (gold) district, Tibet. Acta Petrol. Sin. 2019, 35, 879–896. [Google Scholar] [CrossRef] [Green Version]
- Yang, H.H.; Wang, Q.; Li, Y.B.; Lin, B.; Song, Y.; Wang, Y.Y.; He, W.; Li, H.W.; Li, S.; Li, J.L.; et al. Geology and mineralization of the Tiegelongnan supergiant porphyry-epithermal Cu (Au, Ag) deposit (10 Mt) in western Tibet, China: A review. China Geol. 2022, 5, 136–159. [Google Scholar]
- Geng, Q.R.; Zhang, Z.; Peng, Z.M.; Guan, J.L.; Zhu, X.P.; Mao, X.C. Jurassic-Cretaceous granitoids and related tectono-metallogenesis in the Zapug-Duobuza arc, western Tibet. Ore Geol. Rev. 2016, 77, 163–175. [Google Scholar] [CrossRef]
- Song, Y.; Yang, H.H.; Lin, B.; Liu, Z.B.; Wang, Q.; Gao, K.; Yang, C.; Fang, X. The preservation system of epithermal deposits in South Qiangtang terrane of central Tibetan Plateau and its significance: A case study of the Tiegelongnan superlarge deposit. Acta Geosci. Sin. 2017, 38, 659–669. [Google Scholar]
- Liu, Z.B.; Wang, W.L.; Song, Y.; Wang, Q. Geo-information extraction and integration of ore-controlling structure in the Duolong ore concentration area of Tibet. Acta Petrol. Sin. 2017, 38, 803–812. [Google Scholar]
- Wei, S.G.; Song, Y.; Tang, J.X.; Liu, Z.B.; Wang, Q.; Lin, B.; Feng, J.; Hou, L.; Dan, Z.; Wang, X. Geochronology, geochemistry, Sr-Nd-Hf isotopic compositions, and petrogenetic and tectonic implications of Early Cretaceous intrusions associated with the Duolong porphyry-epithermal Cu-Au deposit, central Tibet. Int. Geol. Rev. 2018, 60, 1116–1139. [Google Scholar] [CrossRef]
- Wang, W.L.; Cheng, Q.M.; Tang, J.X.; Pubuciren; Song, Y.; Li, Y.B.; Liu, Z.B. Fractal/multifractal analysis in support of mineral exploration in the Duolong mineral district, Tibet, China. Geochem. Explor. Environ. Anal. 2017, 17, 261–276. [Google Scholar] [CrossRef]
- Xie, S.Y.; Ke, X.Z.; Huang, K.J.; Cheng, Q.M.; Bao, Z.Y. Evaluation of ore-forming potential by fractal/multifractal analysis. Geochim. Et Cosmochim. Acta 2010, 74, A1157. [Google Scholar]
- Zuo, R.G.; Wang, J. Fractal/multifractal modeling of geochemical data: A review. J. Geochem. Explor. 2016, 164. [Google Scholar] [CrossRef]
- Russell, D.A.; Hanson, J.D.; Ott, E. Dimension of Strange Attractors. Phys. Rev. Lett. 1980, 45, 1175–1178. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W.H. Freeman and Company: New York, NY, USA, 1983; Volume 495. [Google Scholar]
- Evertsz, C.J.G.; Mandelbrot, B.B. Multifractal Measures. Chaos Fractals 1992, 1992, 922–953. [Google Scholar]
- Stanley, H.E.; Meakin, P. Multifractal phenomena in physics and chemistry. Nature 1988, 335, 405–409. [Google Scholar] [CrossRef]
- Halsey, T.C.; Jensen, M.H.; Kadanoff, L.P.; Procaccia, I.; Shraiman, B.I. Fractal measures and their singularities: The characterization of strange sets. Phys. Rev. A 1986, 33, 1141–1151. [Google Scholar] [CrossRef]
- Ai, T.; Zhang, R.; Zhou, H.W.; Pei, J.L. Box-counting methods to directly estimate the fractal dimension of a rock surface. Appl. Surf. Sci. 2014, 314, 610–621. [Google Scholar] [CrossRef]
- Bashan, A.; Bartsch, R.; Kantelhardt, J.W.; Havlin, S. Comparison of detrending methods for fluctuation analysis. Phys. A Stat. Mech. Its Appl. 2008, 387, 5080–5090. [Google Scholar] [CrossRef] [Green Version]
- Xie, H.P.; Wang, J.A.; Kwasniewski, M.A. Multifractal characterization of rock fracture surfaces. Int. J. Rock Mech. Min. Sci. 1999, 36, 19–27. [Google Scholar] [CrossRef]
- Cheng, Q.M. Generalized binomial multiplicative cascade processes and asymmetrical multifractal distributions. Nonlinear Process. Geophys. 2014, 21, 477–487. [Google Scholar] [CrossRef] [Green Version]
- Xie, S.Y.; Bao, Z.Y. Fractal and multifractal properties of geochemical fields. Math. Geol. 2004, 36, 847–864. [Google Scholar] [CrossRef]
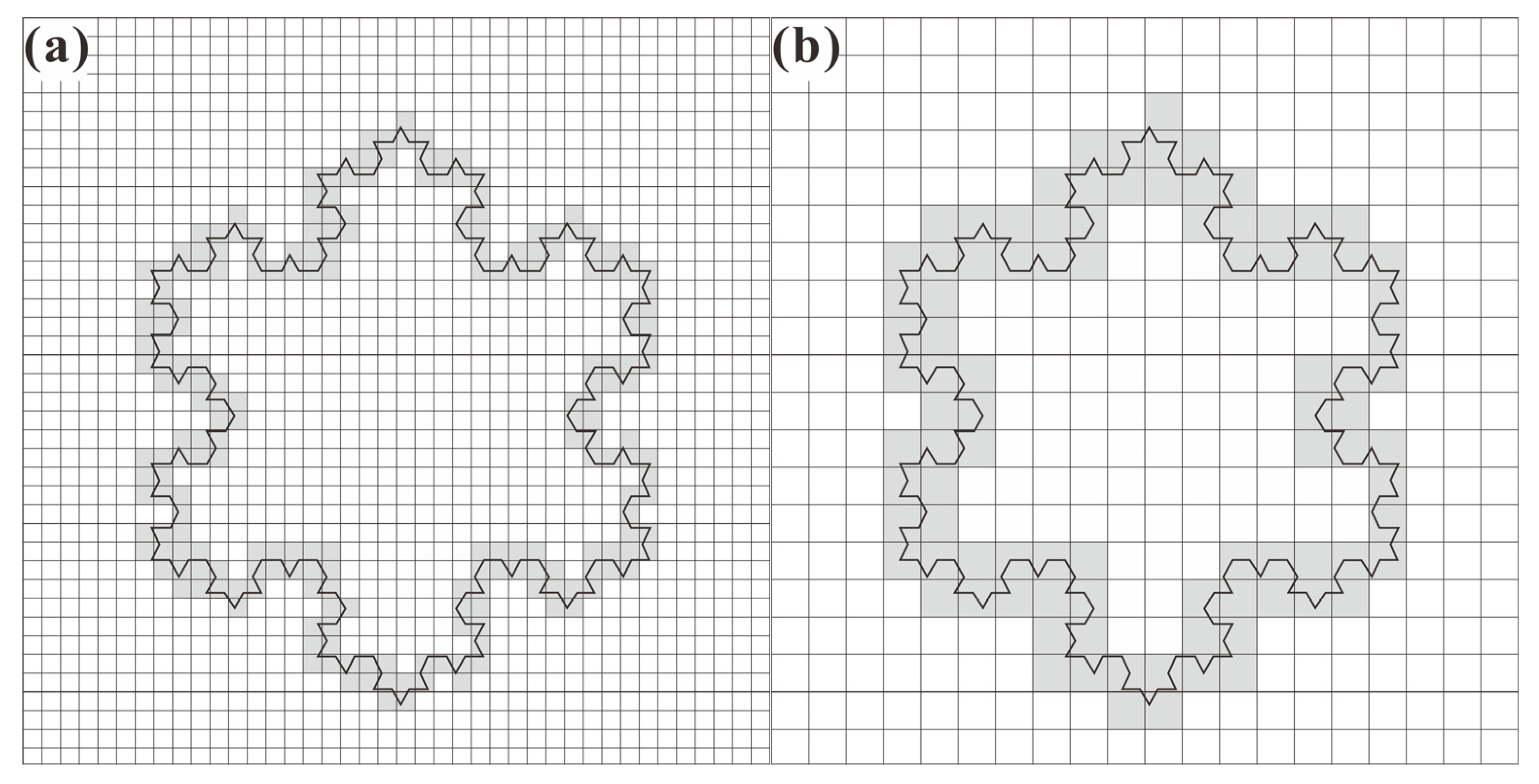
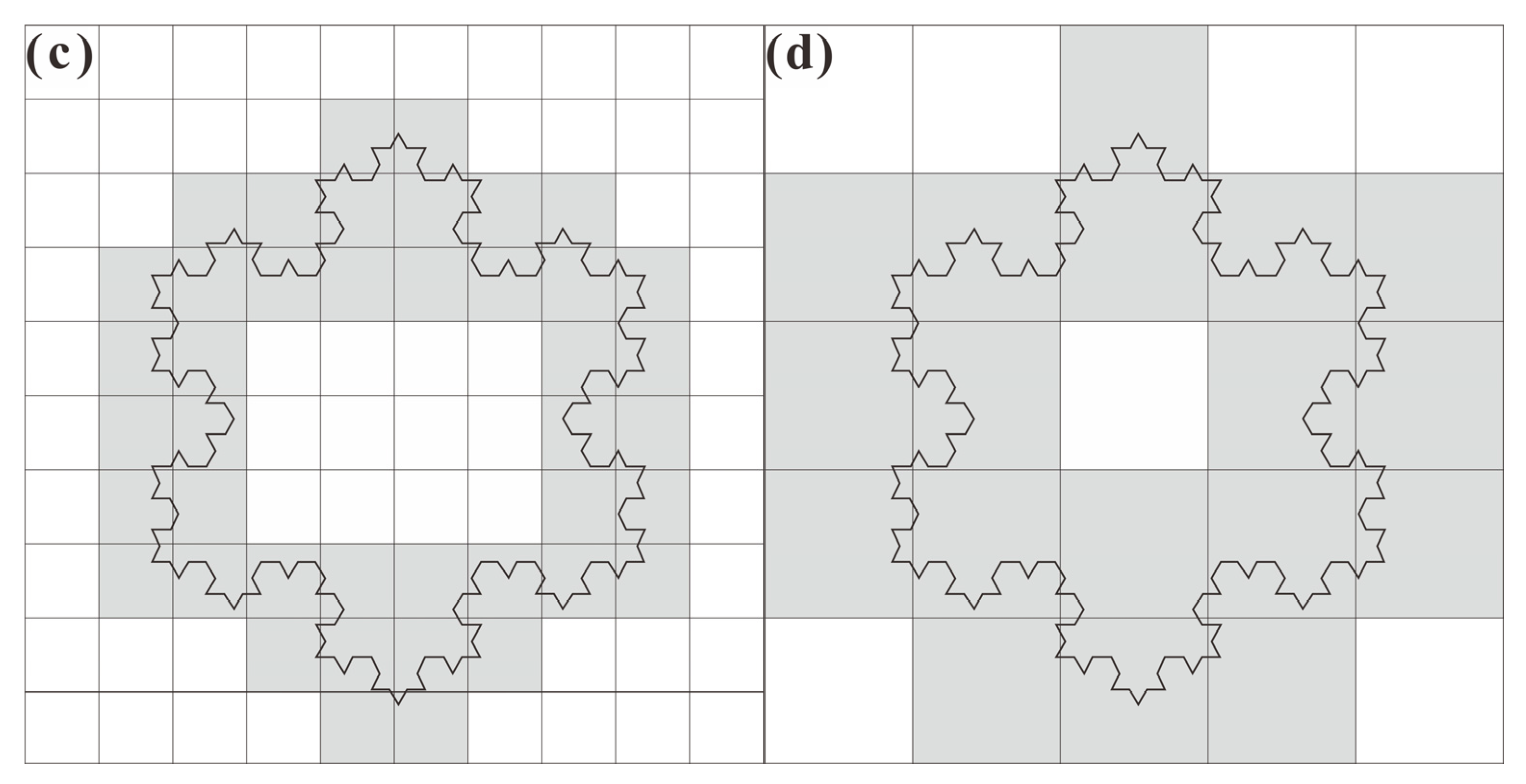





| Max | Min | Mean | Standard Deviation | CV | Median | Skewness | |
|---|---|---|---|---|---|---|---|
| Cu (in ppm) | 854.00 | 6.20 | 38.51 | 51.99 | 1.35 | 26.84 | 8.67 |
| Au (in ppb) | 1058.50 | 0.40 | 4.76 | 25.00 | 5.25 | 2.15 | 29.58 |
| Box Size εi | 1 | 2 | 4 | 8 |
|---|---|---|---|---|
| Box Count N(εi) | 221 | 93 | 42 | 18 |
| αmin | α(0) | αmax | Δα | R | f(αmin) | f(αmax) | Δf | |
|---|---|---|---|---|---|---|---|---|
| Cu | 1.39 | 2.02 | 2.18 | 0.79 | 3.94 | 0.24 | 0.87 | −0.63 |
| Au | 0.96 | 2.02 | 2.68 | 1.72 | 1.61 | 0.07 | −1.22 | 1.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, J.; Wang, W.; Yuan, C. A New Anisotropic Singularity Algorithm to Characterize Geo-Chemical Anomalies in the Duolong Mineral District, Tibet, China. Minerals 2023, 13, 988. https://doi.org/10.3390/min13070988
Tang J, Wang W, Yuan C. A New Anisotropic Singularity Algorithm to Characterize Geo-Chemical Anomalies in the Duolong Mineral District, Tibet, China. Minerals. 2023; 13(7):988. https://doi.org/10.3390/min13070988
Chicago/Turabian StyleTang, Jie, Wenlei Wang, and Changjiang Yuan. 2023. "A New Anisotropic Singularity Algorithm to Characterize Geo-Chemical Anomalies in the Duolong Mineral District, Tibet, China" Minerals 13, no. 7: 988. https://doi.org/10.3390/min13070988
APA StyleTang, J., Wang, W., & Yuan, C. (2023). A New Anisotropic Singularity Algorithm to Characterize Geo-Chemical Anomalies in the Duolong Mineral District, Tibet, China. Minerals, 13(7), 988. https://doi.org/10.3390/min13070988







