3D Multicomponent Self-Potential Inversion: Theory and Application to the Exploration of Seafloor Massive Sulfide Deposits on Mid-Ocean Ridges
Abstract
:1. Introduction
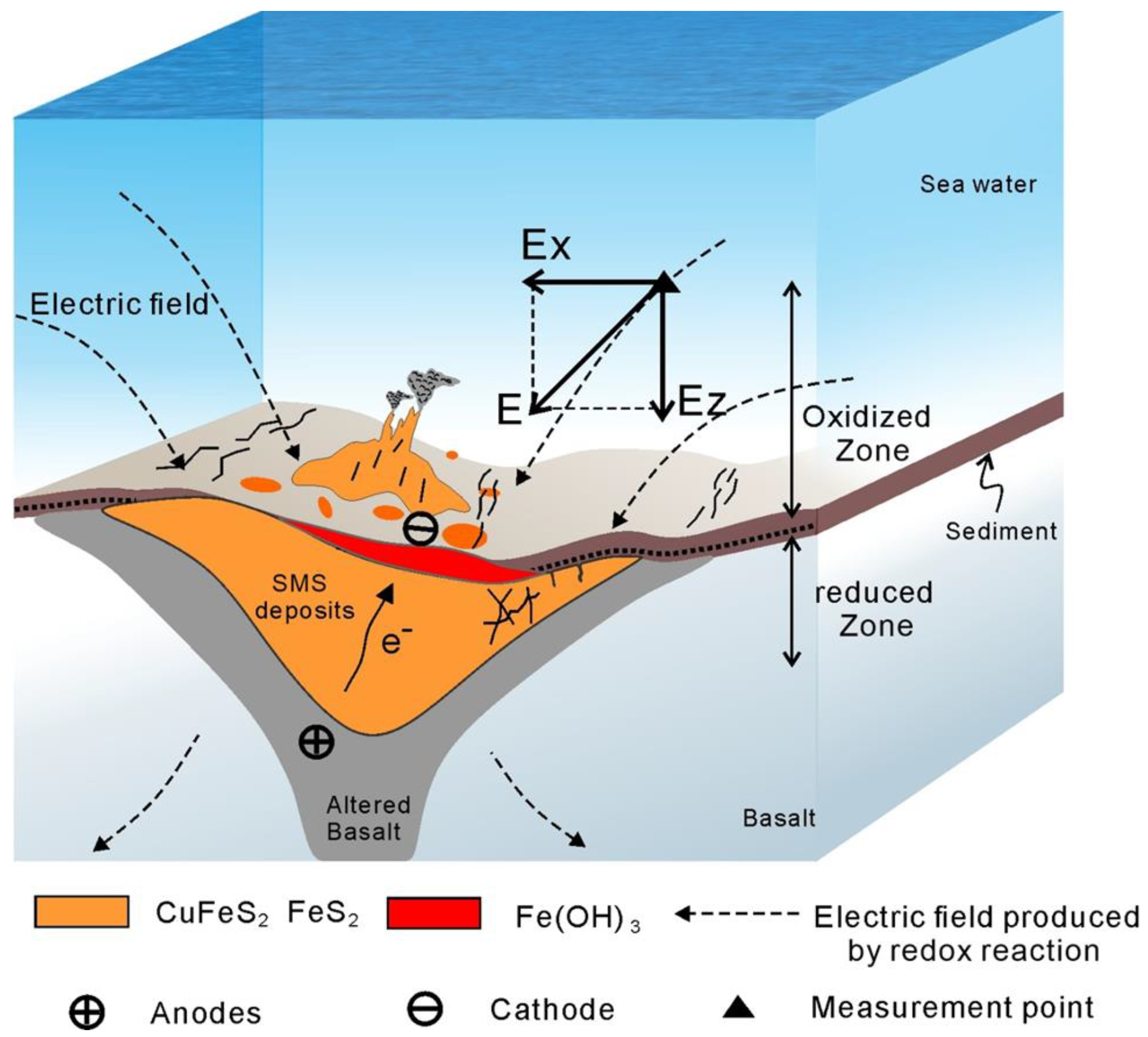
2. The Causative Source of Negative SP Anomalies above the Seafloor
3. Forward and Inversion Methods of SP Method
3.1. Governing Equations for the Self-Potential Anomalies
3.2. Jacobian Matrix
3.3. Multicomponent SP Data Inversion
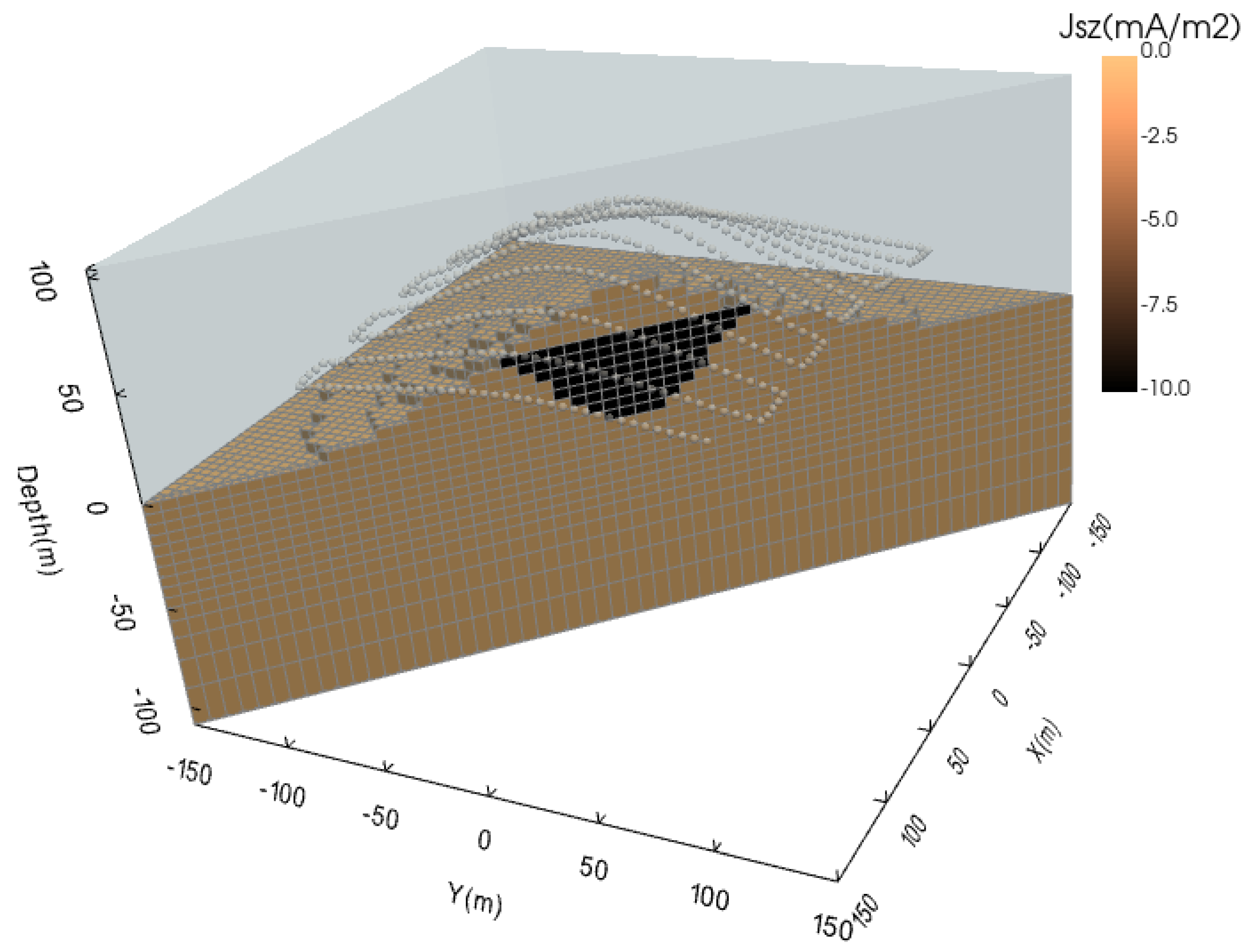
4. Synthetic Model Test
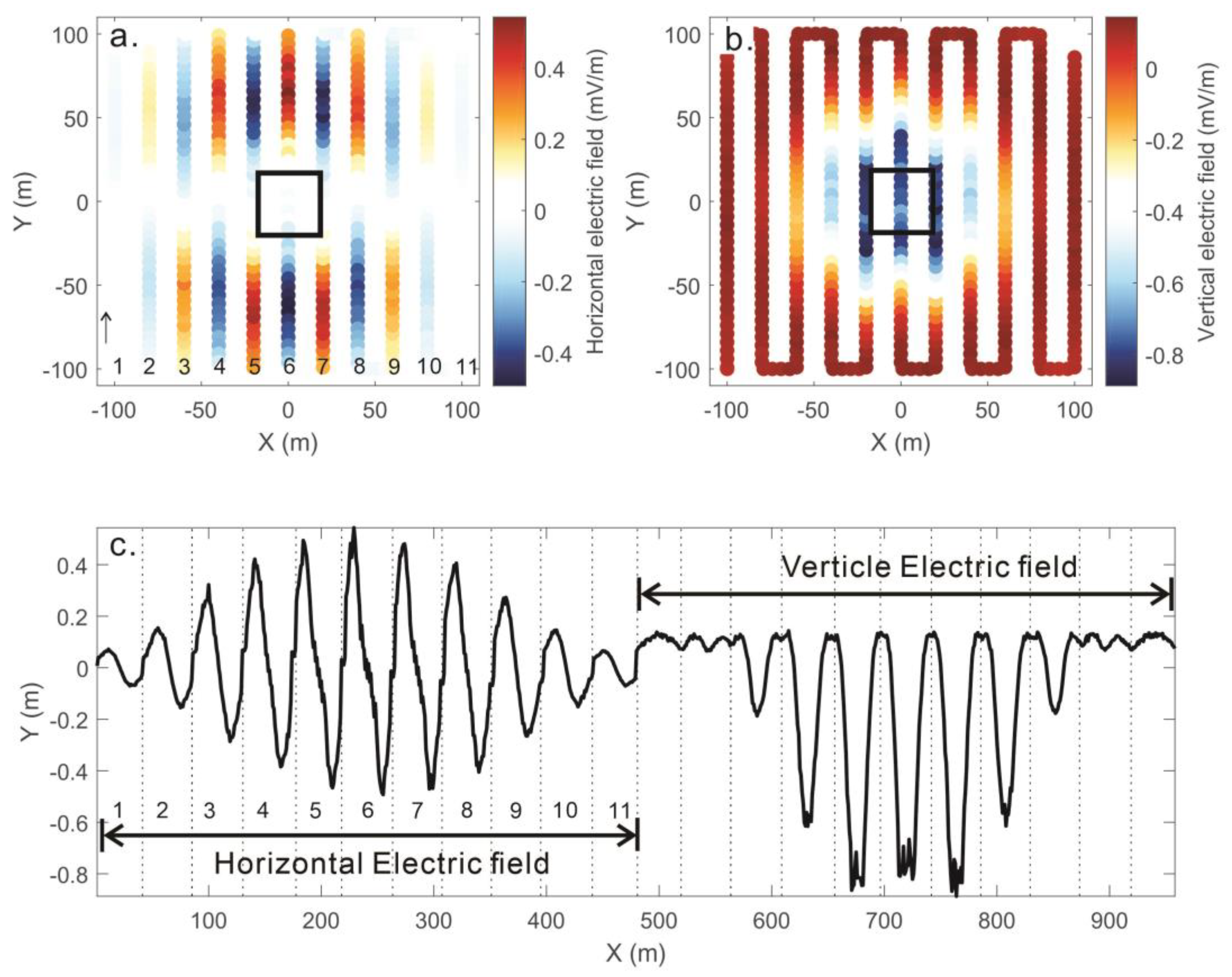
4.1. The Characteristics of Different Electric Field Components
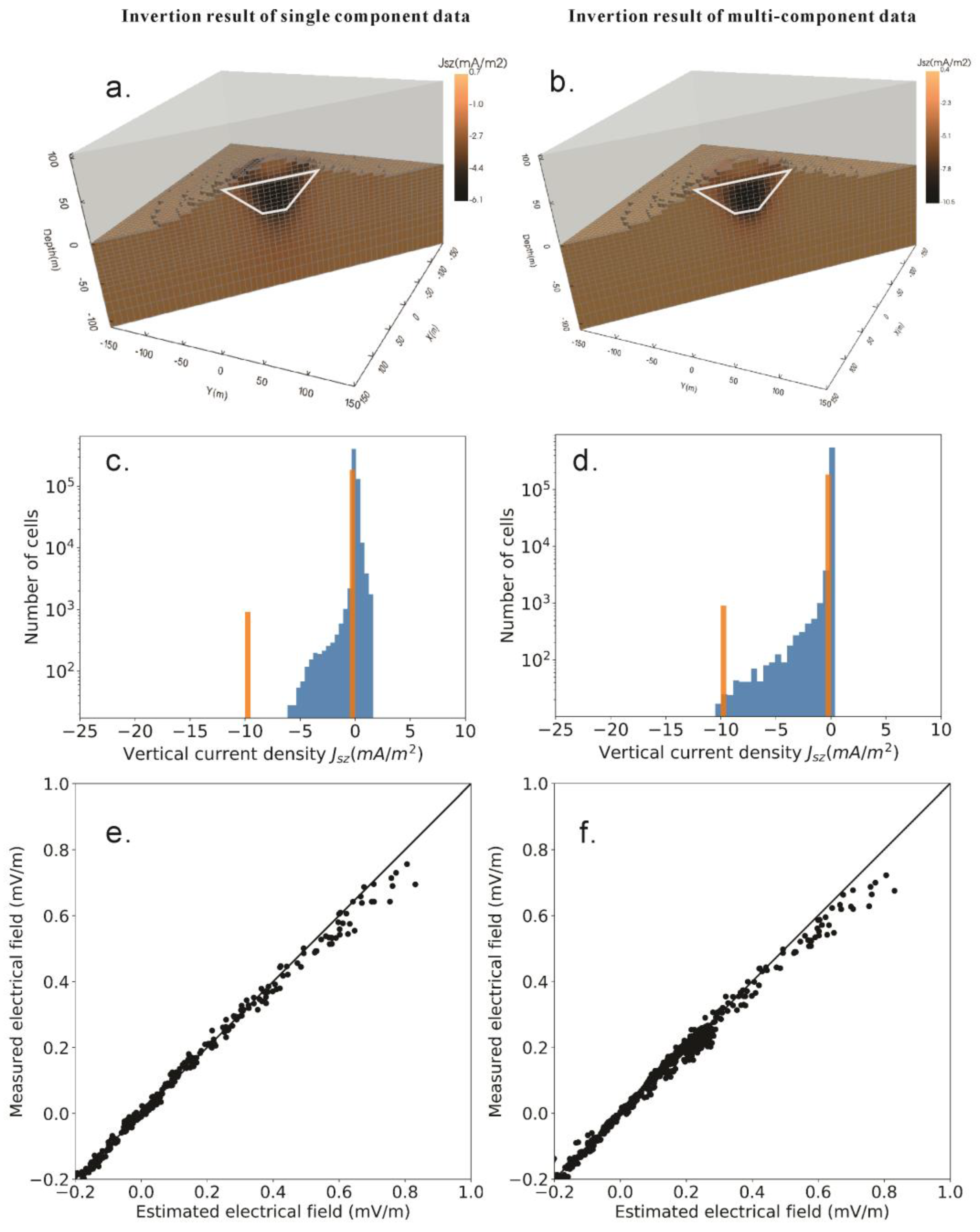
4.2. Single-Component versus Multicomponent Electric Field Results
4.3. Comparing the Computation Times and Memory for the Different Inversion
5. Field Data Application
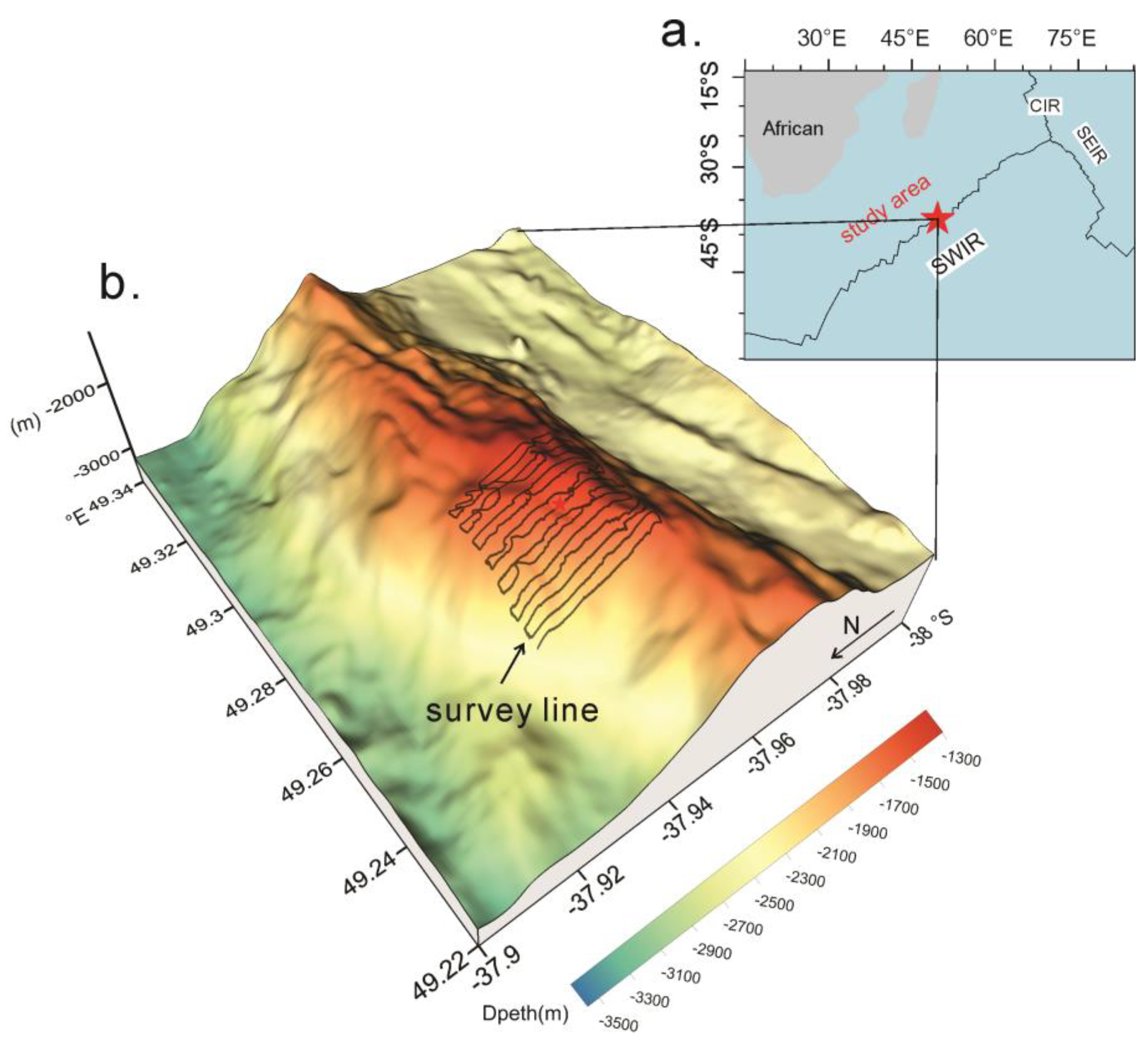
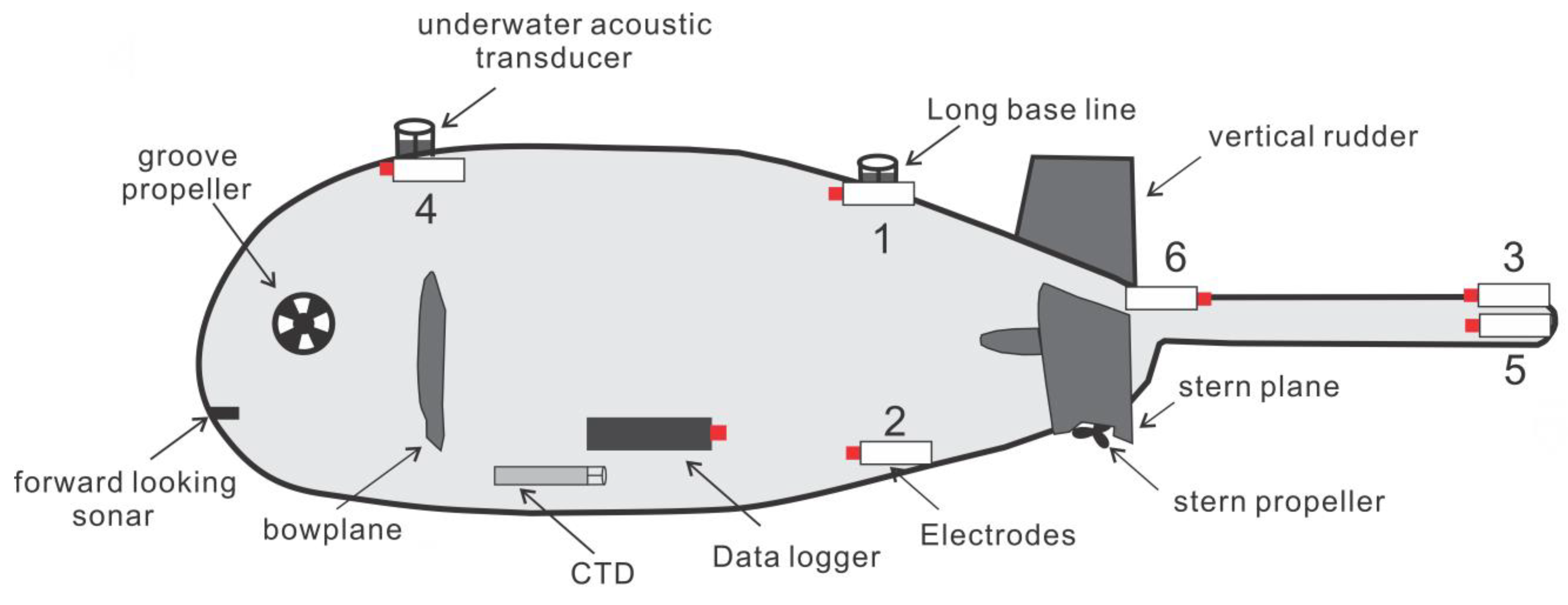
5.1. Data Acquisition
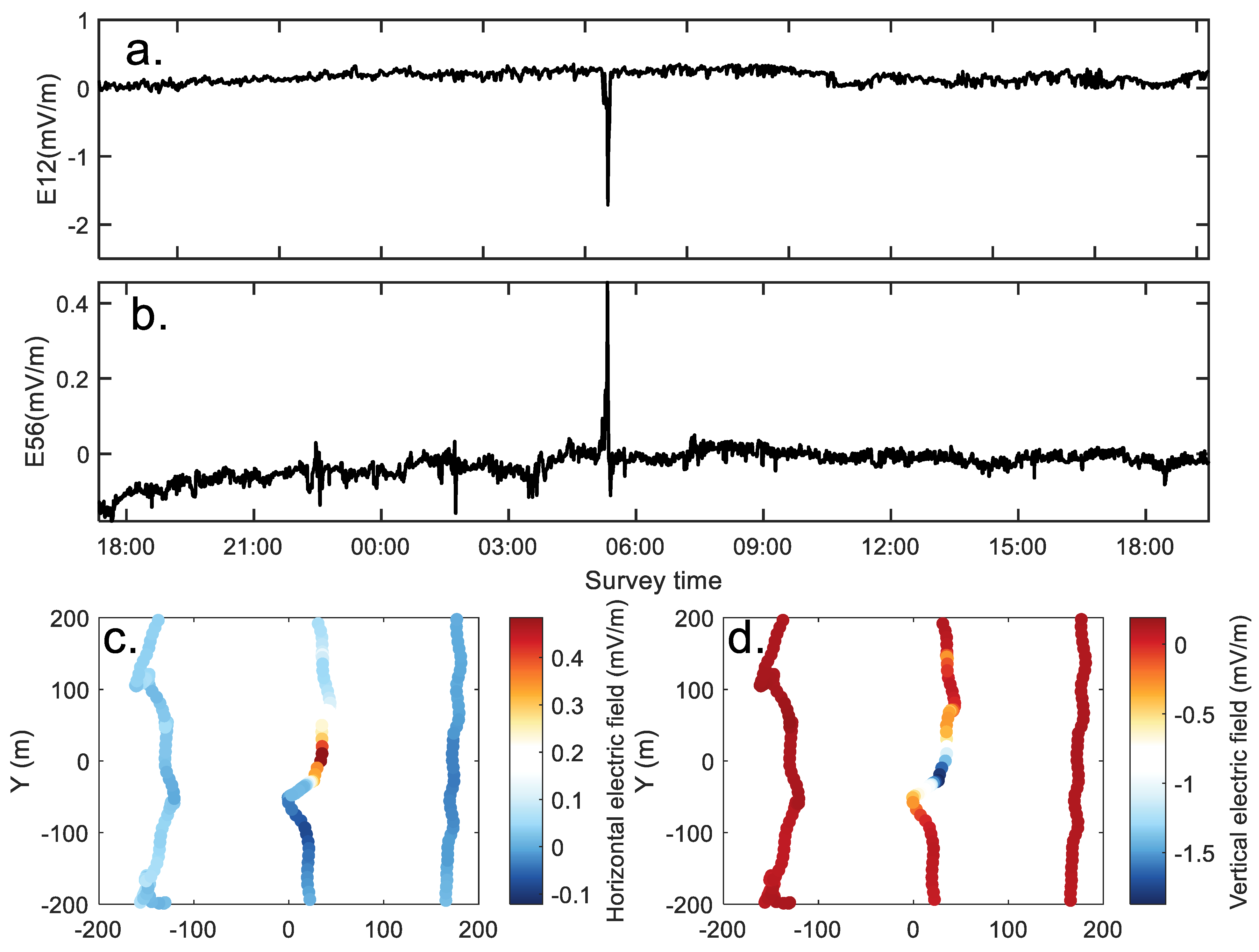
5.2. Data Processing
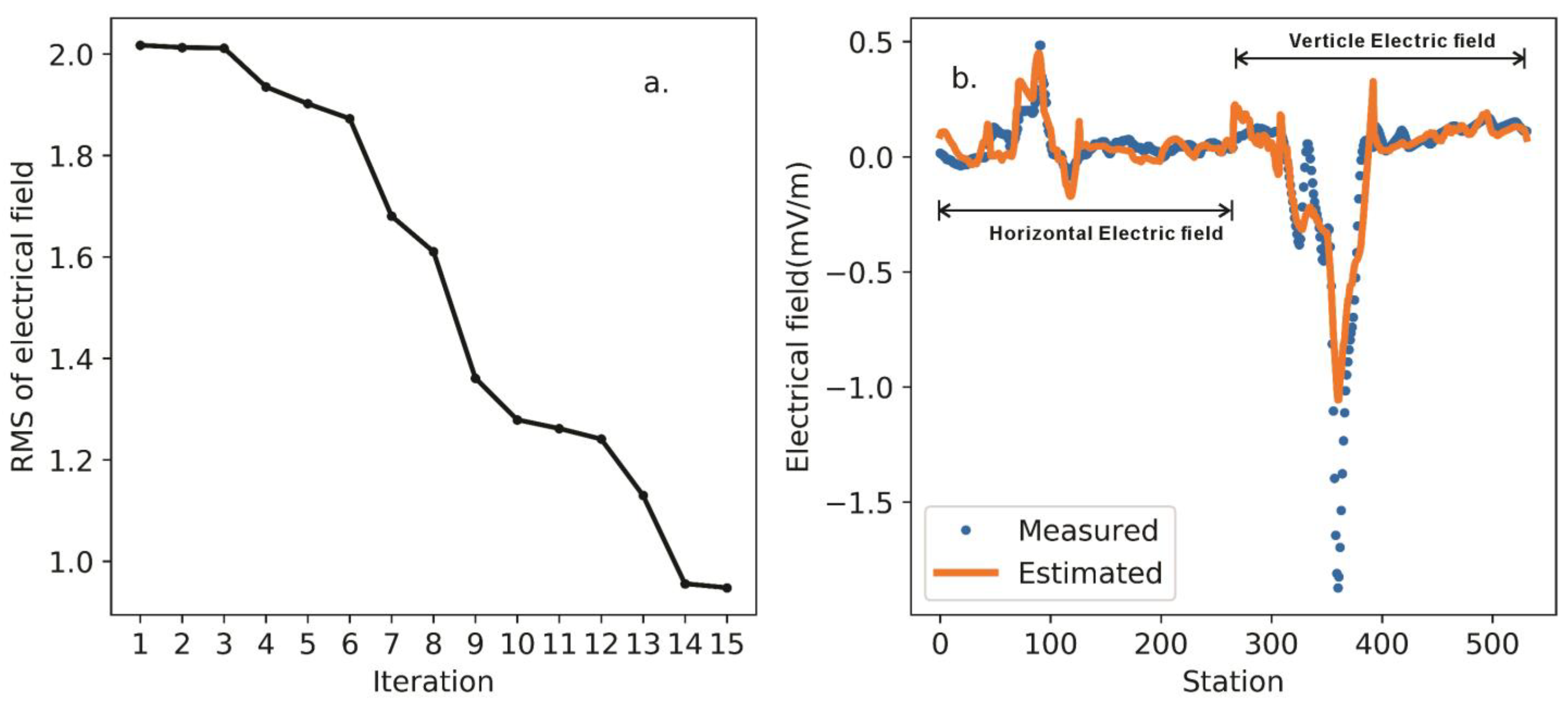
5.3. Inversion Results of Multicomponent Data
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hannington, M.; Jamieson, J.; Monecke, T.; Petersen, S.; Beaulieu, S. The abundance of seafloor massive sulfide deposits. Geology 2011, 39, 1155–1158. [Google Scholar] [CrossRef]
- Müller, H.; Schwalenberg, K.; Reeck, K.; Barckhausen, U.; Schwarz-Schampera, U.; Hilgenfeldt, C.; von Dobeneck, T. Mapping seafloor massive sulfides with the Golden Eye frequency-domain EM profiler. First Break 2018, 36, 61–67. [Google Scholar] [CrossRef]
- Ishizu, K.; Goto, T.; Ohta, Y.; Kasaya, T.; Iwamoto, H.; Vachiratienchai, C.; Siripunvaraporn, W.; Tsuji, T.; Kumagai, H.; Koike, K. Internal structure of a seafloor massive sulfide deposit by electrical resistivity tomography, Okinawa Trough. Geophys. Res. Lett. 2019, 46, 11025–11034. [Google Scholar] [CrossRef]
- Galley, C.; Lelièvre, P.; Haroon, A.; Graber, S.; Jamieson, J.; Szitkar, F.; Yeo, I.; Farquharson, C.; Petersen, S.; Evans, R. Magnetic and Gravity Surface Geometry Inverse Modeling of the TAG Active Mound. J. Geophys. Res. Solid Earth 2021, 126, e22228. [Google Scholar] [CrossRef]
- Haroon, A.; Hölz, S.; Gehrmann, R.A.S.; Attias, E.; Jegen, M.; Minshull, T.A.; Murton, B.J. Marine dipole-dipole controlled source electromagnetic and coincident-loop transient electromagnetic experiments to detect seafloor massive sulphides: Effects of three-dimensional bathymetry. Geophys. J. Int. 2018, 215, 2156–2171. [Google Scholar] [CrossRef]
- Gehrmann, R.; North, L.J.; Graber, S.; Szitkar, F.; Petersen, S.; Minshull, T.; Murton, B. Marine mineral exploration with controlled source electromagnetics at the TAG hydrothermal field, 26° N Mid-Atlantic Ridge. Geophys. Res. Lett. 2019, 46, 5808–5816. [Google Scholar] [CrossRef]
- Zhu, Z.; Tao, C.; Shen, J.; Revil, A.; Deng, X.; Liao, S.; Zhou, J.; Wang, W.; Nie, Z.; Yu, J. Self-potential tomography of a deep-sea polymetallic sulfide deposit on Southwest Indian Ridge. J. Geophys. Res. Solid Earth 2020, 125, e2020JB019738. [Google Scholar] [CrossRef]
- Ishizu, K.; Siripunvaraporn, W.; Goto, T.-N.; Koike, K.; Kasaya, T.; Iwamoto, H. A cost-effective three-dimensional marine controlled-source electromagnetic survey: Exploring seafloor massive sulfides. Geophysics 2022, 87, E219–E241. [Google Scholar] [CrossRef]
- Revil, A.; Jardani, A. The Self-Potential Method: Theory and Applications in Environmental Geosciences; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Constable, S.; Kowalczyk, P.; Bloomer, S. Measuring marine self-potential using an autonomous underwater vehicle. Geophys. J. Int. 2018, 215, 49–60. [Google Scholar] [CrossRef]
- Kawada, Y.; Kasaya, T. Self-potential mapping using an autonomous underwater vehicle for the Sunrise deposit, Izu-Ogasawara arc, southern Japan. Earth Planets Space 2018, 70, 142. [Google Scholar] [CrossRef]
- Szitkar, F.; Hölz, S.; Tarits, P.; Petersen, S. Deep-Sea Electric and Magnetic Surveys Over Active and Inactive Basalt-Hosted Hydrothermal Sites of the TAG Segment (26°, MAR): An Optimal Combination for Seafloor Massive Sulfide Exploration. J. Geophys. Res. Solid Earth 2021, 126, e2021JB022082. [Google Scholar] [CrossRef]
- Su, Z.; Tao, C.; Shen, J.; Revil, A.; Zhu, Z.; Deng, X.; Nie, Z.; Li, Q.; Liu, L.; Wu, T. 3D self-potential tomography of seafloor massive sulfide deposits using an autonomous underwater vehicle. Geophysics 2022, 87, B255–B267. [Google Scholar] [CrossRef]
- Revil, A.; Karaoulis, M.; Srivastava, S.; Byrdina, S. Thermoelectric self-potential and resistivity data localize the burning front of underground coal fires. Geophysics 2013, 78, B259–B273. [Google Scholar] [CrossRef]
- Kasaya, T.; Iwamoto, H.; Kawada, Y.; Hyakudome, T.J.T. Marine DC resistivity and self-potential survey in the hydrothermal deposit areas using multiple AUVs and ASV. TAO Terr. Atmos. Ocean. Sci. 2020, 31, 579–588. [Google Scholar] [CrossRef]
- Su, Z.; Tao, C.; Zhu, Z.; Revil, A.; Shen, J.; Nie, Z.; Li, Q.; Deng, X.; Zhou, J.; Liu, L. Joint Interpretation of Marine Self-Potential and Transient Electromagnetic Survey for Seafloor Massive Sulfide (SMS) Deposits: Application at TAG Hydrothermal Mound, Mid-Atlantic Ridge. J. Geophys. Res. Solid Earth 2022, 127, e2022JB024496. [Google Scholar] [CrossRef]
- Yamamoto, M.; Nakamura, R.; Takai, K. Deep-sea hydrothermal fields as natural power plants. ChemElectroChem 2018, 5, 2162–2166. [Google Scholar] [CrossRef]
- Petersen, S.; Krätschell, A.; Augustin, N.; Jamieson, J.; Hein, J.R.; Hannington, M.D.J.M.P. News from the seabed—Geological characteristics and resource potential of deep-sea mineral resources. Mar. Policy 2016, 70, 175–187. [Google Scholar] [CrossRef]
- Murton, B.J.; Lehrmann, B.; Dutrieux, A.M.; Martins, S.; de la Iglesia, A.G.; Stobbs, I.J.; Barriga, F.J.; Bialas, J.; Dannowski, A.; Vardy, M.E. Geological fate of seafloor massive sulphides at the TAG hydrothermal field (Mid-Atlantic Ridge). Ore Geol. Rev. 2019, 107, 903–925. [Google Scholar] [CrossRef]
- Nyquist, J.E.; Corry, C.E. Self-potential: The ugly duckling of environmental geophysics. Lead. Edge 2002, 21, 446–451. [Google Scholar] [CrossRef]
- Sato, M.; Mooney, H.M. The electrochemical mechanism of sulfide self-potentials. Geophysics 1960, 25, 226–249. [Google Scholar] [CrossRef]
- Jekeli, C. A review of gravity gradiometer survey system data analyses. Geophysics 1993, 58, 508–514. [Google Scholar] [CrossRef]
- Corwin, R.F.; Hoover, D.B. The self-potential method in geothermal exploration. Geophysics 1979, 44, 226–245. [Google Scholar] [CrossRef]
- Kawada, Y.; Kasaya, T. Marine self-potential survey for exploring seafloor hydrothermal ore deposits. Sci. Rep. 2017, 7, 13552. [Google Scholar] [CrossRef] [PubMed]
- Sudarikov, S.M.; Roumiantsev, A.B. Structure of hydrothermal plumes at the Logatchev vent field, 14°45′ N, Mid-Atlantic Ridge: Evidence from geochemical and geophysical data. J. Volcanol. Geotherm. Res. 2000, 101, 245–252. [Google Scholar] [CrossRef]
- Zhu, Z.; Shen, J.; Tao, C.; Deng, X.; Wu, T.; Nie, Z.; Wang, W.; Su, Z. Autonomous-underwater-vehicle-based marine multicomponent self-potential method: Observation scheme and navigational correction. Geosci. Instrum. Methods Data Syst. 2021, 10, 35–43. [Google Scholar] [CrossRef]
- MacGregor, L.; Kowalczyk, P.; Galley, C.; Weitemeyer, K.; Bloomer, S.; Phillips, N.; Proctor, A. Characterization of Seafloor Mineral Deposits Using Multiphysics Datasets Acquired from an AUV. First Break 2021, 39, 63–69. [Google Scholar] [CrossRef]
- Okamoto, A.; Seta, T.; Sasano, M.; Inoue, S.; Ura, T. Visual and Autonomous Survey of Hydrothermal Vents Using a Hovering-Type AUV: Launching Hobalin Into the Western Offshore of Kumejima Island. Geochem. Geophys. Geosyst. 2019, 20, 6234–6243. [Google Scholar] [CrossRef]
- García, M.; Dowdeswell, J.A.; Noormets, R.; Hogan, K.; Evans, J.; Cofaigh, C.Ó.; Larter, R.D. Geomorphic and shallow-acoustic investigation of an Antarctic Peninsula fjord system using high-resolution ROV and shipboard geophysical observations: Ice dynamics and behaviour since the Last Glacial Maximum. Quat. Sci. Rev. 2016, 153, 122–138. [Google Scholar] [CrossRef]
- Patella, D. Self-potential global tomography including topographic effects. Geophys. Prospect. 1997, 45, 843–863. [Google Scholar] [CrossRef]
- Chou, Y. Spatial distribution of spontaneous potential of metallic orebody and its application. Geophys. Geochem. Explor. 1985, 9, 268–273. (In Chinese) [Google Scholar]
- Revil, A.; Ehouarne, L.; Thyreault, E. Tomography of self-potential anomalies of electrochemical nature. Geophys. Res. Lett. 2001, 28, 4363–4366. [Google Scholar] [CrossRef]
- Biswas, A.; Sharma, S.P. Interpretation of self-potential anomaly over 2-D inclined thick sheet structures and analysis of uncertainty using very fast simulated annealing global optimization. Acta Geod. Geophys. 2017, 52, 439–455. [Google Scholar] [CrossRef]
- Jardani, A.; Revil, A.; Bolève, A.; Dupont, J.P. Three-dimensional inversion of self-potential data used to constrain the pattern of groundwater flow in geothermal fields. J. Geophys. Res. Solid Earth 2008, 113, B9. [Google Scholar] [CrossRef]
- Mendonça, C.A. Forward and inverse self-potential modeling in mineral exploration. Geophysics 2007, 73, F33–F43. [Google Scholar] [CrossRef]
- Zhu, X.; Cui, Y.; Chen, Z. Inversion for self-potential sources based on the least squares regularization. Prog. Geophys. 2016, 31, 2313. (In Chinese) [Google Scholar]
- Miller, C.A.; Kang, S.; Fournier, D.; Hill, G. Distribution of vapor and condensate in a hydrothermal system: Insights from self-potential inversion at Mount Tongariro, New Zealand. Geophys. Res. Lett. 2018, 45, 8190–8198. [Google Scholar] [CrossRef]
- Cockett, R.; Kang, S.; Heagy, L.J.; Pidlisecky, A.; Oldenburg, D.W. SimPEG: An open source framework for simulation and gradient based parameter estimation in geophysical applications. Comput. Geosci. 2015, 85, 142–154. [Google Scholar] [CrossRef]
- Heagy, L.J.; Cockett, R.; Kang, S.; Rosenkjaer, G.K.; Oldenburg, D.W. A framework for simulation and inversion in electromagnetics. Comput. Geosci. 2017, 107, 1–19. [Google Scholar] [CrossRef]
- Revil, A.; Vaudelet, P.; Su, Z.; Chen, R. Induced Polarization as a Tool to Assess Mineral Deposits: A Review. Minerals 2022, 12, 571. [Google Scholar] [CrossRef]
- Revil, A.; Su, Z.; Zhu, Z.; Maineult, A. Self-Potential as a Tool to Monitor Redox Reactions at an Ore Body: A Sandbox Experiment. Minerals 2023, 13, 716. [Google Scholar] [CrossRef]
- Sill, W.R. Self-potential modeling from primary flows. Geophysics 1983, 48, 76–86. [Google Scholar] [CrossRef]
- Cockett, R.; Heagy, L.J.; Oldenburg, D.W. Pixels and their neighbors: Finite volume. Lead. Edge 2016, 35, 703–706. [Google Scholar] [CrossRef]
- Haber, E. Computational Methods in Geophysical Electromagnetics; Mathematics in Industry; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2014. [Google Scholar]
- Minsley, B.J.; Sogade, J.; Morgan, F.D. Three-dimensional source inversion of self-potential data. J. Geophys. Res. 2007, 112, B2. [Google Scholar] [CrossRef]
- Liu, Y.; Yin, C.; Qiu, C.; Hui, Z.; Zhang, B.; Ren, X.; Weng, A. 3-D inversion of transient EM data with topography using unstructured tetrahedral grids. Geophys. J. Int. 2019, 217, 301–318. [Google Scholar] [CrossRef]
- Hansen, P.C.; O’Leary, D.P. The Use of the L-Curve in the Regularization of Discrete Ill-Posed Problems. SIAM J. Sci. Comput. 1993, 14, 1487–1503. (In English) [Google Scholar] [CrossRef]
- Spinelli, L. Analyse Spatiale de L’activité Electrique Cérébrale: Nouveaux Développements. Ph.D. Thesis, Université Joseph-Fourier-Grenoble I, Grenoble, France, 1999. [Google Scholar]
- Hannington, M.D.; Galley, A.G.; Herzig, P.M.; Petersen, S. Comparison of the TAG mound and stockwork complex with Cyprus-type massive sulfide deposits. Oceanogr. Lit. Rev. 1998, 158, 1557–1558. [Google Scholar]
- Nocedal, J.; Wright, S.J. Numerical Optimization; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Oldenburg, D.W.; Li, Y.J.N.-S.G. Inversion for applied geophysics: A tutorial. Near-Surf. Geophys. 2005, 89–150. [Google Scholar]

| Data for Inversion | Number of Data | Mesh | Time (min) | Memory (MB) | Iterations |
|---|---|---|---|---|---|
| Ex | 479 | 90 × 90 × 43 | 12.19 | 561 | 10 |
| Ex + Ez | 958 | 90 × 90 × 43 | 17.23 | 615 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Z.; Tao, C.; Shan, Z.; Revil, A.; Su, Z.; Nie, Z.; Shen, J.; Deng, X.; Zhou, J. 3D Multicomponent Self-Potential Inversion: Theory and Application to the Exploration of Seafloor Massive Sulfide Deposits on Mid-Ocean Ridges. Minerals 2023, 13, 1098. https://doi.org/10.3390/min13081098
Zhu Z, Tao C, Shan Z, Revil A, Su Z, Nie Z, Shen J, Deng X, Zhou J. 3D Multicomponent Self-Potential Inversion: Theory and Application to the Exploration of Seafloor Massive Sulfide Deposits on Mid-Ocean Ridges. Minerals. 2023; 13(8):1098. https://doi.org/10.3390/min13081098
Chicago/Turabian StyleZhu, Zhongmin, Chunhui Tao, Zhigang Shan, André Revil, Zhaoyang Su, Zuofu Nie, Jinsong Shen, Xianming Deng, and Jianping Zhou. 2023. "3D Multicomponent Self-Potential Inversion: Theory and Application to the Exploration of Seafloor Massive Sulfide Deposits on Mid-Ocean Ridges" Minerals 13, no. 8: 1098. https://doi.org/10.3390/min13081098
APA StyleZhu, Z., Tao, C., Shan, Z., Revil, A., Su, Z., Nie, Z., Shen, J., Deng, X., & Zhou, J. (2023). 3D Multicomponent Self-Potential Inversion: Theory and Application to the Exploration of Seafloor Massive Sulfide Deposits on Mid-Ocean Ridges. Minerals, 13(8), 1098. https://doi.org/10.3390/min13081098






