Viscosity, Boson Peak and Elastic Moduli in the Na2O-SiO2 System
Abstract
:1. Introduction
2. Materials and Methods
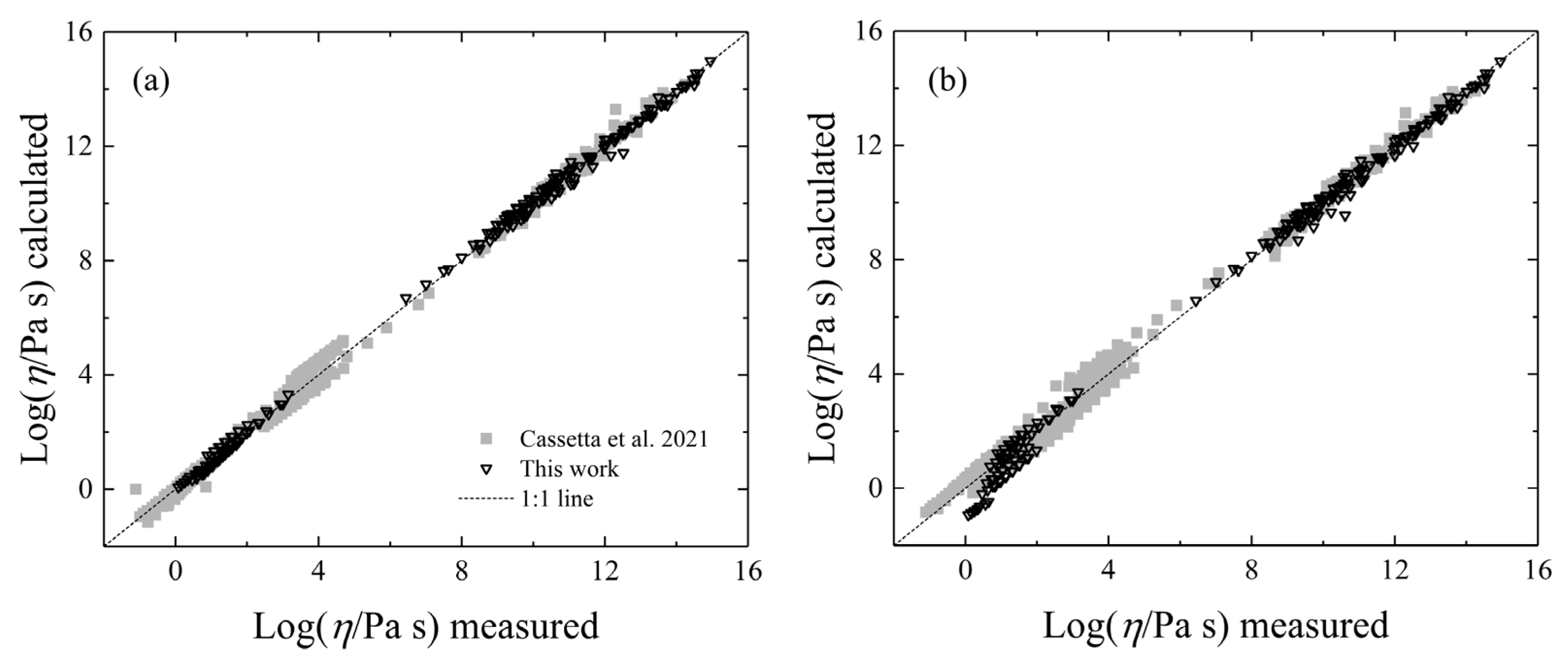
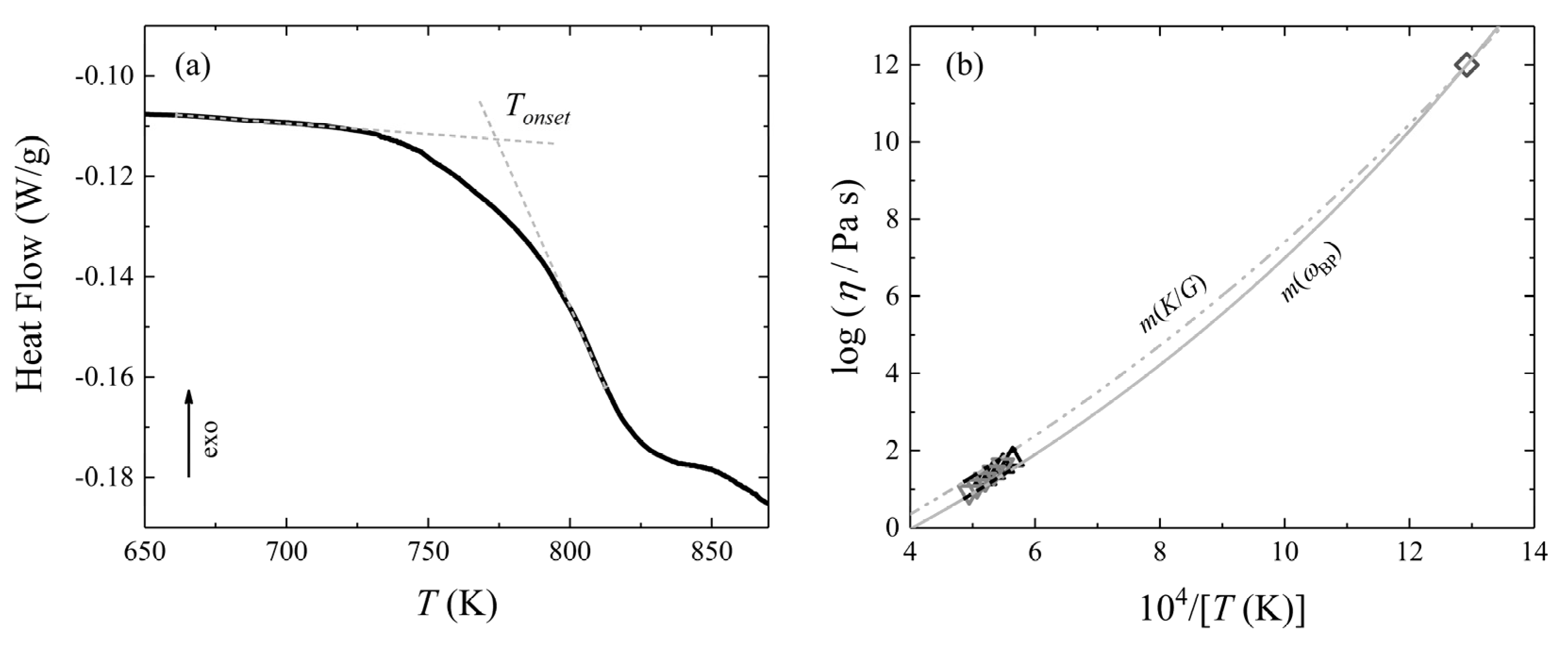
3. Results and Discussions
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Maxwell, J.C. On the Dynamical Theory of Gases. Philos. Trans. R. Soc. Lond. 1867, 157, 49–88. [Google Scholar]
- Zanotto, E.D.; Cassar, D.R. The race within supercooled liquids—Relaxation versus crystallization. J. Chem. Phys. 2018, 149, 2. [Google Scholar] [CrossRef]
- Gonnermann, H.M.; Manga, M. The Fluid Mechanics Inside a Volcano. Annu. Rev. Fluid Mech. 2007, 39, 321–356. [Google Scholar] [CrossRef]
- Dingwell, D.B. Volcanic dilemma: Flow or blow? Science 1996, 273, 1054–1055. [Google Scholar] [CrossRef]
- Zanotto, E.D.; Mauro, J.C. The glassy state of matter: Its definition and ultimate fate. J. Non-Cryst. Solids 2017, 471, 490–495. [Google Scholar] [CrossRef]
- Vetere, F.; Iezzi, G.; Behrens, H.; Holtz, F.; Ventura, G.; Misiti, V.; Cavallo, A.; Mollo, S.; Dietrich, M. Glass forming ability and crystallisation behaviour of sub-alkaline silicate melts. Earth-Sci. Rev. 2015, 150, 25–44. [Google Scholar] [CrossRef]
- Di Genova, D.; Brooker, R.A.; Mader, H.; Drewitt, J.W.E.; Longo, A.; Deubener, J.; Neuville, D.R.; Fanara, S.; Shebanova, O.; Anzellini, S.; et al. In situ observation of nanolite growth in volcanic melt: A driving force for explosive eruptions. Sci. Adv. 2020, 6, eabb0413. [Google Scholar] [CrossRef]
- Giordano, D.; Russel, J.K.; Dingwell, D.B. Viscosity of magmatic liquids: A model. Earth Planet. Sci. Lett. 2008, 271, 123–134. [Google Scholar] [CrossRef]
- Vetere, F.; Holtz, F. Rheological Behavior of Partly Crystallized Silicate Melts under Variable Shear Rate. Dyn. Magma Evol. Geophys. Monogr. 2021, 1, 152–167. [Google Scholar]
- Scopigno, T. La Transizione Vetrosa; KOS: Milano, Italy, 2005; pp. 28–31. [Google Scholar]
- Anderson, P.W. The deepest and most interesting unsolved problem in solid state theory. Science 1995, 267, 1615–1616. [Google Scholar] [CrossRef]
- Poole, J.P. Low-Temperature Viscosity of Alkali Silicate Glasses. J. Am. Ceram. Soc. 1949, 32, 230–233. [Google Scholar] [CrossRef]
- Bockris, J.O.; Lowe, D.C. Viscosity and the structure of molten silicates. Proc. R. Soc. 1954, 226, 423–435. [Google Scholar]
- Hannon, A.C.; Vaishnav, S.; Alderman, O.L.G.; Bingham, P.A. The structure of sodium silicate glass from neutron diffraction and modeling of oxygen- oxygen correlations. J. Am. Ceram. Soc. 2021, 104, 6155–6171. [Google Scholar] [CrossRef]
- Inoue, K.; Kataoka, H.; Nagai, Y.; Hasegawa, M.; Kobayashi, Y. Short and medium range order in two-component silica glasses by positron annihilation spectroscopy. J. Appl. Phys. 2014, 115, 20. [Google Scholar] [CrossRef]
- Deubener, J.; Behrens, H.; Müller, R. An overview on the effect of dissolved water on the viscosity of soda lime silicate melts. J. Non-Cryst. Solids 2023, 19, 100195. [Google Scholar] [CrossRef]
- Vetere, F.; Rossi, S.; Namur, O.; Morgavi, D.; Misiti, V.; Mancinelli, P.; Petrelli, M.; Pauselli, C.; Perugini, D. Experimental constraints on the rheology, eruption, and emplacement dynamics of analog lavas comparable to Mercury’s northern volcanic plains. J. Geophys. Res. Planets 2017, 122, 1522–1538. [Google Scholar] [CrossRef]
- Richet, P. Viscosity and configurational entropy of silicate melts. Geochim. Cosmochim. ACTA 1984, 48, 471–483. [Google Scholar] [CrossRef]
- Greaves, G.N.; Sen, S. Inorganic glasses, glass-forming liquids and amorphizing solids. Adv. Phys. 2007, 56, 1–166. [Google Scholar] [CrossRef]
- Micoulaut, M. Constrained interactions, rigidity, adaptative networks, and their role for the description of silicates. Am. Mineral. 2008, 93, 1732–1748. [Google Scholar] [CrossRef]
- Angell, C.A. Formation of glasses from liquids and biopolymers. Science 1995, 267, 1924–1935. [Google Scholar] [CrossRef]
- Jarry, P.; Richet, P. Unmixing in sodium-silicate melts: Influence on viscosity and heat capacity. J. Non-Cryst. Solids 2001, 293–295, 232–237. [Google Scholar] [CrossRef]
- Le Losq, C.; Neuville, D.R. Molecular structure, configurational entropy and viscosity of silicate melts: Link through the Adam and Gibbs theory of viscous flow. J. Non-Cryst. Solids 2017, 463, 175–188. [Google Scholar] [CrossRef]
- Cassetta, M.; Di Genova, D.; Zanatta, M.; Ballaran, T.B.; Kurnosov, A.; Giarola, M.; Mariotto, G. Estimating the viscosity of volcanic melts from the vibrational properties of their parental glasses. Sci. Rep. 2021, 11, 13072. [Google Scholar] [CrossRef] [PubMed]
- Mauro, J.C.; Yue, Y.; Ellison, A.J.; Gupta, P.K.; Allan, D.C. Viscosity of glass-forming liquids. Proc. Natl. Acad. Sci. USA 2009, 106, 19780–19784. [Google Scholar] [CrossRef] [PubMed]
- Jochum, K.P.; Stoll, B.; Herwig, K.; Willbold, M.; Hofmiann, A.W.; Amini, M.; Aarburg, S.; Abouchami, W.; Hellebrand, E.; Mocek, B.; et al. MPI-DING reference glasses for in situ microanalysis: New reference values for element concentrations and isotope ratios. Geochem. Geophys. Geosyst. 2006, 7, 2. [Google Scholar] [CrossRef]
- Cassetta, M.; Zanatta, M.; Biesuz, M.; Giarola, M.; Mariotto, G. New insights about the role of Na–K ratio on the vibrational dynamics of synthetic-basalt glasses. J. Raman Spectrosc. 2022, 53, 540–549. [Google Scholar] [CrossRef]
- Enrichi, F.; Cassetta, M.; Daldosso, N.; Cattaruzza, E.; Riello, P.; Zairov, R.; Vomiero, A.; Righini, G.C. Effect of the crystal structure on the optical properties and Ag sensitization of Tb3+/Yb3+ ions in silica-zirconia glasses and glass-ceramics. Ceram. Int. 2022, in press. [CrossRef]
- Cassetta, M.; Giannetta, B.; Enrichi, F.; Zaccone, C.; Mariotto, G.; Giarola, M.; Nodari, L.; Zanatta, M.; Daldosso, N. Effect of the alkali vs iron ratio on glass transition temperature and vibrational properties of synthetic basalt-like glasses. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2023, 293, 122430. [Google Scholar] [CrossRef]
- Cassetta, M.; Vetere, F.; Zanatta, M.; Perugini, D.; Alvaro, M.; Giannetta, B.; Zaccone, C.; Daldosso, N. Micro-Raman spectroscopy for a comprehensive understanding of the structural evolution of Basaltic-Andesite and Trachybasalt multiphase systems. Chem. Geol. 2023, 616, 121241. [Google Scholar] [CrossRef]
- Furukawa, T.; Fox, K.E.; White, W.B. Raman spectroscopic investigation of the structure of silicate glasses. III. Raman intensities and structural units in sodium silicate glasses. J. Chem. Phys. 1981, 75, 3226–3237. [Google Scholar] [CrossRef]
- O’Shaughnessy, C.; Henderson, G.S.; Nesbitt, H.W.; Bancroft, G.M.; Neuville, D.R. The influence of modifier cations on the Raman stretching modes of Qn species in alkali silicate glasses. J. Am. Ceram. Soc. 2020, 103, 3991–4001. [Google Scholar] [CrossRef]
- Malfait, W.J.; Zakaznova-Herzog, V.P.; Halter, W.E. Quantitative Raman spectroscopy: Speciation of Na-silicate glasses and melts. Am. Mineral. 2008, 93, 1505–1518. [Google Scholar] [CrossRef]
- Mazurin, O.V.; Streltsina, M.V.; Shvaiko-Svaikovskaya, T.P. Handbook of Glass Data Part A: Silica Glass and Binary Silicate Glasses, A; Elsevier: Amsterdam, The Netherlands, 1983. [Google Scholar]
- Knoche, R.; Dingwell, D.B.; Seifert, F.A.; Webb, S.L. Non-linear properties of supercooled liquids in the system Na2OSiO2. Chem. Geol. 1994, 116, 1–16. [Google Scholar] [CrossRef]
- Sipp, A.; Bottinga, Y.; Richet, P. New high viscosity data for 3D network liquids and new correlations between old parameters. J. Non-Cryst. Solids 2001, 288, 166–174. [Google Scholar] [CrossRef]
- Le Losq, C.; Neuville, D.R.; Florian, P.; Henderson, G.S.; Massiot, D. The role of Al3+ on rheology and structural changes in sodium silicate and aluminosilicate glasses and melts. Geochim. Cosmochim. Acta 2014, 126, 495–517. [Google Scholar] [CrossRef]
- Vaills, Y.; Luspin, Y.; Hauret, G. Two opposite effects of sodium on elastic constants of silicate binary glasses. Mater. Sci. Eng. B 1996, 40, 199–202. [Google Scholar] [CrossRef]
- Hehlen, B.; Neuville, D.R.; Kilymis, D.; Ispas, S. Bimodal distribution of Si–O–Si angles in sodo-silicate glasses. J. Non-Cryst. Solids 2017, 469, 39–44. [Google Scholar] [CrossRef]
- Zhao, Q.; Guerette, M.; Huang, L. Nanoindentation and Brillouin light scattering studies of elastic moduli of sodium silicate glasses. J. Non-Cryst. Solids 2012, 358, 652–657. [Google Scholar] [CrossRef]
- Galeener, F.L. Band limits and the vibrational spectra of tetrahedral glasses. Phys. Rev. B 1979, 19, 4292–4297. [Google Scholar] [CrossRef]
- Wang, Z.; Cooney, T.F.; Sharma, S.K. High temperature structural investigation of Na2O·0.5Fe2O3·3SiO2 and Na2O·FeO3 SiO2 melts and glasses. Contrib. Mineral. Petrol. 1993, 115, 112–122. [Google Scholar] [CrossRef]
- Hehlen, B.; Simon, G. The vibrations of vitreous silica observed in hyper-Raman scattering. J. Raman Spectrosc. 2012, 43, 1941–1950. [Google Scholar] [CrossRef]
- Baldi, G.; Fontana, A.; Monaco, G.; Orsingher, L.; Rols, S.; Rossi, F.; Ruta, B. Connection between Boson Peak and Elastic Properties in Silicate Glasses. Phys. Rev. Lett. 2009, 102, 195502. [Google Scholar] [CrossRef] [PubMed]
- Fontana, A.; Dell’Anna, R.; Montagna, M.; Rossi, F.; Viliani, G.; Ruocco, G.; Sampoli, M.; Buchenau, U.; Wischnewski, A. The Raman coupling function in amorphous silica and the nature of the long-wavelength excitations in disordered systems. Europhys. Lett. 1999, 47, 56–62. [Google Scholar] [CrossRef]
- Fontana, A.; Rossi, F.; Viliani, G.; Caponi, S.; Fabiani, E.; Baldi, G.; Ruocco, G.; Maschio, R.D. The Raman coupling function in disordered solids: A light and neutron scattering study on glasses of different fragility. J. Phys. Condens. Matter. 2007, 19, 205145. [Google Scholar] [CrossRef]
- Surovtsev, N.V.; Sokolov, A.P. Frequency behavior of raman coupling coefficient in glasses. Phys. Rev. B Condens. Matter Mater. Phys. 2002, 66, 054205. [Google Scholar] [CrossRef]
- Malinovsky, V.K.; Novikov, V.N.; Sokolov, A.P. Log-normal spectrum of low-energy vibrational excitations in glasses. Phys. Lett. A 1991, 153, 63–66. [Google Scholar] [CrossRef]
- Weinberg, M.C.; Neilson, G.F. Phase separation behaviour of a metal-organic derived sodium silicate glass. J. Mater. Sci. 1978, 13, 1206–1216. [Google Scholar] [CrossRef]
- Chen, P.; Holbrook, C.; Boolchand, P.; Georgiev, D.G.; Jackson, K.A.; Micoulaut, M. Intermediate phase, network demixing, boson and floppy modes, and compositional trends in glass transition temperatures of binary AsxS1−x system. Phys. Rev. B Condens. Matter Mater. Phys. 2008, 78, 224208. [Google Scholar] [CrossRef]
- Le Losq, C.; Neuville, D.R.; Chen, W.; Florian, P.; Massiot, D.; Zhou, Z.; Greaves, G.N. Percolation channels: A universal idea to describe the atomic structure and dynamics of glasses and melts. Sci. Rep. 2017, 7, 16490. [Google Scholar] [CrossRef]
- Bauchy, M. Topological Constraint Theory and Rigidity of Glasses. arXiv 2020, arXiv:2005.04603. [Google Scholar]
- Bauchy, M.; Micoulaut, M. Atomic scale foundation of temperature-dependent bonding constraints in network glasses and liquids. J. Non-Cryst. Solids 2011, 357, 2530–2537. [Google Scholar] [CrossRef]
- Jabraoui, H.; Vaills, Y.; Hasnaoui, A.; Badawi, M.; Ouaskit, S. Effect of sodium oxide modifier on structural and elastic properties of silicate glass. J. Phys. Chem. B 2016, 120, 13193–13205. [Google Scholar] [CrossRef]
- Nakamura, K.; Takahashi, Y.; Osada, M.; Fujiwara, T. Low-frequency Raman scattering in binary silicate glass: Boson peak frequency and its general expression. J. Ceram. Soc. Jpn. 2013, 121, 1012–1014. [Google Scholar] [CrossRef]
- Chemarin, C.; Champagnon, B. Medium range order in sodium silicate glasses: Role of the network modifier. J. Non-Cryst. Solids 1999, 243, 281–284. [Google Scholar] [CrossRef]
- Richet, N.F. Heat capacity and low-frequency vibrational density of states. Inferences for the boson peak of silica and alkali silicate glasses. Phys. B Condens. Matter. 2009, 404, 3799–3806. [Google Scholar] [CrossRef]
- Zheng, Q.; Zheng, J.; Solvang, M.; Yue, Y.; Mauro, J.C. Determining the liquidus viscosity of glass-forming liquids through differential scanning calorimetry. J. Am. Ceram. Soc. 2020, 103, 6070–6074. [Google Scholar] [CrossRef]
- Novikov, V.N.; Sokolov, A.P. Poisson’s ratio and the fragility of glass-forming liquids. Nature 2004, 431, 961–963. [Google Scholar] [CrossRef]
- McIntosh, C.; Toulouse, J.; Tick, P. The Boson peak in alkali silicate glasses. J. Non-Cryst. Solids 1997, 222, 335–341. [Google Scholar] [CrossRef]
- Whittington, A.G.; Richet, P.; Polian, A. Amorphous materials: Properties, structure, and durability: Water and the compressibility of silicate glasses: A Brillouin spectroscopic study. Am. Mineral. 2012, 97, 455–467. [Google Scholar] [CrossRef]
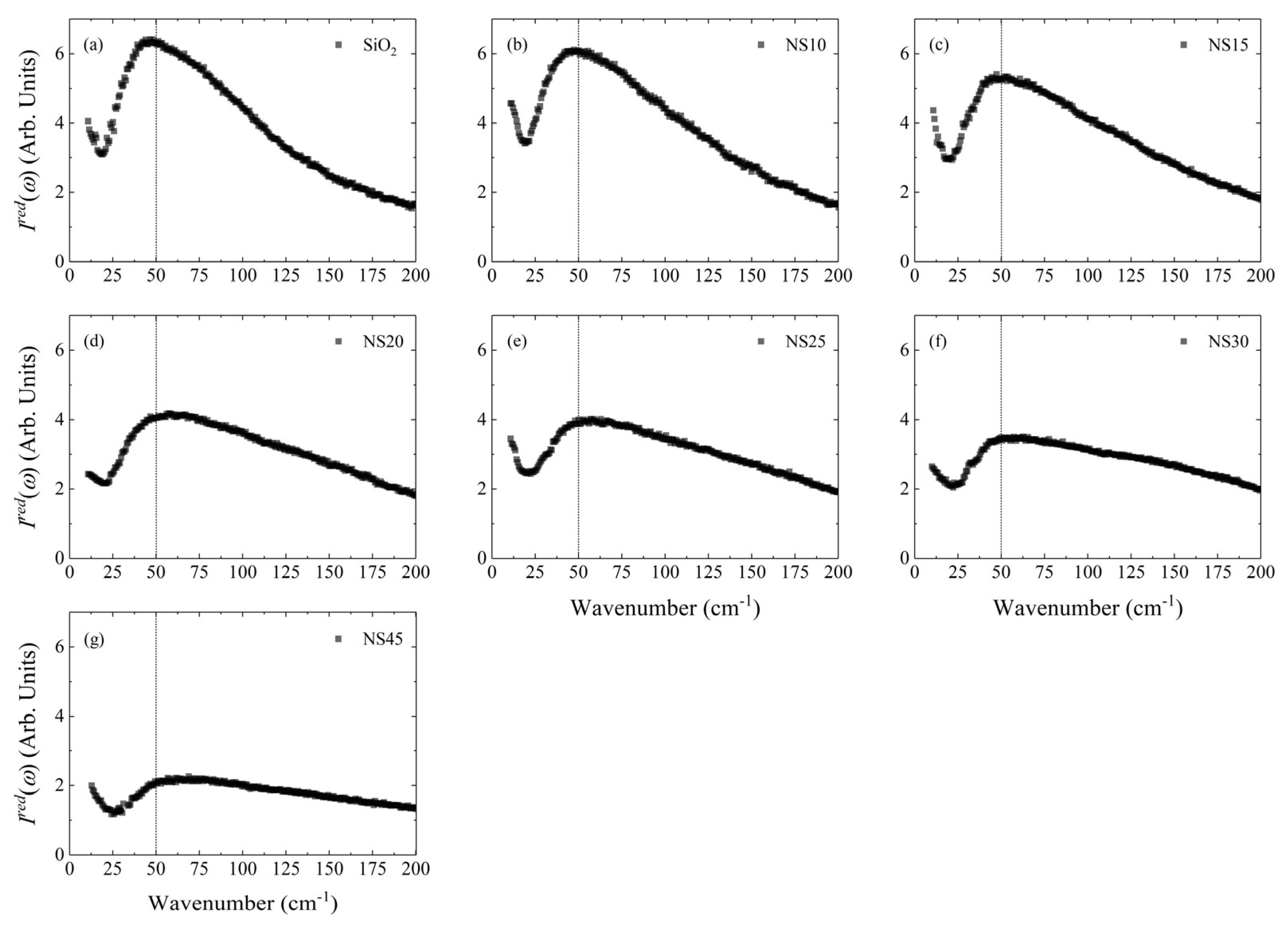


| ωBP | ρ | Tg | m | vl | vt | K/G | Reference | |
|---|---|---|---|---|---|---|---|---|
| (cm−1) | (g cm−3) | (K) | (m s−1) | (m s−1) | ||||
| SiO2 | 48.5(5) | 2.20(2) | 1427(8) | 24.0(4) | 5972 | 3769 | 1.18 | [24] |
| NS10 | 49.7(6) | 2.28(4) | - | - | 5654 | 3531 | 1.23 | () [13,34,35] (vl, vt) |
| NS15 | 51.0(1) | 2.34(4) | 779.9(5) | 26.6(1) | 5559 | 3421 | 1.31 | () [12,13,34,35,36], (vl, vt) [37,38] |
| NS20 | 60.1(7) | 2.39(2) | 750.2(7) | 29.8(2) | 5493 | 3330 | 1.39 | () [12,13,22,34,35,36], (vl, vt) [38] |
| NS25 | 60.0(7) | 2.44(3) | 731.0(1) | 29.9(3) | 5457 | 3257 | 1.47 | () [12,13,35,37], (vl, vt) [38] |
| NS30 | 63.8(8) | 2.47(2) | 720.0(1) | 30.8(2) | 5450 | 3204 | 1.56 | () [13,35], (vl, vt) [38] |
| NS45 | 71.0(1) | 2.58(2) | 679.7(5) | 36.4(2) | 5604 | 3154 | 1.82 | () [35], (vl, vt) [38] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cassetta, M.; Mariotto, G.; Daldosso, N.; De Bona, E.; Biesuz, M.; Sorarù, G.D.; Almeev, R.; Zanatta, M.; Vetere, F. Viscosity, Boson Peak and Elastic Moduli in the Na2O-SiO2 System. Minerals 2023, 13, 1166. https://doi.org/10.3390/min13091166
Cassetta M, Mariotto G, Daldosso N, De Bona E, Biesuz M, Sorarù GD, Almeev R, Zanatta M, Vetere F. Viscosity, Boson Peak and Elastic Moduli in the Na2O-SiO2 System. Minerals. 2023; 13(9):1166. https://doi.org/10.3390/min13091166
Chicago/Turabian StyleCassetta, Michele, Gino Mariotto, Nicola Daldosso, Emanuele De Bona, Mattia Biesuz, Gian Domenico Sorarù, Renat Almeev, Marco Zanatta, and Francesco Vetere. 2023. "Viscosity, Boson Peak and Elastic Moduli in the Na2O-SiO2 System" Minerals 13, no. 9: 1166. https://doi.org/10.3390/min13091166
APA StyleCassetta, M., Mariotto, G., Daldosso, N., De Bona, E., Biesuz, M., Sorarù, G. D., Almeev, R., Zanatta, M., & Vetere, F. (2023). Viscosity, Boson Peak and Elastic Moduli in the Na2O-SiO2 System. Minerals, 13(9), 1166. https://doi.org/10.3390/min13091166








