What Extra Information Can Be Provided by Multi-Component Seismic Data: A Case Study of 2D3C Prospecting of a Copper–Molybdenum Mine in Inner Mongolia, China
Abstract
:1. Introduction
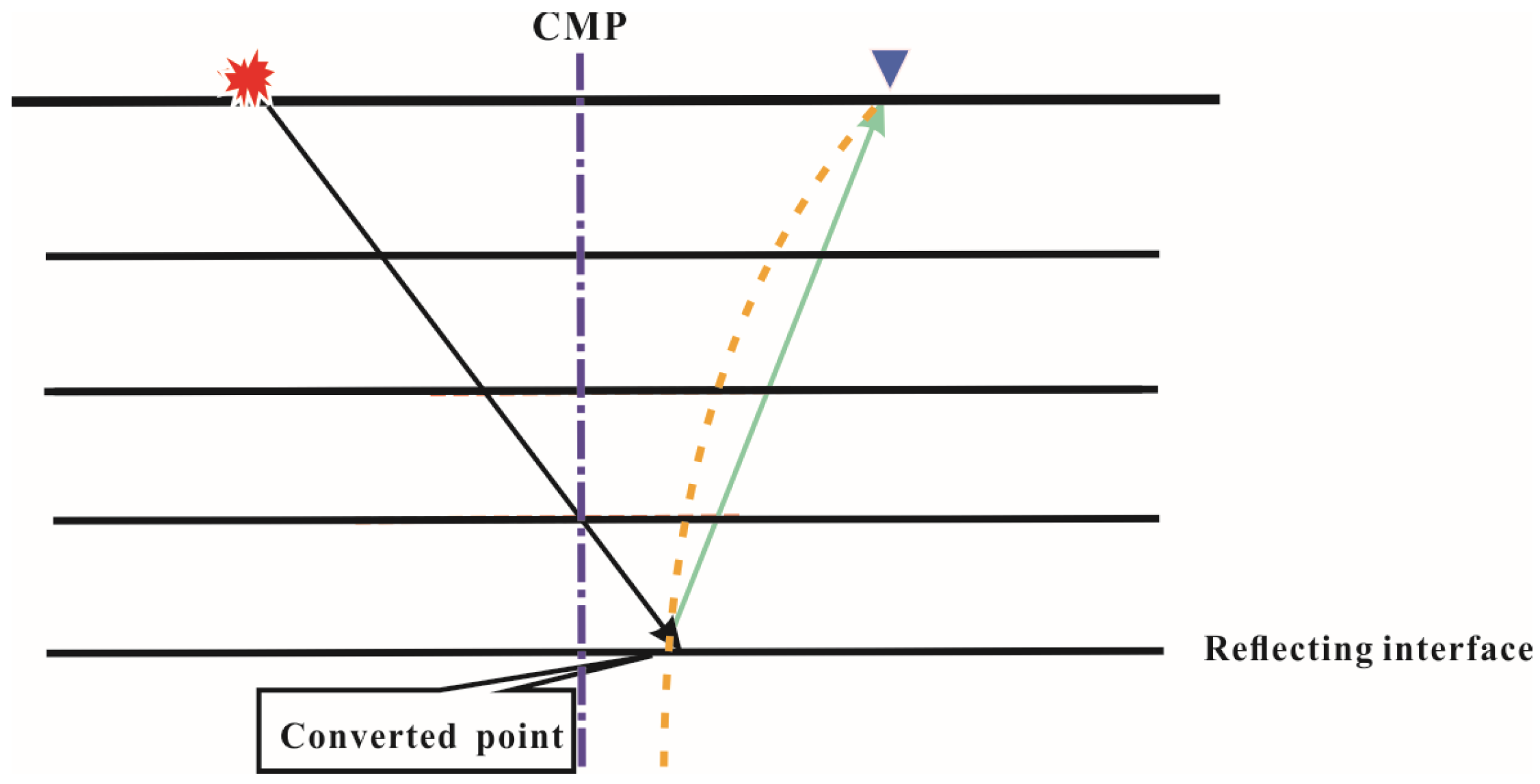
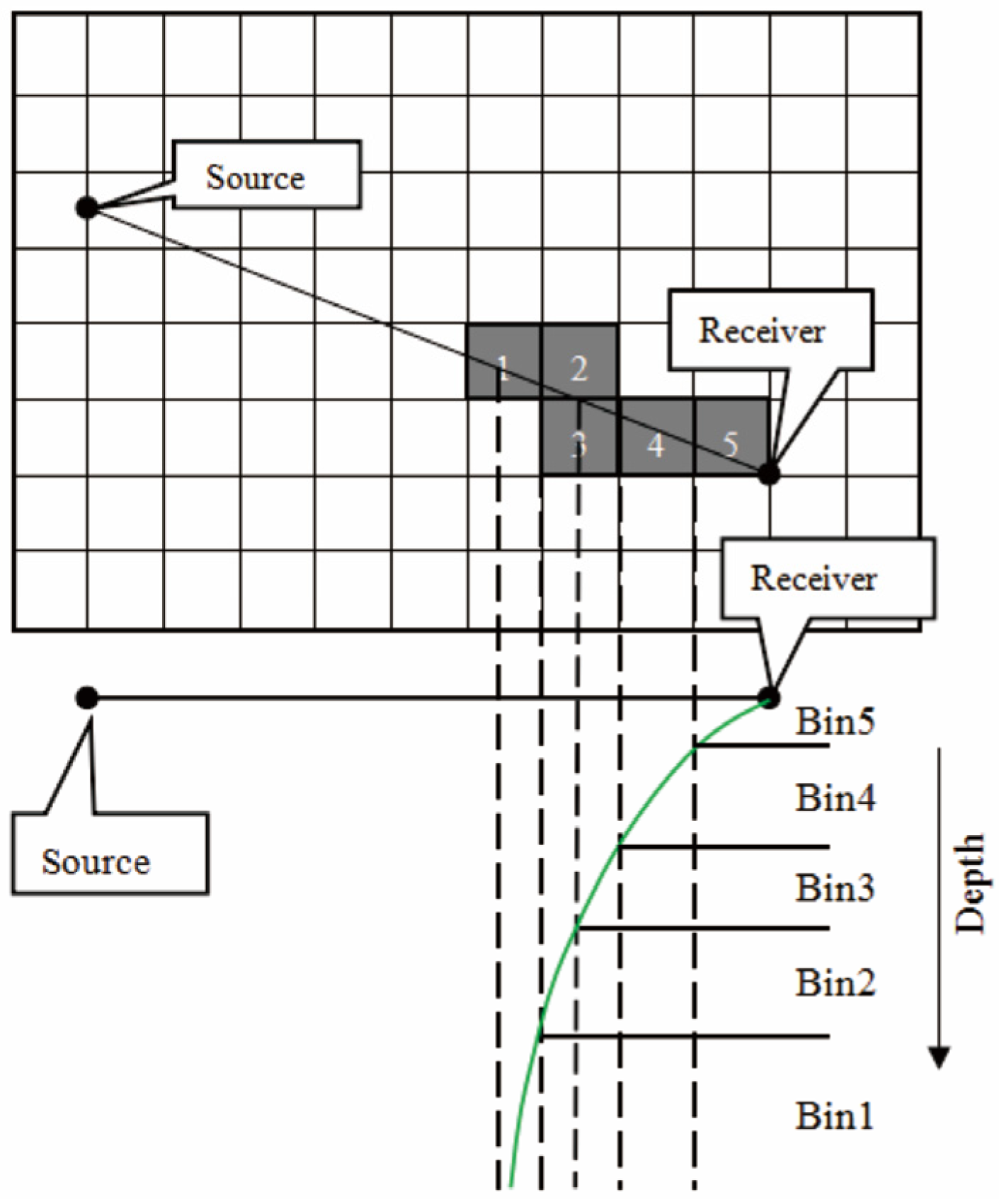
2. Seismic Geological Characteristics and Imaging Methods of Metallic Ores
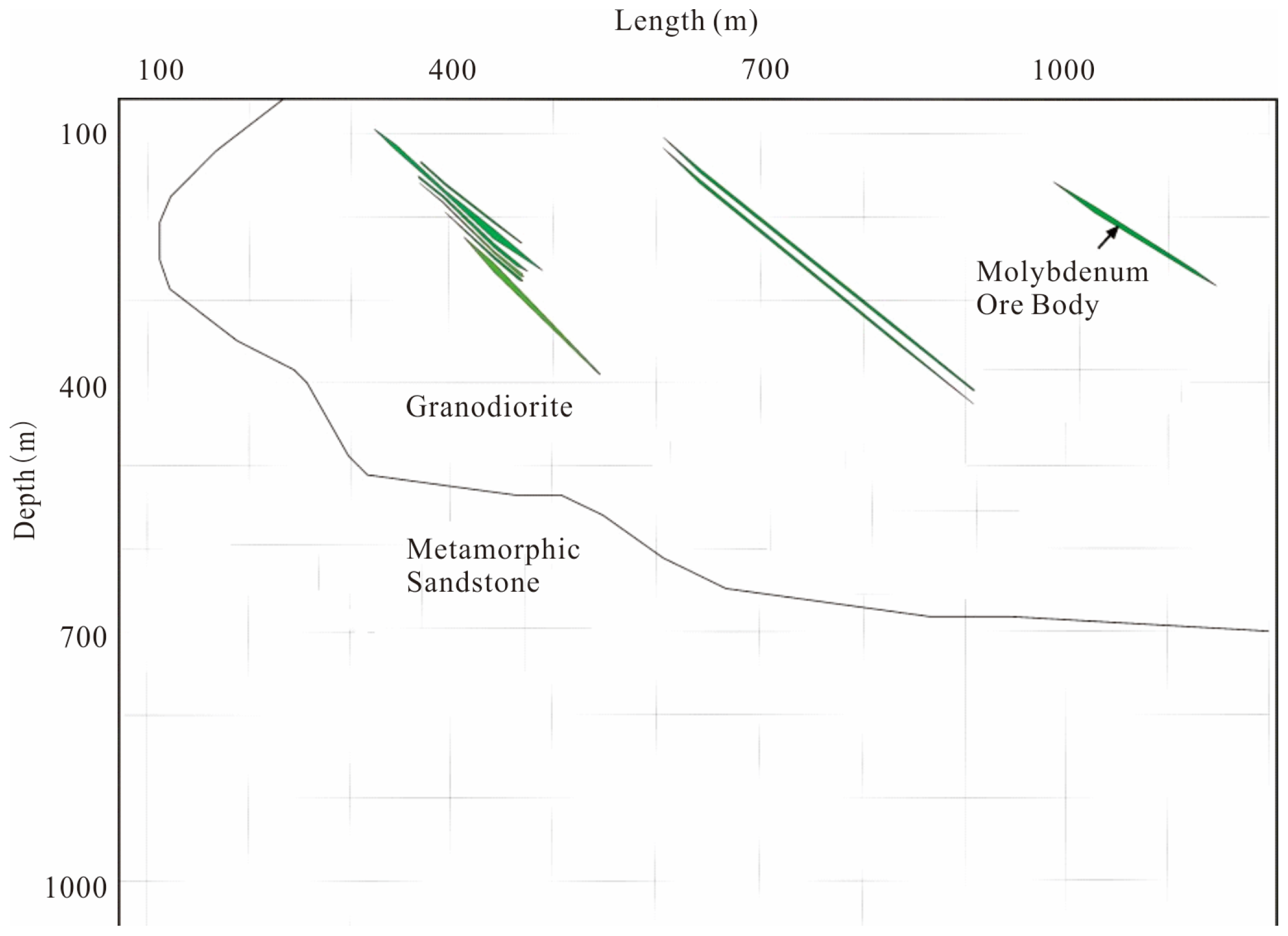
3. Numerical Examples
4. A Case Study of 2D3C Seismic Exploration for Copper–Molybdenum Deposits in Inner Mongolia
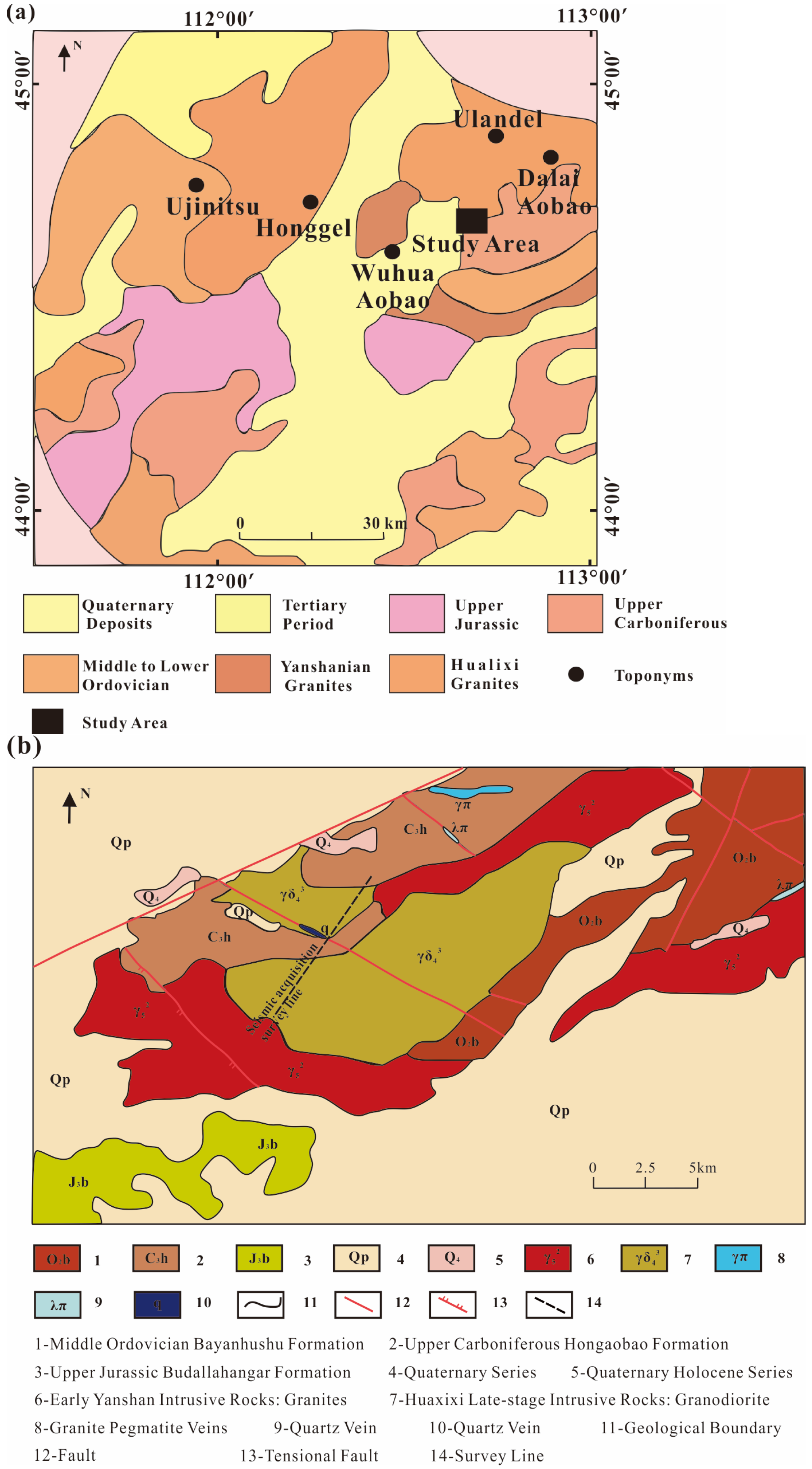
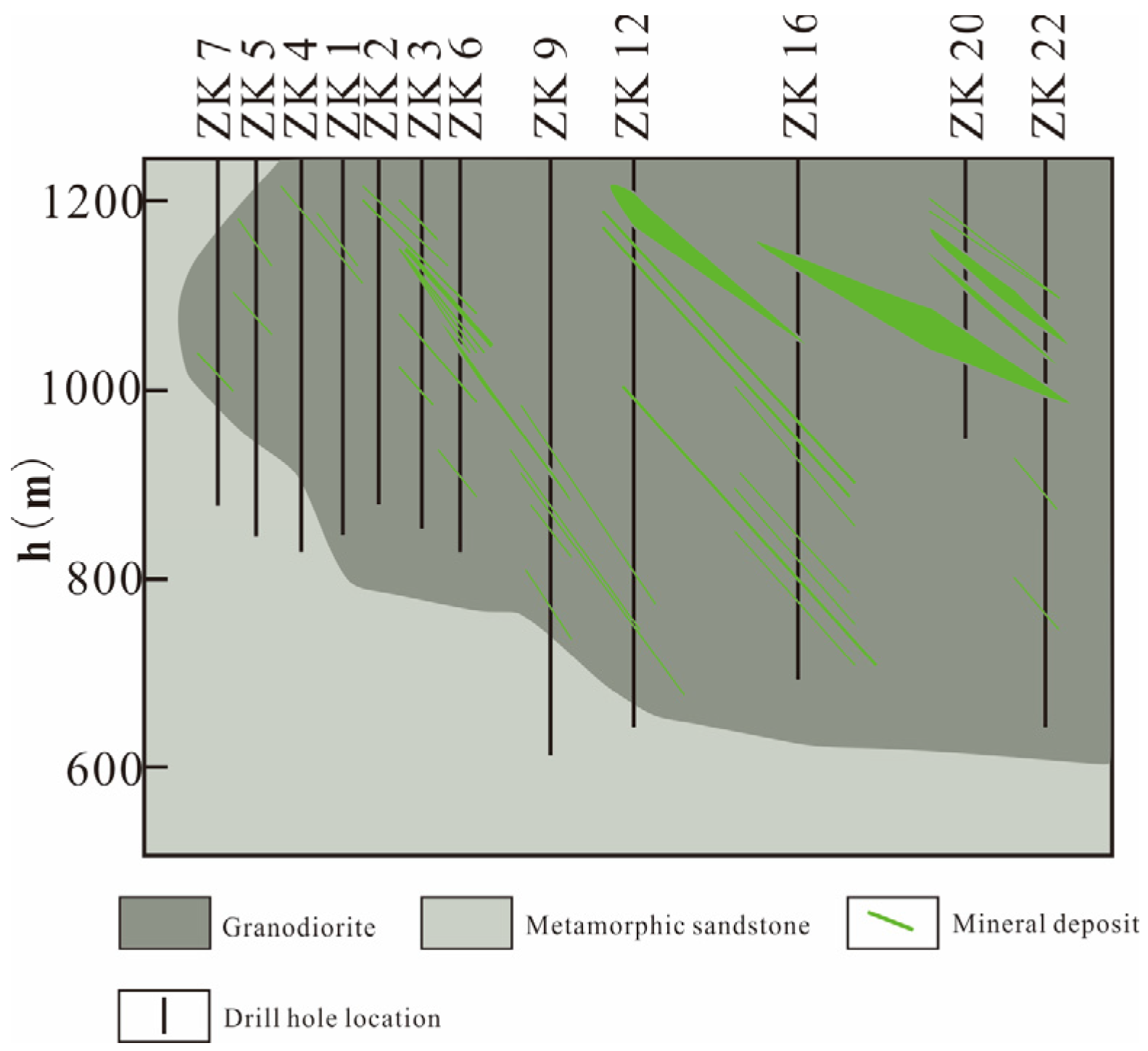
4.1. Geological Overview
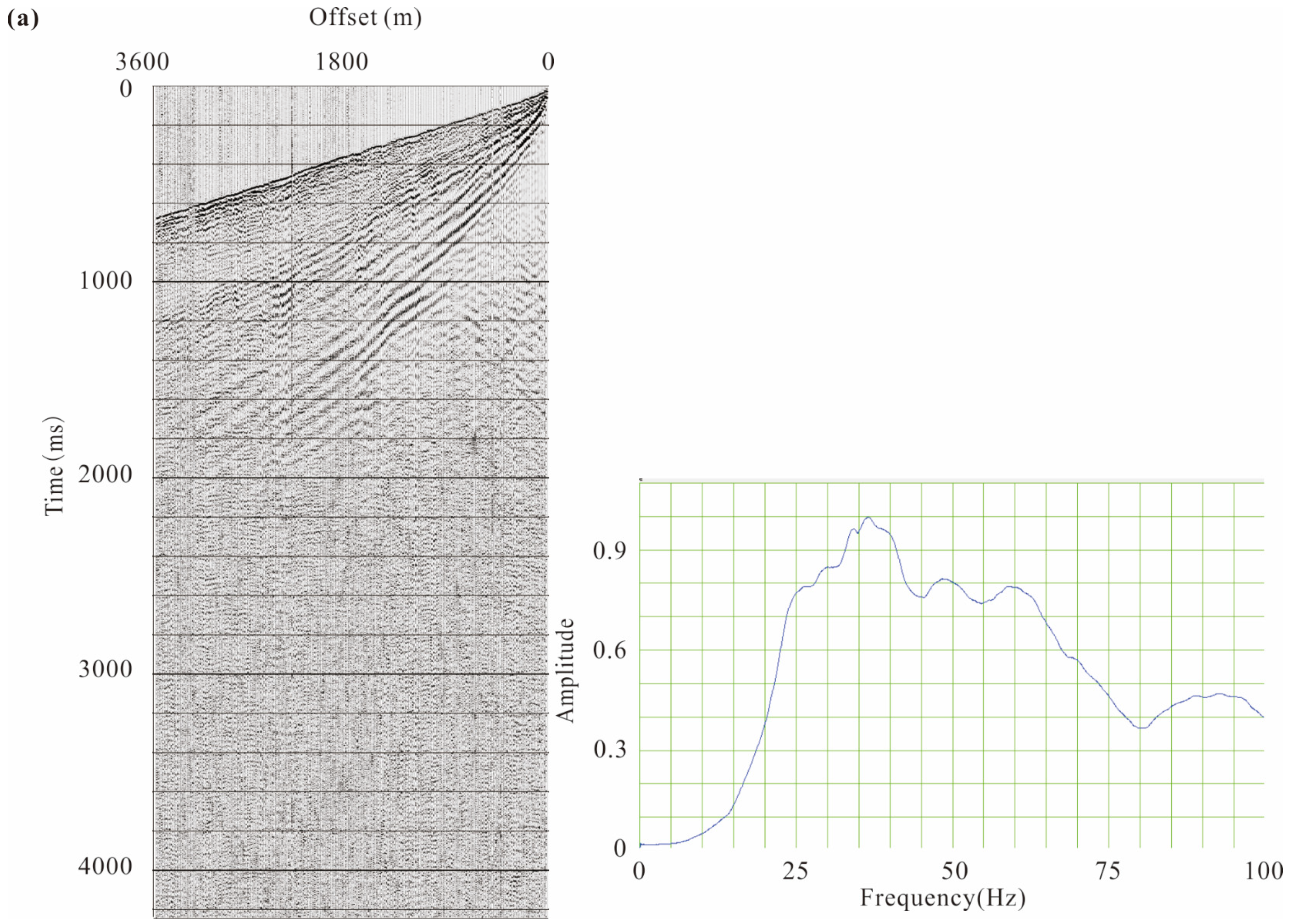
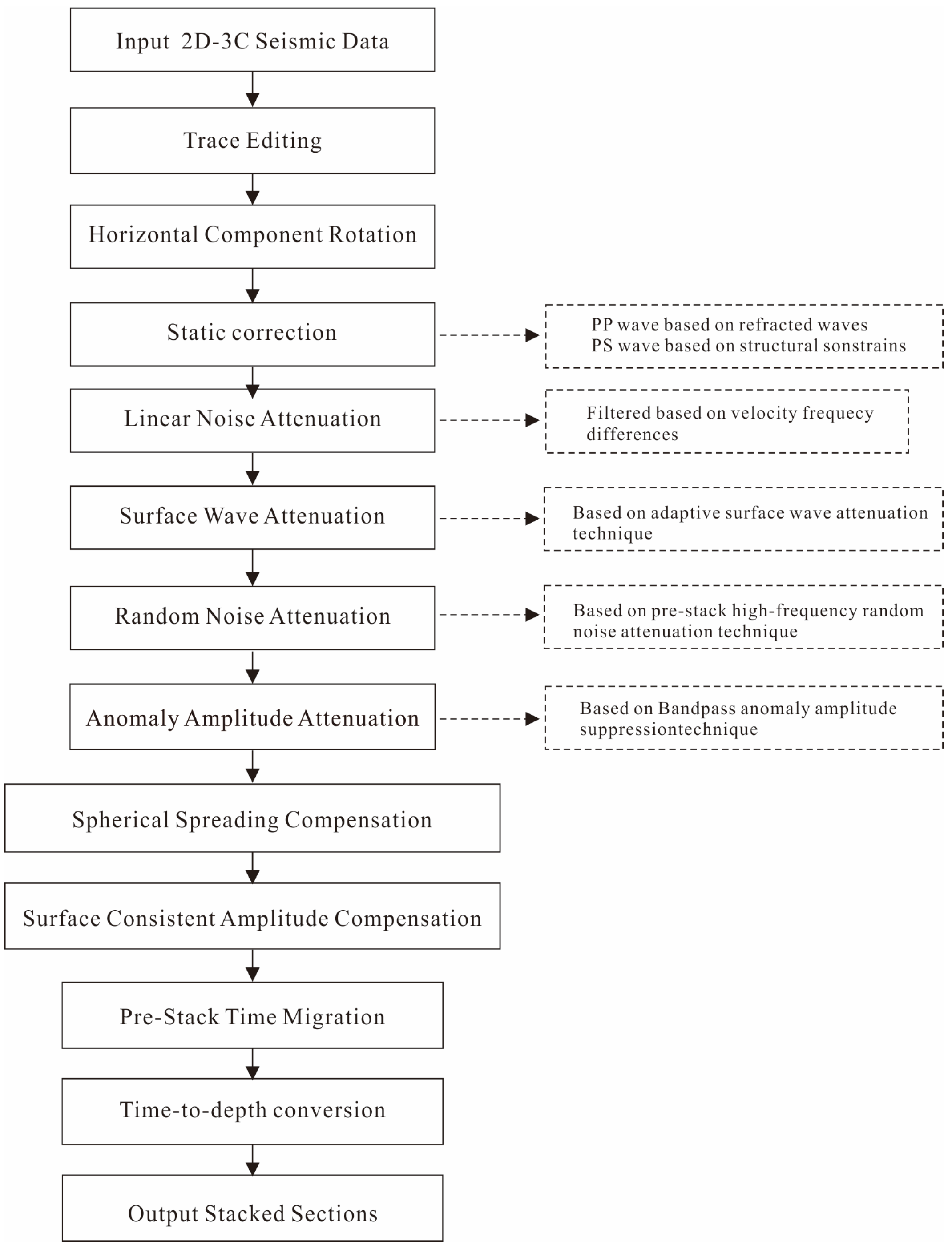
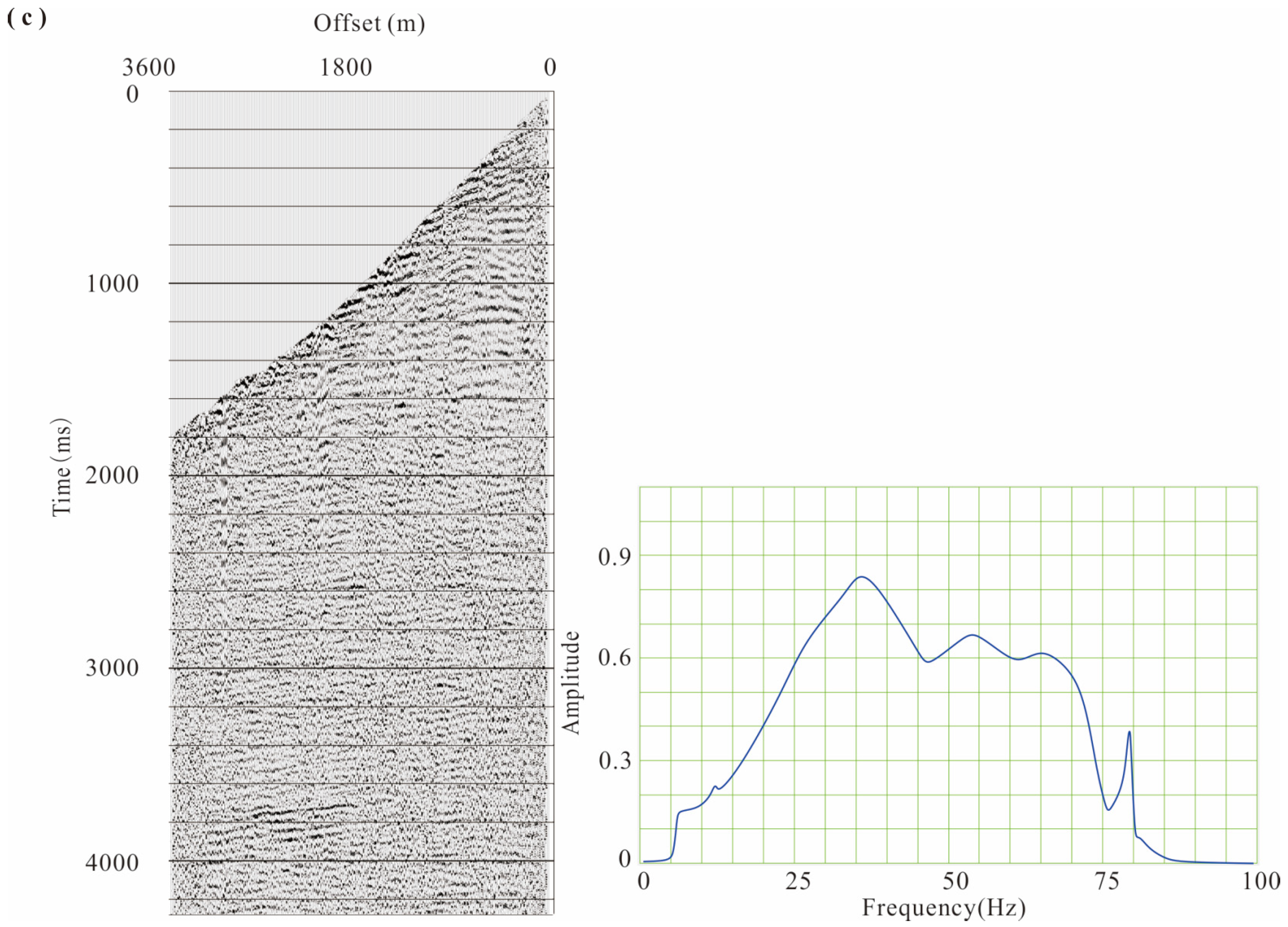
4.2. Data Analysis and Processing
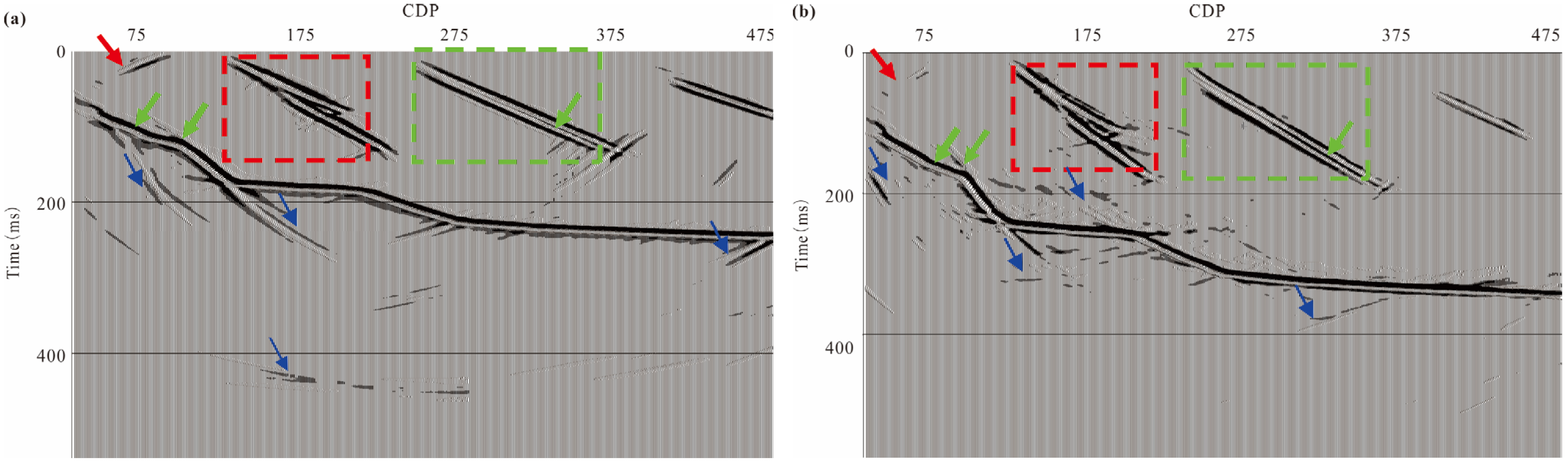
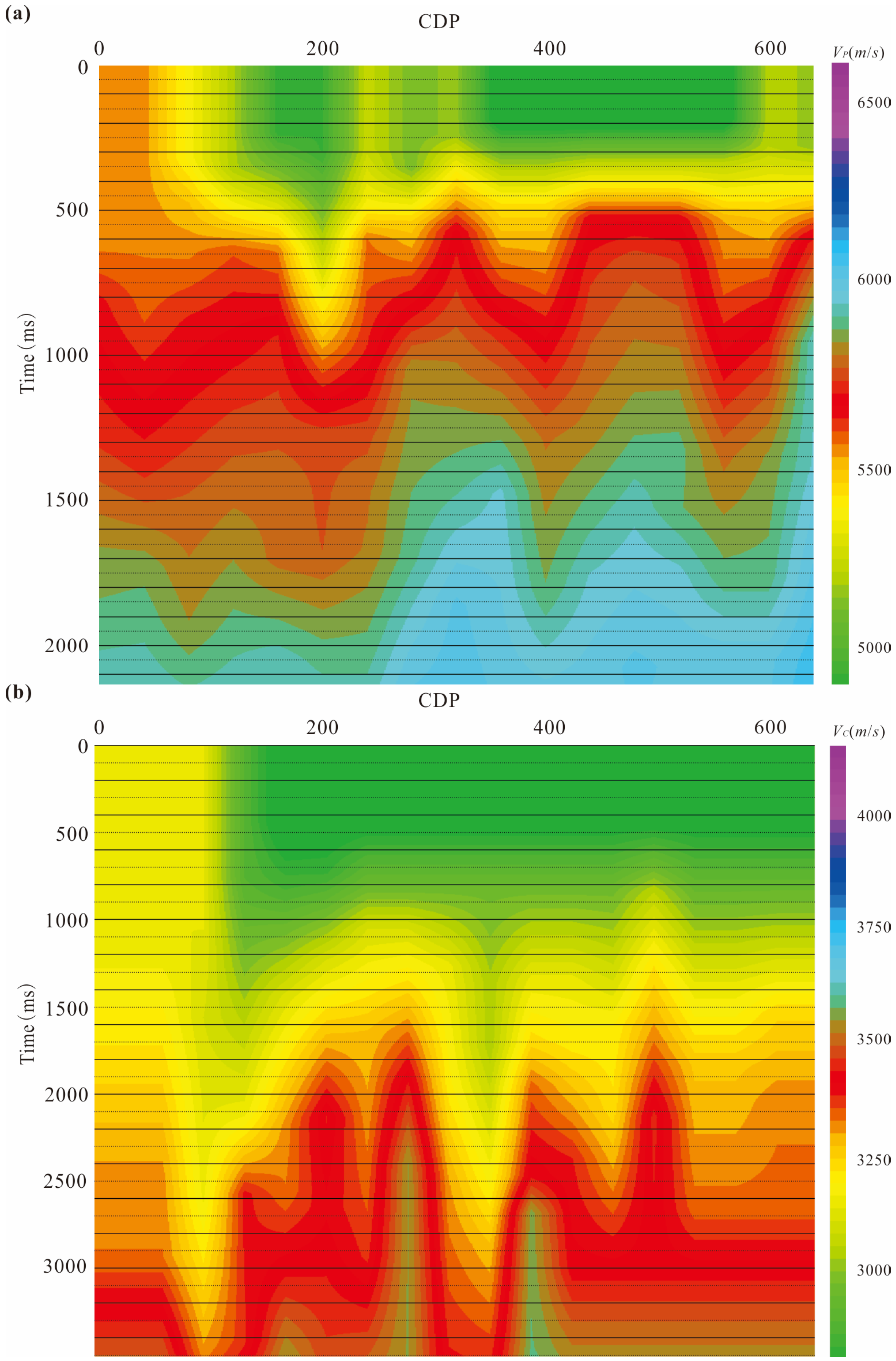
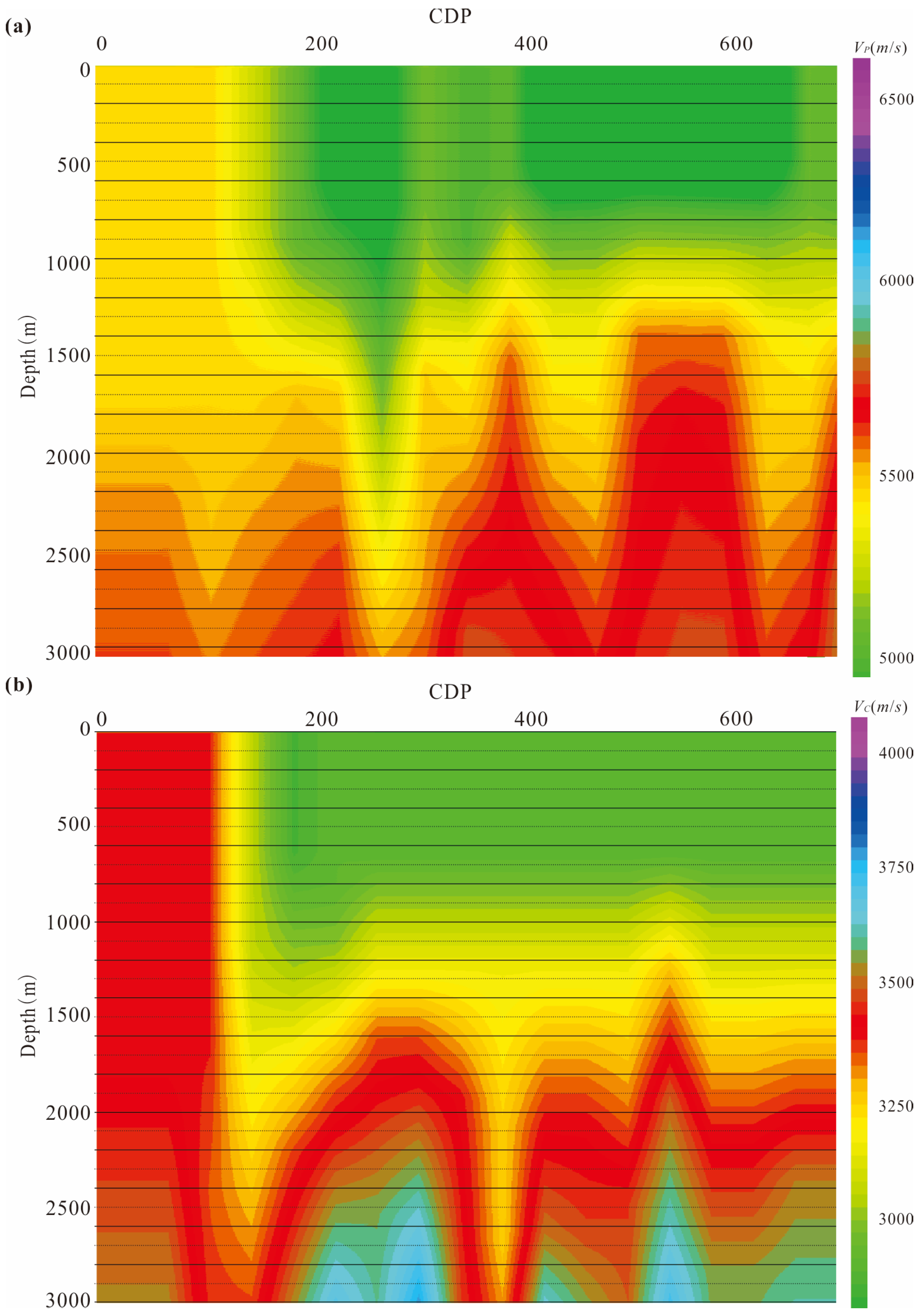
4.3. Imaging
5. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, Y.; Mao, J. Increase in Technological Investment for Mineral Exploration and Development in China. Sci. Technol. Ind. China 2022, 8, 6–10. (In Chinese) [Google Scholar] [CrossRef]
- Dong, S.; Li, T.; Chen, X.; Gao, R.; Lü, Q.; Shi, Y.; Huang, D.; Yang, J.; Wang, X.; Wei, W.; et al. SinoProbe revealed crustal structures, deep processes, and metallogenic background within China continent. Earth Sci. Front. 2014, 21, 201–225. (In Chinese) [Google Scholar]
- Teng, J. Strengthening geophysical exploration and exploitation of metallic minerals in the second deep space of the crustal interior. Geol. Bull. China 2006, 25, 767–771. (In Chinese) [Google Scholar]
- Teng, J.; Liu, J.; Liu, C.; Yao, J.; Han, L.; Zhang, Y. Prospecting for Metal Ore Deposits in Second Deep Space of Crustal Interior, the Building of Strategy Reserve Base of Northeast China. J. Jilin Univ. (Earth Sci. Ed.) 2007, 37, 633–651. [Google Scholar]
- Liang, G.; Cai, X.; Zhang, B.; Xu, X. Application of shallow seismic exploration methods in deep prediction of gold mines. Geol. Explor. 2001, 37, 29–33. (In Chinese) [Google Scholar]
- Eaton, D.W.; Milkereit, B.; Salisbury, M. Seismic methods for deep mineral exploration: Mature technologies adapted to new targets. Lead. Edge 2003, 22, 580–585. [Google Scholar] [CrossRef]
- Lü, Q.; Hou, Z.; Shi, D.; Zhao, J.; Xu, M.; Chai, M. Seismic reflection results of the Shizishan metal mine in Tongling and its significance for regional exploration. Miner. Depos. 2004, 23, 390–398. (In Chinese) [Google Scholar]
- Gou, L.; Liu, X.; Lei, P.; Liu, S. Review of seismic survey in mining exploration: Theory and reflection seismic method. Prog. Explor. Geophys. 2007, 30, 16–24. (In Chinese) [Google Scholar]
- Xu, M.; Gao, J. Seismic Exploration for Metallic Deposits; Geological Publishing House: Beijing, China, 2009; pp. 1–263. [Google Scholar]
- Schmidt, G. Results of underground seismic reflection investigations in siderite district of the Siegerland. Geophys. Prospect. 1959, 7, 287–290. [Google Scholar] [CrossRef]
- Milkereit, B.; Eaton, D.; Wu, J.; Perron, G.; Berrer, E.; Morrison, G. Seismic imaging of massive sulphide deposits: Part II. Reflection seismic profiling. Econ. Geol. 1996, 91, 829–834. [Google Scholar] [CrossRef]
- Milkereit, B.; Berrer, E.K.; King, A.R.; Watts, A.H.; Roberts, B.; Erick, A.; Eaton, D.W. Development of 3D seismic exploration technology for deep nickel-copper deposits-A case history from the Sudbury basin, Canada. Geophysics 2000, 65, 1890–1899. [Google Scholar] [CrossRef]
- Malehmir, A.; Bellefleur, G. 3D seismic reflection imaging of volcanic-hosted massive sulfide deposits: Insights from reprocessing Halfimile Lake data, New Brunswick, Canada. Geophysics 2009, 74, B209–B219. [Google Scholar] [CrossRef]
- Cheraghi, S.; Malehmir, A.; Bellefleur, G. 3D imaging challenges in steeply dipping mining environment: New lights on acquisition geometry and processing from the Brunswick no. 6 seismic data, Canada. Geophysics 2012, 77, WC109–WC122. [Google Scholar] [CrossRef]
- Drummond, B.J.; Goleby, B.R.; Goncharov, A.G.; Wyborn, L.A.I.; Collins, C.D.N.; MacCreadyb, T. Crustal-scale struc tures in the Proterozoic Mount Isa Inlier of north Australia: Their seismic response and influence on mineralization. Tectonophysics 1998, 288, 43–56. [Google Scholar] [CrossRef]
- Goleby, B.R.; Korsch, R.J.; Fomin, T.; Bell, B.; Nicoll, M.G.; Drummond, B.J.; Owen, A.J. Preliminary 3-D geological model of the Kalgoorlie region, Yilgarn Craton, Western Australia, based on deep seismic reflection and potential-field data. Aust. J. Earth Sci. 2002, 49, 917–933. [Google Scholar] [CrossRef]
- Pretorius, C.C.; Muller, M.R.; Larroque, M.; Wilkins, C. A review of 16 years of hard rock seismics on the Kaapvaal Craton. In Hardrock Seismic Exploration; Eaton, D.W., Milkereit, B., Salisbury, M.H., Eds.; SEG: Houston, TX, USA, 2003; pp. 247–268. [Google Scholar] [CrossRef]
- Kukkonen, I.T.; Heinonen, S.; Heikkinen, P.; Sorjonen-Ward, P. Delineating ophiolite-derived host rocks of massive sulfide Cu-Co-Zn deposits with 2D high-resolution seismic reflection data in Outokumpu, Finland. Geophysics 2012, 77, WC213–WC222. [Google Scholar] [CrossRef]
- Malehmir, A.; Durrheim, R.; Bellefleur, G.; Urosevic, M.; Juhlin, C.; White, J.D.; Milkereit, B.; Campbell, G. Seismic methods in mineral exploration and mine planning: A general overview of past and present case histories and a look into the future. Geophysics 2012, 77, WC173–WC190. [Google Scholar] [CrossRef]
- Bancroft, J.C.; Geigert, H.D.; Margrave, G.F. The equivalent offset method of prestack time migration. Geophysics 1998, 63, 2042–2053. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, W.; Yin, J. A modified EOM method for PS wave mi gration. Explor. Geophys. 2012, 43, 156–161. [Google Scholar] [CrossRef]
- Fleury, C.; Vasconcelos, I. Imaging condition for nonlinear scattering-based imaging: Estimate of power loss in scattering. Geophysics 2012, 77, S1–S18. [Google Scholar] [CrossRef]
- Fang, X.; Fehler, C.; Zhu, Z.; Zheng, Y.; Burns, D.R. Reservoir fracture characterization from seismic scattered waves. Geophys. J. Int. 2014, 196, 481–492. [Google Scholar] [CrossRef]
- Yan, T.; Liu, Y. Fracture detection using scattered waves in the angle domain. Geophysics 2021, 86, S257–S269. [Google Scholar] [CrossRef]
- Li, Z.; Yin, J.; Wang, Y. Application of seismic scattered wave simulation imaging in metal ore exploration. Geol. Explor. 2009, 45, 80–84. (In Chinese) [Google Scholar]
- Malcolm, A.E.; Hoop, M.V.; Ursin, B. Recursive imaging with multiply scattered waves using partial image regularization: A North Sea case study. Geophysics 2011, 76, B33–B42. [Google Scholar] [CrossRef]
- Hu, R.Z.; Wen, H.; Ye, L.; Chen, W.; Xia, Y.; Fan, H.; Huang, Y.; Zhu, J.; Fu, S. Metallogeny of critical metals in the Southwestern Yangtze Block. Chin. Sci. Bull. 2020, 65, 3700–3714. (In Chinese) [Google Scholar] [CrossRef]
- XU, J.; Yang, J.; Wang, Y.; Huang, J.; Guo, W.; Yang, Y. Full-wavefield migration method by amplitude-preserving inverse scattering imaging condition. Oil Geophys. Prospect. 2024, 59, 98–109. (In Chinese) [Google Scholar]
- Lu, L.; Vincent, E.; Xu, J. Imaging diffractors using wave-equation migration. Geophysics 2016, 81, S459–S468. [Google Scholar] [CrossRef]
- Wang, Z.; Lü, Q. Separation and Imaging of Seismic Diffractions on Metal Deposit: Two Cases in Luzong Deposit Concentration Area and Qinhang Metallogenic Belt. Acta Geosci. Sin. 2017, 38, 79–82. (In Chinese) [Google Scholar]
- Li, W.; Liu, Y.; Chen, R.; Xu, S.; Tan, Y.; He, Y.; Hua, X.; Jia, J. Removing the complex nearsurface scattered wave via an angle-domain vector resolution method. Geophys. Prospect. Pet. 2021, 60, 565–573. (In Chinese) [Google Scholar]
- Yang, J.; Sun, J.; Huang, J.; Li, Z.; Qin, S.; Yu, Y. Intelligent diffractions imaging method for fault-karst reservoir. Jourmal China Univ. Pet. (Ed. Nat. Sci.) 2024, 48, 67–73. [Google Scholar]
- Bellefleur, G.; Müller, C.; Snyder, D.; Matthews, L. Downhole seismic imaging of a massive sulfide orebody with mode-converted waves, Halfmile lake, New Brunswick, Canada. Geophysics 2004, 69, 318–329. [Google Scholar] [CrossRef]
- Snyder, D.B.; Cary, P.; Salisbury, M. 2D-3C high-resolution seismic data from the Abitibi Greenstone Belt, Canada. Tectonophysics 2009, 472, 226–237. [Google Scholar] [CrossRef]
- Malinowski, M.; White, D. Converted wave seismic imaging in the Flin Flon mining camp, Canada. J. Appl. Geophys. 2011, 75, 719–730. [Google Scholar] [CrossRef]
- Malehmir, A.; Wang, S.; Lamminen, J.; Brodic, B.; Bastani, M.; Vaittinen, K.; Juhlin, C.; Place, J. Delineating structures controlling sandstone-hosted base-metal deposits using high-resolution multicomponent seismic and radio-magnetotelluric methods: A case study from Northern Sweden. Geophys. Prospect. 2015, 63, 774–797. [Google Scholar] [CrossRef]
- Hu, R.Z.; Mao, J.W.; Hua, R. Intracontinental Metallogeny of South China Block; Science Press: Beijing, China, 2015. [Google Scholar]
- Tang, C.; Fu, L.; Xiao, F.; Du, Q. Review of progress in seismic exploration in metallic deposits. Rev. Geophys. Planet. Phys. 2022, 53, 187–203. [Google Scholar] [CrossRef]
- Zhou, J.; Xu, M.; Liu, J.; Gao, J.; Wang, X.; Zhang, B. Application of seismic reflection imaging in the Karatungk Cu–Ni deposit of Xinjiang. Geol. Explor. 2016, 52, 0910–0917. (In Chinese) [Google Scholar]
- Guo, W. Basic characteristics of the ore-forming conditions of major mineral resources in China. Sci. Bull. 1965, 3, 189–201. (In Chinese) [Google Scholar]
- Xu, M.; Chai, M.; Gao, J. Characteristics of seismic waves and physical properties of rocks and minerals in the Zhunsujihua mine of Inner Mongolia. Geol. Explor. 2015, 51, 1168–1174. (In Chinese) [Google Scholar]
- Khoshnavaz, M.J.; Bóna, A.; Hossain, M.S.; Urosevic, M.; Chambers, K. Diffractivity-another attribute for the interpretation of seismic data in hard rock environment, a case study. Interpretation 2016, 4, B23–B32. [Google Scholar] [CrossRef]
- Salisbury, M.H.; Harvey, C.W.; Matthews, L. The Acoustic Properties of Ores and Host Rocks in Hardrock Terrane//Hardrock Seismic Exploration. Soc. Econ. Geol. 2003, 10, 9–19. [Google Scholar]
- Qin, F.; Guo, Y.; Wang, M. Elastic wave Kirchhoff integral migration method. Chin. J. Geophys. 1988, 05, 577–587. (In Chinese) [Google Scholar]
- Yu, G.; Yao, C. The sorting method of CCP gathers and influencing factors in slanting interface. Coal Geol. Explor. 2007, 04, 65–69. (In Chinese) [Google Scholar]
- Yao, C.; Yu, G.; Cai, M. Angle-domain CDP and angle-domain CCP stacking. In 21st Annual Meeting of the Chinese Geophysical Society; Jilin University Press: Changchun, China, 2005; p. 1. (In Chinese) [Google Scholar]
- Li, Y.; Lu, J.; Wang, Y.; Zhang, Y.; Wu, Z. Converted PS-wave imaging based on offset vector tiles. Geophysics 2023, 88, S151–S161. [Google Scholar] [CrossRef]
- Lu, J.; Wang, Y.; Yao, C. Separating P- and S-waves in an affine coordinate system. J. Geophys. Eng. 2012, 9, 12–18. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, J.; Liu, J.; Wang, S.; Wang, Q.; Kang, S.; Zhang, J.; Zhao, Y. Isotopic geochemical characteristics of the Wunugetu tungsten-molybdenum deposit in Sunitezuo Banner, Inner Mongolia. Geol. Rev. 2013, 27, 13–23. [Google Scholar]
- Kong, W.; Liu, C.; Deng, J.; Xu, L.; Zhao, G. Zircon U-Pb geochronology of quartz porphyry from the Wuhua’aobao molybdenum deposit in Erenhot area, Inner Mongolia, and its constraints on the molybdenum mineralization age. Miner. Depos. 2010, 29, 454–455. [Google Scholar]
- Xu, M.; Jiang, C.; Chai, M.; Gao, J. Three-component seismic experimental study of the Zhunsujihua Cu-Mo mine in Inner Mongolia. Prog. Geophys. 2016, 31, 1229–1236. (In Chinese) [Google Scholar] [CrossRef]
- Xu, M.; Zhou, J.; Chai, M.; Gao, J.; Liu, J.; Zhang, B. Seismic reflection detection in the Zhunsujihua porphyry molybdenum ore district and its periphery, Inner Mongolia. Geophys. Geochem. Explor. 2016, 40, 639–647. (In Chinese) [Google Scholar] [CrossRef]
- Yang, W.; Zhu, G.; Yang, Z.; Wang, H.; Xu, G.; Zhou, Y.; Yao, H.; Li, G. Three component seismic profiling at the Chinese Continent al Scientific Drilling site. Chin. J. Geophys. 2007, 50, 780–790. (In Chinese) [Google Scholar]




| Rock Type | P-Wave Velocity (m/s) | S-Wave Velocity (m/s) | Density (g/cm3) |
|---|---|---|---|
| Metamorphic Sandstone | 5580 | 3250 | 2.8 |
| Granodiorite | 5270 | 2970 | 2.74 |
| Molybdenum Ore Body | 4879 | 2600 | 3.77 |
| Rock Types | P-Wave Velocity (m/s) | S-Wave Velocity (m/s) | Density (g/cm3) |
|---|---|---|---|
| Granodiorite | 5271.4 | 2973.7 | 2.7402 |
| Diorite (Vein) | 5566.0 | 3189.0 | 2.9094 |
| Mineralized granite diorite | 5576.4 | 3251.5 | 2.8003 |
| Copper–molybdenum mineralized Granite diorite (ore) | 5297.5 | 2769.3 | 2.8467 |
| Granodiorite | 4879.0 | 2600.0 | 3.7670 |
| Rock Types | Granodiorite | Diorite (Vein) | Metamorphic Sandstone | Mineralized Granite Diorite | Copper–Molybdenum Mineralized Granite Diorite (Ore) |
|---|---|---|---|---|---|
| Granodiorite | — | 1749 | 1171 | 636 | 3935 |
| Diorite (vein) | — | — | 578 | 1113 | 3934 |
| Mineralized granite diorite | — | — | — | 535 | 2764 |
| Copper–molybdenum mineralized granite diorite (ore) | — | — | — | — | 3299 |
| Rock Types | Granodiorite | Diorite (Vein) | Metamorphic Sandstone | Mineralized Granite Diorite | Copper–Molybdenum Mineralized Granite Diorite (Ore) |
|---|---|---|---|---|---|
| Granodiorite | — | 1130 | 957 | 265 | 1646 |
| Diorite (vein) | — | — | 172 | 1395 | 516 |
| Mineralized granite diorite | — | — | — | 1222 | 682 |
| Copper–molybdenum mineralized granite diorite (ore) | — | — | — | — | 1911 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Gu, Y.; Zhang, Y.; Wang, Y.; Yu, G.; Xu, M. What Extra Information Can Be Provided by Multi-Component Seismic Data: A Case Study of 2D3C Prospecting of a Copper–Molybdenum Mine in Inner Mongolia, China. Minerals 2024, 14, 689. https://doi.org/10.3390/min14070689
Li Y, Gu Y, Zhang Y, Wang Y, Yu G, Xu M. What Extra Information Can Be Provided by Multi-Component Seismic Data: A Case Study of 2D3C Prospecting of a Copper–Molybdenum Mine in Inner Mongolia, China. Minerals. 2024; 14(7):689. https://doi.org/10.3390/min14070689
Chicago/Turabian StyleLi, Yingda, Yutian Gu, Yi Zhang, Yun Wang, Guangming Yu, and Mingcai Xu. 2024. "What Extra Information Can Be Provided by Multi-Component Seismic Data: A Case Study of 2D3C Prospecting of a Copper–Molybdenum Mine in Inner Mongolia, China" Minerals 14, no. 7: 689. https://doi.org/10.3390/min14070689
APA StyleLi, Y., Gu, Y., Zhang, Y., Wang, Y., Yu, G., & Xu, M. (2024). What Extra Information Can Be Provided by Multi-Component Seismic Data: A Case Study of 2D3C Prospecting of a Copper–Molybdenum Mine in Inner Mongolia, China. Minerals, 14(7), 689. https://doi.org/10.3390/min14070689







