Estimating Content of Rare Earth Elements in Marine Sediments Using Hyperspectral Technology: Experiment and Method Series
Abstract
1. Introduction
2. Data and Methods
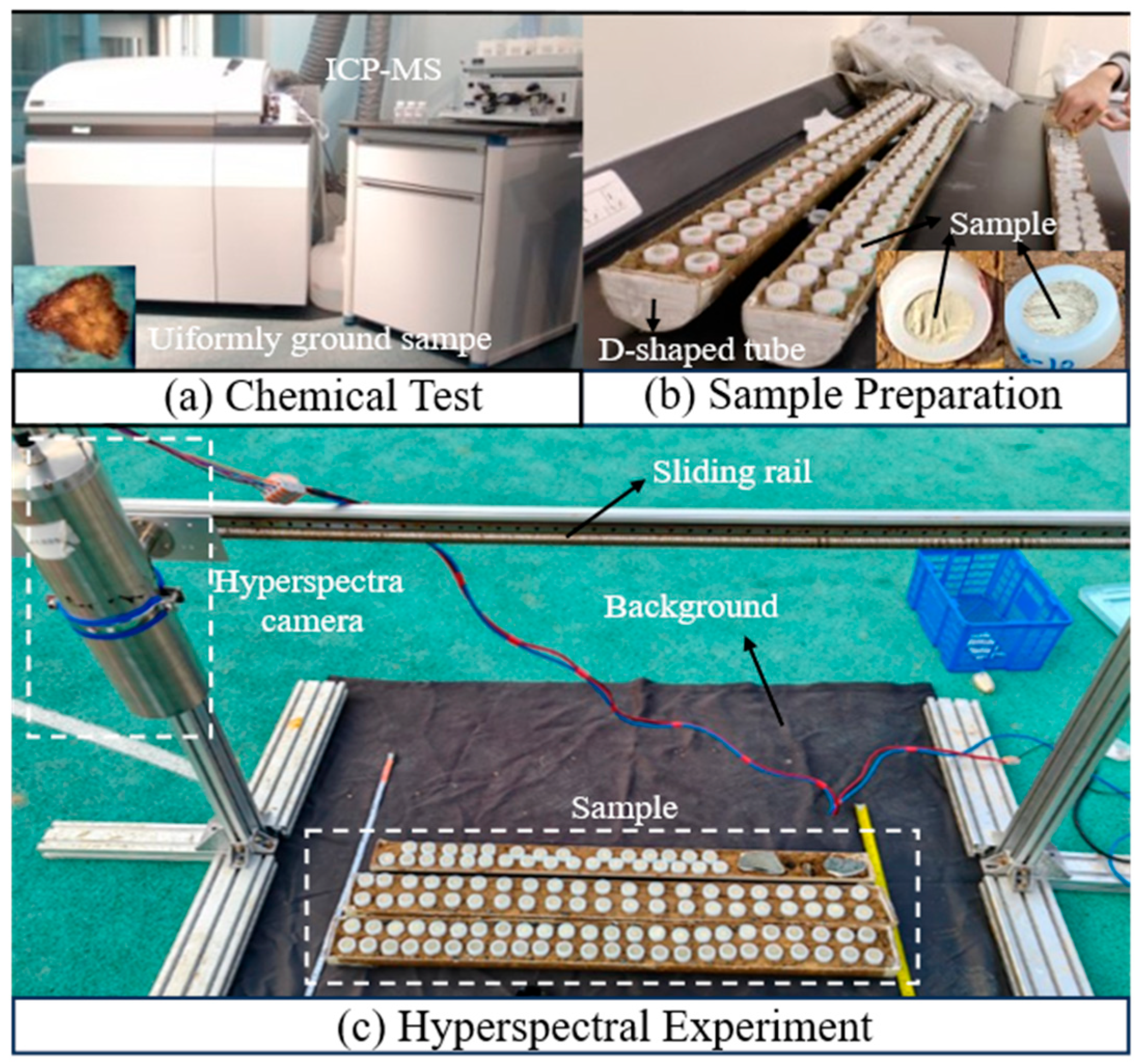
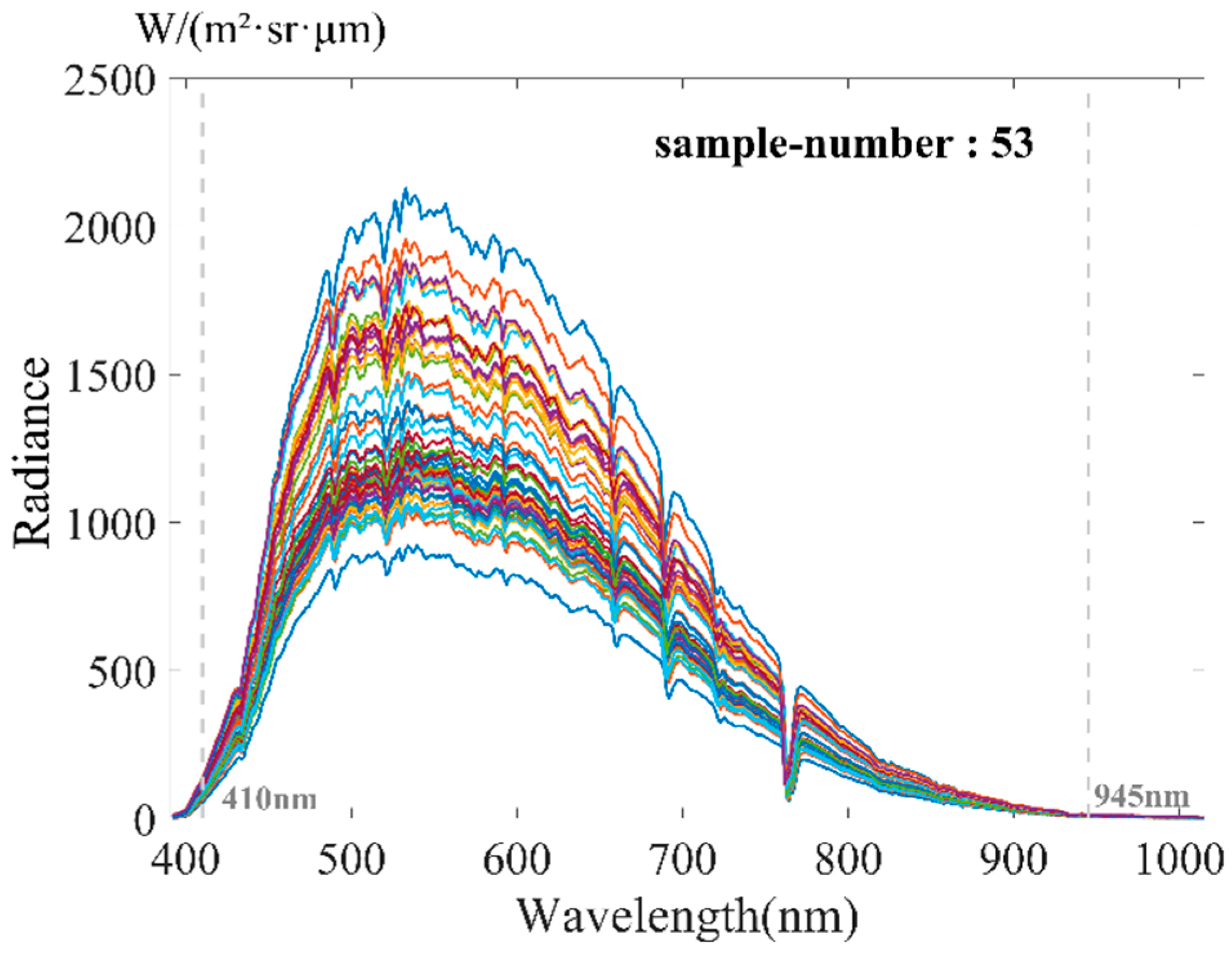
2.1. Date
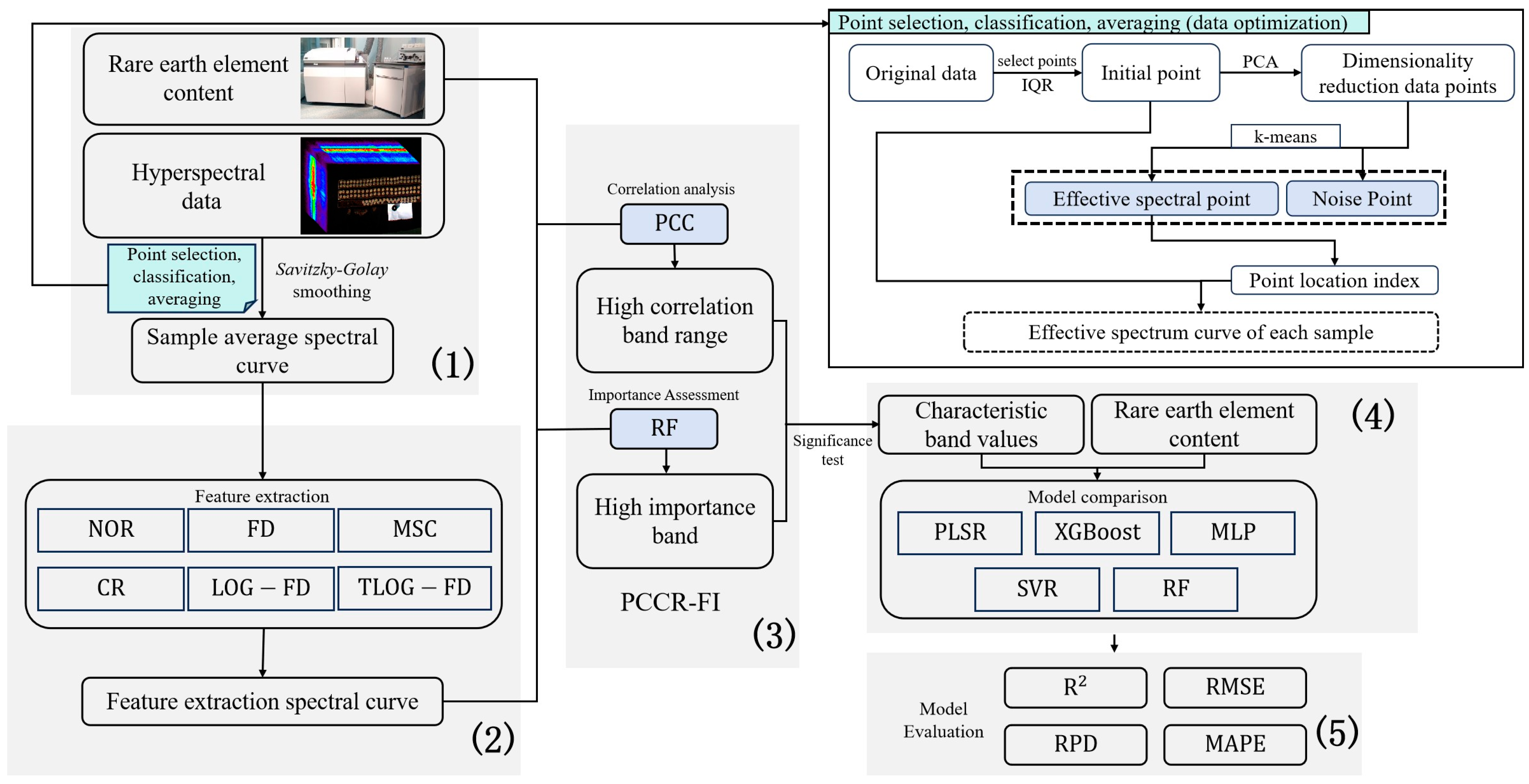
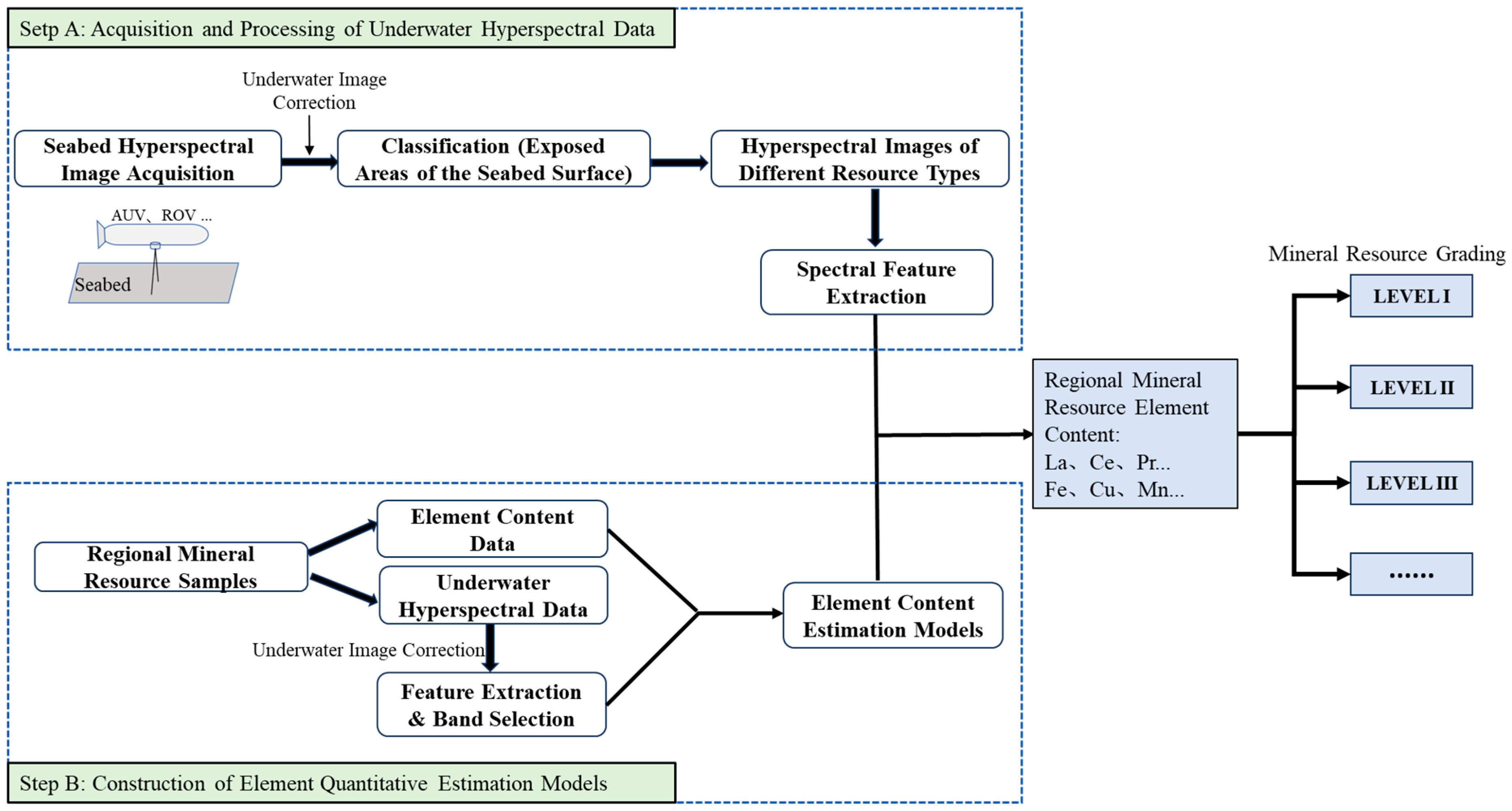
2.2. Workflow
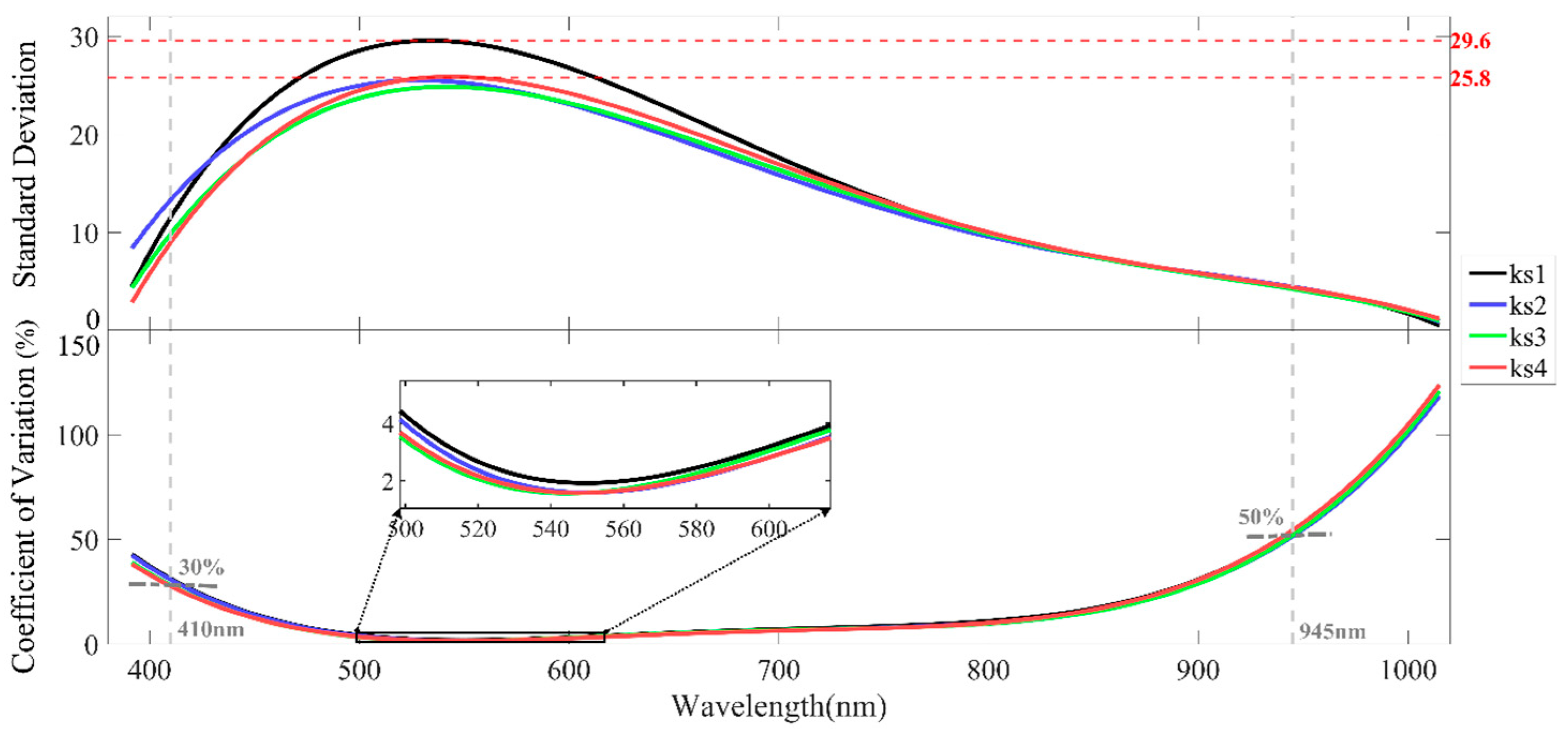
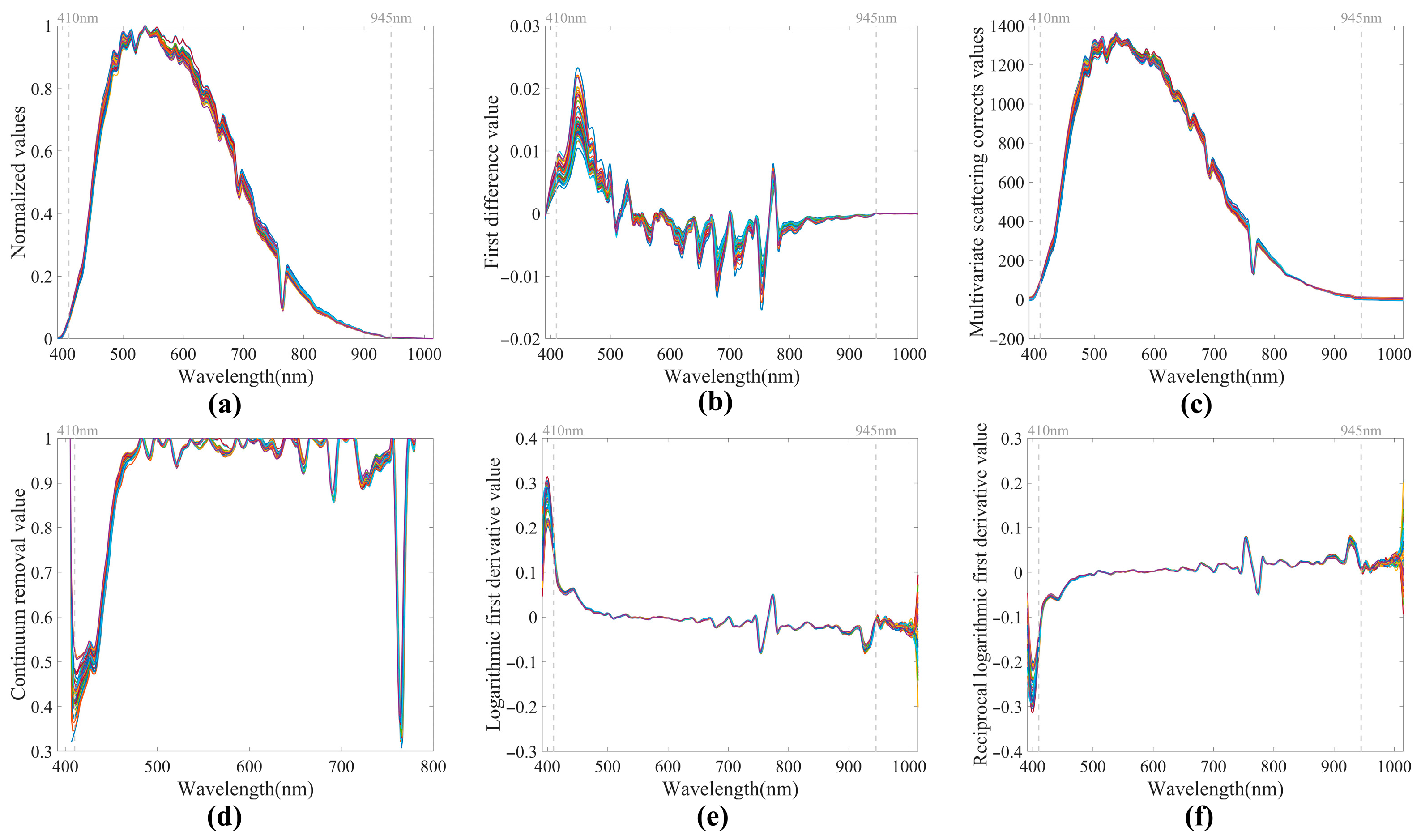
2.3. Hyperspectral Data Anomaly Detection and Removal
2.4. Spectral Feature Extraction
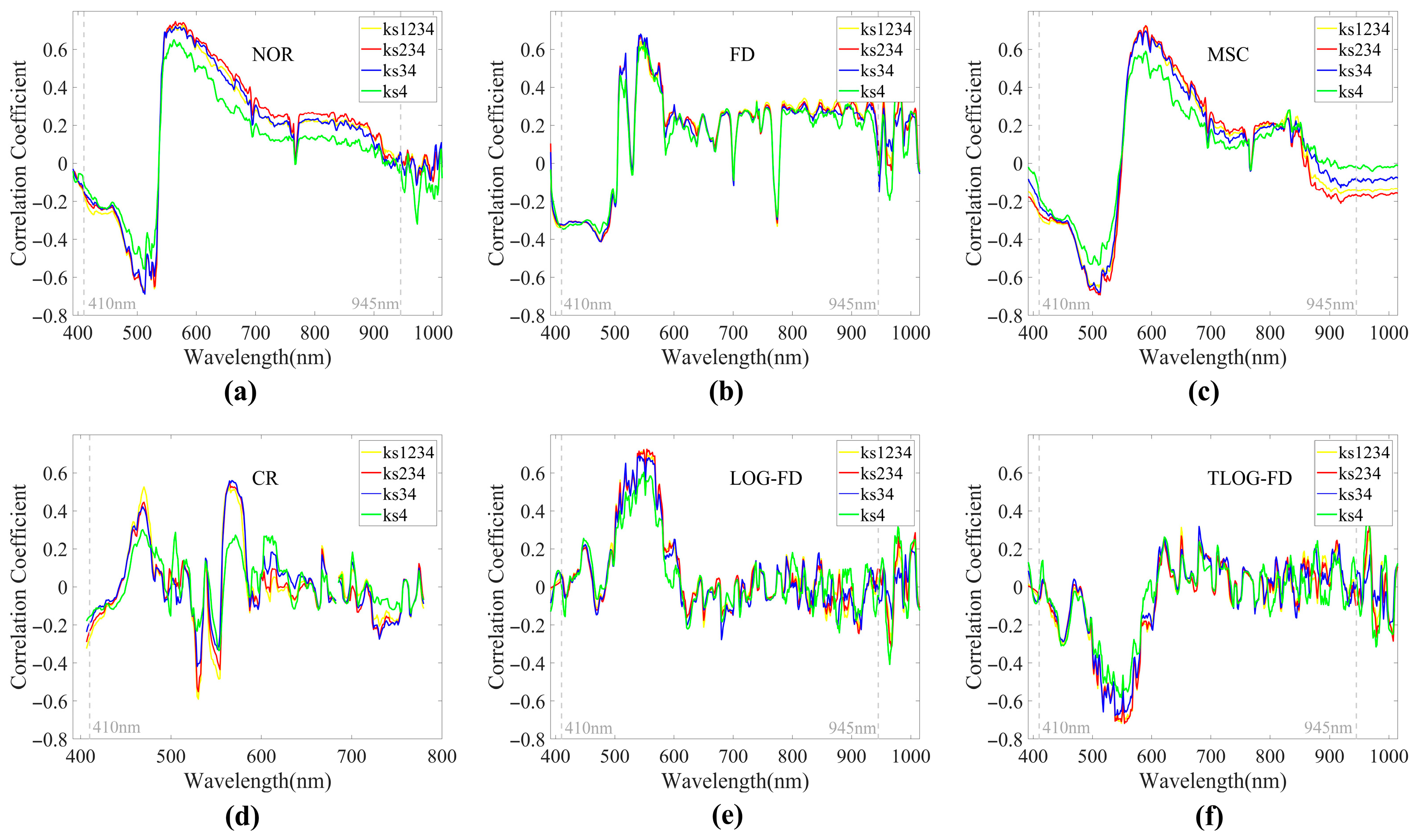
2.5. Characteristic Band Selection
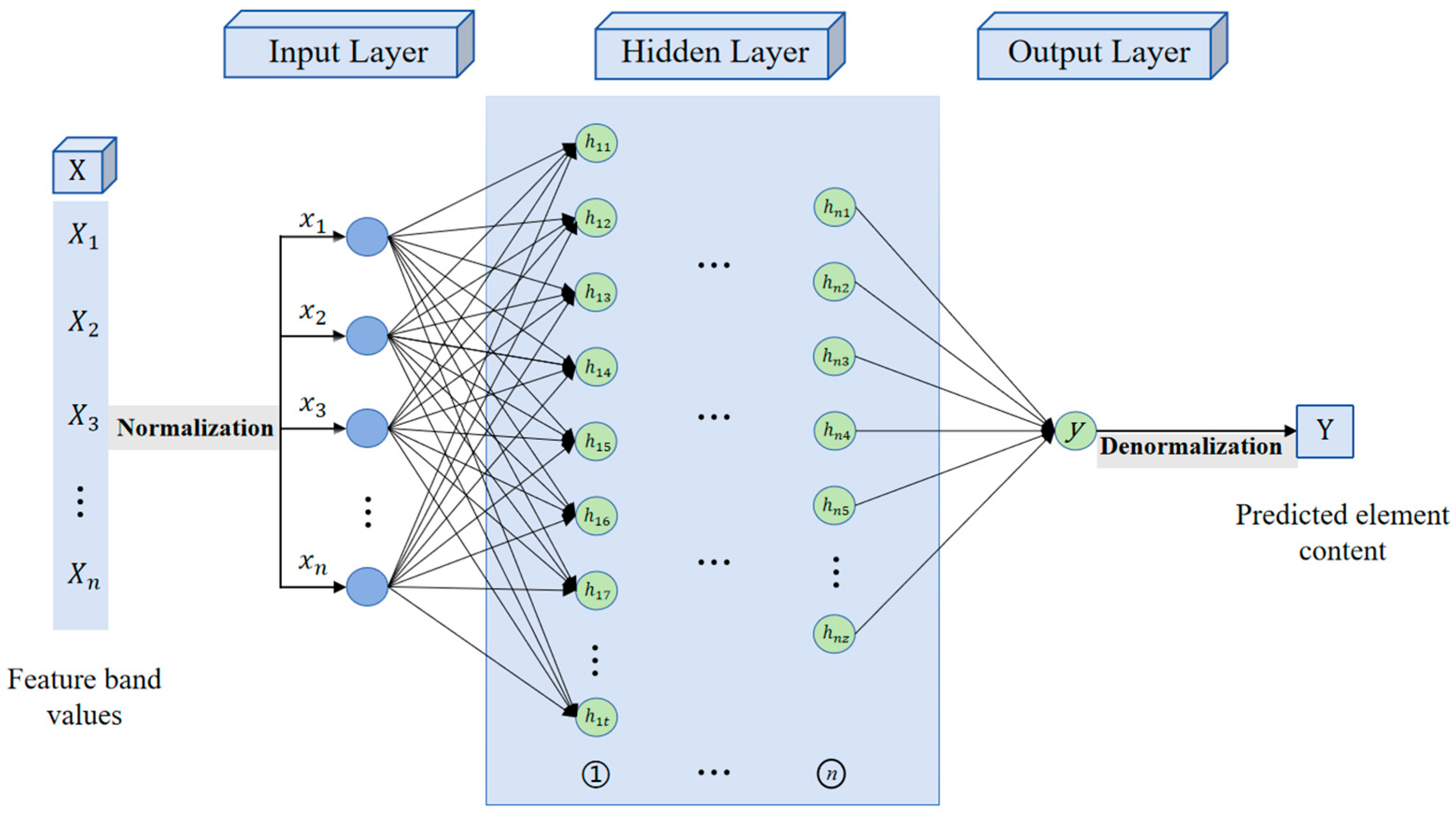
2.6. Estimation Model
2.7. Model Evaluation
3. Results and Discussion
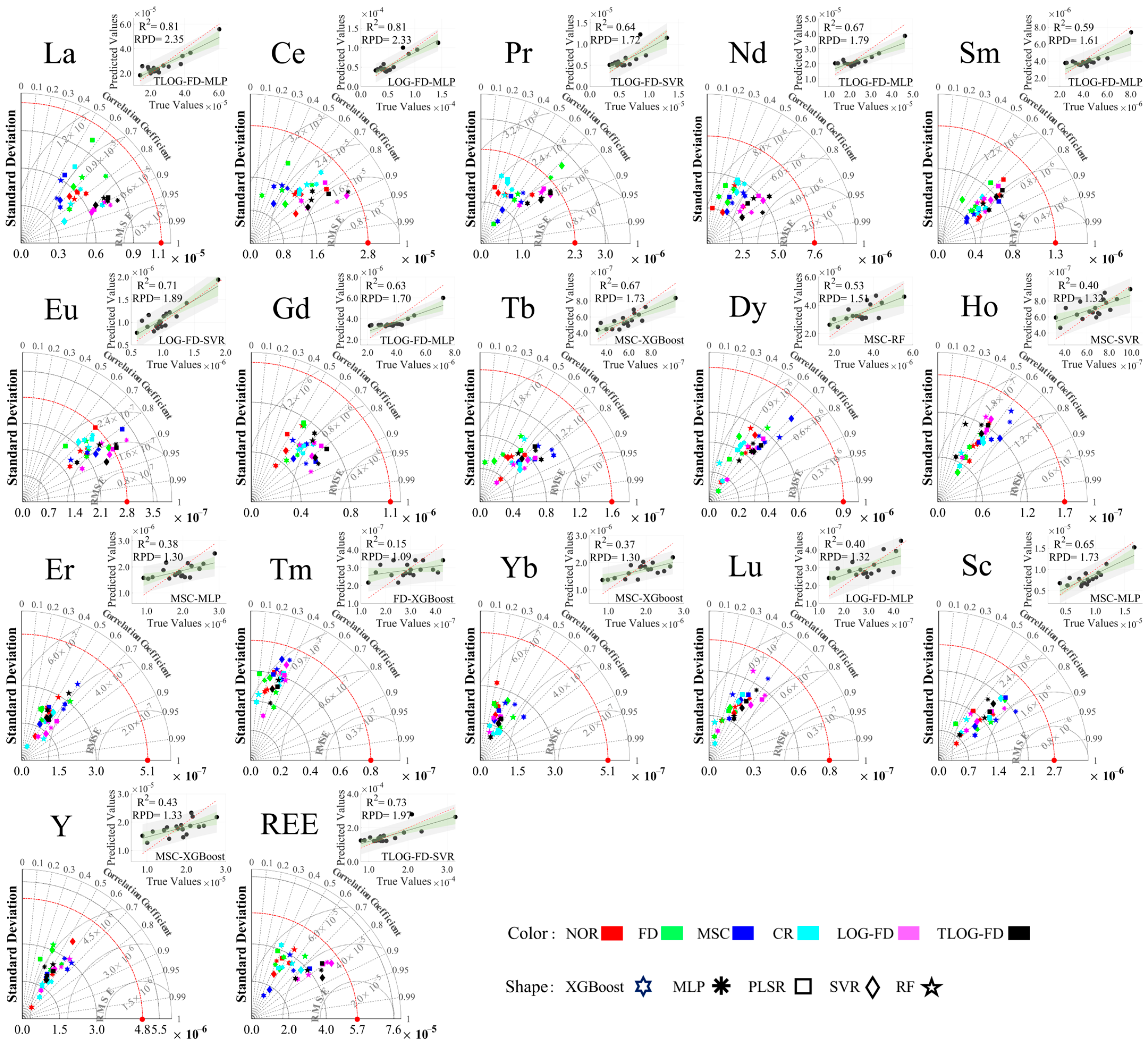
3.1. Estimation Results of Rare Earth Elements
3.2. Discussion on the Quantitative Estimation of Rare Earth Element Content Using Hyperspectral Data
3.3. Effectiveness and Generalization Ability of Experimental and Method Models
3.4. The Limitations and Feasibility of Hyperspectral Estimation of Rare Earth Elements in Sediments
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kato, Y.; Fujinaga, K.; Nakamura, K.; Takaya, Y.; Kitamura, K.; Ohta, J.; Toda, R.; Nakashima, T.; Iwamori, H. Deep-sea mud in the Pacific Ocean as a potential resource for rare-earth elements. Nat. Geosci. 2011, 4, 535–539. [Google Scholar] [CrossRef]
- Shi, X.; Bi, D.; Huang, M.; Yu, M.; Luo, Y.; Zhou, T.; Zhang, Z.; Liu, J. Distribution and metallogenesis of deep-sea rare earth elements. Geol. Bull. China 2021, 40, 195–208. [Google Scholar]
- Lu, D.; Mao, J.; Ye, H.; Wang, P.; Chao, W.; Yu, M. Geochemistry of scheelite from Jiangligou skarn W-(Cu-Mo) deposit in the West Qinling orogenic belt, Northwest China: Implication on the multistage ore-forming processes. Ore Geol. Rev. 2023, 159, 105525. [Google Scholar] [CrossRef]
- Huang, M.; Shi, X.; Bi, D.; Yu, M.; Li, L.; Li, J.; Zhang, P.; Zhang, X.; Liu, J.; Yang, G.; et al. Advances on the study of exploration and development of deep-sea rare earth resources. Chin. J. Nonferrous Met. 2021, 31, 2665–2681. [Google Scholar]
- Ding, Z.; Liu, B.; Liu, Z.; Xin, H. Research on multi-function in-situ detect miniature probe of sea sediment. J. Electron. Meas. Instrum. 2009, 23, 44–48. [Google Scholar]
- Kan, G.; Liu, B.; Han, G.; Li, G.; Zhao, Y. Application of in-situ measurement technology to the survey of seafloor sediment acoustic properties in the Huanghai Sea. Acta Oceanol. Sin. 2010, 32, 88–94. [Google Scholar]
- Zhu, Y.; Bao, R.; Zhu, L.; Jiang, S.; Chen, H.; Zhang, L.; Zhou, Y. Investigating the provenances and transport mechanisms of surface sediments in the offshore muddy area of Shandong Peninsula: Insights from REE analyses. J. Mar. Syst. 2022, 226, 103671. [Google Scholar] [CrossRef]
- Graul, S.; Kallaste, T.; Pajusaar, S.; Urston, K.; Gregor, A.; Moilanen, M.; Ndiaye, M.; Hints, R. REE + Y distribution in Tremadocian shelly phosphorites (Toolse, Estonia): Multi-stages enrichment in shallow marine sediments during early diagenesis. J. Geochem. Explor. 2023, 254, 107311. [Google Scholar] [CrossRef]
- Ouyang, A.; Xiong, W.; Li, X.; Chen, D.; Zhang, L.; Jiang, P. Occurrence and screening- flotation separation for the beneficiation of rare earth elements and yttrium (REY) in core sediments from the Pacific Ocean. Mar. Geol. 2023, 462, 107097. [Google Scholar] [CrossRef]
- Jia, Y.; Zhang, L.; Wu, D.; Song, C.; Yuan, W.; Li, L. Comparative analysis of grassland biomass inversion models based on unmanned aerial vehicle multispectral data. Acta Ecol. Sin. 2024, 44, 6854–6864. [Google Scholar]
- Liang, W.; Wu, Y.; Shi, Y.; Wang, D.; Wang, Y. Inversion of Taipu River water quality parameters by UAV hyperspectral imaging technology. Bull. Surv. Mapp. 2024, 4, 29–34. [Google Scholar] [CrossRef]
- Patel, A.K.; Ghosh, J.K.; Pande, S.; Sayyad, S.U. Deep-Learning-Based Approach for Estimation of Fractional Abundance of Nitrogen in Soil From Hyperspectral Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 6495–6511. [Google Scholar] [CrossRef]
- Xu, L.; Shi, S.; Gong, W.; Shi, Z.; Qu, F.; Tang, X.; Chen, B.; Sun, J. Improving leaf chlorophyll content estimation through constrained PROSAIL model from airborne hyperspectral and LiDAR data. Int. J. Appl. Earth Obs. Geoinf. 2022, 115, 103128. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, T.; Gu, X.; Kuai, Y.; Wang, C.; Chen, D.; Zhao, C. UAV-borne hyperspectral estimation of nitrogen content in tobacco leaves based on ensemble learning methods. Comput. Electron. Agric. 2023, 211, 108008. [Google Scholar] [CrossRef]
- Bian, Z.; Sun, L.; Tian, K.; Liu, B.; Huang, B.; Wu, L. Estimation of multi-media metal(loid)s around abandoned mineral processing plants using hyperspectral technology and extreme learning machine. Environ. Sci. Pollut. Res. 2022, 30, 19495–19512. [Google Scholar] [CrossRef]
- Zhang, Z.-H.; Guo, F.; Xu, Z.; Yang, X.-Y.; Wu, K.-Z. On retrieving the chromium and zinc concentrations in the arable soil by the hyperspectral reflectance based on the deep forest. Ecol. Indic. 2022, 144, 109440. [Google Scholar] [CrossRef]
- Zhu, C.; Ding, J.; Zhang, Z.; Wang, Z. Exploring the potential of UAV hyperspectral image for estimating soil salinity: Effects of optimal band combination algorithm and random forest. Spectrochim. Acta A 2022, 279, 121416. [Google Scholar] [CrossRef]
- Tan, J.; Ding, J.; Wang, Z.; Han, L.; Wang, X.; Li, Y.; Zhang, Z.; Meng, S.; Cai, W.; Hong, Y. Estimating soil salinity in mulched cotton fields using UAV-based hyperspectral remote sensing and a Seagull Optimization Algorithm-Enhanced Random Forest Model. Comput. Electron. Agric. 2024, 221, 109017. [Google Scholar] [CrossRef]
- Zhong, L.; Yang, S.; Chu, X.; Sun, Z.; Li, J. Inversion of heavy metal copper content in soil-wheat systems using hyperspectral techniques and enrichment characteristics. Sci. Total Environ. 2024, 907, 168104. [Google Scholar] [CrossRef]
- Tan, K.; Zhu, L.; Wang, X. A Hyperspectral Feature Selection Method for Soil Organic Matter Estimation Based on an Improved Weighted Marine Predators Algorithm. IEEE Trans. Geosci. Remote Sens. 2025, 63, 1–11. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, M.; Li, P. Study on the Geochemical Anomalies Identification of REE Based on HJ-1A-HSI. Spectrosc. Spectr. Anal. 2015, 35, 3172–3175. [Google Scholar]
- Zimmermann, R.; Brandmeier, M.; Andreani, L.; Mhopjeni, K.; Gloaguen, R. Remote Sensing Exploration of Nb-Ta-LREE-Enriched Carbonatite (Epembe/Namibia). Remote Sens. 2016, 8, 620. [Google Scholar] [CrossRef]
- Lorenz, S.; Beyer, J.; Fuchs, M.; Seidel, P.; Turner, D.; Heitmann, J.; Gloaguen, R. The Potential of Reflectance and Laser Induced Luminescence Spectroscopy for Near-Field Rare Earth Element Detection in Mineral Exploration. Remote Sens. 2019, 11, 21. [Google Scholar] [CrossRef]
- Cheng, G.; Li, J.; Wang, C.; Hu, Z.; Ning, Q. Study on Hyperspectral Quantitative Inversion of Ionic Rare Earth Ores. Spectrosc. Spectr. Anal. 2019, 39, 1571–1578. [Google Scholar]
- Cheng, G.; Zhang, H.; Li, H.; Deng, X.; Elatikpo, S.M.; Li, J.; Hu, Z.; Li, G. Quantitative Inversion of REEs in Ion-Adsorbed Rare Earth Ores from the Liutang Area (South China), Based on Measured Hyperspectral Data. J. Earth Sci. 2023, 34, 1068–1082. [Google Scholar] [CrossRef]
- Jia, X.; Hu, B.; Marchant, B.P.; Zhou, L.; Shi, Z.; Zhu, Y. A methodological framework for identifying potential sources of soil heavy metal pollution based on machine learning: A case study in the Yangtze Delta, China. Environ. Pollut. 2019, 250, 601–609. [Google Scholar] [CrossRef]
- Acosta, I.C.C.; Khodadadzadeh, M.; Tolosana-Delgado, R.; Gloaguen, R. Drill-Core Hyperspectral and Geochemical Data Integration in a Superpixel-Based Machine Learning Framework. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 4214–4228. [Google Scholar] [CrossRef]
- Boesche, N.K.; Rogass, C.; Lubitz, C.; Brell, M.; Herrmann, S.; Mielke, C.; Tonn, S.; Appelt, O.; Altenberger, U.; Kaufmann, H. Hyperspectral REE (Rare Earth Element) Mapping of Outcrops—Applications for Neodymium Detection. Remote Sens. 2015, 7, 5160–5186. [Google Scholar] [CrossRef]
- Huang, Z.; Huang, W.; Li, S.; Ni, B.; Zhang, Y.; Wang, M.; Chen, M.; Zhu, F. Inversion Evaluation of Rare Earth Elements in Soil by Visible-Shortwave Infrared Spectroscopy. Remote Sens. 2021, 13, 4886. [Google Scholar] [CrossRef]
- Shen, Q.; Xia, K.; Zhang, S.; Kong, C.; Hu, Q.; Yang, S. Hyperspectral indirect inversion of heavy-metal copper in reclaimed soil of iron ore area. Spectrochim. Acta A 2019, 222, 117191. [Google Scholar] [CrossRef]
- Ye, M.; Zhu, L.; Li, X.; Ke, Y.; Huang, Y.; Chen, B.; Yu, H.; Li, H.; Feng, H. Estimation of the soil arsenic concentration using a geographically weighted XGBoost model based on hyperspectral data. Sci. Total Environ. 2023, 858, 159798. [Google Scholar] [CrossRef]
- Zhang, T.; Fu, Q.; Tian, R.; Zhang, Y.; Sun, Z. A spectrum contextual self-attention deep learning network for hyperspectral inversion of soil metals. Ecol. Indic. 2023, 152, 110351. [Google Scholar] [CrossRef]
- Ma, X.; Wang, J.; Zhou, K.; Zhang, W.; Zhang, Z.; De Maeyer, P.; Van de Voorde, T. New data-driven estimation of metal element in rocks using a hyperspectral data and geochemical data. Ore Geol. Rev. 2024, 165, 105877. [Google Scholar] [CrossRef]
- Subi, X.; Eziz, M.; Zhong, Q.; Li, X. Estimating the chromium concentration of farmland soils in an arid zone from hyperspectral reflectance by using partial least squares regression methods. Ecol. Indic. 2024, 161, 111987. [Google Scholar] [CrossRef]
- Chen, L.; Lai, J.; Tan, K.; Wang, X.; Chen, Y.; Ding, J. Development of a soil heavy metal estimation method based on a spectral index: Combining fractional-order derivative pretreatment and the absorption mechanism. Sci. Total Environ. 2022, 813, 151882. [Google Scholar] [CrossRef]
- Wang, G.; Lee, Z.; Mishra, D.R.; Ma, R. Retrieving absorption coefficients of multiple phytoplankton pigments from hyperspectral remote sensing reflectance measured over cyanobacteria bloom waters. Limnol. Oceanogr. Methods 2016, 14, 432–447. [Google Scholar] [CrossRef]
- Wang, M.; Yang, J.; Liu, S.; Gu, Y.; Xu, M.; Ma, Y.; Zhang, J.; Wan, J. Quantitative Inversion of Oil Film Thickness Based on Airborne Hyperspectral Data Using the 1DCNN_GRU Model. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–16. [Google Scholar] [CrossRef]
- Niu, C.; Tan, K.; Wang, X.; Du, P.; Pan, C. A semi-analytical approach for estimating inland water inherent optical properties and chlorophyll a using airborne hyperspectral imagery. Int. J. Appl. Earth Obs. Geoinf. 2024, 128, 103774. [Google Scholar] [CrossRef]
- Xue, Q.; Bai, H.; Li, H.; Wang, Y.; Zhang, D. Development of Underwater Hyperspectral Imaging Detecting Technology (Invited). Acta Photonica Sin. 2021, 50, 9–34. [Google Scholar]
- Dumke, I.; Nornes, S.M.; Purser, A.; Marcon, Y.; Ludvigsen, M.; Ellefmo, S.L.; Johnsen, G.; Søreide, F. First hyperspectral imaging survey of the deep seafloor: High-resolution mapping of manganese nodules. Remote Sens. Environ. 2018, 209, 19–30. [Google Scholar] [CrossRef]
- Dumke, I.; Ludvigsen, M.; Ellefmo, S.L.; Søreide, F.; Johnsen, G.; Murton, B.J. Underwater Hyperspectral Imaging Using a Stationary Platform in the Trans-Atlantic Geotraverse Hydrothermal Field. IEEE Trans. Geosci. Remote Sens. 2019, 57, 2947–2962. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M. Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, W.; Cen, Y.; Zhang, L.; Wang, N. Predicting cadmium concentration in soils using laboratory and field reflectance spectroscopy. Sci. Total Environ. 2019, 650, 321–334. [Google Scholar] [CrossRef]
- Hanafi, M.; Ouertani, S.S.; Boccard, J.; Mazerolles, G.; Rudaz, S. Multi-way PLS regression: Monotony convergence of tri-linear PLS2 and optimality of parameters. Comput. Stat. Data Anal. 2015, 83, 129–139. [Google Scholar] [CrossRef]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Ma, M.; Zhao, G.; He, B.; Li, Q.; Dong, H.; Wang, S.; Wang, Z. XGBoost-based method for flash flood risk assessment. J. Hydrol. 2021, 598, 126382. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Zhang, J.; Jing, X.; Song, X.; Zhang, T.; Duan, W.; Su, J. Hyperspectral estimation of wheat stripe rust using fractional order differential equations and Gaussian process methods. Comput. Electron. Agric. 2023, 206, 107671. [Google Scholar] [CrossRef]
- Batsanov, S.S.; Derbeneva, S.S.; Batsanova, L.R. Electronic spectra of fluorides, oxyfluorides, and oxides of rare-earth metals. Appl. Spectrosc. 1969, 10, 240–242. [Google Scholar] [CrossRef]
- Möller, V.; Williams-Jones, A.E. A hyperspectral study (V-NIR-SWIR) of the Nechalacho REE-Nb-Zr deposit, Canada. Geochem. Explor. 2018, 188, 194–215. [Google Scholar] [CrossRef]
- Dai, J.; Wu, Y.; Ling, T. Reflectance Spectroscopy and Hyperspectral Detection of Rare Earth Element. Spectrosc. Spectr. Anal. 2018, 38, 3801–3808. [Google Scholar]
- Koerting, F.; Koellner, N.; Kuras, A.; Boesche, N.K.; Rogass, C.; Mielke, C.; Elger, K.; Altenberger, U. A solar optical hyperspectral library of rare-earth-bearing minerals, rare-earth oxide powders, copper-bearing minerals and Apliki mine surface samples. Earth Syst. Sci. Data 2021, 13, 923–942. [Google Scholar] [CrossRef]
- Bi, D.; Shi, X.; Huang, M.; Yu, M.; Zhou, T.; Zhang, Y.; Zhu, A.; Shi, M.; Fang, X. Geochemical and mineralogical characteristics of deep-sea sediments from the western North Pacific Ocean: Constraints on the enrichment processes of rare earth elements. Ore Geol. Rev. 2021, 138, 104318. [Google Scholar] [CrossRef]
- Li, J.; Sun, C.; Jiang, F.; Gao, F.; Zheng, Y. Distribution pattern and geochemical analysis of rare earth elements in deep-ocean sediments. J. Oceanol. Limnol. 2021, 39, 79–88. [Google Scholar] [CrossRef]
- Feng, X.; Chen, H.; Chen, Y.; Zhang, C.; Liu, X.; Weng, H.; Xiao, S.; Nie, P.; He, Y. Rapid detection of cadmium and its distribution in Miscanthus sacchariflorus based on visible and near-infrared hyperspectral imaging. Sci. Total Environ. 2019, 659, 1021–1031. [Google Scholar] [CrossRef] [PubMed]
- Dai, X.; Wang, Z.; Liu, S.; Yao, Y.; Zhao, R.; Xiang, T.; Fu, T.; Feng, H.; Xiao, L.; Yang, X.; et al. Hyperspectral imagery reveals large spatial variations of heavy metal content in agricultural soil—A case study of remote-sensing inversion based on Orbita Hyperspectral Satellites (OHS) imagery. J. Clean. Prod. 2022, 380, 134878. [Google Scholar] [CrossRef]
- Xu, M.; Wu, S.; Zhou, S.; Liao, F.; Ma, C.; Zhu, C. Hyperspectral reflectance models for retrieving heavy metal content: Application in the archaeological soil. J. Infrared Millim. Waves 2012, 30, 109–114. [Google Scholar] [CrossRef]
- Jeong, Y.S.; Yu, J.; Wang, L.; Lee, K.-J. Bulk scanning method of a heavy metal concentration in tailings of a gold mine using SWIR hyperspectral imaging system. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102382. [Google Scholar] [CrossRef]
- Priester, M.; Ericsson, M.; Dolega, P.; Löf, O. Mineral grades: An important indicator for environmental impact of mineral exploitation. Miner. Econ. 2019, 32, 49–73. [Google Scholar] [CrossRef]
- Rosera, J.M.; Lederer, G.W.; Schuenemeyer, J.H. Statistical approaches for modeling correlated grade and tonnage distributions and applications for mineral resource assessments. Appl. Comput. Geosci. 2025, 26, 100240. [Google Scholar] [CrossRef]
- Neave, D.A.; Black, M.; Riley, T.R.; Gibson, S.A.; Ferrier, G.; Wall, F.; Broom-Fendley, S. On the Feasibility of Imaging Carbonatite-Hosted Rare Earth Element Deposits Using Remote Sensing. Econ. Geol. 2016, 111, 641–665. [Google Scholar] [CrossRef]

| Max | Min | Mean | SD | C.V./% | |
|---|---|---|---|---|---|
| La | 67.10 | 11.67 | 27.29 | 11.90 | 0.44 |
| Ce | 158.23 | 23.78 | 58.37 | 30.57 | 0.52 |
| Pr | 14.46 | 2.94 | 6.25 | 2.44 | 0.39 |
| Nd | 50.36 | 11.82 | 23.35 | 8.12 | 0.35 |
| Sm | 8.59 | 2.40 | 4.33 | 1.32 | 0.31 |
| Eu | 1.89 | 0.55 | 1.01 | 0.29 | 0.29 |
| Gd | 7.66 | 2.15 | 3.89 | 1.18 | 0.30 |
| Tb | 1.07 | 0.29 | 0.59 | 0.17 | 0.28 |
| Dy | 5.68 | 1.49 | 3.40 | 0.95 | 0.28 |
| Ho | 1.01 | 0.27 | 0.66 | 0.18 | 0.27 |
| Er | 2.88 | 0.79 | 1.89 | 0.51 | 0.27 |
| Tm | 0.43 | 0.11 | 0.29 | 0.08 | 0.28 |
| Yb | 2.72 | 0.73 | 1.87 | 0.51 | 0.27 |
| Lu | 0.43 | 0.12 | 0.29 | 0.08 | 0.28 |
| Sc | 17.19 | 3.29 | 8.88 | 2.81 | 0.32 |
| Y | 27.79 | 7.43 | 18.31 | 4.90 | 0.27 |
| REEs | 367.36 | 77.61 | 160.67 | 63.16 | 0.39 |
| Element | RMSE | RPD | MAPE | Method | Model | |
|---|---|---|---|---|---|---|
| La | 0.81 | 2.35 | 16.26% | TLOG-FD | MLP | |
| Ce | 0.76 | 2.11 | 21.72% | TLOG-FD | MLP | |
| 0.81 | 2.33 | 20.53% | LOG-FD | MLP | ||
| Pr | 0.62 | 1.66 | 18.62% | TLOG-FD | MLP | |
| 0.64 | 1.72 | 18.37% | TLOG-FD | SVR | ||
| Nd | 0.67 | 1.79 | 16.97% | TLOG-FD | MLP | |
| Sm | 0.59 | 1.61 | 17.03% | TLOG-FD | MLP | |
| Eu | 0.60 | 1.62 | 14.17% | TLOG-FD | MLP | |
| 0.71 | 1.89 | 13.67% | LOG-FD | SVR | ||
| Gd | 0.63 | 1.70 | 16.09% | TLOG-FD | MLP | |
| Tb | 0.67 | 1.73 | 14.14% | MSC | XGBoost | |
| Dy | 0.53 | 1.51 | 17.25% | MSC | RF | |
| Ho | 0.40 | 1.32 | 19.90% | MSC | SVR | |
| Er | 0.38 | 1.30 | 21.55% | MSC | MLP | |
| Tm | 0.15 | 1.09 | 24.74% | FD | XGBoost | |
| Yb | 0.37 | 1.30 | 18.61% | MSC | XGBoost | |
| Lu | 0.40 | 1.32 | 21.46% | LOG-FD | MLP | |
| Sc | 0.65 | 1.73 | 19.50% | MSC | MLP | |
| Y | 0.43 | 1.33 | 19.04% | MSC | XGBoost | |
| REEs | 0.73 | 1.97 | 18.14% | TLOG-FD | SVR | |
| 0.67 | 1.79 | 18.05% | TLOG-FD | MLP |
| Element | Number of Characteristic Bands | Element | Number of Characteristic Bands |
|---|---|---|---|
| La | 15 | Dy | 11 |
| Ce | 13 | Ho | 11 |
| Pr | 17 | Er | 9 |
| Nd | 7 | Tm | 4 |
| Sm | 12 | Yb | 12 |
| Eu | 13 | Lu | 4 |
| Gd | 22 | Sc | 18 |
| Tb | 22 | Y | 8 |
| REEs | 19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, D.; Yan, S.; Yang, G.; Ye, J.; Yuan, C.; Huang, M.; Luo, Y.; Hao, Y.; Zhang, Y.; Liu, X.; et al. Estimating Content of Rare Earth Elements in Marine Sediments Using Hyperspectral Technology: Experiment and Method Series. Minerals 2025, 15, 1102. https://doi.org/10.3390/min15111102
Liu D, Yan S, Yang G, Ye J, Yuan C, Huang M, Luo Y, Hao Y, Zhang Y, Liu X, et al. Estimating Content of Rare Earth Elements in Marine Sediments Using Hyperspectral Technology: Experiment and Method Series. Minerals. 2025; 15(11):1102. https://doi.org/10.3390/min15111102
Chicago/Turabian StyleLiu, Dalong, Shijuan Yan, Gang Yang, Jun Ye, Chunhui Yuan, Mu Huang, Yiping Luo, Yue Hao, Yuxue Zhang, Xiaofeng Liu, and et al. 2025. "Estimating Content of Rare Earth Elements in Marine Sediments Using Hyperspectral Technology: Experiment and Method Series" Minerals 15, no. 11: 1102. https://doi.org/10.3390/min15111102
APA StyleLiu, D., Yan, S., Yang, G., Ye, J., Yuan, C., Huang, M., Luo, Y., Hao, Y., Zhang, Y., Liu, X., Ren, X., Chen, Z., & Du, D. (2025). Estimating Content of Rare Earth Elements in Marine Sediments Using Hyperspectral Technology: Experiment and Method Series. Minerals, 15(11), 1102. https://doi.org/10.3390/min15111102







