A Comparative Study of Gold Leaching Kinetics Using Alternative Reagents from Concentrates of Low-Grade Ores
Abstract
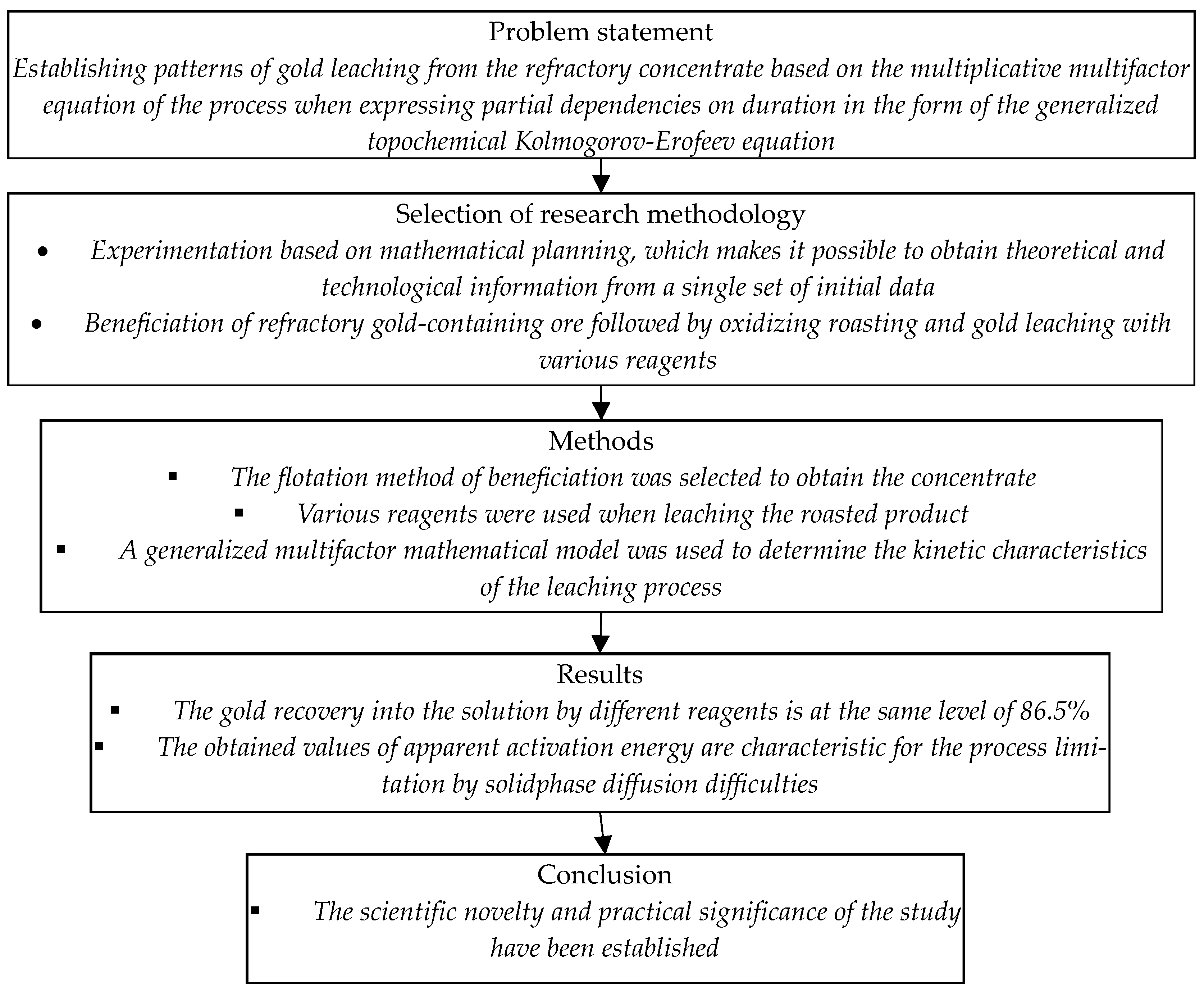
1. Introduction
- Ensuring the safety of operating personnel;
- Cyanide neutralization in the tailings;
- Environmental requirements for cyanide waste disposal.
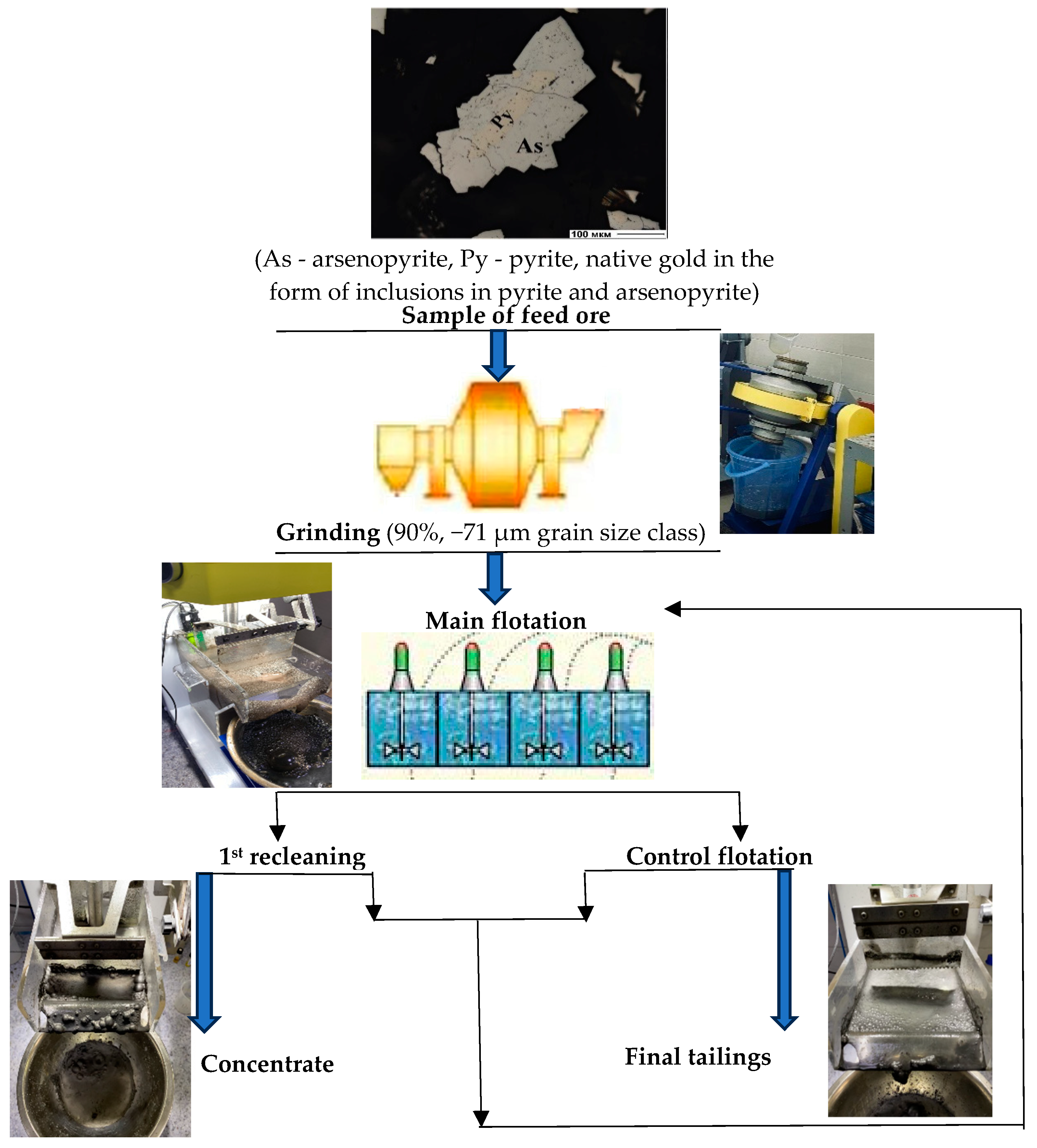
2. Materials and Methods
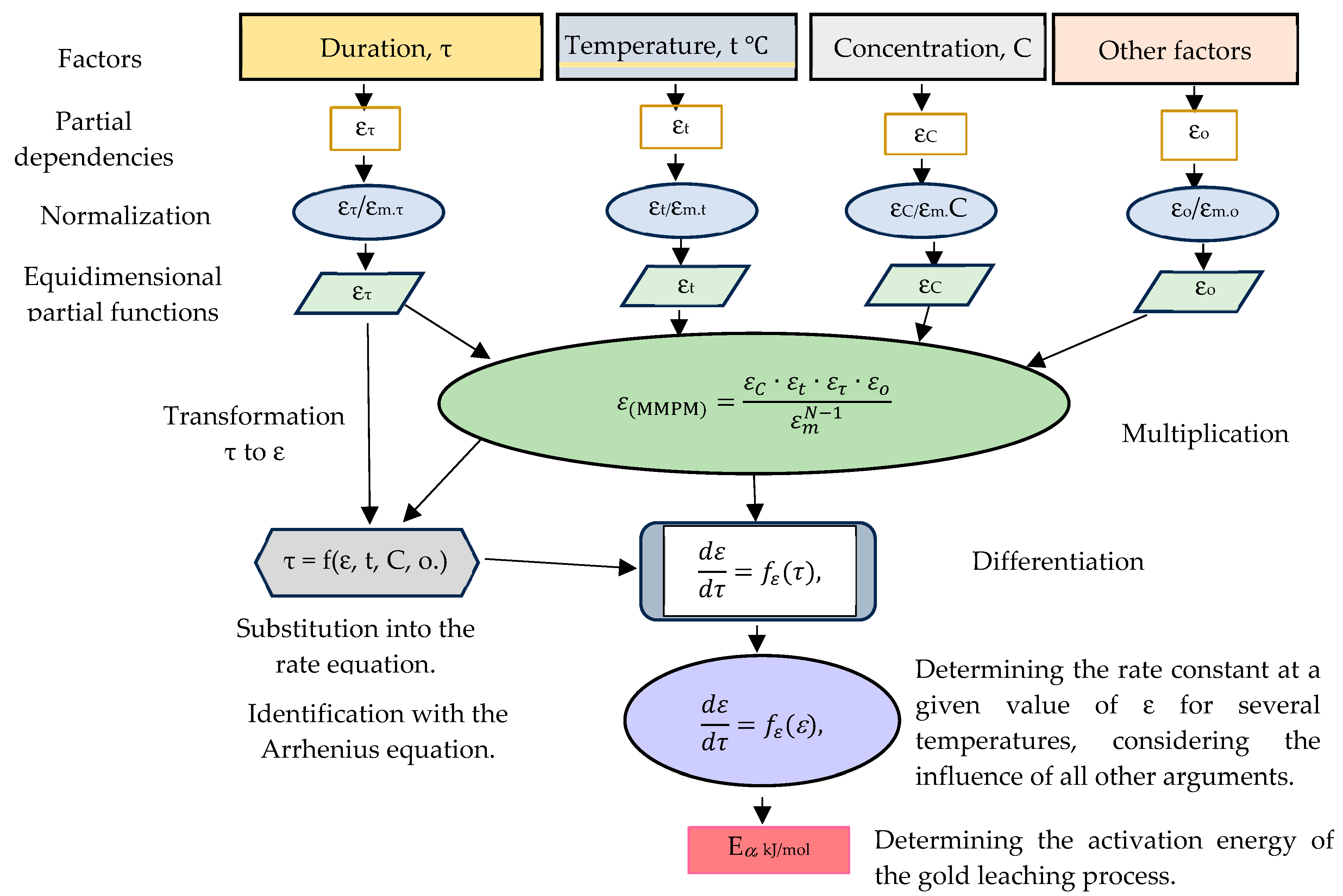
- Factors are selected in the experiment;
- Their partial dependencies and R(6) and tR(7) are found;
- They are entered into the multiplicative model;
- Under the experimental conditions for obtaining each factor, the dependence of this factor is calculated as a part of the multiplicative model, and is directly compared with the experimental results for R and tR:
- From the topochemical kinetics of the Kolmogorov–Erofeev equation, the dependence of the duration on all other factors was released (excluded), with the subsequent introduction of the rate (the partial derivative of τ) into the equation instead of the duration. From these analytical procedures, the dependence of the process rate on the degree of transformation was determined.
- The apparent activation energy is calculated under the temperature variation using the Arrhenius equation.
3. Results and Discussion
4. Conclusions
4.1. Implications and Explanation of the Findings
4.2. Strengths and Limitations of the Study
4.3. Recommendations and Next Steps
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Clary, R.; DiNuzzo, P.; Hunter, T.; Varghese, S. Making the Right Selection: A Comparative Analysis for the Treatment of Refractory Gold Concentrates. In The Minerals, Metals & Materials Series; Springer: Berlin/Heidelberg, Germany, 2018; pp. 1327–1338. [Google Scholar] [CrossRef]
- Grigoreva, V.A.; Boduen, A.Y. Prospects for Refractory Gold-Sulfide Ore Processing. Izv. Non-Ferr. Metall. 2024, 6, 22–34. [Google Scholar] [CrossRef]
- Çelik, H.; Mordoğan, H.; İpekoğlu, Ü. Siyanürlü Altin Üretim Tesisi Atiklarini Aritma Yöntemleri. Bilimsel Madencilik Derg. 1997, 36, 33–46. [Google Scholar]
- Yessengarayev, Y.; Baimbetov, B.S.; Mamyachenkov, S.V.; Surimbayev, B.N.; Prozor, N.G. Study of the Process of Cyanide Leaching of Gold Using Sodium Acetate at Different Ore Sizes. Kompleks. Ispolz. Miner. Syra = Complex Use Miner. Resour. 2020, 312, 59–68. [Google Scholar] [CrossRef]
- Kholov, K.I.; Sharifboev, N.T.; Samikhov, S.R.; Dzhurakulov, S.R.; Zarifova, M.S. Gold Leaching by Various Solutions, Alternative of Cyanide and Their Prospects in the Future. J. Sib. Fed. Univ. Eng. Technol. 2021, 14, 433–447. [Google Scholar] [CrossRef]
- Chan, J. Environmental-Friendly Gold Dressing Agent. Available online: http://www.gxshgk.com/senhe_en/index.php/content/index/pid/15.html (accessed on 6 June 2024).
- Beyuo, M.; Abaka-Wood, G.B.; Asamoah, R.K.; Kabenlah, A.; Amankwah, R.K. A Comparative Study of Sodium Cyanide and Jinchan TM Leaching Reagents: A Case Study at Goldfields Ghana Limited. In Proceedings of the 4th UMaT Biennial International Mining and Mineral Conference, Tarkwa, Ghana, 3–6 July 2016; pp. 195–199. [Google Scholar]
- Guangxi Senhe Hi-Tech. Available online: https://jinchan.en.ecplaza.net/ (accessed on 6 June 2024).
- Guo, X.-Y.; Liu, Z.-W.; Tian, Q.-H.; Li, D.; Zhang, L. Gold Extraction from Carlin-Type Concentrate by a Novel Environmentally Friendly Lixiviant. Hydrometallurgy 2022, 211, 105884. [Google Scholar] [CrossRef]
- Bayat, O.; Vapur, H.; Akyol, F.; Poole, C. Effects of Oxidising Agents on Dissolution of Gumuskoy Silver Ore in Cyanide Solution. Miner. Eng. 2003, 16, 395–398. [Google Scholar] [CrossRef]
- Dai, X.; Jeffrey, M.I. The Effect of Sulfide Minerals on the Leaching of Gold in Aerated Cyanide Solutions. Hydrometallurgy 2006, 82, 118–125. [Google Scholar] [CrossRef]
- Nunan, T.O.; Viana, I.L.; Peixoto, G.C.; Ernesto, H.; Verster, D.M.; Pereira, J.H.; Bonfatti, J.M.; Teixeira, L.A.C. Improvements in Gold Ore Cyanidation by Pre-Oxidation with Hydrogen Peroxide. Miner. Eng. 2017, 108, 67–70. [Google Scholar] [CrossRef]
- Gurov, V.A.; Dorofeev, Y.N.; Koltsov, V.Y.; Snigir, A.N. Ecologically Pure of Extraction of Noble Metals from Materials Containing Such Metals. Google Patent RU 2167211 C1, 20 May 2001. (In Russian). [Google Scholar]
- Samsonov, A.S.; Kurochkina, I.A.; Polyakov, M.L. The Method of Extraction of Gold from Ores. Google Patent RU2275436C2, 27 April 2006. (In Russian). [Google Scholar]
- Chryssoulis, S.L.; McMullen, J. Mineralogical Investigation of Gold Ores. In Gold Ore Processing; Elsevier: Amsterdam, The Netherlands, 2016; pp. 57–93. [Google Scholar] [CrossRef]
- Evdokimov, A.V. Search for new reagent-accelerators intensifying the process of cyanidation. Bull. Irkutsk State Tech. Univ. 2010, 4, 139–143. [Google Scholar]
- Sorokin, I.P. An Investigation of Gold and Silver. Dissolution in Cyanic Solutions at Low Temperatures. Trudy VNII-1 Magadan 1958, 33, 13–79. (In Russian) [Google Scholar]
- Blokhin, N.N.; Fetodov, G.P.; Khmelevskaya, G.A.; Zabelsky, V.K.; Avargin, V.A. The Composition and Method for Leaching Gold. Google Patent RU2093672C1, 20 October 1997. (In Russian). [Google Scholar]
- Surimbayev, B.; Baikonurova, A.; Bolotova, L.; Mishra, B. Intensive Leaching of Gold from Gravity Concentrate at Low Concentration of Sodium Cyanide. Kompleks. Ispolz. Miner. Syra = Complex Use Miner. Resour. 2018, 307, 65–70. [Google Scholar] [CrossRef]
- Surimbayev, B.N.; Bolotova, L.S.; Shalgymbayev, S.T.; Baikonurova, A.O. Method of Processing Gold-Containing Gravity Concentrate. Google Patent No. 4536 (KZ), 17 January 2019. [Google Scholar]
- Surimbayev, B.N. Development of Technology for the Extraction of Gold from Sulphide Ores Using Reagent-Activator with Intensive Cyanidation. Ph.D. Thesis, Satbayev University, Almaty, Kazakhstan, 2018. (In Russian). [Google Scholar]
- Abubakriev, A.T.; Koizhanova, A.K.; Magomedov; Erdenova, M.B.; Abdyldaev, N.N. Leaching of Gold-Containing Ores with Application of Oxidation Activators. Kompleks. Ispolz. Miner. Syra = Complex Use Miner. Resour. 2019, 310, 10–15. [Google Scholar] [CrossRef]
- Kenzhaliyev, B.K. Innovative Technologies Providing Enhancement of Nonferrous, Precious, Rare and Rare Earth Metals Extraction. Kompleks. Ispolz. Miner. Syra = Complex Use Miner. Resour. 2019, 310, 64–75. [Google Scholar] [CrossRef]
- Surimbayev, B.; Bolotova, L.; Baikonurova, A.; Shalgymbayev, S. Application of acetic acid as a reagent-activator in intensive cyanidation of gravity concentrates. Kompleks. Ispolz. Miner. Syra = Complex Use Miner. Resour. 2019, 308, 83–88. [Google Scholar] [CrossRef]
- Surimbayev, B.; Bolotova, L.; Mishra, B.; Baikonurova, A. Intensive cyanidation of gold from gravity concentrates ina drum-type apparatus. NEWS Natl. Acad. Sci. Repub. Kazakhstan 2018, 431, 32–37. [Google Scholar] [CrossRef]
- McNulty, T. Cyanide substitutes. Min. Mag. 2001, 184, 256–261. [Google Scholar]
- Kurkov, A.V.; Anufrieva, S.I.; Sokolova, V.N.; Mamoshin, M.Y.; Likhnikevich, E.G.; Permyakova, N.A. Information and Analytical Materials: World Achievements in the Development of Methods, Techniques, and Technologies for Processing Mineral Raw Materials. Series: Hydrometallurgical and Geotechnological Processing of Mineral Raw Materials; VIMS: Moscow, Russia, 2020. (In Russian) [Google Scholar]
- Asamoah, R.K.; Zanin, M.; Gascooke, J.; Skinner, W.; Addai-Mensah, J. Refractory Gold Ores and Concentrates Part 1: Mineralogical and Physico-Chemical Characteristics. Miner. Process. Extr. Metall. Trans. Inst. Min. Metall. 2019, 130, 240–252. [Google Scholar] [CrossRef]
- Asamoah, R.K.; Skinner, W.; Addai-Mensah, J. Alkaline Cyanide Leaching of Refractory Gold Flotation Concentrates and Bio-Oxidised Products: The Effect of Process Variables. Hydrometallurgy 2018, 179, 79–93. [Google Scholar] [CrossRef]
- Sitando, O.; Senanayake, G.; Dai, X.; Breuer, P. The Adsorption of Gold(I) on Minerals and Activated Carbon (Preg-Robbing) in Non-Ammoniacal Thiosulfate Solutions—Effect of Calcium Thiosulfate, Silver(I), Copper(I) and Polythionate Ions. Hydrometallurgy 2018, 184, 206–217. [Google Scholar] [CrossRef]
- Gordeev, D.V.; Petrov, G.V.; Hasanov, A.V.; Severinova, O.V. Review of modern technologies for processing of refractory gold-containing ores and concentrates using nitric acid. Bull. Tomsk Polytech. Univ. Geo Assets Eng. 2022, 333, 214–223. [Google Scholar] [CrossRef]
- Rogozhnikov, D.A.; Dizer, O.A.; Karimov, K.A.; Zakharian, S.V. Nitric Acid Leaching of the Copper-Bearing Arsenic Sulphide Concentrate of Akzhal. Tsvetnye Met. 2020, 8, 11–17. [Google Scholar] [CrossRef]
- Abdullayevich, Y.A.; Tilovkabulovich, B.B.; Turdaliyevich, M.S.; Ilkhomjonovich, R.A.; Ilkhomjonovna, R.G. Improvement of Technology of Processing of Persistent Gold-Bearing Ores and Concentrates Using Oxidative Burning. Int. J. Eng. Adv. Technol. 2019, 9, 4793–4796. [Google Scholar] [CrossRef]
- Tolibov, B.I. Research of the process of oxidative firing of gold-containing sulfide materials for the development of optimal. Eurasian Union Sci. 2020, 4, 41–49. [Google Scholar] [CrossRef]
- Karimova, L.M.; Oleinikova, T.O.; Mansurov, B.E.; Saganbek, S. Oxidizing Roasting and Cyanidation for the Processing of Refractory Gold Concentrates. Obogashchenie Rud 2023, 3, 10–15. [Google Scholar] [CrossRef]
- Ljubetic, K.; Liu, W. Kinetic Limitations of Gold Leaching in Ferric Chloride Media Part I: Batch Reactor Studies. Miner. Eng. 2022, 178, 107397. [Google Scholar] [CrossRef]
- Deschênes, G. Advances in the Cyanidation of Gold. In Developments in Mineral Processing; Elsevier: Amsterdam, The Netherlands, 2005; pp. 479–500. [Google Scholar] [CrossRef]
- Cheremisina, O.; Vasiliev, R.; Fedorov, A. Effect of Potassium Salt Addition on Silver Precipitation during Hydrothermal Synthesis of Argentojarosites. Metals 2024, 15, 24. [Google Scholar] [CrossRef]
- Karimova, L.M.; Korabaev, A.S.; Oleinikova, T.O.; Terent’eva, I.V.; Magaz, A.M. Studying the Process of Gold Leaching after the Oxidative Roasting of a Refractory Gold-Bearing Concentrate. Theor. Found. Chem. Eng. 2024, 58, 444–449. [Google Scholar] [CrossRef]
- Musayev, V.V.; Klyushnikov, A.M.; Galimov, R.R. Study on the Extraction of Metals from Tails of Flotation Enrichment of Copper Sulfide Ores. Butlerov Commun. 2019, 57, 50–59. [Google Scholar] [CrossRef]
- Boldyrev, A.V.; Balikov, S.V.; Yemelianov, Y.E.; Kopylova, N.V.; Nikolaev, Y.L.; Posedko, E.Y. Comparative evaluation of various processing methods for refractory gold-sulphide flotation concentrate. Ipolytech J. 2017, 21, 161–170. [Google Scholar] [CrossRef]
- Yılmaz, H.; Sayın, Z.E. Sodyum Siyanür ve Jin Chan Kimyasallarının Cevherden Altın Kazanımına Etkisi. J. Polytech. 2023, 27, 1387–1397. [Google Scholar] [CrossRef]
- Karimova, L.M.; Terentyeva, I.V.; Oleinikova, T.O.; Magaz, A.A. Research on hydrometallurgical processing of dump silver-containing tailings. Izv. Vyss. Uchebnykh Zaved. Khimiya Khimicheskaya Tekhnologiya 2023, 66, 101–110. [Google Scholar] [CrossRef]
- Malyshev, V.P.; Makasheva, A.M.; Bekturganov, N.S.; Kazhikenova, S.S. Probabilistic and deterministic mapping as a natural-scientific basis for understanding, creation and management of technological processes. In Proceedings of the International Scientific and Practical Conference “Innovations in the field of natural sciences as a basis for export-oriented industrialization of Kazakhstan”, Almaty, Kazakhstan, 4–5 April 2019; pp. 387–392. (In Russian). [Google Scholar]
- Malyshev, V.P. Kinetic and technological analysis of generalizing mathematical models of chemical-metallurgical processes. Rep. Natl. Acad. Sci. Repub. Kazakhstan 2008, 2, 13–18. (In Russian) [Google Scholar]
- Cheremisina, O.V.; Vasiliev, R.E.; Netrusov, A.O.; Ter-Oganesyants, A.K. Hot Curing and Lime Boiling of High-Arsenic Copper Concentrate Pressure Oxidation Product and Their Effect on Precious Metals Recovery during Subsequent Cyanidation. Tsvetnye Met. 2024, 2, 19–26. [Google Scholar] [CrossRef]
- Yussupov, K.; Aben, E.; Akhmetkanov, D.; Abenk, K.; Yussupova, S. Investigation of the Solid Oxidizer Effect on the Metal Geotechnology Efficiency. Min. Miner. Depos. 2023, 17, 12–17. [Google Scholar] [CrossRef]
- Nie, Y.; Chen, J.; Wang, Q.; Zhang, C.; Shi, C.; Zhao, J. Use of Dry Grinding Process to Increase the Leaching of Gold from a Roasted Concentrate Containing Hematite in the Thiosulfate System. Hydrometallurgy 2021, 201, 105582. [Google Scholar] [CrossRef]
- Fedotov, P.K.; Senchenko, A.E.; Fedotov, K.V.; Burdonov, A.E. Hydrometallurgical Processing of Gold-Containing Ore and Its Enrichment Products. Metallurgist 2021, 65, 214–227. [Google Scholar] [CrossRef]
- Zavyalov, S.S.; Mamonov, R.S. Mixed-Type Dry Pretreatment Technology for Gold-Bearing Ore. Min. Informational Anal. Bull. 2021, 11, 338–345. [Google Scholar] [CrossRef]
- Karimova, L.; Makasheva, G.; Malyshev, V.; Kharchenko, Y.; Kairalapov, Y. Permissible Extrapolation Justification of the Multiplicative Multifactorial Model and Its Application to the White Soot Production Technology. HighTech Innov. J. 2024, 5, 663–676. [Google Scholar] [CrossRef]
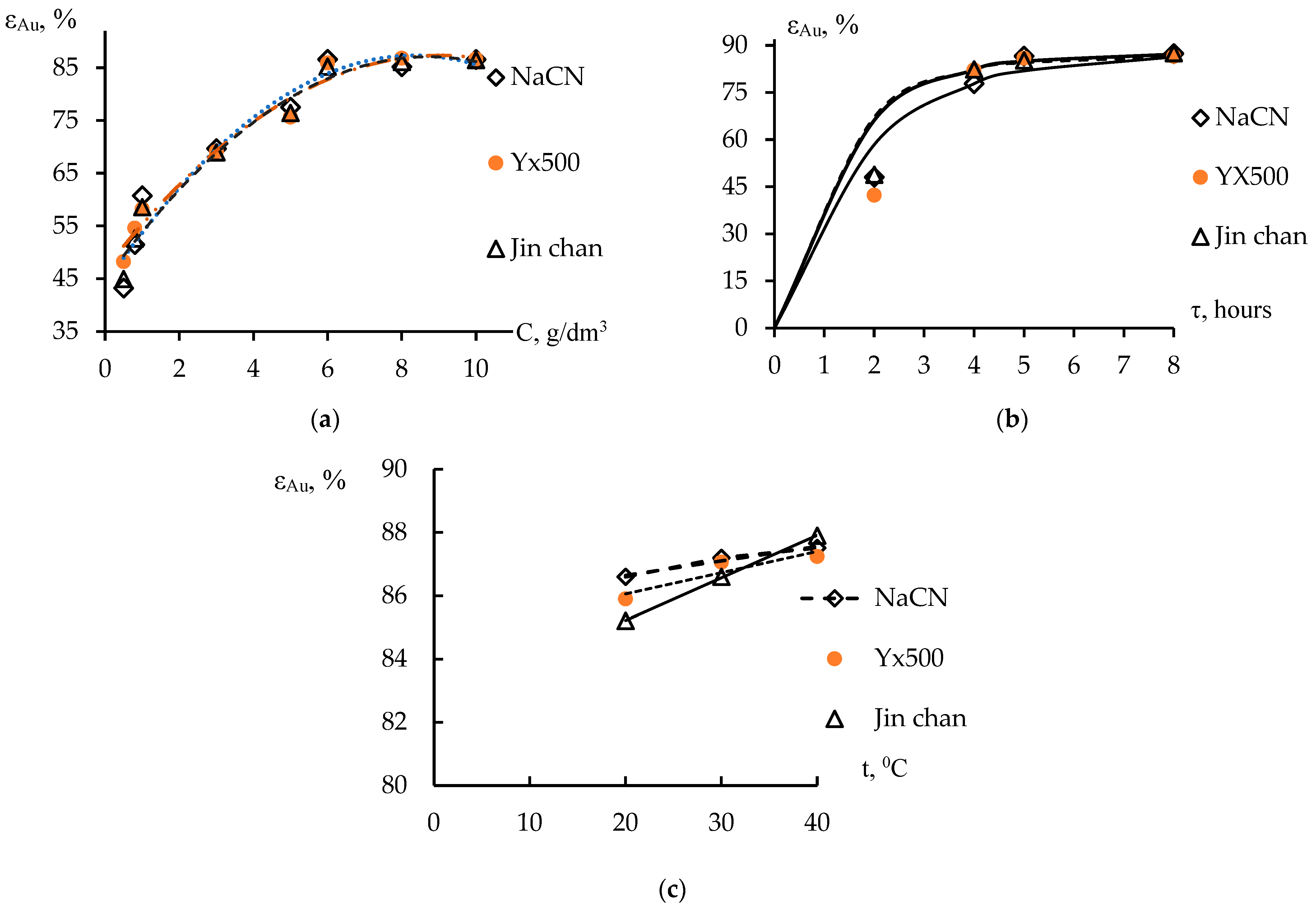
| Process and Basic Principles | Au and Ag Recovery, % | |
|---|---|---|
| Oxidizing roasting | ||
| Oxidation of S, As, and C in the concentrate; the destruction of the mineral structure that includes gold. | Leaching using Jinchan and NaCN for 4 h | 88.5 [39]; 88.7 [35,39]. |
| Roasting in a multiple hearth furnace at 550–600 °C. | NaCN—at a concentration of 2 g/L and a specific consumption of 0.83 kg/t of pyrite concentrate; L:S = 2:1, for 2 h. | 78.05; throughout recovery into the marketable product—66% [40]. |
| Roasting in two stages: (1) At 300–400 °C with restricted access to air (dearsenization); (2) At 450–550 °C with access to air, with a stirring of the material (desulfurization). | Cinder cyanidation at a concentration of 1.5 g/L for 24 h at a NaCN consumption of 1.7 kg/t. | 92.6 [41]. |
| Hydrometallurgical methods | ||
| Leaching of Kaimaz ore under the conditions: L:S = 0.4, concentration −300 mg/L, Jinchan consumption—1.27 kg/t and NaCN—0.95 kg/t. | Jinchan NaCN | 81.55; 82.86 [42]. |
| Leaching of 150 μm grain size ore at 80% yield. | NaCN Jinchan | 97.31; 90.30 [7]. |
| Ag leaching from waste copper tailings with Ag content of 1.7 g/t (specific consumption—0.9 kg/t tailings). | NaCN Jinchan | Ag −72.416; Ag −72.372 [43]. |
| YX 500 | Jinchan | ||
|---|---|---|---|
| Chemical Formula | Content, % | Chemical Formula | Content, % |
| Na2CO3 | 16.3 | Na2CO3 | 45.1 |
| NaCN | 66.6 | NaCN | 41.7 |
| Na2SO4 | 7.0 | NaCNO | 13.2 |
| NaCNO | 10.1 | ||
| NaCN | YX500 | Jinchan | |||
|---|---|---|---|---|---|
| Symbol | Weight % | Symbol | Weight % | Symbol | Weight % |
| Na | 46.9 | Na | 44.18 | Na | 43.82 |
| C | 24.5 | C | 20.02 | C | 17.75 |
| N | 28.6 | N | 21.20 | N | 14.76 |
| O | 13.02 | O | 23.67 | ||
| S | 1.58 | ||||
| Component | Au, g/t | Ag, g/t | Cu | Pb | Zn | Fe | P | Mo | As |
|---|---|---|---|---|---|---|---|---|---|
| Weight % | 0.38 | 0.15 | 0.012 | 0.006 | 0.01 | 4.60 | 0.087 | 0.0001 | 0.08 |
| Component | Sn | Sb | Bi | Cd | SiO2 | Al2O3 | CaO | C | S total |
| Weight % | - | 0.0015 | - | 0.0002 | 62.80 | 15.70 | 3.64 | 4.17 | 0.51 |
| Operation | Content of −0.071 mm Grain Size Class, % | Time, min | pH | Consumption of Reagents, g/t | ||
|---|---|---|---|---|---|---|
| CuSO4 | Kx | T-92 | ||||
| Grinding | 90 | - | - | - | - | - |
| 1st main flotation | - | 10 | 8.5 | 80 | 65 | 20 |
| Control flotation | - | 10 | - | 60 | 25 | 5 |
| 1st recleaning | - | 4 | - | - | - | - |
| Products | Output, % | Au Content, g/t | Au Recovery, % |
|---|---|---|---|
| Concentrate of the 1st recleaning | 5.82 | 5.3 | 81.40 |
| Tailings | 94.18 | 0.075 | 18.60 |
| Initial ore sample | 100.0 | 0.38 | 100.0 |
| Material | Chemical Formula | Content, % |
|---|---|---|
| Quartz | SiO2 | 37.1 |
| Albite | K[AlSi3O8] | 41 |
| Hematite | Fe2O3 | 6.7 |
| Calcium sulfate | CaSO4 | 15.2 |
| Total | 100 |
| Reagent | Functions | tR > 2 | R |
|---|---|---|---|
| NaCN | 36.280 | 0.9668 | |
| 6.598 | 0.8985 | ||
| 29.380 | 0.9372 | ||
| YX500 | 84.755 | 0.9856 | |
| 2.160 | 0.7249 | ||
| 4.865 | 0.7244 | ||
| Jinchan | 67.545 | 0.9820 | |
| 2.298 | 0.7386 | ||
| 498.00 | 0.9960 |
| Given | Reagent | t, °C | E, kJ/mol | Given | Reagent | t, °C | E, kJ/mol | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 40 | NaCN | 20 | 27.628 | 3.319 | 0.718 | 80 | NaCN | 20 | 5.5402 | 1.712 | 3.454 |
| 30 | 27.891 | 3.328 | 30 | 5.8030 | 1.758 | ||||||
| 40 | 28.154 | 3.337 | 40 | 6.0658 | 1.802 | ||||||
| YX500 | 20 | 34.837 | 3.550 | 1.090 | YX500 | 20 | 4.8451 | 1.578 | 7.225 | ||
| 30 | 35.342 | 3.565 | 30 | 5.3506 | 1.677 | ||||||
| 40 | 35.848 | 3.579 | 40 | 5.8560 | 1.767 | ||||||
| Jinchan | 20 | 33.110 | 3.499 | 2.167 | Jinchan | 20 | 4.8784 | 1.585 | 12.757 | ||
| 30 | 34.079 | 3.528 | 30 | 5.8473 | 1.766 | ||||||
| 40 | 35.048 | 3.556 | 40 | 6.8161 | 1.919 | ||||||
| 50 | NaCN | 20 | 22.106 | 3.096 | 0.895 | 85 | NaCN | 20 | 2.7792 | 1.022 | 6.604 |
| 30 | 22.369 | 3.107 | 30 | 3.0420 | 1.112 | ||||||
| 40 | 22.632 | 3.119 | 40 | 3.3048 | 1.195 | ||||||
| YX500 | 20 | 27.339 | 3.308 | 1.383 | YX500 | 20 | 1.0961 | 0.092 | 24.948 | ||
| 30 | 27.844 | 3.326 | 30 | 1.6016 | 0.471 | ||||||
| 40 | 28.350 | 3.345 | 40 | 2.1070 | 0.745 | ||||||
| Jinchan | 20 | 26.052 | 3.260 | 2.734 | Jinchan | 20 | 1.3494 | 0.299 | 34.010 | ||
| 30 | 27.021 | 3.297 | 30 | 2.3183 | 0.841 | ||||||
| 40 | 27.990 | 3.332 | 40 | 3.2871 | 1.190 | ||||||
| 60 | NaCN | 20 | 16.584 | 2.808 | 1.189 | 86.5 | NaCN | 20 | 1.9509 | 0.668 | 9.097 |
| 30 | 16.847 | 2.824 | 30 | 2.2137 | 0.795 | ||||||
| 40 | 17.110 | 2.839 | 40 | 2.4765 | 0.907 | ||||||
| YX500 | 20 | 19.841 | 2.988 | 1.894 | YX500 | 20 | −0.028 | - | - | ||
| 30 | 20.346 | 3.013 | 30 | 0.4769 | −0.740 | 56.980 | |||||
| 40 | 20.852 | 3.037 | 40 | 0.9823 | −0.018 | ||||||
| Jinchan | 20 | 18.994 | 2.944 | 3.702 | Jinchan | 20 | 0.2907 | −1.235 | 77.989 | ||
| 30 | 19.963 | 2.994 | 30 | 1.2596 | 0.2308 | ||||||
| 40 | 20.932 | 3.041 | 40 | 2.2284 | 0.801 | ||||||
| 70 | NaCN | 20 | 11.062 | 2.403 | 1.769 | ||||||
| 30 | 11.325 | 2.427 | |||||||||
| 40 | 11.588 | 2.450 | |||||||||
| YX500 | 20 | 12.343 | 2.513 | 3.000 | |||||||
| 30 | 12.848 | 2.553 | |||||||||
| 40 | 13.354 | 2.592 | |||||||||
| Jinchan | 20 | 11.936 | 2.479 | 5.735 | |||||||
| 30 | 12.905 | 2.557 | |||||||||
| 40 | 13.874 | 2.630 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malyshev, V.; Karimova, L.; Sagatbek, S.; Kharchenko, Y.; Magaz, A. A Comparative Study of Gold Leaching Kinetics Using Alternative Reagents from Concentrates of Low-Grade Ores. Minerals 2025, 15, 282. https://doi.org/10.3390/min15030282
Malyshev V, Karimova L, Sagatbek S, Kharchenko Y, Magaz A. A Comparative Study of Gold Leaching Kinetics Using Alternative Reagents from Concentrates of Low-Grade Ores. Minerals. 2025; 15(3):282. https://doi.org/10.3390/min15030282
Chicago/Turabian StyleMalyshev, Vitaliy, Lyutsiya Karimova, Sunkar Sagatbek, Yelena Kharchenko, and Adilet Magaz. 2025. "A Comparative Study of Gold Leaching Kinetics Using Alternative Reagents from Concentrates of Low-Grade Ores" Minerals 15, no. 3: 282. https://doi.org/10.3390/min15030282
APA StyleMalyshev, V., Karimova, L., Sagatbek, S., Kharchenko, Y., & Magaz, A. (2025). A Comparative Study of Gold Leaching Kinetics Using Alternative Reagents from Concentrates of Low-Grade Ores. Minerals, 15(3), 282. https://doi.org/10.3390/min15030282





