Comparative Study of Particle-Resolved and Point-Particle Simulations of Particle–Bubble Collisions in Homogeneous Isotropic Turbulence
Abstract
:1. Introduction
2. Materials and Methods
2.1. Point-Particle Method
2.2. Particle-Resolved Method
3. Results and Discussion
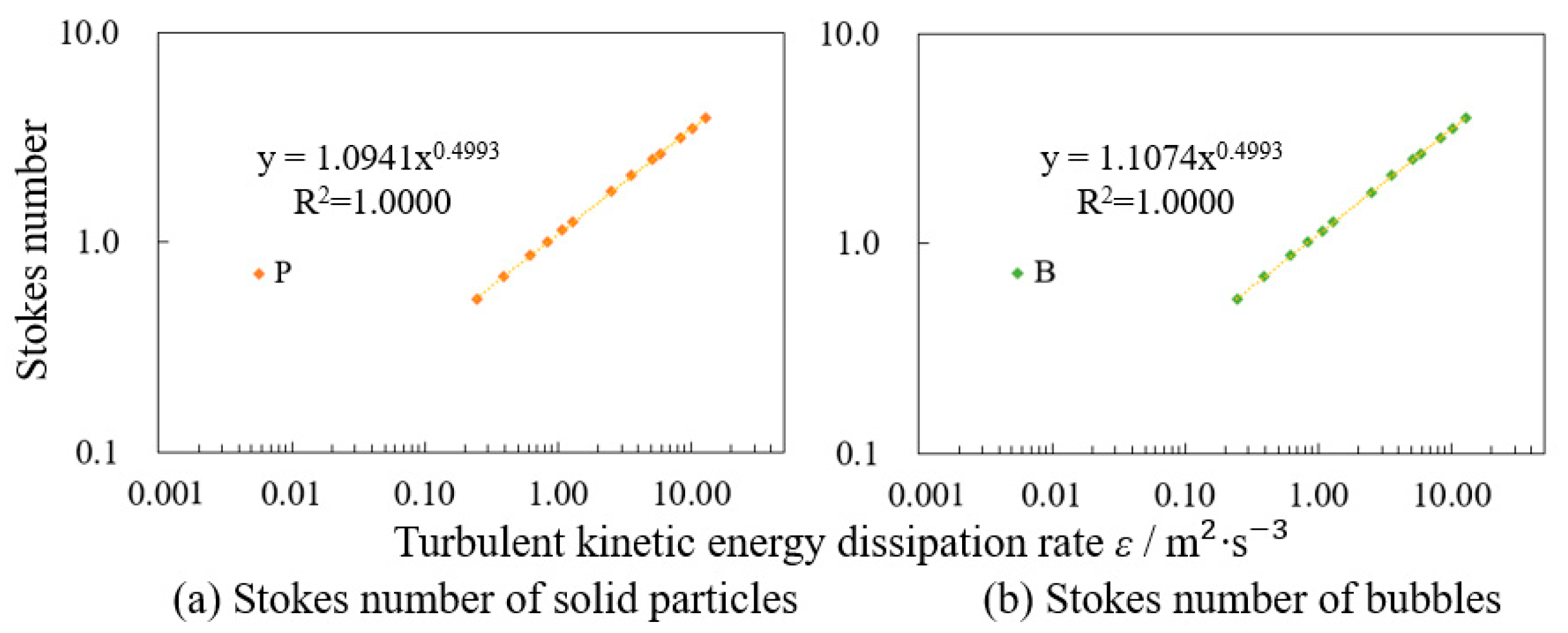
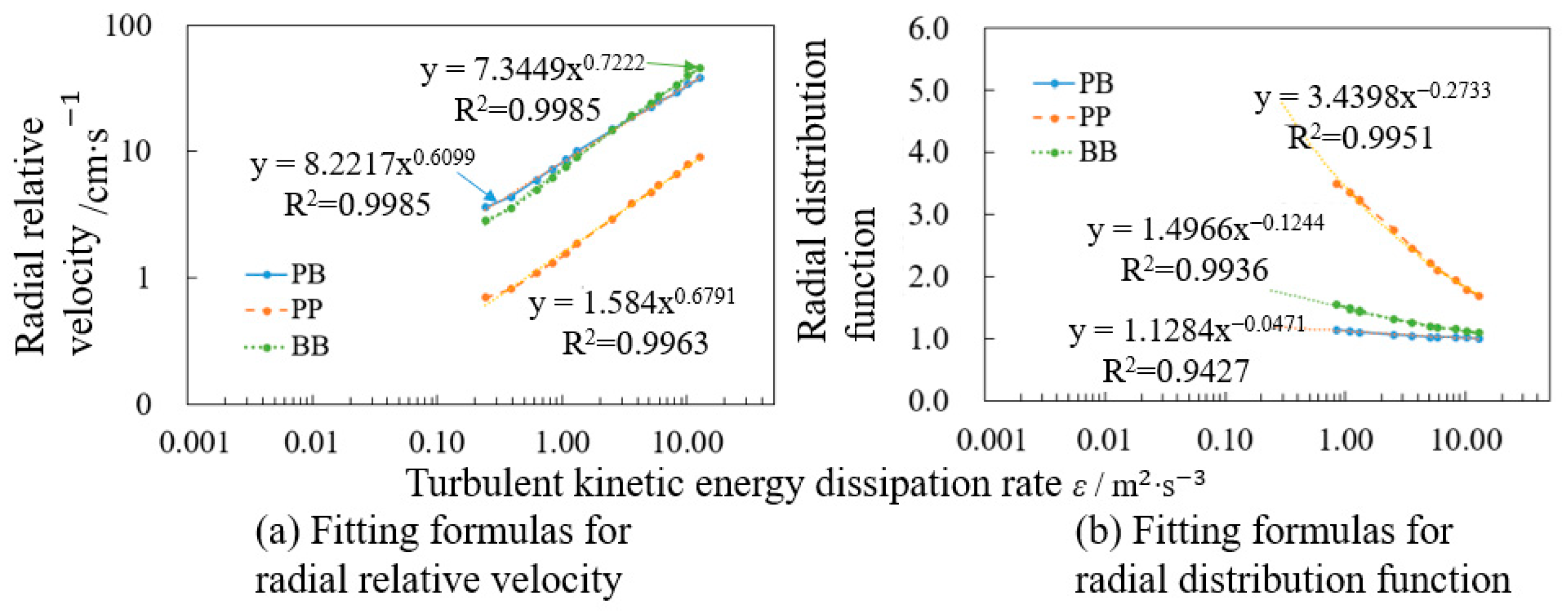
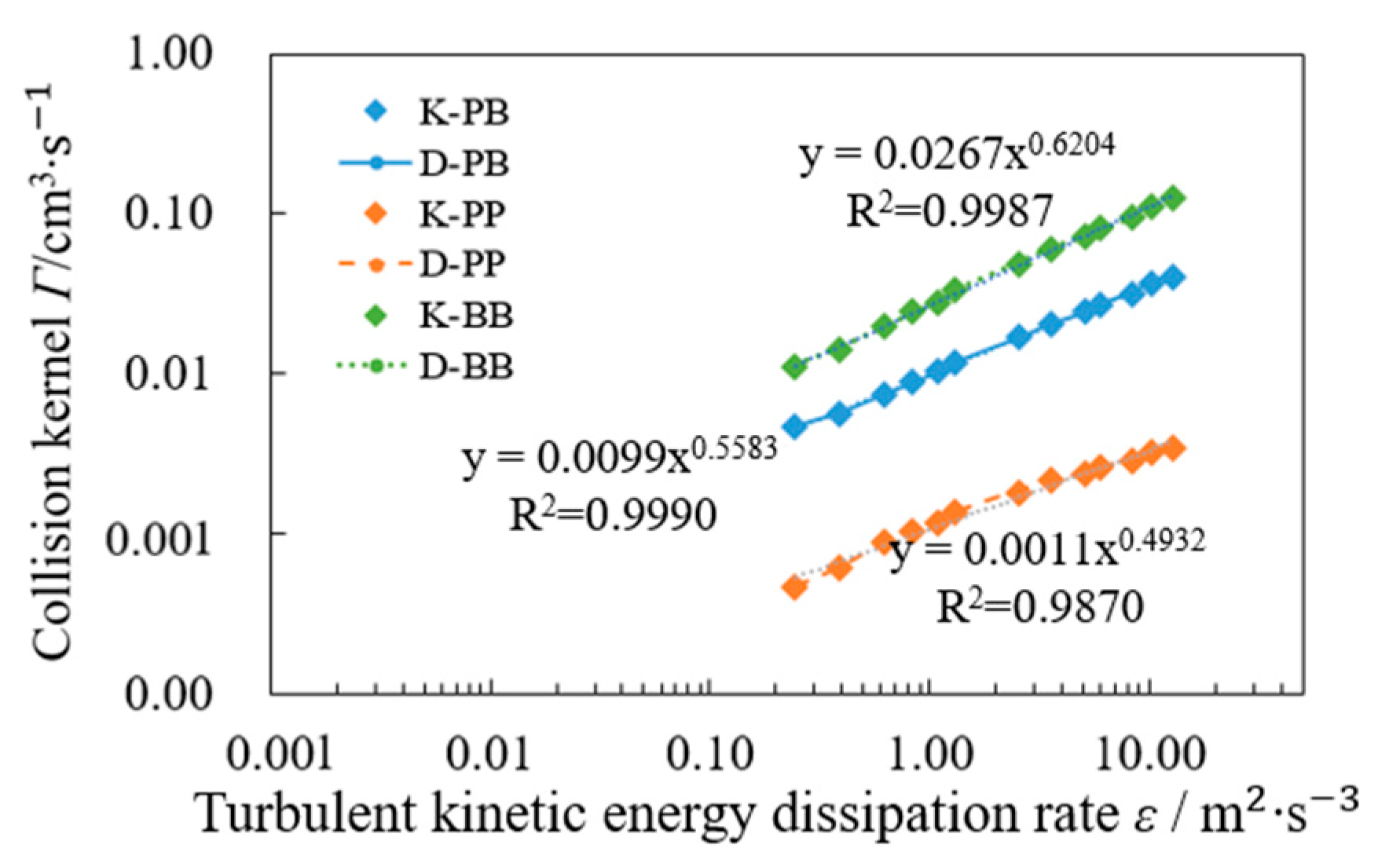
3.1. Fitting and Prediction of the Point-Particle Model
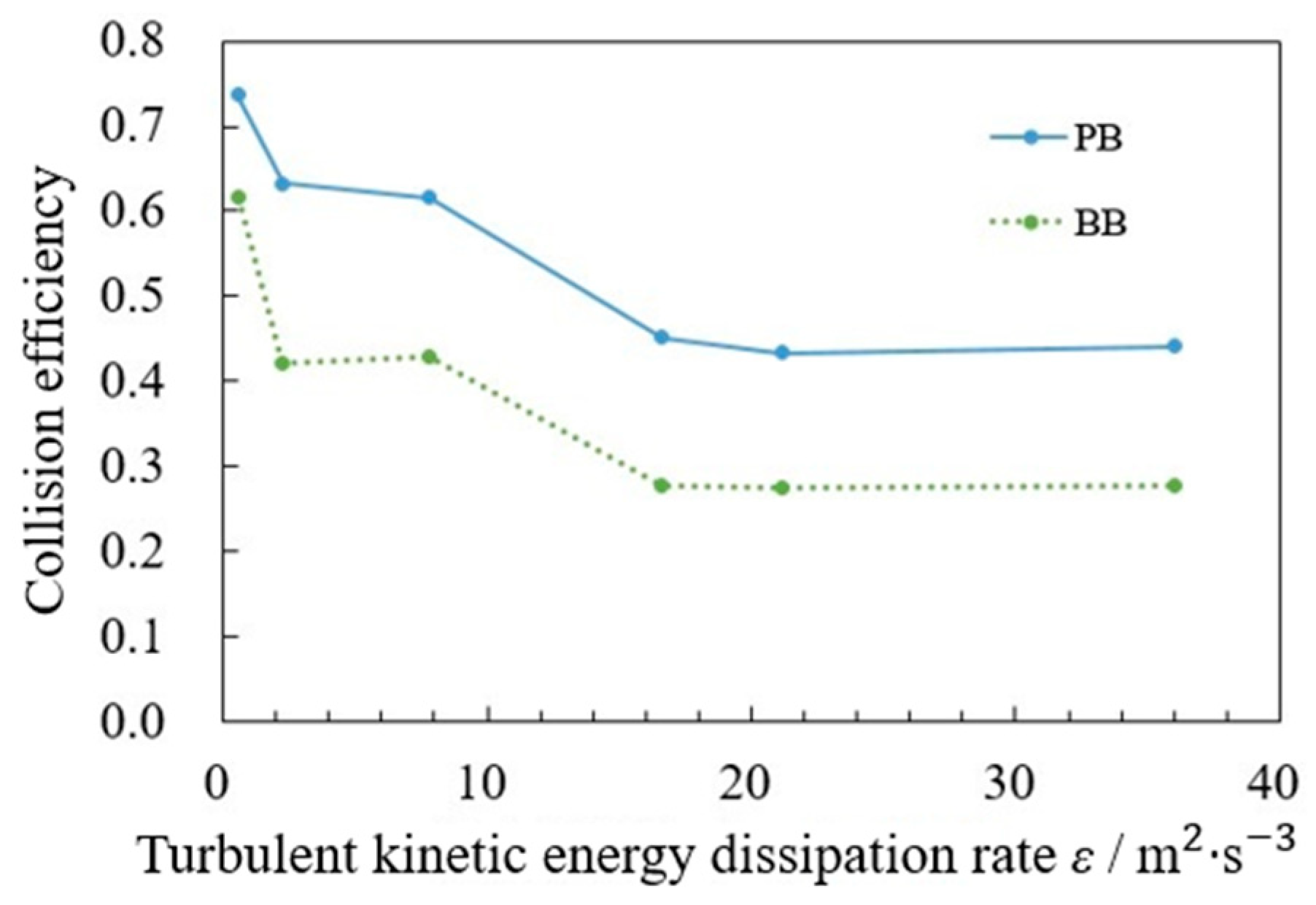
3.2. Comparison and Analysis of Results from the Two Models
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LBM | Lattice Boltzmann method |
| DNS | Direct numerical simulation |
| CFD | Computational fluid dynamics |
| HDI | Hydrodynamic interactions |
| PPS | Point-particle model |
| PRS | Fully resolved particle simulation |
References
- Schubert, H. On the turbulence-controlled microprocesses in flotation machines. Int. J. Miner. Process. 1999, 56, 257–276. [Google Scholar] [CrossRef]
- Saffman, P.G.; Turner, J.S. On the Collision of Drops in Turbulent Clouds. J. Fluid Mech. 1956, 1, 16–30. [Google Scholar] [CrossRef]
- Wang, L.-P.; Ayala, O.; Kasprzak, S.E.; Grabowski, W.W. Theoretical formulation of collision rate and collision efficiency of hydrodynamically interacting cloud droplets in turbulent atmosphere. J. Atmos. Sci. 2005, 62, 2433–2450. [Google Scholar] [CrossRef]
- Abrahamson, J. Collision rates of small particles in a vigorously turbulent fluid. Chem. Eng. Sci. 1975, 30, 1371–1379. [Google Scholar] [CrossRef]
- Meyer, C.J.; Deglon, D.A. Particle collision modeling—A review. Miner. Eng. 2011, 24, 719–730. [Google Scholar] [CrossRef]
- Dai, Z.; Fornasiero, D.; Ralston, J. Particle–bubble collision models—A review. Adv. Colloid Interface Sci. 2000, 85, 231–256. [Google Scholar] [CrossRef]
- Wang, G.; Ge, L.; Mitra, S.; Evans, G.M.; Joshi, J.; Chen, S. A review of CFD modelling studies on the flotation process. Miner. Eng. 2018, 127, 153–177. [Google Scholar] [CrossRef]
- Yao, N.; Liu, J.; Sun, X.; Liu, Y.; Chen, S.; Wang, G. A Rational Interpretation of the Role of Turbulence in Particle-Bubble Interactions. Minerals 2021, 11, 1006. [Google Scholar] [CrossRef]
- Yao, N.; Liu, J.; Sun, X.; Liu, Y.; Chen, S.; Wang, G. Estimation of turbulent dissipation rates and its implications for the particle-bubble interactions in flotation. Miner. Eng. 2023, 201, 108230. [Google Scholar] [CrossRef]
- Zhou, Y.; Wexler, A.S.; Wang, L.-P. On the collision rate of small particles in isotropic turbulence. II. Finite Inertia Case. Phys. Fluids 1998, 10, 1206–1216. [Google Scholar] [CrossRef]
- Wang, L.-P.; Wexler, A.S.; Zhou, Y. Statistical mechanical description and modelling of turbulent collision of inertial particles. J. Fluid Mech. 2000, 415, 117–153. [Google Scholar] [CrossRef]
- Maxey, M.R. The Gravitational Settling of Aerosol-Particles in Homogeneous Turbulence and Random Flow-Fields. J. Fluid Mech. 1987, 174, 441–465. [Google Scholar] [CrossRef]
- Maxey, M.R.; Corrsin, S. Gravitational Settling of Aerosol-Particles in Randomly Oriented Cellular-Flow Fields. J. Atmos. Sci. 1986, 43, 1112–1134. [Google Scholar] [CrossRef]
- Sundaram, S.; Collins, L.R. Collision statistics in an isotropic particle-laden turbulent suspension. Part 1. Direct numerical simulations. J. Fluid Mech. 1997, 335, 75–109. [Google Scholar] [CrossRef]
- Fayed, H.E.; Ragab, S.A. Direct numerical simulation of particles-bubbles collisions kernel in homogeneous isotropic turbulence. J. Comput. Multiph. Flows 2013, 5, 167–188. [Google Scholar] [CrossRef]
- Wang, A.; Hoque, M.M.; Evans, G.; Mitra, S. Effect of turbulence dispersion on bubble-particle collision efficiency. Miner. Eng. 2022, 177, 107374. [Google Scholar] [CrossRef]
- Chan, T.T.K.; Ng, C.S.; Krug, D. Bubble–particle collisions in turbulence: Insights from point-particle simulations. J. Fluid Mech. 2023, 959, A6. [Google Scholar] [CrossRef]
- Balachandar, S.; Eaton, J.K. Turbulent Dispersed Multiphase Flow. Annu. Rev. Fluid Mech. 2010, 42, 111–133. [Google Scholar] [CrossRef]
- Chen, S.; Chen, X.; Wan, D.; Yi, X.; Sun, X.; Ji, L.; Wang, G. A lattice Boltzmann study of the collisions in a particle-bubble system under turbulent flows. Powder Technol. 2020, 361, 759–768. [Google Scholar] [CrossRef]
- Chen, S.; Chen, X.; Wan, D.; Sun, X.; Ji, L.; Wu, K.; Yang, F.; Wang, G. Particle-resolved direct numerical simulation of collisions of bidisperse inertial particles in a homogeneous isotropic turbulence. Powder Technol. 2020, 376, 72–79. [Google Scholar] [CrossRef]
- Wan, D.; Yi, X.; Wang, L.-P.; Sun, X.; Chen, S.; Wang, G. Study of collisions between particles and unloaded bubbles with point-particle model embedded in the direct numerical simulation of turbulent flows. Miner. Eng. 2020, 146, 106137. [Google Scholar] [CrossRef]
- Maxey, M.R.; Riley, J.J. Equation of Motion for a Small Rigid Sphere in a Nonuniform Flow. Phys. Fluids 1983, 26, 883–889. [Google Scholar] [CrossRef]
- Lallemand, P.; Luo, L.S. Lattice Boltzmann method for moving boundaries. J. Comput. Phys. 2003, 184, 406–421. [Google Scholar] [CrossRef]
- de Motta, J.C.B.; Breugem, W.-P.; Gazanion, B.; Estivalezes, J.-L.; Vincent, S.; Climent, E. Numerical modelling of finite-size particle collisions in a viscous fluid. Phys. Fluids 2013, 25, 083302. [Google Scholar] [CrossRef]
- Karakashev, S.; Grozev, N.; Ozdemir, O.; Guven, O.; Ata, S.; Bournival, G.; Batjargal, K.; Boylu, F.; Hristova, S.; Çelik, M.S. Physical restrictions of the flotation of fine particles and ways to overcome them. Physicochem. Probl. Miner. Process. 2022, 58, 153944. [Google Scholar] [CrossRef]
| Parameter | Physics | DNS |
|---|---|---|
| Domain size | 6 mm | 256 |
| Fluid density | 1.0000 g/cm3 | 1 |
| Fluid kinematic viscosity | 0.01 cm2/s | 0.0058 |
| Time step | s | 1 |
| Parameter | Physics | DNS |
|---|---|---|
| Solid particle diameter | m | 8 |
| Fluid density | 1.0000 g/cm3 | 1 |
| Fluid kinematic viscosity | 0.01 cm2/s | 0.0058 |
| Time step | s | 1 |
| Project | Group 1 | Group 2 | Group 3 | Group 4 | Group 5 | Group 6 |
|---|---|---|---|---|---|---|
| Turbulent kinetic energy dissipation rate | 0.56 | 2.26 | 7.84 | 16.63 | 21.13 | 36.06 |
| Stokes number of solid particles | 0.82 | 1.64 | 3.06 | 4.45 | 5.02 | 6.55 |
| Stokes number of bubbles | 0.83 | 1.66 | 3.10 | 4.51 | 5.08 | 6.63 |
| PP radial distribution function | 4.04 | 2.75 | 1.96 | 1.60 | 1.49 | 1.29 |
| PB radial distribution function | 1.16 | 1.09 | 1.02 | 0.99 | 0.98 | 0.95 |
| BB radial distribution function | 1.61 | 1.35 | 1.16 | 1.05 | 1.02 | 0.96 |
| PP radial relative velocity | 1.06 | 2.76 | 6.41 | 10.69 | 12.57 | 18.08 |
| PB radial relative velocity | 5.75 | 13.53 | 28.86 | 45.67 | 52.84 | 73.21 |
| BB radial relative velocity | 4.81 | 13.24 | 32.49 | 55.94 | 66.50 | 97.82 |
| PP collision kernel | 0.001 | 0.002 | 0.003 | 0.004 | 0.005 | 0.006 |
| PB collision kernel | 0.01 | 0.02 | 0.03 | 0.05 | 0.05 | 0.07 |
| BB collision kernel | 0.02 | 0.04 | 0.10 | 0.15 | 0.18 | 0.25 |
| Project | Group 1 | Group 2 | Group 3 | Group 4 | Group 5 | Group 6 |
|---|---|---|---|---|---|---|
| Turbulent kinetic energy dissipation rate | 0.56 | 2.26 | 7.84 | 16.63 | 21.13 | 36.06 |
| Stokes number of solid particles | −0.005 | −0.004 | −0.003 | −0.005 | −0.003 | −0.005 |
| Stokes number of bubbles | −0.17 | −0.17 | −0.17 | −0.17 | −0.17 | −0.17 |
| PP radial distribution function | 0.43 | −0.47 | −0.69 | −0.76 | −0.77 | −0.81 |
| PB radial distribution function | −0.52 | −0.65 | −0.73 | −0.75 | −0.74 | −0.76 |
| BB radial distribution function | −0.27 | −0.45 | −0.57 | −0.62 | −0.68 | −0.64 |
| PP radial relative velocity | 14.46 | 16.17 | 20.49 | 21.18 | 20.07 | 20.29 |
| PB radial relative velocity | 40.77 | 44.34 | 49.30 | 52.79 | 53.83 | 58.08 |
| BB radial relative velocity | 18.06 | 18.24 | 21.47 | 31.94 | 35.22 | 39.21 |
| PP kinematic collision kernel | 17.73 | 7.78 | 6.05 | 5.01 | 4.55 | 3.95 |
| PB kinematic collision kernel | 19.17 | 14.75 | 12.30 | 12.90 | 12.92 | 12.91 |
| BB kinematic collision kernel | 12.26 | 9.34 | 8.70 | 13.28 | 10.84 | 14.16 |
| PP dynamic collision kernel | −0.20 | −0.25 | −0.24 | −0.13 | −0.06 | −0.12 |
| PB dynamic collision kernel | 0.36 | 0.58 | 0.63 | 1.21 | 1.31 | 1.26 |
| BB dynamic collision kernel | 0.62 | 1.37 | 1.33 | 2.60 | 2.63 | 2.61 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Lin, J.; Wang, J.; Mao, Y.; Chen, S.; Wang, G. Comparative Study of Particle-Resolved and Point-Particle Simulations of Particle–Bubble Collisions in Homogeneous Isotropic Turbulence. Minerals 2025, 15, 338. https://doi.org/10.3390/min15040338
Wang J, Lin J, Wang J, Mao Y, Chen S, Wang G. Comparative Study of Particle-Resolved and Point-Particle Simulations of Particle–Bubble Collisions in Homogeneous Isotropic Turbulence. Minerals. 2025; 15(4):338. https://doi.org/10.3390/min15040338
Chicago/Turabian StyleWang, Junwen, Jichao Lin, Jianchun Wang, Yongwei Mao, Songying Chen, and Guichao Wang. 2025. "Comparative Study of Particle-Resolved and Point-Particle Simulations of Particle–Bubble Collisions in Homogeneous Isotropic Turbulence" Minerals 15, no. 4: 338. https://doi.org/10.3390/min15040338
APA StyleWang, J., Lin, J., Wang, J., Mao, Y., Chen, S., & Wang, G. (2025). Comparative Study of Particle-Resolved and Point-Particle Simulations of Particle–Bubble Collisions in Homogeneous Isotropic Turbulence. Minerals, 15(4), 338. https://doi.org/10.3390/min15040338






