SAG Mill Grinding Media Stress Evaluation—A DEM Approach
Abstract
1. Introduction
2. The Discrete Element Method (DEM)
3. Materials and Methods
Sag Mill Configuration and Simulation Set-Up
4. Results and Discussion
4.1. Charge Motion Inside the SAG Mill
4.2. Mill Power Draw
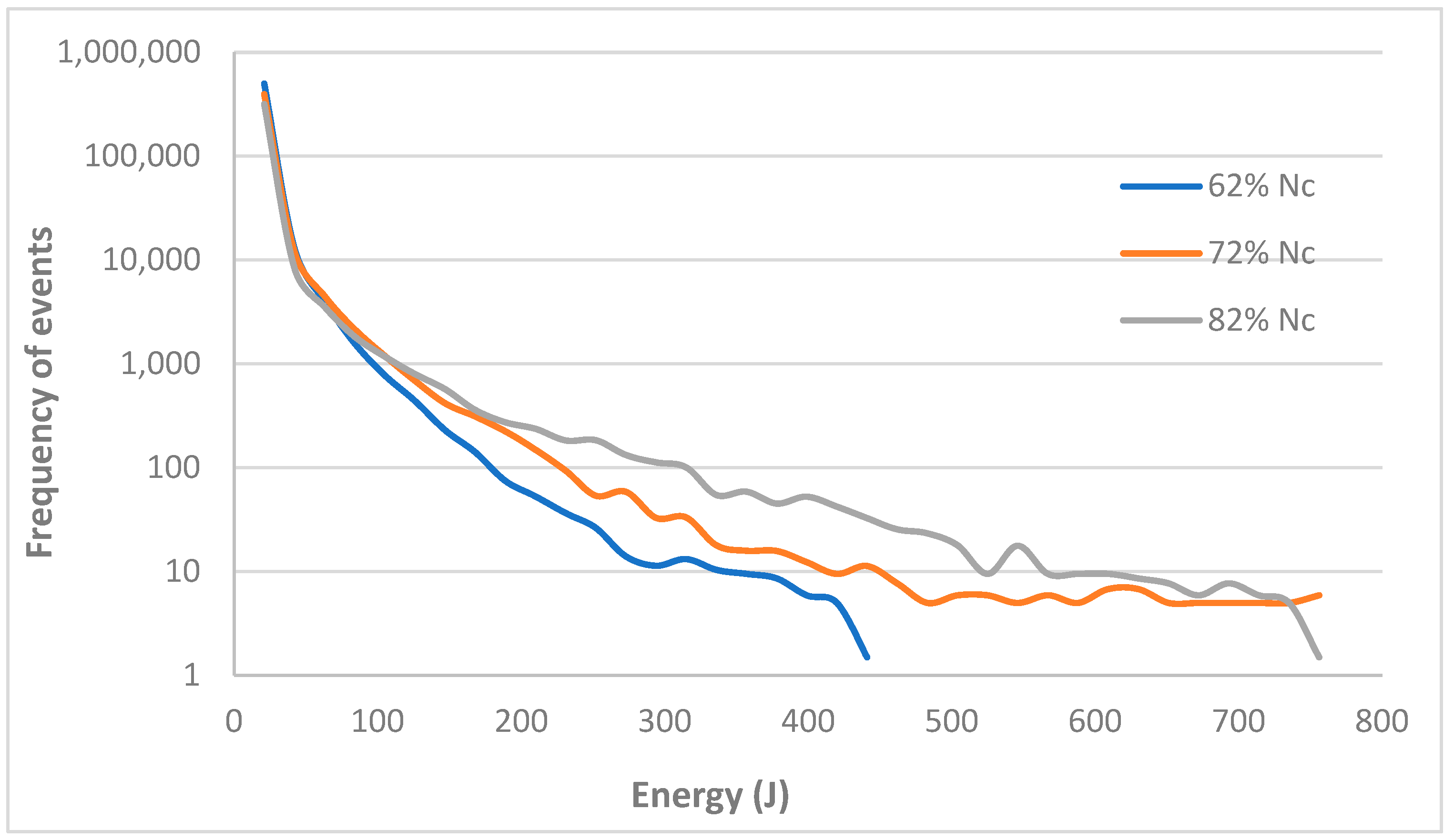
4.3. Energy Dissipation
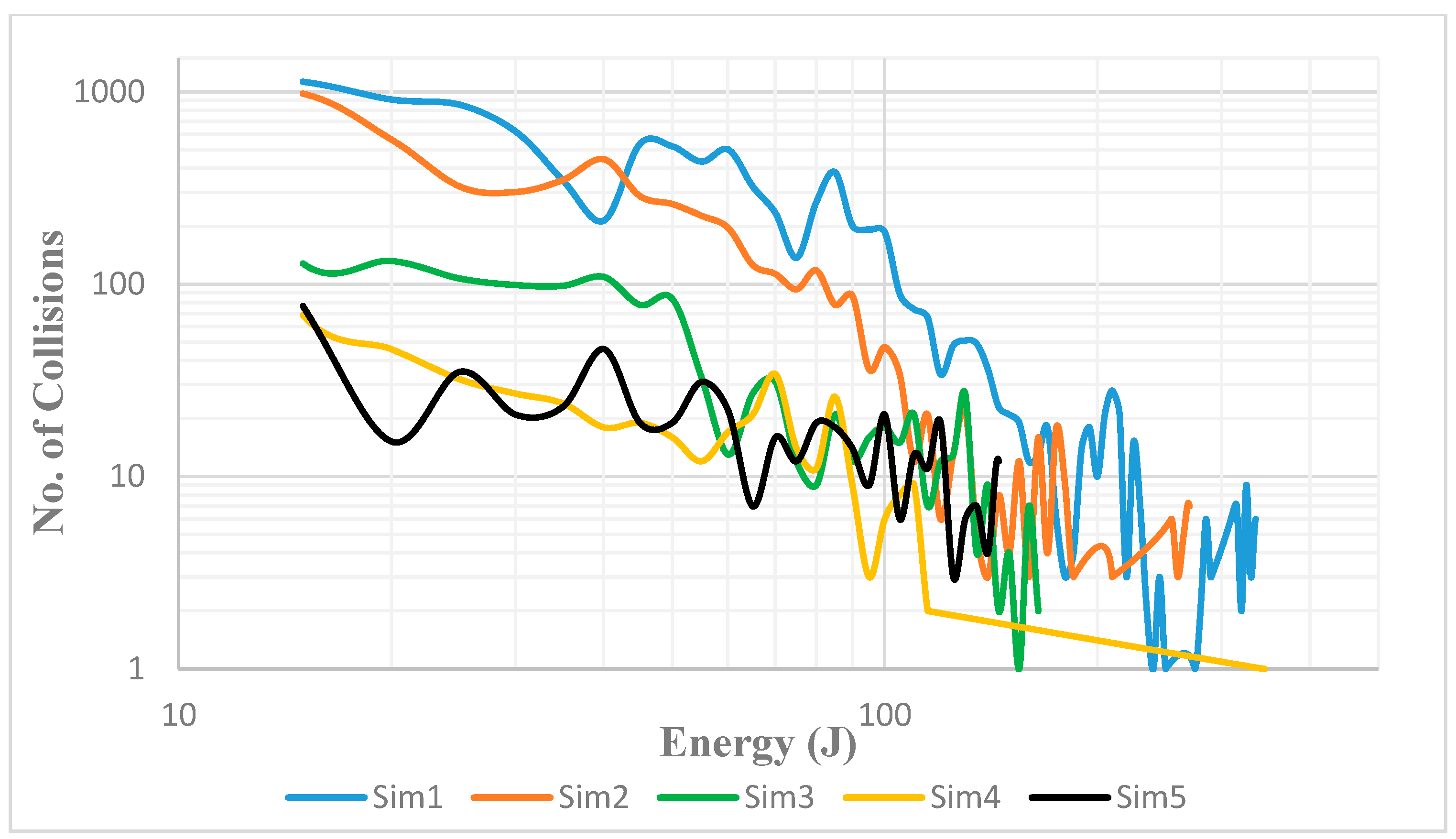
4.4. Impact Energy Spectra (IES)
- -
- lower ball load results in more cushioning of the high-energy collisions that have the potential to fracture the balls;
- -
- a reduction in ball load results in a SAG operation that is more power effective;
- -
- reducing the ball load of the charge will significantly reduce the cost of grinding since grinding media replenishment can account for up to 45% of grinding costs;
- -
- using smaller ball sizes reduces ball damage probability.
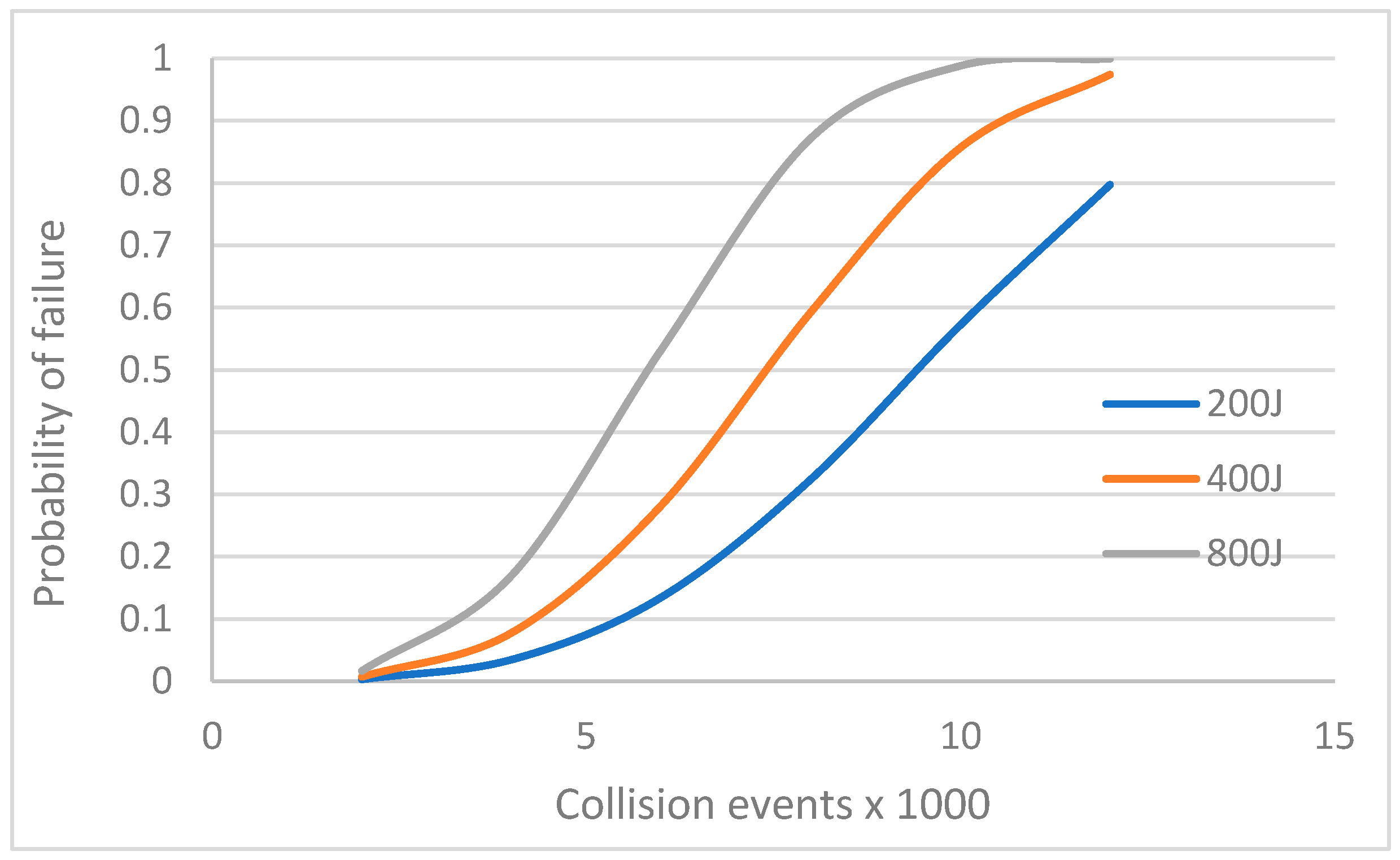
4.5. Predicting Fracture of Steel Balls in SAG Mills
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Royston, D. Semi-autogenous grinding (SAG) mill liner design and development. Miner. Metall. Process. 2007, 23, 121–132. [Google Scholar] [CrossRef]
- Owusu, K.B.; Zanin, M.; Skinner, W.; Asamoah, R.K. AG/SAG mill acoustic emissions characterisation under different operating conditions. Miner. Eng. 2021, 171, 107098. [Google Scholar] [CrossRef]
- Yang, F.X. Research on Optimization of Working Parameters of SAG Mill. Master’s Thesis, Central South University, Changsha, China, 2013. [Google Scholar]
- Xie, Q.; Zhong, C.; Liu, D.; Fu, Q.; Wang, X.; Shen, Z. Operation Analysis of a SAG Mill under Different Conditions Based on DEM and Breakage Energy Method. Energies 2020, 13, 5247. [Google Scholar] [CrossRef]
- Owen, P.; Clearly, P.W. The relationship between charge shape characteristics and fill level and lifter height for a SAG mill. Miner. Eng. 2015, 83, 19–32. [Google Scholar] [CrossRef]
- Pourasiabi, H.; Gates, J.D. Ball mill abrasion test (BMAT): Method development and statistical evaluations. MethodsX 2022, 9, 101900. [Google Scholar] [CrossRef]
- Pax, R.A.; Cornish, B. Understanding Size Effects of Semi-autogenous Grinding (SAG) Mill Operation as a Pathway to Solving Feed Disturbances—Case Study Using the MMG Century SAG Mill. In Proceedings of the 13th AusIMM Mill Operators’ Conference 2016, Perth, Australia, 10–12 October 2016; The Australasian Institute of Mining and Metallurgy: Perth, WA, Australia, 2016; pp. 321–329. [Google Scholar]
- Pax, R.; Thornton, A. Real time measurement and fast control strategies for the optimal operation of grinding circuits. In Proceedings of the MetPlant Conference, Perth, Australia, 10–11 September 2019; pp. 132–147. [Google Scholar]
- Sun, Y.I.; Dong, M.; Mao, Y.; Fan, D. Analysis on Grinding media Motion in Ball Mill by Discrete Element Method. In Proceedings of the 1st International Conference on Manufacturing Engineering, Quality and Production Systems, Brasov, Romania, 24–26 September 2009; Volume I, pp. 227–231. [Google Scholar]
- Jonsén, P.; Pålsson, B.I. and Häggblad, H.Å.A novel method for full-body modelling of grinding charges in tumbling mills. Miner. Eng. 2012, 33, 2–12. [Google Scholar] [CrossRef]
- Weerasekara, N.S.; Powell, M.S.; Cleary, P.W.; Tavares, L.M.; Evertsson, M.; Morrison, R.D.; Quist, J.; Carvalho, R.M. The contribution of DEM to the science of comminution. Powder Technol. 2013, 248, 3–4. [Google Scholar] [CrossRef]
- Cleary, P.W. and Sinnott, M.D. Simulation of particle flows and breakage in crushers using DEM: Part 1—Compression crushers. Miner. Eng. 2015, 74, 178–197. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, Z.S.; Yang, J.C.; Wassgren, C.; Curtis, J.S.; Guo, Y. Discrete Element Method Investigation of Binary Granular Flows with Different Particle Shapes. Energies 2020, 13, 1841. [Google Scholar] [CrossRef]
- Cleary, P.W.; Sinnott, M.D.; Morrison, R.D. Prediction of slurry transport in SAG mills using SPH fluid flow in a dynamic DEM-based porous media. Miner. Eng. 2006, 19, 1517–1527. [Google Scholar] [CrossRef]
- Mishra, B.K. and Rajamani, R.K. The discrete element method for the simulation of ball mills. Appl. Math. Model. 1992, 16, 598–604. [Google Scholar] [CrossRef]
- Bwalya, M.M. Using the Discrete Element Method to Guide the Modelling of Semi and Fully Autogenous Milling. Ph.D. Thesis, University of the Witwatersrand, Johannesburg, South Africa, 2005. [Google Scholar]
- Collinao, E.; Poblete, M.; Tavares, M. Preliminary validation of DEM-FEM coupling to predict mechanical stresses in SAG mill liners. In Proceedings of the International Conference on Semi-Autogenous and High Pressure Grinding Technology, Vancouer, BC, Canada, 20–24 September 2015. [Google Scholar]
- Paul, C.; Rob, W.; Morrison, D.; Sinnott, M.D. Prediction of slurry grinding due to media and coarse rock interactions in a 3D pilot SAG mill using a coupled DEM+ SPH model. Miner. Eng. 2020, 159, 106614. [Google Scholar]
- Delaney, G.W.; Cleary, P.W.; Morrison, R.D.; Cummins, S.; Loveday, B. Predicting breakage and the evolution of rock size and shape distributions in Ag and SAG mills using DEM. Miner. Eng. 2013, 50–51, 132–139. [Google Scholar] [CrossRef]
- Cleary, P.W.; Morrison, R.D. Understanding fine ore breakage in a laboratory scale ball mill using DEM. Miner. Eng. 2011, 24, 352–366. [Google Scholar] [CrossRef]
- Govender, N.; Rajamani, R.K.; Kok, S.; Wilke, D.N. Discrete element simulation of mill charge in 3D using the BLAZE-DEM GPU framework. Miner. Eng. 2015, 79, 152–168. [Google Scholar] [CrossRef]
- Polycarpou, A.A. Measurement and Modeling of Normal Contact Stiffness and Contact Damping at the Meso Scale. J. Vib. Acoust. 2005, 127, 52–60. [Google Scholar]
- Bond, F.C. Grinding Ball Size Selection. Mining Engineering. AIME Trans. 1958, 211, 592. [Google Scholar]
- Hogg, R.; Fuerstenau, D.W. Power Relationship for Tumbling Mills. Trans. Soc. Min. Eng.–AIME 1972, 252, 418–432. [Google Scholar]
- Moys, M. A model of mill power as affected by mill speed, load volume, and liner design. J. S. Afr. Inst. Min. Met. 1993, 93, 135. [Google Scholar]
- Loveday, B.K. Prediction of Autogenous Milling from Pilot Plant Tests. In Proceedings of the 11th Commonwealth Mining and Metallurgical Congress, Hong Kong; The Institution of Mining and Metallurgy: London, UK, 1978. [Google Scholar]
- Austin, L.G. A mill power equation for SAG mills. Miner. Metall. Process. Soc. Min. Metall. Explor. 1990, 7, 57–63. [Google Scholar] [CrossRef]
- Dunne, R.; Morrell, S.; Lane, G.; Valery, W.; Hart, S. Design of the 40 Foot Diameter SAG Mill Installed at the Cadia Gold Copper Mine. In Proceedings of the International Conference on Autogenous and Semiautogenous Grinding Technology 2001, Vancouver, BC, Canada, 30 September–3 October 2001; pp. I-43–I-58. [Google Scholar]
- Lameck, N.; Kiangi, K.; Moys, M. Effects of grinding media shapes on load behaviour and mill power in a dry ball mill. Miner. Eng. 2006, 19, 1357–1361. [Google Scholar] [CrossRef]
- Bwalya, M.M.; Moys, M.H.; Hinden, A.L. The use of the discrete element method and fracture mechanics to improve grinding rate prediction. Miner. Eng. 2001, 14, 565–573. [Google Scholar] [CrossRef]
- Rajamani, R.; Callahan, S.; Schreiner, J. DEM Simulation of Mill Charge in 3D VIA GPU Computing. Miner. Eng. 2010, 12, 1–12. [Google Scholar]
- Dabeet, A.; Wijewickreme, D.; Byrne, P. Application of discrete element modeling for simulation of the cyclic direct simple shear response of granular materials. In Proceedings of the 10th National Conference in Earthquake Engineering, Earthquake Engineering Research Institute, Anchorage, AK, USA, 21–25 July 2014. [Google Scholar]
- Cleary, P.W. Effect of rock shape representation in DEM on flow and energy utilisation in a pilot SAG mill. Comput. Part. Mech. 2019, 6, 461–477. [Google Scholar] [CrossRef]
- Cleary, P.W.; Owen, P. Effect of operating condition changes on the collisional environment in a SAG mill. Miner. Eng. 2019, 132, 297–315. [Google Scholar] [CrossRef]
- Chimwani, N.; Bwalya, M.; Samukute, O. Using Discrete Element Method to Analyse the Drop Ball Test. Minerals 2024, 14, 220. [Google Scholar] [CrossRef]
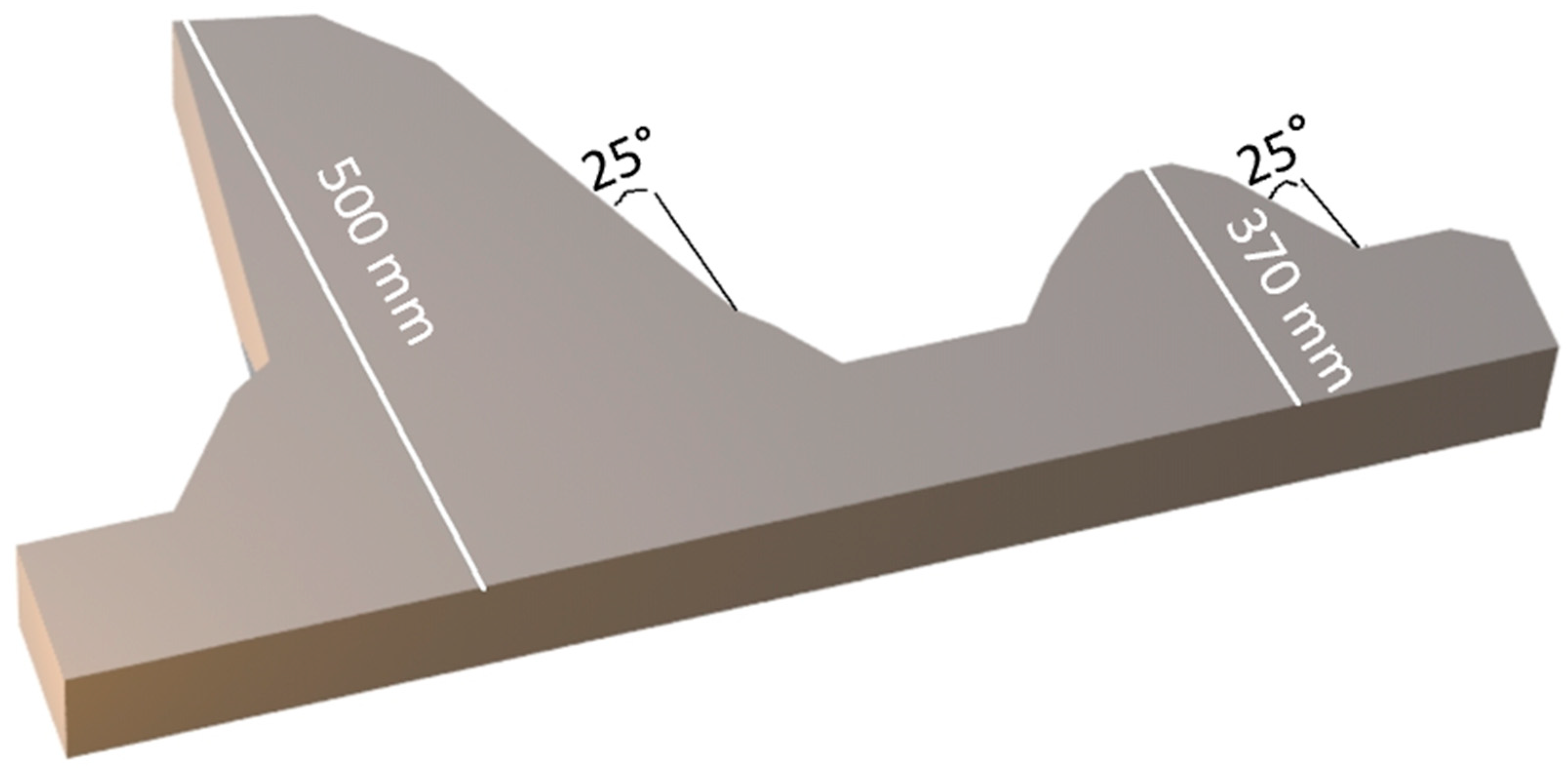
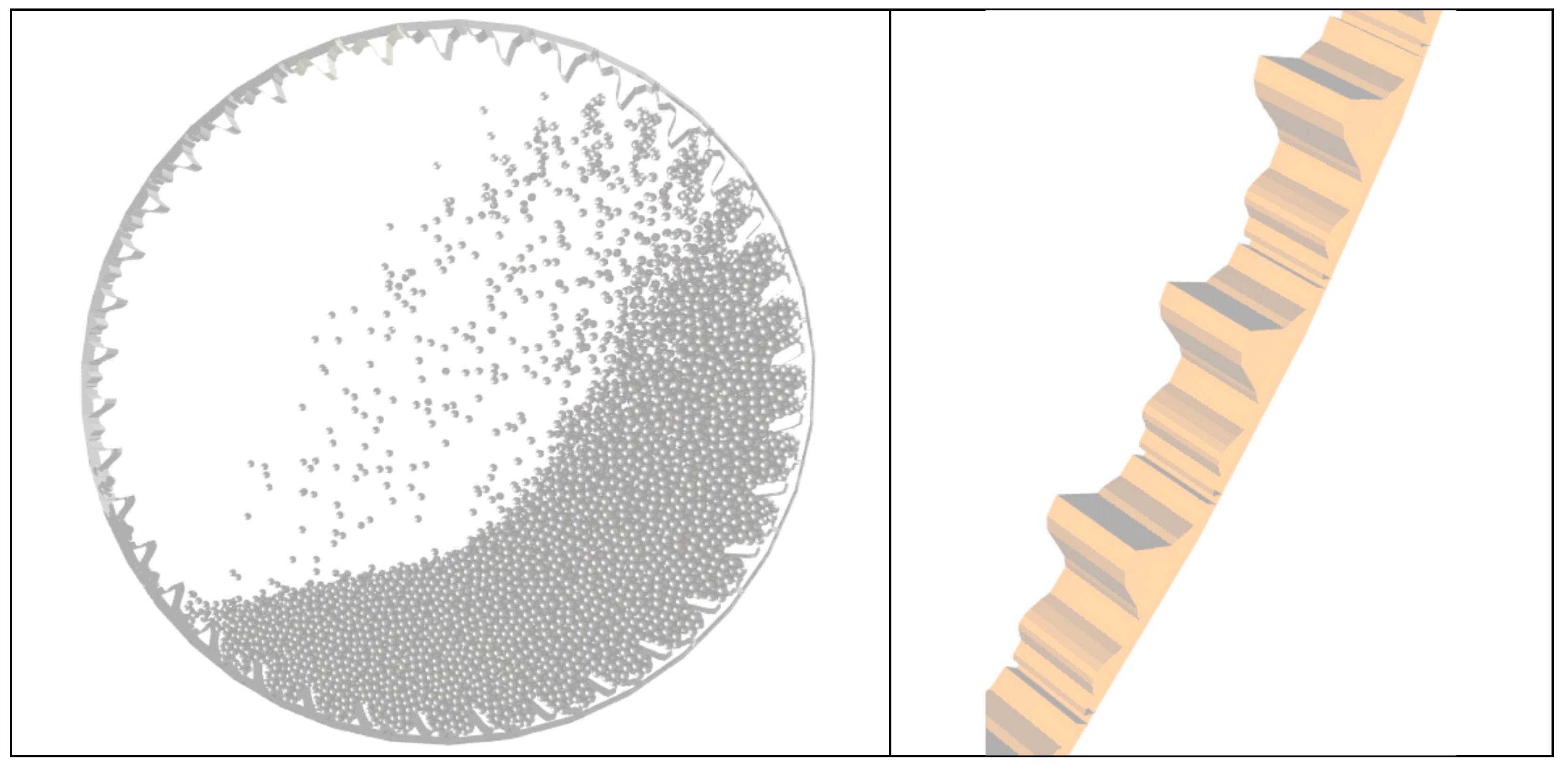

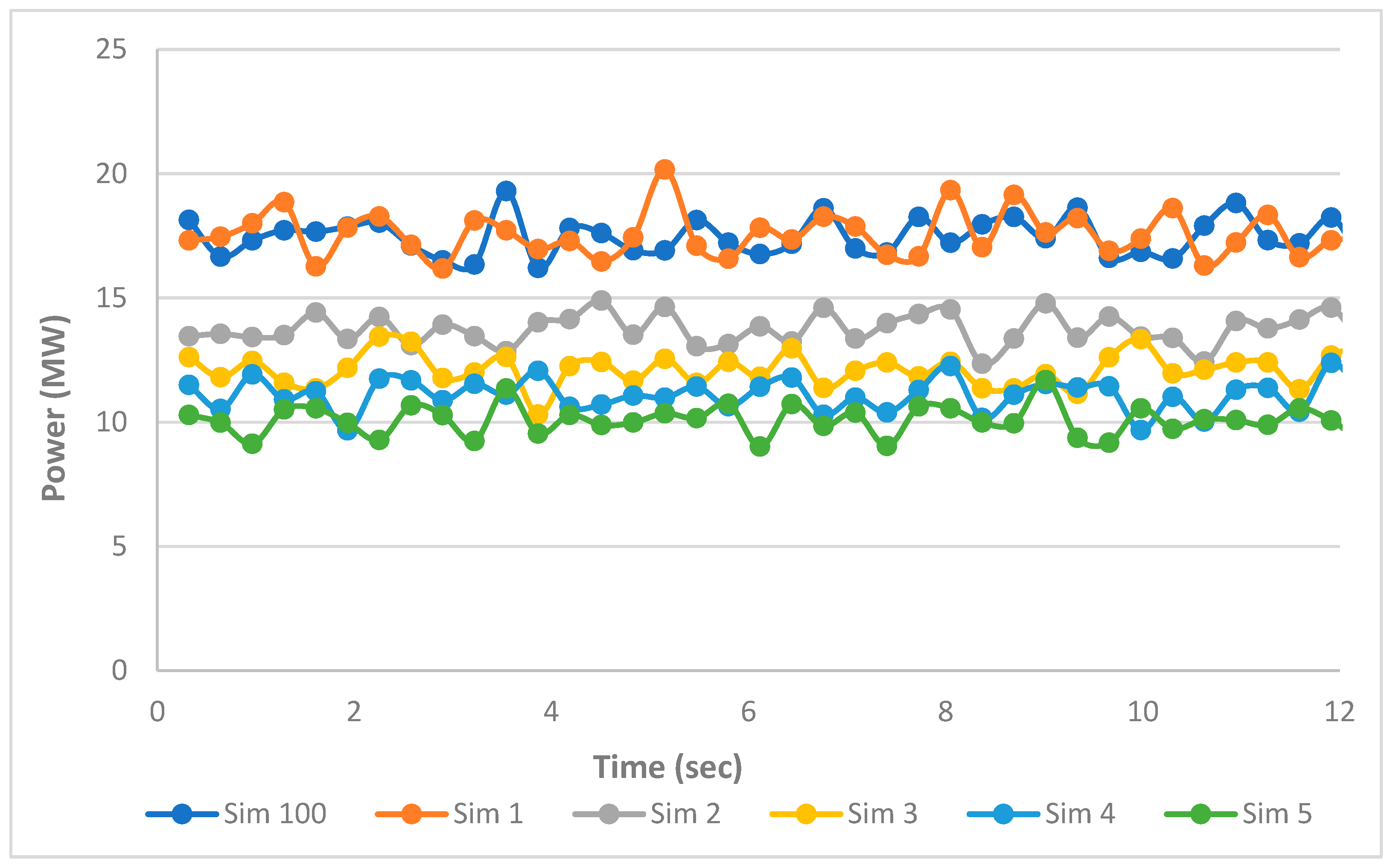


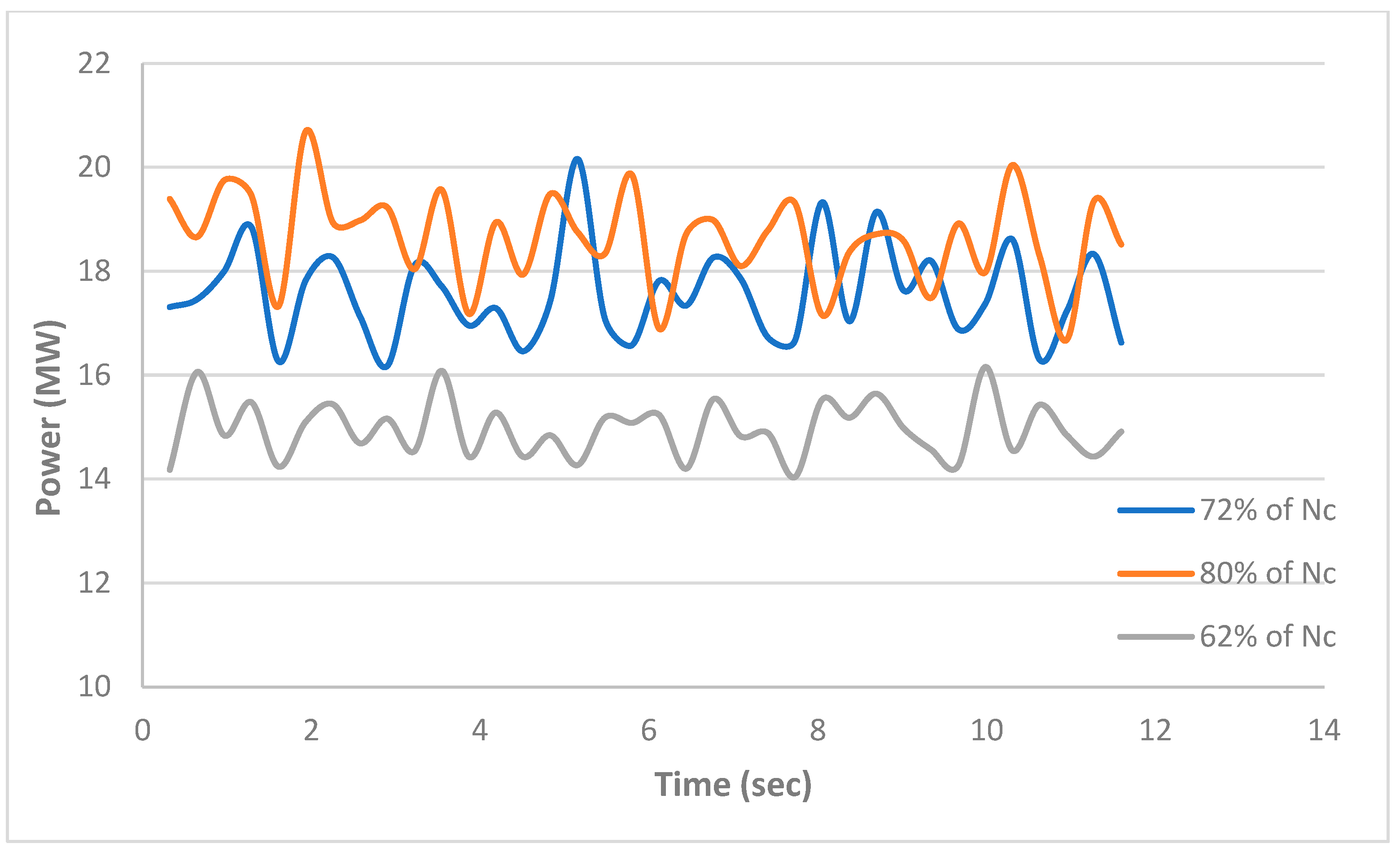



| Parameter | Value | Units |
|---|---|---|
| Inside shell diameter | 11.6 | m |
| Length of mill slice | 0.5 | m |
| % critical speed | 72 | Nc |
| Total filling | 24 | % |
| Lifters | Hi-Lo, 650 lifter face | |
| Number of lifters | 36 |
| Sim ID | Total Mill Filling (% v/v) | Ball Filling (% v/v) | Ore Filling (% v/v) | Ore Particle Fractions (% v/v) | ||||
|---|---|---|---|---|---|---|---|---|
| 150 mm | 120 mm | 90 mm | 60 mm | 30 mm | ||||
| Sim1 | 24 | 24 | 0 | 0 | 0 | 0 | 0 | 0 |
| Sim2 | 24 | 13 | 11 | 2 | 2 | 3 | 2 | 2 |
| Sim3 | 24 | 10 | 14 | 2 | 3 | 4 | 3 | 2 |
| Sim4 | 24 | 8 | 16 | 2 | 3.5 | 5 | 3.5 | 2 |
| Sim5 | 24 | 6 | 18 | 2 | 2 | 4 | 6 | 4 |
| Property | Value | Units |
|---|---|---|
| Coefficient of restitution (ϵ) | 0.6 | |
| Coefficient of friction (µ) | 0.4 | |
| Normal stiffness (kn) | 400 | kN/m |
| Shear stiffness (kt) | 300 | kN/m |
| Power sampling time interval | 0.1 | s |
| Energy scale | 5.0 | J |
| Ball size | 125 | mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bwalya, M.M.; Samukute, O.S.; Chimwani, N. SAG Mill Grinding Media Stress Evaluation—A DEM Approach. Minerals 2025, 15, 431. https://doi.org/10.3390/min15040431
Bwalya MM, Samukute OS, Chimwani N. SAG Mill Grinding Media Stress Evaluation—A DEM Approach. Minerals. 2025; 15(4):431. https://doi.org/10.3390/min15040431
Chicago/Turabian StyleBwalya, Murray Mulenga, Oliver Shwarzkopf Samukute, and Ngonidzashe Chimwani. 2025. "SAG Mill Grinding Media Stress Evaluation—A DEM Approach" Minerals 15, no. 4: 431. https://doi.org/10.3390/min15040431
APA StyleBwalya, M. M., Samukute, O. S., & Chimwani, N. (2025). SAG Mill Grinding Media Stress Evaluation—A DEM Approach. Minerals, 15(4), 431. https://doi.org/10.3390/min15040431






