How Can Additives Control the Early Stages of Mineralisation?
Abstract
:1. Introduction
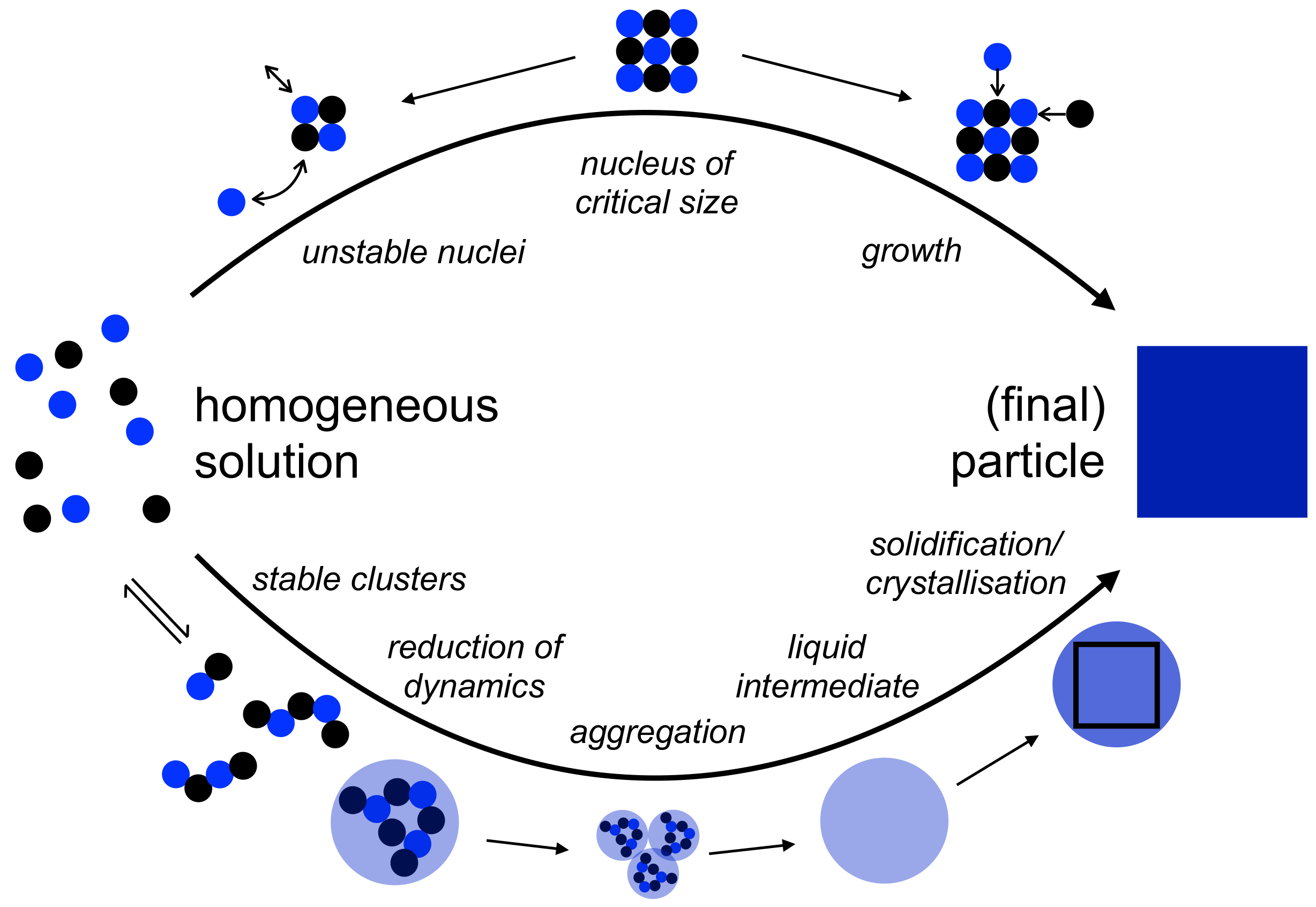
2. Possible Modes of Additive Control within the Notions of Classical Nucleation Theory
2.1. Additive Incorporation into the Nascent Phase
2.2. Interfacial Adsorption of Additives on Nascent Nuclei
2.3. Additive Mesophases as Environments for Nucleation
3. Additive Control Patterns in “Non-Classical” Nucleation
3.1. Adsorption of Free Ions and Pre-Nucleation Clusters
3.2. Additives and Liquid Intermediates
3.3. Additives and Nascent Solid Amorphous Intermediates
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Ruiz-Agudo, E.; Putnis, C.V.; Rodriguez-Navarro, C. Reactions between minerals and aqueous solutions. In Mineral Reaction Kinetics: Microstructures, Textures, Chemical and Isotopic Signatures; Mineralogical Society of Great Britain & Ireland: Chantilly, GA, USA, 2017; pp. 419–467. [Google Scholar]
- Cölfen, H.; Antonietti, M. Mesocrystals and Nonclassical Crystallization; John Wiley & Sons, Ltd.: Chichester, UK, 2008. [Google Scholar]
- Meldrum, F.C.; Cölfen, H. Controlling Mineral Morphologies and Structures in Biological and Synthetic Systems. Chem. Rev. 2008, 108, 4332–4432. [Google Scholar] [CrossRef] [PubMed]
- Evans, J.S. ‘Apples’ and ‘oranges’: Comparing the structural aspects of biomineral- and ice-interaction proteins. Curr. Opin. Colloid Interface Sci. 2003, 8, 48–54. [Google Scholar] [CrossRef]
- Evans, J.S. “Liquid-like” biomineralization protein assemblies: A key to the regulation of non-classical nucleation. CrystEngComm 2013, 15, 8388–8394. [Google Scholar] [CrossRef]
- Evans, J. Polymorphs, Proteins, and Nucleation Theory: A Critical Analysis. Minerals 2017, 7, 62. [Google Scholar] [CrossRef]
- Evans, J.S. Principles of Molecular Biology and Biomacromolecular Chemistry. Rev. Min. Geochem. 2003, 54, 31–56. [Google Scholar] [CrossRef]
- Ibsen, C.J.S.; Birkedal, H. Pyrophosphate-Inhibition of Apatite Formation Studied by In Situ X-Ray Diffraction. Minerals 2018, 8, 65. [Google Scholar] [CrossRef]
- Boulahlib-Bendaoud, Y.; Ghizellaoui, S.; Tlili, M. Inhibition of CaCO3 scale formation in ground waters using mineral phosphates. Desal. Water Treat. 2012, 38, 382–388. [Google Scholar] [CrossRef]
- Ruiz-Agudo, E.; Burgos-Cara, A.; Ruiz-Agudo, C.; Ibañez-Velasco, A.; Cölfen, H.; Rodriguez-Navarro, C. A non-classical view on calcium oxalate precipitation and the role of citrate. Nat. Commun. 2017, 8, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez-Navarro, C.; Benning, L.G. Control of Crystal Nucleation and Growth by Additives. Elements 2013, 9, 203–209. [Google Scholar] [CrossRef]
- Mann, S. Biomimetic Materials Chemistry; VCH: New York, NY, USA, 1996. [Google Scholar]
- Eyring, H. The activated complex in chemical reactions. Chem. Rev. 1935, 17, 65–77. [Google Scholar] [CrossRef]
- Gebauer, D.; Kellermeier, M.; Gale, J.D.; Bergström, L.; Cölfen, H. Pre-nucleation clusters as solute precursors in crystallisation. Chem. Soc. Rev. 2014, 43, 2348–2371. [Google Scholar] [CrossRef] [PubMed]
- Flory, P.J. Molecular size distribution in linear condensation polymers. J. Am. Chem. Soc. 1936, 58, 1877–1885. [Google Scholar] [CrossRef]
- Demichelis, R.; Raiteri, P.; Gale, J.D.; Quigley, D.; Gebauer, D. Stable prenucleation mineral clusters are liquid-like ionic polymers. Nat. Commun. 2011, 2, 590. [Google Scholar] [CrossRef] [PubMed]
- Hu, Q.; Nielsen, M.H.; Freeman, C.L.; Hamm, L.M.; Tao, J.; Lee, J.R.I.; Han, T.Y.J.; Becker, U.; Harding, J.H.; Dove, P.M.; et al. The thermodynamics of calcite nucleation at organic interfaces: Classical vs. non-classical pathways. Faraday Discuss. 2012, 159, 509–523. [Google Scholar] [CrossRef]
- Smeets, P.J.M.; Finney, A.R.; Habraken, W.J.E.M.; Nudelman, F.; Friedrich, H.; Laven, J.; De Yoreo, J.J.; Rodger, P.M.; Sommerdijk, N.A.J.M. A classical view on nonclassical nucleation. Proc. Natl. Acad. Sci. USA 2017, 114, E7882–E7890. [Google Scholar] [CrossRef] [PubMed]
- Cartwright, J.H.E.; Checa, A.G.; Gale, J.D.; Gebauer, D.; Sainz-Díaz, C.I. Calcium carbonate polyamorphism and its role in biomineralization: How many amorphous calcium carbonates are there? Angew. Chem. Int. Ed. 2012, 51, 11960–11970. [Google Scholar] [CrossRef] [PubMed]
- De Yoreo, J.J.; Vekilov, P.G. Principles of crystal nucleation and growth. Rev. Min. Geochem. 2003, 54, 57–93. [Google Scholar] [CrossRef]
- Nielsen, A.E. Kinetics of Precipitation; Pergamon Press: New York, NY, USA, 1964. [Google Scholar]
- Li, H.; Xin, H.L.; Muller, D.A.; Estroff, L.A. Visualizing the 3D Internal Structure of Calcite Single Crystals Grown in Agarose Hydrogels. Science 2009, 326, 1244–1247. [Google Scholar] [CrossRef] [PubMed]
- Davis, K.J.; Dove, P.M.; De Yoreo, J.J. The Role of Mg2+ as an Impurity in Calcite Growth. Science 2000, 290, 1134–1137. [Google Scholar] [CrossRef] [PubMed]
- Dörfler, H.D. Grenzflächen- und Kolloidchemie [Interface and Colloid Chemistry]; VCH: Weinheim, Germany, 1994. [Google Scholar]
- Sun, W.; Jayaraman, S.; Chen, W.; Persson, K.A.; Ceder, G. Nucleation of metastable aragonite CaCO3 in seawater. Proc. Natl. Acad. Sci. USA 2015, 112, 3199–3204. [Google Scholar] [CrossRef] [PubMed]
- Navrotsky, A. Nanoscale Effects on Thermodynamics and Phase Equilibria in Oxide Systems. ChemPhysChem 2011, 12, 2207–2215. [Google Scholar] [CrossRef] [PubMed]
- Israelachvili, J.N. Intermolecular and Surface Forces, 3rd ed.; Academic Press: Burlington, MA, USA, 2011. [Google Scholar]
- Smeets, P.J.M.; Cho, K.R.; Kempen, R.G.E.; Sommerdijk, N.A.J.M.; De Yoreo, J.J. Calcium carbonate nucleation driven by ion binding in a biomimetic matrix revealed by in situ electron microscopy. Nat. Mater. 2015, 14, 394–399. [Google Scholar] [CrossRef] [PubMed]
- Vekilov, P.G. Nucleation. Cryst. Growth Des. 2010, 10, 5007–5019. [Google Scholar] [CrossRef] [PubMed]
- Vekilov, P.G. The two-step mechanism of nucleation of crystals in solution. Nanoscale 2010, 2, 2346–2357. [Google Scholar] [CrossRef] [PubMed]
- De Yoreo, J.J. Crystal nucleation: More than one pathway. Nat. Mater. 2013, 12, 284–285. [Google Scholar] [CrossRef] [PubMed]
- Stephens, C.J.; Ladden, S.F.; Meldrum, F.C.; Christenson, H.K. Amorphous Calcium Carbonate is Stabilized in Confinement. Adv. Funct. Mater. 2010, 20, 2108–2115. [Google Scholar] [CrossRef]
- Kröger, R. Andreas Verch Liquid Cell Transmission Electron Microscopy and the Impact of Confinement on the Precipitation from Supersaturated Solutions. Minerals 2018, 8, 21. [Google Scholar] [CrossRef]
- Mao, L.B.; Xue, L.; Gebauer, D.; Liu, L.; Yu, X.F.; Liu, Y.Y.; Cölfen, H.; Yu, S.H. Anisotropic nanowire growth via a self-confined amorphous template process: A reconsideration on the role of amorphous calcium carbonate. Nano Res. 2016, 9, 1334–1345. [Google Scholar] [CrossRef]
- Gebauer, D.; Cölfen, H.; Verch, A.; Antonietti, M. The multiple roles of additives in CaCO3 crystallization: A quantitative case study. Adv. Mater. 2009, 21, 435–439. [Google Scholar] [CrossRef]
- Rao, A.; Gebauer, D.; Cölfen, H. Modulating Nucleation by Kosmotropes and Chaotropes: Testing the Waters. Crystals 2017, 7, 302. [Google Scholar] [CrossRef]
- Burgos-Cara, A.; Putnis, C.; Rodriguez-Navarro, C.; Ruiz-Agudo, E. Hydration Effects on the Stability of Calcium Carbonate Pre-Nucleation Species. Minerals 2017, 7, 126. [Google Scholar] [CrossRef]
- Kellermeier, M.; Raiteri, P.; Berg, J.K.; Kempter, A.; Gale, J.D.; Gebauer, D. Entropy Drives Calcium Carbonate Ion Association. ChemPhysChem 2016, 17, 3535–3541. [Google Scholar] [CrossRef] [PubMed]
- Sinn, C.G.; Dimova, R.; Antonietti, M. Isothermal Titration Calorimetry of the Polyelectrolyte/Water Interaction and Binding of Ca2+: Effects Determining the Quality of Polymeric Scale Inhibitors. Macromolecules 2004, 37, 3444–3450. [Google Scholar] [CrossRef]
- Scheck, J.; Drechsler, M.; Ma, X.; Stöckl, M.T.; Konsek, J.; Schwaderer, J.B.; Stadler, S.M.; De Yoreo, J.J.; Gebauer, D. Polyaspartic acid facilitates oxolation within iron(III) oxide pre-nucleation clusters and drives the formation of organic-inorganic composites. J. Chem. Phys. 2016, 145, 211917–211919. [Google Scholar] [CrossRef] [PubMed]
- Gower, L.B. Biomimetic model systems for investigating the amorphous precursor pathway and its role in biomineralization. Chem. Rev. 2008, 108, 4551–4627. [Google Scholar] [CrossRef] [PubMed]
- Gebauer, D. Prenucleation Clusters. In Encyclopedia of Nanotechnology; Springer: Dordrecht, The Netherlands, 2015; pp. 1–7. [Google Scholar]
- Jiang, Y.; Gower, L.; Volkmer, D.; Cölfen, H. The existence region and composition of a polymer-induced liquid precursor phase for DL-glutamic acid crystals. Phys. Chem. Chem. Phys. 2012, 14, 914–919. [Google Scholar] [CrossRef] [PubMed]
- Cantaert, B.; Kim, Y.Y.; Ludwig, H.; Nudelman, F.; Sommerdijk, N.A.J.M.; Meldrum, F.C. Think positive: Phase separation enables a positively charged additive to induce dramatic changes in calcium carbonate morphology. Adv. Funct. Mater. 2012, 22, 907–915. [Google Scholar] [CrossRef]
- Sebastiani, F.; Stefan, L.P.W.; Born, B.; Luong, T.Q.; Cölfen, H.; Gebauer, D.; Havenith, M. Water Dynamics from THz Spectroscopy Reveal the Locus of a Liquid-Liquid Binodal Limit in Aqueous CaCO3 Solutions. Angew. Chem. Int. Ed. 2016, 56, 490–495. [Google Scholar] [CrossRef] [PubMed]
- Kellermeier, M.; Gebauer, D.; Melero-García, E.; Drechsler, M.; Talmon, Y.; Kienle, L.; Cölfen, H.; García-Ruiz, J.M.; Kunz, W. Colloidal stabilization of calcium carbonate prenucleation clusters with silica. Adv. Funct. Mater. 2012, 22, 4301–4311. [Google Scholar] [CrossRef]
- Berg, J.K.; Jordan, T.; Binder, Y.; Börner, H.G.; Gebauer, D. Mg2+ tunes the wettability of liquid precursors of CaCO3: Toward controlling mineralization sites in hybrid materials. J. Am. Chem. Soc. 2013, 135, 12512–12515. [Google Scholar] [CrossRef] [PubMed]
- Khouzani, M.F.; Schütz, C.; Durak, G.M.; Fornell, J.; Sort, J.; Salazar-Alvarez, G.; Bergström, L.; Gebauer, D. A CaCO3/nanocellulose-based bioinspired nacre-like material. J. Mater. Chem. A 2017, 5, 16128–16133. [Google Scholar] [CrossRef]
- Bewernitz, M.A.; Gebauer, D.; Long, J.R.; Cölfen, H.; Gower, L.B. A meta-stable liquid precursor phase of calcium carbonate and its interactions with polyaspartate. Faraday Discuss. 2012, 159, 291–312. [Google Scholar] [CrossRef]
- Ruiz-Agudo, E.; Putnis, C.V.; Putnis, A. Coupled dissolution and precipitation at mineral–fluid interfaces. Chem. Geol. 2014, 383, 132–146. [Google Scholar] [CrossRef]
- Ihli, J.; Wong, W.C.; Noel, E.H.; Kim, Y.Y.; Kulak, A.N.; Christenson, H.K.; Duer, M.J.; Meldrum, F.C. Dehydration and crystallization of amorphous calcium carbonate in solution and in air. Nat. Commun. 2014, 5, 3169. [Google Scholar] [CrossRef] [PubMed]
- Sturm, E.V.; Cölfen, H. Mesocrystals: Past, Presence, Future. Crystals 2017, 7, 207. [Google Scholar]
- Sturm, E.V.; Cölfen, H. Mesocrystals: Structural and morphogenetic aspects. Chem. Soc. Rev. 2016, 45, 5821–5833. [Google Scholar] [CrossRef] [PubMed]
- Addadi, L.; Raz, S.; Weiner, S. Taking advantage of disorder: Amorphous calcium carbonate and its roles in biomineralization. Adv. Mater. 2003, 15, 959–970. [Google Scholar] [CrossRef]
- Gebauer, D.; Verch, A.; Börner, H.G.; Cölfen, H. Influence of selected artificial peptides on calcium carbonate precipitation—A quantitative study. Cryst. Growth Des. 2009, 9, 2398–2403. [Google Scholar] [CrossRef]
- Scheck, J.; Wu, B.; Drechsler, M.; Rosenberg, R.; Van Driessche, A.E.S.; Stawski, T.M.; Gebauer, D. The Molecular Mechanism of Iron(III) Oxide Nucleation. J. Phys. Chem. Lett. 2016, 7, 3123–3130. [Google Scholar] [CrossRef] [PubMed]
- Wolf, S.L.P.; Jähme, K.; Gebauer, D. Synergy of Mg2+ and poly(aspartic acid) in additive-controlled calcium carbonate precipitation. CrystEngComm 2015, 17, 6857–6862. [Google Scholar] [CrossRef]



© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gebauer, D. How Can Additives Control the Early Stages of Mineralisation? Minerals 2018, 8, 179. https://doi.org/10.3390/min8050179
Gebauer D. How Can Additives Control the Early Stages of Mineralisation? Minerals. 2018; 8(5):179. https://doi.org/10.3390/min8050179
Chicago/Turabian StyleGebauer, Denis. 2018. "How Can Additives Control the Early Stages of Mineralisation?" Minerals 8, no. 5: 179. https://doi.org/10.3390/min8050179
APA StyleGebauer, D. (2018). How Can Additives Control the Early Stages of Mineralisation? Minerals, 8(5), 179. https://doi.org/10.3390/min8050179




