Inertial Accelerated Algorithm for Fixed Point of Asymptotically Nonexpansive Mapping in Real Uniformly Convex Banach Spaces
Abstract
:1. Introduction
- (i)
- Nonexpansive if
- (ii)
- Asymptotically nonexpansive (see [1] ) if there exists a sequence , with such thatand
- (iii)
- Uniformly L-Lipschitzian if there exists a constant such that, for all ,
- (C1)
- .
- (C2)
- .
- (C3)
- is bounded.
- (D1) is bounded; and
- (D2) is bounded for any
2. Preliminaries
- (i)
- for weak convergence and → for strong convergence.
- (ii)
- to denote the set of w-weak cluster limits of .
- (1)
- Demiclosed at , if for any sequence in C which converges weakly to and , it holds that .
- (2)
- Semicompact, if for any bounded sequence in C such that there exists a subsequence such that .
- (i)
- The sequence converges.
- (ii)
- In particular, if , then .
3. Main Results
- (i)
- Choose sequences , and with which means .
- (ii)
- Let be arbitrary points, for the iterates and for each , choose such that where, for anyThis idea was obtained from the recent inertial extrapolation step introduced in [32].
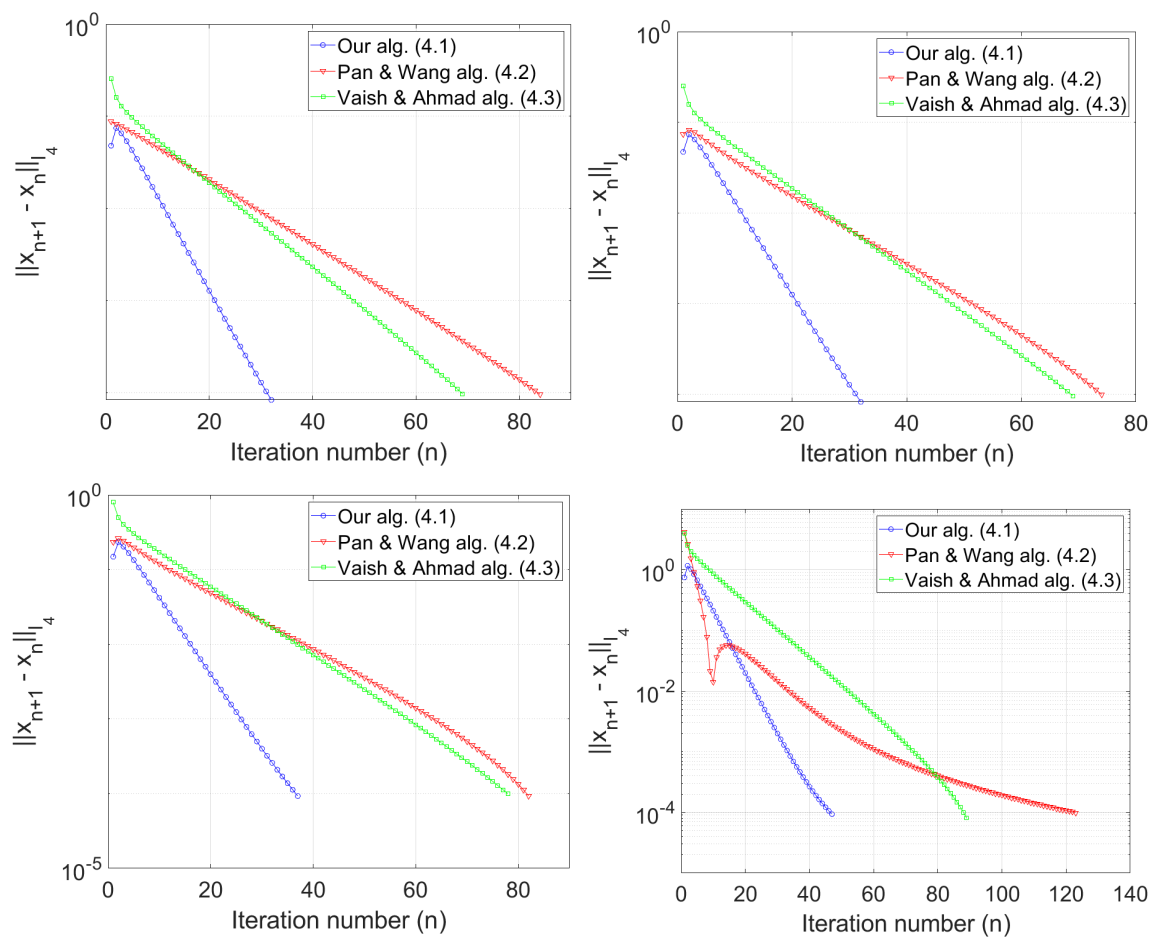
4. Numerical Examples
- Case I:
- and
- Case II:
- and
- Case III:
- and
- Case IV:
- and
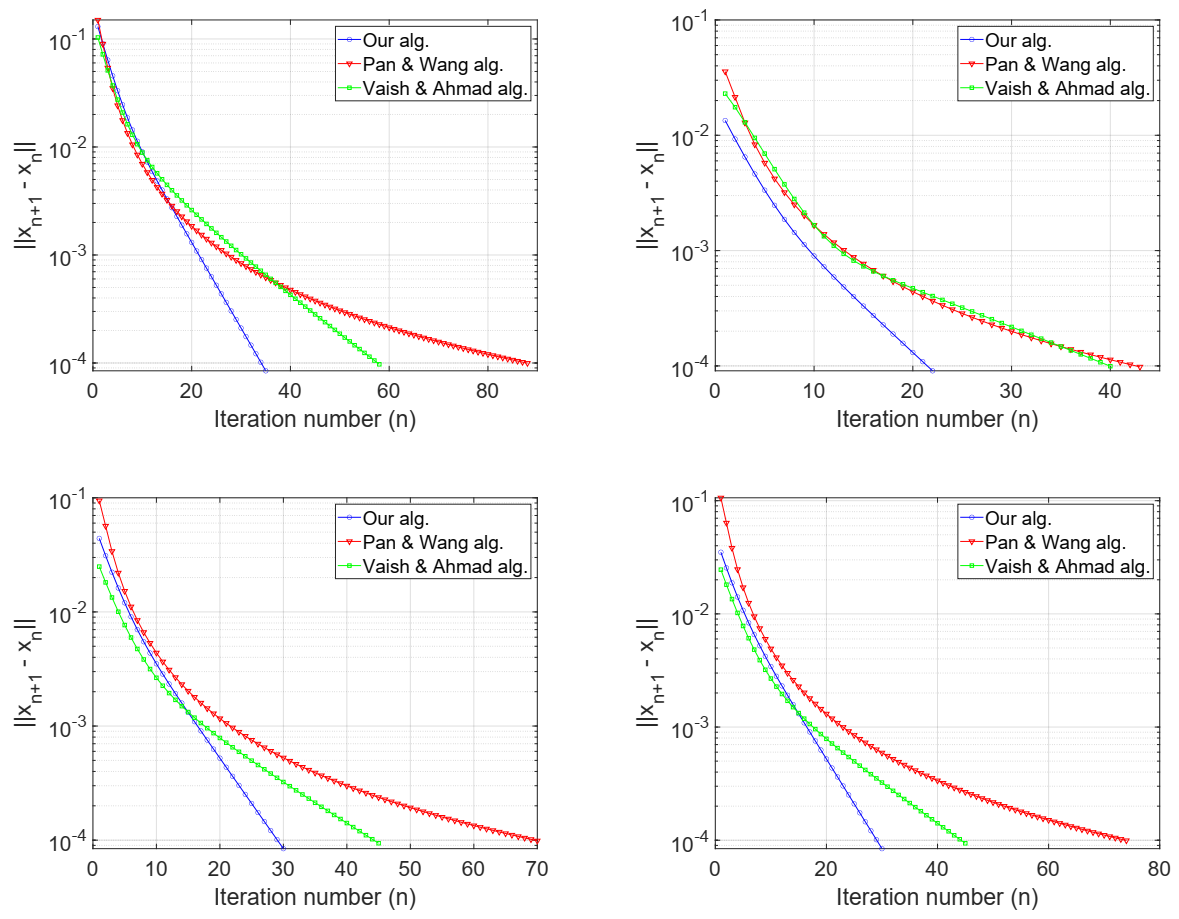
- Case I:
- Case II:
- Case III:
- Case IV:
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Goebel, K.; Kirk, W.A. A fixed point theorem for asymptotically nonexpansive mappings. Proc. Am. Math. Soc. 1972, 35, 171–174. [Google Scholar] [CrossRef]
- Ali, B.; Harbau, M.H. Covergence theorems for pseudomonotone equilibrium problems, split feasibility problems and multivalued strictly pseudocontractive mappings. Numer. Funct. Anal. Opt. 2019, 40. [Google Scholar] [CrossRef]
- Castella, M.; Pesquet, J.-C.; Marmin, A. Rational optimization for nonlinear reconstruction with approximate penalization. IEEE Trans. Signal Process. 2019, 67, 1407–1417. [Google Scholar] [CrossRef]
- Combettes, P.L.; Eckstein, J. Asynchronous block-iterative primal-dual decomposition methods for monotone inclusions. Math. Program. 2018, B168, 645–672. [Google Scholar] [CrossRef] [Green Version]
- Noor, M.A. New approximation Schemes for General Variational Inequalities. J. Math. Anal. Appl. 2000, 251, 217–229. [Google Scholar] [CrossRef] [Green Version]
- Xu, H.K. A variable Krasnosel’skii-Mann algorithm and the multiple-set split feasibility problem. Inverse Probl. 2006, 22, 2021–2034. [Google Scholar] [CrossRef]
- Cai, G.; Shehu, Y.; Iyiola, O.S. Iterative algorithms for solving variational inequalities and fixed point problems for asymptotically nonexpansive mappings in Banach spaces. Numer. Algorithms 2016, 73, 869–906. [Google Scholar] [CrossRef]
- Halpern, B. Fixed points of nonexpansive maps. Bull. Am. Math. Soc. 1967, 73, 957–961. [Google Scholar] [CrossRef] [Green Version]
- Mann, W.R. Mean value methods in iteration. Proc. Am. Math. Soc. 1953, 4, 506–510. [Google Scholar] [CrossRef]
- Picard, E. Mémoire sur la théorie des équations aux dérivées partielles et la méthode des approximations successives. J. Math. Pures Appl. 1890, 6, 145–210. [Google Scholar]
- Tan, K.K.; Xu, H.K. Fixed Point Iteration Proccesses for Asymtotically Nonnexpansive Mappings. Proc. Am. Math. Soc. 1994, 122, 733–739. [Google Scholar] [CrossRef]
- Bose, S.C. Weak convergence to the fixed point of an asymptotically nonexpansive map. Proc. Am. Math. Soc. 1978, 68, 305–308. [Google Scholar] [CrossRef]
- Schu, J. Weak and strong convergence to fixed points of asymptotically nonexpansive mappings. Bull. Aust. Math. Soc. 1991, 43, 153–159. [Google Scholar] [CrossRef] [Green Version]
- Schu, J. Iterative construction of fixed points of asymptotically nonexpansive mappings. J. Math. Anal. Appl. 1991, 158, 407–413. [Google Scholar] [CrossRef] [Green Version]
- Osilike, M.O.; Aniagbosor, S.C. Weak and Strong Convergence Theorems for Fixed Points of Asymtotically Nonexpansive Mappings. Math. Comput. Model. 2000, 32, 1181–1191. [Google Scholar] [CrossRef]
- Dong, Q.L.; Yuan, H.B. Accelerated Mann and CQ algorithms for finding a fixed point of a nonexpansive mapping. Fixed Point Theory Appl. 2015, 125. [Google Scholar] [CrossRef] [Green Version]
- Nocedal, J.; Wright, S.J. Numerical Optimization, 2nd ed.; Springer Series in Operations Research and Financial Engineering; Springer: Berlin, Germany, 2006. [Google Scholar]
- Attouch, H.; Peypouquet, J.; Redont, P. A dynamical approach to an inertial forward–backward algorithm for convex minimization. SIAM J. Optim. 2014, 24, 232–256. [Google Scholar] [CrossRef]
- Attouch, H.; Goudon, X.; Redont, P. The heavy ball with friction. I. The continuous dynamical system. Commun. Contemp. Math. 2000, 2, 1–34. [Google Scholar] [CrossRef]
- Attouch, H.; Peypouquent, J. The rate of convergence of Nesterov’s accelarated forward-backward method is actually faster than . SIAM J. Optim. 2016, 26, 1824–1834. [Google Scholar] [CrossRef]
- Bot, R.I.; Csetnek, E.R.; Hendrich, C. Inertial Douglas-Rachford splitting for monotone inclusion problems. Appl. Math. Comput. 2015, 256, 472–487. [Google Scholar] [CrossRef] [Green Version]
- Dong, Q.L.; Yuan, H.B.; Je, C.Y.; Rassias, T.M. Modified inertial Mann algorithm and inertial CQ-algorithm for nonexpansive mappings. Optim. Lett. 2016, 12, 87–102. [Google Scholar] [CrossRef]
- Dong, Q.L.; Kazmi, K.R.; Ali, R.; Li, H.X. Inertial Krasnol’skii-Mann type hybrid algorithms for solving hierarchical fixed point problems. J. Fixed Point Theory Appl. 2019, 21, 57. [Google Scholar] [CrossRef]
- Lorenz, D.A.; Pock, T. An inertial forward-backward algorithm for monotone inclusions. J. Math. Imaging Vis. 2015, 51, 311–325. [Google Scholar] [CrossRef] [Green Version]
- Polyak, B.T. Some methods of speeding up the convergence of iteration methods. USSR Comput. Math. Math. Phys. 1964, 4, 1–17. [Google Scholar] [CrossRef]
- Shehu, Y.; Gibali, A. Inertial Krasnol’skii-Mann method in Banach spaces. Mathematics 2020, 8, 638. [Google Scholar] [CrossRef] [Green Version]
- Browder, F.E. Convergence theorems for sequence of nonlinear mappings in Hilbert spaces. Math. Z. 1967, 100, 201–225. [Google Scholar] [CrossRef]
- Opial, Z. Weak convergence of the sequence of successive approximations for nonexpansive mappings. Bull. Am. Math. Soc. 1967, 73, 591–597. [Google Scholar] [CrossRef] [Green Version]
- Browder, F.E. Fixed point theorems for nonlinear semicontractive mappings in Banach spaces. Arch. Ration. Mech. Anal. 1966, 21, 259–269. [Google Scholar] [CrossRef]
- Gossez, J.-P.; Dozo, E.L. Some geometric properties related to the fixed point theory for nonexpansive mappings. Pac. J. Math. 1972, 40, 565–573. [Google Scholar] [CrossRef] [Green Version]
- Xu, H.K. Inequalities in Banach Spaces with Applications. Nonlinear Anal. 1991, 16, 1127–1138. [Google Scholar] [CrossRef]
- Beck, A.; Teboulle, M. A fast iterative shrinkage thresholding algorithm for linear inverse problem. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef] [Green Version]
- Agarwal, R.P.; Regan, D.O.; Sahu, D.R. Fixed Point Theory for Lipschitzian-Type Mappings with Applications; Springer: Berlin, Germany, 2009. [Google Scholar]
- Pan, C.; Wang, Y. Generalized viscosity implicit iterative process for asymptotically non-expansive mappings in Banach spaces. Mathematics 2019, 7, 379. [Google Scholar] [CrossRef] [Green Version]
- Vaish, R.; Ahmad, M.K. Generalized viscosity implicit schemewith Meir-Keeler contraction for asymptotically nonexpansive mapping in Banach spaces. Numer. Algorithms 2020, 84, 1217–1237. [Google Scholar] [CrossRef]
- Figueiredo, M.A.T.; Nowak, R.D.; Wright, S.J. Gradient projection for sparse reconstruction: Application to compressed sensing and other inverse problems. IEEE J. Sel. Top. Signal Process. 2007, 1, 586–597. [Google Scholar] [CrossRef] [Green Version]
- Shehu, Y.; Vuong, P.T.; Cholamjiak, P. A self-adaptive projection method with an inertial technique for split feasibility problems in Banach spaces with applications to image restoration problems. J. Fixed Point Theory Appl. 2019, 21, 1–24. [Google Scholar] [CrossRef]
- Shehu, Y.; Iyiola, O.S.; Ogbuisi, F.U. Iterative method with inertial terms for nonexpansive mappings, Applications to compressed sensing. Numer. Algorithms 2020, 83, 1321–1347. [Google Scholar] [CrossRef]


| Alg. (25) | Alg. (26) | Alg. (27) | ||||
|---|---|---|---|---|---|---|
| Iter. | CPU (sec) | Iter. | CPU (sec) | Iter. | CPU (sec) | |
| Case I | 32 | 0.0063 | 84 | 0.0750 | 69 | 0.0102 |
| Case II | 33 | 0.0065 | 74 | 0.0724 | 69 | 0.0120 |
| Case III | 38 | 0.0084 | 87 | 0.0847 | 78 | 0.0103 |
| Case IV | 48 | 0.0095 | 123 | 0.0781 | 89 | 0.0131 |
| Our Alg. | Pan and Wang Alg. | Vaish and Ahmad Alg. | ||||
|---|---|---|---|---|---|---|
| Iter. | CPU (sec) | Iter. | CPU (sec) | Iter. | CPU (sec) | |
| Case I | 35 | 0.0103 | 88 | 0.0382 | 58 | 0.0156 |
| Case II | 22 | 0.0067 | 43 | 0.0163 | 40 | 0.0104 |
| Case III | 30 | 0.0090 | 70 | 0.0487 | 45 | 0.0175 |
| Case IV | 30 | 0.0072 | 74 | 0.0368 | 45 | 0.0175 |
| Our Alg. | Pan and Wang Alg. | Vaish and Ahmad Alg. | |
|---|---|---|---|
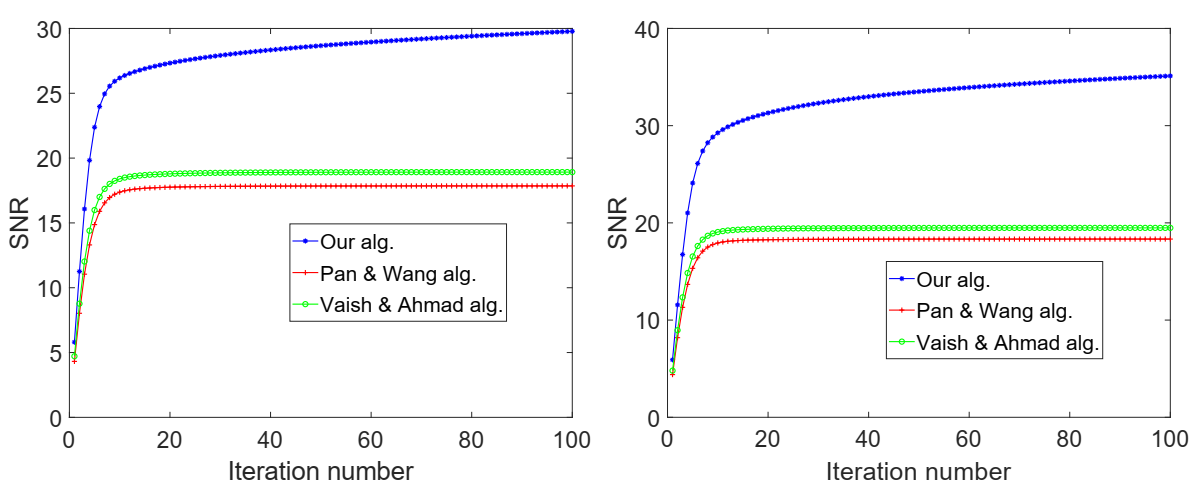
| Cameraman image | 2.7928 | 2.6422 | 2.6709 |
| Pout image | 4.8237 | 4.4248 | 3.45630 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Harbau, M.H.; Ugwunnadi, G.C.; Jolaoso, L.O.; Abdulwahab, A. Inertial Accelerated Algorithm for Fixed Point of Asymptotically Nonexpansive Mapping in Real Uniformly Convex Banach Spaces. Axioms 2021, 10, 147. https://doi.org/10.3390/axioms10030147
Harbau MH, Ugwunnadi GC, Jolaoso LO, Abdulwahab A. Inertial Accelerated Algorithm for Fixed Point of Asymptotically Nonexpansive Mapping in Real Uniformly Convex Banach Spaces. Axioms. 2021; 10(3):147. https://doi.org/10.3390/axioms10030147
Chicago/Turabian StyleHarbau, Murtala Haruna, Godwin Chidi Ugwunnadi, Lateef Olakunle Jolaoso, and Ahmad Abdulwahab. 2021. "Inertial Accelerated Algorithm for Fixed Point of Asymptotically Nonexpansive Mapping in Real Uniformly Convex Banach Spaces" Axioms 10, no. 3: 147. https://doi.org/10.3390/axioms10030147
APA StyleHarbau, M. H., Ugwunnadi, G. C., Jolaoso, L. O., & Abdulwahab, A. (2021). Inertial Accelerated Algorithm for Fixed Point of Asymptotically Nonexpansive Mapping in Real Uniformly Convex Banach Spaces. Axioms, 10(3), 147. https://doi.org/10.3390/axioms10030147







