Random Walk Analysis in a Reliability System under Constant Degradation and Random Shocks
Abstract
:1. Introduction
1.1. Background
1.2. Pertinent Literature
1.2.1. Shock Models
1.2.2. Cumulative Shock Models
1.2.3. Extreme Shock Models
1.2.4. -Shock Models
1.2.5. Run Shock Models
1.2.6. Mixed Shock Models
1.2.7. Shock and Degradation Models
- (a)
- Soft failures are caused by continuous wear degradation and vocational non-fatal and extreme shocks that arrive in accordance with a marked Poisson process of rate for its support counting measure with position independent marking and with marks ’s and ’s independent of each other. A soft failure occurs when the cumulative degradation process (due to wear and periodic shocks ’s) crosses a fixed threshold Additionally, ;
- (b)
- Hard failures caused by extreme shocks (also referred to as shock loads) affect a different unit of the system and that causes a catastrophic failure. Only in this case does the system fail if any such shock exceeds some level D.
1.3. Our Model
1.3.1. Our Methodology
1.3.2. Paper’s Layout
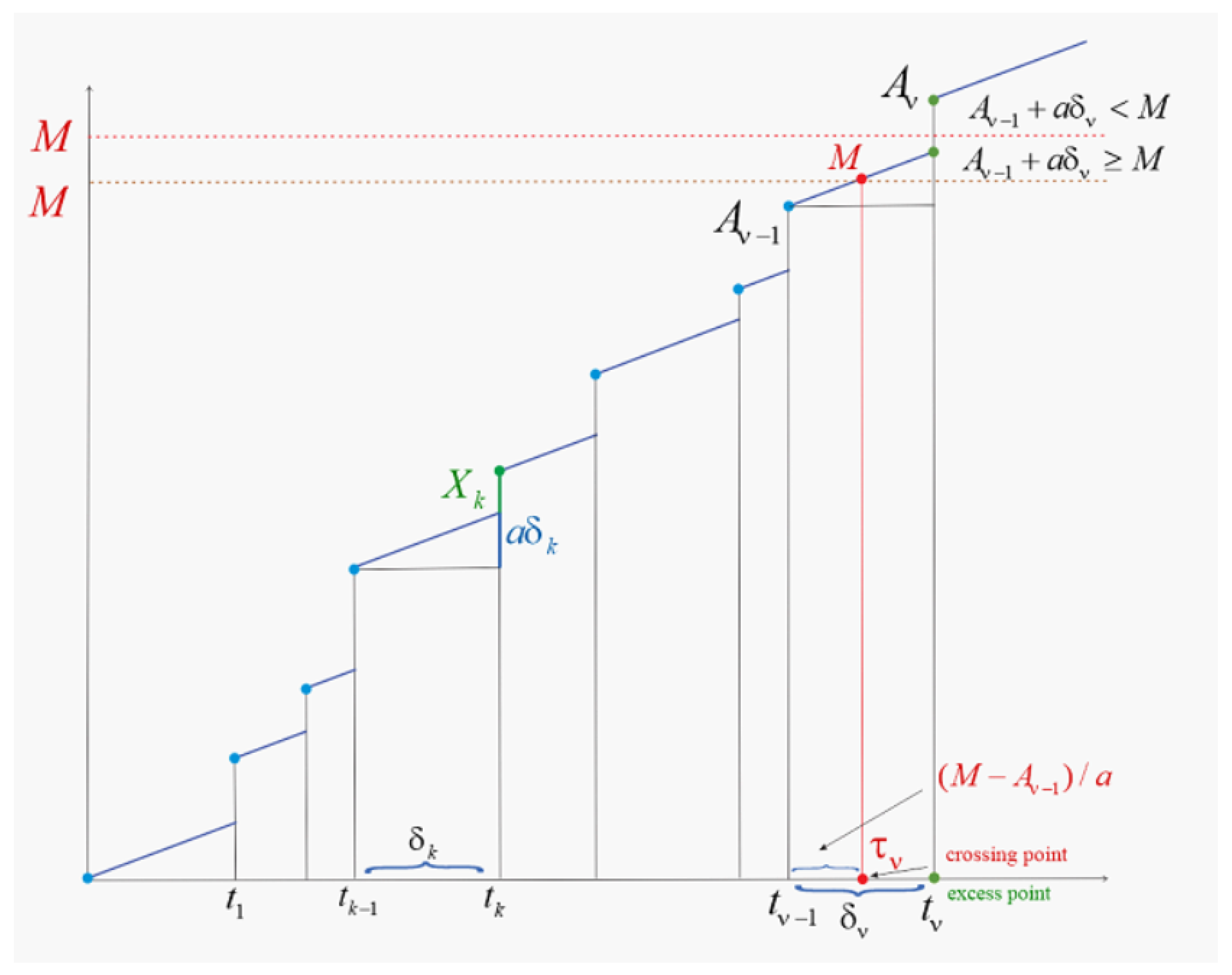
2. Fluctuation Analysis of the Linear Degradation Process with Shocks
3. Results for a Dual-Exponential Shock Process
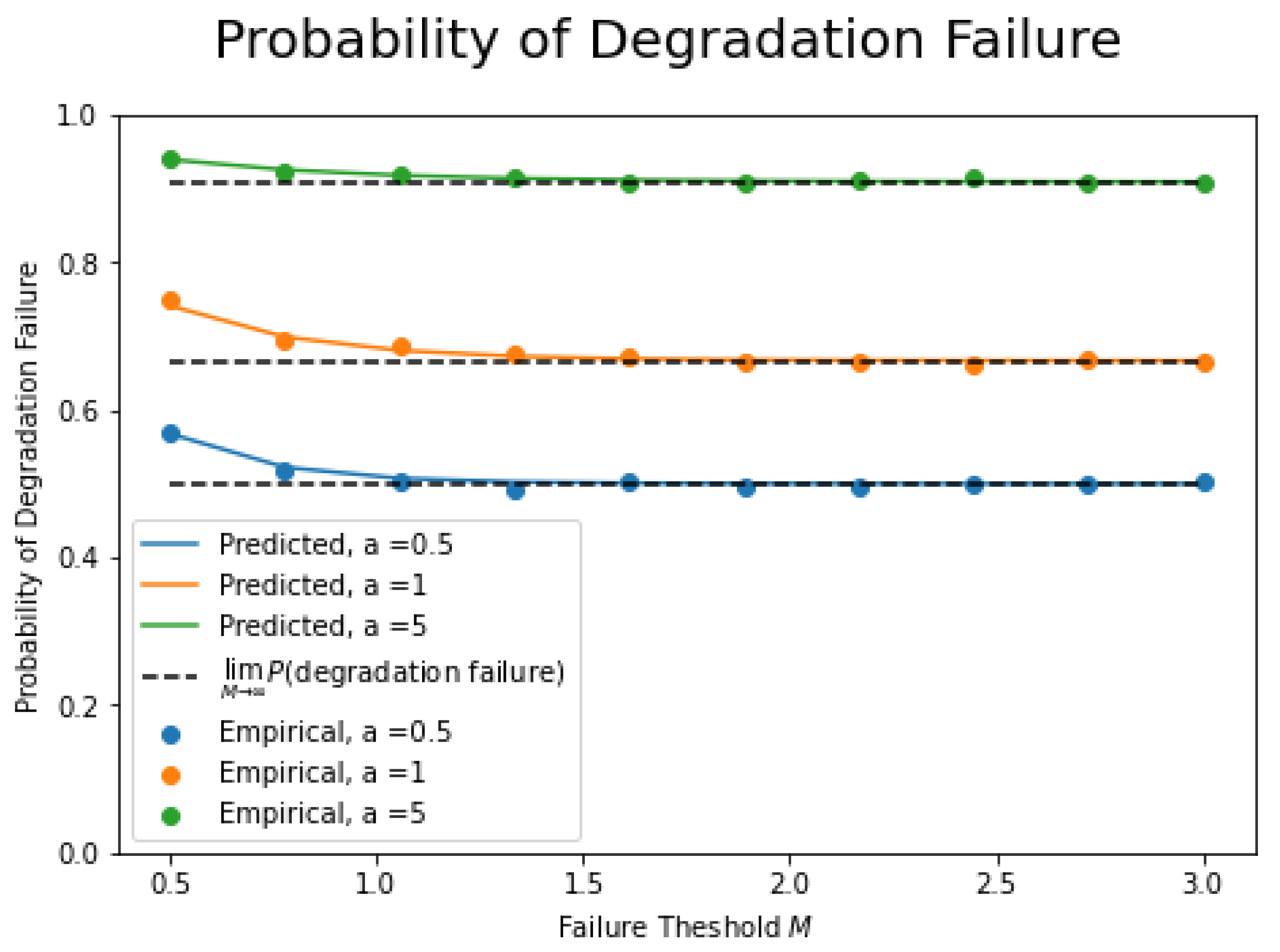
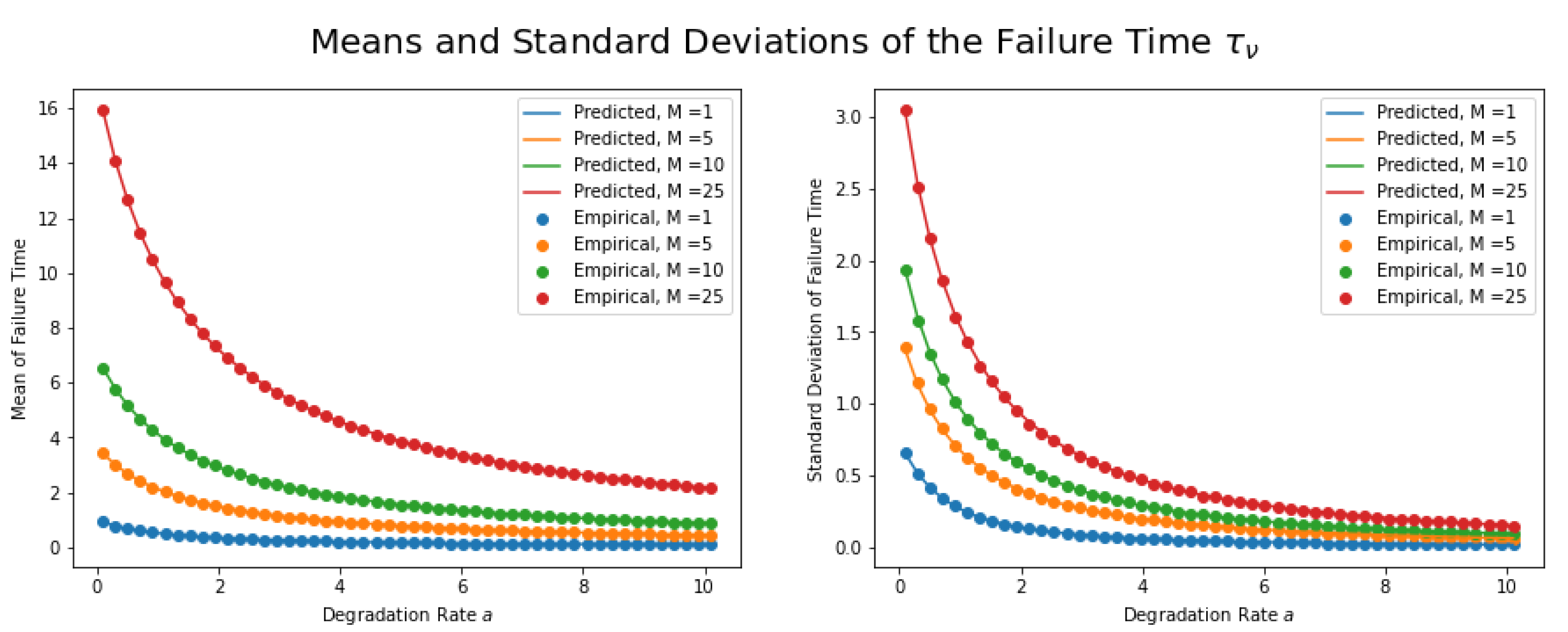
4. Comparison with Stochastic Simulation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| General Acronyms | |
| i.i.d. | independent and identically distributed |
| LST | Laplace-Stieltjes transform |
| probability distribution function | |
| probability density function | |
| PGF | probability-generating function |
| r.v. | random variable |
| Notation in the Literature Review | |
| soft shocks marked point process in cumulative shock model | |
| associated support counting measure of shocks’ arrivals | |
| the number of shocks in time interval | |
| Dirac point mass (unity measure) | |
| magnitudes of soft shocks | |
| the time of the nth shock | |
| pure degradation process | |
| magnitudes of hard shocks | |
| marked point measure of hard shocks | |
| lower threshold in -shock policy models | |
| x | failure threshold |
| M | soft failure threshold |
| D | hard failure threshold |
| number of soft shocks until soft failure with respect to threshold x | |
| number of hard shocks until hard failure with respect to threshold x | |
| A | the set that process escapes |
| Notation in Our Model | |
| number of the first shock where degradation exceeds M | |
| pre-failure time | |
| soft failure time (the escape from set A) | |
| pre-failure cumulative damage | |
| cumulative damage to the system at the failure | |
| operator | |
| modified Bessel function of order zero | |
| soft shocks and degradation marked point process | |
| cumulative degradation process including shocks | |
| M | failure threshold |
| failure time if it occurs upon constant degradation | |
| failure time if it occurs upon a shock | |
| Laplace transform | |
| inverse Laplace transform | |
| p | failure threshold |
| standard Gaussian PDF | |
| equivalence class of all exponential distributions with parameter | |
| equivalence classs of all geometric random variables with parameter | |
| equivalence class of all gamma distributions with parameters | |
| equivalence class of all Gaussian distributions with parameters | |
Appendix A
Appendix A.1. Simulation Code
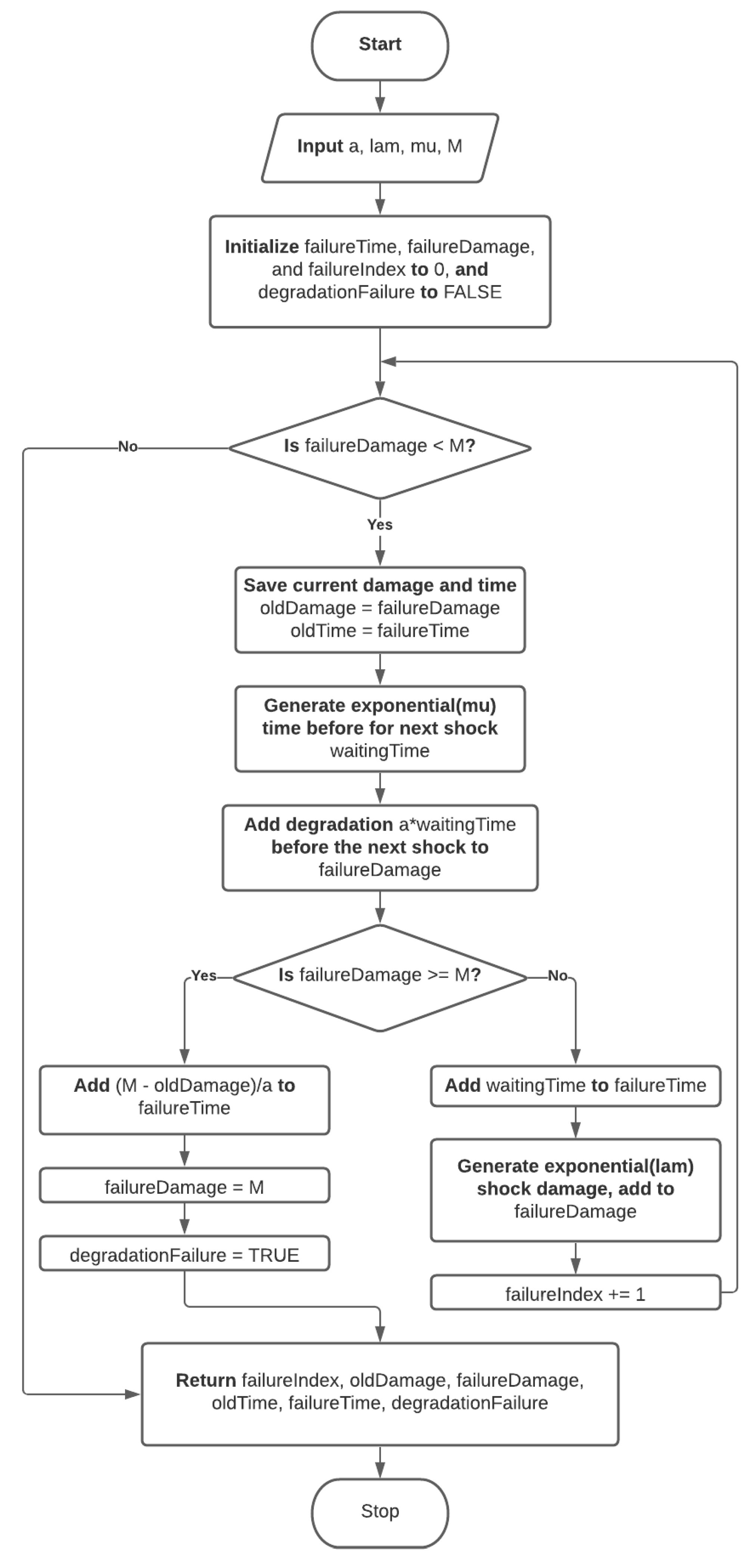
- import numpy as~np
- def simulatePath(a, lam, mu, M):
- # initialize outputs
- failureTime = 0
- failureDamage = 0
- failureIndex = 0
- degradationFailure = False
- # simulate the process
- while failureDamage < M:
- # save A_j-1
- oldDamage = failureDamage
- # save t_j-1
- oldTime = failureTime
- # compute waiting time before the next shock
- waitingTime = np.random.exponential(1/mu)
- # add degradation between shocks
- failureDamage += a ∗ waitingTime
- # if degradation causes damage to reach M...
- if failureDamage >= M:
- # compute tau_nu
- failureTime += (M - oldDamage)/a
- # set S_nu (total damage) to M
- failureDamage = M
- # mark degradation as the cause of the failure
- degradationFailure = True
- # exit the loop
- break
- # else, add the shock
- else:
- # add the waiting time
- failureTime += waitingTime
- # add the shock damage
- failureDamage += np.random.exponential(1/lam)
- # add 1 to the shock counter
- failureIndex += 1
- # gather the output values into a tuple
- outputs = (failureIndex, oldDamage, failureDamage,
- oldTime, failureTime, degradationFailure)
- # return values nu, A_nu-1, S_nu, t_nu-1, tau_nu, flag for
- # failure type
- return outputs
- simulatePath(a, lam, mu, M)
- def degradationProbability(a, lam, mu, M):
- term = a ∗ lam + mu ∗ np.exp(-(lam + mu / a) ∗ M)
- return term / (a ∗ lam + mu)
- def failureTimeMean(a, lam, mu, M):
- term = lam ∗ M + 1 - degradationProbability(a, lam, mu, M)
- return term / (a ∗ lam + mu)
- def failureTimeVariance(a, lam, mu, M):
- dTerm = a ∗ lam + mu
- eTerm = np.exp(-(lam + mu / a) ∗ M)
- term1 = 2 ∗ lam ∗ mu ∗ M / dTerm ∗∗ 3
- term2 = mu ∗ (mu - 4 ∗ a ∗ lam) / dTerm ∗∗ 4
- term3 = 2 ∗ mu
- term3 ∗= 2 ∗ a ∗∗ 2 ∗ lam + (a ∗ lam) ∗∗ 2 ∗ M - 2 ∗ mu ∗∗ 2 ∗ M
- term3 ∗= eTerm / (a ∗ dTerm ∗∗ 4)
- term4 = 2 ∗ mu ∗∗ 2 ∗ eTerm ∗∗ 2 / dTerm ∗∗ 4
- return term1 + term2 + term3 - term4
- def failureDamageMean(a, lam, mu, M):
- return M + (1 - degradationProbability(a, lam, mu, M)) / lam
- def failureDamageVariance(a, lam, mu, M):
- dTerm = a ∗ lam + mu
- eTerm = np.exp(-(lam + mu / a) ∗ M)
- term1 = 2 ∗ a ∗ mu ∗ (1 - eTerm) / (lam ∗ dTerm ∗∗ 2)
- term2 = mu ∗∗ 2 ∗ (1 - eTerm ∗∗ 2) / (lam ∗ dTerm) ∗∗ 2
- return term1 + term2
References
- Tsai, C.C.; Tseng, S.T.; Balakrishnan, N. Mis-specification analyses of gamma and Wiener degradation processes. J. Stat. Plan. Inference 2011, 141, 3725–3735. [Google Scholar] [CrossRef]
- Gut, A. Cumulative shock models. Adv. Appl. Probab. 1990, 22, 504–507. [Google Scholar] [CrossRef] [Green Version]
- Gut, A.; Hüsler, J. Shock models. In Advances in Degradation Modeling: Applications to Reliability, Survival Analysis, and Finance; Nikulin, M.S., Limnios, N., Balakrishnan, N., Kahle, W., Huber-Carol, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Chapter 5; pp. 56–124. [Google Scholar]
- Sumita, U.; Shanthikumar, J.G. A class of correlated cumulative shock models. Adv. Appl. Probab. 1985, 17, 347–366. [Google Scholar] [CrossRef]
- Abolnikov, L.; Dshalalow, J.H. A first passage problem and its applications to the analysis of a class of stochastic models. J. Appl. Math. Stoch. Anal. 1992, 5, 83–97. [Google Scholar] [CrossRef] [Green Version]
- Dshalalow, J.H.; Huang, W. On noncooperative hybrid stochastic games. Nonlinear Anal. Hybrid Syst. 2008, 2, 803–811. [Google Scholar] [CrossRef]
- Dshalalow, J.H.; Robinson, R. On one-sided stochastic games and their applications to finance. Stoch. Model. 2012, 28, 1–14. [Google Scholar] [CrossRef]
- Gut, A.; Hüsler, J. Extreme shock models. Extremes 1999, 2, 295–307. [Google Scholar] [CrossRef]
- Li, Z.; Kong, X. Life behavior of δ-shock model. Stat. Probab. Lett. 2007, 77, 577–587. [Google Scholar] [CrossRef]
- Eryilmaz, S.; Bayramoglu, K. Life behavior of δ-shock models for uniformly distributed interarrival times. Stat. Pap. 2013, 55, 841–852. [Google Scholar] [CrossRef]
- Eryılmaz, S. Generalized δ-shock model via runs. Stat. Probab. Lett. 2012, 82, 326–331. [Google Scholar] [CrossRef]
- Mallor, F.; Omey, E. Shocks, runs and random sums. J. Appl. Probab. 2001, 38, 438–448. [Google Scholar] [CrossRef]
- Mallor, F.; Santos, J. Reliability of systems subject to shocks with a stochastic dependence for the damages. Test 2003, 12, 427–444. [Google Scholar] [CrossRef]
- Mallor, F.; Omey, E.; Santos, J. Asymptotic results for a run and cumulative mixed shock model. J. Math. Sci. 2006, 138, 5410–5414. [Google Scholar] [CrossRef]
- Ozkut, M.; Eryilmaz, S. Reliability analysis under Marshall–Olkin run shock model. J. Comput. Appl. Math. 2019, 349, 52–59. [Google Scholar] [CrossRef]
- Marshall, A.W.; Olkin, I. A multivariate exponential distribution. J. Am. Stat. Assoc. 1967, 62, 30–44. [Google Scholar] [CrossRef]
- Marshall, A.W.; Olkin, I. A generalized bivariate exponential distribution. J. Appl. Probab. 1967, 4, 291–302. [Google Scholar] [CrossRef]
- Eryilmaz, S.; Tekin, M. Reliability evaluation of a system under a mixed shock model. J. Comput. Appl. Math. 2019, 352, 255–261. [Google Scholar] [CrossRef]
- Zhao, X.; Guo, X.; Wang, X. Reliability and maintenance policies for a two-stage shock model with self-healing mechanism. Reliab. Eng. Syst. Saf. 2018, 172, 185–194. [Google Scholar] [CrossRef]
- Peng, H.; Feng, Q.; Coit, D.W. Reliability and maintenance modeling for systems subject to multiple dependent competing failure processes. IIE Trans. 2010, 43, 12–22. [Google Scholar] [CrossRef]
- Hao, H.; Su, C.; Qu, Z. Reliability analysis for mechanical components subject to degradation process and random shock with Wiener process. In The 19th International Conference on Industrial Engineering and Engineering Management; Springer: Berlin/Heidelberg, Germany, 2013; pp. 531–543. [Google Scholar] [CrossRef]
- Rafiee, K.; Feng, Q.; Coit, D.W. Reliability assessment of competing risks with generalized mixed shock models. Reliab. Eng. Syst. Saf. 2017, 159, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Hao, S.; Yang, J.; Ma, X.; Zhao, Y. Reliability modeling for mutually dependent competing failure processes due to degradation and random shocks. Appl. Math. Model. 2017, 51, 232–249. [Google Scholar] [CrossRef]
- Yousefi, N.; Coit, D.W.; Song, S.; Feng, Q. Optimization of on-condition thresholds for a system of degrading components with competing dependent failure processes. Reliab. Eng. Syst. Saf. 2019, 192, 106547. [Google Scholar] [CrossRef] [Green Version]
- Cao, Y.; Liu, S.; Fang, Z.; Dong, W. Modeling ageing effects in the context of continuous degradation and random shock. Comput. Ind. Eng. 2020, 145, 106539. [Google Scholar] [CrossRef]
- Oliveira, R.P.; Achcar, J.A.; Mazucheli, J.; Bertoli, W. A new class of bivariate Lindley distributions based on stress and shock models and some of their reliability properties. Reliab. Eng. Syst. Saf. 2021, 211, 107528. [Google Scholar] [CrossRef]
- Dshalalow, J.H.; White, R.T. Current trends in random walks on random lattices. Mathematics 2021, 9, 1148. [Google Scholar] [CrossRef]
- Dshalalow, J.H. On the level crossing of multi-dimensional delayed renewal processes. J. Appl. Math. Stoch. Anal. 1997, 10, 355–361. [Google Scholar] [CrossRef] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dshalalow, J.H.; White, R.T. Random Walk Analysis in a Reliability System under Constant Degradation and Random Shocks. Axioms 2021, 10, 199. https://doi.org/10.3390/axioms10030199
Dshalalow JH, White RT. Random Walk Analysis in a Reliability System under Constant Degradation and Random Shocks. Axioms. 2021; 10(3):199. https://doi.org/10.3390/axioms10030199
Chicago/Turabian StyleDshalalow, Jewgeni H., and Ryan T. White. 2021. "Random Walk Analysis in a Reliability System under Constant Degradation and Random Shocks" Axioms 10, no. 3: 199. https://doi.org/10.3390/axioms10030199
APA StyleDshalalow, J. H., & White, R. T. (2021). Random Walk Analysis in a Reliability System under Constant Degradation and Random Shocks. Axioms, 10(3), 199. https://doi.org/10.3390/axioms10030199





