A Shortcut Method to Solve for a 1D Heat Conduction Model under Complicated Boundary Conditions
Abstract
:1. Introduction
2. Basic Model
- (1)
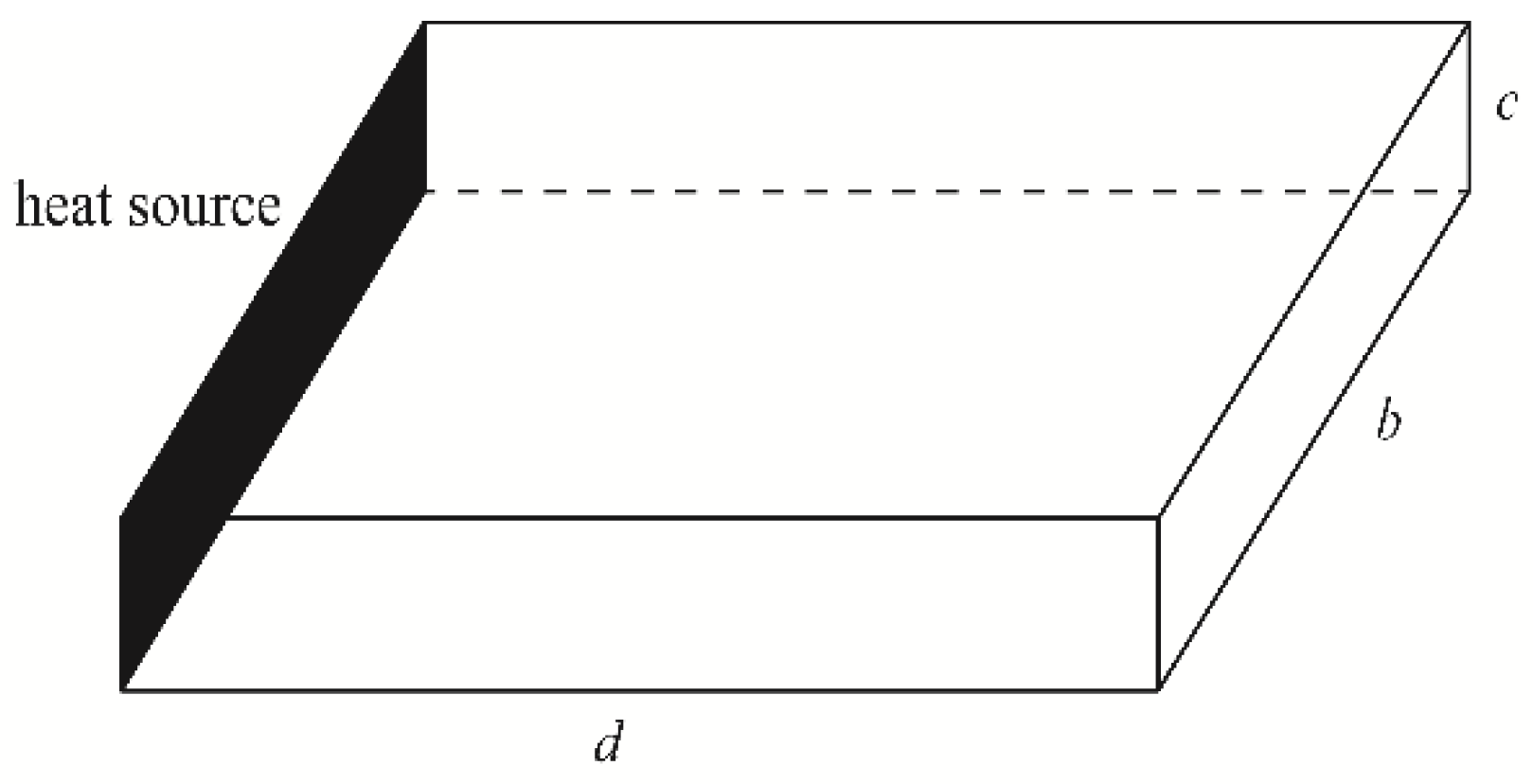
- The material is homogeneous, isotropic, and extends infinitely in the x-direction.
- (2)
- The material has a heat source set at one end, forming a Dirichlet boundary. The outer surface of both the material and its boundary are insulated surfaces.
- (3)
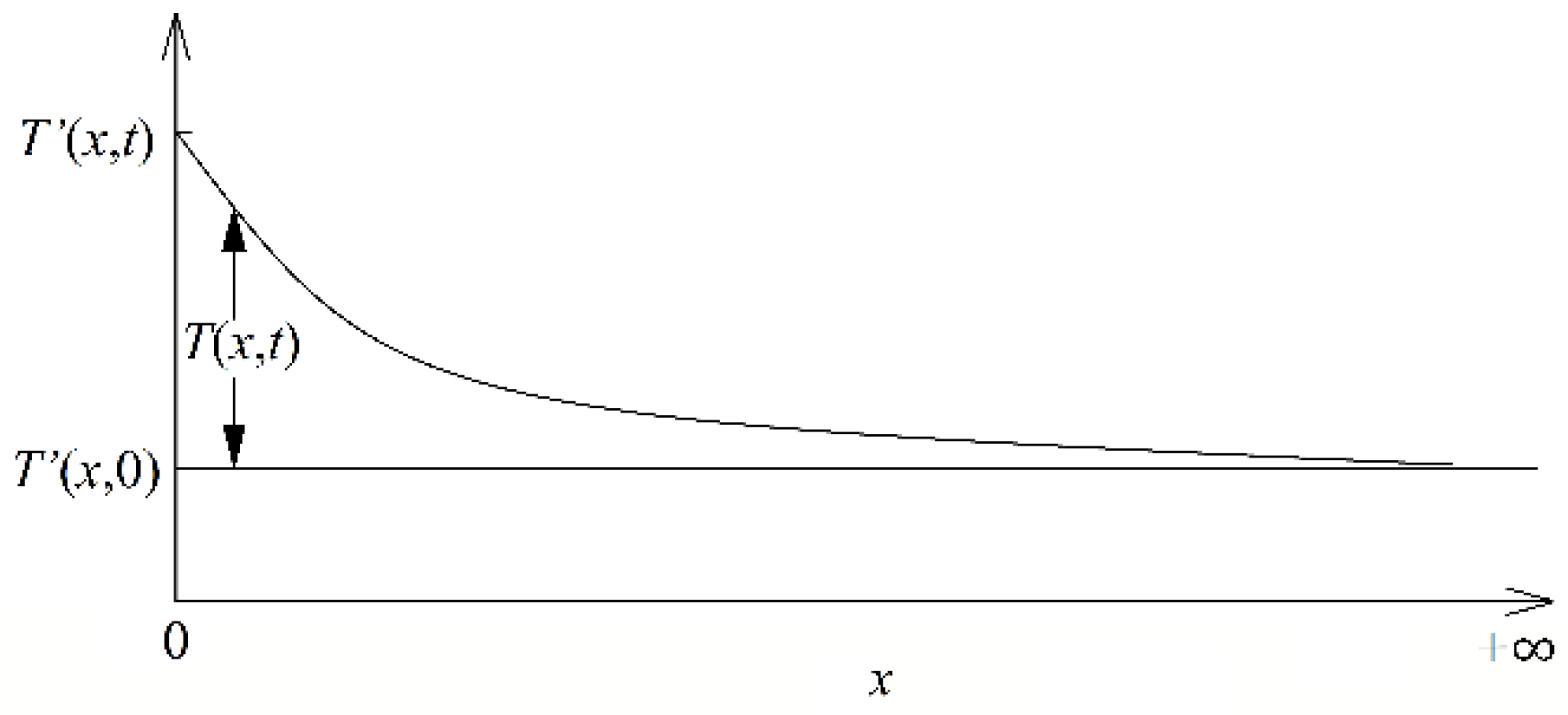
- The temperature of the material at moment t from the boundary x is noted as T’(x, t), and the initial temperature of both the material and the boundary is T’(x, 0); the excess temperature at distance x from the boundary is noted as T(x,t) = T’(x,t) − T’(x,0) (as shown in Figure 2).
- (4)
- The excess temperature of the boundary as a function of time is denoted as f(t).
- (5)
- The heat transfer from the heat source to the thin-layer material is regarded as a one-dimensional process.
3. Solutions
3.1. Theoretical Solution
3.2. Analytical Solution
3.3. Specific Analytical Solutions under Particular Conditions
3.3.1. f(t) = ΔT0
3.3.2. ΔT0 ≠ 0 ∩ i = 1
4. Methods
4.1. Curve Fitting Method
4.2. Inflection Point Method
5. Results
5.1. Curve Fitting Method
5.2. Inflection Point Method
6. Discussion
6.1. Comparison to Traditional Solving Method
6.2. Comparison of Thermal Diffusivity Obtained by the Two Methods
6.3. Variation Laws of the Appearance Moment of the Inflection Point
7. Conclusions
- When it is difficult to give a specific and accurate expression for boundary temperature, due to its complicated variation process, the properties of the Fourier transform and the differential characteristic of the convolution integral can be fully utilized for deriving the theoretical solution to the 1D heat conduction model, without considering the detailed transformation process of f(t). In addition, the piecewise linear interpolation method is adopted to discretize the actual temperature variation process, followed by substituting the interpolation function into the theoretical solution, thus providing a shortcut method to obtain a solution composed of more commonly used functions with a relatively simple form. For the study of similar problems based on this sort of heat conduction model, this resolving method can also be referenced.
- Based on the derived solution and the variation characteristics of the temperature variation rate φ(x,t) with time t, the curve fitting method and the inflection point method used to calculate the thermal diffusivity a are given, and the values of a calculated by the two methods are basically consistent.
- For a certain material (i.e., a is a fixed value), the higher the initial temperature of the heat source, the slower the temperature of the heat source decreases, and the further away from the heat source, then the later the inflection point of the φ(x,t)-t curve (the curve of temperature variation velocity curve at distance x from the boundary with time t) appears.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| a | thermal diffusivity, m2/d |
| f | boundary temperature, °C |
| F | Fourier transform operator |
| F−1 | inverse Fourier transform operator |
| t | time, d |
| tg | the appearance moment of inflection point, h |
| T | temperature of calculation point, °C |
| image function for Fourier transform | |
| ΔT0 | instantaneous change of boundary temperature, °C |
| x | distance from the boundary of the calculation point, m |
| β | boundary temperature variation rate, °C/d |
| φ | temperature variation rate of the calculation point, °C/h |
| ω | Fourier operator |
| * | convolution operator |
References
- Fourier, J. The Analytical Theory of Heat; Peking University Press: Beijing, China, 2008; pp. 90–91. [Google Scholar]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids; Oxford University Press: Oxford, UK, 1986; pp. 62–64. [Google Scholar]
- Asogwa, K.K.; Goud, B.S.; Shah, N.A.; Yook, S. Rheology of electromagnetohydrodynamic tangent hyperbolic nanofluid over a stretching riga surface featuring dufour effect and activation energy. Sci. Rep. 2022, 12, 14602. [Google Scholar] [CrossRef] [PubMed]
- Bejawada, S.G.; Jamshed, W.; Safdar, R.; Reddy, Y.D.; Alanazi, M.M.; Zahran, H.Y.; Eid, M.R. Chemical reactive and viscous dissipative flow of magneto nanofluid via natural convection by employing Galerkin finite element technique. Coatings 2022, 12, 151. [Google Scholar] [CrossRef]
- Goud, B.S. Thermal radiation influences on MHD stagnation point stream over a stretching sheet with slip boundary conditions. Int. J. Sci. Technol. 2020, 7, 70201. [Google Scholar] [CrossRef]
- Kumar, P.P.; Goud, B.S.; Malga, B.S. Finite element study of Soret number effects on MHD flow of Jeffrey fluid through a vertical permeable moving plate. Part. Differ. Equ. Appl. Math. 2020, 1, 100005. [Google Scholar] [CrossRef]
- Shankar Goud, B. Heat generation/absorption influence on steady stretched permeable surface on MHD flow of a micropolar fluid through a porous medium in the presence of variable suction/injection. Int. J. Thermofluids 2020, 7–8, 100044. [Google Scholar] [CrossRef]
- Hu, X.; Deng, S.; Wang, Y.; Chen, J.; Zhang, L.; Guo, W.; Han, Y. Study progress on analytical solution of static temperature field with artificial ground freezing. Mine Constr. Technol. 2015, 36, 1–9. [Google Scholar]
- Xie, H.; Zhang, C.; Jiang, Y. An analytical solution to organic contaminants diffusion through composite liners consisting of a geomembrane,a GCL and an attenuation layer considering degradation. J. Hydraul. Eng. 2014, 45, 52–60. [Google Scholar]
- Suk, H.J.; Chen, J.S.; Park, E.Y.; Kihm, Y.H. Practical Application of the Galerkin Finite Element Method with a Mass Conservation Scheme under Dirichlet Boundary Conditions to Solve Groundwater Problems. Sustainability 2020, 12, 5627. [Google Scholar] [CrossRef]
- Shah, N.A.; Rauf, A.; Vieru, D.; Sitthithakerngkiet, K.; Kumam, P. Analytical Solutions of the Diffusion–Wave Equation of Groundwater Flow with Distributed-Order of Atangana–Baleanu Fractional Derivative. Appl. Sci. 2021, 11, 4142. [Google Scholar] [CrossRef]
- Falta, R.W.; Wang, W.W. A semi-analytical method for simulating matrix diffusion in numerical transport models. J. Contam. Hydrol. 2017, 197, 39–49. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Q.; Oldenburg, C.M.; Rutqvist, J. Revisiting the analytical solutions of heat transport in fractured reservoirs using a generalized multirate memory function. Water Resour. Res. 2019, 55, 1405–1428. [Google Scholar] [CrossRef]
- BniLam, N.; Al-Khoury, R.; Shiri, A.; Sluys, L.J. A semi-analytical model for detailed 3D heat flow in shallow geothermal systems. Int. J. Heat Mass Transf. 2018, 123, 911–927. [Google Scholar] [CrossRef]
- Li, Y.; Shu, L.; Xiao, R.; Tao, Y.; Niu, S.; Wang, Z. Effect of pumping-recharge well structures on heat transfer characteristics of double-well groundwater heat pump systems considering hydrothermal coupling. Energy Convers. Manag. 2021, 249, 114871. [Google Scholar] [CrossRef]
- Wu, D. Study on Heat Transfer Model of High Efficient Heat Exchange System in Ground Source Heat Pump. Ph.D. Dissertation, Hefei University of Technology, Hefei, China, 2019. [Google Scholar]
- Povstenko, Y.; Klekot, J. Fractional heat conduction with heat absorption in a sphere under Dirichlet boundary condition. Comput. Appl. Math. 2018, 37, 4475–4483. [Google Scholar] [CrossRef] [Green Version]
- Hua, Y.C.; Zhao, T.; Guo, Z.Y. Optimization of the one-dimensional transient heat conduction problems using extended entransy analyses. Int. J. Heat Mass Transf. 2018, 116, 166–172. [Google Scholar] [CrossRef]
- Huang, D.; Li, Y.; Pei, D. Identification of a time-dependent coefficient in heat conduction problem by new iteration method. Adv. Math. Phys. 2018, 2018, 4918256. [Google Scholar] [CrossRef]
- Kot, V.A. Integral method of boundary characteristics: The Dirichlet condition. Principles. Heat Transf. Res. 2016, 47, 1035–1055. [Google Scholar] [CrossRef]
- Fabre, A.; Hristov, J. On the integral-balance approach to the transient heat conduction with linearly temperature-dependent thermal diffusivity. Heat Mass Transf. 2017, 53, 177–204. [Google Scholar] [CrossRef]
- Kot, V.A. Integral method of boundary characteristics in solving the Stefan problem: Dirichlet condition. J. Eng. Phys. Thermophys. 2016, 89, 1289–1314. [Google Scholar] [CrossRef]
- Dell’Oro, F.; Goubet, O.; Mammeri, Y.; Pata, V. A semidiscrete scheme for evolution equations with memory. Discret. Contin. Dyn. Syst. 2019, 39, 5637–5658. [Google Scholar] [CrossRef] [Green Version]
- Gasilov, N.A.; Amrahov, S.E.; Fatullayev, A.G. On a solution of the fuzzy Dirichlet problem for the heat equation. Int. J. Therm. Sci. 2016, 103, 67–76. [Google Scholar] [CrossRef]
- Zhang, W.Z. Calculation of Unsteady Flow of Groundwater and Evaluation of Groundwater Resources; Science Press: Beijing, China, 1983; pp. 222–224. [Google Scholar]
- Shan, K.; Zhang, X.S.; Li, S.H. A method for measuring thermal properties of ground. Acta Energ. Sol. Sin. 2010, 31, 22–26. [Google Scholar]
- Kodikara, J.; Rajeev, P.; Rhoden, N.J. Determination of thermal diffusivity of soil using infrared thermal imaging. Can. Geotech. J. 2011, 48, 1295–1302. [Google Scholar] [CrossRef]
- Proskurnin, M.A.; Korte, D.; Rogova, O.B.; Volkov, D.S.; Franko, M. Photothermal Beam Deflection Spectroscopy for the Determination of Thermal Diffusivity of Soils and Soil Aggregates. Int. J. Thermophys. 2018, 39, 10765. [Google Scholar] [CrossRef]
- Beardsmore, G.; Egan, S.; Sandiford, M. A Fourier Spectral Method to Measure the Thermal Diffusivity of Soil. Geotech. Test. J. 2020, 43, 20180300. [Google Scholar] [CrossRef]
- Yoon, S.; Kim, M. Prediction of ground thermal diffusivity from thermal response tests. Energy Build. 2019, 185, 239–246. [Google Scholar] [CrossRef]
- Carson, J.K. A Versatile Effective Thermal Diffusivity Model for Porous Materials. Int. J. Thermophys. 2021, 42, 141. [Google Scholar] [CrossRef]
- Teng, Y.M. Some problems in integeral transform. Coll. Math. 2015, 31, 105–109. [Google Scholar]
- Zhang, Y.H.; Xi, M.C.; Chen, X.Q. Numerical Calculation Method and Algorithm; Science Press: Beijing, China, 2002; Volume 73, pp. 9–27. [Google Scholar]
- Li, G.; Sheng, Y.; Jin, H.; Ma, W.; Qi, J.; Wen, Z.; Zhang, B.; Mu, Y.; Bi, G. Forecasting the oil temperatures along the proposed China-Russia Crude Oil Pipeline using quasi 3-D transient heat conduction model. Cold Reg. Sci. Technol. 2010, 64, 235–242. [Google Scholar] [CrossRef]
- Zhou, C.; Chen, Y.; Wei, L.; Cheng, L.; Huang, Q.; Cao, X. Application of fitting-curve method to frequency analysis of POT flood series. Water Resour. Power 2011, 29, 48–50. [Google Scholar]
- Zeng, Q.; Mo, H.; Liu, J. Inflection point method to analyze the stability of soft soil embankment during construction. J. China Foreign Highw. 2006, 26, 21–25. [Google Scholar]

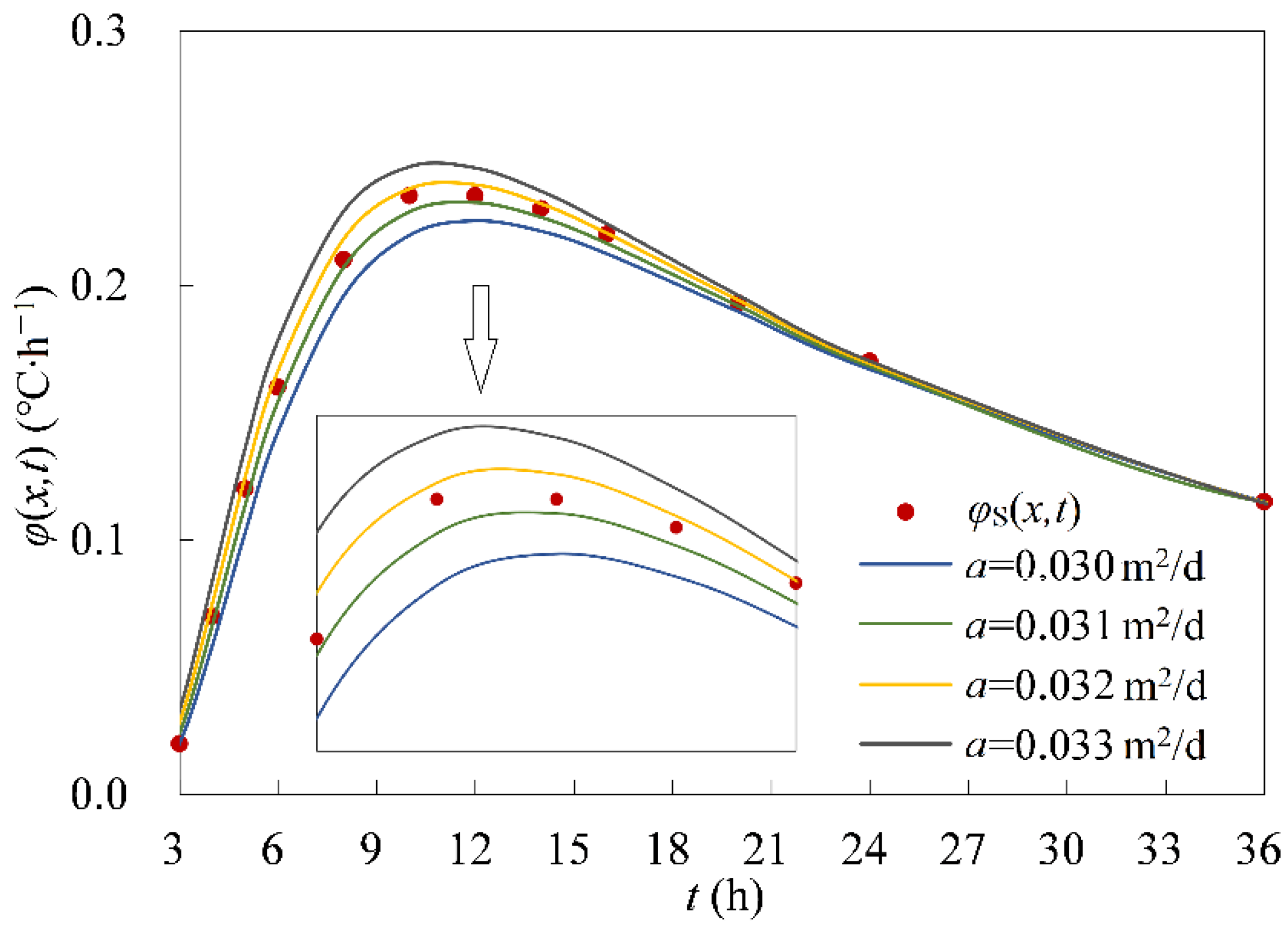
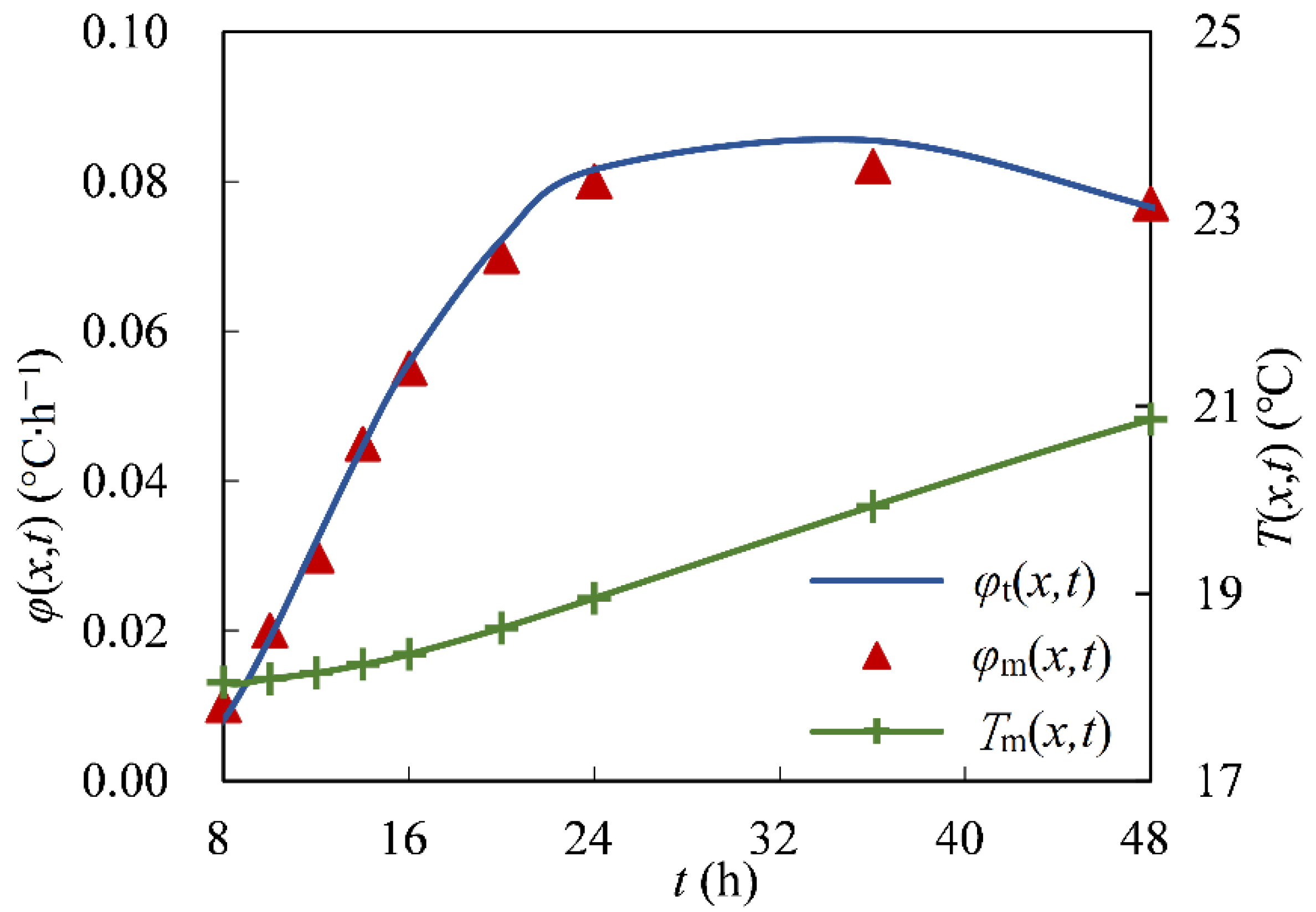
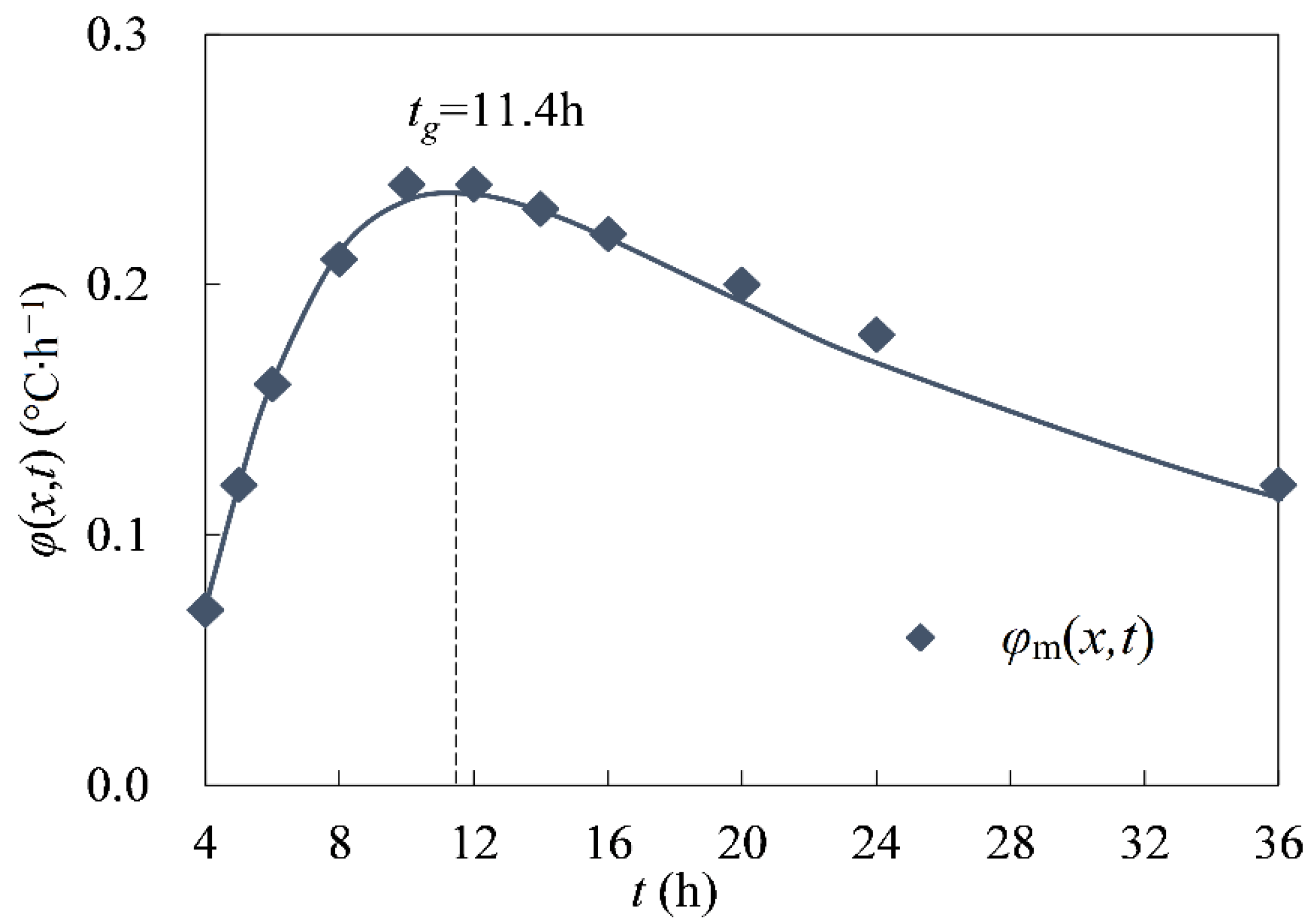

| t (h) | Tm(x,t) (°C) | φm(x,t) (°C∙h−1) |
|---|---|---|
| 3 * | 18.03 | 0.020 |
| 4 | 18.10 | 0.070 |
| 5 | 18.22 | 0.120 |
| 6 | 18.38 | 0.160 |
| 8 | 18.80 | 0.210 |
| 10 | 19.27 | 0.235 |
| 12 | 19.74 | 0.235 |
| 14 | 20.20 | 0.230 |
| 16 | 20.64 | 0.220 |
| 20 | 21.41 | 0.193 |
| 24 | 22.09 | 0.170 |
| 36 * | 23.47 | 0.115 |
| t (h) | Tm(x,t) (°C) | φm(x,t) (°C∙h−1) | φt(x,t) (°C∙h−1) |
|---|---|---|---|
| 8 * | 18.05 | 0.010 | 0.008 |
| 10 | 18.09 | 0.020 | 0.019 |
| 12 | 18.15 | 0.030 | 0.032 |
| 14 | 18.24 | 0.045 | 0.045 |
| 16 | 18.35 | 0.055 | 0.056 |
| 20 | 18.63 | 0.070 | 0.072 |
| 24 | 18.95 | 0.080 | 0.082 |
| 36 | 19.93 | 0.082 | 0.085 |
| 48 | 20.86 | 0.077 | 0.077 |
| ΔT0 (°C) | tg (h) |
|---|---|
| 10 | 11.375 |
| 14 | 11.400 |
| 18 | 11.415 |
| 22 | 11.424 |
| 26 | 11.430 |
| β (°C·d−1) | tg (h) |
|---|---|
| −0.15 | 11.435 |
| −0.20 | 11.425 |
| −0.25 | 11.415 |
| −0.30 | 11.405 |
| −0.35 | 11.395 |
| x (m) | tg (h) |
|---|---|
| 0.20 | 5.086 |
| 0.25 | 7.937 |
| 0.30 | 11.415 |
| 0.35 | 15.512 |
| 0.40 | 20.224 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, T.; Tao, Y.; Ren, H.; Lin, F. A Shortcut Method to Solve for a 1D Heat Conduction Model under Complicated Boundary Conditions. Axioms 2022, 11, 556. https://doi.org/10.3390/axioms11100556
Wei T, Tao Y, Ren H, Lin F. A Shortcut Method to Solve for a 1D Heat Conduction Model under Complicated Boundary Conditions. Axioms. 2022; 11(10):556. https://doi.org/10.3390/axioms11100556
Chicago/Turabian StyleWei, Ting, Yuezan Tao, Honglei Ren, and Fei Lin. 2022. "A Shortcut Method to Solve for a 1D Heat Conduction Model under Complicated Boundary Conditions" Axioms 11, no. 10: 556. https://doi.org/10.3390/axioms11100556
APA StyleWei, T., Tao, Y., Ren, H., & Lin, F. (2022). A Shortcut Method to Solve for a 1D Heat Conduction Model under Complicated Boundary Conditions. Axioms, 11(10), 556. https://doi.org/10.3390/axioms11100556






