Solving Time-Fractional Partial Differential Equation Using Chebyshev Cardinal Functions
Abstract
1. Introduction
2. Chebyshev Cardinal Functions
2.1. Operational Matrix of Derivation
- 1.
- If , due to the fact that , we have
- 2.
- If , according to Equation (14), we get
2.2. Operational Matrix of Fractional Integration
2.3. Operational Matrix of Fractional Derivation
3. Galerkin Method
Convergence Analysis
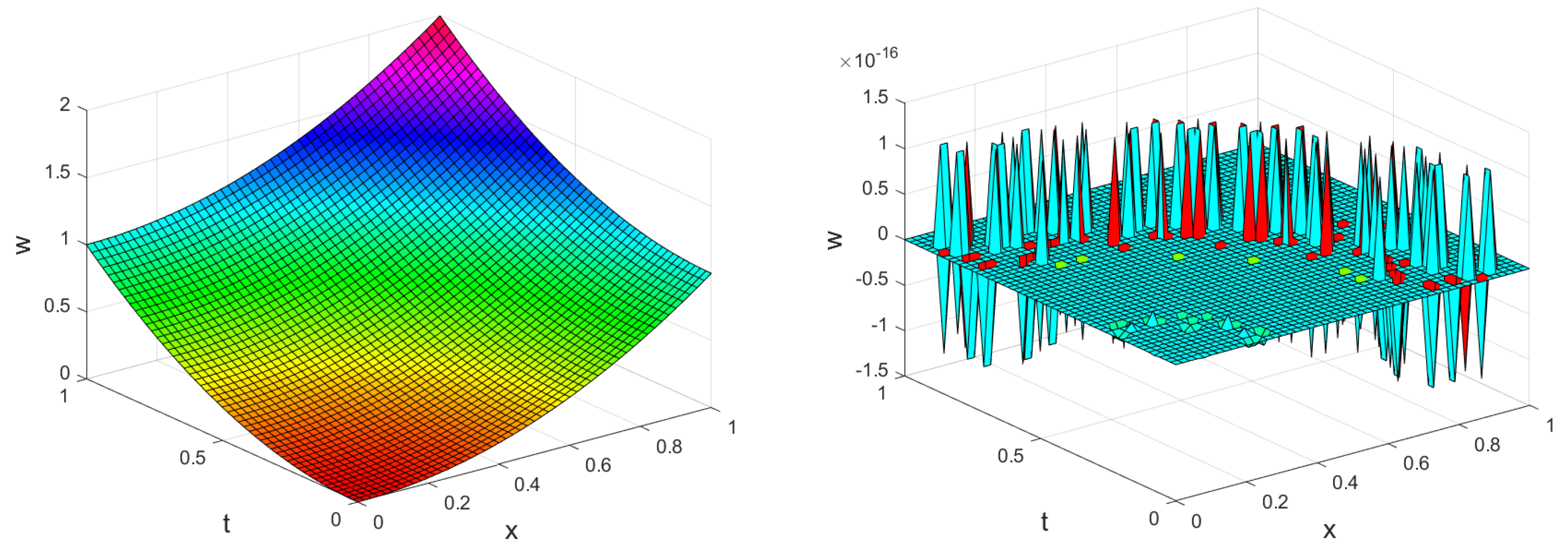
4. Numerical Experiments
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| TFPDEs | Time-fractional partial differential equations |
| CCFs | Chebyshev cardinal functions |
| RBFs | Radial basis functions |
References
- Udita, N.K. A New Approach To Generalized Fractional Derivatives. Bull. Math. Anal. Appl. 2014, 6, 1–15. [Google Scholar]
- Arif, M.; Ali, F.; Khan, I.; Nisar, K.S. A time fractional model with non-singular kernel the generalized couette flow of couple stress nanofluid. IEEE Access 2020, 8, 77378–77395. [Google Scholar] [CrossRef]
- Chang, A.; Sun, H.; Zheng, C.; Lu, B.; Lu, C.; Ma, R.; Zhang, Y. A Time Fractional Convection-Diffusion Equation to Model Gas Transport through Heterogeneous Soil and Gas Reservoirs. Physica A 2018, 502, 356–369. [Google Scholar] [CrossRef]
- Tenreiro, M.; Silva, M.F.; Barbosa, R.S.; Jesus, I.S.; Reis Cecília, M.; Marcos, M.G.; Galhano, A.F. Some Applications of Fractional Calculus in Engineering. Math. Probl. Eng. 2010, 2010, 639801. [Google Scholar]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity; Imperial College Press: London, UK, 2010. [Google Scholar]
- Shiri, B.; Wu, G.C.; Baleanu, D. Terminal value problems for the nonlinear systems of fractional differential equations. Appl. Numer. Math. 2021, 170, 162–178. [Google Scholar] [CrossRef]
- Benkerrouche, B.; Baleanu, D.; Souid, M.S.; Hakem, A.; Inc, M. Boundary value problem for nonlinear fractional differential equations of variable order via Kuratowski MNC technique. Adv. Differ. Equ.-N. Y. 2021, 2021, 365. [Google Scholar] [CrossRef]
- Arshad, S.; Saleem, I.; Defterli, O.; Tang, Y.; Baleanu, D. Simpson’s method for fractional differential equations with a non-singular kernel applied to a chaotic tumor model. Phys. Scr. 2021, 96, 124019. [Google Scholar] [CrossRef]
- Asadzadeh, M.; Saray, B.N. On a multiwavelet spectral element method for integral equation of a generalized Cauchy problem. BIT Numer. Math. 2022, 1–34. [Google Scholar] [CrossRef]
- Lakestani, M.; Dehghan, M. The use of Chebyshev cardinal functions for the solution of a partial differential equation with an unknown time-dependent coefficient subject to an extra measurement. J. Comput. Appl. Math. 2010, 235, 669–678. [Google Scholar] [CrossRef][Green Version]
- Daftardar-Gejji, V.; Jafari, A. Adomian decomposition: A tool for solving a system of fractional differential equations. J. Math. Anal. Appl. 2005, 301, 508–518. [Google Scholar] [CrossRef]
- Fix, G.J.; Roop, J.P. Least squares finite element solution of a fractional order two-point boundary value problem. Comput. Math. Appl. 2004, 48, 1017–1033. [Google Scholar] [CrossRef]
- Luchko, Y.F.; Gorenflo, R. An operational method for solving fractional differential equations with the Caputo derivatives. Acta Math. Vietnam 1999, 24, 207–233. [Google Scholar]
- Asad Iqbal, M.; Shakeel, M.; Mohyud-Din, S.T.; Rafiq, M. Modified wavelets–based algorithm for nonlinear delay differential equations of fractional order. Adv. Mech. Eng. 2017, 9, 1–8. [Google Scholar] [CrossRef]
- Alikhanov, A.A. A new difference scheme for the time fractional diffusion equation. J. Comput. Phys. 2015, 280, 424–438. [Google Scholar] [CrossRef]
- Du, R.; Yan, Y.; Liang, Z. A high-order scheme to approximate the Caputo fractional derivative and its application to solve the fractional diffusion wave equation. J. Comput. Phys. 2019, 376, 1312–1330. [Google Scholar] [CrossRef]
- Langlands, T.A.M.; Henry, B.I. The accuracy and stability of an implicit solution method for the fractional diffusion equation. J. Comput. Phys. 2005, 205, 719–736. [Google Scholar] [CrossRef]
- Lakestani, M.; Dehghan, M.; Irandoust-Pakchin, S. The construction of operational matrix of fractional derivatives using B-spline functions. Commun. Nonlinear Sci. 2012, 17, 1149–1162. [Google Scholar] [CrossRef]
- Mustahsan, M.; Younas, H.M.; Iqbal, S.; Rathore, S.; Nisar, K.S.; Singh, J. An Efficient Analytical Technique for Time-Fractional Parabolic Partial Differential Equations. Front. Phys. 2020, 8, 1–8. [Google Scholar] [CrossRef]
- Uddin, M.; Haq, S. RBFs approximation method for time fractional partial differential equations. Commun. Nonlinear Sci. Numer. Simulat. 2011, 16, 4208–4214. [Google Scholar] [CrossRef]
- Qu, H.; Liu, X.; Lu, X.; Ur Rahman, M.; She, Z. Neural network method for solving nonlinear fractional advection-diffusion equation with spatiotemporal variable-order. Chaos Soliton Fract. 2022, 156, 111856. [Google Scholar] [CrossRef]
- Mahmood, T.; Rahman, M.; Arfan, M.; Ilyas Kayani, S.; Sun, M. Mathematical study of Algae as a bio-fertilizer using fractal–fractional dynamic model. Math. Comput. Simulat. 2023, 203, 207–222. [Google Scholar] [CrossRef]
- Xu, C.; Ur Rahman, M.; Baleanu, D. On fractional-order symmetric oscillator with offset-boosting control. Nonlinear Anal.-Model. 2022, 27, 994–1008. [Google Scholar] [CrossRef]
- Zhang, L.; Ur Rahman, M.; Ahmad, S.H.; Riaz, M.B.; Jarad, F. Dynamics of fractional order delay model of coronavirus disease. AIMS Math. 2021, 7, 4211–4232. [Google Scholar] [CrossRef]
- Boyd, J.P. Chebyshev and Fourier Spectral Methods: Second Revised Edition; Dover Publications: New York, NY, USA, 2000. [Google Scholar]
- Afarideh, A.; Dastmalchi Saei, F.; Lakestani, M.; Saray, B.N. Pseudospectral method for solving fractional Sturm-Liouville problem using Chebyshev cardinal functions. Phys. Scr. 2021, 96, 125267. [Google Scholar] [CrossRef]
- Dehghan, M.; Lakestani, M. The use of Chebyshev cardinal functions for solution of the second-order one-dimensional telegraph equation. Numer. Math. Part. Differ. Equ. 2009, 25, 931–938. [Google Scholar] [CrossRef]
- Tchier, F.; Dassios, I.; Tawfiq, F.; Ragoub, L. On the Approximate Solution of Partial Integro-Differential Equations Using the Pseudospectral Method Based on Chebyshev Cardinal Functions. Mathematics 2021, 9, 286. [Google Scholar] [CrossRef]
- Canuto, C.; Hussaini, M.Y.; Quarteroni, A.; Zang, T.A. Spectral Methods Fundamentals in Single Domains; Springer: Berlin, Germany, 2006. [Google Scholar]
- Sayev, K.; Arab, H. An efficient extension of the Chebyshev cardinal functions for differential equations with coordinate derivatives of non-integer order. Comput. Methods Differ. Equ. 2018, 6, 339–352. [Google Scholar]
- Beezer, R.A. A First Course in Linear Algebra, 3rd ed.; Congruent Press: Washington, DC, USA, 2012. [Google Scholar]
- Kilbas, A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier B. V.: Amsterdam, The Netherlands, 2006; Volume 24. [Google Scholar]
- Dahlquist, G.; Björck, A. Numerical Methods; Prentice Hall: Englewood Cliffs, NJ, USA, 1974. [Google Scholar]
- Zaid, O.; Shaher, M. The Variational iteration method: An efficient scheme for handling fractional partial differential equations in fluid mechanics. Comput. Math. Appl. 2009, 58, 2199–2208. [Google Scholar]


| RBFs method (m = 51) | ||||
| CCFs method (m = 3) | ||||
| RBFs method (m = 121) | ||||
| CCFs method (m = 9) | ||||
| m | |||||
|---|---|---|---|---|---|
| 3 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 7 | |||||
| 8 | |||||
| 9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bin Jebreen, H.; Cattani, C. Solving Time-Fractional Partial Differential Equation Using Chebyshev Cardinal Functions. Axioms 2022, 11, 642. https://doi.org/10.3390/axioms11110642
Bin Jebreen H, Cattani C. Solving Time-Fractional Partial Differential Equation Using Chebyshev Cardinal Functions. Axioms. 2022; 11(11):642. https://doi.org/10.3390/axioms11110642
Chicago/Turabian StyleBin Jebreen, Haifa, and Carlo Cattani. 2022. "Solving Time-Fractional Partial Differential Equation Using Chebyshev Cardinal Functions" Axioms 11, no. 11: 642. https://doi.org/10.3390/axioms11110642
APA StyleBin Jebreen, H., & Cattani, C. (2022). Solving Time-Fractional Partial Differential Equation Using Chebyshev Cardinal Functions. Axioms, 11(11), 642. https://doi.org/10.3390/axioms11110642







