The Role of Risk Forecast and Risk Tolerance in Portfolio Management: A Case Study of the Chinese Financial Sector
Abstract
:1. Introduction
2. Risk Forecasting
2.1. Model for Marginal Distribution
2.2. Simulation
- FDG copula with Cuadras–Augé generators
- 2.
- FDG copula with Fréchet generators
2.3. Risk Measurement
3. Portfolio Allocation with Risk Tolerance Restrictions
3.1. CVaR Minimization
3.2. Weight Allocation with Risk Tolerance Restrictions
- Conservative: Allocate the smallest weight to the stock with the highest risk contribution. The portfolio return will be
- 2.
- Aggressive: Allocate the largest weight to the stock with the highest risk contribution. The portfolio return will be
- 3.
- Moderate: Allocate equal weight to the remaining companies. The portfolio return will be the average return of the remaining stocks.
3.3. Joint Extreme Risk Probability
- For return forecasting, we follow the same procedure as the one we use in the calculation of CES.
- The 1%-VaR for each stock is calculated, which is denoted by .
- A threshold, , is defined for , which is given bywith
- 4.
- Steps one–three are repeated 100 times (M = 100), and K/N is set to be 60%. JERP is then given by
4. Case Study
4.1. The Data
4.2. Empirical Results
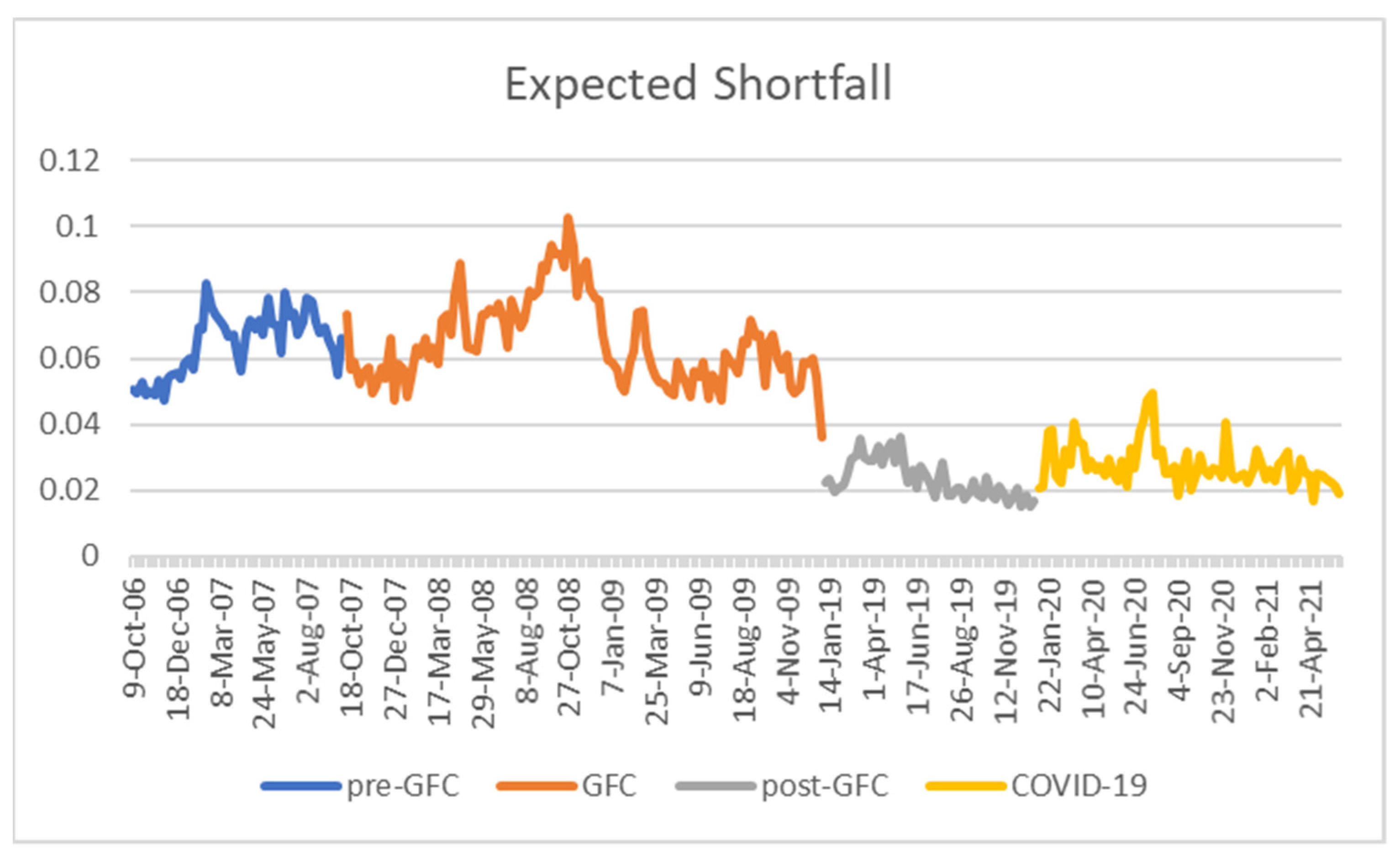
4.2.1. Market Risk
4.2.2. Portfolio Management
4.3. Joint Extreme Risk Probability
5. Discussion
6. Conclusions
7. Limitations of the Study and Future Directions of Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bernoulli, D. Exposition of a new theory on the measurement of risk. Econometrica 1954, 22, 22–36. [Google Scholar] [CrossRef] [Green Version]
- Corter, J.E.; Chen, Y.J. Do Investment Risk Tolerance Attitudes Predict Portfolio Risk? J. Bus. Psychol. 2006, 20, 369–381. [Google Scholar] [CrossRef]
- Gibson, R.; Michayluk, D.; Van de Venter, G. Financial risk tolerance: An analysis of unexplored factors. Financ. Serv. Rev. 2013, 22, 23–50. [Google Scholar]
- Markowitz, H. Portfolio selection. J. Financ. 1952, 7, 77–91. [Google Scholar]
- Chopra, V.K.; Ziemba, W.T. The Effect of Errors in Means, Variance and Covariance of Optimal Portfolio Choice. J. Portf. Manag. 1993, 19, 6–11. [Google Scholar] [CrossRef]
- Hiroaki, K.; Hiroaki, Y. Mean-Absolute Deviation Portfolio Optimization Model and its Application to Tokyo Stock Market. Manag. Sci. 1991, 37, 519–531. [Google Scholar]
- Green, R.C.; Hollifield, B. When Will Mean-Variance Efficient Portfolios Be Well Diversified? J. Financ. 1992, 47, 1785–1809. [Google Scholar] [CrossRef]
- Leung, P.L.; Ng, H.Y.; Wong, W.K. An improved estimation to make Markowitz’s portfolio optimization theory users friendly and estimation accurate with application on the US stock market investment. Eur. J. Oper. Res. 2012, 222, 85–95. [Google Scholar] [CrossRef]
- Bemporad, A.; Puglia, L.; Gabbriellini, T. A stochastic model predictive control approach to dynamic option hedging with transaction costs. In Proceedings of the 2011 American Control Conference, San Francisco, CA, USA, 29 June–1 July 2011; pp. 3862–3867. [Google Scholar]
- Rockafellar, R.T.; Uryasev, S. Optimization of conditional value-at-risk. J. Risk 2000, 2, 21–42. [Google Scholar] [CrossRef] [Green Version]
- Grable, J.E. Financial risk tolerance and additional factors that affect risk taking in everyday money matters. J. Bus. Psychol. 2000, 14, 625–630. [Google Scholar] [CrossRef]
- Gerrans, P.; Faff, R.; Hartnett, N. Individual financial risk tolerance and the global financial crisis. Account. Financ. 2015, 55, 165–185. [Google Scholar] [CrossRef]
- Nguyen, L.; Gallery, G.; Newton, C. The joint influence of financial risk perception and risk tolerance on individual investment decision-making. Account. Financ. 2017, 59, 747–771. [Google Scholar] [CrossRef]
- Yilmazer, T.; Lich, S. Portfolio choice and risk attitudes: A household bargaining approach. Rev. Econ. Househ. 2015, 13, 219–241. [Google Scholar] [CrossRef]
- Romprasert, S. Taxonomy of Economic Perspective on Cognitive Domain for Older Workers Government Policy. Int. J. Econ. Res. 2017, 14, 1–14. [Google Scholar]
- Sung, J.; Hanna, S.D. Factors Related to Risk Tolerance. Financ. Couns. Plan. 1996, 7, 11–19. [Google Scholar] [CrossRef] [Green Version]
- Fisher, P.J.; Yao, R. Gender differences in financial risk tolerance. J. Econ. Psychol. 2017, 61, 191–202. [Google Scholar] [CrossRef]
- Pyles, M.K.; Li, Y.; Wu, S.; Dolvin, S.D. Cultural influences on risk tolerance and portfolio creation. J. Behav. Exp. Financ. 2016, 9, 43–55. [Google Scholar] [CrossRef]
- Hawley, C.B.; Fujii, E.T. An empirical analysis of preferences for financial risk: Further evidence on the Friedman-Savage model. J. Post Keynes. Econ. 1993, 16, 197–204. [Google Scholar] [CrossRef]
- Ferreira, S.; Dickason-Koekemoer, Z. A structural equation model of financial risk tolerance in South Africa. Cogent Bus. Manag. 2020, 7, 1811595. [Google Scholar] [CrossRef]
- Lawrenson, J.; Dickason-Koekemoer, Z. A model for female South African investors’ financial risk tolerance. Cogent Econ. Financ. 2020, 8, 1794493. [Google Scholar] [CrossRef]
- Wahl, I.; Kirchler, E. RIsk SCreening on the Financial Market (RISC-FM): A tool to assess investors’ financial risk tolerance. Cogent Psychol. 2020, 7, 1714108. [Google Scholar] [CrossRef]
- Chiang, T.F.; Xiao, J.J. Household characteristics and the change of financial risk tolerance during the financial crisis in the United States. Int. J. Consum. Stud. 2017, 41, 484–493. [Google Scholar] [CrossRef]
- Heo, W.; Rabbani, A.; Grable, J.E. An Evaluation of the Effect of the COVID-19 Pandemic on the Risk Tolerance of Financial Decision Makers. Financ. Res. Lett. 2021, 41, 101842. [Google Scholar] [CrossRef]
- Zhang, W.G.; Zhang, X.L.; Xu, W.J. A risk tolerance model for portfolio adjusting problem with transaction costs based on possibilistic moments. Insur. Math. Econ. 2010, 46, 493–499. [Google Scholar] [CrossRef]
- Gong, X.M.; Min, L.Y.; Yu, C. Multi-period portfolio selection under the coherent fuzzy environment with dynamic risk-tolerance and expected-return levels. Appl. Soft Comput. 2022, 114, 108104. [Google Scholar] [CrossRef]
- Wei, Z.; Kim, D. Measure of asymmetric association for ordinal contingency tables via the bilinear extension copula. Stat. Probab. Lett. 2021, 178, 109183. [Google Scholar] [CrossRef]
- Glosten, L.R.; Jagannathan, R.; Runkle, D.E. On the Relation between the Expected Value and the Volatility of the Nominal Excess Return on Stocks. J. Financ. 1993, 48, 1779–1801. [Google Scholar] [CrossRef]
- Mazo, G.; Girard, S.; Forbes, F. A flexible and tractable class of one-factor copulas. Stat. Comput. 2016, 26, 965–979. [Google Scholar] [CrossRef] [Green Version]
- Banulescu, G.D.; Dumitrescu, E.I. Which are the SIFIs? A Component Expected Shortfall approach to systemic risk. J. Bank. Financ. 2015, 50, 575–588. [Google Scholar] [CrossRef]
- Browne, M.; Jaeger, V.; Steinorth, P. The impact of economic conditions on individual and managerial risk taking. Geneva Risk Insur. Rev. 2019, 44, 27–53. [Google Scholar] [CrossRef]
- Hoffmann, A.O.I.; Post, T.; Pennings, J.M.E. Individual investor perceptions and behavior during the financial crisis. J. Bank. Financ. 2013, 37, 60–74. [Google Scholar] [CrossRef]




| Code | Name | Period |
|---|---|---|
| 000627 | Hubei Biocause Pharmaceutical Co., Ltd., Jingmen, China | 1 |
| 000666 | Jingwei Textile Machinery Company Limited, Beijing, China | 1 |
| 000958 | Spic Dongfang New Energy Corporation, Shijiazhuang, China | 1 |
| 600643 | Shanghai AJ Group Co., Ltd., Shanghai, China | 1 |
| 600783 | Luxin Venture Capital Group Co., Ltd., Jinan, China | 1 |
| 600061 | SDIC Capital Co., Ltd., Beijing, China | 2 |
| 600830 | Sunny Loan Top Co., Ltd., Ningbo, China | 2 |
| 600120 | Zhejiang Orient Financial Holdings Group Co., Ltd., Hangzhou, China | 1,2 |
| 000046 | Oceanwide Holdings Co., Ltd., Beijing, China | 1,2 |
| 000416 | Minsheng Holdings Co., Ltd., Beijing, China | 1,2 |
| 000567 | Hainan Haide Capital Management Co., Ltd., Beijing, China | 1,2 |
| 600390 | Minmetals Capital Company Limited, Changsha, China | 1,2 |
| 000890 | Jiangsu Fasten Company Limited, Jiangyin, China | 1,2 |
| 000987 | Guangzhou Yuexiu Financial Holdings Group Co., Ltd., Guangzhou, China | 1,2 |
| 600621 | Shanghai Chinafortune Co., Ltd., Shanghai, China | 1,2 |
| 601788 | Everbright Securities Company Limited, Shanghai, China | 3 |
| 601901 | Founder Securities Co., Ltd., Changsha, China | 3 |
| 000617 | Cnpc Capital Company Limited, Beijing, China | 4 |
| 600015 | Hua Xia Bank Co., Ltd., Beijing, China | 4 |
| 601009 | Bank Of Nanjing Co., Ltd., Nanjing, China | 3,4 |
| 601166 | Industrial Bank Co., Ltd., Fuzhou, China | 3,4 |
| 601169 | Bank of Beijing Co., Ltd., Beijing, China | 3,4 |
| 601288 | Agricultural Bank Of China Limited, Beijing, China | 3,4 |
| 601328 | Bank Of Communications Co., Ltd., Shanghai, China | 3,4 |
| 601398 | Industrial Additionally, Commercial Bank Of China Limited, Beijing, China | 3,4 |
| 601818 | China Everbright Bank Co., Ltd., Beijing, China | 3,4 |
| 601939 | China Construction Bank Corporation, Beijing, China | 3,4 |
| 601988 | Bank Of China Limited, Beijing, China | 3,4 |
| 601998 | China Citic Bank Corporation Limited, Beijing, China | 3,4 |
| 000776 | Gf Securities Co., Ltd., Guangzhou, China | 3,4 |
| 002736 | Guosen Securities Co., Ltd., Shenzhen, China | 3,4 |
| 600837 | Haitong Securities Co., Ltd., Shanghai, China | 3,4 |
| 600958 | Orient Securities Company Limited, Shanghai, China | 3,4 |
| 600999 | China Merchants Securities Co., Ltd., Shenzhen, China | 3,4 |
| 601211 | Guotai Junan Securities Co., Ltd., Shanghai, China | 3,4 |
| 601318 | Ping An Insurance (Group) Company Of China, Ltd., Shenzhen, China | 3,4 |
| 601336 | New China Life Insurance Company Ltd., Beijing, China | 3,4 |
| 601601 | China Pacific Insurance(group) Co., Ltd., Shanghai, China | 3,4 |
| 601628 | China Life Insurance Company Limited, Beijing, China | 3,4 |
| 601688 | Huatai Securities Co., Ltd., Nanjing, China | 3,4 |
| 300059 | East Money Information Co., Ltd., Shanghai, China | 3,4 |
| 002142 | Bank of Ningbo Co., Ltd., Ningbo, China | 3,4 |
| 000001 | Ping An Bank Co., Ltd., Shenzhen, China | 1,3,4 |
| 600000 | Shanghai Pudong Development Bank Co., Ltd., Shanghai, China | 2,3,4 |
| 600016 | China Minsheng Banking Corp., Ltd., Beijing, China | 1,2,3,4 |
| 600036 | China Merchants Bank Co., Ltd., Shenzhen, China | 1,2,3,4 |
| 600030 | CITTI Securities Company Limited, Shenzhen, China | 1,2,3,4 |
| Period | Company | Days Invested | Average Return | Average Weight (%) |
|---|---|---|---|---|
| CVaR-minimized (pre-GFC) | Ping An Bank Co., Ltd., Shenzhen, China | 218/242 | 0.007 (0.032) | 15.1 (0.105) |
| Shanghai AJ Group Co., Ltd., Shanghai, China | 228/242 | 0.005 (0.031) | 14.5 (0.074) | |
| China Merchants Bank Co., Ltd., Shenzhen, China | 232/242 | 0.006 (0.031) | 11.6 (0.059) | |
| Conservative (GFC) | China Minsheng Banking Corp., Ltd., Beijing, China | 392/500 | 0.001 (0.030) | 15.7 (0.083) |
| Shanghai Pudong Development Bank Co., Ltd., Shanghai, China | 454/550 | −0.002 (0.042) | 14.3 (0.104) | |
| China Merchants Bank Co., Ltd., Shenzhen, China | 305/550 | −0.001 (0.035) | 14.0 (0.080) | |
| Aggressive (post-GFC) | Everbright Securities Company Limited, Shanghai, China | 12/244 | 0.009 (0.027) | 25.4 (0.130) |
| East Money Information Co., Ltd., Shanghai, China | 27/244 | 0.016 (0.028) | 25.4 (0.129) | |
| Guosen Securities Co., Ltd., Shenzhen, China | 63/244 | 0.004 (0.021) | 23.6 (0.143) | |
| Aggressive (COVID-19) | East Money Information Co., Ltd., Shanghai, China | 11/354 | 0.014 (0.030) | 44.0 (0.160) |
| CITTI Securities Company Limited, Shenzhen, China | 8/354 | 0.0002 (0.021) | 37.7 (0.100) | |
| Industrial Bank CO.,LTD., Fuzhou, China | 109/354 | 0.002 (0.024) | 34.8 (0.193) |
| Period (K/N) | Date | Forecasted Market Risk | Mean Return of the Portfolio | Max. Return in the Portfolio | Min. Return in the Portfolio | JERP |
|---|---|---|---|---|---|---|
| Pre-GFC (10/17) | 7 August 2007 | 0.094 | −0.005 | 0.040 | −0.075 | 100% |
| 29 June 2007 | 0.090 | −0.035 | 0.095 | −0.105 | 90% | |
| GFC (9/14) | 3 November 2008 | 0.110 | −0.011 | 0.018 | −0.065 | 100% |
| 23 September 2008 | 0.102 | −0.060 | 0.033 | −0.105 | 100% | |
| Post-GFC (18/30) | 23 May 2019 | 0.053 | −0.006 | 0.029 | −0.029 | 100% |
| 26 March 2019 | 0.052 | −0.014 | 0.012 | −0.042 | 100% | |
| COVID−19 (18/30) | 27 July 2020 | 0.069 | −0.005 | 0.009 | −0.045 | 100% |
| 21 July 2020 | 0.062 | −0.011 | 0.033 | −0.044 | 100% |
| Date | Conservative | Aggressive | Moderate | CVaR-Minimized |
|---|---|---|---|---|
| 7 August 2007 | 64,835 | 31,815 | 56,639 | 52,522 |
| 29 June 2007 | 31,362 | 22,401 | 27,382 | 42,766 |
| 3 November 2008 | 19,288 | 10,716 | 13,219 | 15,982 |
| 23 September 2008 | 25,396 | 15,911 | 17,542 | 20,912 |
| 23 May 2019 | 3562 | 1029 | 526 | 2415 |
| 26 March 2019 | 3629 | 1043 | 535 | 2424 |
| 27 July 2020 | 10,283 | 9388 | 9084 | 7959 |
| 21 July 2020 | 7524 | 5628 | 6342 | 4342 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Cheng, Y.; Li, X.; Sriboonchitta, S. The Role of Risk Forecast and Risk Tolerance in Portfolio Management: A Case Study of the Chinese Financial Sector. Axioms 2022, 11, 134. https://doi.org/10.3390/axioms11030134
Liu J, Cheng Y, Li X, Sriboonchitta S. The Role of Risk Forecast and Risk Tolerance in Portfolio Management: A Case Study of the Chinese Financial Sector. Axioms. 2022; 11(3):134. https://doi.org/10.3390/axioms11030134
Chicago/Turabian StyleLiu, Jianxu, Yangnan Cheng, Xiaoqing Li, and Songsak Sriboonchitta. 2022. "The Role of Risk Forecast and Risk Tolerance in Portfolio Management: A Case Study of the Chinese Financial Sector" Axioms 11, no. 3: 134. https://doi.org/10.3390/axioms11030134
APA StyleLiu, J., Cheng, Y., Li, X., & Sriboonchitta, S. (2022). The Role of Risk Forecast and Risk Tolerance in Portfolio Management: A Case Study of the Chinese Financial Sector. Axioms, 11(3), 134. https://doi.org/10.3390/axioms11030134






