Mathematical Modeling Research Output Impacting New Technological Development: An Axiomatization to Build Novelty
Abstract
:1. Introduction
Problem Statement
2. Methods and Source of Axiomatization
Location and Participants’ Selection Technique
3. Results
3.1. Qualitative Axiomatization of Mathematical Modeling Research Output
3.1.1. Axiomatization 1 (A1): Mathematical Modeling for System Theorizing and the Impact on Technological Development
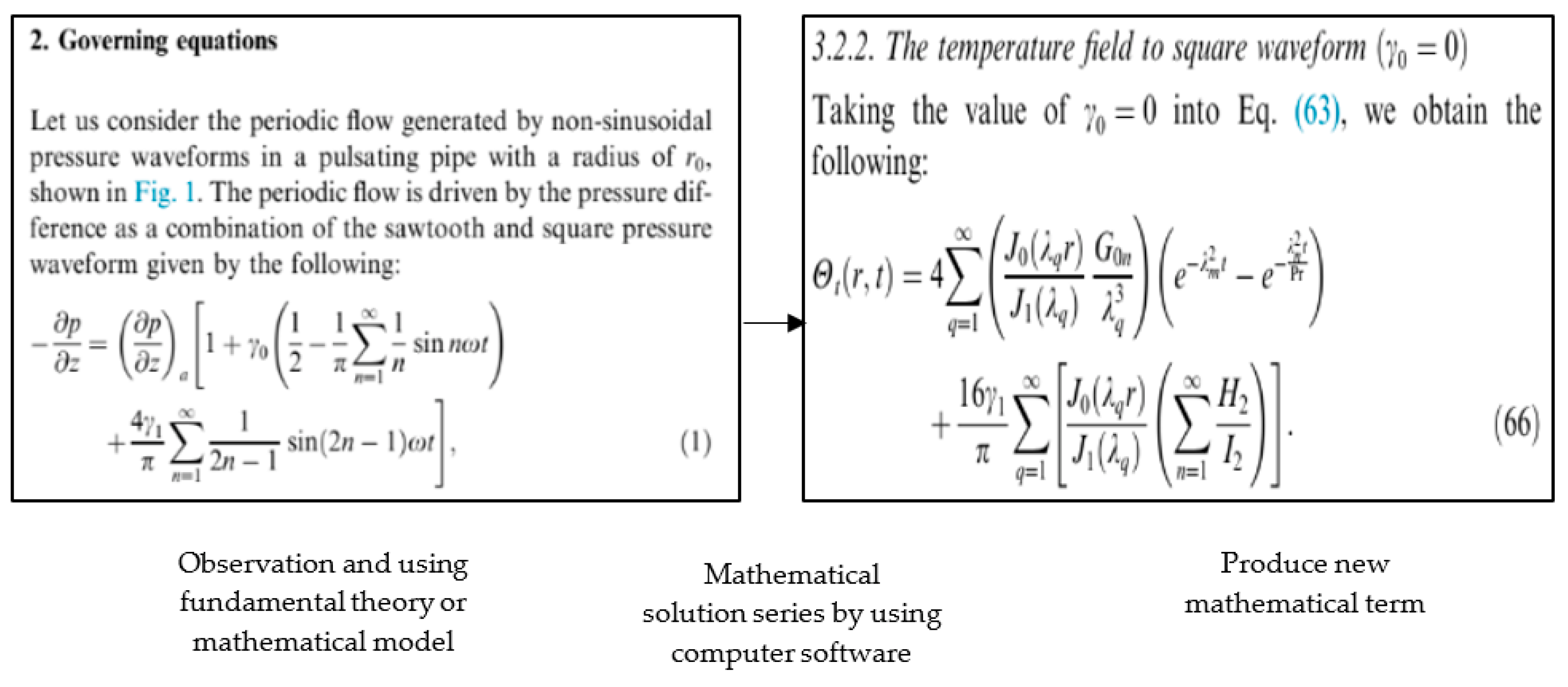
“…using past data, we can generate a mathematical model by observing changes…using the simplest pattern that we observe…we can generate an equation from the original equation to describe the system of a phenomenon… for the complicated ones, we included other factors in the equation such as economic factors or price factor…”Source (P4, 4:28)
“We will solve the equation using computer software…but the danger is when we don’t really understand the software and we don’t know what we really want, and we just put in some random values…of course, the software will produce an output…but we don’t know what the value means—is it right?…it might just be due to a missing negative sign…if we don’t understand the system for example, and we just take the result at face value…the result might be reversed…for example, the result might cause a person to go backwards instead of going forward when we keep entering the wrong value. This can be caused by having a weak background in the topic or theory”.Source (P2, 2:12)
“The important thing is to set up the geometry diagram…a free body diagram… then determine what other people have done on the studied phenomena, and what do you want to do on that particular phenomenon…based on that diagram, what’s a new term that can be generated…and what is the purpose of the equation for the new thing…then we can derive in mathematical terms, and we can get a new mathematical model…”Source: (P1: 1:12)
“We would need to have knowledge in mathematics and other disciplines…your math skills must be strong…if not, it may be difficult to even start working on the problem…but the first thing is the issue, how do we find the issue…”Source: (P2, 2:55)
3.1.2. Axiomatization 2 (A2): Mathematical Modeling for Simulation and the Impact on Technology Development
“For example, in gun fire pattern recognition, yes, we have evidence for gun fire identification study, so how do we translate the image into mathematics, to the numbers, yes, in fact the image for example on the inner side of the bullet casing, we can translate it into a mathematical model and simulate the image…”Source: (P5: 10:16)
“In the case of forensics, we can’t get a 100% accuracy, but we say that we only can get close to 90%, and we say it might be gang A, gang B, or gang C, let’s say in Malaysia that there are 7 gangs involved in gun-related crimes, so this might be done by gang A, gang B or gang C, so we go back to the lab and select a particular analysis using a microscope, and only then will we can get closer to suspect”Source: (P5: 10:28)
“But the court has not accepted the result of the analysis using computers so far, they also need human beings to verify the analysis, but we have made it easier, our real purpose is to screen people, or as we call it, the screening phase, it means that we have reduced 90% of the work and only 10% would require human intervention…”Source: (P5: 10:29)
“The first cycle of the project was done manually, the second cycle was conducted automatically, and has managed to come out with important images from the inside of the bullet casing, meaning that before this we had to ask an expert, we had to hand draw a little bit, and in this second part, the part that I’m interested in, is done automatically…”Source: (P5: 10:31)
“…We can’t get a lot of data, and there were only a few new papers, and there were also some comments from outside on our paper that we did not have enough in terms of samples used, but these will incur a big cost, and it’s from PDRM…we get some contribution from them”Source: (P5: 10:26)
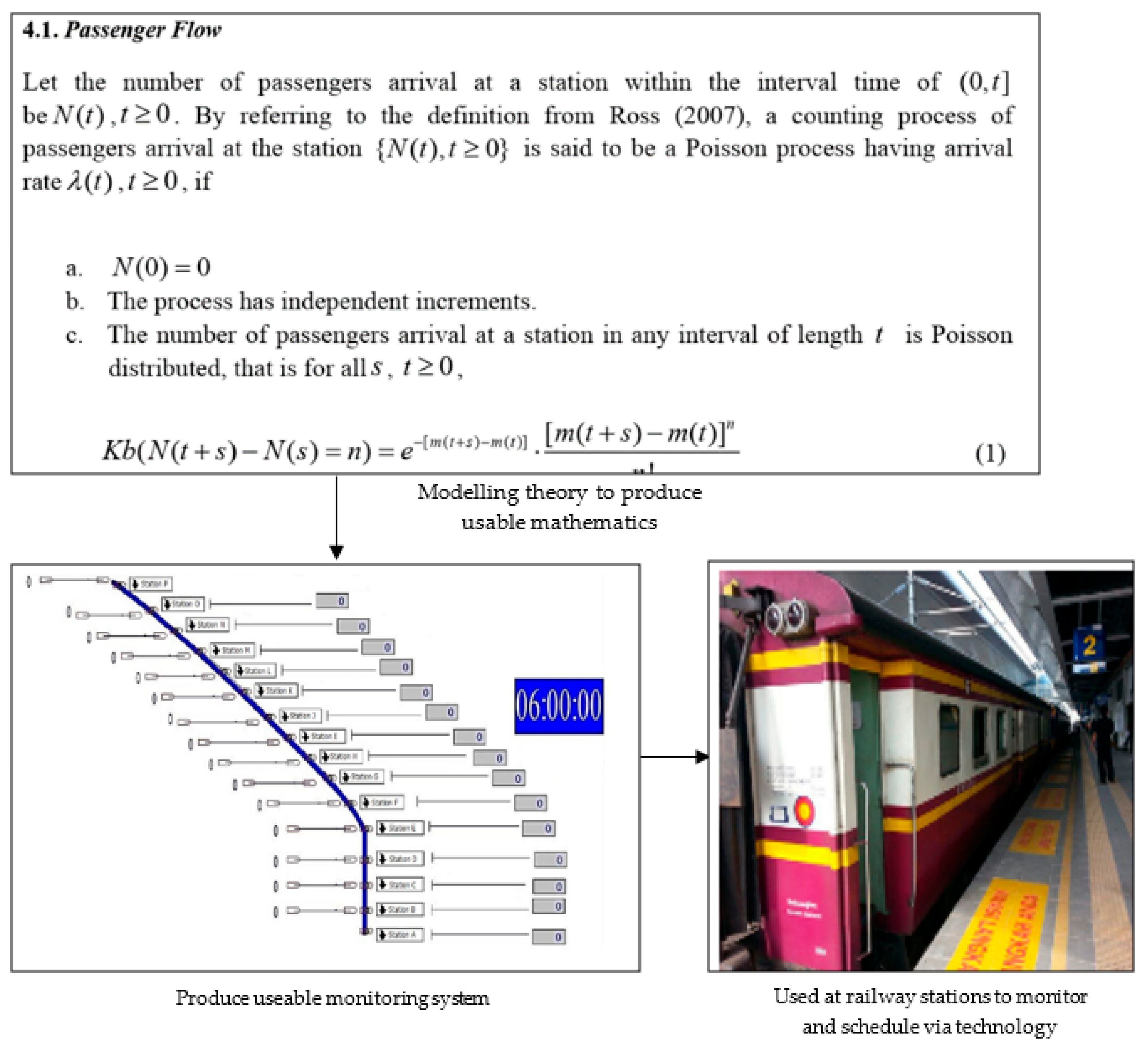
“…Another interesting thing is the simulation, a simulation modelling that we have done was for the performance of the commuter system, our commuter system that is KTM, indeed the KTM has come to us to ask for consultant for modelling simulation, they wanted to see the train journey of KTM…”Source: (P3: 10:12)
“Sometimes we don’t really understand the mathematics, it’s half of it…for example like scheduling, because we want to build a constraint for scheduling simulation…we have to understand…”Source: (P3: 10:56)
3.1.3. Axiomatization 3 (A3): Mathematical Modeling for Useable Innovation Output the Impact on Technology Development
“So, what I mean by mathematical model for me is a model that we try to benefit it to the public instead, we only use in self-books in the library…the example that I presented earlier is something that can actually be used for society…”Source: (P3: 3:16)
“Actually, by using mathematical modelling…in other words it is not a mathematical solution only…it’s more on the model that we can apply it”Source: (P2: 2:40)
“…There are not many knee experts…we were looking for experts to collaborate with…we could not find many knee experts in our University Hospital…I’d try searching on the website…people don’t even know…”Source: (P7: 9:53)
“Because the model they have now is only used in the operating room, but we have it in the computer and software that can be taken anywhere, that’s the advantage of the system itself…”Source: (P7: 10:14)
“For the example, loading bay optimization, it is about methods of loading the goods. How practical is it? Past studies show to what extent? and why can’t it be solved with the software or optimization package that is available now?”Source: (P5: 10:47)
3.1.4. Axiomatization 4 (A4): Patent and Commercialization Output
“Ortho-knee is ready, Ortho-Hip is being made…Ortho-Knee is being patented and also is being trademarked…it has been used at our University Hospital… now this product has been used for two years already…if two years our University Hospital is acceptable, then we can spread the use of this product to other hospitals…”Source: (P7: 9:68)
“We developed, built and sold to people…we have used it for two years already…we made it and we are using it at the first stage…”Source: (P7: 9:69)
“Now I already have five patents, but others have dozens already…I’m still a small fish…five patents…”Source: (P7: 9:70)
“When I commercialize my product, not really commercialize but what I mean is, when I patent my research outcome, they were surprised at how can mathematicians could come out with the product…people talk like that…then I said…the reason is that the development of the product is actually very simple…you don’t need to be bombastic with development like you want to wait for the engineer to build that thing right…it is not necessary…that thing is very simple…it is about what we learn…because it involves the circuit, what we learned in school before…and we have a program…that’s all…”Source: (P2: 2:65)
3.1.5. Formulization of Novelty in Mathematical Modeling
“People never do this kind of simulation…it’s using FAP…Frequency Assignment Problem…mobile network…I tried to solve it to optimize the frequency assignment…to the channels, I managed to run a simulation of the cells.…”Source: (P2: 4:11)
“According to the comments that we have received…our image simulation is very accurate…it has an error of just 0.02%…they said that 0.02% is ok…they said that if we could get it to 0.07% error, then it would be enough…and getting 0.02%, thank God…It’s very good…so they are confident with our findings…We were able to give a solution where patients do not have to wait for a long period of time and reduce the time it takes for imaging to be available prior to surgery”Source: (P7: 9:72)
“For PhD research, it needs to get something new, produce something new, and in science, we are really interested to discover something new, look for something… something easy, in the case of gun loaded with bullets, the based-side bullet imaging is much easier than the inside, because the features of the inside shell are difficult to render, because there is lighting on the stretch that comes out, then we look at the mathematics, it is also sophisticated, it just so happens that in my PhD, I also used concept of moments, I know concept of moments can give unique features, the term now bitara, uniqueness for each image…”Source: (P5: 10:23)
“…There is a classic one… there are areas that people don’t study… there is a boundary condition, the boundary that people always study on this type, but at the other areas, they don’t study on it, and I tried to look into it, then I have the result that other researcher don’t have…I changed the boundary condition…”Source: (P1: 8:53)
“I once competed with a professor over the submission of a paper, I know that this professor is expert in mathematics, but he is not an expert in fluid mechanics…his expertise is in numerical methods…it so happened that when I submitted the manuscript, it was him who reviewed my manuscript…he held onto my manuscript for a long time…maybe he kept it…he is an expert in numerical methods but not in fluid mechanics…so when he saw my mathematical equation, he likely kept them from being published…”Source: (P1: 8:34)
“In my case, at that time there are no other techniques available to detected things by weight…it used to be a problem…that was the problem that I had studied before…I did an experiment…of school children carrying heavy bags to school, so how much weight can a child carry…of course the weight of the each student is not the same…so we have to standardize it first…then we looked at how much weight schools children are able to carry, finding the critical value that would cause back aches…at that time carrying a heavy bag to school was an issue. Such a thing could result in children suffering from back problems.”Source: (P2: 2:17)
“It’s like the research I’m doing…if there’s field integration…knowledge, it’ll take us further…if not, we’ll be stuck at that stage…for example, if you’re good at programming, but if you don’t relate it with real-world applications, you will remain at that stage…”Source: (P1: 8:15)
4. Formulization and Discussion
Data Triangulation and Consensus
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kyurkchiev, N. Selected Topics in Mathematical Modelling: Some New Trends; Lambert Academic Publishing: Chisinau, Moldova, 2020. [Google Scholar]
- Paul, S.K.; Chowdhury, P.; Chakrabortty, R.K.; Ivanov, D.; Sallam, K. A mathematical model for managing the multi-dimensional impacts of the COVID-19 pandemic in supply chain of a high-demand item. Ann. Oper. Res. 2022, 1–46. [Google Scholar] [CrossRef] [PubMed]
- Riyanto, B.; Zulkardi, Z.; Sriwijaya, U.; Ilma, R.; Putri, I.; Sriwijaya, U. Mathematical modelling in realistic mathematics education. J. Phys. Conf. Ser. 2017, 943, 012049. [Google Scholar] [CrossRef] [Green Version]
- Serovajsky, S. Mathematical Modelling; CRC Press: New York, NY, USA, 2022. [Google Scholar]
- Khudzari, J.; Kurian, J.; Tartakovsky, B.; Raghavan, G.S.V. Bibliometric analysis of global research trends on microbial fuel cells using Scopus database. Biochem. Eng. J. 2018, 136, 51–60. [Google Scholar] [CrossRef]
- Molina-Toro, J.F.; Rendon-mesa, P.A.; Villa-Ochoa, J.A. Research trends in digital technologies and modelling in mathematics education. Eurasia J. Math. Sci. Technol. Educ. 2019, 15, 1–13. [Google Scholar] [CrossRef]
- Jang, H.; Kim, H. Research output of science, technology and bioscience publications in Asia. Sci. Ed. 2014, 1, 62–70. [Google Scholar] [CrossRef]
- Tecson-mendoza, E.M. Case study scientific and academic journals in the Philippines: Status and challenges. Sci. Ed. 2015, 2, 73–78. [Google Scholar] [CrossRef] [Green Version]
- Wan Lanang, W.N.S.; Turan, F.M.; Johan, K. Systematic assessment through mathematical model for sustainability reporting in Malaysia context. IOP Conf. Ser. Mater. Sci. Eng. 2017, 226, 012049. [Google Scholar] [CrossRef] [Green Version]
- Bajuri, M.R.; Abdul Rahim, S.S.; Mohd Shahali, E.H.; Maat, S.M. Influence of spirituality in the career and STEM-based research approach of scientists for sustainable development: A study on the perspective of scientists from a public research university in Malaysia. Sustainability 2021, 13, 11161. [Google Scholar] [CrossRef]
- Long, B.T.; Toan, N.D. Scientific and technological journals in Vietnam: The current state and direction of development. Sci. Ed. 2015, 2, 18–21. [Google Scholar] [CrossRef] [Green Version]
- Temime, L.; Hejblum, G.; Setbon, M.; Valleron, A. The rising impact of mathematical modelling in epidemiology: Antibiotic resistance research as a case study. Epidemiol. Infect. 2008, 163, 289–298. [Google Scholar] [CrossRef]
- Porgo, T.V.; Norris, S.L.; Salanti, G.; Johnson, L.F.; Simpson, J.A.; Low, N.; Egger, M.; Althaus, C.L. The use of mathematical modelling studies for evidence synthesis and guideline development: A glossary. Wiley Res. Synth. Methods 2017, 10, 125–133. [Google Scholar] [CrossRef] [Green Version]
- Hansson, S.O. Technology and Mathematics. Philos. Technol. 2020, 33, 113–139. [Google Scholar] [CrossRef] [Green Version]
- Legatiuk, D. Mathematical modelling by help of category theory: Models and relations between them. Mathematics 2021, 9, 1946. [Google Scholar] [CrossRef]
- Rosyidi, A.H.; Fadhilah, L.F.; Hartono, S. Students’ Mathematical modeling on PISA quantity problems of formulation category: Explicit model vs implicit model. Adv. Eng. Res. 2021, 209, 409–416. [Google Scholar]
- Gibbs, A.M.; Park, J.Y. Unboxing mathematics: Creating a culture of modeling as critic. Educ. Stud. Math. 2022, 110, 167–192. [Google Scholar] [CrossRef]
- Gambier, A. Control of Large Wind Energy Systems; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Regmi, S. Optimized Iterative Methods with Applications in Diverse Disciplines; Nova Science Publisher: New York, NY, USA, 2021. [Google Scholar]
- Soboleva, E.V.; Zhumakulov, K.K.; Umurkulov, K.P.; Ibragimov, G.I.; Kochneva, L.V.; Timofeeva, M.O. Developing a personalised learning model based on interactive novels to improve the quality of mathematics education. Eurasia J. Math. Sci. Technol. Educ. 2022, 18, em2078. [Google Scholar] [CrossRef]
- Nance, D.A. The reference class problem and mathematical models of inference. Int. J. Evid. Proof 2007, 11, 259–273. [Google Scholar] [CrossRef]
- Barrow-Green, J. Knowledge gained by experience: Olaus Henrici—Engineer, geometer and maker of mathematical models. Hist. Math. 2021, 54, 41–76. [Google Scholar] [CrossRef]
- Bulturbayevich, M.B.; Yusufxonovich, K.P. Development of innovative activities of enterprises on the basis of vertical integration processes. Turk. J. Com. Math. Edu. 2021, 12, 5020–5031. [Google Scholar]
- Yin, R.K. Qualitative Research from Start to Finish, 2nd ed.; The Guilford Press: New York, NY, USA, 2016. [Google Scholar]
- Chun, C.; Eric, M. A Case study on developing a teacher’s capacity in mathematical modelling. Math. Educ. 2015, 16, 47–76. [Google Scholar]
- Yin, R.K. Applications of Case Study Research, 2nd ed.; Sage Publications: Thousand Oaks, CA, USA, 2003; Volume 34. [Google Scholar]
- Flick, U. An Introduction to Qualitative, 4th ed.; SAGE Publications: Thousand Oaks, CA, USA, 2009. [Google Scholar]
- Robnett, R.D.; Nelson, P.A.; Zurbriggen, E.L.; Crosby, F.J.; Chemers, M.M. The form and function of STEM research mentoring: A mixed-methods analysis focusing on ethnically diverse undergraduates and their mentors. Emerg. Adulthood 2018, 7, 180–193. [Google Scholar] [CrossRef]
- Hidiroglu, C.N.; Bukova Guzel, E. Metacognitive structures occurring in mathematical modelling within a technology enhanced environment. Turk. J. Comput. Math. Educ. 2015, 6, 179–208. [Google Scholar]
- Majid, F.A. Creativity and innovation in research: The perceptions of Malaysian postgraduate students. Publ. Asian J. Univ. Educ. 2010, 6, 49–73. [Google Scholar]
- Li, C.C.; Dong, Y.; Herrera, F.; Herrera-Viedma, E.; Martínez, L. Personalized individual semantics in computing with words for supporting linguistic group decision making. An application on consensus reaching. Inf. Fusion 2017, 33, 29–40. [Google Scholar] [CrossRef] [Green Version]
- Dimitrov, B. The axioms in my understanding from many years of experience. Axioms 2021, 10, 176. [Google Scholar] [CrossRef]
- Bazeley, P. Qualitative Data Analysis; SAGE Publications: Thousand Oaks, CA, USA, 2013. [Google Scholar]
- Roslan, R.; Abdulhameed, M.; Hashim, I.; Chamkha, A.J. Non-sinusoidal waveform effects on heat transfer performance in pulsating pipe flow. Alex. Eng. J. 2016, 55, 3309–3319. [Google Scholar] [CrossRef] [Green Version]
- Abdul Rahman, S.A.; Rambely, A.S.; Ahmad, R.R. Effect of load carriage on the backpack vibration system. Appl. Mech. Mater. 2012, 165, 295–299. [Google Scholar] [CrossRef]
- Kechil, S.A.; Hashim, I. Series solutions of boundary-layer flows in porous media with lateral mass flux. Heat Mass Transf. 2008, 44, 1179–1186. [Google Scholar] [CrossRef]
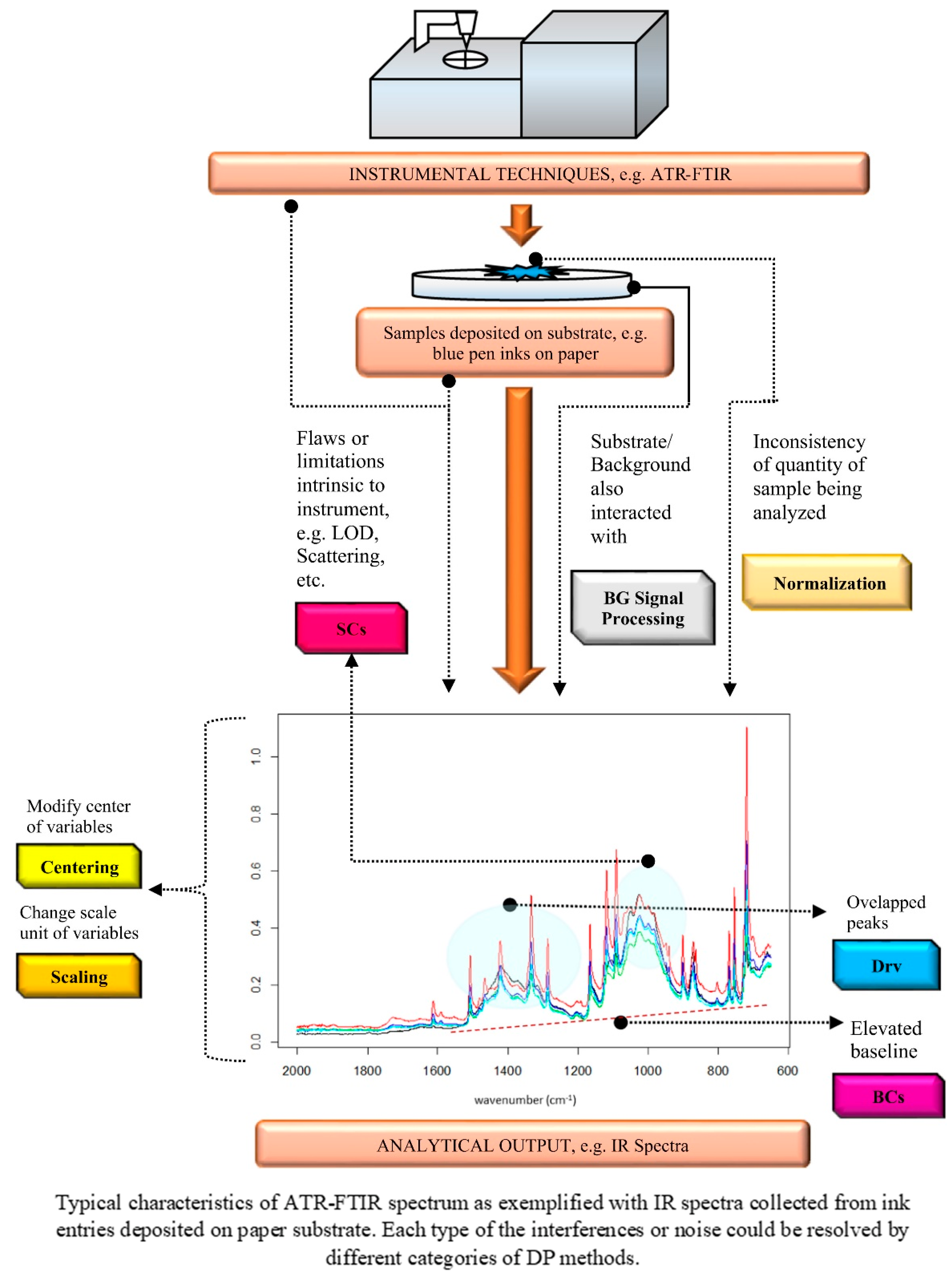
- Lee, L.C.; Liong, C.Y.; Jemain, A.A. A Contemporary review on data preprocessing (DP) practice strategy in ATR-FTIR spectrum. Chemom. Intell. Lab. Syst. 2017, 163, 64–75. [Google Scholar] [CrossRef]
- Low, S.K.; Liong, C.Y. Simulation modelling for evaluating performance of commuter system with ARENA. J. Qual. Meas. Anal. 2015, 11, 47–60. [Google Scholar]
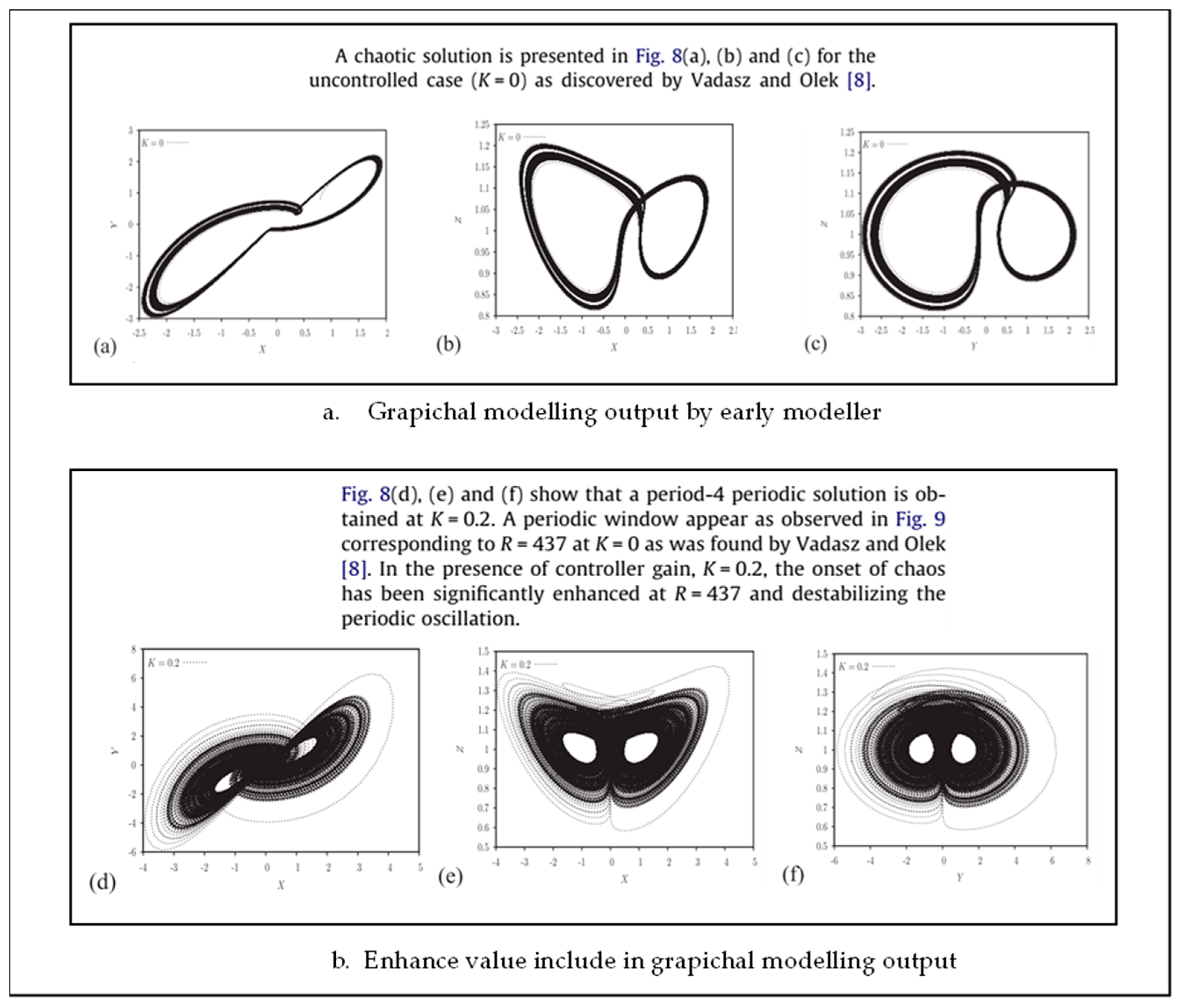
- Roslan, R.; Mahmud, M.N.; Hashim, I. Effects of feedback control on chaotic convection in fluid-saturated porous media. Int. J. Heat Mass Transf. 2011, 54, 404–412. [Google Scholar] [CrossRef]
- Wagner, C.S.; Whetsell, T.A.; Mukherjee, S. International research collaboration: Novelty, conventionality, and atypicality in knowledge recombination. Res. Policy 2019, 48, 1260–1270. [Google Scholar] [CrossRef]
- Willig, C. Introducing Qualitative Research in Psychology Adventures in Theory and Method, 2nd ed.; Open University Press: New York, NY, USA, 2008. [Google Scholar]
- Farzaneh, V.; Weinstock, V. Mathematical modelling of cities as complex systems and simulations in design. In Proceedings of the 39th Annual Conference of The Association for Computer Aided Design in Architecture, Austin, TX, USA, 24–26 October 2019; pp. 554–563. [Google Scholar]
- Brown, J.P.; Ikeda, T. Conclusions and future lines of inquiry in mathematical modelling research in education. In Lines of Inquiry in Mathematical Modelling Research in Education; Stillman, G.A., Brown, J.P., Eds.; Springer: Cham, Switzerland, 2019; pp. 233–253. [Google Scholar]
- Morawski, R.Z. Technoscientific Research: Methodological and Ethical Aspects; Walter de Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Suh, J.M.; Seshaiyer, P. Modelling Mathematical Ideas; Rowman and Littlefield: New York, NY, USA, 2017. [Google Scholar]
- Gould, H.; Murray, D.R.; Sanfratello, A. Mathematical Modeling Handbook; Columbia University: New York, NY, USA, 2012. [Google Scholar]
- Tung, K. Topics in Mathematical Modelling; Princeton University Press: Oxford, UK, 2007. [Google Scholar]
- Eaton, C.D.; Highlander, H.C.; Dahlquist, K.D.; Ledder, G.; LaMar, M.D.; Schugart, R.C. A ‘Rule-of-Five’ framework for models and modelling to unify mathematicians and biologists and improve student learning. Primus 2019, 29, 799–829. [Google Scholar] [CrossRef] [Green Version]
- Marshall, J.A.R.; Reina, A.; Bose, T. Multiscale modelling tool: Mathematical modelling of collective behaviour without the maths. PLoS ONE 2019, 14, e0222906. [Google Scholar] [CrossRef]
- Sutaphan, S.; Yuenyong, C. STEM Education teaching approach: Inquiry from the context based. J. Phys. 2018, 1340, 012003. [Google Scholar] [CrossRef] [Green Version]
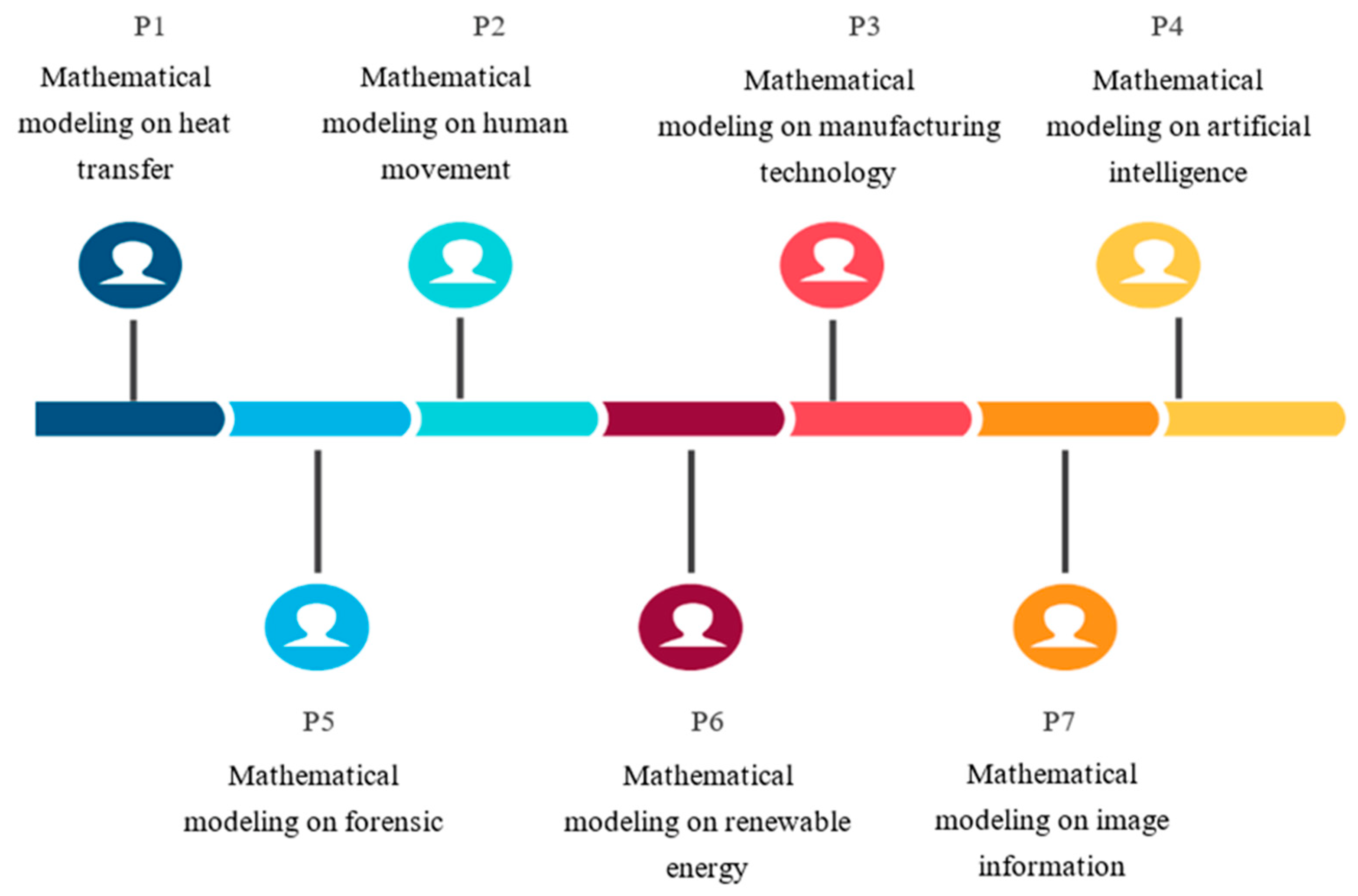



| Central Axiom | Axiom A(X)n; n = 1, 2, 3, … | Mathematical Modeling Axiom Element E(X)n; n = 1, 2, 3, … |
|---|---|---|
| Mathematical modeling novelty towards building new technology F(N) | System theorizing output modeling (X~T) | E(T)n: 1. Mastering specific field of knowledge. 2. Rooted from system observed and has fundamental principles. 3. Observation can also be carried out based on sets of previous data. 4. Involves assumptions that need to be set for system under review. 5. To develop a theory for explanation and system phenomena prediction. 6. Consideration of existing theories, concepts and models under specific study. 7. Using free body and schematic diagrams. 8. Strong mathematical background. 9. Using mathematical equations or a set of equations that govern together. 10. Involves system pattern properties determination. 11. Using digital technology to assist the problem-solving processes. 12. Contribution of theory to the specific field. |
| System simulation output modeling (X~S) | E(S)n: 1. Used to break human being limitation (i.e., thinking, visualizing and physical). 2. Used in multi-discipline research objectives. 3. Need to understand certain analyzing techniques. 4. Some investigations need to be conducted in laboratories. 5. Combination of methods that have the potential to develop new precise technology. 6. Some different methods of analysis could enhance precession. 7. Could involve cyclic investigations and several parties in the study. 8. Has been advantageous due to the advancement of computer technology. | |
| Useable innovation output (tangible/intangible) (X~I) | E(I)n: 1. Using the first and second axiom to develop and innovate new technology. 2. Can be in tangible or intangible innovation. 3. Useable and can benefit society. 4. Solve real-world problems. 5. Collaboration could also be carried out with those involved in different fields. 6. Improve and expand the understanding of a field. | |
| Patent and commercialization output (Product) (X~C) | E(C)n: 1. Establish mathematical modeling for usability innovation. 2. Patents to protect uniqueness. 3. Patent claims for idea or product of research output. 4. Solve real-life problems and situation. |
| Formulization | Axiom A(X)n | Element E(X)n | Source of Data (P1 to P7) | Participant Consensus | |
|---|---|---|---|---|---|
| Interview | Document | Yes or No | |||
| Mathematical modeling novelty towards building new technology | A(T)1: System theorizing output modeling | E(T)1 | all | all | Yes |
| E(T)2 | P1, P2, P5 | all | Yes | ||
| E(T)3 | P2, P4, P5 | P2, P4, P5 | Yes | ||
| E(T)4 | all | all | Yes | ||
| E(T)5 | P1, P5 | P1, P5 | Yes | ||
| E(T)6 | all | all | Yes | ||
| E(T)7 | P1, P2 | P1, P2, P5 | Yes | ||
| E(T)8 | P1, P2, P4 | all | Yes | ||
| E(T)9 | P1, P2, P5 | all | Yes | ||
| E(T)10 | P1, P4, P5 | P1, P4, P5 | Yes | ||
| E(T)11 | all | all | Yes | ||
| E(T)12 | P1, P5, P6 | P1, P5 | Yes | ||
| A(S)2: System simulation output modeling | E(S)1 | all | all | Yes | |
| E(S)2 | P2, P4, P7 | P2, P4, P7 | Yes | ||
| E(S)3 | P1, P2, P4 | P1, P2, P4 | Yes | ||
| E(S)4 | P1, P2, P7 | P1, P2, P4 | Yes | ||
| E(S)5 | P1, P4, P7 | P1, P4 | Yes | ||
| E(S)6 | P1, P4, P7 | P4, P5, P7 | Yes | ||
| E(S)7 | P2, P4, P7 | P1, P2, P5 | Yes | ||
| E(S)8 | all | all | Yes | ||
| A(I)3: Useable innovation output modeling (tangible/intangible) | E(I)1 | P1, P2, P3, P5, P7 | P2, P3, P5, P7 | Yes | |
| E(I)2 | P2, P3, P4, P5, P7 | P2, P3, P4, P5 | Yes | ||
| E(I)3 | P1, P2, P6 | P1, P2, P5, P6 | Yes | ||
| E(I)4 | all | all | Yes | ||
| E(I)5 | P1, P2, P4, P5, P7 | all | Yes | ||
| A(C)4: Patent and commercialization of modeling output (Product) | E(C)1 | P2, P3, P5, P7 | P1–P6 | Yes | |
| E(C)2 | P2, P3, P5, P7 | P1–P6 | Yes | ||
| E(C)3 | P2, P5, P7 | P1–P6 | Yes | ||
| E(C)4 | P2, P3, P4, P5, P7 | P1–P6 | Yes | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bajuri, M.R.; Siri, Z.; Abdullah, M.N.S. Mathematical Modeling Research Output Impacting New Technological Development: An Axiomatization to Build Novelty. Axioms 2022, 11, 264. https://doi.org/10.3390/axioms11060264
Bajuri MR, Siri Z, Abdullah MNS. Mathematical Modeling Research Output Impacting New Technological Development: An Axiomatization to Build Novelty. Axioms. 2022; 11(6):264. https://doi.org/10.3390/axioms11060264
Chicago/Turabian StyleBajuri, Mohd Razip, Zailan Siri, and Mohd Nor Syahrir Abdullah. 2022. "Mathematical Modeling Research Output Impacting New Technological Development: An Axiomatization to Build Novelty" Axioms 11, no. 6: 264. https://doi.org/10.3390/axioms11060264
APA StyleBajuri, M. R., Siri, Z., & Abdullah, M. N. S. (2022). Mathematical Modeling Research Output Impacting New Technological Development: An Axiomatization to Build Novelty. Axioms, 11(6), 264. https://doi.org/10.3390/axioms11060264






