1. Introduction
On the routes of transportation systems, bridges serve as crucial elements that connect people and facilitate a variety of economic activity. In use today are more than two million bridges globally [
1]. Over time, both nationally and internationally, the construction of bridges has steadily increased. On the eastern and southern branches of highway Corridor X in Serbia, contracts for the construction of about 200 reinforced concrete bridges totaling more than 100 million euros were signed from 2009 to 2015 [
2,
3].
The current idea of how bridge construction is organized assumes that activities will be planned, and resources will be assessed in order to build the bridge at the best possible cost and with the best quality. In the early stages of project development, ensuring accurate resource assessment is crucial because it has a significant impact on all following stages. The creation of a model for such an assessment will serve as a foundation for further examination and assessment of the technological solution to the project from a techno-economic perspective.
It is essential information from the perspective of the project’s execution to create a model that will enable a quick and accurate assessment of costs and materials during the early stages of project preparation while taking into account the fundamental properties of future bridges.
Key components for the construction of bridges over the Nile River in Egypt were analyzed by Marcous et al. in 2001 [
4], with 22 prestressed concrete bridges represented in the data collection. Material consumption was modeled using a neural network. The maximum span, type of contract, bearing structure of the bridge (box girder, I girder), static system, and method of bridge construction were all taken into consideration as input variables for the model. The weight of the prestressing steel and the volume of concrete were chosen as output variables. Neural network models with various numbers of neurons in the middle layer were examined. The model’s accuracy was demonstrated by an error size of 7.5% for the amount of concrete and 11.5% for the forecast of the amount of prestressing steel.
In 2001, Flyvbjerg and Skamris [
5] conducted research on the use of several techniques for estimating the cost of traffic infrastructure facilities. The railway infrastructure facilities, tunnels, bridges, and roadways were examined. The total value of the analyzed projects was over USD 90 billion. The outcome showed a sizable percentage of error in calculating the construction costs of all the facilities. While the overall average error for all evaluated projects was 27.6%, the average percentage error in the estimation for bridges and tunnels was 33.8%.
A technique for calculating the expenses of constructing bridges and culverts using multiple regression analysis was developed by Mostafa in 2003 [
6]. There were data for 54 bridges and 72 culverts in the database. The models that were built were given as prediction equations.
Fragkakis and others are working on models for estimating the costs of building a super-structure of bridges in 2010 [
7]. Regression analysis and the bootstrap approach were both discussed. The research’s basis was data pertaining to the construction of 68 bridges on Greece’s Egnatia highway. Analysis was conducted on how the fundamental variables found during the preliminary phase affect costs. Ten-fold cross-validation was used for model evaluation. The maximum accuracy measured by the MAPE value using the mentioned models was 20%.
In another study in 2010 [
8], Fragkakis and others proposed the use of computer-aided models for calculating the construction costs of prestressed concrete road bridges. Greece’s Egnatia highway bridges were analyzed once again. The volume of concrete and ribbed steel, two crucial components in the construction of bridge piers, were modeled using regression analysis. When calculating the volume of concrete, the values of the coefficient of determination R
2 of 72% were achieved. The R
2 coefficient of determination for estimating steel consumption was 85%.
In 2010 [
9], Kim and others discussed the application of genetic algorithms and the case-based reasoning (CBR) method in the preliminary cost estimation of bridge construction. Costs were broken down and expressed per square foot. The model was developed using information from 216 prestressed bridges constructed in South Korea between 2000 and 2005. To quantify the accuracy attained when utilizing CBR, the mean absolute error rate (MAER) of 5.99% was obtained.
A technique for calculating construction costs early in a project was developed in 2011 by Arafa and Alqedra [
10]. As a test model, an ANN was examined. The database contained information on 71 projects. The ground floor area, typical floor area, number of floors, number of pillars, method of foundation, number of elevators, and number of rooms were all taken into consideration as input variables. The model was constructed using a multi-layer perceptron model. The model’s attained accuracy in this study, as measured by the R
2 coefficient of determination, was 97%.
Fragkakis and others modeled the consumption of steel and concrete for bridge foundations in 2011 to estimate expenses at the conceptual stage of the project [
11]. The coefficient of determination R
2, whose value surpassed 77% for the examined models, was used in the study to evaluate models using regression analysis.
In 2013 [
12], Mohamid dealt with cost estimation during the conceptual stage of road construction projects, with 52 completed Saudi Arabian projects included in the statistics. The application of several regression models was examined. The volume of soil excavated, the final layer expressed per surface unit, the length of the road, and the width of the road were all examined as input factors. The results of the MAPE and R
2 criteria, which were used to assess the model, fell between the ranges of 17.2% to 32.1% and 0.88 to 0.97, respectively.
A design cost-estimation research for bridge projects in North Carolina, USA, was carried out in 2013 by Hollar et al. [
13]. Analyses of 461 projects’ costs from 2001 to 2009 were performed, and the study used 16 categorical variables to identify the major cost factors. For modeling, multiple linear regression was employed. The MAPE value of 42.7% was obtained as a measure of the model’s accuracy.
In order to estimate construction costs, Chou et al. used multiple regression, neural networks, and the CBR technique in 2015 [
14]. The database used to examine the contract price for bridge construction contained information on 275 projects that were contracted in Taiwan during 2008 and 2009. Numerous input variables were examined. A ten-fold cross-validation procedure was employed to rate the model’s forecasting capability. Using MAPE criteria, models’ accuracy was assessed. The study found that, with a MAPE value of 13.09%, the neural network model performed best.
In 2015 [
15], Fragkakis and others addressed the issue of culvert construction costs. The database used to create the model contained information on 104 culverts on the Greek Egnatia motorway. The research led to the definition of regression equations that calculate the amount of concrete and steel used per long meter of the culvert. Ten-fold cross-validation was used to test the models, and they were assessed using MAPE standards. The outcome demonstrated the estimation accuracy, which was 13.78% and 19.79%, respectively, for the concrete and steel used.
A neural network model was used by Marinelli et al. in 2015 [
16] to develop a model for evaluating the material consumption of bridge superstructures, and 68 bridges completed in Greece provided the data used to train the model. A multi-layer perceptron neural network model was used. The models were evaluated using Pearson’s linear correlation coefficient R. The training, validation, and test data sets all produced similar results, with values of 0.99937, 0.99288, and 0.9973, correspondingly.
Antoniou et al. conducted an analysis of the actual construction costs and concrete and steel consumption for underpasses in 2015 [
17], with 28 underpasses in Greece represented in the database. The study provided average material consumption and actual construction costs for such buildings, both given in terms of square meters.
In their investigation of the accuracy of artificial intelligence methods’ ability to estimate cost and time in building projects, Pesko et al. analyzed SVM and ANN models [
18]. When calculating expenses, SVM demonstrated greater precision with a MAPE of 7.06% as opposed to the most accurate ANNs, which attained a precision of 25.38%. However, estimating the length of the work proved to be more challenging, and for SVM and ANNs, the best MAPEs were 22.77% and 26.26%, respectively.
A methodology for calculating the consumption of essential resources during the construction of road bridges was developed by Dimitriou and others in 2018 [
19]. The use of neural network models and linear regression models was covered in the study. Concrete and steel consumption were modeled. The study made use of data from 68 Greek bridges. The accuracy of the model was evaluated using the MAPE and R
2 values. Depending on the applied span structure, the MAPE value ranged from 11.48% to 16.12% when predicting the consumption of concrete alone for the superstructure of the bridge, whereas the values for R
2 ranged from 0.979 to 0.995. The obtained MAPE and R
2 values were 37% and 0.962, respectively, for concrete and 31% and 0.962 for steel in terms of consumption per column.
In 2021 [
20], Kovačević et al. developed various models for estimating the cost of reinforced concrete (RC) and prestressed concrete (PC) bridges. The database for the completed 181 bridges on Serbia’s Corridor X included information about the project’s characteristics and the tender papers. A model based on Gaussian random processes was chosen as the research’s best option, and its accuracy, as measured by the MAPE criterion, was 10.86%.
Hanak and Vitkova, in their research in 2022, aimed to identify dispute factors and the related consequences of a case study involving the construction of a road to commercial premises [
21]. The research explored a specific case study: a private road construction project implemented in the Czech Republic. The analysis consisted of identifying potential problems and discussing their implications. The problem was investigated on three levels: economic, technical, and legal.
In 2022, Tijanić et al. [
22] investigated road construction projects on the territory of the Republic of Croatia that went over budget. Artificial neural networks were used to estimate costs at various stages of the project life cycle using data on construction costs gathered from previous projects. The database of roads built in Croatia was used during the modeling process. The general regression neural network (GRNN) achieved the best accuracy with a MAPE of 13% and a coefficient of determination of 0.9595.
Kovačević and Bulajić in 2022 [
23] conducted research on the best model that can be used to forecast the consumption of prestressed steel in the construction of PC bridges using machine learning (ML) techniques. The database contained information on 75 completed pre-stressed bridges in Serbia’s Corridor X. According to the established criterion MAPE, the model’s achieved accuracy for estimating prestressed steel consumption per square meter of the bridge superstructure was 6.55%.
The basic hypothesis of the investigation is that in the early stages of project development, methods based on artificial intelligence can quickly and sufficiently accurately estimate the consumption of key materials in RC and PC road bridges based on the basic characteristics of future bridges and the database of historical data on contracted bridges on which the model would be trained.
Resource estimation in current practice is based mainly on expert estimation of construction resources and previous experience of experts, very often subjectively and with significant errors in estimation. The formed model for assessing the consumption of concrete in bridge construction in this research is analog to an expert assessment, with a significant difference in that the previous experience is incorporated in the model itself, and the process is fast, automated, objective, significantly more accurate, and cheaper.
As part of the research, a large number of models for estimating the consumption of concrete for their construction was developed, analyzed, and verified. The established database enables future resource estimates to be made systematically and on a scientific basis, and any expansion of the historical database could be easily incorporated into the model and increase the accuracy of the model.
2. Methods
The most modern ML methodologies are presented and examined in this research in order to measure the resource consumption of reinforced concrete and prestressed concrete road bridges. The use of artificial neural networks, an ensemble of s, models based on the method of support vectors, and Gaussian random processes were all examined. All models were analyzed in the Matlab programming environment.
2.1. MLP Neural Network
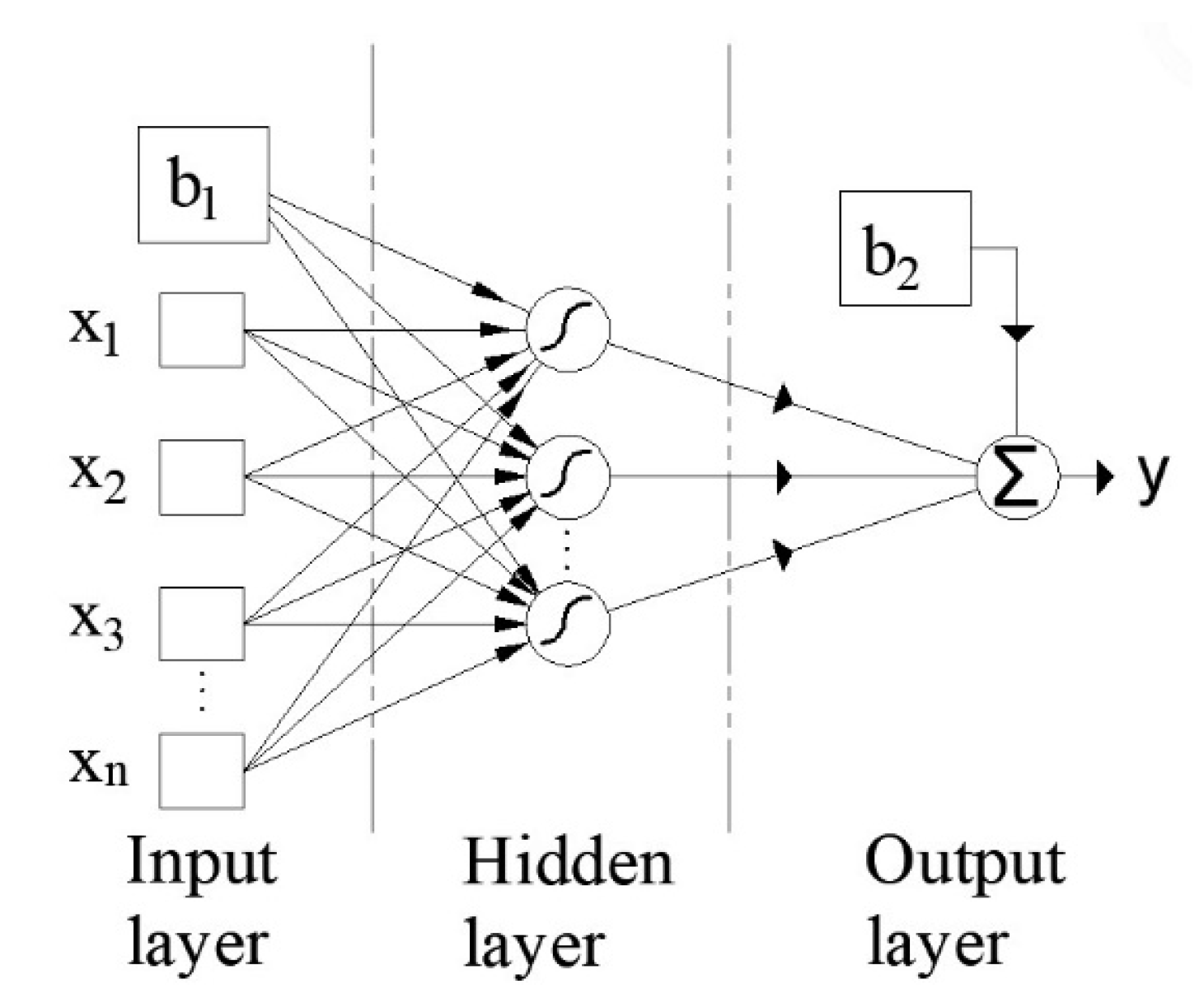
A multi-layer perceptron (MLP) is a feed-forward neural network made up of at least three layers of neurons: an input layer, a hidden layer, and an output layer. As illustrated in
Figure 1, a three-layer MLP network with
n inputs and one output is an example of an MLP.
The characteristics of the neurons and the type of activation function determine the properties of the network. Consider using the network as a universal approximator. Then, in order to approximate nonlinear relationships between input and output variables, it must apply nonlinear activation functions in the hidden layer. The use of the sigmoid activation function (1) in the hidden layer has produced excellent results in a sizable number of studies:
The dimensions of the input vector affect how many input neurons there are, and the dimensions of the output vector affect how many output neurons there are. The number of inputs and outputs, the number of training pairs, the size of the noise in the training pairs, the complexity of the error function, the network architecture, and the training algorithm are just a few of the variables that affect the optimal number of neurons in the hidden layer neurons.
The optimal number of neurons for the hidden layer is still primarily determined by experimentation. In this situation, it is recommended [
20,
23,
24] to start with a simple structure, such as a network with just one neuron in the hidden layer, before progressively increasing the number of neurons and evaluating the outcomes.
It is advised [
20,
23,
24] to use the following equations to calculate the maximum number of hidden layer neurons [
25]:
where
denotes the number of inputs in the neural network, and
is the number of instances used for training. The lower of the two determined numbers is adopted based on the obtained values for the number of neurons.
The main drawback of this approach is the sheer volume of networks that need to be tested and trained.
The optimal number of neurons in the hidden layer is important for the successful operation of the model because it directly influences the generalization properties [
3]. Too many neurons will form a network with too many parameters, which will be prone to overfitting. On the other hand, a network with insufficient neurons cannot accurately approximate the given nonlinear relationships, and a problem with underfitting occurs.
2.2. Regression Trees Models
An example of supervised machine learning in which data are continuously divided based on particular parameter values is a RT. Nodes, branches, and leaves make up a tree. One variable from the problem being modeled is represented by each node. The appropriate branch is taken depending on the value in the node. Until the terminal leaves are reached, the process is repeated iteratively.
Trees divide the area or domain of input variables of the considered domain into several regions in order to apply a linear model to each of these regions instead of applying a single linear model to the entire domain.
The variables and their values that will be used to divide the nodes in the tree must be decided before the tree is created. The so-called greedy technique is applied in this study [
26]. In this method, only the current division in the current iteration—which ought to have the minimum squared error relative to the target value—is taken into account. However, it is not taken into account if such a division is more optimal than other iterations, and as a result, it is referred to as greedy. In this context, the Equation (4) is used [
26]:
where
=
and
=
(see
Appendix A).
In this case, the division is made into
regions
and the RT model provides a prediction by assigning a point to a certain region depending on the values of the input variables and the values
of the splitting in the nodes (
Figure 2). In the assigned region, the considered point is assigned the value of the output variable, which is equal to the average value of the output variable of the samples for that region.
Individual RTs often represent base models that form ensembles of RTs (
Figure 3). Bootstrap sampling is used to create a dataset for each tree in the ensemble. The procedure essentially involves sampling with replacement from the original dataset. As a result, the datasets of the same size as the original are formed for training individual ensemble models. When ensembles constructed in this way are used for regression, the mean value of the individual trees that make up the ensemble is taken for prediction for some test sample x (
Figure 3).
When creating individual trees, a subset of
randomly selected input variables from
possible variables of the analyzed problem can be considered in the case of the random forest (RF) algorithm. Alternatively, an entire set of input variables can be considered in the case of the TreeBagger (TB) algorithm [
26,
27,
28,
29].
When using the boosted trees (BT) model [
30,
31,
32], the initial RT adheres to the established limitations for the maximum number of splits of the tree (
Figure 4). The following tree can be used to model differences once the gap between the target value and the value of the output variable provided by that model has been established. The preceding tree is then combined with a subsequent tree that modeled its residuals. The previous model is enhanced in this way. Typically, the values of differences or residuals are multiplied by a quantity smaller than one, known as the learning rate, rather than being fully modeled. The reason for the gradual modeling of the residuals is to prevent an overtraining of the model. Applying the aforementioned process repeatedly results in an ensemble of enhanced trees. BT models are developed sequentially as opposed to RF and TB models, which can be created in parallel.
2.3. Support Vector Machines for Regression (SVR)
The basic idea of the SVM method is the transformation of the input space and the use of the linear model in the transformed space.
Let us assume that we have a set of training data from which we may infer the input-output dependence, i.e., mapping f. The training data set contains pairs , ,…, , where inputs are -dimensional vectors , and outputs are continuous values.
The approximation function [
33] is analyzed by the SVM method and has the following form [
33,
34]:
where the functions
are referred to as attributes. Although it is not explicitly displayed, the bias
value is factored into the value of the weight vector
. The best way to understand the SVR approach by first examining linear regression [
33]:
In order to build the model, it is necessary to define the so-called Vapnik’s error function [
34], which is equal to zero if the difference between the predicted value
and the observed value is less than some value
(
Figure 5).
The error function defined in this way can be defined as an
cylinder or tube. If the prediction values are inside the tube, the error is zero. For all other prediction values outside the pipe, the error is equal to the amount of the discrepancy between the forecasted value and the diameter
of the pipe [
33]:
The empirical risk function is established to apply the SVR regression [
33,
34]:
The objective of the SVM algorithm for a regression problem (SVR) is to concurrently minimize the empirical risk
and the
value [
33]. In order to find the hyperplane
in linear regression, the following equation must be minimized:
Equations for linear regression can be employed in the case of non-linear regression (
Figure 5) by substituting K for the scalar product
.
The constant
C is a penalty parameter that balances the approximation error and the norm of the weight vector ||
||. If the slack variables
and
(
Figure 5) are introduced, the previous equation reduces to the following equation, which needs to be optimized [
33]:
As a result of the optimization, Lagrange multipliers are acquired in the form of pairs (
), and utilizing them, the optimal weight vector values are discovered by applying the equation [
33]:
as well as the optimal value for bias
:
The optimal hyperplane is defined by the equation [
33]:
Equations for linear regression can be employed in the case of non-linear regression (
Figure 5) by substituting the scalar product
for
.
For the case of non-linear regression, the same equations as for linear regression are obtained [
33]:
The mapping function need not be chosen explicitly when using the kernel . A subset of training data vectors is linearly combined to obtain the optimal solution. We may train nonlinear models using essentially the same method as for linear SVM models by employing the so-called kernel trick.
In this study, the sequential minimal optimization (SMO) algorithm was used with the LIBSVM software for optimization [
35,
36,
37]. LIBSVM software was used within the MATLAB 2020a program [
38].
2.4. Gaussian Process for Regression (GPR)
When modeling an unknown function from the experimental data itself, the Gaussian process implies that each subset of these functions has a Gaussian normal distribution. A Gaussian process (GP) is a collection of random variables, any finite number of which have a joint Gaussian distribution [
39].
GP for the regression problem (GPR) models solves a regression task to find a function that returns a real value, denoted as f: ⟼ ℝ for a given data set in pairs ), ,…, ), where denotes the input vector, and represents the scalar value of the output. An input can be thought of as a location where an unknown function (that stands for a random variable) following a normal distribution is approximated.
Let represent the input vector values for the training set and represent the function values that correspond to those values. The input vector values for the test data set will be marked with and their corresponding function values with . The lengths of the vectors and are and , respectively.
If the values of the functions
and
are observed as realized values that follow the multidimensional Gaussian distribution, the following equation can be written:
where
stands for the mean vector for random variable
when
is the mean vector for random variable
when
and
is the covariance function.
The covariance function, whose determination is a crucial step in the GPR application process, assesses how similar two different function values are at two different locations. The random variables f(xᵢ) and f(xⱼ) are correlated at separate locations, xᵢ and xⱼ, and the degree of correlation between f(xᵢ) and f(xⱼ) depends on the distance between xᵢ and xⱼ. The assumption is that the values of the functions corresponding to the points will be closer together the closer the points are. This correlation is modeled differently by using various covariance functions , which has a substantial impact on the generalization of the model.
The following equation, for example, defines the exponential covariance function [
35]:
In this equation, stands for the signal variance, stands for the so-called length scale parameter, while and are model parameters. The term “prior” refers to the joint probability density over the random variables and .
When modeling specific output values of an unknown function, the values of the output variables of the functions followed by noise are measured, and these values can be expressed as [
39]:
where
,
is noise variance, and
is the identity matrix of size
.
Given that there was noise used to monitor the experimental measurements, the marginal probability can be expressed as the following equation [
39] by applying the Gaussian marginalization rule and the Gaussian transformation rule:
Model parameters are derived by maximising the equation for .
The equation for the joint distribution of
and
, which denotes a multidimensional Gaussian distribution, is used to obtain the distribution for the posterior
. The posterior equation
is obtained by applying the conditional rule to a multivariate Gaussian distribution, and its mean value and variance are given by the following equations [
39]:
Given that = distribution for may be obtained by applying the Gaussian linear transformation rule.
4. Results
The MLP neural network type was used to form a neural network model for forecasting the concrete consumption of bridges. For modeling, the architecture of a three-layer network with one input, hidden, and an output layer of neurons was analyzed. A neuron with a linear activation function was used in the output layer and neurons with a nonlinear activation function in the hidden layer. In addition, the application of the tansigmoid activation function was analyzed. An architecture with six neurons in the input layer and one neuron in the output layer was taken into consideration because in the specific problem of concrete consumption prediction, which is a regression problem, there must be one neuron in the output layer. All model variables were transformed before training. Variable scaling is applied to ensure the equality of all variables because the absolute size of the variable does not have to be equivalent to the actual influence of the variable.
In the paper, the variables were transformed into the interval [–1, 1], where the corresponding minimum value was mapped to –1 and the corresponding maximum value to 1, and linear scaling was used for the values that are in between. Numerous studies mentioned in
Section 2.1 gave a recommendation for the number of neurons in the hidden layer
. It is proposed to examine architectures that have up to 12 neurons in the hidden layer, which is obtained by adopting a smaller value from Equations (2) and (3), which represents the value of the upper limit of the number of neurons of the hidden layer.
The LM algorithm [
20] was used to train the model, and three criteria were used as stopping criteria: the maximum number of epochs, which is limited to 1000; the minimum gradient magnitude, which is limited to
; and the network performance, which is evaluated using the MSE value and adjusted to a value of 0.
The training is interrupted at the moment when any of the aforementioned criteria is met. All architectures were evaluated by using four defined model-accuracy criteria, namely RMSE, MAE, R, and MAPE.
According to the three criteria MAE, R, and MAPE, the architecture of the MLP-ANN model with three neurons in the hidden layer has optimal values (
Figure 9). On the other hand, the model with nine neurons is the optimal model based on the value of the RMSE criterion.
The optimization of parameter values was carried out for the following adjustable parameters when using the random forest and TreeBagger models:
Number of variables that are taken into account in the node when branching trees (Num of variables);
The minimum amount of data assigned to the terminal leaf when creating the tree model (Min leaf size).
Regarding the number of variables, models with the set of variables for splitting containing one variable or the full set of six variables were taken into consideration. There are recommendations to use one-third of all model variables for the random forest model, which is also the default value in the Matlab program. In this instance, several RF model variations were taken into account. These variations consisted of 500 base models, and during the analysis, subsets of variables with a maximum of five variables were taken into consideration. TreeBagger models were composed of 500 basis elements, and all model variables were included in the set of variables that might be divided. It is not necessary to scale the model variables when using these models.
Figure 10 illustrates how the model’s considered hyperparameters affect the model’s accuracy in relation to four specified criteria.
The following variables were taken into account when using the boosted trees model:
The ensemble for BT can only have a maximum of 100 base models due to the sequential nature of model training. The learning parameters under test have values of 0, 0.01, 0.10, 0.25, 0.75, and 1.00. The model was trained using the MSE criterion. The optimal model was determined to have the following hyperparameters (
Figure 11): the number of trees, 7; the maximum number of splits, 8; and the learning parameter, 0.50. The optimal model was then assessed using the RMSE, MAE, R, and MAPE criteria.
Regarding the application of the SVM method, there is no universal recommendation at which kernel function gives optimal results. This study investigated the application of the following kernel functions: linear, RBF, and sigmoid. When using the SVM approach, scaling the model variables is advised. In this case, the model variables are converted into the range (0, 1). After scaling, the model was trained and tested. By the grid search procedure and the MSE criteria employed as the optimality criterion, the optimal kernel function parameters were (C = 1.3765 and ε = 0.0285 for the linear kernel; C = 76.1093; ε = 0.00058067; γ = 8.7242 for the RBF kernel; C = 649.6989; ε = 0.0299; γ = 0.0020 for sigmoid kernel). Following the selection of the optimal model, the accuracy was evaluated using the RMSE, MAE, R, and MAPE criteria.
The GPR model was applied, and various covariance functions were taken into account. The covariance functions convert the similarity between input vectors into the similarity between the functions or output variables that correspond to those vectors in the right manner. It is crucial to investigate the use of a greater variety of covariance functions because of this. The use of ten distinct covariance functions was investigated in this study.
Exponential, quadratic-exponential, Matern 3/2, Matern 5/2, and rational quadratic covariance functions were analyzed (
Table 2) as well as their ARD variants with distinct parameters for each coordinate axis (
Table 3). The analyses were performed on models with constant basis functions. The so-called z-score was used to scale the variable values prior to modeling. By maximizing the equation for the log marginal probability, the parameter values were derived.
The significance of each variable in the model can be established (
Figure 12) using the model with the highest accuracy (
Table 4) and the values of the length scale parameters. In this particular instance, the model with the ARD exponential covariance function will be the subject of this analysis.
By comparing the values of the length scale parameters to the parameters that describe the other variables, it can be seen that the variable
, which represents the construction method in the model with the ARD exponential function, has the highest value of the length scale parameter (the importance of the variable is inversely proportional to the value of the length scale parameter) (
Figure 12). The length of the bridge—variable
—is the most important variable for the model; however, the other variables are also important for model accuracy.
In
Table 5, a binary value (0 or 1) designates whether a certain variable is incorporated into the model or not.
By examining the preceding table (
Table 5), it is clear that model 1 produced better results for the RMSE accuracy criteria, but these differences are insignificant for the MAE, R, and MAPE criteria.
Figure 13 compares the modeled values for the total amount of concrete used expressed in
per bridge to the target values which are stated in the same unit.
The so-called regression diagram between the target and modeled values can be seen in
Figure 14. Regression plots show how accurate a model is, and in an ideal regression plot, the points are situated on a line that is 45 degrees above or below the horizontal. Thus, it can be seen from
Figure 14 analysis that the model has a good level of accuracy.
5. Conclusions
The primary hypothesis that in the early stages of project development, it is possible to quickly and sufficiently accurately estimate the consumption of concrete during their construction using methods based on artificial intelligence was confirmed by this research.
The developed models could be applied by investors, designers, consultants, contractors, and other interested parties. In order to make a decision about starting the construction of a reinforced concrete or prestressed road bridge, it is necessary for the preparatory phase of the investment project to carry out an early techno-economic analysis, which necessarily includes the planned resource consumption.
Therefore, as part of the research, a large number of predictive models were developed, analyzed, and verified for the early assessment of concrete consumption. At the same time, it is possible to estimate the costs of building bridges using an amount of concrete consumption.
A database of the consumption of reinforced concrete and the design characteristics of 181 reinforced concrete road bridges in the eastern and southern branches of Corridor X in Serbia, with a value of more than 100 million euros, was used for the creation of the assessment model. Models based on artificial neural networks, decision trees, the SVM method, and the GP process were among the machine learning models that were under consideration for application to the considered study.
All models were trained and tested under equal conditions using cross-validation, and measures of model accuracy included RMSE, MAE, R, and MAPE.
The results revealed that the GPR model’s accuracy is the highest when the ARD exponential function is used. In terms of accuracy criteria, the following results were obtained for the optimal model: RMSE = 325.7768; MAE = 159.2796; R = 0.9899; MAPE = 11.6461.
A suitable solution was found, as evidenced by the values of the attained correlation coefficient, which was 98.99%, and the mean absolute percentage error, which was 11.64%.
Because ARD covariance functions provide models with the highest accuracy, it is advised to build a model for estimating concrete consumption using the ARD exponential function of covariance. The suggested model makes it possible to rank the impact of different variables on the model’s accuracy. It is demonstrated that a model with approximately the same accuracy may be obtained by removing variables of minimal importance and utilizing a smaller collection of variables. Additionally, the model’s complexity is decreased, and the model-training process is expedited.
Based on everything presented, the proposed method for early cost estimation can be successfully used in practice as a support in the management of investment projects for the construction of reinforced and prestressed concrete road bridges.
6. Future Developments
The directions of further research must be aimed at expanding the existing base with subsequently obtained data related to the construction of other reinforced concrete and prestressed bridges.
The problem in this research was set as a problem of prediction of a continuous variable, that is, a regression problem. In the future, this problem can also be set as a classification problem (instead regression problem) in such a way that the concrete consumption of bridges would be assigned to a certain number of classes and then applied to ML algorithms for classification problems. After that, the accuracy of those models could be compared with the regression models presented in the paper.
The model implementation could be investigated for other markets for which there is a possibility of forming a suitable database. Furthermore, the applied methodology in the research, with certain adjustments, could also be applied to the cost estimation of other phases in the life cycle of the project and also to other types of construction facilities.
With a more significant expansion of the database for model building, the application of unsupervised learning methods can be investigated, where the data would be grouped into a certain number of clusters, and then, individual regression models instead of one integral model would be formed for each of the clusters.
The application of hybrid models of ensembles that would be simultaneously composed of models of ANNs, RTs, and models based on SVM could also be explored in future research.