A Reliable Combination of Double Laplace Transform and Homotopy Analysis Method for Solving a Singular Nonlocal Problem with Bessel Operator
Abstract
:1. Introduction
2. Existence and Uniqueness of the Solution
3. Method Development
4. Application of the Method
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Muravei, L.A.; Philinovskii, A.V. On a certain nonlocal boundary value problem for hyperbolic equation. Matem. Zametki 1993, 54, 98–116. [Google Scholar]
- Nakhushev, A.N. An approximate method for solving boundary value problems for differential equations and its application to the dynamics of ground moisture and ground water. Differ. Uravn. 1982, 18, 72–81. [Google Scholar]
- Pulkina, L.S. A nonlocal problem with integral conditions for hyperbolic equations. Electron. J. Differ. Equ. 1999, 45, 1–6. [Google Scholar] [CrossRef]
- Pulkina, L.S. On the solvability in L2 of a nonlocal problem with integral conditions for a hyperbolic equation. Differ. Equ. 2000, 36, 316–318. [Google Scholar] [CrossRef]
- Samarskii, A.A. Some problems in differential equations theory. Differ. Uravn. 1980, 16, 1221–1228. [Google Scholar]
- Shi, P.; Shillor, M. Design of Contact Patterns in One Dimensional Thermoelasticity in Theoretical Aspects of Industrial Design; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1992. [Google Scholar]
- Cannon, J.R. The solution of heat equation subject to the specification of energy. Q. Appl. Math. 1963, 21, 155–160. [Google Scholar] [CrossRef]
- Ionkin, N.I.; Moiseev, E.I. A problem for heat conduction equation with two point boundary condition. Differ. Uravn. 1979, 15, 1284–1295. [Google Scholar]
- Kacur, J.; van Keer, R. On the numerical solution of semilinear parabolic problems in multicomponent structures with Volterra operators in the transmission conditions and in the boundary conditions. Z. Fuer Angew. Math. Und Mech. 1995, 75, 91–103. [Google Scholar] [CrossRef]
- Dehghan, M. The one-dimensional heat equation subject to a boundary integral specification. Chaos Solitons Fractals 2007, 32, 661–675. [Google Scholar] [CrossRef]
- Taki-Eddine, O.; Abdelfatah, B.; Gattal, N. Numerical Solution of Mixed Problem of Parabolic Equation with an Integral Conditions by using Finite Difference and Orthogonal Function Approximation. Math. Moravica 2012, 16, 89–98. [Google Scholar] [CrossRef]
- Ramezani, M.; Dehghan, M.; Razzaghi, M. Combined finite difference and spectral methods for the numerical solution of hyperbolic equation with an integral condition. Numer. Methods Partial. Differ. Equ. 2008, 24, 1–8. [Google Scholar] [CrossRef]
- Singh, H. Chebyshev spectral method for solving a class of local and nonlocal elliptic boundary value problems. Int. J. Nonlinear Sci. Numer. Simul. 2023, 24, 899–915. [Google Scholar] [CrossRef]
- Gudi, T. Finite element method for a nonlocal problem of Kirchhoff type. SIAM J. Numer. Anal. 2012, 50, 657–668. [Google Scholar] [CrossRef]
- Chang, S.H.; Chang, I.L. A new algorithm for calculating one-dimensional differential transform of nonlinear functions. Appl. Math. Comput. 2008, 195, 799–808. [Google Scholar] [CrossRef]
- Arikoglu, A.; Ozkol, I. Solution of fractional differential equations by using differential transform method. Chaos Solitons Fractals 2007, 34, 1473–1481. [Google Scholar] [CrossRef]
- Adomian, G. Nonlinear Stochastic Operator Equations; Kluwer Academic Publishers: Alphen aan den Rijn, The Netherlands, 1986; ISBN 978-0-12-044375-8. [Google Scholar]
- Adomian, G. A Review of the Decomposition Method in Applied Mathematics. J. Math. Anal. Appl. 1988, 135, 501–544. [Google Scholar] [CrossRef]
- Adomian, G. A review of the decomposition method and some recent results for nonlinear equations. Comput. Math. Appl. 1991, 21, 101–127. [Google Scholar]
- Khuri, S.A. A Laplace decomposition algorithm applied to a class of nonlinear differential equations. J. Appl. Math. 2001, 1, 141–155. [Google Scholar] [CrossRef]
- Khuri, S.A. A new approach to Bratu’s problem. Appl. Math. Comput. 2004, 147, 131–136. [Google Scholar] [CrossRef]
- He, J.H. Variational iteration method a kind of non-linear analytical technique: Some examples. Int. J. Non-Linear Mech. 1999, 34, 699–708. [Google Scholar] [CrossRef]
- He, J.H. Variational iteration method for autonomous ordinary differential systems. Appl. Math. Comput. 2000, 114, 115–123. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation technique. Comput. Methods Appl. Mech. Eng. 1999, 178, 257–262. [Google Scholar] [CrossRef]
- He, J.H. A coupling method of a homotopy technique and a perturbation technique for non-linear problems. Int. J. Nonlinear Mech. 2000, 35, 37–43. [Google Scholar] [CrossRef]
- He, J.H. New interpretation of homotopy perturbation method. Int. J. Mod. Phys. B 2006, 20, 2561–2568. [Google Scholar] [CrossRef]
- Liao, S.J. The Proposed Homotopy Analysis Technique for the Solution of Nonlinear Problems. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 1992. [Google Scholar]
- Liao, S.J. Homotopy analysis method a new analytical technique for nonlinear problems. Commun. Nonlinear Sci. Numer. Simul. 1997, 2, 95–100. [Google Scholar] [CrossRef]
- Liao, S.J. An explicit, totally analytic approximation of Blasius’ viscous flow problems. Int. J. Non-Linear Mech. 1999, 34, 759–778. [Google Scholar] [CrossRef]
- Liao, S.J. Beyond Perturbation: Introduction to the Homotopy Analysis Method; Chapman & Hall/CRC Press: Boca Raton, FL, USA, 2003; ISBN 978-1-58488-407-1. [Google Scholar]
- Liao, S.J. On the homotopy analysis method for nonlinear problems. Appl. Math. Comput. 2004, 147, 499–513. [Google Scholar] [CrossRef]
- Mesloub, S.; Obaidat, S. On the application of the homotopy analysis method for a nonlocal mixed problem with Bessel operator. Appl. Math. Comput. 2012, 219, 3477–3485. [Google Scholar] [CrossRef]
- Eltayeb, H.; Kiliçman, A. A note on solutions of wave, Laplace’s and heat equations with convolution terms by using a double Laplace transform. Appl. Math. Lett. 2008, 21, 1324–1329. [Google Scholar] [CrossRef]
- Kiliçman, A.; Eltayeb, H. A note on defining singular integral as distribution and partial differential equations with convolution term. Math. Comput. Model. 2009, 49, 327–336. [Google Scholar] [CrossRef]
- Kiliçman, A.; Gadain, H.E. On the applications of Laplace and Sumudu transforms. J. Frankl. Inst. 2010, 347, 848–862. [Google Scholar] [CrossRef]
- Mesloub, S.; Bouziani, A. Mixed problem with a weighted integral condition for a parabolic equation with the Bessel operator. J. Appl. Math. Stoch. Anal. 2000, 15, 277–286. [Google Scholar] [CrossRef]
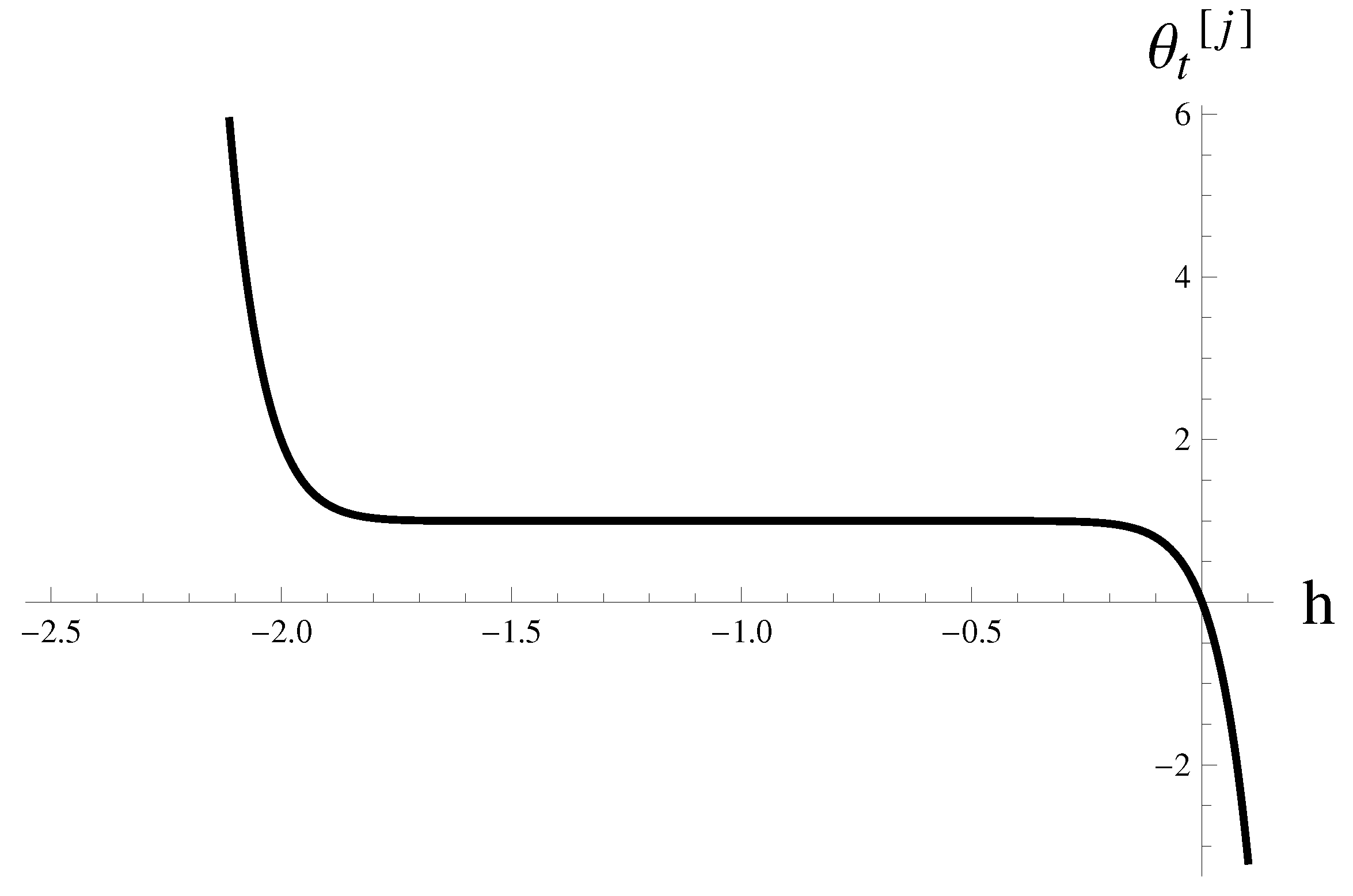
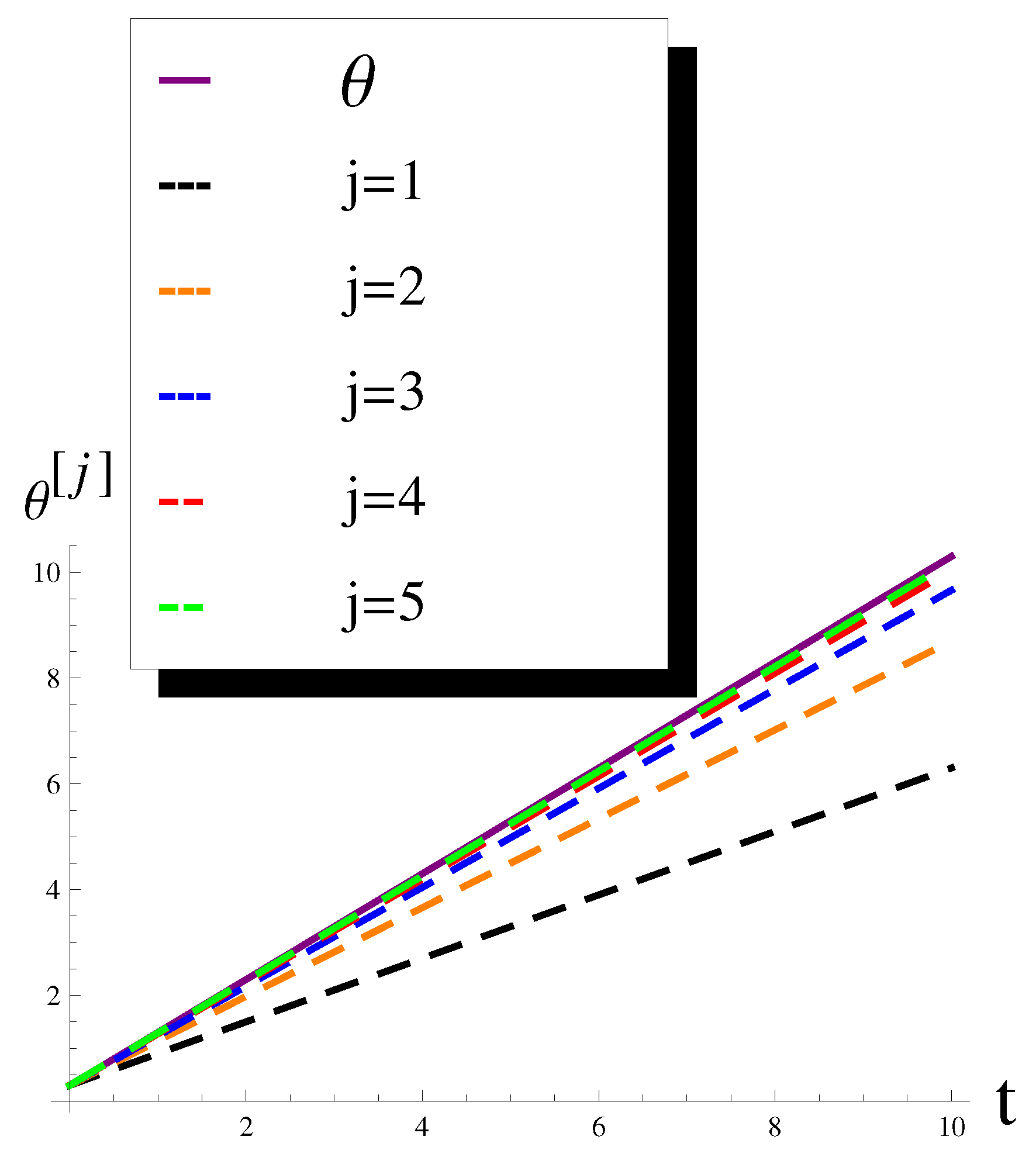
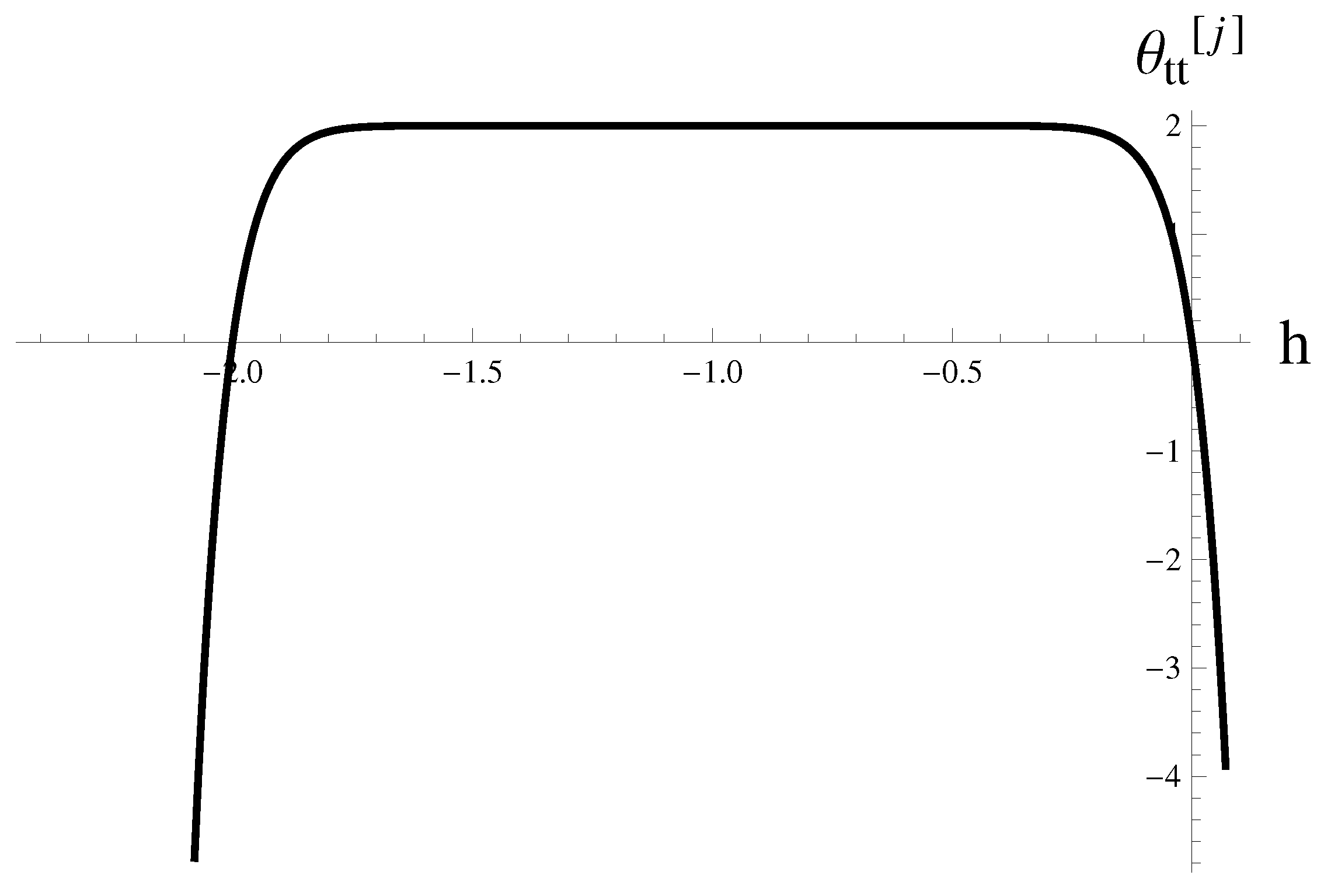
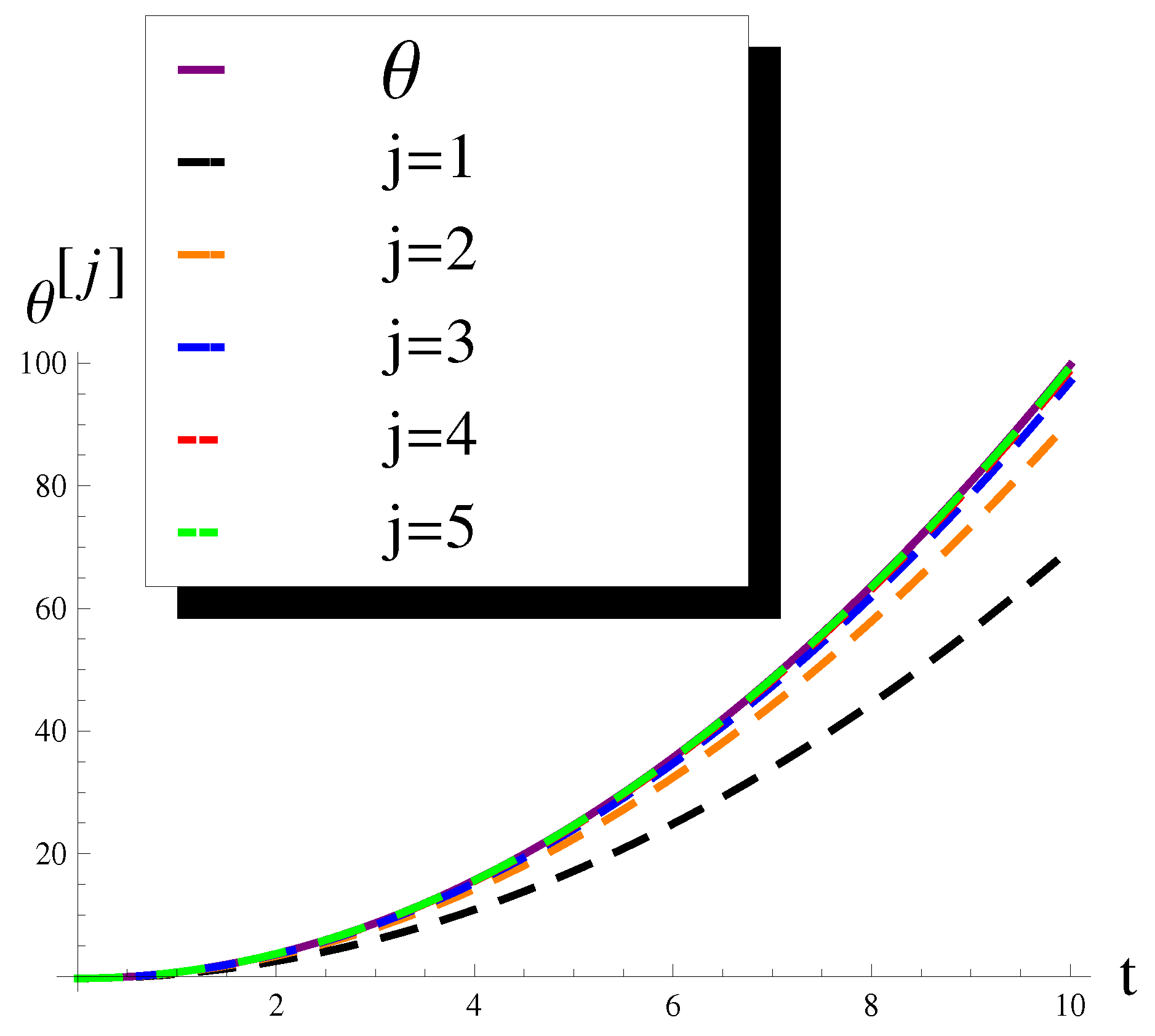
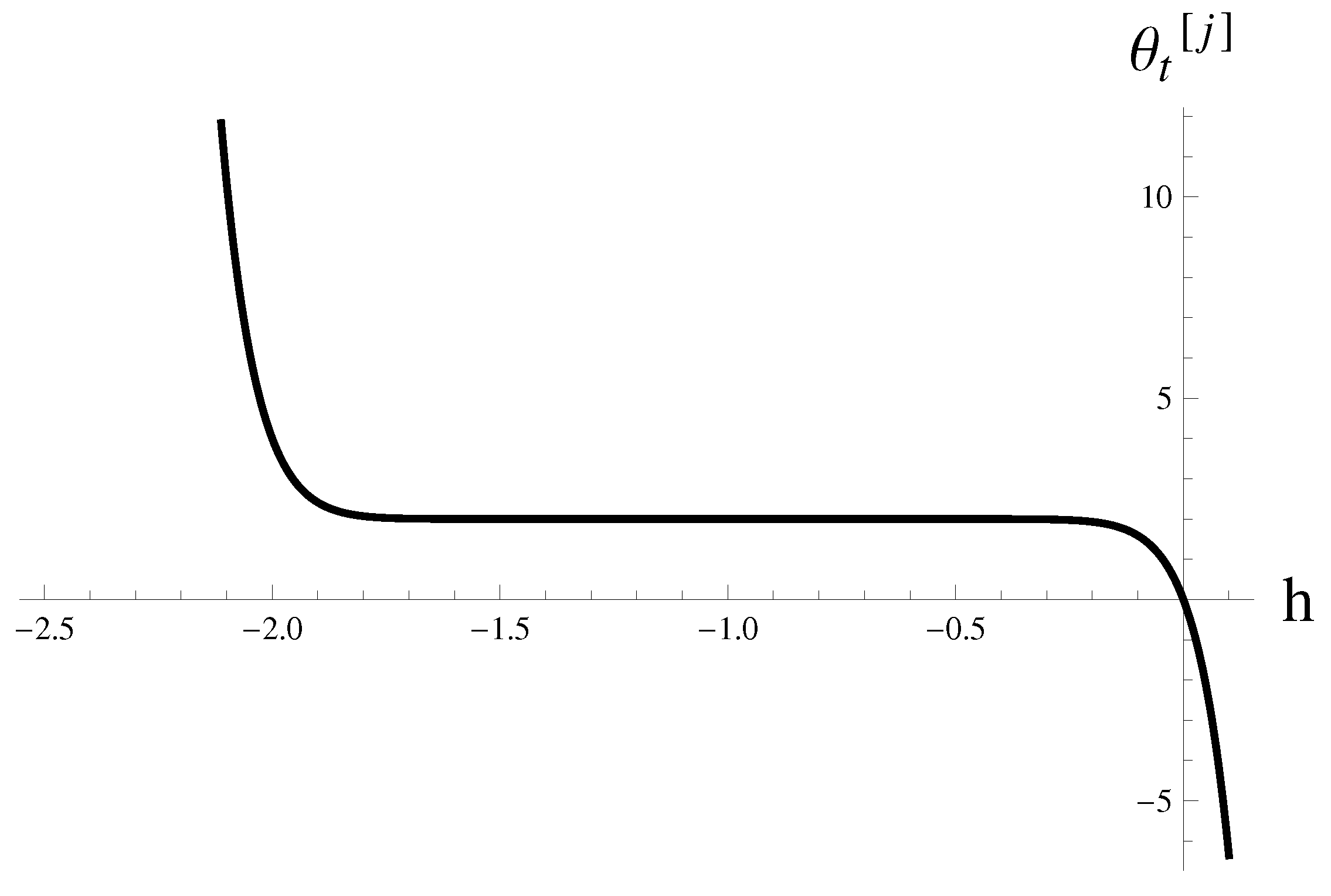
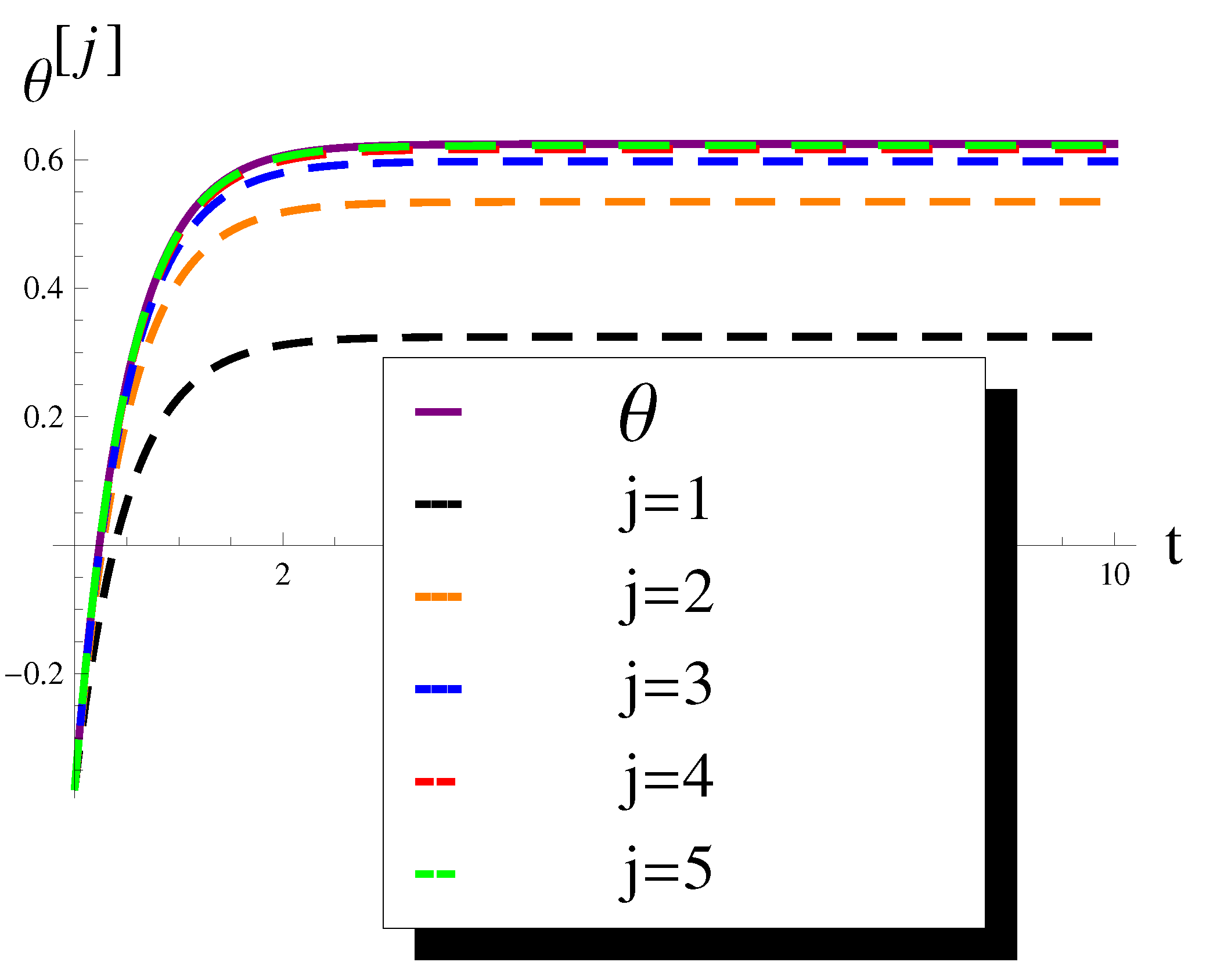
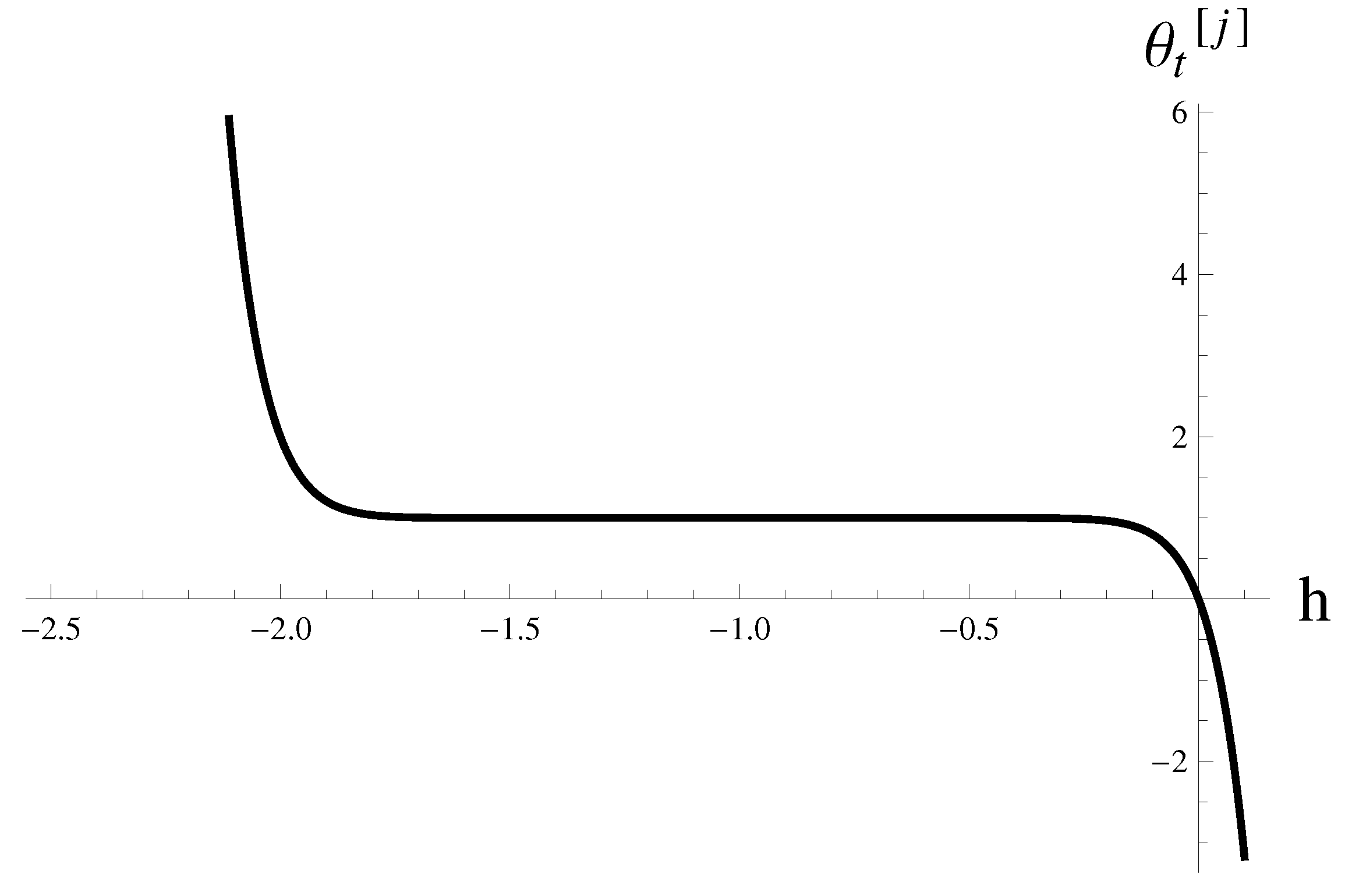
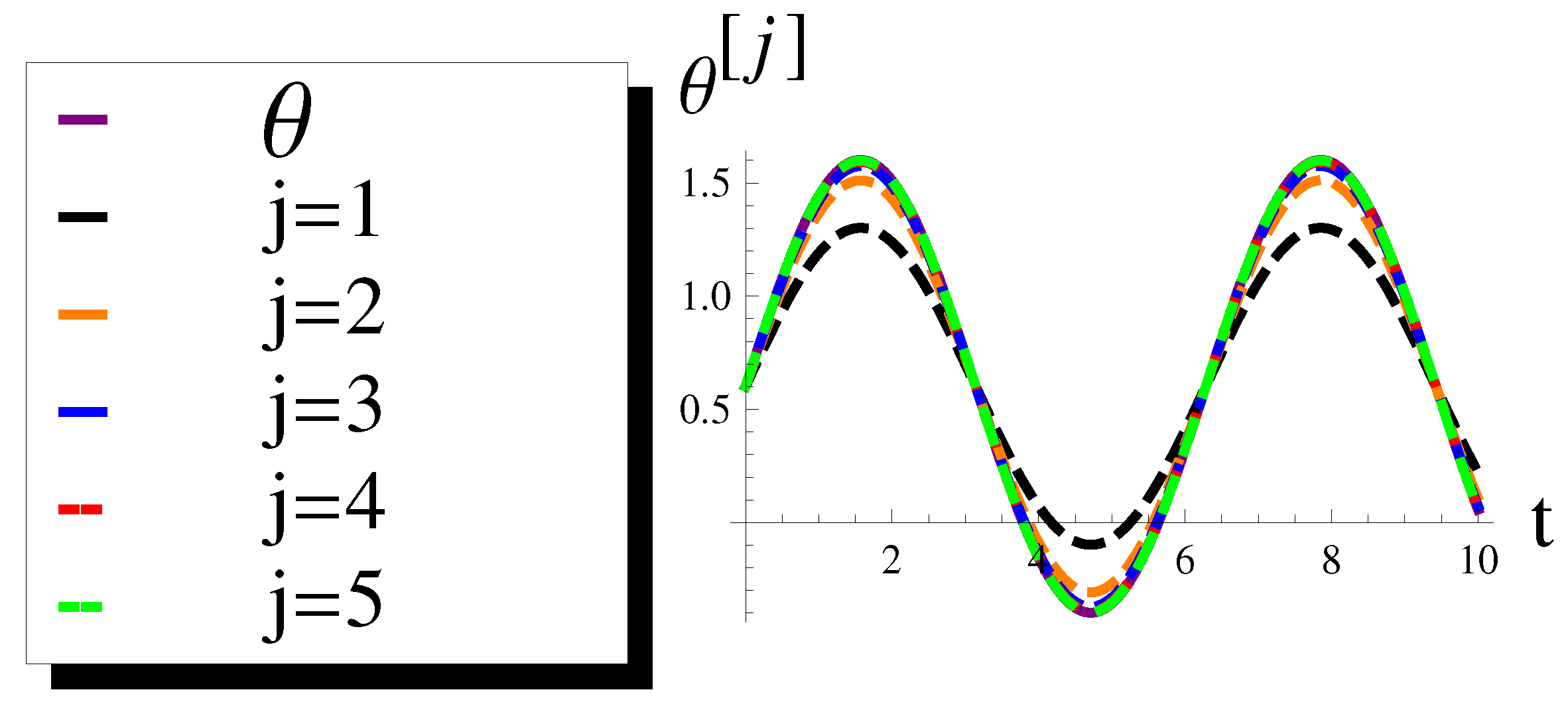
| t | |||||
|---|---|---|---|---|---|
| 0.1 | 0.5 | 1 | 5 | ||
| 0.1 | 2 | 0.001 | 0.005 | 0.01 | 0.05 |
| 5 | 1 | 5 | 0.00001 | 0.00005 | |
| 10 | 1 | ||||
| 14 | |||||
| 0.5 | 2 | 0.001 | 0.005 | 0.01 | 0.05 |
| 5 | 1 | 5 | 0.00001 | 0.00005 | |
| 10 | |||||
| 14 | |||||
| 0.7 | 2 | 0.001 | 0.005 | 0.01 | 0.05 |
| 5 | 1 | 5 | 0.00001 | 0.00005 | |
| 10 | |||||
| 14 | |||||
| 0.9 | 2 | 0.001 | 0.005 | 0.01 | 0.05 |
| 5 | 1 | 5 | 0.00001 | 0.00005 | |
| 10 | |||||
| 14 | |||||
| t | |||||
|---|---|---|---|---|---|
| 0.1 | 0.5 | 1 | 5 | ||
| 0.1 | 2 | 0.0001 | 0.0025 | 0.01 | 0.25 |
| 5 | 1 | 0.00001 | 0.00025 | ||
| 10 | |||||
| 14 | |||||
| 0.5 | 2 | 0.0001 | 0.0025 | 0.01 | 0.25 |
| 5 | 1 | 0.00001 | 0.00025 | ||
| 10 | |||||
| 14 | |||||
| 0.7 | 2 | 0.0001 | 0.0025 | 0.01 | 0.25 |
| 5 | 1 | 0.00001 | 0.00025 | ||
| 10 | |||||
| 14 | |||||
| 0.9 | 2 | 0.0001 | 0.0025 | 0.01 | 0.25 |
| 5 | 1 | 0.00001 | 0.00025 | ||
| 10 | |||||
| 14 | |||||
| t | |||||
|---|---|---|---|---|---|
| 0.1 | 0.5 | 1 | 5 | ||
| 0.1 | 2 | 0.00181269 | 0.00632121 | 0.00864665 | 0.00999955 |
| 5 | |||||
| 10 | |||||
| 14 | |||||
| 0.5 | 2 | 0.00181269 | 0.00632121 | 0.00864665 | 0.00999955 |
| 5 | |||||
| 10 | |||||
| 14 | |||||
| 0.7 | 2 | 0.00181269 | 0.00632121 | 0.00864665 | 0.00999955 |
| 5 | |||||
| 10 | |||||
| 14 | |||||
| 0.9 | 2 | 0.00181269 | 0.00632121 | 0.00864665 | 0.00999955 |
| 5 | |||||
| 10 | |||||
| 14 | |||||
| t | |||||
|---|---|---|---|---|---|
| 0.1 | 0.5 | 1 | 5 | ||
| 0.1 | 2 | 0.000998334 | 0.00479426 | 0.00841471 | 0.00958924 |
| 5 | |||||
| 10 | |||||
| 14 | |||||
| 0.5 | 2 | 0.000998334 | 0.00479426 | 0.00841471 | 0.00958924 |
| 5 | |||||
| 10 | |||||
| 14 | |||||
| 0.7 | 2 | 0.000998334 | 0.00479426 | 0.00841471 | 0.00958924 |
| 5 | |||||
| 10 | |||||
| 14 | |||||
| 0.9 | 2 | 0.000998334 | 0.00479426 | 0.00841471 | 0.00958924 |
| 5 | |||||
| 10 | |||||
| 14 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mesloub, S.; Gadain, H.E.; Bachar, I. A Reliable Combination of Double Laplace Transform and Homotopy Analysis Method for Solving a Singular Nonlocal Problem with Bessel Operator. Axioms 2023, 12, 933. https://doi.org/10.3390/axioms12100933
Mesloub S, Gadain HE, Bachar I. A Reliable Combination of Double Laplace Transform and Homotopy Analysis Method for Solving a Singular Nonlocal Problem with Bessel Operator. Axioms. 2023; 12(10):933. https://doi.org/10.3390/axioms12100933
Chicago/Turabian StyleMesloub, Said, Hassan Eltayeb Gadain, and Imed Bachar. 2023. "A Reliable Combination of Double Laplace Transform and Homotopy Analysis Method for Solving a Singular Nonlocal Problem with Bessel Operator" Axioms 12, no. 10: 933. https://doi.org/10.3390/axioms12100933
APA StyleMesloub, S., Gadain, H. E., & Bachar, I. (2023). A Reliable Combination of Double Laplace Transform and Homotopy Analysis Method for Solving a Singular Nonlocal Problem with Bessel Operator. Axioms, 12(10), 933. https://doi.org/10.3390/axioms12100933






